Hostname: page-component-8448b6f56d-xtgtn Total loading time: 0 Render date: 2024-04-18T14:30:31.942Z Has data issue: false hasContentIssue false
  • English
  • Français

Multiscale preferential sweeping of particles settling in turbulence

Published online by Cambridge University Press:  20 May 2019

Josin Tom Open the ORCID record for Josin Tom [Opens in a new window]  and
Andrew D. Bragg Open the ORCID record for Andrew D. Bragg [Opens in a new window]
Josin Tom
Affiliation:
Department of Civil and Environmental Engineering, Duke University, Durham, NC 27708, USA
Andrew D. Bragg*
Affiliation:
Department of Civil and Environmental Engineering, Duke University, Durham, NC 27708, USA
*
†Email address for correspondence: andrew.bragg@duke.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

In a seminal article, Maxey (J. Fluid Mech., vol. 174, 1987, pp. 441–465) presented a theoretical analysis showing that enhanced particle settling speeds in turbulence occur through the preferential sweeping mechanism, which depends on the preferential sampling of the fluid velocity gradient field by the inertial particles. However, recent direct numerical simulation (DNS) results in Ireland et al. (J. Fluid Mech., vol. 796, 2016b, pp. 659–711) show that even in a portion of the parameter space where this preferential sampling is absent, the particles nevertheless exhibit enhanced settling velocities. Further, there are several outstanding questions concerning the role of different turbulent flow scales on the enhanced settling, and the role of the Taylor Reynolds number 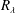$R_{\unicode[STIX]{x1D706}}$. The analysis of Maxey does not explain these issues, partly since it was restricted to particle Stokes numbers 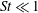$St\ll 1$. To address these issues, we have developed a new theoretical result, valid for arbitrary 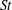$St$, that reveals the multiscale nature of the mechanism generating the enhanced settling speeds. In particular, it shows how the range of scales at which the preferential sweeping mechanism operates depends on 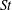$St$. This analysis is complemented by results from DNS where we examine the role of different flow scales on the particle settling speeds by coarse graining the underlying flow. The results show how the flow scales that contribute to the enhanced settling depend on 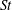$St$, and that contrary to previous claims, there can be no single turbulent velocity scale that characterizes the enhanced settling speed. The results explain the dependence of the particle settling speeds on 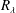$R_{\unicode[STIX]{x1D706}}$, and show how the saturation of this dependence at sufficiently large 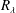$R_{\unicode[STIX]{x1D706}}$ depends upon 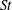$St$. The results also show that as the Stokes settling velocity of the particles is increased, the flow scales of the turbulence responsible for enhancing the particle settling speed become larger. Finally, we explored the multiscale nature of the preferential sweeping mechanism by considering how particles preferentially sample the fluid velocity gradients coarse grained at various scales. The results show that while rapidly settling particles do not preferentially sample the fluid velocity gradients, they do preferentially sample the fluid velocity gradients coarse grained at scales outside of the dissipation range. This explains the findings of Ireland et al., and further illustrates the truly multiscale nature of the mechanism generating enhanced particle settling speeds in turbulence.

JFM classification

Turbulent Flows: Isotropic turbulence Multiphase and Particle-laden Flows: Multiphase flow Multiphase and Particle-laden Flows: Particle/fluid flow
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 871 , 25 July 2019 , pp. 244 - 270
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aliseda, A., Cartellier, A., Hainaux, F. & Lasheras, J. C. 2002 Effect of preferential concentration on the settling velocity of heavy particles in homogeneous isotropic turbulence. J. Fluid Mech. 468, 77–105.Google Scholar
Ayyalasomayajula, S., Warhaft, Z. & Collins, L. R. 2008 Modeling inertial particle acceleration statistics in isotropic turbulence. Phys. Fluids 20, 094104.Google Scholar
Baker, L., Frankel, A., Mani, A. & Coletti, F. 2017 Coherent clusters of inertial particles in homogeneous turbulence. J. Fluid Mech. 833, 364–398.Google Scholar
Batchelor, G. K. 1967 An Introduction to Fluid Dynamics. Cambridge University Press.Google Scholar
Bec, J., Biferale, L., Boffetta, G., Celani, A., Cencini, M., Lanotte, A. S., Musacchio, S. & Toschi, F. 2006 Acceleration statistics of heavy particles in turbulence. J. Fluid Mech. 550, 349–358.Google Scholar
Bec, J., Homann, H. & Ray, S. S. 2014 Gravity-driven enhancement of heavy particle clustering in turbulent flow. Phys. Rev. Lett. 112, 184501.Google Scholar
Bragg, A. D. & Collins, L. R. 2014 New insights from comparing statistical theories for inertial particles in turbulence: I. Spatial distribution of particles. New J. Phys. 16, 055013.Google Scholar
Bragg, A., Swailes, D. C. & Skartlien, R. 2012a Drift-free kinetic equations for turbulent dispersion. Phys. Rev. E 86, 056306.Google Scholar
Bragg, A., Swailes, D. C. & Skartlien, R. 2012b Particle transport in a turbulent boundary layer: Non-local closures for particle dispersion tensors accounting for particle-wall interactions. Phys. Fluids 24, 103304.Google Scholar
Bragg, A. D., Ireland, P. J. & Collins, L. R. 2015 Mechanisms for the clustering of inertial particles in the inertial range of isotropic turbulence. Phys. Rev. E 92, 023029.Google Scholar
Bragg, A. D., Ireland, P. J. & Collins, L. R. 2015 On the relationship between the non-local clustering mechanism and preferential concentration. J. Fluid Mech. 780, 327–343.Google Scholar
Chan, C. C. & Fung, J. C. H. 1999 The change in settling velocity of inertial particles in cellular flow. Fluid Dyn. Res. 25 (5), 257–273.Google Scholar
Clift, R., Grace, J. R. & Weber, M. E. 1978 Bubbles, Drops, and Particles. Academic Press.Google Scholar
Elghobashi, S. E. & Truesdell, G. C. 1993 On the two-way interaction between homogeneous turbulence and dispersed particles. 1. Turbulence modification. Phys. Fluids A 5, 1790–1801.Google Scholar
Eyink, G. L. & Aluie, H. 2009 Localness of energy cascade in hydrodynamic turbulence. 1. Smooth coarse graining. Phys. Fluids 21 (11), 115107.Google Scholar
Fornari, W., Picano, F., Sardina, G. & Brandt, L. 2016 Reduced particle settling speed in turbulence. J. Fluid Mech. 808, 153–167.Google Scholar
Fung, J. C. H. 1993 Gravitational settling of particles and bubbles in homogeneous turbulence. J. Geophys. Res. 98, 20287–20297.Google Scholar
Fung, J. C. H. 1998 Effect of nonlinear drag on the settling velocity of particles in homogeneous isotropic turbulence. J. Geophys. Res.: Oceans 103 (C12), 27905–27917.Google Scholar
Good, G. H., Ireland, P. J., Bewley, G. P., Bodenschatz, E., Collins, L. R. & Warhaft, Z. 2014 Settling regimes of inertial particles in isotropic turbulence. J. Fluid Mech. 759, R3.Google Scholar
Grabowski, W. W. & Wang, L.-P. 2013 Growth of cloud droplets in a turbulent environment. Annu. Rev. Fluid Mech. 45, 293–324.Google Scholar
Guseva, K., Daitche, A., Feudel, U. & Tél, T. 2016 History effects in the sedimentation of light aerosols in turbulence: The case of marine snow. Phys. Rev. Fluids 1, 074203.Google Scholar
Gustavsson, K. & Mehlig, B. 2011 Ergodic and non-ergodic clustering of inertial particles. Eur. Phys. Lett. 96, 60012.Google Scholar
van Hinsberg, M. A. T., Thije Boonkkamp, J. H. M., Toschi, F. & Clercx, H. J. H. 2012 On the efficiency and accuracy of interpolation methods for spectral codes. SIAM J. Sci. Comput. 34 (4), B479–B498.Google Scholar
Huck, P. D., Bateson, C., Volk, R., Cartellier, A., Bourgoin, M. & Aliseda, A. 2018 The role of collective effects on settling velocity enhancement for inertial particles in turbulence. J. Fluid Mech. 846, 1059–1075.Google Scholar
Ireland, P. J., Bragg, A. D. & Collins, L. R. 2016a The effect of Reynolds number on inertial particle dynamics in isotropic turbulence. Part 1. Simulations without gravitational effects. J. Fluid Mech. 796, 617–658.Google Scholar
Ireland, P. J., Bragg, A. D. & Collins, L. R. 2016b The effect of Reynolds number on inertial particle dynamics in isotropic turbulence. Part 2. Simulations with gravitational effects. J. Fluid Mech. 796, 659–711.Google Scholar
Ireland, P. J., Vaithianathan, T., Sukheswalla, P. S., Ray, B. & Collins, L. R. 2013 Highly parallel particle-laden flow solver for turbulence research. Comput. Fluids 76, 170–177.Google Scholar
Kawanisi, K. & Shiozaki, R. 2008 Turbulent effects on the settling velocity of suspended sediment. J. Hydrol. Engng 134, 261–266.Google Scholar
Kiorboe, T. 1997 Small-scale turbulence, marine snow formation, and planktivorous feeding. Sci. Mar. 61 (Suppl. 1), 141–158.Google Scholar
Maxey, M. R. 1987 The gravitational settling of aerosol particles in homogeneous turbulence and random flow fields. J. Fluid Mech. 174, 441–465.Google Scholar
Maxey, M. R. & Corrsin, S. 1986 Gravitational settling of aerosol particles in randomly oriented cellular flow fields. J. Aero. Sci. 43, 1112–1134.Google Scholar
Maxey, M. R. & Riley, J. J. 1983 Equation of motion for a small rigid sphere in a nonuniform flow. Phys. Fluids 26, 883–889.Google Scholar
Mei, R. 1994 Effect of turbulence on the particle settling velocity in the nonlinear drag range. Intl J. Multiphase Flow 20, 273–284.Google Scholar
Momenifar, M., Dhariwal, R. & Bragg, A. D.2018 The influence of Reynolds and Froude number on the motion of settling, bidisperse inertial particles in turbulence. arXiv e-prints arXiv:1808.01537.Google Scholar
Monchaux, R. & Dejoan, A. 2017 Settling velocity and preferential concentration of heavy particles under two-way coupling effects in homogeneous turbulence. Phys. Rev. Fluids 2, 104302.Google Scholar
Nemes, A., Dasari, T., Hong, J., Guala, M. & Coletti, F. 2017 Snowflakes in the atmospheric surface layer: observation of particle turbulence dynamics. J. Fluid Mech. 814, 592–613.Google Scholar
Nielsen, P. 1984 On the motion of suspended sand particles. J. Geophys. Res.: Oceans 89 (C1), 616–626.Google Scholar
Nielsen, P. 1993 Turbulence effects on the settling of suspended particles. J. Sedim. Petrol. 63, 835–838.Google Scholar
Papanicolaou, A. (Thanos) N., Elhakeem, M., Krallis, G., Prakash, S. & Edinger, J. 2008 Sediment transport modeling review – current and future developments. J. Hydraul. Engng 134 (1), 1–14.Google Scholar
Petersen, A. J., Baker, L. & Coletti, F. 2019 Experimental study of inertial particles clustering and settling in homogeneous turbulence. J. Fluid Mech. 864, 925–970.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Reeks, M. W. 1977 On the dispersion of small particles suspended in an isotropic turbulent fluid. J. Fluid Mech. 83, 529–546.Google Scholar
Riley, J. J. & Lindborg, E. 2012 Recent Progress in Stratified Turbulence, pp. 269–317. Cambridge University Press.Google Scholar
Rosa, B., Parishani, H., Ayala, O. & Wang, L.-P. 2016 Settling velocity of small inertial particles in homogeneous isotropic turbulence from high-resolution DNS. Intl J. Multiphase Flow 83, 217–231.Google Scholar
Rosa, B. & Pozorski, J. 2017 Impact of subgrid fluid turbulence on inertial particles subject to gravity. J. Turbul. 18 (7), 634–652.Google Scholar
Schneborn, P.-R. 1975 The interaction between a single particle and an oscillating fluid. Intl J. Multiphase Flow 2 (3), 307–317.Google Scholar
Shaw, R. A. 2003 Particle-turbulence interactions in atmospheric clouds. Annu. Rev. Fluid Mech. 35, 183–227.Google Scholar
Squires, K. D. & Eaton, J. K. 1991 Preferential concentration of particles by turbulence. Phys. Fluids A 3, 1169–1178.Google Scholar
Sundaram, S. & Collins, L. R. 1997 Collision statistics in an isotropic, particle-laden turbulent suspension I. Direct numerical simulations. J. Fluid Mech. 335, 75–109.Google Scholar
Towns, J., Cockerill, T., Dahan, M., Foster, I., Gaither, K., Grimshaw, A., Hazlewood, V., Lathrop, S., Lifka, D., Peterson, G. D., Roskies, R., Scott, J. R. & Wilkins-Diehr, N. 2014 Xsede: Accelerating scientific discovery. Comput. Sci. Engng 16 (5), 62–74.Google Scholar
Tunstall, E. B. & Houghton, G. 1968 Retardation of falling spheres by hydrodynamic oscillations. Chem. Engng Sci. 23 (9), 1067–1081.Google Scholar
Wang, L. P. & Maxey, M. R. 1993 Settling velocity and concentration distribution of heavy particles in homogeneous isotropic turbulence. J. Fluid Mech. 256, 27–68.Google Scholar
Wilkinson, M. & Mehlig, B. 2005 Caustics in turbulent aerosols. Europhys. Lett. 71, 186–192.Google Scholar
Yang, C. Y. & Lei, U. 1998 The role of turbulent scales in the settling velocity of heavy particles in homogeneous isotropic turbulence. J. Fluid Mech. 20, 179–205.Google Scholar
Yang, T. S. & Shy, S. S. 2003 The settling velocity of heavy particles in an aqueous near-isotropic turbulence. Phys. Fluids 15, 868–880.Google Scholar
Zaichik, L. I. & Alipchenkov, V. M. 2009 Statistical models for predicting pair dispersion and particle clustering in isotropic turbulence and their applications. New J. Phys. 11, 103018.Google Scholar