Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-18T18:50:12.706Z Has data issue: false hasContentIssue false
  • English
  • Français

Modelling the dynamics of a sphere approaching and bouncing on a wall in a viscous fluid

Published online by Cambridge University Press:  17 April 2014

Edouard Izard ,
Thomas Bonometti  and
Laurent Lacaze
Edouard Izard
Affiliation:
Université de Toulouse; INPT, UPS; IMFT (Institut de Mécanique des Fluides de Toulouse), Allée Camille Soula, F-31400 Toulouse, France CNRS; IMFT, F-31400 Toulouse, France
Thomas Bonometti
Affiliation:
Université de Toulouse; INPT, UPS; IMFT (Institut de Mécanique des Fluides de Toulouse), Allée Camille Soula, F-31400 Toulouse, France CNRS; IMFT, F-31400 Toulouse, France
Laurent Lacaze*
Affiliation:
Université de Toulouse; INPT, UPS; IMFT (Institut de Mécanique des Fluides de Toulouse), Allée Camille Soula, F-31400 Toulouse, France CNRS; IMFT, F-31400 Toulouse, France
*
†Email address for correspondence: lacaze@imft.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

The canonical configuration of a solid particle bouncing on a wall in a viscous fluid is considered here, focusing on rough particles as encountered in most of the laboratory experiments or applications. In that case, the particle deformation is not expected to be significant prior to solid contact. An immersed boundary method (IBM) allowing the fluid flow around the solid particle to be numerically described is combined with a discrete element method (DEM) in order to numerically investigate the dynamics of the system. Particular attention is paid to modelling the lubrication force added in the discrete element method, which is not captured by the fluid solver at very small scale. Specifically, the proposed numerical model accounts for the surface roughness of real particles through an effective roughness length in the contact model, and considers that the time scale of the contact is small compared to that of the fluid. The present coupled method is shown to quantitatively reproduce available experimental data and in particular is in very good agreement with recent measurement of the dynamics of a particle approaching very close to a wall in the viscous regime 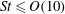$St \le {O}(10)$, where 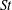$St$ is the Stokes number which represents the balance between particle inertia and viscous dissipation. Finally, based on the reliability of the numerical results, two predictive models are proposed, namely for the dynamics of the particle close to the wall and the effective coefficient of restitution. Both models use the effective roughness height and assume the particle remains rigid prior to solid contact. They are shown to be pertinent to describe experimental and numerical data for the whole range of investigated parameters.

JFM classification

Low-Reynolds-number flows: Lubrication theory Multiphase and Particle-laden Flows: Particle/fluid flow
Type
Papers
Information
Journal of Fluid Mechanics , Volume 747 , 25 May 2014 , pp. 422 - 446
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ardekani, A. M. & Rangel, R. H. 2008 Numerical investigation of particle–particle and particle–wall collisions in a viscous fluid. J. Fluid Mech. 596, 437–466.Google Scholar
Barnocky, G. & Davis, R. H. 1988 Elastohydrodynamic collision and rebound of spheres: experimental verification. Phys. Fluids 31, 1324–1329.CrossRefGoogle Scholar
Barnocky, G. & Davis, R. H. 1989 The influence of pressure-dependent density and viscosity on the elastohydrodynamic collision and rebound of two spheres. J. Fluid Mech. 209, 501–519.Google Scholar
Bigot, B., Bonometti, T., Lacaze, L. & Thual, O. 2013 A simple immersed-boundary method for solid–fluid interaction in constant- and stratified-density flows. Comput. Fluids, doi:10.1016/j.compfluid.2014.03.030.CrossRefGoogle Scholar
Brändle de Motta, J. C., Breugem, W.-P., Gazanion, B., Estivalezes, J.-L., Vincent, S. & Climent, E. 2013 Numerical modelling of finite-size particle collisions in a viscous fluid. Phys. Fluids 25, 083302.Google Scholar
Brenner, H. 1961 The slow motion of a sphere through a viscous fluid towards a plane surface. Chem. Engng Sci. 16, 242–251.Google Scholar
Breugem, W.-P.2010 A combined soft-sphere collision/immersed boundary method for resolved simulations of particulate flows. Proceedings of the ASME FED SM 2010 30634.CrossRefGoogle Scholar
Breugem, W.-P. 2012 A second-order accurate immersed boundary method for fully resolved simulations of particle-laden flows. J. Comput. Phys. 231, 4469–4498.Google Scholar
Cox, R. G. & Brenner, H. 1967 The slow motion of a sphere through a viscous fluid towards a plane surface–II small gap widths, including inertial effects. Chem. Engng Sci. 22, 1753–1777.CrossRefGoogle Scholar
Cundall, P. A. & Strack, O. D. L. 1979 A discrete numerical model for granular assemblies. Gèotechnique 29, 47–65.Google Scholar
Davis, R. H. 1987 Elastohydrodynamic collisions of particles. Physico-Chem. Hydrodyn. 9, 41–52.Google Scholar
Davis, R. H., Serayssol, J.-M. & Hinch, E. J. 1986 Elastohydrodynamic collision of two spheres. J. Fluid Mech. 163, 479–497.Google Scholar
Fabre, D., Tchoufag, J. & Magnaudet, J. 2012 The steady oblique path of buoyancy-driven disks and spheres. J. Fluid Mech. 707, 24–36.Google Scholar
Fadlun, E. A., Verzicco, R., Orlandi, P. & Mohd-Yusof, J. 2000 Combined immersed-boundary finite-difference methods for three-dimensional complex flow simulations. J. Comput. Phys. 161, 35–60.Google Scholar
Feng, Z. G., Michaelides, E. E. & Mao, S. 2010 A three-dimensional resolved discrete particle method for studying particle-wall collision in a viscous fluid. J. Comput. Phys. 161, 35–60.Google Scholar
Foerster, S. F., Louge, M. Y., Chang, H. & Allia, K. 1994 Measurements of the collision properties of small spheres. Phys. Fluids 6, 1108–1115.Google Scholar
Gondret, P., Lance, M. & Petit, L. 2002 Bouncing motion of spherical particles in fluids. Phys. Fluids 14, 643–652.CrossRefGoogle Scholar
Jenny, M., Dusek, J. & Bouchet, G. 2004 Instabilities and transition of a sphere falling or ascending freely in a Newtonian fluid. J. Fluid Mech. 508, 201–239.CrossRefGoogle Scholar
Joseph, G. G. & Hunt, M. L. 2004 Oblique particle-wall collisions in a liquid. J. Fluid Mech. 510, 71–93.Google Scholar
Joseph, G. G., Zenit, R., Hunt, M. L. & Rosenwinkel, A. M. 2001 Particle-wall collisions in a viscous fluid. J. Fluid Mech. 433, 329–346.Google Scholar
Kempe, T. & Fröhlich, J. 2012 Collision modelling for the interface-resolved simulation of spherical particles in viscous fluids. J. Fluid Mech. 709, 445–489.CrossRefGoogle Scholar
Kim, J., Kim, D. & Choi, H. 2001 An immersed-boundary finite-volume method for simulations of flow in complex geometries. J. Comput. Phys. 171, 132–150.Google Scholar
Lacaze, L., Phillips, J. C. & Kerswell, R. R. 2008 Planar collapse of a granular column: experiments and discrete element simulations. Phys. Fluids 20, 063302.Google Scholar
Lecoq, N., Anthore, R., Cichocki, B., Szymczak, P. & Feuillebois, F. 2004 Drag force on a sphere moving towards a corrugated wall. J. Fluid Mech. 513, 247–264.CrossRefGoogle Scholar
Legendre, D., Daniel, C. & Guiraud, P. 2005 Experimental study of a drop bouncing on a wall in a liquid. Phys. Fluids 17, 097105.Google Scholar
Legendre, D., Zenit, R., Daniel, C. & Guiraud, P. 2006 A note on the modelling of the bouncing of spherical drops or solid spheres on a wall in viscous fluid. Chem. Engng Sci. 61, 3543–3549.Google Scholar
Li, X., Hunt, M. L. & Colonius, T. 2012 A contact model for normal immersed collisions between a particle and a wall. J. Fluid Mech. 691, 123–145.Google Scholar
Lian, G., Adams, M. J. & Thornton, C. 1996 Elastohydrodynamic collisions of solid spheres. J. Fluid Mech. 311, 141–152.Google Scholar
Lundberg, J. & Shen, H. H. 1992 Collisional restitution dependence on viscosity. J. Engng Mech. ASCE 118, 979–989.Google Scholar
Mongruel, A., Chastel, T., Asmolov, E. S. & Vinogradova, O. I. 2013 Effective hydrodynamic boundary conditions for microtextured surfaces. Phys. Rev. E 87, 011002.Google Scholar
Mongruel, A., Lamriben, C., Yahiaoui, S. & Feuillebois, F. 2010 The approach of a sphere to a wall at finite Reynolds number. J. Fluid Mech. 661, 229–238.Google Scholar
Peskin, C. S. 2002 The immersed boundary method. Acta Numerica 11, 479–517.Google Scholar
Pianet, G., Ten Cate, A., Derksen, J. J. & Arquis, E. 2007 Assessment of the 1-fluid method for dns of particulate flows: sedimentation of a single sphere at moderate to high Reynolds numbers. Comput. Fluids 36, 359–375.Google Scholar
Richard, D. & Quéré, D. 2000 Bouncing water drops. Europhys. Lett. 50, 769–775.Google Scholar
Schäfer, J., Dippel, S. & Wolf, D. E. 1996 Force schemes in simulations of granular materials. J. Phys. I France 6, 5–20.Google Scholar
Simeonov, J. A. & Calantoni, J. 2012 Modeling mechanical contact and lubrication in direct numerical simulations of colliding particles. Intl J. Multiphase Flow 46, 38–53.Google Scholar
Smart, J. R. & Leighton, D. T. 1989 Measurement of the hydrodynamic surface roughness of noncolloidal spheres. Phys. Fluids A 1, 52–60.Google Scholar
Ten Cate, A., Nieuwstad, C. H., Derksen, J. J. & Van den Akker, H. E. A. 2002 Particle imaging velocimetry experiments and lattice-Boltzmann simulations on a single sphere settling under gravity. Phys. Fluids 14, 4012–4025.Google Scholar
Thompson, J. F., Warsi, Z. U. A. & Mastin, C. W. 1985 Numerical Grid Generation: Foundations and Applications. Elsevier.Google Scholar
Uhlmann, M. 2005 An immersed boundary method with direct forcing for the simulation of particulate flows. J. Comput. Phys. 209, 448–476.Google Scholar
Yang, F.-L. & Hunt, M. L. 2006 Dynamics of particle–particle collisions in a viscous liquid. Phys. Fluids 18, 121506.Google Scholar
Yang, F.-L. & Hunt, M. L. 2008 A mixed contact model for an immersed collision between two solid surfaces. Phil. Trans. R. Soc. Lond. A 366, 2205–2218.Google Scholar
Yuki, Y., Takeuchi, S. & Kajishima, T. 2007 Efficient immersed boundary method for strong interaction problem of arbitrary shape object with the self-induced flow. J. Fluid Sci. Technol. 2, 1–11.Google Scholar