Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-18T06:04:31.189Z Has data issue: false hasContentIssue false
  • English
  • Français

Mixing and entrainment are suppressed in inclined gravity currents

Published online by Cambridge University Press:  28 June 2019

Maarten van Reeuwijk Open the ORCID record for Maarten van Reeuwijk [Opens in a new window] ,
Markus Holzner  and
C. P. Caulfield Open the ORCID record for C. P. Caulfield [Opens in a new window]
Maarten van Reeuwijk*
Affiliation:
Department of Civil and Environmental Engineering, Imperial College London, London SW7 2AZ, UK
Markus Holzner
Affiliation:
Institute of Environmental Engineering, ETH Zürich, CH-8039 Zürich, Switzerland
C. P. Caulfield
Affiliation:
BP Institute, University of Cambridge, Madingley Rise, Madingley Road, Cambridge CB3 0EZ, UK Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK
*
†Email address for correspondence: m.vanreeuwijk@imperial.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

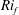We explore the dynamics of inclined temporal gravity currents using direct numerical simulation, and find that the current creates an environment in which the flux Richardson number $\mathit{Ri}_{f}$, gradient Richardson number 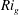$\mathit{Ri}_{g}$ and turbulent flux coefficient 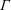$\unicode[STIX]{x1D6E4}$ are constant across a large portion of the depth. Changing the slope angle $\unicode[STIX]{x1D6FC}$ modifies these mixing parameters, and the flow approaches a maximum Richardson number 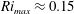$\mathit{Ri}_{max}\approx 0.15$ as 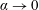$\unicode[STIX]{x1D6FC}\rightarrow 0$ at which the entrainment coefficient 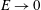$E\rightarrow 0$. The turbulent Prandtl number remains 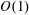$O(1)$ for all slope angles, demonstrating that 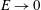$E\rightarrow 0$ is not caused by a switch-off of the turbulent buoyancy flux as conjectured by Ellison (J. Fluid Mech., vol. 2, 1957, pp. 456–466). Instead, 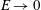$E\rightarrow 0$ occurs as the result of the turbulence intensity going to zero as 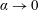$\unicode[STIX]{x1D6FC}\rightarrow 0$, due to the flow requiring larger and larger shear to maintain the same level of turbulence. We develop an approximate model valid for small $\unicode[STIX]{x1D6FC}$ which is able to predict accurately 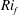$\mathit{Ri}_{f}$, 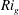$\mathit{Ri}_{g}$ and 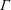$\unicode[STIX]{x1D6E4}$ as a function of $\unicode[STIX]{x1D6FC}$ and their maximum attainable values. The model predicts an entrainment law of the form 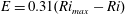$E=0.31(\mathit{Ri}_{max}-\mathit{Ri})$, which is in good agreement with the simulation data. The simulations and model presented here contribute to a growing body of evidence that an approach to a marginally or critically stable, relatively weakly stratified equilibrium for stratified shear flows may well be a generic property of turbulent stratified flows.

JFM classification

Geophysical and Geological Flows: Gravity currents Geophysical and Geological Flows: Stratified flows Mixing: Turbulent mixing
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 873 , 25 August 2019 , pp. 786 - 815
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bak, P., Tang, C. & Wiesenfeld, K. 1987 Self-organized criticality – an explanation of 1/f noise. Phys. Rev. Lett. 59, 381–384.Google Scholar
Billant, P. & Chomaz, J.-M. 2001 Self-similarity of strongly stratified inviscid flows. Phys. Fluids 13, 1645–1651.Google Scholar
Brethouwer, G., Billant, P., Lindborg, E. & Chomaz, J.-M. 2007 Scaling analysis and simulation of strongly stratified turbulent flows. J. Fluid Mech. 585, 343–368.Google Scholar
Caulfield, C. C. P. & Woods, A. W. 1995 Plumes with nonmonotonic mixing behaviour. Geophys. Astrophys. Fluid Dyn. 79, 173–199.Google Scholar
Caulfield, C. P. & Woods, A. W. 1998 Turbulent gravitational convection from a point source in a non-uniformly stratified environment. J. Fluid Mech. 360, 229–248.Google Scholar
Da Silva, C. B., Hunt, J. C. R., Eames, I. & Westerweel, J. 2014 Interfacial layers between regions of different turbulence intensity. Annu. Rev. Fluid Mech. 46, 567–590.Google Scholar
Deusebio, E., Caulfield, C. P. & Taylor, J. R. 2015 The intermittency boundary in stratified plane Couette flow. J. Fluid Mech. 781, 298–329.Google Scholar
Ellison, T. H. 1957 Turbulent transport of heat and momentum from an infinite rough plane. J. Fluid Mech. 2, 456–466.Google Scholar
Ellison, T. H. & Turner, J. S. 1959 Turbulent entrainment in stratified flows. J. Fluid Mech. 6, 423–448.Google Scholar
Falder, M., White, N. J. & Caulfield, C. P. 2016 Seismic imaging of rapid onset of stratified turbulence in the south Atlantic Ocean. J. Phys. Oceanogr. 46 (4), 1023–1044.Google Scholar
Fedorovich, E. & Shapiro, A. 2009 Structure of numerically simulated katabatic and anabatic flows along steep slopes. Acta Geophys. 57 (4), 981–1010.Google Scholar
Ferrari, R., Mashayek, A., McDougall, T. J., Nikurashin, M. & Campin, J. M. 2016 Turning ocean mixing upside down. J. Phys. Oceanogr. 46, 2239–2261.Google Scholar
Ferrari, R. & Wunsch, C. 2009 The distribution of eddy kinetic and potential energies in the global ocean. Annu. Rev. Fluid Mech. 41, 253–282.Google Scholar
Howard, L. N. 1961 Note on a paper of John W. Miles. J. Fluid Mech. 10 (4), 509–512.Google Scholar
Hunt, G. R. & Kaye, N. G. 2001 Virtual origin correction for lazy plumes. J. Fluid Mech. 435, 377–396.Google Scholar
Ivey, G. N., Winters, K. B. & Koseff, J. R. 2008 Density stratification, turbulence, but how much mixing? Annu. Rev. Fluid Mech. 40, 169–184.Google Scholar
Krug, D., Holzner, M., Lüthi, B., Wolf, M., Kinzelbach, W. & Tsinober, A. 2013 Experimental study of entrainment and interface dynamics in a gravity current. Exp. Fluids 54, 1530.Google Scholar
Krug, D., Holzner, M., Lüthi, B., Wolf, M., Kinzelbach, W. & Tsinober, A. 2015 The turbulent/non-turbulent interface in an inclined dense gravity current. J. Fluid Mech. 765, 303–324.Google Scholar
Krug, D., Holzner, M., Marusic, I. & van Reeuwijk, M. 2017 Fractal scaling of the turbulence interface in gravity currents. J. Fluid Mech. 820, R3.Google Scholar
Lighthill, M. 1950 Contributions to the theory of heat transfer through a laminar boundary layer. Proc. R. Soc. Lond. A 202, 350–377.Google Scholar
Lindborg, E. 2006 The energy cascade in a strongly stratified fluid. J. Fluid Mech. 550, 207–242.Google Scholar
Linden, P. F. 1979 Mixing in stratified fluids. Geophys. Astrophys. Fluid Dyn. 13, 3–23.Google Scholar
Mater, B. D. & Venayagamoorthy, S. K. 2014 A unifying framework for parameterizing stably stratified shear-flow turbulence. Phys. Fluids 26, 036601.Google Scholar
Miles, J. W. 1961 On the stability of heterogeneous shear flows. J. Fluid Mech. 10 (4), 496–508.Google Scholar
Monin, A. S. & Obukhov, A. M. 1954 Basic laws of turbulent mixing in the surface layer of the atmosphere. Contrib. Geophys. Inst. Acad. Sci. USSR 151, 163–187.Google Scholar
Morton, B. R. & Middleton, J. 1973 Scale diagrams for forced plumes. J. Fluid Mech. 58, 165–176.Google Scholar
Nieuwstadt, F. T. M. 1984 The turbulent structure of the stable, nocturnal boundary layer. J. Atmos. Sci. 41 (14), 2202–2216.Google Scholar
Obukhov, A. M. 1971 Turbulence in an atmosphere with a non-uniform temperature. Boundary-Layer Meterol. 2, 7–29.Google Scholar
Odier, P., Chen, J. & Ecke, R. E. 2014 Entrainment and mixing in a laboratory model of oceanic overflow. J. Fluid Mech. 746, 498–535.Google Scholar
Odier, P., Chen, J., Rivera, M. K. & Ecke, R. E. 2009 Fluid mixing in stratified gravity currents: The Prandtl mixing length. Phys. Rev. Lett. 102, 134504.Google Scholar
Osborn, T. R. 1980 Estimates of the local-rate of vertical diffusion from dissipation measurements. J. Phys. Oceanogr. 10, 83–89.Google Scholar
van Reeuwijk, M., Jonker, H. J. J. & Hanjalić, K. 2008 Wind and boundary layers in Rayleigh–Bénard convection. I. Analysis and modelling. Phys. Rev. E 77, 036311.Google Scholar
van Reeuwijk, M., Krug, D. & Holzner, M. 2018 Small-scale entrainment in inclined gravity currents. Environ. Fluid Mech. 18 (1), 225–239.Google Scholar
Salehipour, H. & Peltier, W. R. 2015 Diapycnal diffusivity, turbulent Prandtl number and mixing efficiency in Boussinesq stratified turbulence. J. Fluid Mech. 775, 464–500.Google Scholar
Salehipour, H., Peltier, W. R. & Caulfield, C. P. 2018 Self-organised criticality of turbulence in strongly stratified mixing layers. J. Fluid Mech. 856, 228–256.Google Scholar
Schlichting, H. & Gersten, K. 2000 Boundary Layer Theory. Springer.Google Scholar
Scotti, A. 2015 Biases in Thorpe-scale estimates of turbulence dissipation. Part II. Energetics arguments and turbulence simulations. J. Geophys. Res. 45, 2522–2543.Google Scholar
Sher, D. & Woods, A. W. 2015 Gravity currents: entrainment, stratification and self-similarity. J. Fluid Mech. 784, 130–162.Google Scholar
Shih, L. H., Koseff, J. R., Ivey, G. N. & Ferziger, J. H. 2005 Parameterization of turbulent fluxes and scales using homogenous sheared stably stratified turbulence simulations. J. Fluid Mech. 525, 193–214.Google Scholar
Simpson, J. E. 1999 Gravity Currents. Cambridge University Press.Google Scholar
Smyth, W. D. & Moum, J. N. 2013 Marginal instability and deep cycle turbulence in the eastern equatorial pacific occean. Geophys. Res. Lett. 40, 6181–6185.Google Scholar
Spalding, D. 1954 Mass transfer in laminar flow. Proc. R. Soc. Lond. A 221, 78–99.Google Scholar
Tailleux, R. 2013 Available potential energy and exergy in stratified fluids. Annu. Rev. Fluid Mech. 45, 35–58.Google Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT Press.Google Scholar
Thorpe, S. A. & Liu, Z. 2009 Marginal instability? J. Phys. Oceanogr. 39 (9), 2373–2381.Google Scholar
Turner, J. S. 1973 Buoyancy Effects in Fluids. Cambridge University Press.Google Scholar
Turner, J. S. 1986 Turbulent entrainment: the development of the entrainment assumption, and its application to geophysical flows. J. Fluid Mech. 173, 431–471.Google Scholar
Verstappen, R. W. C. P. & Veldman, A. E. P. 2003 Symmetry-preserving discretization of turbulent flow. J. Comput. Phys. 187 (1), 343–368.Google Scholar
Wahlin, A. K. & Cenedese, C. 2006 How entraining density currents influence the stratification in a one-dimensional ocean basin. Deep Sea Res. II 53, 172–193.Google Scholar
Wells, M., Cenedese, C. & Caulfield, C. P. 2010 The relationship between flux coefficient and entrainment ratio in density currents. J. Phys. Oceanogr. 40 (12), 2713–2727.Google Scholar
Wells, M. G. & Wettlaufer, J. S. 2005 Two-dimensional density currents in a confined basin. Geophys. Astrophys. Fluid Mech. 99, 199–218.Google Scholar
Zhou, Q., Taylor, J. R. & Caulfield, C. P. 2017 Self-similar mixing in stratified plane Couette flow for varying Prandtl number. J. Fluid Mech. 820, 86–120.Google Scholar