Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-18T16:42:44.984Z Has data issue: false hasContentIssue false
  • English
  • Français

Inertial particle acceleration in strained turbulence

Published online by Cambridge University Press:  12 November 2015

C.-M. Lee ,
Á. Gylfason ,
P. Perlekar  and
F. Toschi
C.-M. Lee
Affiliation:
Department of Mathematics and Statistics, California State University Long Beach, 1250 Bellflower Blvd, Long Beach, CA 90840, USA Department of Applied Physics, Eindhoven University of Technology, 5600 MB Eindhoven, The Netherlands
Á. Gylfason*
Affiliation:
School of Science and Engineering, Reykjavík University, Menntavegur 1, 101, Iceland
P. Perlekar
Affiliation:
TIFR Centre for Interdisciplinary Sciences, Tata Institute of Fundamental Research, 21 Brundavan Colony, Narsingi, Hyderabad 500075, India
F. Toschi
Affiliation:
Department of Applied Physics, Eindhoven University of Technology, 5600 MB Eindhoven, The Netherlands Department of Mathematics and Computer Science, Eindhoven University of Technology, 5600 MB Eindhoven, The Netherlands Istituto per le Applicazioni del Calcolo CNR, Via dei Taurini 19, 00185 Rome, Italy
*
†Email address for correspondence: armann@ru.is
Get access Rights & Permissions [Opens in a new window]

Abstract

The dynamics of inertial particles in turbulence is modelled and investigated by means of direct numerical simulation of an axisymmetrically expanding homogeneous turbulent strained flow. This flow can mimic the dynamics of particles close to stagnation points. The influence of mean straining flow is explored by varying the dimensionless strain rate parameter 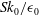$Sk_{0}/{\it\epsilon}_{0}$ from 0.2 to 20, where 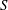$S$ is the mean strain rate, 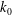$k_{0}$ and 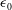${\it\epsilon}_{0}$ are the turbulent kinetic energy and energy dissipation rate at the onset of straining. We report results relative to the acceleration variances and probability density functions for both passive and inertial particles. A high mean strain is found to have a significant effect on the acceleration variance both directly by an increase in the frequency of the turbulence and indirectly through the coupling of the fluctuating velocity and the mean flow field. The influence of the strain on the normalized particle acceleration probability distribution functions is more subtle. For the case of a passive particle we can approximate the acceleration variance with the aid of rapid-distortion theory and obtain good agreement with simulation data. For the case of inertial particles we can write a formal expression for the accelerations. The magnitude changes in the inertial particle acceleration variance and the effect on the probability density function are then discussed in a wider context for comparable flows, where the effects of the mean flow geometry and of the anisotropy at small scales are present.

JFM classification

Multiphase and Particle-laden Flows: Particle/fluid flow Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulence theory
Type
Papers
Information
Journal of Fluid Mechanics , Volume 785 , 25 December 2015 , pp. 31 - 53
Check for updates
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alipchenkov, V. M. & Beketov, A. I. 2013 On clustering of aerosol particles in homogeneous turbulent shear flows. J. Turbul. 14, 1–9.CrossRefGoogle Scholar
Ayyalasomayajula, S., Gylfason, A., Collins, L. R., Bodenschatz, E. & Warhaft, Z. 2006 Lagrangian measurements of inertial particle accelerations in grid generated wind tunnel turbulence. Phys. Rev. Lett. 97, 144507.CrossRefGoogle ScholarPubMed
Ayyalasomayajula, S. & Warhaft, Z. 2006 Nonlinear interactions in strained axi-symmetric high Reynolds number turbulence. J. Fluid Mech. 566, 273–307.CrossRefGoogle Scholar
Batchelor, G. K. 1953 The Theory of Homogeneous Turbulence. Cambridge University Press.Google Scholar
Bec, J., Biferale, L., Boffetta, G., Celani, A., Cencini, M., Lanotte, A., Musacchio, S. & Toschi, F. 2006 Acceleration statistics of heavy particles in turbulence. J. Fluid Mech. 550, 349–358.CrossRefGoogle Scholar
Betchov, R. 1956 An inequality concerning the production of vorticity in isotropic turbulence. J. Fluid Mech. 1, 497–504.CrossRefGoogle Scholar
Biferale, L. & Procaccia, I. 2005 Anisotropy in turbulent flows and in turbulent transport. Phys. Rep. 414 (2–3), 43–164.CrossRefGoogle Scholar
Celani, A. 2007 The frontiers of computing in turbulence: challenges and perspectives. J. Turbul. 8, N34.CrossRefGoogle Scholar
Chen, J., Meneveau, C. & Katz, J. 2006 Scale interaction of turbulence subjected to a straining–relaxation–destraining cycle. J. Fluid Mech. 562, 123–150.CrossRefGoogle Scholar
Davidson, P. A. 2004 Turbulence: An Introduction for Scientists and Engineers. Oxford University Press.Google Scholar
Gerashchenco, S., Sharp, N. S., Neuscamman, S. & Warhaft, Z. 2008 Lagrangian measurements of inertial particle accelerations in a turbulent boundary layer. J. Fluid Mech. 617, 255–281.CrossRefGoogle Scholar
Gualtieri, P. & Meneveau, C. 2010 Direct numerical simulations of turbulence subjected to a straining and destraining cycle. Phys. Fluids 22, 065104.CrossRefGoogle Scholar
Gualtieri, P., Picano, F. & Casciola, C. M. 2009 Anisotropic clustering of inertial particles in homogeneous shear flow. J. Fluid Mech. 629, 25–39.CrossRefGoogle Scholar
Gualtieri, P., Picano, F., Sardina, G. & Casciola, C. M. 2012 Statistics of particle pair relative velocity in the homogeneous shear flow. Physica D 241, 245–250.CrossRefGoogle Scholar
Gylfason, A., Ayyalasomayajula, S. & Warhaft, Z. 2004 Intermittency, pressure and acceleration statistics from hot-wire measurements in wind-tunnel turbulence. J. Fluid Mech. 501, 213–229.CrossRefGoogle Scholar
Gylfason, A., Lee, C., Perlekar, P. & Toschi, F. 2011 Direct numerical simulation on strained turbulent flows and particles within. J. Phys.: Conf. Ser. 318, 052003.Google Scholar
Han, Z. & Reitz, R. D. 1995 Turbulence modeling of internal combustion engines using RNG ${\it\kappa}$ – ${\it\epsilon}$ models. Combust. Sci. Technol. 106, 267–295.CrossRefGoogle Scholar
Hunt, J. C. R. 1973 A theory of turbulent flow round two-dimensional bluff bodies. J. Fluid Mech. 61, 625–706.CrossRefGoogle Scholar
Hunt, J. C. R. & Carruthers, D. J. 1990 Rapid distortion theory and the problems of turbulence. J. Fluid Mech. 212, 497–532.CrossRefGoogle Scholar
Klein, A. 1995 Characteristics of combustor diffuser. Prog. Aerosp. Sci. 31, 171–271.CrossRefGoogle Scholar
Lavezzo, V., Soldati, A., Gerashchenko, S., Warhaft, Z. & Collins, L. R. 2010 On the role of gravity and shear on inertial particle accelerations in near-wall turbulence. J. Fluid Mech. 658, 229–246.CrossRefGoogle Scholar
Maxey, M. R. & Riley, J. R. 1983 Equation of motion for a small rigid sphere in a nonuniform flow. Phys. Fluids 26 (4), 883–889.CrossRefGoogle Scholar
Ott, S. & Mann, J. 2000 An experimental investigation of the relative diffusion of particle pairs in three-dimensional turbulence. J. Fluid Mech. 422, 207–223.CrossRefGoogle Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
Rogallo, R. S.1981 Numerical experiments in homogeneous turbulence. Tech. Rep. 81835. NASA Tech. Mem.Google Scholar
Shaw, R. 2003 Particle turbulence interactions in atmospheric clouds. Annu. Rev. Fluid Mech. 35, 183–227.CrossRefGoogle Scholar
Shotorban, B. & Balachandar, S. 2006 Particle concentration in homogeneous shear turbulence simulated via Lagrangian and equilibrium Eulerian approaches. Phys. Fluids 18, 065105.CrossRefGoogle Scholar
Toschi, F. & Bodenschatz, E. 2009 Lagrangian properties of particles in turbulence. Annu. Rev. Fluid Mech. 41, 375–404.CrossRefGoogle Scholar
Townsend, A. A. 1951 On the finescale structure of turbulence. Proc. R. Soc. Lond. A 208, 534–542.Google Scholar
Virant, M. & Dracos, T. 1997 PTV and its application on Lagrangian motion. Meas. Sci. Technol. 8, 1539–1552.CrossRefGoogle Scholar
Voth, G. A., Porta, A. La, Crawford, A. M., Alexander, J. & Bodenschatz, E. 2002 Measurements of particle accelerations in fully developed turbulence. J. Fluid Mech. 469, 121–160.CrossRefGoogle Scholar
Warhaft, Z. 1980 An experimental study of the effect of uniform strain on thermal fluctuations in grid generated turbulence. J. Fluid Mech. 99, 545–573.CrossRefGoogle Scholar
Xu, H., Ouelette, N. T. & Bodenschatz, E. 2008 Evolution of geometric structures in intense turbulence. New J. Phys. 10, 013012.CrossRefGoogle Scholar
Yeung, P. K. & Pope, S. B. 1998 Lagrangian statistics from direct numerical simulations of isotropic turbulence. J. Comput. Phys. 79, 373–416.CrossRefGoogle Scholar