Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-18T08:41:42.744Z Has data issue: false hasContentIssue false
  • English
  • Français

Frequency–wavenumber spectral analysis of spatio-temporal flows

Published online by Cambridge University Press:  08 June 2018

Christopher J. Geoga Open the ORCID record for Christopher J. Geoga [Opens in a new window] ,
Charlotte L. Haley ,
Andrew R. Siegel  and
Mihai Anitescu
Christopher J. Geoga*
Affiliation:
Argonne National Laboratory, Mathematics and Computer Science Division, 9700 S. Cass Ave., Lemont, IL 60439, USA
Charlotte L. Haley
Affiliation:
Argonne National Laboratory, Mathematics and Computer Science Division, 9700 S. Cass Ave., Lemont, IL 60439, USA
Andrew R. Siegel
Affiliation:
Argonne National Laboratory, Mathematics and Computer Science Division, 9700 S. Cass Ave., Lemont, IL 60439, USA University of Chicago, Department of Computer Science, 1100 E. 58th Street, Chicago, IL 60637, USA
Mihai Anitescu
Affiliation:
Argonne National Laboratory, Mathematics and Computer Science Division, 9700 S. Cass Ave., Lemont, IL 60439, USA University of Chicago, Department of Statistics, George Herbert Jones Laboratory 5747 S. Ellis Ave., Chicago, IL 60637, USA
*
†Email address for correspondence: cgeoga@anl.gov
Get access Rights & Permissions [Opens in a new window]

Abstract

We propose a fully spatio-temporal approach for identifying spatially varying modes of oscillation in fluid dynamics simulation output by means of multitaper frequency–wavenumber spectral analysis. One-dimensional spectrum estimation has proven to be a valuable tool in the analysis of turbulence data applied spatially to determine the rate of energy transport between spatial scales, or temporally to determine frequencies of oscillatory flows. It also allows for the quantitative comparison of flow characteristics between two scenarios using a standard basis. It has the limitation, however, that it neglects coupling between spatial and temporal structures. Two-dimensional frequency–wavenumber spectral analysis allows one to decompose waveforms into standing or travelling variety. The extended higher-dimensional multitaper method proposed here is shown to have improved statistical properties over conventional non-parametric spectral estimators, and is accompanied by confidence intervals which estimate their uncertainty. Multitaper frequency–wavenumber analysis is applied to a canonical benchmark problem, namely, a direct numerical simulation of von Kármán vortex shedding off a square wall-mounted cylinder with two inflow scenarios with matching momentum-thickness Reynolds numbers 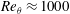$Re_{\unicode[STIX]{x1D703}}\approx 1000$ at the obstacle. Frequency–wavenumber analysis of a two-dimensional section of these data reveals that although both the laminar and turbulent inflow scenarios show a turbulent 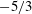$-5/3$ cascade in wavenumber ($\unicode[STIX]{x1D708}$) and frequency (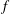$f$), the flow characteristics differ in that there is a significantly more prominent discrete harmonic oscillation near 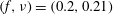$(f,\unicode[STIX]{x1D708})=(0.2,0.21)$ in wavenumber and frequency in the laminar inflow scenario than the turbulent scenario. This frequency–wavenumber pair corresponds to a travelling wave with velocity near one near the centre path of the vortex street.

JFM classification

Mathematical Foundations: Mathematical Foundations Vortex Flows: Vortex Flows Wakes/Jets: Vortex streets
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 848 , 10 August 2018 , pp. 545 - 559
Check for updates
Copyright
© Cambridge University Press 2018. This is a work of the U.S. Government and is not subject to copyright protection in the United States. 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Berkooz, G., Holmes, P. & Lumley, J. L. 1993 The proper orthogonal decomposition in the analysis of turbulent flows. Annu. Rev. Fluid Mech. 25, 539–575.Google Scholar
Cressie, N. 1981 Transformations and the jackknife. J. Roy. Statist. Soc. B 43, 177–182.Google Scholar
Cressie, N. & Wikle, C. K. 2011 Statistics for Spatio-Temporal Data. Wiley.Google Scholar
Efron, B. & Stein, C. 1981 The jackknife estimate of variance. Ann. Stat. 9, 586–596.Google Scholar
Grünbaum, F. A. 1981 Toeplitz matrices commuting with tridiagonal matrices. Linear Algebr. Applics. 40, 25–36.CrossRefGoogle Scholar
Hanssen, A. 1997 Multidimensional multitaper spectral estimation. Signal Process. 58, 327–332.CrossRefGoogle Scholar
Hayashi, Y. 1979 Space–time spectral analysis of rotary vector series. J. Atmos. Sci. 36, 757–766.Google Scholar
Holmes, P., Lumley, J. L. & Berkooz, G. 1998 Turbulence, Coherent Structures, Dynamical Systems and Symmetry. Cambridge University Press.Google Scholar
Kirby, J. F. 2014 Estimation of the effective elastic thickness of the lithosphere using inverse spectral methods: the state of the art. Tectonophysics 631, 87–116.CrossRefGoogle Scholar
Mallows, C. L. 1967 Linear processes are nearly Gaussian. J. Appl. Probab. 4, 313–329.Google Scholar
Percival, D. B. & Walden, A. T. 1993 Spectral Analysis for Physical Applications: Multitaper and Conventional Univariate Techniques. Cambridge University Press.Google Scholar
Pratt, R. W. 1976 The interpretation of space–time spectral quantities. J. Atmos. Sci. 33 (6), 1060–1066.2.0.CO;2>CrossRefGoogle Scholar
Rowley, C. W. 2005 Model reduction for fluids, using balanced proper orthogonal decomposition. Intl J. Bifurcation Chaos 15, 997–1013.Google Scholar
Rowley, C. W., Mezić, I., Bagheri, S., Schlatter, P. & Henningson, D. S. 2009 Spectral analysis of nonlinear flows. J. Fluid Mech. 641, 115–127.CrossRefGoogle Scholar
Schmidt, O. T., Towne, A., Colonius, T., Cavalieri, A. V. G., Jordan, P. & Brès, G. A. 2017 Wavepackets and trapped acoustic modes in a turbulent jet: coherent structure eduction and global stability. J. Fluid Mech. 825, 1153–1181.Google Scholar
Simons, F. J. & Wang, D. V. 2011 Spatiospectral concentration in the Cartesian plane. Intl J. Geomath. 2 (1), 1–36.Google Scholar
Slepian, D. 1964 Prolate spheroidal wave functions, Fourier analysis and uncertainty IV. Bell System Tech. J. 43, 3009–3057.Google Scholar
Slepian, D. 1978 Prolate spheroidal wave functions, Fourier analysis, and uncertainty V: the discrete case. Bell System Tech. J. 57 (5), 1371–1429.Google Scholar
von Storch, H. & Zwiers, F. W. 1999 Statistical Analysis in Climate Research. Cambridge University Press.Google Scholar
Thomson, D. J. 1982 Spectrum estimation and harmonic analysis. Proc. IEEE 70 (9), 1055–1096.CrossRefGoogle Scholar
Thomson, D. J. 1990 Quadratic-inverse spectrum estimates: applications to paleoclimatology. Phil. Trans. R. Soc. Lond. A 332, 539–597.Google Scholar
Thomson, D. J. 1994 An overview of multiple-window and quadratic-inverse spectrum estimation methods. Proc. ICASSP VI, 185–194; invited plenary lecture.Google Scholar
Thomson, D. J. & Chave, A. D. 1991 Jackknifed error estimates for spectra, coherences, and transfer functions. In Advances in Spectrum Analysis and Array Processing (ed. Haykin, S.), vol. 1, chap. 2, pp. 58–113. Prentice-Hall.Google Scholar
Vinuesa, R., Schlatter, P., Malm, J., Mavriplis, C. & Henningson, D. S. 2015 Direct numerical simulation of the flow around a wall-mounted square cylinder under various inflow conditions. J. Turbul. 16, 555–587.Google Scholar
Wilks, D. S. 2011 Statistical Methods in the Atmospheric Sciences. Academic Press.Google Scholar