Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-18T06:03:33.708Z Has data issue: false hasContentIssue false
  • English
  • Français

Fractal scaling of the turbulence interface in gravity currents

Published online by Cambridge University Press:  09 May 2017

Dominik Krug Open the ORCID record for Dominik Krug [Opens in a new window] ,
Markus Holzner ,
Ivan Marusic  and
Maarten van Reeuwijk
Dominik Krug*
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Victoria 3010, Australia
Markus Holzner
Affiliation:
Institute of Environmental Engineering, ETH Zürich, CH-8039 Zürich, Switzerland
Ivan Marusic
Affiliation:
Department of Mechanical Engineering, University of Melbourne, Victoria 3010, Australia
Maarten van Reeuwijk
Affiliation:
Department of Civil and Environmental Engineering, Imperial College London, SW7 2AZ London, UK
*
†Email address for correspondence: dkrug@unimelb.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

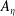It was previously observed by Krug et al. (J. Fluid Mech., vol. 765, 2015, pp. 303–324) that the surface area $A_{\unicode[STIX]{x1D702}}$ of the turbulent/non-turbulent interface (TNTI) in gravity currents decreases with increasing stratification, significantly reducing the entrainment rate. Here, we consider the multiscale properties of this effect using direct numerical simulations of temporal gravity currents with different gradient Richardson numbers 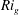$Ri_{g}$. Our results indicate that the reduction of 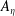$A_{\unicode[STIX]{x1D702}}$ is caused by a decrease of the fractal scaling exponent 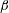$\unicode[STIX]{x1D6FD}$, while the scaling range remains largely unaffected. We further find that convolutions of the TNTI are characterized by different length scales in the streamwise and wall-normal directions, namely the integral scale 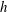$h$ and the shear scale 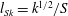$l_{Sk}=k^{1/2}/S$ (formed using the mean shear 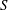$S$ and the turbulent kinetic energy 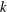$k$) respectively. By recognizing that the anisotropy implied by the different scaling relations increases with increasing 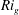$Ri_{g}$, we are able to model the 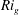$Ri_{g}$ dependence of 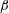$\unicode[STIX]{x1D6FD}$ in good agreement with the data.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Geophysical and Geological Flows: Gravity currents Turbulent Flows: Stratified turbulence
Type
Rapids
Information
Journal of Fluid Mechanics , Volume 820 , 10 June 2017 , R3
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Corrsin, S. & Kistler, A.1954 The free-stream boundaries of turbulent flows. NACA TN-3133, TR-1244, 1033–1064.Google Scholar
Craske, J. & van Reeuwijk, M. 2015 Energy dispersion in turbulent jets. Part 1. Direct simulation of steady and unsteady jets. J. Fluid Mech. 763, 500–537.Google Scholar
Da Silva, C. B., Hunt, J. C. R., Eames, I. & Westerweel, J. 2014 Interfacial layers between regions of different turbulence intensity. Annu. Rev. Fluid Mech. 46, 567–590.Google Scholar
Dimotakis, P. E. & Catrakis, H. J. 1999 Turbulence, fractals, and mixing. In Mixing: Chaos and Turbulence (ed. Chaté, H., Villermaux, E. & Chomaz, J.-M.), pp. 59–143. Springer.CrossRefGoogle Scholar
Ellison, T. H. & Turner, J. S. 1959 Turbulent entrainment in stratified flows. J. Fluid Mech. 6 (03), 423–448.Google Scholar
Holzner, M. & Lüthi, B. 2011 Laminar superlayer at the turbulence boundary. Phys. Rev. Lett. 106 (13), 134503.Google Scholar
Kneller, B., Nasr-Azadani, M. M., Radhakrishnan, S. & Meiburg, E. 2016 Long-range sediment transport in the world’s oceans by stably stratified turbidity currents. J. Geophys. Res. Oceans 121, 8608–8620.Google Scholar
Krug, D., Holzner, M., Lüthi, B., Wolf, M., Kinzelbach, W. & Tsinober, A. 2015 The turbulent/non-turbulent interface in an inclined dense gravity current. J. Fluid Mech. 765, 303–324.Google Scholar
Mandelbrot, B. B. 1982 The Fractal Geometry of Nature. W.H. Freeman.Google Scholar
Mater, P. D. & Venayagamoorthy, S. K. 2014 A unifying framework for parameterizing stably stratified shear-flow turbulence. Phys. Fluids 26 (3), 036601.Google Scholar
Mistry, D., Philip, J., Dawson, J. R. & Marusic, I. 2016 Entrainment at multi-scales across the turbulent/non-turbulent interface in an axisymmetric jet. J. Fluid Mech. 802, 690–725.Google Scholar
Paizis, S. T. & Schwarz, W. H. 1974 An investigation of the topography and motion of the turbulent interface. J. Fluid Mech. 63 (02), 315–343.Google Scholar
Pollard, R. T., Rhines, P. B. & Thompson, R. O. R. Y. 1972 The deepening of the wind-mixed layer. Geophys. Astrophys. Fluid Dyn. 4 (1), 381–404.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
van Reeuwijk, M. & Holzner, M. 2014 The turbulence boundary of a temporal jet. J. Fluid Mech. 739, 254–275.CrossRefGoogle Scholar
van Reeuwijk, M., Krug, D. & Holzner, M. 2017 Small-scale entrainment in inclined gravity currents. Environ. Fluid Mech. doi:10.1007/s10652-017-9514-3.Google Scholar
Schmid, P. J. & Henningson, D. S. 2000 Stability and Transition in Shear Flows. Springer.Google Scholar
Sequeiros, O. E. 2012 Estimating turbidity current conditions from channel morphology: a Froude number approach. J. Geophys. Res. 117, C04003.Google Scholar
Sequeiros, O. E., Spinewine, B., Beaubouef, R. T., Sun, T., García, M. H. & Parker, G. 2010 Characteristics of velocity and excess density profiles of saline underflows and turbidity currents flowing over a mobile bed. J. Hydraul. Engng ASCE 136 (7), 412–433.Google Scholar
de Silva, C. M., Philip, J., Chauhan, K., Meneveau, C. & Marusic, I. 2013 Multiscale geometry and scaling of the turbulent–nonturbulent interface in high Reynolds number boundary layers. Phys. Rev. Lett. 111, 044501.Google Scholar
Sreenivasan, K. R. 1991 Fractals and multifractals in fluid turbulence. Annu. Rev. Fluid Mech. 23 (1), 539–604.Google Scholar
Sreenivasan, K. R., Ramshankar, R. & Meneveau, C. 1989 Mixing, entrainment and fractal dimensions of surfaces in turbulent flows. Proc. R. Soc. Lond. A 421 (1860), 79–108.Google Scholar
Thiesset, F., Maurice, G., Halter, F., Mazellier, N., Chauveau, C. & Gökalp, I. 2016 Geometrical properties of turbulent premixed flames and other corrugated interfaces. Phys. Rev. E 93 (1), 013116.Google Scholar
Turner, J. S. 1986 Turbulent entrainment – the development of the entrainment assumption, and its application to geophysical flows. J. Fluid Mech. 173, 431–471.Google Scholar