Article contents
Flow structures in spanwise rotating plane Poiseuille flow based on thermal analogy
Published online by Cambridge University Press: 23 December 2021
Abstract
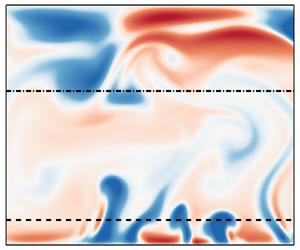
The analogy between rotating shear flow and thermal convection suggests the existence of plumes, inertial waves and plume currents in plane Poiseuille flow under spanwise rotation. The existence of these flow structures is examined with the results of three-dimensional and two-dimensional three-component direct numerical simulations. The dynamics of plumes near the unstable side is embodied in a truncated exponential distribution of turbulent fluctuations. For large rotation numbers, inertial waves are identified near the stable side, and these can be used to explain the abnormal flow statistics, such as the large root-mean-square of the streamwise velocity fluctuation and the nearly negligible Reynolds shear stress. For small or medium rotation numbers, plumes generated from the unstable side form large-scale plume currents and the patterns of the plume currents show different capabilities in scalar transport.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
REFERENCES
Zhang et al. supplementary movie 1
Contour of $u'$ in the $y-z$ plane from the 2-D case at $Re_\tau=180, Ro_\tau=5$. The dashed and dash-dotted lines denote the horizontal locations at $y=y_1$ and $y=y_2$ with $N_b(y_1)=0.1N_b(-1)$ and $N_b(y_2)=0.1N_b(1)$ respectively.
Zhang et al. supplementary movie 2
Contour of $u'$ in the $y-z$ plane from the 2-D case at $Re_\tau=180, Ro_\tau=40$. The dashed and dash-dotted lines denote the horizontal locations at $y=y_1$ and $y=y_2$ with $N_b(y_1)=0.1N_b(-1)$ and $N_b(y_2)=0.1N_b(1)$ respectively.
Zhang et al. supplementary movie 3
Contour of $u'$ in the $y-z$ plane at $x=0$ from the 3-D case at $Re_\tau=180, Ro_\tau=5$. The dashed and dash-dotted lines denote the horizontal locations at $y=y_1$ and $y=y_2$ with $N_b(y_1)=0.1N_b(-1)$ and $N_b(y_2)=0.1N_b(1)$ respectively.
- 4
- Cited by



