Article contents
Flow rate–pressure drop relation for shear-thinning fluids in narrow channels: approximate solutions and comparison with experiments
Published online by Cambridge University Press: 30 July 2021
Abstract
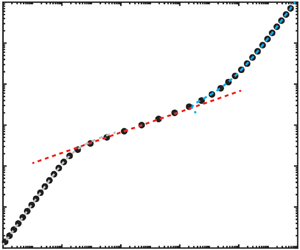
Non-Newtonian fluids are characterized by complex rheological behaviour that affects the hydrodynamic features, such as the flow rate–pressure drop relation. While flow rate–pressure drop measurements of such fluids are common in the literature, a comparison of experimental data with theory is rare, even for shear-thinning fluids at low Reynolds number, presumably due to the lack of analytical expressions for the flow rate–pressure drop relation covering the entire range of pressures and flow rates. Such a comparison, however, is of fundamental importance as it may provide insight into the adequacy of the constitutive model that was used and the values of the rheological parameters. In this work, we present a theoretical approach to calculating the flow rate–pressure drop relation of shear-thinning fluids in long, narrow channels that can be used for comparison with experimental measurements. We utilize the Carreau constitutive model and provide a semi-analytical expression for the flow rate–pressure drop relation. In particular, we derive three asymptotic solutions for small, intermediate and large values of the dimensionless pressures or flow rates, which agree with distinct limits previously known and allow us to approximate analytically the entire flow rate–pressure drop curve. We compare our semi-analytical and asymptotic results with the experimental measurements of Pipe et al. (Rheol. Acta, vol. 47, 2008, pp. 621–642) and find excellent agreement. Our results rationalize the change in the slope of the flow rate–pressure drop data, when reported in log–log coordinates, at high flow rates, which cannot be explained using a simple power-law model.
- Type
- JFM Rapids
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
REFERENCES
- 13
- Cited by





