Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Hu, Ruifeng
and
Wang, Lifeng
2014.
Motion transitions of falling plates via quasisteady aerodynamics.
Physical Review E,
Vol. 90,
Issue. 1,
Hamed, Ali M.
Jin, Yaqing
and
Chamorro, Leonardo P.
2015.
On the transient dynamics of the wake and trajectory of free falling cones with various apex angles.
Experiments in Fluids,
Vol. 56,
Issue. 11,
Zhang, Chuanhong
Zhu, Yiding
Chen, Xi
Yuan, Huijing
Wu, Jiezhi
Chen, Shiyi
Lee, Cunbiao
and
Gad-el-Hak, Mohamed
2015.
Transition in hypersonic boundary layers.
AIP Advances,
Vol. 5,
Issue. 10,
Wang, Y.
Shu, C.
Teo, C. J.
and
Yang, L. M.
2016.
Numerical study on the freely falling plate: Effects of density ratio and thickness-to-length ratio.
Physics of Fluids,
Vol. 28,
Issue. 10,
Zhu, Yiding
Zhang, Chuanhong
Chen, Xi
Yuan, Huijing
Wu, Jiezhi
Chen, Shiyi
Lee, Cunbiao
and
Gad-el-Hak, Mohamed
2016.
Transition in Hypersonic Boundary Layers: Role of Dilatational Waves.
AIAA Journal,
Vol. 54,
Issue. 10,
p.
3039.
Bai Ye
Jia Yong-Xia
Li Cun-Biao
and
Zhu Yi-Ding
2016.
Experimental Study of a Periodical Flapping Flag.
Acta Physica Sinica,
Vol. 65,
Issue. 12,
p.
124701.
Wang, Y.
Shu, C.
Teo, C.J.
and
Yang, L.M.
2016.
An efficient immersed boundary-lattice Boltzmann flux solver for simulation of 3D incompressible flows with complex geometry.
Computers & Fluids,
Vol. 124,
Issue. ,
p.
54.
Jia, L C
Zhu, Y D
Jia, Y X
Yuan, H J
and
Lee, C B
2017.
Image pre-processing method for near-wall PIV measurements over moving curved interfaces.
Measurement Science and Technology,
Vol. 28,
Issue. 3,
p.
035201.
Sun, Y.
Shu, C.
Wang, Y.
Teo, C.J.
and
Chen, Z.
2017.
An immersed boundary-gas kinetic flux solver for simulation of incompressible flows
.
Computers & Fluids,
Vol. 142,
Issue. ,
p.
45.
Wang, Y.
Shu, C.
Yang, L.M.
and
Teo, C.J.
2017.
An immersed boundary-lattice boltzmann flux solver in a moving frame to study three-dimensional freely falling rigid bodies.
Journal of Fluids and Structures,
Vol. 68,
Issue. ,
p.
444.
Wang, Y.
Shu, C.
Yang, L. M.
and
Sun, Y.
2017.
On the immersed boundary‐lattice Boltzmann simulations of incompressible flows with freely moving objects.
International Journal for Numerical Methods in Fluids,
Vol. 83,
Issue. 4,
p.
331.
YUAN, Xulong
LIU, Xiyan
CHEN, Cheng
REN, Yao
and
ZHANG, Biancheng
2018.
The Dynamics Modeling of the Underwater Falling Motion of the Irregular Body.
p.
1.
Kim, Taehyun
Chang, Jaehyeock
and
Kim, Daegyoum
2018.
Free-fall dynamics of a pair of rigidly linked disks.
Physics of Fluids,
Vol. 30,
Issue. 3,
Du, Zhifang
and
Li, Jiequan
2018.
A Hermite WENO reconstruction for fourth order temporal accurate schemes based on the GRP solver for hyperbolic conservation laws.
Journal of Computational Physics,
Vol. 355,
Issue. ,
p.
385.
Luo, Lan
and
Tomac, Ingrid
2018.
Particle Image Velocimetry (PIV) Analysis of Particle Settling in Narrow Fracture Experiments.
Geotechnical Testing Journal,
Vol. 41,
Issue. 2,
p.
354.
Blay Esteban, Luis
Shrimpton, John
and
Ganapathisubramani, Bharathram
2018.
Edge effects on the fluttering characteristics of freely falling planar particles.
Physical Review Fluids,
Vol. 3,
Issue. 6,
Salomone, Horacio D
Olivieri, Néstor A
Véliz, Maximiliano E
and
Raviola, Lisandro A
2018.
A non-traditional fluid problem: transition between theoretical models from Stokes’ to turbulent flow.
European Journal of Physics,
Vol. 39,
Issue. 3,
p.
035002.
Du, Zhifang
and
Li, Jiequan
2018.
A two-stage fourth order time-accurate discretization for Lax–Wendroff type flow solvers II. High order numerical boundary conditions.
Journal of Computational Physics,
Vol. 369,
Issue. ,
p.
125.
Li, Bing-Hua
Huang, Xian-Wen
Zheng, Yao
Xie, Fang-Fang
Wang, Jing
and
Zou, Jian-Feng
2018.
Performance of flapping airfoil propulsion with LBM method and DMD analysis.
Modern Physics Letters B,
Vol. 32,
Issue. 12n13,
p.
1840024.
Xiang, Yang
Qin, Suyang
Huang, Wentao
Wang, Fuxin
and
Liu, Hong
2018.
Trajectory modes and wake patterns of freely falling plates.
Journal of Visualization,
Vol. 21,
Issue. 3,
p.
433.
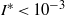 ${I}^{\ast } \lt 1{0}^{- 3} $) was investigated experimentally. The transition from two-dimensional zigzag motion to three-dimensional spiral motion occurs due to the growth of three-dimensional disturbances. Oscillations in the direction normal to the zigzag plane increase with the development of this instability. At the same time, the oscillation of the nutation angle decreases to zero and the angle remains constant. The effects of initial conditions (release angle) were investigated. Two kinds of transition modes, zigzag–spiral transition and zigzag–spiral–zigzag intermittence transition, were observed to be separated by a critical Reynolds number. In addition, the solution of the generalized Kirchhoff equations shows that the small
${I}^{\ast } \lt 1{0}^{- 3} $) was investigated experimentally. The transition from two-dimensional zigzag motion to three-dimensional spiral motion occurs due to the growth of three-dimensional disturbances. Oscillations in the direction normal to the zigzag plane increase with the development of this instability. At the same time, the oscillation of the nutation angle decreases to zero and the angle remains constant. The effects of initial conditions (release angle) were investigated. Two kinds of transition modes, zigzag–spiral transition and zigzag–spiral–zigzag intermittence transition, were observed to be separated by a critical Reynolds number. In addition, the solution of the generalized Kirchhoff equations shows that the small 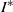 ${I}^{\ast } $ is responsible for the growth of disturbances in the third dimension (perpendicular to the planar motion).
${I}^{\ast } $ is responsible for the growth of disturbances in the third dimension (perpendicular to the planar motion).

