Article contents
Dynamics of viscous backflow from a model fracture network
Published online by Cambridge University Press: 12 December 2017
Abstract
Hydraulic fracturing for production of oil and gas from shale formations releases fluid waste, by-products that must be managed carefully to avoid significant harm to human health and the environment. These fluids are presumed to result from a variety of fracture relaxation processes, and are commonly referred to as ‘flowback’ and ‘produced water’, depending primarily on the time scale of their appearance. Here, a model is presented for investigating the dynamics of backflows caused by the elastic relaxation of a pre-strained medium, namely a single fracture and two model fracture network systems: a single bifurcated channel and its generalization for  $n$ bifurcated fracture generations. Early- and late-time asymptotic solutions are obtained for the model problems and agree well with numerical solutions. In the late-time period, the fracture apertures and backflow rates exhibit a time dependence of
$n$ bifurcated fracture generations. Early- and late-time asymptotic solutions are obtained for the model problems and agree well with numerical solutions. In the late-time period, the fracture apertures and backflow rates exhibit a time dependence of 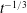 $t^{-1/3}$ and
$t^{-1/3}$ and 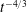 $t^{-4/3}$, respectively. In addition, the pressure distributions collapse to universal curves when scaled by the maximum pressure in the system, which we calculate as a function of
$t^{-4/3}$, respectively. In addition, the pressure distributions collapse to universal curves when scaled by the maximum pressure in the system, which we calculate as a function of  $n$. The pressure gradient along the network is steepest near the outlet while the bulk of the network serves as a ‘reservoir’. Fracture networks with larger
$n$. The pressure gradient along the network is steepest near the outlet while the bulk of the network serves as a ‘reservoir’. Fracture networks with larger  $n$ are less efficient at evicting fluids, manifested through a longer time required for a given fractional reduction of the initial volume. The developed framework may be useful for informing engineering design and environmental regulations.
$n$ are less efficient at evicting fluids, manifested through a longer time required for a given fractional reduction of the initial volume. The developed framework may be useful for informing engineering design and environmental regulations.
- Type
- JFM Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 16
- Cited by



