Article contents
Development of gravity currents on slopes under different interfacial instability conditions
Published online by Cambridge University Press: 07 October 2019
Abstract
We present experimental results on the development of gravity currents moving onto sloping boundaries with slope angles 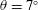 $\unicode[STIX]{x1D703}=7^{\circ }$,
$\unicode[STIX]{x1D703}=7^{\circ }$, 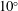 $10^{\circ }$ and
$10^{\circ }$ and 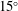 $15^{\circ }$. Different regimes of flow development are observed depending on the slope angle and on the initial velocity and density profiles, characterized by the Richardson number
$15^{\circ }$. Different regimes of flow development are observed depending on the slope angle and on the initial velocity and density profiles, characterized by the Richardson number 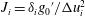 $J_{i}=\unicode[STIX]{x1D6FF}_{i}{g_{0}}^{\prime }/\unicode[STIX]{x0394}u_{i}^{2}$, where
$J_{i}=\unicode[STIX]{x1D6FF}_{i}{g_{0}}^{\prime }/\unicode[STIX]{x0394}u_{i}^{2}$, where 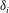 $\unicode[STIX]{x1D6FF}_{i}$,
$\unicode[STIX]{x1D6FF}_{i}$, 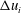 $\unicode[STIX]{x0394}u_{i}$ and
$\unicode[STIX]{x0394}u_{i}$ and 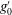 $g_{0}^{\prime }$ are, respectively, the velocity interface thickness, the maximum velocity difference and reduced gravity at the beginning of the slope. For
$g_{0}^{\prime }$ are, respectively, the velocity interface thickness, the maximum velocity difference and reduced gravity at the beginning of the slope. For 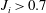 $J_{i}>0.7$ and the larger slope angle, the flow strongly accelerates, reaches a maximum at the beginning of the Kelvin–Helmholtz instability, then decelerates and re-accelerates again. For
$J_{i}>0.7$ and the larger slope angle, the flow strongly accelerates, reaches a maximum at the beginning of the Kelvin–Helmholtz instability, then decelerates and re-accelerates again. For 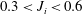 $0.3<J_{i}<0.6$, instability occurs earlier and velocity oscillations are less. When
$0.3<J_{i}<0.6$, instability occurs earlier and velocity oscillations are less. When 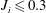 $J_{i}\leqslant 0.3$ the increase in velocity is smooth. The magnitude of velocity oscillation depends on the combined effect of
$J_{i}\leqslant 0.3$ the increase in velocity is smooth. The magnitude of velocity oscillation depends on the combined effect of 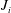 $J_{i}$ and slope angle, expressed by an overall acceleration parameter
$J_{i}$ and slope angle, expressed by an overall acceleration parameter 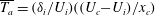 $\overline{T_{a}}=(\unicode[STIX]{x1D6FF}_{i}/U_{i})((U_{c}-U_{i})/x_{c})$, which, to first order, is given by
$\overline{T_{a}}=(\unicode[STIX]{x1D6FF}_{i}/U_{i})((U_{c}-U_{i})/x_{c})$, which, to first order, is given by 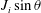 $J_{i}\sin \unicode[STIX]{x1D703}$, where
$J_{i}\sin \unicode[STIX]{x1D703}$, where 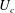 $U_{c}$ and
$U_{c}$ and 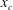 $x_{c}$ are, respectively, the velocity and position at instability onset. The velocity increases smoothly up to an equilibrium state when
$x_{c}$ are, respectively, the velocity and position at instability onset. The velocity increases smoothly up to an equilibrium state when 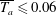 $\overline{T_{a}}\leqslant 0.06$ and exhibits an irregular behaviour at larger values of
$\overline{T_{a}}\leqslant 0.06$ and exhibits an irregular behaviour at larger values of 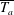 $\overline{T_{a}}$. The critical Richardson number
$\overline{T_{a}}$. The critical Richardson number 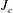 $J_{c}$ decreases with increasing
$J_{c}$ decreases with increasing 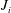 $J_{i}$ (increasing
$J_{i}$ (increasing 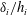 $\unicode[STIX]{x1D6FF}_{i}/h_{i}$) which is due to wall effects and
$\unicode[STIX]{x1D6FF}_{i}/h_{i}$) which is due to wall effects and 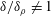 $\unicode[STIX]{x1D6FF}/\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70C}}\neq 1$. After the beginning of Kelvin–Helmholtz instability, entrainment rates are close to those of a mixing layer, decreasing to values of a gravity current after the mixing layer reaches the boundary. It is shown here that the interfacial instability during current development affects the bottom shear stress which can reach values of
$\unicode[STIX]{x1D6FF}/\unicode[STIX]{x1D6FF}_{\unicode[STIX]{x1D70C}}\neq 1$. After the beginning of Kelvin–Helmholtz instability, entrainment rates are close to those of a mixing layer, decreasing to values of a gravity current after the mixing layer reaches the boundary. It is shown here that the interfacial instability during current development affects the bottom shear stress which can reach values of 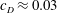 $c_{D}\approx 0.03$ regardless of initial conditions. By solving numerically the depth integrated governing equations, the gravity flow velocity, depth and buoyant acceleration in the flow direction can be well predicted for all the performed experiments over the full measurement domain. The numerical results for the experiments with
$c_{D}\approx 0.03$ regardless of initial conditions. By solving numerically the depth integrated governing equations, the gravity flow velocity, depth and buoyant acceleration in the flow direction can be well predicted for all the performed experiments over the full measurement domain. The numerical results for the experiments with 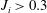 $J_{i}>0.3$ predict that the current requires a distance of at least
$J_{i}>0.3$ predict that the current requires a distance of at least 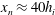 $x_{n}\approx 40h_{i}$ to reach a normal state of constant velocity, which is much larger than the distance
$x_{n}\approx 40h_{i}$ to reach a normal state of constant velocity, which is much larger than the distance 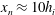 $x_{n}\approx 10h_{i}$ required in the case of a current with
$x_{n}\approx 10h_{i}$ required in the case of a current with 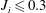 $J_{i}\leqslant 0.3$ that is commonly assumed for downslope currents.
$J_{i}\leqslant 0.3$ that is commonly assumed for downslope currents.
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 13
- Cited by


