Article contents
Convective heat transfer along ratchet surfaces in vertical natural convection
Published online by Cambridge University Press: 28 June 2019
Abstract
We report on a combined experimental and numerical study of convective heat transfer along ratchet surfaces in vertical natural convection (VC). Due to the asymmetry of the convection system caused by the asymmetric ratchet-like wall roughness, two distinct states exist, with markedly different orientations of the large-scale circulation roll (LSCR) and different heat transport efficiencies. Statistical analysis shows that the heat transport efficiency depends on the strength of the LSCR. When a large-scale wind flows along the ratchets in the direction of their smaller slopes, the convection roll is stronger and the heat transport is larger than the case in which the large-scale wind is directed towards the steeper slope side of the ratchets. Further analysis of the time-averaged temperature profiles indicates that the stronger LSCR in the former case triggers the formation of a secondary vortex inside the roughness cavity, which promotes fluid mixing and results in a higher heat transport efficiency. Remarkably, this result differs from classical Rayleigh–Bénard convection (RBC) with asymmetric ratchets (Jiang et al., Phys. Rev. Lett., vol. 120, 2018, 044501), wherein the heat transfer is stronger when the large-scale wind faces the steeper side of the ratchets. We reveal that the reason for the reversed trend for VC as compared to RBC is that the flow is less turbulent in VC at the same 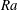 $Ra$. Thus, in VC the heat transport is driven primarily by the coherent LSCR, while in RBC the ejected thermal plumes aided by gravity are the essential carrier of heat. The present work provides opportunities for control of heat transport in engineering and geophysical flows.
$Ra$. Thus, in VC the heat transport is driven primarily by the coherent LSCR, while in RBC the ejected thermal plumes aided by gravity are the essential carrier of heat. The present work provides opportunities for control of heat transport in engineering and geophysical flows.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 11
- Cited by



