Hostname: page-component-8448b6f56d-42gr6 Total loading time: 0 Render date: 2024-04-19T16:45:57.484Z Has data issue: false hasContentIssue false
  • English
  • Français

Continuously forced transient growth in oblique breakdown for supersonic boundary layers

Published online by Cambridge University Press:  09 September 2016

Andreas C. Laible  and
H. F. Fasel
Andreas C. Laible
Affiliation:
Department of Aerospace and Mechanical Engineering, Tucson, AZ 85721, USA
H. F. Fasel*
Affiliation:
Department of Aerospace and Mechanical Engineering, Tucson, AZ 85721, USA
*
†Email address for correspondence: faselh@email.arizona.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

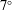The early nonlinear transition process initiated by a small-amplitude pair of oblique waves is studied using both temporal numerical simulation and theoretical considerations. This investigation is performed under the flow conditions of the experiments by Corke et al. (AIAA J., vol. 40, 2002, pp. 1015–1018) who investigated a sharp $7^{\circ }$ cone in the NASA Mach 3.5 Quiet Tunnel. In particular, both the linear and the nonlinear mechanisms prior to transition onset are investigated in great detail as the physics of this regime predetermine the flow topology of the nonlinear transition zone. The objective of this study is (i) to advance the understanding of the underlying physical mechanisms relevant for the early nonlinear transition regime of oblique breakdown and (ii) to make the connection to oblique transition, the incompressible scenario for bypass transition investigated by Schmid & Henningson (Phys. Fluids A, vol. 4, 1992, pp. 1986–1989). The dominance of the longitudinal vortex mode in oblique breakdown is shown to be a consequence of a constantly forced transient growth instability. In particular, the primary pair of oblique waves serves as an ‘actuator’ that is permanently introducing disturbances into the longitudinal mode where these disturbances exhibit transient growth. The effect of the transient growth instability on the longitudinal mode is to raise its amplitude rather than change the growth rate of this mode.

JFM classification

Boundary Layers: Boundary layer stability Compressible Flows: Compressible boundary layers Instability: Transition to turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 804 , 10 October 2016 , pp. 323 - 350
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: Bettina-von-Arnim-Str. 41, 73760, Ostfildern, Germany

References

Berlin, S., Lundbladh, A. & Henningson, D. 1994 Spatial simulations of oblique transition in a boundary layer. Phys. Fluids 6, 1949.CrossRefGoogle Scholar
Canuto, C., Hussaini, M. Y., Quateroni, A. & Zang, T. A. 1988 Spectral Methods in Fluid Dynamics. Springer.CrossRefGoogle Scholar
Chang, C. L. & Malik, M. R. 1994 Oblique-mode breakdown and secondary instability in supersonic boundary layers. J. Fluid Mech. 273, 323–360.CrossRefGoogle Scholar
Corke, T. C., Cavalieri, D. A. & Matlis, E. 2002 Boundary-layer instability on sharp cone at Mach 3.5 with controlled input. AIAA J. 40, 1015–1018.CrossRefGoogle Scholar
Ermolaev, Y. G., Kosinov, A. D. & Semionov, N. V. 1996 Experimental investigation of laminar-turbulent transition process in supersonic boundary layer using controlled disturbances. In IUTAM Symposium on Nonlinear Instability and Transition in Three-Dimensional Boundary Layers (ed. Duck, P. W. & Hall, P.), pp. 17–26. Kluwer Academic.CrossRefGoogle Scholar
Fasel, H., Thumm, A. & Bestek, H. 1993 Direct numerical simulation of transition in supersonic boundary layers: oblique breakdown. In Transitional and Turbulent Compressible Flows (ed. Kral, L. D. & Zang, T. A.), vol. FED 151, pp. 77–92. ASME.Google Scholar
Fezer, A. & Kloker, M. 2003 DNS of transition mechanisms at Mach 6.8 – flat plate vs. sharp cone. In West East High Speed Flow Fields, 2002, Proc. W.E.H.S.F.F. Conference, Marseille, France, April 22–26, 2002 (ed. Zeitoun, D. E., Periaux, J., Desideri, J. A. & Marini, M.), pp. 434–441. CIMNE, see ResearchGate.Google Scholar
Jiang, L., Choudhari, M., Chang, C. L. & Liu, C.2006 Numerical simulations of laminar-turbulent transition in supersonic boundary layer. AIAA Paper 2006-3324.CrossRefGoogle Scholar
Kloker, M. J. & Stemmer, C. 2003 Three-dimensional steady disturbance modes in the Blasius boundary layer – a DNS study. In Recent Results in Laminar-Turbulent Transition, Notes on Numerical Fluid Mechanics and Multidisciplinary Design (NNFM), vol. 86, pp. 91–110. Springer.Google Scholar
Laible, A. C., Mayer, C. S. J. & Fasel, H. F.2009 Numerical Investigation of Transition for a Cone at Mach 3.5: oblique breakdown. AIAA Paper 2009-3557.CrossRefGoogle Scholar
Laurien, E. & Kleiser, L. 1989 Numerical simulation of boundary-layer transition and transition control. J. Fluid Mech. 199, 403–440.CrossRefGoogle Scholar
van Leer, B. 1982 Flux-vector splitting for the Euler equations. In International Conference on Numerical Methods in Fluid Dynamics, Lecture Notes in Physics, vol. 170, pp. 507–512. Springer.Google Scholar
Mack, L. M.1984 Boundary-layer linear stability theory. In Special Course on Stability and Transition of Laminar Flow, Advisory Group for Aerospace Research and Development, AGARD Rep. 709. Defense Technical Information Center.Google Scholar
Mayer, C. S. J., Wernz, S. & Fasel, H. F.2007 Investigation of oblique breakdown in a supersonic boundary layer at Mach 2 using DNS. AIAA Paper 2007-0949.CrossRefGoogle Scholar
Mayer, C. J. S., von Terzi, D. A. & Fasel, H. F. 2010 Direct numerical simulation of complete transition to turbulence via oblique breakdown at Mach 3. J. Fluid Mech. 674, 5–42.CrossRefGoogle Scholar
Sandberg, R. D. & Fasel, H. F. 2006 Numerical investigation of transitional supersonic axisymmetric wakes. J. Fluid Mech. 563, 1–41.CrossRefGoogle Scholar
Schmid, P. J. & Henningson, D. S. 1992 A new mechanism for rapid transition involving a pair of oblique waves. Phys. Fluids A 4, 1986–1989.CrossRefGoogle Scholar
Spalart, P. R. & Yang, K.-S. 1987 Numerical study of ribbon-induced transition in Blasius flow. J. Fluid Mech. 178, 345–365.CrossRefGoogle Scholar
Squire, H. B. 1933 On the stability for three-dimensional disturbances of viscous fluid flow between parallel walls. Proc. R. Soc. Lond. A 142, 621–628.Google Scholar
Stemmer, C. & Kloker, M. 2000 Navier–Stokes simulation of harmonic point disturbances in an airfoil boundary layer. AIAA J. 38, 1369–1376.CrossRefGoogle Scholar
Thumm, A.1991 Numerische Untersuchungen zum laminar-turbulenten Strömungsumschlag in transsonischen Grenzschichtströmungen. PhD thesis, Universität Stuttgart.Google Scholar
Thumm, A., Wolz, W. & Fasel, H. 1989 Numerical simulation of spatially growing three-dimensional disturbance waves in compressible boundary layers. In Laminar-Turbulent Transition (ed. Arnal, D. & Michel, R.), International Union of Theoretical and Applied Mechanics, pp. 303–308. IUTAM Symposium, Toulouse/France. Springer.Google Scholar
Zhong, X. 1998 High-order finite-difference schemes for numerical simulation of hypersonic boundary-layer transition. J. Comput. Phys. 144, 662–709.CrossRefGoogle Scholar
Zhong, X. & Tatineni, M. 2003 High-order non-uniform grid schemes for numerical simulation of hypersonic boundary-layer stability and transition. J. Comput. Phys. 190, 419–458.CrossRefGoogle Scholar