Skip to main content Accessibility help

We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.

Close cookie message
×
Home
  • Home
Hostname: page-component-559fc8cf4f-d5zgf Total loading time: 0.341 Render date: 2021-03-06T07:12:37.943Z Has data issue: true Feature Flags: { "shouldUseShareProductTool": true, "shouldUseHypothesis": true, "isUnsiloEnabled": true, "metricsAbstractViews": false, "figures": false, "newCiteModal": false, "newCitedByModal": true }
EnglishFrançais
Journal of Fluid Mechanics Journal of Fluid Mechanics

Article contents

Cascades of temperature and entropy fluctuations in compressible turbulence

Published online by Cambridge University Press:  20 March 2019

Jianchun Wang [Opens in a new window] ,
Minping Wan [Opens in a new window] ,
Song Chen ,
Chenyue Xie ,
Lian-Ping Wang [Opens in a new window]  and
Shiyi Chen
Jianchun Wang
Affiliation:
Department of Mechanics and Aerospace Engineering, Southern University of Science and Technology, Shenzhen, Guangdong 518055, PR China
Minping Wan
Affiliation:
Department of Mechanics and Aerospace Engineering, Southern University of Science and Technology, Shenzhen, Guangdong 518055, PR China
Song Chen
Affiliation:
Department of Mechanics and Aerospace Engineering, Southern University of Science and Technology, Shenzhen, Guangdong 518055, PR China
Chenyue Xie
Affiliation:
Department of Mechanics and Aerospace Engineering, Southern University of Science and Technology, Shenzhen, Guangdong 518055, PR China
Lian-Ping Wang
Affiliation:
Department of Mechanics and Aerospace Engineering, Southern University of Science and Technology, Shenzhen, Guangdong 518055, PR China Department of Mechanical Engineering, University of Delaware, Newark, DE 19716, USA
Shiyi Chen
Affiliation:
Department of Mechanics and Aerospace Engineering, Southern University of Science and Technology, Shenzhen, Guangdong 518055, PR China State Key Laboratory of Turbulence and Complex Systems, Center for Applied Physics and Technology, College of Engineering, Peking University, Beijing 100871, PR China
Corresponding
E-mail address:
wangjc@sustech.edu.cn
wanmp@sustech.edu.cn
Get access
Rights & Permissions[Opens in a new window]

Abstract

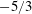Cascades of temperature and entropy fluctuations are studied by numerical simulations of stationary three-dimensional compressible turbulence with a heat source. The fluctuation spectra of velocity, compressible velocity component, density and pressure exhibit the $-5/3$ scaling in an inertial range. The strong acoustic equilibrium relation between spectra of the compressible velocity component and pressure is observed. The 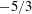$-5/3$ scaling behaviour is also identified for the fluctuation spectra of temperature and entropy, with the Obukhov–Corrsin constants close to that of a passive scalar spectrum. It is shown by Kovasznay decomposition that the dynamics of the temperature field is dominated by the entropic mode. The average subgrid-scale (SGS) fluxes of temperature and entropy normalized by the total dissipation rates are close to 1 in the inertial range. The cascade of temperature is dominated by the compressible mode of the velocity field, indicating that the theory of a passive scalar in incompressible turbulence is not suitable to describe the inter-scale transfer of temperature in compressible turbulence. In contrast, the cascade of entropy is dominated by the solenoidal mode of the velocity field. The different behaviours of cascades of temperature and entropy are partly explained by the geometrical properties of SGS fluxes. Moreover, the different effects of local compressibility on the SGS fluxes of temperature and entropy are investigated by conditional averaging with respect to the filtered dilatation, demonstrating that the effect of compressibility on the cascade of temperature is much stronger than on the cascade of entropy.

JFM classification

Turbulent Flows: Compressible turbulence Turbulent Flows: Isotropic turbulence
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 867 , 25 May 2019 , pp. 195 - 215
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below.
If you should have access and can't see this content please contact technical support.

References

Aluie, H. 2011 Compressible turbulence: the cascade and its locality. Phys. Rev. Lett. 106, 174502.CrossRefGoogle ScholarPubMed
Aluie, H. 2013 Scale decomposition in compressible turbulence. Physica D 247, 54–65.Google Scholar
Aluie, H., Li, S. & Li, H. 2012 Conservative cascade of kinetic energy in compressible turbulence. Astrophys. J. Lett. 751, L29.CrossRefGoogle Scholar
Balsara, D. S. & Shu, C. W. 2000 Monotonicity preserving weighted essentially non-oscillatory schemes with increasingly high order of accuracy. J. Comp. Phys. 160, 405–452.CrossRefGoogle Scholar
Bayly, B. J., Levermore, C. D. & Passot, T. 1992 Density variations in weakly compressible flows. Phys. Fluids A 4, 945–954.CrossRefGoogle Scholar
Benzi, R., Biferale, L., Fisher, R. T., Kadanoff, L. P., Lamb, D. Q. & Toschi, F. 2008 Intermittency and universality in fully developed inviscid and weakly compressible turbulent flows. Phys. Rev. Lett. 100, 234503.CrossRefGoogle ScholarPubMed
Cardy, J., Falkovich, G. & Gawedzki, K. 2008 Non-equilibrium Statistical Mechanics and Turbulence. Cambridge University Press.CrossRefGoogle Scholar
Chassaing, P., Antoniz, R., Anselmet, F., Joly, L. & Sarkar, S. 2002 Variable Density Fluid Turbulence, Fluid Mechanics and its Applications, vol. 69. Kluwer.CrossRefGoogle Scholar
Chen, S. & Cao, N. 1997 Anomalous scaling and structure instability in three-dimensional passive scalar turbulence. Phys. Rev. Lett. 78, 3459–3462.CrossRefGoogle Scholar
Chen, S., Wang, J., Li, H., Wan, M. & Chen, S. Y. 2018 Spectra and Mach number scaling in compressible homogeneous shear turbulence. Phys. Fluids 30, 065109.CrossRefGoogle Scholar
Corrsin, S. 1951 On the spectrum of isotropic temperature fluctuations in an isotropic turbulence. J. Appl. Phys. 22, 469–473.CrossRefGoogle Scholar
Donzis, D. A. & Maqui, A. F. 2016 Statistically steady states of forced isotropic turbulence in thermal equilibrium and non-equilibrium. J. Fluid Mech. 797, 181–200.CrossRefGoogle Scholar
Drivas, T. D. & Eyink, G. L. 2018 An Onsager singularity theorem for turbulent solutions of compressible Euler equations. Commun. Math. Phys. 359, 733–763.CrossRefGoogle Scholar
Eyink, G. L. & Drivas, T. D. 2018 Cascades and dissipative anomalies in compressible fluid turbulence. Phys. Rev. X 8, 011022.Google Scholar
Falkovich, G., Fouxon, I. & Oz, Y. 2010 New relations for correlation functions in Navier–Stokes turbulence. J. Fluid Mech. 644, 465–472.CrossRefGoogle Scholar
Frisch, U. 1995 Turbulence: The Legacy of A. N. Kolmogorov. Cambridge University Press.CrossRefGoogle Scholar
Galtier, S. & Banerjee, S. 2011 Exact relation for correlation functions in compressible isothermal turbulence. Phys. Rev. Lett. 107, 134501.CrossRefGoogle ScholarPubMed
Gauthier, S. 2017 Compressible Rayleigh–Taylor turbulent mixing layer between Newtonian miscible fluids. J. Fluid Mech. 830, 211–256.CrossRefGoogle Scholar
Gotoh, T. & Watanabe, T. 2015 Power and nonpower laws of passive scalar moments convected by isotropic turbulence. Phys. Rev. Lett. 115, 114502.CrossRefGoogle ScholarPubMed
Jagannathan, S. & Donzis, D. A. 2016 Reynolds and Mach number scaling in solenoidally-forced compressible turbulence using high-resolution direct numerical simulations. J. Fluid Mech. 789, 669–707.CrossRefGoogle Scholar
Kovasznay, L. S. G. 1953 Turbulence in supersonic flow. J. Aeronaut. Sci. 20, 657–674.CrossRefGoogle Scholar
Kritsuk, A. G., Wagner, R. & Norman, M. L. 2013 Energy cascade and scaling in supersonic isothermal turbulence. J. Fluid Mech. 729, R1.CrossRefGoogle Scholar
Lele, S. K. 1992 Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 103, 16–42.CrossRefGoogle Scholar
Livescu, D. & Li, Z. 2017 Subgrid-scale backscatter after the shock–turbulence interaction. AIP Conf. Proc. 1793, 150009.CrossRefGoogle Scholar
Obukhov, A. M. 1949 Structure of the temperature field in turbulent flows. Isv. Akad. Nauk SSSR Geogr. Geofiz. 13, 58–69.Google Scholar
Pan, L. & Scannapieco, E. 2010 Mixing in supersonic turbulence. Astrophys. J. 721, 1765–1782.CrossRefGoogle Scholar
Pan, L. & Scannapieco, E. 2011 Passive scalar structures in supersonic turbulence. Phys. Rev. E 83, 045302(R).Google ScholarPubMed
Sagaut, P. & Cambon, C. 2008 Homogeneous Turbulence Dynamics. Cambridge University Press.CrossRefGoogle Scholar
Samtaney, R., Pullin, D. I. & Kosovic, B. 2001 Direct numerical simulation of decaying compressible turbulence and shocklet statistics. Phys. Fluids 13, 1415–1430.CrossRefGoogle Scholar
Sarkar, S., Erlebacher, G., Hussaini, M. Y. & Kreiss, H. O. 1991 The analysis and modelling of dilatational terms in compressible turbulence. J. Fluid Mech. 227, 473–493.CrossRefGoogle Scholar
Sreenivasan, K. R. 1996 The passive scalar spectrum and the Obukhov–Corrsin constant. Phys. Fluids 8, 189–196.CrossRefGoogle Scholar
Suman, S. & Girimaji, S. S. 2011 Dynamical model for velocity-gradient evolution in compressible turbulence. J. Fluid Mech. 683, 289–319.CrossRefGoogle Scholar
Wagner, R., Falkovich, G., Kritsuk, A. G. & Norman, M. L. 2012 Flux correlations in supersonic isothermal turbulence. J. Fluid Mech. 713, 482–490.CrossRefGoogle Scholar
Wang, J., Gotoh, T. & Watanabe, T. 2017 Spectra and statistics in compressible isotropic turbulence. Phys. Rev. Fluids 2, 013403.Google Scholar
Wang, J., Shi, Y., Wang, L.-P., Xiao, Z., He, X. T. & Chen, S. 2011 Effect of shocklets on the velocity gradients in highly compressible isotropic turbulence. Phys. Fluids 23, 125103.CrossRefGoogle Scholar
Wang, J., Shi, Y., Wang, L.-P., Xiao, Z., He, X. T. & Chen, S. 2012 Effect of compressibility on the small scale structures in isotropic turbulence. J. Fluid Mech. 713, 588–631.CrossRefGoogle Scholar
Wang, J., Wan, M., Chen, S. & Chen, S. Y. 2018a Kinetic energy transfer in compressible isotropic turbulence. J. Fluid Mech. 841, 581–613.CrossRefGoogle Scholar
Wang, J., Wan, M., Chen, S., Xie, C. & Chen, S. Y. 2018b Effect of shock waves on the statistics and scaling in compressible isotropic turbulence. Phys. Rev. E 97, 043108.Google Scholar
Wang, J., Wang, L.-P., Xiao, Z., Shi, Y. & Chen, S. 2010 A hybrid numerical simulation of isotropic compressible turbulence. J. Comput. Phys. 229, 5257–5259.CrossRefGoogle Scholar
Wang, J., Yang, Y., Shi, Y., Xiao, Z., He, X. T. & Chen, S. 2013 Cascade of kinetic energy in three-dimensional compressible turbulence. Phys. Rev. Lett. 110, 214505.CrossRefGoogle ScholarPubMed
Yeung, P. K., Donzis, D. A. & Sreenivasan, K. R. 2005 High-Reynolds-number simulation of turbulent mixing. Phys. Fluids 17, 081703.CrossRefGoogle Scholar
Zank, G. P. & Matthaeus, W. H. 1990 Nearly incompressible hydrodynamics and heat conduction. Phys. Rev. Lett. 64, 1243–1246.CrossRefGoogle ScholarPubMed
Zank, G. P. & Matthaeus, W. H. 1991 The equations of nearly incompressible fluids. I. Hydrodynamics, turbulence, and waves. Phys. Fluids A 3, 69–82.CrossRefGoogle Scholar

Full text views

Full text views reflects PDF downloads, PDFs sent to Google Drive, Dropbox and Kindle and HTML full text views.

Total number of HTML views: 31
Total number of PDF views: 436 *
View data table for this chart

* Views captured on Cambridge Core between 20th March 2019 - 6th March 2021. This data will be updated every 24 hours.

13 Cited by

Send article to Kindle

To send this article to your Kindle, first ensure no-reply@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about sending to your Kindle. Find out more about sending to your Kindle.

Note you can select to send to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be sent to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.

Find out more about the Kindle Personal Document Service.

Cascades of temperature and entropy fluctuations in compressible turbulence
Available formats
×

Send article to Dropbox

To send this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your <service> account. Find out more about sending content to Dropbox.

Cascades of temperature and entropy fluctuations in compressible turbulence
Available formats
×

Send article to Google Drive

To send this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your <service> account. Find out more about sending content to Google Drive.

Cascades of temperature and entropy fluctuations in compressible turbulence
Available formats
×
×

Reply to: Submit a response

Your details

Conflicting interests

Do you have any conflicting interests? *