Article contents
Bistabilities in two parallel Kármán wakes
Published online by Cambridge University Press: 19 October 2021
Abstract
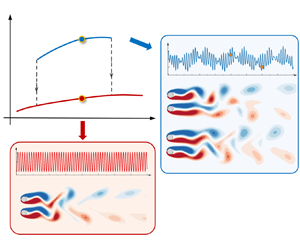
Bistabilities of two equilibrium states discovered in the coupled side-by-side Kármán wakes are investigated through Floquet analysis and direct numerical simulation (DNS) with different initial conditions over a range of gap-to-diameter ratio ( $g^*= 0.2\text {--}3.5$) and Reynolds number (
$g^*= 0.2\text {--}3.5$) and Reynolds number ( $Re = 47\text {--}100$). Two bistabilities are found in the transitional
$Re = 47\text {--}100$). Two bistabilities are found in the transitional  $g^*-Re$ regions from in-phase (IP) to anti-phase (AP) vortex shedding states. By initialising the flow in DNS with zero initial conditions, the flow in the first bistable region (i.e. bistable IP/FF
$g^*-Re$ regions from in-phase (IP) to anti-phase (AP) vortex shedding states. By initialising the flow in DNS with zero initial conditions, the flow in the first bistable region (i.e. bistable IP/FF $_C$ at
$_C$ at  $g^*= 1.4 \text {--} 2.0$, where FF
$g^*= 1.4 \text {--} 2.0$, where FF $_C$ denotes the conditional flip-flop flow) attains flip-flop (FF) flow, it settles into the IP state by initialising the flow with an IP flow. The second bistability is observed between cylinder-scale IP and AP states at large
$_C$ denotes the conditional flip-flop flow) attains flip-flop (FF) flow, it settles into the IP state by initialising the flow with an IP flow. The second bistability is observed between cylinder-scale IP and AP states at large  $g^*$ (
$g^*$ ( $=$ 2.0–3.5). The transition from the FF
$=$ 2.0–3.5). The transition from the FF $_C$ to IP is dependent on initial conditions and irreversible over the parameter space, meaning that the flow cannot revert back to the FF
$_C$ to IP is dependent on initial conditions and irreversible over the parameter space, meaning that the flow cannot revert back to the FF $_C$ state once it jumps to the IP state irrespective of the direction of
$_C$ state once it jumps to the IP state irrespective of the direction of  $Re$ variations. Its counterpart for the bistable IP/AP state is reversible. We also found that the FF
$Re$ variations. Its counterpart for the bistable IP/AP state is reversible. We also found that the FF $_C$ flow in the first bistable region is primarily bifurcated from synchronised AP with cluster-scale features, possibly because the cluster-scale AP flow is inherently unstable to FF flow instabilities. It is demonstrated that the irreversible bistability exists in other interacting wakes around multiple cylinders. A good understanding of flow bistabilities is pivotal to flow control applications and the interpretation of desynchronised flow features observed at high
$_C$ flow in the first bistable region is primarily bifurcated from synchronised AP with cluster-scale features, possibly because the cluster-scale AP flow is inherently unstable to FF flow instabilities. It is demonstrated that the irreversible bistability exists in other interacting wakes around multiple cylinders. A good understanding of flow bistabilities is pivotal to flow control applications and the interpretation of desynchronised flow features observed at high  $Re$ values.
$Re$ values.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
REFERENCES
- 8
- Cited by



