Article contents
An almost subharmonic instability in the flow past rectangular cylinders
Published online by Cambridge University Press: 21 October 2022
Abstract
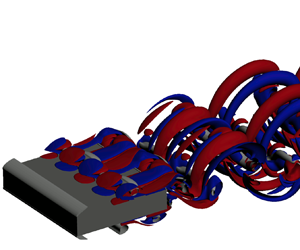
The three-dimensional instability of the flow past a 5 : 1 rectangular cylinder is investigated via Floquet analysis and direct numerical simulations. A quasi-subharmonic (QS) unstable mode is detected, marking an important difference with the flow past bodies with lower aspect ratio and/or with smooth leading edge. The QS mode becomes unstable at Reynolds number (based on the cylinder thickness and free-stream velocity)  $Re \approx 480$; its spanwise wavelength is approximately three times the cylinder thickness. The structural sensitivity locates the wavemaker region over the longitudinal sides of the cylinder, indicating that the instability is triggered by the mutual inviscid interaction of vortices generated by the leading edge shear layer.
$Re \approx 480$; its spanwise wavelength is approximately three times the cylinder thickness. The structural sensitivity locates the wavemaker region over the longitudinal sides of the cylinder, indicating that the instability is triggered by the mutual inviscid interaction of vortices generated by the leading edge shear layer.
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
References
REFERENCES
- 3
- Cited by



