New Frontiers in Applied Probability (Journal of Applied Probability Special Volume 48A)
Other
Søren Asmussen
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. vii-ix
-
- Article
-
- You have access
- Export citation
Publications of Søren Asmussen
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. xi-xviii
-
- Article
-
- You have access
- Export citation
Part 1. Risk Theory
Ruin excursions, the G/G/∞ queue, and tax payments in renewal risk models
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 3-14
-
- Article
-
- You have access
- Export citation
On the ruin probability of the generalised Ornstein–Uhlenbeck process in the cramér case
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 15-28
-
- Article
-
- You have access
- Export citation
Threshold strategies for risk processes and their relation to queueing theory
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 29-38
-
- Article
-
- You have access
- Export citation
Ruin probabilities in a diffusion environment
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 39-50
-
- Article
-
- You have access
- Export citation
Exit times for a class of random walks exact distribution results
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 51-63
-
- Article
-
- You have access
- Export citation
Asymptotics of conditional moments of the summand in Poisson compounds
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 65-76
-
- Article
-
- You have access
- Export citation
Part 2. Lévy Processes
On the excursions of reflected local-time processes and stochastic fluid queues
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 79-98
-
- Article
-
- You have access
- Export citation
Loss rate for a general Lévy process with downward periodic barrier
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 99-108
-
- Article
-
- You have access
- Export citation
A piecewise linear stochastic differential equation driven by a Lévy process
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 109-119
-
- Article
-
- You have access
- Export citation
Part 3. Heavy Tail Phenomena
Characterization of tails through hazard rate and convolution closure properties
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 123-132
-
- Article
-
- You have access
- Export citation
A large deviation principle for Minkowski sums of heavy-tailed random compact convex sets with finite expectation
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 133-144
-
- Article
-
- You have access
- Export citation
Part 4. Simulation
Efficient simulation of tail probabilities of sums of dependent random variables
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 147-164
-
- Article
-
- You have access
- Export citation
On exact sampling of stochastic perpetuities
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 165-182
-
- Article
-
- You have access
- Export citation
A comparison of cross-entropy and variance minimization strategies
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 183-194
-
- Article
-
- You have access
- Export citation
Checkpointing for the RESTART problem in Markov networks
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 195-207
-
- Article
-
- You have access
- Export citation
Exact simulation of the stationary distribution of the FIFO M/G/c queue
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 209-213
-
- Article
-
- You have access
- Export citation
Part 5. Stochastic Growth and Branching
On some tractable growth-collapse processes with renewal collapse epochs
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 217-234
-
- Article
-
- You have access
- Export citation
The size of a major epidemic of a vector-borne disease
- Part of:
-
- Published online by Cambridge University Press:
- 14 July 2016, pp. 235-247
-
- Article
-
- You have access
- Export citation



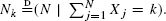 In particular, we want to know the asymptotic behavior of the conditional mean E
In particular, we want to know the asymptotic behavior of the conditional mean E