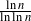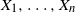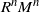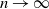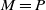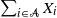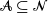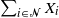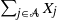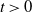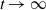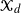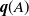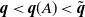Research Papers
Oscillations for order statistics of some discrete processes
- Part of:
-
- Published online by Cambridge University Press:
- 04 September 2020, pp. 703-719
-
- Article
- Export citation
Perron–Frobenius theory for kernels and Crump–Mode–Jagers processes with macro-individuals
- Part of:
-
- Published online by Cambridge University Press:
- 04 September 2020, pp. 720-733
-
- Article
- Export citation
On branching models with alarm triggerings
- Part of:
-
- Published online by Cambridge University Press:
- 04 September 2020, pp. 734-759
-
- Article
- Export citation
Explicit results on conditional distributions of generalized exponential mixtures
- Part of:
-
- Published online by Cambridge University Press:
- 04 September 2020, pp. 760-774
-
- Article
- Export citation
Existence of Gibbs point processes with stable infinite range interaction
- Part of:
-
- Published online by Cambridge University Press:
- 04 September 2020, pp. 775-791
-
- Article
- Export citation
Stochastically modeled weakly reversible reaction networks with a single linkage class
- Part of:
-
- Published online by Cambridge University Press:
- 04 September 2020, pp. 792-810
-
- Article
- Export citation
The probabilities of extinction in a branching random walk on a strip
- Part of:
-
- Published online by Cambridge University Press:
- 04 September 2020, pp. 811-831
-
- Article
- Export citation
Stochastic comparisons of largest-order statistics for proportional reversed hazard rate model and applications
- Part of:
-
- Published online by Cambridge University Press:
- 04 September 2020, pp. 832-852
-
- Article
- Export citation
Strong convergence of infinite color balanced urns under uniform ergodicity
- Part of:
-
- Published online by Cambridge University Press:
- 04 September 2020, pp. 853-865
-
- Article
- Export citation
On some threshold-one attractive interacting particle systems on homogeneous trees
- Part of:
-
- Published online by Cambridge University Press:
- 04 September 2020, pp. 866-898
-
- Article
- Export citation
On the behavior of the failure rate and reversed failure rate in engineering systems
- Part of:
-
- Published online by Cambridge University Press:
- 04 September 2020, pp. 899-910
-
- Article
- Export citation
Trees grown under young-age preferential attachment
- Part of:
-
- Published online by Cambridge University Press:
- 04 September 2020, pp. 911-927
-
- Article
- Export citation
Decorrelation of a class of Gibbs particle processes and asymptotic properties of U-statistics
- Part of:
-
- Published online by Cambridge University Press:
- 04 September 2020, pp. 928-955
-
- Article
- Export citation
Flooding and diameter in general weighted random graphs
- Part of:
-
- Published online by Cambridge University Press:
- 04 September 2020, pp. 956-980
-
- Article
- Export citation
Randomised rules for stopping problems
- Part of:
-
- Published online by Cambridge University Press:
- 04 September 2020, pp. 981-1004
-
- Article
- Export citation
On moderate deviations in Poisson approximation
- Part of:
-
- Published online by Cambridge University Press:
- 04 September 2020, pp. 1005-1027
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
JPR volume 57 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 04 September 2020, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
JPR volume 57 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 04 September 2020, pp. b1-b2
-
- Article
-
- You have access
- Export citation