Hostname: page-component-8448b6f56d-42gr6 Total loading time: 0 Render date: 2024-04-20T14:23:23.902Z Has data issue: false hasContentIssue false
  • English
  • Français

Lyapunov-type conditions for non-strong ergodicity of Markov processes

Part of: Markov processes Stochastic processes

Published online by Cambridge University Press:  25 February 2021

Yong-Hua Mao  and
Tao Wang
Yong-Hua Mao*
Affiliation:
Beijing Normal University
Tao Wang*
Affiliation:
Beijing Normal University
*
*Postal address: School of Mathematical Sciences, Laboratory of Mathematics and Complex Systems, Ministry of Education, Beijing100875, People’s Republic of China.
*Postal address: School of Mathematical Sciences, Laboratory of Mathematics and Complex Systems, Ministry of Education, Beijing100875, People’s Republic of China.
Get access Rights & Permissions [Opens in a new window]

Abstract

We present Lyapunov-type conditions for non-strong ergodicity of Markov processes. Some concrete models are discussed, including diffusion processes on Riemannian manifolds and Ornstein–Uhlenbeck processes driven by symmetric $\alpha$-stable processes. In particular, we show that any process of d-dimensional Ornstein–Uhlenbeck type driven by $\alpha$-stable noise is not strongly ergodic for every 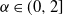$\alpha\in (0,2]$.

Keywords

Non-strong ergodicityLyapunov-type functiondiffusion processOrnstein–Uhlenbeck processα-stable process

MSC classification

Primary: 60J25: Continuous-time Markov processes on general state spaces
Secondary: 60J60: Diffusion processes 60G51: Processes with independent increments; L'evy processes
Type
Research Papers
Information
Journal of Applied Probability , Volume 58 , Issue 1 , March 2021 , pp. 238 - 253
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramowitz, M. and Stegun, I. A. (eds) (1984). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. John Wiley & Sons Inc., New York.Google Scholar
Chen, M. F. (2004). From Markov Chains to Non-Equilibrium Particle Systems. World Scientific, Singapore.CrossRefGoogle Scholar
Chen, M. F. (2005). Eigenvalues, Inequalities, and Ergodic Theory. Springer, London.Google Scholar
Chen, Z. Q. and Wang, J. (2014). Ergodicity for time-changed symmetric stable processes. Stoch. Process. Appl. 124, 2799–2823.CrossRefGoogle Scholar
Down, D. Meyn, S. P. and Tweedie, R. T. (1995). Exponential and uniform ergodicity of Markov processes. Ann. Prob. 23, 1671–1691.CrossRefGoogle Scholar
Fayolle, G. Malyshev, V. A. and Menshikov M. V. (1995). Random walks in a quarter plane with zero drifts I: Ergodicity and null recurrence. Ann. Inst. H. Poincaré Prob. Statist. 28, 179–194.Google Scholar
Mao, Y. H. (2002). Strong ergodicity for Markov processes by coupling methods. J. Appl. Prob. 39, 839–852.CrossRefGoogle Scholar
Mao, Y. H. (2006). Convergence rates in strong ergodicity for Markov processes. Stoch. Process. Appl. 116, 1964–1976.CrossRefGoogle Scholar
Menshikov, M. and Petritis, D. (2014). Explosion, implosion, and moments of passage times for continuous-time Markov chains: A semimartingale approach. Stoch. Process. Appl. 124, 2388–2414.CrossRefGoogle Scholar
Meyn, S. P. and Tweedie, R. T. (1993). Markov Chains and Stochastic Stability. Springer, London.CrossRefGoogle Scholar
Meyn, S. P. and Tweedie, R. T. (1993). Stability of Markovian processes III: Foster–Lyapunov criteria for continuous-time processes. Adv. Appl. Prob. 25, 518–548.CrossRefGoogle Scholar
Pinsky Ross, G. (1995). Positive Harmonic Functions and Diffusion. Cambridge University Press.CrossRefGoogle Scholar
Sandrić, N. (2013). Long-time behavior of stable-like processes. Stoch. Process. Appl. 123, 1276–1300.CrossRefGoogle Scholar
Stramer, O. and Tweedie, R. T. (1994). Stability and instability of continuous-time Markov processes. In Probability, Statistics and Optimisation, ed. N. H. Bingham, Wiley, Chichester, pp. 173–184.Google Scholar
Wang, J. (2012). On the exponential ergodicity for Lévy driven Ornstein–Uhlenbeck processes. J. Appl. Prob. 49, 990–1104.CrossRefGoogle Scholar
Wang, J. (2013). Exponential ergodicity and strong ergodicity for SDEs driven by symmetric α-stable processes. Appl. Math. Lett. 26, 654–658.CrossRefGoogle Scholar
Zhang, Y. H. (2001). Strong ergodicity for single birth processes. J. Appl. Prob. 38, 270–277.CrossRefGoogle Scholar