Hostname: page-component-76fb5796d-25wd4 Total loading time: 0 Render date: 2024-04-25T16:43:40.866Z Has data issue: false hasContentIssue false
  • English
  • Français

Generalizations of forest fires with ignition at the origin

Part of: Time-dependent statistical mechanics (dynamic and nonequilibrium) Special processes

Published online by Cambridge University Press:  24 October 2022

Francis Comets ,
Mikhail Menshikov  and
Stanislav Volkov Open the ORCID record for Stanislav Volkov [Opens in a new window]
Francis Comets
Affiliation:
Université de Paris
Mikhail Menshikov*
Affiliation:
Durham University
Stanislav Volkov*
Affiliation:
Lund University
*
*Postal address: Department of Mathematical Sciences, Durham University, DH1 3LE, UK. Email address: mikhail.menshikov@durham.ac.uk
**Postal address: Centre for Mathematical Sciences, Lund University, SE-22100, Sweden. Email address: stanislav.volkov@matstat.lu.se
Get access Rights & Permissions [Opens in a new window]

Abstract

We study generalizations of the forest fire model introduced in [4] and [10] by allowing the rates at which the trees grow to depend on their location, introducing long-range burning, as well as a continuous-space generalization of the model. We establish that in all the models in consideration the expected time required to reach a site at distance x from the origin is of order 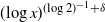$(\!\log x)^{(\!\log 2)^{-1}+\delta}$ for any 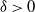$\delta>0$ .

Keywords

Forest fire modellong-range interactionstime-dependent percolationself-organized criticality

MSC classification

Primary: 60K35: Interacting random processes; statistical mechanics type models; percolation theory
Secondary: 82C43: Time-dependent percolation 92D25: Population dynamics (general)
Type
Original Article
Information
Journal of Applied Probability , Volume 60 , Issue 2 , June 2023 , pp. 418 - 434
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Asmussen, S., Ivanovs, J. and Rønn Nielsen, A. (2017). Time inhomogeneity in longest gap and longest run problems. Stoch. Process. Appl. 127, 574–589.CrossRefGoogle Scholar
van den Berg, J. and Brouwer, R. (2006). Self-organized forest-fires near the critical time. Commun. Math. Phys. 267, 265–277.CrossRefGoogle Scholar
van den Berg, J. and Járai, A. A. (2005). On the asymptotic density in a one-dimensional self-organized critical forest-fire model. Commun. Math. Phys. 253, 633–644.CrossRefGoogle Scholar
van den Berg, J. and Tóth, B. (2001). A signal-recovery system: asymptotic properties, and construction of an infinite-volume process. Stoch. Process. Appl. 96, 177–190.CrossRefGoogle Scholar
Bressaud, X. and Fournier, N. (2013). One-Dimensional General Forest Fire Processes (Mémoires de la Société Mathématique de France 132). Société Mathématique de France.CrossRefGoogle Scholar
Crane, E., Freeman, N. and Tóth, B. (2015). Cluster growth in the dynamical Erdős–Rényi process with forest fires. Electron. J. Prob. 20, 33.CrossRefGoogle Scholar
den Hollander, F. (2000). Large Deviations (Fields Institute Monographs 14). American Mathematical Society.Google Scholar
Kiss, D., Manolescu, I. and Sidoravicius, V. (2015). Planar lattices do not recover from forest fires. Ann. Prob. 43, 3216–3238.CrossRefGoogle Scholar
Martin, J. and Ráth, B. (2017). Rigid representations of the multiplicative coalescent with linear deletion. Electron. J. Prob. 22, 47.CrossRefGoogle Scholar
Volkov, S. (2009). Forest fires on $\mathbb{Z}_+$ with ignition only at 0. ALEA Lat. Am. J. Prob. Math. Statist. 6, 399–414.Google Scholar