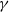1. Introduction
Stochastic dominance has been studied extensively in applied probability, particularly in the financial and economic literature concerning investment decision-making under uncertainty. The concept of stochastic dominance is quite old and has served as one of the main ways to rank risk prospects or distributions. Of special importance are first-order stochastic dominance (FSD) and second-order stochastic dominance (SSD). We refer the reader to [Reference Levy15], [Reference Müller and Stoyan24], and [Reference Shaked and Shanthikumar26] for an overview of the SD relations and other stochastic orders. The stochastic dominance relation has an equivalent characterization by a certain class of utility functions. Let X and Y be two random variables (risk prospects). Y dominates X in the FSD means that
![]() $\mathbb{E} u(Y)\ge \mathbb{E} u(X)$
for all increasing utility functions u for which the expectations exist, and Y dominates X in the SSD means that
$\mathbb{E} u(Y)\ge \mathbb{E} u(X)$
for all increasing utility functions u for which the expectations exist, and Y dominates X in the SSD means that
![]() $\mathbb{E} u(Y)\ge \mathbb{E} u(X)$
for all increasing and concave utilityfunctions u.
$\mathbb{E} u(Y)\ge \mathbb{E} u(X)$
for all increasing and concave utilityfunctions u.
In the literature of expected utility theory, it is known that a utility function with local convexities is able to explain many individual behaviors, for example, many people buy insurance and also gamble; see [Reference Baucells and Heukamp2], [Reference Friedman and Savage11], [Reference Kahneman and Tversky13], [Reference Markowitz21], among others. Motivated by this, Huang, Tzeng, and Zhao [Reference Huang, Tzeng and Zhao12] and Müller, Scarsini, Tsetlin, and Winkler [Reference Müller, Scarsini and Tsetlin25] proposed two notions of fractional SD, both serving a continuum of FSD and SSD. However, their approaches are different. For
![]() $\gamma\in [0,1]$
, Müller et al. [Reference Müller, Scarsini and Tsetlin25] developed one notion of
$\gamma\in [0,1]$
, Müller et al. [Reference Müller, Scarsini and Tsetlin25] developed one notion of
![]() $(1+\gamma)$
-stochastic dominance, denoted by
$(1+\gamma)$
-stochastic dominance, denoted by
![]() $(1+\gamma)$
-SD, by adding constraints to the ratio of marginal utilities. The formal definition of
$(1+\gamma)$
-SD, by adding constraints to the ratio of marginal utilities. The formal definition of
![]() $(1+\gamma)$
-SD will be given in Definition 2.1. Huang et al. [Reference Huang, Tzeng and Zhao12] introduced another notion of fractional SD, denoted by
$(1+\gamma)$
-SD will be given in Definition 2.1. Huang et al. [Reference Huang, Tzeng and Zhao12] introduced another notion of fractional SD, denoted by
![]() $(1+\eta)_{{}_{\mathrm{HTZ}}}$
-SD, by adding constraints to the lower bound of the Arrow–Pratt index of absolute risk aversion, where
$(1+\eta)_{{}_{\mathrm{HTZ}}}$
-SD, by adding constraints to the lower bound of the Arrow–Pratt index of absolute risk aversion, where
![]() $\eta\in [0,1]$
. Both the degree parameters
$\eta\in [0,1]$
. Both the degree parameters
![]() $\gamma$
and
$\gamma$
and
![]() $\eta$
have intuitive interpretations. Compared with [Reference Müller, Scarsini and Tsetlin25], the approach of [Reference Huang, Tzeng and Zhao12] can be used to introduce
$\eta$
have intuitive interpretations. Compared with [Reference Müller, Scarsini and Tsetlin25], the approach of [Reference Huang, Tzeng and Zhao12] can be used to introduce
![]() $(n+\eta)$
th-degree SD between nth-degree SD and
$(n+\eta)$
th-degree SD between nth-degree SD and
![]() $(n+1)$
th-degree SD, where
$(n+1)$
th-degree SD, where
![]() $\eta\in [0,1]$
and n is any positive integer. It should be pointed out that, for
$\eta\in [0,1]$
and n is any positive integer. It should be pointed out that, for
![]() $\gamma\in [0,1]$
, the notion of
$\gamma\in [0,1]$
, the notion of
![]() $\gamma$
-risk aversion introduced in [Reference Mao and Wang20] is equivalent to consistency with
$\gamma$
-risk aversion introduced in [Reference Mao and Wang20] is equivalent to consistency with
![]() $(1+\gamma)$
-SD of [Reference Müller, Scarsini and Tsetlin25].
$(1+\gamma)$
-SD of [Reference Müller, Scarsini and Tsetlin25].
The purpose of this paper is to investigate further properties of
![]() $(1+\gamma)$
-SD in the sense of [Reference Müller, Scarsini and Tsetlin25]. The rest of this paper is organized as follows. Section 2 recalls from [Reference Müller, Scarsini and Tsetlin25] the definition of
$(1+\gamma)$
-SD in the sense of [Reference Müller, Scarsini and Tsetlin25]. The rest of this paper is organized as follows. Section 2 recalls from [Reference Müller, Scarsini and Tsetlin25] the definition of
![]() $(1+\gamma)$
-SD and its basic properties, including the characterization theorem in terms of integral conditions of distribution functions or their inverse functions and closure properties under transformation and mixture. In this section we also introduce the concept of
$(1+\gamma)$
-SD and its basic properties, including the characterization theorem in terms of integral conditions of distribution functions or their inverse functions and closure properties under transformation and mixture. In this section we also introduce the concept of
![]() $(1+\gamma)$
-pure stochastic dominance, denoted by
$(1+\gamma)$
-pure stochastic dominance, denoted by
![]() $(1+\gamma)$
‐PSD, which will enable one to understand
$(1+\gamma)$
‐PSD, which will enable one to understand
![]() $(1+\gamma)$
-SD. Section 3 consists of the main results of this paper, including the generating processes of
$(1+\gamma)$
-SD. Section 3 consists of the main results of this paper, including the generating processes of
![]() $(1+\gamma)$
-PSD via
$(1+\gamma)$
-PSD via
![]() $\gamma$
-transfers of probability, Yaari’s dual characterization by utilizing the special class of distortion functions, the separation theorem in terms of FSD and
$\gamma$
-transfers of probability, Yaari’s dual characterization by utilizing the special class of distortion functions, the separation theorem in terms of FSD and
![]() $(1+\gamma)$
-PSD, Strassen’s representation, and bivariate characterization of
$(1+\gamma)$
-PSD, Strassen’s representation, and bivariate characterization of
![]() $(1+\gamma)$
-SD. Applications of the main results are given in Section 4. We establish several closure properties of
$(1+\gamma)$
-SD. Applications of the main results are given in Section 4. We establish several closure properties of
![]() $(1+\gamma)$
-SD under p-quantile truncation, under comonotonic sums, and under distortion, as well as its equivalence characterization. Examples of distributions ordered in the sense of
$(1+\gamma)$
-SD under p-quantile truncation, under comonotonic sums, and under distortion, as well as its equivalence characterization. Examples of distributions ordered in the sense of
![]() $(1+\gamma)$
-SD are provided in Section 5.
$(1+\gamma)$
-SD are provided in Section 5.
Throughout this paper, let
![]() $(\Omega, \mathcal{A}, \mathbb{P})$
be a probability space, and let
$(\Omega, \mathcal{A}, \mathbb{P})$
be a probability space, and let
![]() $L^1=L^1(\Omega,\mathcal{A}, \mathbb{P})$
be the set of all random variables in the probability space with finite expectations. For any distribution function F, the inverse
$L^1=L^1(\Omega,\mathcal{A}, \mathbb{P})$
be the set of all random variables in the probability space with finite expectations. For any distribution function F, the inverse
![]() $F^{-1}$
of F is taken to be the left continuous version defined by
$F^{-1}$
of F is taken to be the left continuous version defined by
with
![]() $F^{-1}(0)=\inf\{x\colon F(x)>0\}$
. For any
$F^{-1}(0)=\inf\{x\colon F(x)>0\}$
. For any
![]() $x\in\mathbb{R}$
,
$x\in\mathbb{R}$
,
![]() $x_+=\max\{x, 0\}$
and
$x_+=\max\{x, 0\}$
and
![]() $x_-=\max\{-x, 0\}$
. All expectations are implicitly assumed to exist whenever they are written.
$x_-=\max\{-x, 0\}$
. All expectations are implicitly assumed to exist whenever they are written.
2. Preliminaries
2.1. Definitions
The following definition of stochastic dominance of order
![]() $(1+\gamma)$
was given in [Reference Müller, Scarsini and Tsetlin25]. We first introduce the following notation. Let
$(1+\gamma)$
was given in [Reference Müller, Scarsini and Tsetlin25]. We first introduce the following notation. Let
![]() $\mathcal U$
be the set of all increasing functions on
$\mathcal U$
be the set of all increasing functions on
![]() $\mathbb{R}$
. For
$\mathbb{R}$
. For
![]() $\gamma\in [0,1]$
, define
$\gamma\in [0,1]$
, define
Definition 2.1. ([Reference Müller, Scarsini and Tsetlin25].)Let X and Y be two random variables in
![]() $\mathbb{R}$
. We say that X is dominated by Y in stochastic dominance of order
$\mathbb{R}$
. We say that X is dominated by Y in stochastic dominance of order
![]() $(1+\gamma)$
, denoted by
$(1+\gamma)$
, denoted by
![]() $X\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} Y$
, if
$X\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} Y$
, if
The order
![]() $\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}}$
cannot be defined for any
$\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}}$
cannot be defined for any
![]() $\gamma>1$
because
$\gamma>1$
because
![]() $\mathcal U_\gamma$
is empty except for constant functions in this case. For
$\mathcal U_\gamma$
is empty except for constant functions in this case. For
![]() $0\le \gamma_1<\gamma_2\le 1$
,
$0\le \gamma_1<\gamma_2\le 1$
,
![]() $X\preccurlyeq_{\mathrm{(1+\gamma_1)\hbox{-}SD}} Y$
implies
$X\preccurlyeq_{\mathrm{(1+\gamma_1)\hbox{-}SD}} Y$
implies
![]() $X\preccurlyeq_{\mathrm{(1+\gamma_2)\hbox{-}SD}} Y$
since
$X\preccurlyeq_{\mathrm{(1+\gamma_2)\hbox{-}SD}} Y$
since
![]() $\mathcal U_{\gamma_2} \subseteq \mathcal U_{\gamma_1}$
. This means that lower-degree stochastic dominance always implies higher-degree stochastic dominance. In Definition 2.1, the class
$\mathcal U_{\gamma_2} \subseteq \mathcal U_{\gamma_1}$
. This means that lower-degree stochastic dominance always implies higher-degree stochastic dominance. In Definition 2.1, the class
![]() $\mathcal U_\gamma$
of functions can be replaced by
$\mathcal U_\gamma$
of functions can be replaced by
![]() $\mathcal U_\gamma^\ast$
defined by
$\mathcal U_\gamma^\ast$
defined by
It is obvious that
![]() $\preccurlyeq_{\mathrm{1\hbox{-}SD}}$
is equivalent to FSD while
$\preccurlyeq_{\mathrm{1\hbox{-}SD}}$
is equivalent to FSD while
![]() $\preccurlyeq_{\mathrm{2\hbox{-}SD}}$
is equivalent to SSD. The orders
$\preccurlyeq_{\mathrm{2\hbox{-}SD}}$
is equivalent to SSD. The orders
![]() $\preccurlyeq_{\mathrm{1\hbox{-}SD}}$
and
$\preccurlyeq_{\mathrm{1\hbox{-}SD}}$
and
![]() $\preccurlyeq_{\mathrm{2\hbox{-}SD}}$
are also denoted by
$\preccurlyeq_{\mathrm{2\hbox{-}SD}}$
are also denoted by
![]() $\preccurlyeq_{\mathrm{FSD}}$
and
$\preccurlyeq_{\mathrm{FSD}}$
and
![]() $\preccurlyeq_{\mathrm{SSD}}$
, respectively. Thus
$\preccurlyeq_{\mathrm{SSD}}$
, respectively. Thus
![]() $(1+\gamma)$
-SD establishes an interpolation between FSD and SSD. For more properties of FSD, SSD, and other related stochastic orders, refer to [Reference Müller and Stoyan24] and [Reference Shaked and Shanthikumar26].
$(1+\gamma)$
-SD establishes an interpolation between FSD and SSD. For more properties of FSD, SSD, and other related stochastic orders, refer to [Reference Müller and Stoyan24] and [Reference Shaked and Shanthikumar26].
To investigate the properties of
![]() $(1+\gamma)$
-SD, we introduce the following
$(1+\gamma)$
-SD, we introduce the following
![]() $(1+\gamma)$
-pure stochastic dominance, denoted by
$(1+\gamma)$
-pure stochastic dominance, denoted by
![]() $(1+\gamma)$
-PSD.
$(1+\gamma)$
-PSD.
Definition 2.2. Let
![]() $X,Y\in L^1$
, and define
$X,Y\in L^1$
, and define
with the convention that
![]() $0/0=0$
. X is said to be smaller than Y in the pure stochastic dominance of order
$0/0=0$
. X is said to be smaller than Y in the pure stochastic dominance of order
![]() $(1+\gamma)$
if
$(1+\gamma)$
if
![]() $\gamma\in [0,1]$
and
$\gamma\in [0,1]$
and
![]() $X\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} Y$
. We denote this by
$X\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} Y$
. We denote this by
![]() $X\preccurlyeq_{\mathrm{(1+\gamma)-PSD}} Y$
.
$X\preccurlyeq_{\mathrm{(1+\gamma)-PSD}} Y$
.
In fact (2.1) can be replaced by
The motivation of the constraint condition (2.1) or (2.1) comes from Proposition 2.1, which gives a characterization of the order
![]() $\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}}$
. For
$\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}}$
. For
![]() $\gamma=1$
, (2.1) is equivalent to
$\gamma=1$
, (2.1) is equivalent to
![]() $\mathbb{E}[X]=\mathbb{E}[Y]$
. Thus 2-PSD is exactly the concave order. Equation (2.1) appears to be similar to that used in [Reference Leshno and Levy14] to define
$\mathbb{E}[X]=\mathbb{E}[Y]$
. Thus 2-PSD is exactly the concave order. Equation (2.1) appears to be similar to that used in [Reference Leshno and Levy14] to define
![]() $\epsilon$
-almost FSD as follows: Y dominates X by
$\epsilon$
-almost FSD as follows: Y dominates X by
![]() $\epsilon$
-almost FSD, denoted by
$\epsilon$
-almost FSD, denoted by
![]() $X\preccurlyeq_1^{{\mathrm{almost}}(\epsilon)} Y$
, if and only if
$X\preccurlyeq_1^{{\mathrm{almost}}(\epsilon)} Y$
, if and only if
where
![]() $0<\epsilon<1/2$
. Therefore
$0<\epsilon<1/2$
. Therefore
![]() $X\preccurlyeq_{\mathrm{(1+\gamma)-PSD}} Y$
implies
$X\preccurlyeq_{\mathrm{(1+\gamma)-PSD}} Y$
implies
![]() $X\preccurlyeq_1^{{\mathrm{almost}}(\epsilon)} Y$
with
$X\preccurlyeq_1^{{\mathrm{almost}}(\epsilon)} Y$
with
![]() $\epsilon={\gamma}/{(1+\gamma)}$
. However, the converse is not true.
$\epsilon={\gamma}/{(1+\gamma)}$
. However, the converse is not true.
Hence
![]() $(1+\gamma)$
-PSD enables one to understand
$(1+\gamma)$
-PSD enables one to understand
![]() $(1+\gamma)$
-SD well. First,
$(1+\gamma)$
-SD well. First,
![]() $(1+\gamma)$
-PSD can be used to characterize
$(1+\gamma)$
-PSD can be used to characterize
![]() $(1+\gamma)$
-SD (see Theorem 3.2). Second, if Y dominates X in
$(1+\gamma)$
-SD (see Theorem 3.2). Second, if Y dominates X in
![]() $(1+\gamma)$
-SD, and if there does not exist
$(1+\gamma)$
-SD, and if there does not exist
![]() $Z\in L^1$
, not identically distributed with Y, such that Y dominates Z in the FSD and Z dominates X in
$Z\in L^1$
, not identically distributed with Y, such that Y dominates Z in the FSD and Z dominates X in
![]() $(1+\gamma)$
-SD, then Y dominates X in
$(1+\gamma)$
-SD, then Y dominates X in
![]() $(1+\gamma)$
-PSD (seeRemark 3.4). These two points are the motivation for us to introduce
$(1+\gamma)$
-PSD (seeRemark 3.4). These two points are the motivation for us to introduce
![]() $(1+\gamma)$
-PSD.
$(1+\gamma)$
-PSD.
It should be pointed out that the order
![]() $\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}PSD}}$
for
$\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}PSD}}$
for
![]() $\gamma\in (0,1)$
is not a partial order because it does not possess transitivity, as illustrated by the following example.
$\gamma\in (0,1)$
is not a partial order because it does not possess transitivity, as illustrated by the following example.
Example 2.1. Let X, Y, and Z be three random variables with probability mass functions (PMFs)
![]() $\mathbb{P}(X=-1)=0.4$
,
$\mathbb{P}(X=-1)=0.4$
,
![]() $\mathbb{P}(X=2)=0.1$
,
$\mathbb{P}(X=2)=0.1$
,
![]() $\mathbb{P}(X=3)=0.5$
,
$\mathbb{P}(X=3)=0.5$
,
![]() $\mathbb{P}(Y=0)=\mathbb{P}(Y=3)=1/2$
, and
$\mathbb{P}(Y=0)=\mathbb{P}(Y=3)=1/2$
, and
![]() $\mathbb{P}(Z=2)=1$
. By Theorem 2.7 in [Reference Müller, Scarsini and Tsetlin25], it can be seen from the probability mass movement illustrated in Figure 1 that
$\mathbb{P}(Z=2)=1$
. By Theorem 2.7 in [Reference Müller, Scarsini and Tsetlin25], it can be seen from the probability mass movement illustrated in Figure 1 that
However,
This means that the order
![]() $\preccurlyeq_{\mathrm{(1\,+\,1/2)\hbox{-}PSD}}$
does not possess transitivity.
$\preccurlyeq_{\mathrm{(1\,+\,1/2)\hbox{-}PSD}}$
does not possess transitivity.

Figure 1. Probability mass movement from Z to Y and then to X.
Let
![]() $X\sim F$
and
$X\sim F$
and
![]() $Y\sim G$
. For convenience, we will write
$Y\sim G$
. For convenience, we will write
![]() $X\preccurlyeq_{\mathrm{order}} Y$
and
$X\preccurlyeq_{\mathrm{order}} Y$
and
![]() $F\preccurlyeq_{\mathrm{order}} G$
interchangeably for any order relation
$F\preccurlyeq_{\mathrm{order}} G$
interchangeably for any order relation
![]() $\preccurlyeq_{\mathrm{order}}$
.
$\preccurlyeq_{\mathrm{order}}$
.
2.2. Basic properties
In this subsection we list three basic properties of
![]() $(1+\gamma)$
-SD from [Reference Müller, Scarsini and Tsetlin25]. The first characterizes
$(1+\gamma)$
-SD from [Reference Müller, Scarsini and Tsetlin25]. The first characterizes
![]() $(1+\gamma)$
-SD by using integral conditions, and the second and third are concerned with preservation properties of
$(1+\gamma)$
-SD by using integral conditions, and the second and third are concerned with preservation properties of
![]() $(1+\gamma)$
-SD under transformations and under mixture, respectively.
$(1+\gamma)$
-SD under transformations and under mixture, respectively.
Proposition 2.1. ([Reference Müller, Scarsini and Tsetlin25].)Let F and G be the distribution functions of X and Y, respectively. For
![]() $\gamma\in [0,1]$
,
$\gamma\in [0,1]$
,
![]() $X\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}{\rm SD}}} Y$
if and only if
$X\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}{\rm SD}}} Y$
if and only if
or, equivalently,
In view ofProposition 2.1, it is seen that
![]() $X\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}PSD}} Y$
if and only if (2.1) and
$X\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}PSD}} Y$
if and only if (2.1) and
Proposition 2.2. ([Reference Müller, Scarsini and Tsetlin25].)If
![]() $X\preccurlyeq_{\mathrm{(1+\gamma_1\gamma_2)\hbox{-}{\rm SD}}} Y$
for
$X\preccurlyeq_{\mathrm{(1+\gamma_1\gamma_2)\hbox{-}{\rm SD}}} Y$
for
![]() $\gamma_1, \gamma_2\in [0,1]$
, then
$\gamma_1, \gamma_2\in [0,1]$
, then
![]() $u(X) \preccurlyeq_{\mathrm{(1+\gamma_2)\hbox{-}{\rm SD}}} u(Y)$
for all
$u(X) \preccurlyeq_{\mathrm{(1+\gamma_2)\hbox{-}{\rm SD}}} u(Y)$
for all
![]() $u\in \mathcal{U}_{\gamma_1}$
.
$u\in \mathcal{U}_{\gamma_1}$
.
Proposition 2.3. ([Reference Müller, Scarsini and Tsetlin25].)If random variables X, Y, and
![]() $\Theta$
satisfy
$\Theta$
satisfy
for some
![]() $\gamma\in [0,1]$
and all
$\gamma\in [0,1]$
and all
![]() $\theta$
in the support of
$\theta$
in the support of
![]() $\Theta$
, then
$\Theta$
, then
![]() $X \preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}{\rm SD}}} Y$
.
$X \preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}{\rm SD}}} Y$
.
Immediate consequences of Proposition 2.3 are as follows. (i) Let
![]() $F_i$
and
$F_i$
and
![]() $G_i$
be the distribution functions of
$G_i$
be the distribution functions of
![]() $X_i$
and
$X_i$
and
![]() $Y_i$
, respectively. For
$Y_i$
, respectively. For
![]() $\alpha\in (0,1)$
, assume that
$\alpha\in (0,1)$
, assume that
![]() $Z_1\sim \alpha F_1 + (1-\alpha)F_2$
and
$Z_1\sim \alpha F_1 + (1-\alpha)F_2$
and
![]() $Z_2\sim \alpha G_1 + (1-\alpha)G_2$
. If
$Z_2\sim \alpha G_1 + (1-\alpha)G_2$
. If
![]() $X_i\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} Y_i$
for
$X_i\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} Y_i$
for
![]() $i=1, 2$
, then
$i=1, 2$
, then
![]() $Z_1 \preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} Z_2$
. (ii) Let
$Z_1 \preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} Z_2$
. (ii) Let
![]() $X_1$
and
$X_1$
and
![]() $X_2$
be independent, and let
$X_2$
be independent, and let
![]() $Y_1$
and
$Y_1$
and
![]() $Y_2$
be independent. If
$Y_2$
be independent. If
![]() $X_i\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} Y_i$
for
$X_i\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} Y_i$
for
![]() $i=1, 2$
, then
$i=1, 2$
, then
3. Further properties
3.1. Generating processes
For a better understanding of
![]() $(1+\gamma)$
-SD and
$(1+\gamma)$
-SD and
![]() $(1+\gamma)$
-PSD, we recall the definition of
$(1+\gamma)$
-PSD, we recall the definition of
![]() $\gamma$
-transfer, which is due to [Reference Müller, Scarsini and Tsetlin25].
$\gamma$
-transfer, which is due to [Reference Müller, Scarsini and Tsetlin25].
Definition 3.1. (
![]() $\gamma$
-transfer.) Let X and Y be two discrete random variables with PMFs f and g, respectively. We say that Y is obtained from X via a
$\gamma$
-transfer.) Let X and Y be two discrete random variables with PMFs f and g, respectively. We say that Y is obtained from X via a
![]() $\gamma$
-transfer if there exist
$\gamma$
-transfer if there exist
![]() $x_1<x_2<x_3<x_4$
and
$x_1<x_2<x_3<x_4$
and
![]() $\eta_1,\eta_2>0$
with
$\eta_1,\eta_2>0$
with
![]() $\eta_2(x_4-x_3)=\gamma \eta_1(x_2-x_1)$
such that
$\eta_2(x_4-x_3)=\gamma \eta_1(x_2-x_1)$
such that
 \begin{align*} g(x_1) & = f(x_1)-\eta_1,\\ g(x_2) & = f(x_2) +\eta_1,\\ g(x_3) & = f(x_3) +\eta_2,\\ g(x_4) & = f(x_4) -\eta_2,\\ g(z)&=f(z)\quad \text{for all other values z.}\end{align*}
\begin{align*} g(x_1) & = f(x_1)-\eta_1,\\ g(x_2) & = f(x_2) +\eta_1,\\ g(x_3) & = f(x_3) +\eta_2,\\ g(x_4) & = f(x_4) -\eta_2,\\ g(z)&=f(z)\quad \text{for all other values z.}\end{align*}
In the definition of
![]() $\gamma$
-transfer,
$\gamma$
-transfer,
![]() $\gamma$
is not necessarily restricted to be in [0,1], which can take any value in
$\gamma$
is not necessarily restricted to be in [0,1], which can take any value in
![]() $\mathbb{R}_+=[0,\infty)$
. Further,
$\mathbb{R}_+=[0,\infty)$
. Further,
![]() $\gamma$
-spread is closely related to
$\gamma$
-spread is closely related to
![]() $\gamma$
-transfer: X is said to be obtained from Y by a
$\gamma$
-transfer: X is said to be obtained from Y by a
![]() $\gamma$
-spread if Y is obtained from X by a
$\gamma$
-spread if Y is obtained from X by a
![]() $\gamma$
-transfer. In a
$\gamma$
-transfer. In a
![]() $\gamma$
-transfer, a mass of size
$\gamma$
-transfer, a mass of size
![]() $\eta_2$
is moved to the left from
$\eta_2$
is moved to the left from
![]() $x_4$
by
$x_4$
by
![]() $\Delta_2=x_4-x_3$
, while a mass of size
$\Delta_2=x_4-x_3$
, while a mass of size
![]() $\eta_1$
is moved to the right from
$\eta_1$
is moved to the right from
![]() $x_1$
by
$x_1$
by
![]() $\Delta_1=x_2-x_1$
such that
$\Delta_1=x_2-x_1$
such that
![]() $\Delta_2\eta_2 =\gamma \Delta_1\eta_1$
. A
$\Delta_2\eta_2 =\gamma \Delta_1\eta_1$
. A
![]() $\gamma$
transfer increases the mean (i.e.
$\gamma$
transfer increases the mean (i.e.
![]() $\mathbb{E} X\le \mathbb{E} Y$
) for
$\mathbb{E} X\le \mathbb{E} Y$
) for
![]() $\gamma\in [0,1]$
. In Example 2.1, Y is obtained from X by a
$\gamma\in [0,1]$
. In Example 2.1, Y is obtained from X by a
![]() $1/2$
-transfer, Z is obtained from Y by a
$1/2$
-transfer, Z is obtained from Y by a
![]() $1/2$
-transfer, and Z is obtained from X by a
$1/2$
-transfer, and Z is obtained from X by a
![]() $5/12$
-transfer.
$5/12$
-transfer.
In Definition 3.1,
![]() $\gamma$
-transfer can also be defined when
$\gamma$
-transfer can also be defined when
![]() $x_1< x_2=x_3< x_4$
. In this case the conditions
$x_1< x_2=x_3< x_4$
. In this case the conditions
![]() $g(x_2)=f(x_2)+\eta_1$
and
$g(x_2)=f(x_2)+\eta_1$
and
![]() $g(x_3)=f(x_3)+\eta_2$
were replaced by
$g(x_3)=f(x_3)+\eta_2$
were replaced by
![]() $g(x_2)=f(x_2)+\eta_1 +\eta_2$
.
$g(x_2)=f(x_2)+\eta_1 +\eta_2$
.
The following proposition states that
![]() $\gamma$
-transfers account for almost all mass transfers of
$\gamma$
-transfers account for almost all mass transfers of
![]() $(1+\gamma)$
-SD. Specifically, part (ii) of Proposition 3.1 can be seen from the proof ofTheorem 2.8 of [Reference Müller, Scarsini and Tsetlin25]. For two random variables X and Y, we use
$(1+\gamma)$
-SD. Specifically, part (ii) of Proposition 3.1 can be seen from the proof ofTheorem 2.8 of [Reference Müller, Scarsini and Tsetlin25]. For two random variables X and Y, we use
![]() $X \buildrel \mathrm{d} \over = Y$
to denote that X and Y have the same distribution, and let
$X \buildrel \mathrm{d} \over = Y$
to denote that X and Y have the same distribution, and let
![]() $\|X\|_\infty =\mathrm{ess\mbox{-}sup} (|X|)$
.
$\|X\|_\infty =\mathrm{ess\mbox{-}sup} (|X|)$
.
Proposition 3.1. ([Reference Müller, Scarsini and Tsetlin25].)Let X and Y be two random variables such that
![]() $X\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}{\rm SD}}} Y$
for
$X\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}{\rm SD}}} Y$
for
![]() $\gamma\in [0,1]$
.
$\gamma\in [0,1]$
.
-
(i) If X and Y both have finite outcomes, then there exist
 $X_1,\ldots,X_n$
such that
$X_1,\ldots,X_n$
such that
 $X \buildrel \mathrm{d} \over = X_1$
,
$X \buildrel \mathrm{d} \over = X_1$
,
 $X_n\le Y$
a.s., and
$X_n\le Y$
a.s., and
 $X_{i}$
is a
$X_{i}$
is a
 $\gamma$
-transfer of
$\gamma$
-transfer of
 $X_{i-1}$
for
$X_{i-1}$
for
 $i=2,\ldots,n$
.
$i=2,\ldots,n$
. -
(ii) If X and Y are bounded, then there exist
 $X_n$
and
$X_n$
and
 $Y_n$
with finite outcomes such that
$Y_n$
with finite outcomes such that
 $\|X_n- X\|_\infty\to 0$
,
$\|X_n- X\|_\infty\to 0$
,
 $\|Y_n -Y\|_{\infty}\to 0$
as
$\|Y_n -Y\|_{\infty}\to 0$
as
 $n\to\infty$
, and
$n\to\infty$
, and
 $X_n\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}{\rm SD}}} Y_n$
for
$X_n\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}{\rm SD}}} Y_n$
for
 $n\in\mathbb{N}$
.
$n\in\mathbb{N}$
. -
(iii) If X and Y are general random variables, then there exist
 $X_n$
and
$X_n$
and
 $Y_n$
with finite outcomes such that
$Y_n$
with finite outcomes such that
 $X_n\to X$
,
$X_n\to X$
,
 $Y_n\to Y$
in distribution,
$Y_n\to Y$
in distribution,
 $\mathbb{E}[X_n]\to\mathbb{E}[X]$
,
$\mathbb{E}[X_n]\to\mathbb{E}[X]$
,
 $\mathbb{E}[Y_n]\to\mathbb{E}[Y]$
as
$\mathbb{E}[Y_n]\to\mathbb{E}[Y]$
as
 $n\to\infty$
, and
$n\to\infty$
, and
 $X_n\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}{\rm SD}}} Y_n$
for
$X_n\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}{\rm SD}}} Y_n$
for
 $n\in\mathbb{N}$
.
$n\in\mathbb{N}$
.
For
![]() $(1+\gamma)$
-PSD, we have the following result analogous to Proposition 3.1.
$(1+\gamma)$
-PSD, we have the following result analogous to Proposition 3.1.
Proposition 3.2. Let X and Y be two random variables such that
![]() $X\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}{\rm PSD}}} Y$
for some
$X\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}{\rm PSD}}} Y$
for some
![]() $\gamma\in [0,1]$
.
$\gamma\in [0,1]$
.
-
(i) If X and Y both have finite outcomes, then there exist
 $X_1,\ldots,X_n$
such that
$X_1,\ldots,X_n$
such that
 $X \buildrel \mathrm{d} \over = X_1$
,
$X \buildrel \mathrm{d} \over = X_1$
,
 $X_n \buildrel \mathrm{d} \over = Y$
a.s., and
$X_n \buildrel \mathrm{d} \over = Y$
a.s., and
 $X_{i}$
is a
$X_{i}$
is a
 $\gamma$
-transfer of
$\gamma$
-transfer of
 $X_{i-1}$
for
$X_{i-1}$
for
 $i=2,\ldots,n$
.
$i=2,\ldots,n$
. -
(ii) If X and Y are bounded, then there exist
 $X_n$
and
$X_n$
and
 $Y_n$
with finite outcomes such that
$Y_n$
with finite outcomes such that
 $\|X_n- X\|_\infty\to 0$
,
$\|X_n- X\|_\infty\to 0$
,
 $\|Y_n -Y\|_{\infty}\to 0$
as
$\|Y_n -Y\|_{\infty}\to 0$
as
 $n\to\infty$
, and
$n\to\infty$
, and
 $X_n\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}{\rm PSD}}} Y_n$
for
$X_n\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}{\rm PSD}}} Y_n$
for
 $n\in\mathbb{N}$
.
$n\in\mathbb{N}$
. -
(iii) If X and Y are general random variables, then there exist
 $X_n$
and
$X_n$
and
 $Y_n$
with finite outcomes such that
$Y_n$
with finite outcomes such that
 $X_n\to X$
,
$X_n\to X$
,
 $Y_n\to Y$
in distribution,
$Y_n\to Y$
in distribution,
 $\mathbb{E}[X_n]\to\mathbb{E}[X]$
,
$\mathbb{E}[X_n]\to\mathbb{E}[X]$
,
 $\mathbb{E}[Y_n]\to\mathbb{E}[Y]$
as
$\mathbb{E}[Y_n]\to\mathbb{E}[Y]$
as
 $n\to\infty$
, and
$n\to\infty$
, and
 $X_n\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}{\rm PSD}}} Y_n$
for
$X_n\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}{\rm PSD}}} Y_n$
for
 $n\in\mathbb{N}$
.
$n\in\mathbb{N}$
.
Proof. Without loss of generality, assume
![]() $\gamma\in (0,1]$
, and let F and G be the distribution functions of X and Y, respectively.
$\gamma\in (0,1]$
, and let F and G be the distribution functions of X and Y, respectively.
(i) The result can be obtained by modifying the proof of Theorem 2.7 in [Reference Müller, Scarsini and Tsetlin25]. We use the same notation as in [Reference Müller, Scarsini and Tsetlin25]. Define
Let w(a) and v(a) be the smallest numbers satisfying
In view of Proposition 2.1, we have
![]() $w(a)\le v(a)$
for all
$w(a)\le v(a)$
for all
![]() $a\in [0, A^-(1)]$
. For each
$a\in [0, A^-(1)]$
. For each
![]() $a\in [0, A^-(1)]$
, define
$a\in [0, A^-(1)]$
, define
Since X and Y both have finite outcomes, there exist
![]() $0=a_1<a_2<\cdots<a_k=A^-(1)$
such that the functions
$0=a_1<a_2<\cdots<a_k=A^-(1)$
such that the functions
![]() $x_1(a), \ldots, x_4(a)$
are constant on
$x_1(a), \ldots, x_4(a)$
are constant on
![]() $(a_{i-1}, a_i]$
. Denote the corresponding values of these functions as
$(a_{i-1}, a_i]$
. Denote the corresponding values of these functions as
![]() $x_{\ell,i}=x_\ell(a)$
for
$x_{\ell,i}=x_\ell(a)$
for
![]() $a\in (a_{i-1}, a_i]$
,
$a\in (a_{i-1}, a_i]$
,
![]() $\ell=1, \ldots, 4$
. It was shown in [Reference Müller, Scarsini and Tsetlin25] that
$\ell=1, \ldots, 4$
. It was shown in [Reference Müller, Scarsini and Tsetlin25] that
![]() $x_{1,i}< x_{2,i}\le x_{3,i}<x_{4,i}$
, and that for each
$x_{1,i}< x_{2,i}\le x_{3,i}<x_{4,i}$
, and that for each
![]() $i\in \{1, \ldots, k\}$
, the probability masses of F at points
$i\in \{1, \ldots, k\}$
, the probability masses of F at points
![]() $x_{1,i}$
and
$x_{1,i}$
and
![]() $x_{4,i}$
, respectively, are moved to the points
$x_{4,i}$
, respectively, are moved to the points
![]() $x_{2,i}$
and
$x_{2,i}$
and
![]() $x_{3,i}$
of G by a
$x_{3,i}$
of G by a
![]() $\gamma$
-transfer.
$\gamma$
-transfer.
Note that when
![]() $X\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}PSD}}Y$
, it follows from (2.2) that
$X\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}PSD}}Y$
, it follows from (2.2) that
![]() $A^{-}(1)=\gamma A^{+}(1)$
. Then
$A^{-}(1)=\gamma A^{+}(1)$
. Then
![]() $G^{-1}(p)\ge F^{-1}(p)$
for
$G^{-1}(p)\ge F^{-1}(p)$
for
![]() $p>v(a_k)$
, and
$p>v(a_k)$
, and
![]() $G^{-1}(p)\le F^{-1}(p)$
for
$G^{-1}(p)\le F^{-1}(p)$
for
![]() $p>w(a_k)$
. This means that
$p>w(a_k)$
. This means that
![]() $F(x)\ge G(x)$
for
$F(x)\ge G(x)$
for
![]() $x>x_{4,k}$
and
$x>x_{4,k}$
and
![]() $F(x)\le G(x)$
for
$F(x)\le G(x)$
for
![]() $x>x_{1,k}$
. Thus
$x>x_{1,k}$
. Thus
![]() $F(x)=G(x)$
for all
$F(x)=G(x)$
for all
![]() $x>x_{4,k}$
and the jumps of F and G occur in the points belonging to the set
$x>x_{4,k}$
and the jumps of F and G occur in the points belonging to the set
![]() $\{x_{\ell,i}\colon i=1,\ldots, k; \ell=1, \ldots, 4\}$
. Therefore G can be obtained from F only by a sequence of k
$\{x_{\ell,i}\colon i=1,\ldots, k; \ell=1, \ldots, 4\}$
. Therefore G can be obtained from F only by a sequence of k
![]() $\gamma$
-transfers.
$\gamma$
-transfers.
(ii) First assume that F and G have finite crossings, that is, there exist
![]() $-\infty<x_0< x_1<\cdots<x_m<\infty$
such that either
$-\infty<x_0< x_1<\cdots<x_m<\infty$
such that either
![]() $F \le G $
or
$F \le G $
or
![]() $F \ge G$
holds in
$F \ge G$
holds in
![]() $(x_{i-1},x_i)$
,
$(x_{i-1},x_i)$
,
![]() $i=1,\ldots,m$
, where the supports of F and G are contained in
$i=1,\ldots,m$
, where the supports of F and G are contained in
![]() $[x_0, x_m]$
. For
$[x_0, x_m]$
. For
![]() $i=1,\ldots,m$
and
$i=1,\ldots,m$
and
![]() $n\in\mathbb{N}$
, denote
$n\in\mathbb{N}$
, denote
Define two random variables
![]() $X_n$
and
$X_n$
and
![]() $Y_n$
with distribution functions
$Y_n$
with distribution functions
![]() $F_n$
and
$F_n$
and
![]() $G_n$
, respectively, where
$G_n$
, respectively, where
for
![]() $x\in [x_{i,j-1}, x_{i,j})$
. It is easy to see that
$x\in [x_{i,j-1}, x_{i,j})$
. It is easy to see that
![]() $X_n$
and
$X_n$
and
![]() $Y_n$
both have finite outcomes. It can be verified that in each interval
$Y_n$
both have finite outcomes. It can be verified that in each interval
![]() $[x_{i,j-1}, x_{i,j})$
, either
$[x_{i,j-1}, x_{i,j})$
, either
![]() $F_n \le G_n$
or
$F_n \le G_n$
or
![]() $F_n\ge G_n$
, and the direction of the inequality is the same as
$F_n\ge G_n$
, and the direction of the inequality is the same as
![]() $F \le G $
or
$F \le G $
or
![]() $F \ge G$
on the same interval. Hence we have
$F \ge G$
on the same interval. Hence we have
and
Then it follows from
![]() $F\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}PSD}} G$
that
$F\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}PSD}} G$
that
![]() $F_n\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}PSD}} G_n$
. On the other hand, it is easy to see that
$F_n\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}PSD}} G_n$
. On the other hand, it is easy to see that
![]() $\max\{|X|, |Y|\} \le M\;:\!=\; x_m-x_0<\infty$
,
$\max\{|X|, |Y|\} \le M\;:\!=\; x_m-x_0<\infty$
,
and
Hence we can easily construct
![]() $X_n\sim F_n$
and
$X_n\sim F_n$
and
![]() $Y_n\sim G_n$
such that
$Y_n\sim G_n$
such that
![]() $|X_n-X|\le 2M/n$
and
$|X_n-X|\le 2M/n$
and
![]() $|Y_n-Y|\le 2M/n$
.
$|Y_n-Y|\le 2M/n$
.
Next, consider that X and Y have infinite crossings, that is, we have infinite intervals
![]() $\{(x_{i-1}, x_{i}),i\in I\}$
such that
$\{(x_{i-1}, x_{i}),i\in I\}$
such that
![]() $G-F$
has the same sign in any one interval. Note that X and Y are both bounded. Then, for
$G-F$
has the same sign in any one interval. Note that X and Y are both bounded. Then, for
![]() $n\in\mathbb{N}$
, the number of intervals with length larger than
$n\in\mathbb{N}$
, the number of intervals with length larger than
![]() $1/n$
is finite. Then we can merge some of the remaining neighboring intervals to make the lengths smaller than
$1/n$
is finite. Then we can merge some of the remaining neighboring intervals to make the lengths smaller than
![]() $2/n$
and the number of intervals finite. Without loss of generality, assume that the transformed intervals are still denoted by
$2/n$
and the number of intervals finite. Without loss of generality, assume that the transformed intervals are still denoted by
![]() $\{(x_{i-1}, x_{i}),i=1,\ldots,m\}$
. In each interval, either
$\{(x_{i-1}, x_{i}),i=1,\ldots,m\}$
. In each interval, either
![]() $G-F$
has the same sign or the length of the interval is less than
$G-F$
has the same sign or the length of the interval is less than
![]() $2/n$
. For the intervals where
$2/n$
. For the intervals where
![]() $G-F$
has the same sign, we use the same method as in the above case to define the values of
$G-F$
has the same sign, we use the same method as in the above case to define the values of
![]() $F_n$
and
$F_n$
and
![]() $G_n$
in the intervals. For the other intervals, take
$G_n$
in the intervals. For the other intervals, take
![]() $(x_{i-1},x_i)$
as an example, where
$(x_{i-1},x_i)$
as an example, where
![]() $G-F$
has different signs on
$G-F$
has different signs on
![]() $(x_{i-1},x_i)$
and
$(x_{i-1},x_i)$
and
![]() $x_i-x_{i-1}< 2/n$
. Let
$x_i-x_{i-1}< 2/n$
. Let
![]() $x^\ast\in (x_{i-1},x_i)$
such that
$x^\ast\in (x_{i-1},x_i)$
such that
![]() $x^\ast-x_{i-1}$
is equal to the length of
$x^\ast-x_{i-1}$
is equal to the length of
![]() $A_i=\{x\in (x_{i-1},x_i)\colon F(x)\ge G(x) \}$
. Denote
$A_i=\{x\in (x_{i-1},x_i)\colon F(x)\ge G(x) \}$
. Denote
![]() $A_i^{c} = (x_{i-1},x_i) \setminus A_i$
and define
$A_i^{c} = (x_{i-1},x_i) \setminus A_i$
and define
for
![]() $x\in (x_{i-1},x^\ast)$
, and
$x\in (x_{i-1},x^\ast)$
, and
for
![]() $x\in (x^\ast,x_i)$
. Then we have
$x\in (x^\ast,x_i)$
. Then we have
and
Then it can be checked that
![]() $F\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}PSD}} G$
implies
$F\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}PSD}} G$
implies
![]() $F_n\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}PSD}} G_n$
. The remaining proof is similar to the above case.
$F_n\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}PSD}} G_n$
. The remaining proof is similar to the above case.
(iii) We modify the proof of Theorem 2.8 in [Reference Müller, Scarsini and Tsetlin25] for our purpose. For unbounded random variables X and Y, define
We approximate X and Y by
![]() $X_n$
and
$X_n$
and
![]() $Y_n$
, respectively, as follows. Define
$Y_n$
, respectively, as follows. Define
 \begin{equation*} X_n=\begin{cases} x_n^\ast & \text{if $ X\le -n$,}\\ X & \text{if $-n<X\le n$,}\\ y_n^\ast & \text{if $ X>n$,} \end{cases}\end{equation*}
\begin{equation*} X_n=\begin{cases} x_n^\ast & \text{if $ X\le -n$,}\\ X & \text{if $-n<X\le n$,}\\ y_n^\ast & \text{if $ X>n$,} \end{cases}\end{equation*}
and
 \begin{equation*} Y_n=\begin{cases} -n & \text{if $ Y\le -n$,}\\ Y & \text{if $ -n<Y\le n$,}\\ n & \text{if $ Y >n$,} \end{cases}\end{equation*}
\begin{equation*} Y_n=\begin{cases} -n & \text{if $ Y\le -n$,}\\ Y & \text{if $ -n<Y\le n$,}\\ n & \text{if $ Y >n$,} \end{cases}\end{equation*}
where
Since
![]() $\xi(t)\ge \psi(t)\ge 0$
for all t, it follows that
$\xi(t)\ge \psi(t)\ge 0$
for all t, it follows that
![]() $x_n^\ast\le -n$
and
$x_n^\ast\le -n$
and
![]() $y_n^\ast\ge n$
. Let
$y_n^\ast\ge n$
. Let
![]() $F_n$
and
$F_n$
and
![]() $G_n$
denote the distribution functions of
$G_n$
denote the distribution functions of
![]() $X_n$
and
$X_n$
and
![]() $Y_n$
, respectively, and define
$Y_n$
, respectively, and define
Then it can be checked that
 \begin{equation*} \psi_n(t)=\begin{cases} 0 & \text{if $ t<-n$,}\\ \psi(t)-\psi(-n) & \text{if $ -n<t\le n$,}\\ \psi(n)-\psi(-n) + (t-n) {\overline F}(n) & \text{if $ n<t\le y_n^\ast$,}\\ \xi(n) & \text{if $ t>y_n^\ast$,} \end{cases}\end{equation*}
\begin{equation*} \psi_n(t)=\begin{cases} 0 & \text{if $ t<-n$,}\\ \psi(t)-\psi(-n) & \text{if $ -n<t\le n$,}\\ \psi(n)-\psi(-n) + (t-n) {\overline F}(n) & \text{if $ n<t\le y_n^\ast$,}\\ \xi(n) & \text{if $ t>y_n^\ast$,} \end{cases}\end{equation*}
and
 \begin{equation*} \xi_n(t)=\begin{cases} \xi(t) & \text{if $ -n\le t\le n$,}\\ \xi(n) & \text{if $ t>n$.} \end{cases}\end{equation*}
\begin{equation*} \xi_n(t)=\begin{cases} \xi(t) & \text{if $ -n\le t\le n$,}\\ \xi(n) & \text{if $ t>n$.} \end{cases}\end{equation*}
Thus
![]() $X_n$
and
$X_n$
and
![]() $Y_n$
are bounded,
$Y_n$
are bounded,
![]() $\psi_n(t)\le \xi_n(t)$
for all
$\psi_n(t)\le \xi_n(t)$
for all
![]() $t\in\mathbb{R}$
, and
$t\in\mathbb{R}$
, and
![]() $\psi_n(+\infty)=\xi(n)=\xi_n$
$\psi_n(+\infty)=\xi(n)=\xi_n$
![]() $(+\infty)$
. This means
$(+\infty)$
. This means
![]() $X_n\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}PSD}} Y_n$
for all
$X_n\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}PSD}} Y_n$
for all
![]() $n\in\mathbb{N}$
. On the other hand,
$n\in\mathbb{N}$
. On the other hand,
![]() $\psi(+\infty)=\xi$
$\psi(+\infty)=\xi$
![]() $(+\infty)$
implies that
$(+\infty)$
implies that
![]() $\mathbb{E} [X_n]\to \mathbb{E} [X]$
and
$\mathbb{E} [X_n]\to \mathbb{E} [X]$
and
![]() $X_n\to X$
in distribution. Obviously,
$X_n\to X$
in distribution. Obviously,
![]() $\mathbb{E} [Y_n]\to \mathbb{E} [Y]$
and
$\mathbb{E} [Y_n]\to \mathbb{E} [Y]$
and
![]() $Y_n\to Y$
in distribution. The desired result now follows from part (ii). This completes the proof.
$Y_n\to Y$
in distribution. The desired result now follows from part (ii). This completes the proof.
3.2. Dual characterization
Let
![]() $\mathcal H$
denote the set of all probability perception functions h (also referred to as distortion functions in the actuarial literature), that is,
$\mathcal H$
denote the set of all probability perception functions h (also referred to as distortion functions in the actuarial literature), that is,
![]() $h\colon [0,1]\to [0,1]$
is increasing, satisfying
$h\colon [0,1]\to [0,1]$
is increasing, satisfying
![]() $h(0)=0$
and
$h(0)=0$
and
![]() $h(1)=1$
. For
$h(1)=1$
. For
![]() $\gamma \in [0,1]$
, define
$\gamma \in [0,1]$
, define
and
where h
′(0) and h
′(1) represent the right derivative at 0 and the left derivative at 1, respectively. Obviously,
![]() $\mathcal H_\gamma$
is the subset of
$\mathcal H_\gamma$
is the subset of
![]() $\mathcal H_\gamma^\ast$
containing all continuously differentiable
$\mathcal H_\gamma^\ast$
containing all continuously differentiable
![]() $h\in\mathcal H_\gamma^\ast$
.
$h\in\mathcal H_\gamma^\ast$
.
In the following theorem, we establish in the framework of Yaari’s dual theory that
![]() $(1+\gamma)$
-SD is equivalent to a common preference among all decision-makers with probability perception function
$(1+\gamma)$
-SD is equivalent to a common preference among all decision-makers with probability perception function
![]() $h\in \mathcal H_\gamma$
. This is a dual characterization of
$h\in \mathcal H_\gamma$
. This is a dual characterization of
![]() $(1+\gamma)$
-SD as the latter is originally defined via a common preference based on utility functions. For Yaari’s dual theory,see [Reference Yaari30].
$(1+\gamma)$
-SD as the latter is originally defined via a common preference based on utility functions. For Yaari’s dual theory,see [Reference Yaari30].
Theorem 3.1. Let F and G be the distribution functions of X and Y, respectively. For
![]() $\gamma\in [0,1]$
, the following statements are equivalent:
$\gamma\in [0,1]$
, the following statements are equivalent:
-
(i)
 $X\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}{\rm SD}}} Y$
,
$X\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}{\rm SD}}} Y$
, -
(ii)
 $\displaystyle \int_0^1 F^{-1}(\alpha)\,{\mathrm{d}} h(\alpha) \le \int_0^1 G^{-1}(\alpha)\,{\mathrm{d}} h(\alpha)$
for all
$\displaystyle \int_0^1 F^{-1}(\alpha)\,{\mathrm{d}} h(\alpha) \le \int_0^1 G^{-1}(\alpha)\,{\mathrm{d}} h(\alpha)$
for all
 $ h\in \mathcal H_\gamma$
,
$ h\in \mathcal H_\gamma$
, -
(iii)
 $\displaystyle \int_0^1 F^{-1}(\alpha)\,{\mathrm{d}} h(\alpha) \le \int_0^1 G^{-1}(\alpha)\,{\mathrm{d}} h(\alpha)$
for all
$\displaystyle \int_0^1 F^{-1}(\alpha)\,{\mathrm{d}} h(\alpha) \le \int_0^1 G^{-1}(\alpha)\,{\mathrm{d}} h(\alpha)$
for all
 $h\in \mathcal H_\gamma^\ast$
.
$h\in \mathcal H_\gamma^\ast$
.
Proof. Part (iii) is equivalent to (ii). It suffices to prove that (iii)
![]() $\Rightarrow$
(2.4)
$\Rightarrow$
(2.4)
![]() $\Rightarrow$
(ii).
$\Rightarrow$
(ii).
To prove (iii)
![]() $\Rightarrow$
(2.4), for
$\Rightarrow$
(2.4), for
![]() $p\in (0,1]$
, define a distortion function
$p\in (0,1]$
, define a distortion function
![]() $h\in\mathcal H$
such that
$h\in\mathcal H$
such that
 \begin{equation*} h'(\alpha) = \begin{cases} \gamma & \text{if $ F^{-1}(\alpha)\le G^{-1}(\alpha)$ and $ \alpha\le p$,}\\ 1 & \text{if $ F^{-1}(\alpha)>G^{-1}(\alpha)$ and $\alpha\le p$,}\\ 0 & \text{if $ \alpha> p$.} \end{cases}\end{equation*}
\begin{equation*} h'(\alpha) = \begin{cases} \gamma & \text{if $ F^{-1}(\alpha)\le G^{-1}(\alpha)$ and $ \alpha\le p$,}\\ 1 & \text{if $ F^{-1}(\alpha)>G^{-1}(\alpha)$ and $\alpha\le p$,}\\ 0 & \text{if $ \alpha> p$.} \end{cases}\end{equation*}
It is easy to verify that
![]() $h\in\mathcal H_\gamma^\ast$
and hence (2.4) holds.
$h\in\mathcal H_\gamma^\ast$
and hence (2.4) holds.
To prove the other direction (2.4)
![]() $\Rightarrow$
(ii), we use arguments similar to those in the proof of Theorem 2.4 of [Reference Müller, Scarsini and Tsetlin25]. For completeness, we give the details. Let
$\Rightarrow$
(ii), we use arguments similar to those in the proof of Theorem 2.4 of [Reference Müller, Scarsini and Tsetlin25]. For completeness, we give the details. Let
![]() $h\in \mathcal H_\gamma$
, i.e. h satisfies
$h\in \mathcal H_\gamma$
, i.e. h satisfies
![]() $0\le \gamma h'(y)\le h'(x)$
for all
$0\le \gamma h'(y)\le h'(x)$
for all
![]() $0\le x\le y\le1$
. Then
$0\le x\le y\le1$
. Then
![]() $R\;:\!=\; \sup_{v\in (0,1)}h'(v)\in (0,\infty)$
since
$R\;:\!=\; \sup_{v\in (0,1)}h'(v)\in (0,\infty)$
since
![]() $0\le h'(v)\le h'(1)/\gamma<\infty.$
For any fixed
$0\le h'(v)\le h'(1)/\gamma<\infty.$
For any fixed
![]() $n\ge 2$
, define
$n\ge 2$
, define
![]() $\epsilon_n=2^{-n}$
and K as the largest integer kfor which
$\epsilon_n=2^{-n}$
and K as the largest integer kfor which
and define a partition of [0,1] into intervals
![]() $[v_k, v_{k+1}]$
as follows:
$[v_k, v_{k+1}]$
as follows:
![]() $v_0=0$
,
$v_0=0$
,
![]() $v_{K+1}=1$
, and
$v_{K+1}=1$
, and
Then we define
It follows that
![]() $\gamma m_{k+1} \le h'(v)\le m_k$
for
$\gamma m_{k+1} \le h'(v)\le m_k$
for
![]() $v\in [v_{k-1}, v_k]$
, i.e.
$v\in [v_{k-1}, v_k]$
, i.e.
![]() $\gamma (m_k - R \epsilon_n) \le h'(v)\le m_k$
for all
$\gamma (m_k - R \epsilon_n) \le h'(v)\le m_k$
for all
![]() $x\in [v_{k-1}, v_k]$
and
$x\in [v_{k-1}, v_k]$
and
![]() $k=1,\ldots,K+1$
. This implies that
$k=1,\ldots,K+1$
. This implies that
 \begin{align*}&\int_{v_{k-1}}^{v_k} (G^{-1}(\alpha)- F^{-1}(\alpha))\,{\mathrm{d}} h(\alpha)\\ & \quad = \int_{v_{k-1}}^{v_k} (G^{-1}(\alpha)- F^{-1}(\alpha))_+h'(\alpha) \,{\mathrm{d}} \alpha - \int_{v_{k-1}}^{v_k} (G^{-1}(\alpha)- F^{-1}(\alpha))_- h'(\alpha)\,{\mathrm{d}} \alpha\\ & \quad \ge \gamma (m_k - R \epsilon_n ) \int_{v_{k-1}}^{v_k}(G^{-1}(\alpha)- F^{-1}(\alpha))_+ {\mathrm{d}} \alpha - m_k \int_{v_{k-1}}^{v_k}(G^{-1}(\alpha)- F^{-1}(\alpha))_-{\mathrm{d}} \alpha\\ & \quad = m_k T_k -\epsilon_n c_k , \end{align*}
\begin{align*}&\int_{v_{k-1}}^{v_k} (G^{-1}(\alpha)- F^{-1}(\alpha))\,{\mathrm{d}} h(\alpha)\\ & \quad = \int_{v_{k-1}}^{v_k} (G^{-1}(\alpha)- F^{-1}(\alpha))_+h'(\alpha) \,{\mathrm{d}} \alpha - \int_{v_{k-1}}^{v_k} (G^{-1}(\alpha)- F^{-1}(\alpha))_- h'(\alpha)\,{\mathrm{d}} \alpha\\ & \quad \ge \gamma (m_k - R \epsilon_n ) \int_{v_{k-1}}^{v_k}(G^{-1}(\alpha)- F^{-1}(\alpha))_+ {\mathrm{d}} \alpha - m_k \int_{v_{k-1}}^{v_k}(G^{-1}(\alpha)- F^{-1}(\alpha))_-{\mathrm{d}} \alpha\\ & \quad = m_k T_k -\epsilon_n c_k , \end{align*}
with
and
Note that (2.4) implies
![]() $\sum_{i=1}^k T_i\ge 0$
for all
$\sum_{i=1}^k T_i\ge 0$
for all
![]() $k=1,\ldots,K+1$
, which in turn implies
$k=1,\ldots,K+1$
, which in turn implies
![]() $\sum_{k=1}^{K+1}m_k T_k \ge0$
for all decreasing non-negative sequences
$\sum_{k=1}^{K+1}m_k T_k \ge0$
for all decreasing non-negative sequences
![]() $m_k$
. Thus
$m_k$
. Thus
 \begin{align*} \int_0^1 (G^{-1}(\alpha)- F^{-1}(\alpha))\,{\mathrm{d}} h(\alpha)\ & \ge\ \sum_{k=1}^{K+1}(m_k T_k-\epsilon_n c_k)\\ & \ge\ -\epsilon_n\gamma R \int_0^1 (G^{-1}(\alpha)- F^{-1}(\alpha))_+ {\mathrm{d}} \alpha.\end{align*}
\begin{align*} \int_0^1 (G^{-1}(\alpha)- F^{-1}(\alpha))\,{\mathrm{d}} h(\alpha)\ & \ge\ \sum_{k=1}^{K+1}(m_k T_k-\epsilon_n c_k)\\ & \ge\ -\epsilon_n\gamma R \int_0^1 (G^{-1}(\alpha)- F^{-1}(\alpha))_+ {\mathrm{d}} \alpha.\end{align*}
Letting
![]() $n\to\infty$
yields part (ii). This completes the proof of the theorem.
$n\to\infty$
yields part (ii). This completes the proof of the theorem.
Remark 3.1. To get a better understanding of the dual characterization of
![]() $(1+\gamma)$
-SD, we introduce the following index
$(1+\gamma)$
-SD, we introduce the following index
![]() $Q_f$
of a probability perception function h:
$Q_f$
of a probability perception function h:
Here we use the convention that
![]() $a/0=+\infty$
for any real number
$a/0=+\infty$
for any real number
![]() $a>0$
and
$a>0$
and
![]() $0/0=0$
. As mentioned in [Reference Chateauneuf, Cohen and Meilijson5],
$0/0=0$
. As mentioned in [Reference Chateauneuf, Cohen and Meilijson5],
![]() $Q_h$
is an index of non-concavity of
$Q_h$
is an index of non-concavity of
![]() $h\in\mathcal H$
,
$h\in\mathcal H$
,
![]() $Q_h\ge 1$
, and
$Q_h\ge 1$
, and
![]() $Q_h=1$
corresponds exactly to concavity. Thus
$Q_h=1$
corresponds exactly to concavity. Thus
![]() $1/Q_h$
can be regarded as an index of the greediness of a decision-maker with probability perception function h (in short, a decision-maker h). That is, for
$1/Q_h$
can be regarded as an index of the greediness of a decision-maker with probability perception function h (in short, a decision-maker h). That is, for
![]() $h_1, h_2\in \mathcal H$
,
$h_1, h_2\in \mathcal H$
,
![]() $Q_{h_1}<Q_{h_2}$
means that
$Q_{h_1}<Q_{h_2}$
means that
![]() $h_1$
is more greedy than
$h_1$
is more greedy than
![]() $h_2$
. Therefore, for
$h_2$
. Therefore, for
![]() $\gamma\in [0,1]$
,
$\gamma\in [0,1]$
,
denotes the set of decision-makers with index of greediness larger than or equal to
![]() $\gamma$
. On the other hand,
$\gamma$
. On the other hand,
![]() ${\mathcal U}_\gamma^\ast$
or
${\mathcal U}_\gamma^\ast$
or
![]() ${\mathcal U}_\gamma^\ast$
has a similar interpretation in terms of risk aversion.
${\mathcal U}_\gamma^\ast$
has a similar interpretation in terms of risk aversion.
The order
![]() $X\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} Y$
is defined in Definition 2.1 by comparing expected utilities
$X\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} Y$
is defined in Definition 2.1 by comparing expected utilities
![]() $\mathbb{E} [u(X)]$
and
$\mathbb{E} [u(X)]$
and
![]() $\mathbb{E} [u(Y)]$
for all utility functions
$\mathbb{E} [u(Y)]$
for all utility functions
![]() $u\in {\mathcal U}_\gamma$
, while the dual characterization in Theorem 3.1 compares the expected values
$u\in {\mathcal U}_\gamma$
, while the dual characterization in Theorem 3.1 compares the expected values
![]() $\mathbb{E} [X_h]$
and
$\mathbb{E} [X_h]$
and
![]() $\mathbb{E} [Y_h]$
of random variables
$\mathbb{E} [Y_h]$
of random variables
![]() $X_h$
and
$X_h$
and
![]() $Y_h$
for all probability perception functions
$Y_h$
for all probability perception functions
![]() $h\in \mathcal H_\gamma$
, where
$h\in \mathcal H_\gamma$
, where
![]() $X_h$
and
$X_h$
and
![]() $Y_h$
have the distorted distribution functions h(F(x)) and h(G(x).
$Y_h$
have the distorted distribution functions h(F(x)) and h(G(x).
3.3. Separation theorem
We establish a separation theorem similar to the classic separation theorem for 2-SD. That is, a
![]() $(1+\gamma)$
-SD can be separated by an FSD and a (
$(1+\gamma)$
-SD can be separated by an FSD and a (
![]() $1+\gamma$
)-PSD.
$1+\gamma$
)-PSD.
Theorem 3.2. For
![]() $X,Y\in L^1$
,
$X,Y\in L^1$
,
![]() $X\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}{\rm SD}}} Y$
if and only if there exist
$X\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}{\rm SD}}} Y$
if and only if there exist
![]() $Z_1, Z_2\in L^1$
such that
$Z_1, Z_2\in L^1$
such that
and
Proof. The sufficiency is trivial. It requires us to prove the necessity. To this end, let F and G denote the distribution functions of X and Y, respectively, and assume that
![]() $X\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} Y$
but
$X\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} Y$
but
![]() $X\not\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}PSD}} Y$
, i.e. (2.1) does not hold. By Proposition 2.1, we have
$X\not\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}PSD}} Y$
, i.e. (2.1) does not hold. By Proposition 2.1, we have
For
![]() $t\in \overline{\mathbb{R}}=[-\infty,\infty]$
, define
$t\in \overline{\mathbb{R}}=[-\infty,\infty]$
, define
where
![]() $\delta_{-\infty}(x)\equiv (G(x)-F(x))_-$
and
$\delta_{-\infty}(x)\equiv (G(x)-F(x))_-$
and
![]() $\delta_{\infty}(x)\equiv0$
. Note that
$\delta_{\infty}(x)\equiv0$
. Note that
![]() $\delta_t(x)$
is decreasing in
$\delta_t(x)$
is decreasing in
![]() $t\in\overline{\mathbb{R}}$
for each fixed x,
$t\in\overline{\mathbb{R}}$
for each fixed x,
![]() $\int_{-\infty}^\infty \delta_t(x)\,{\mathrm{d}} x$
is continuous in
$\int_{-\infty}^\infty \delta_t(x)\,{\mathrm{d}} x$
is continuous in
![]() $t\in\overline{\mathbb{R}}$
, and
$t\in\overline{\mathbb{R}}$
, and
Then there exists
![]() $t_0\in\overline{\mathbb{R}}$
such that
$t_0\in\overline{\mathbb{R}}$
such that
We define
which is an increasing and right-continuous function. From (3.3), we have that
and hence
![]() $H_1$
is a distribution function on
$H_1$
is a distribution function on
![]() $\mathbb{R}$
such that
$\mathbb{R}$
such that
![]() $H_1\preccurlyeq_{\mathrm{FSD}}G$
. From (3.4), one can verify that
$H_1\preccurlyeq_{\mathrm{FSD}}G$
. From (3.4), one can verify that
and
In fact, (3.5) follows from the fact that
![]() $(H_1(x)-F(x))_+=(G(x)-F(x))_+$
and
$(H_1(x)-F(x))_+=(G(x)-F(x))_+$
and
![]() $(H_1(x)-F(x))_-=(G(x)-F(x))_- - \delta_{t_0}(x)$
for all
$(H_1(x)-F(x))_-=(G(x)-F(x))_- - \delta_{t_0}(x)$
for all
![]() $x\in\mathbb{R}$
. Equation (3.6) follows from the facts that
$x\in\mathbb{R}$
. Equation (3.6) follows from the facts that
![]() $H_1(x)=G(x)$
for
$H_1(x)=G(x)$
for
![]() $x<t_0$
and
$x<t_0$
and
![]() $H_1(x)=G(x)\vee F(x)$
for
$H_1(x)=G(x)\vee F(x)$
for
![]() $x \ge t_0$
, which implies the inequality
$x \ge t_0$
, which implies the inequality
This implies that
![]() $F\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} H_1$
. Then (3.1) follows by taking
$F\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} H_1$
. Then (3.1) follows by taking
![]() $Z_1$
as a random variable having distribution function
$Z_1$
as a random variable having distribution function
![]() $H_1$
.
$H_1$
.
A similar argument to the above can be applied to obtain (3.2) by choosing
![]() $H_2(x)= F(x)- \eta_{t_1}(x)$
, where
$H_2(x)= F(x)- \eta_{t_1}(x)$
, where
and
![]() $t_1\in\overline{\mathbb{R}}$
such that
$t_1\in\overline{\mathbb{R}}$
such that
This completes the proof of the theorem.
Remark 3.2. For
![]() $\gamma=1$
, 2-PSD is the concave order. The separation result in Theorem 3.2 reduces to the separation theorem for the SSD:
$\gamma=1$
, 2-PSD is the concave order. The separation result in Theorem 3.2 reduces to the separation theorem for the SSD:
![]() $X\preccurlyeq_{\rm SSD} Y$
if and only if there exists a random variable Z such that
$X\preccurlyeq_{\rm SSD} Y$
if and only if there exists a random variable Z such that
This is a well-known result; see parts (c) and (d) of Theorem 4.A.6 in [Reference Shaked and Shanthikumar26]. There are several proofs of the above separation theorem for the SSD in the literature, for example [Reference Makowski19] and [22]. For
![]() $\gamma=1$
, the proof of Theorem 3.2 is new and differs from those in the literature.
$\gamma=1$
, the proof of Theorem 3.2 is new and differs from those in the literature.
Remark 3.3. The proof of Theorem 3.2 gives us a method for constructing random variables
![]() $Z_1$
and
$Z_1$
and
![]() $Z_2$
such that (3.1) and (3.2) hold, which is illustrated by Example 5.3.
$Z_2$
such that (3.1) and (3.2) hold, which is illustrated by Example 5.3.
Remark 3.4. From the proof of Theorem 3.2, we conclude the following.
-
(i) If
 $X \preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} Y$
, and if there does not exist
$X \preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} Y$
, and if there does not exist
 $Z\in L^1$
such that
$Z\in L^1$
such that
 $Z\not\stackrel {\rm d}{=} Y$
,
$Z\not\stackrel {\rm d}{=} Y$
,
 $Z\preccurlyeq_{\mathrm{FSD}} Y$
and
$Z\preccurlyeq_{\mathrm{FSD}} Y$
and
 $ X \preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} Z$
, then
$ X \preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} Z$
, then
 $X \preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}PSD}} Y$
.
$X \preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}PSD}} Y$
. -
(ii) If
 $X \preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} Y$
, and if there does not exist
$X \preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} Y$
, and if there does not exist
 $Z\in L^1$
such that
$Z\in L^1$
such that
 $Z\not\stackrel {\rm d}{=} X$
,
$Z\not\stackrel {\rm d}{=} X$
,
 $X\preccurlyeq_{\mathrm{FSD}} Z$
and
$X\preccurlyeq_{\mathrm{FSD}} Z$
and
 $Z \preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} Y$
, then
$Z \preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} Y$
, then
 $X \preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}PSD}} Y$
.
$X \preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}PSD}} Y$
.
3.4. Strassen’s representation
A famous result of Strassen [Reference Strassen28] states that
![]() $X\preccurlyeq_{\mathrm{SSD}} Y$
if and only if there exist random variables
$X\preccurlyeq_{\mathrm{SSD}} Y$
if and only if there exist random variables
![]() $\widehat X$
and
$\widehat X$
and
![]() $\widehat Y$
defined on a common probability space with the same distributions as X and Y such that
$\widehat Y$
defined on a common probability space with the same distributions as X and Y such that
![]() $\mathbb{E} [\widehat X \mid \widehat Y ] \le \widehat Y$
, a.s. Müller and Rüschendorf [Reference Müller and Rüschendorf23] presented an elementary and constructive proof of this result on the real line. For more details on Strassen’s theorem and extensions, see [Reference Armbruster1], [Reference Elton and Hill9], [Reference Elton and Hill10], [Reference Lindvall18], and references therein.
$\mathbb{E} [\widehat X \mid \widehat Y ] \le \widehat Y$
, a.s. Müller and Rüschendorf [Reference Müller and Rüschendorf23] presented an elementary and constructive proof of this result on the real line. For more details on Strassen’s theorem and extensions, see [Reference Armbruster1], [Reference Elton and Hill9], [Reference Elton and Hill10], [Reference Lindvall18], and references therein.
For
![]() $(1+\gamma)$
-SD, we have the following partial Strassen’s representation.
$(1+\gamma)$
-SD, we have the following partial Strassen’s representation.
Theorem 3.3. Let X and Y be two random variables. If there exist
![]() $\widehat X$
and
$\widehat X$
and
![]() $\widehat Y$
on the same probability space such that
$\widehat Y$
on the same probability space such that
![]() $\widehat X \buildrel \mathrm{d} \over = X$
,
$\widehat X \buildrel \mathrm{d} \over = X$
,
![]() $\widehat Y \buildrel \mathrm{d} \over = Y$
, and
$\widehat Y \buildrel \mathrm{d} \over = Y$
, and
for some
![]() $\gamma\in [0,1]$
, then
$\gamma\in [0,1]$
, then
![]() $X \preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}{\rm SD}}} Y$
.
$X \preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}{\rm SD}}} Y$
.
Proof. First we assert that, for any random variable Z,
which can be seen by verifying (2.3). Then it follows from (2.5) that for any
![]() $y\in\mathbb{R}$
,
$y\in\mathbb{R}$
,
![]() $Z+y\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} y$
. Let
$Z+y\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} y$
. Let
![]() $\mathrm{supp}(G)$
denote the support of the distribution function of Y. Note that (3.9) implies that, for almost all
$\mathrm{supp}(G)$
denote the support of the distribution function of Y. Note that (3.9) implies that, for almost all
![]() $y\in \mathrm{supp}(G)$
,
$y\in \mathrm{supp}(G)$
,
and hence
![]() $ [\widehat X\mid \widehat Y=y ] \preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} y$
. Then, for any
$ [\widehat X\mid \widehat Y=y ] \preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} y$
. Then, for any
![]() $\phi\in\mathcal U_\gamma^\ast$
, we have
$\phi\in\mathcal U_\gamma^\ast$
, we have
![]() $\mathbb{E} [\phi(\widehat X)\mid \widehat Y=y ] \le \phi(y)$
for almost all
$\mathbb{E} [\phi(\widehat X)\mid \widehat Y=y ] \le \phi(y)$
for almost all
![]() $y\in \mathrm{supp}(G)$
. Hence
$y\in \mathrm{supp}(G)$
. Hence
We thus complete the proof.
For
![]() $\gamma=1$
, (3.9) reduces to
$\gamma=1$
, (3.9) reduces to
![]() $\mathbb{E} [\widehat X \mid \widehat Y ] \le \widehat Y$
a.s. In Theorem 3.3, (3.9) is a sufficient condition for
$\mathbb{E} [\widehat X \mid \widehat Y ] \le \widehat Y$
a.s. In Theorem 3.3, (3.9) is a sufficient condition for
![]() $(1+\gamma)$
-SD. However, it is not a necessary condition, as illustrated by the following counterexample.
$(1+\gamma)$
-SD. However, it is not a necessary condition, as illustrated by the following counterexample.
Example 3.1. Let X and Y be two binary random variables with PMFs
Then Y is a
![]() $1/2$
-transfer of X and hence
$1/2$
-transfer of X and hence
![]() $X\preccurlyeq_{\mathrm{(1+1/2)\hbox{-}SD}} Y$
. Assume that there exist
$X\preccurlyeq_{\mathrm{(1+1/2)\hbox{-}SD}} Y$
. Assume that there exist
![]() $\widehat X$
and
$\widehat X$
and
![]() $\widehat Y$
on the same probability space such that
$\widehat Y$
on the same probability space such that
![]() $\widehat X \buildrel \mathrm{d} \over = X$
,
$\widehat X \buildrel \mathrm{d} \over = X$
,
![]() $\widehat Y \buildrel \mathrm{d} \over = Y$
, and (3.9) holds with
$\widehat Y \buildrel \mathrm{d} \over = Y$
, and (3.9) holds with
![]() $\gamma=1/2$
. Denote
$\gamma=1/2$
. Denote
![]() $b=\mathbb{P}(\widehat X=0\mid \widehat Y=3)$
. From (3.9) it follows that
$b=\mathbb{P}(\widehat X=0\mid \widehat Y=3)$
. From (3.9) it follows that
![]() $b\ge 2$
. However,
$b\ge 2$
. However,
![]() $b\in [0,1]$
. This is a contradiction. Therefore (3.9) is not necessary for
$b\in [0,1]$
. This is a contradiction. Therefore (3.9) is not necessary for
![]() $(1+\gamma)$
-SD.
$(1+\gamma)$
-SD.
To state the next proposition, we recall the definition ofcomonotonicity. A random vector
![]() $(X_1,\ldots$
,
$(X_1,\ldots$
,
![]() $X_n)$
is said to be comonotonic if there exist non-decreasing functions
$X_n)$
is said to be comonotonic if there exist non-decreasing functions
![]() $g_i\ (i=1,\ldots,n)$
, and a random variable W such that
$g_i\ (i=1,\ldots,n)$
, and a random variable W such that
![]() $(X_1,\ldots,X_n) \buildrel \mathrm{d} \over = (g_1(W),\ldots,g_n(W))$
. For more on comonotonicity, see [Reference Deelstra, Dhaene and Vanmaele7], [Reference Dhaene, Denuit, Goovaerts, Kaas and Vyncke8], and references therein.
$(X_1,\ldots,X_n) \buildrel \mathrm{d} \over = (g_1(W),\ldots,g_n(W))$
. For more on comonotonicity, see [Reference Deelstra, Dhaene and Vanmaele7], [Reference Dhaene, Denuit, Goovaerts, Kaas and Vyncke8], and references therein.
Proposition 3.3. Let F and G be two distribution functions. If G is continuous on
![]() $\mathbb{R}$
, then
$\mathbb{R}$
, then
![]() $F\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}{\rm SD}}} G$
for
$F\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}{\rm SD}}} G$
for
![]() $\gamma\in[0,1]$
if and only if there exist
$\gamma\in[0,1]$
if and only if there exist
![]() $X\sim F$
and
$X\sim F$
and
![]() $Y\sim G$
on the same probability space such that they are comonotonic and
$Y\sim G$
on the same probability space such that they are comonotonic and
Proof. To show sufficiency, let U be a random variable uniformly distributed on (0, 1). Then we have
![]() $(X,Y) \buildrel \mathrm{d} \over = (F^{-1}(U),G^{-1}(U))$
and hence, for
$(X,Y) \buildrel \mathrm{d} \over = (F^{-1}(U),G^{-1}(U))$
and hence, for
![]() $y\in\mathbb{R}$
,
$y\in\mathbb{R}$
,
 \begin{align*} \mathbb{E}[(Y-X)_- \mid Y\le y] & = \mathbb{E} [ (G^{-1}(U)-F^{-1}(U) )_- \mid G^{-1}(U)\le y ]\\ & = \mathbb{E} [ (G^{-1}(U)-F^{-1}(U) )_- \mid U\le G(y) ]\\ & = \frac 1{G(y)} \int_0^{G(y)} (G^{-1}(\alpha)-F^{-1}(\alpha) )_- {\mathrm{d}} \alpha.\end{align*}
\begin{align*} \mathbb{E}[(Y-X)_- \mid Y\le y] & = \mathbb{E} [ (G^{-1}(U)-F^{-1}(U) )_- \mid G^{-1}(U)\le y ]\\ & = \mathbb{E} [ (G^{-1}(U)-F^{-1}(U) )_- \mid U\le G(y) ]\\ & = \frac 1{G(y)} \int_0^{G(y)} (G^{-1}(\alpha)-F^{-1}(\alpha) )_- {\mathrm{d}} \alpha.\end{align*}
Similarly,
Since G is continuous, then for any
![]() $p\in (0,1)$
there exists
$p\in (0,1)$
there exists
![]() $y\in\mathbb{R}$
such that
$y\in\mathbb{R}$
such that
![]() $G(y)=p$
. It follows from (3.10) that (2.4) holds for all
$G(y)=p$
. It follows from (3.10) that (2.4) holds for all
![]() $p\in (0,1)$
. It is obvious to check that (2.4) holds for
$p\in (0,1)$
. It is obvious to check that (2.4) holds for
![]() $p=1$
by the continuity of the two functions of (2.4). Therefore we have
$p=1$
by the continuity of the two functions of (2.4). Therefore we have
![]() $F\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} G$
.
$F\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} G$
.
Necessity follows immediately by taking
![]() $(X,Y)\;:\!=\; (F^{-1}(U),G^{-1}(U))$
with U uniformly distributed on (0,1). This completes the proof.
$(X,Y)\;:\!=\; (F^{-1}(U),G^{-1}(U))$
with U uniformly distributed on (0,1). This completes the proof.
3.5. Bivariate characterization
To state the bivariate characterization for
![]() $(1+\gamma)$
-SD, we introduce the following class of bivariate functions:
$(1+\gamma)$
-SD, we introduce the following class of bivariate functions:
Proposition 3.4. Let X and Y be two independent random variables. Then
![]() $X\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}{\rm SD}}} Y$
if and only if
$X\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}{\rm SD}}} Y$
if and only if
Proof. The sufficiency is trivial by noting that, for any
![]() $u\in \mathcal U_\gamma^\ast$
, the bivariate function
$u\in \mathcal U_\gamma^\ast$
, the bivariate function
![]() $\phi(x,y)\;:\!=\; u(x)$
belongs to the set
$\phi(x,y)\;:\!=\; u(x)$
belongs to the set
![]() $\mathcal G_\gamma$
. To see the necessity, for any
$\mathcal G_\gamma$
. To see the necessity, for any
![]() $\phi\in\mathcal G_\gamma$
, define
$\phi\in\mathcal G_\gamma$
, define
It can be easily verified that
![]() $u\in \mathcal U_\gamma^\ast$
and thus
$u\in \mathcal U_\gamma^\ast$
and thus
Necessity then follows, and hence we complete the proof.
It is worth noting that the above result still holds true if all
![]() $\mathcal U_\gamma^\ast$
are replaced by
$\mathcal U_\gamma^\ast$
are replaced by
![]() $\mathcal U_\gamma$
. For
$\mathcal U_\gamma$
. For
![]() $\gamma=1$
, the equivalence characterization was implicitly given in [Reference Shanthikumar and Yao27]; see also Theorem 4.A.7 of [Reference Shaked and Shanthikumar26]. An application of Proposition 3.4 is given in Example 5.6.
$\gamma=1$
, the equivalence characterization was implicitly given in [Reference Shanthikumar and Yao27]; see also Theorem 4.A.7 of [Reference Shaked and Shanthikumar26]. An application of Proposition 3.4 is given in Example 5.6.
4. Applications
4.1. Closure under p-quantile truncation
Proposition 4.1. Let X and Y be two continuous random variables with respective distribution functions F and G. If
![]() $X \preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}{\rm SD}}} Y$
, then
$X \preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}{\rm SD}}} Y$
, then
Proof. Let
![]() $\phi\in\mathcal{U}_\gamma$
, and suppose that
$\phi\in\mathcal{U}_\gamma$
, and suppose that
![]() $X\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} Y$
. From Proposition 2.2 it follows that
$X\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} Y$
. From Proposition 2.2 it follows that
![]() $\phi(X)\preccurlyeq_{\mathrm{SSD}} \phi(Y)$
. Since
$\phi(X)\preccurlyeq_{\mathrm{SSD}} \phi(Y)$
. Since
![]() $F_{\phi(X)}^{-1}(\alpha) =\phi(F^{-1}(\alpha))$
for each
$F_{\phi(X)}^{-1}(\alpha) =\phi(F^{-1}(\alpha))$
for each
![]() $\alpha$
, by Theorems 4.A.1 and 4.A.3 in [Reference Shaked and Shanthikumar26], we have
$\alpha$
, by Theorems 4.A.1 and 4.A.3 in [Reference Shaked and Shanthikumar26], we have
or, equivalently,
![]() $\mathbb{E} [\phi(X) \mid X\le F^{-1}(p) ] \le \mathbb{E} [\phi(Y) \mid Y \le G^{-1}(p) ]$
since F and G are continuous. This means that (4.1) holds.
$\mathbb{E} [\phi(X) \mid X\le F^{-1}(p) ] \le \mathbb{E} [\phi(Y) \mid Y \le G^{-1}(p) ]$
since F and G are continuous. This means that (4.1) holds.
From the proof of Proposition 4.1, we conclude that if X and Y are general random variables (not necessarily continuous), then
![]() $F \preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} G$
implies that
$F \preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} G$
implies that
![]() $ F^{-1}(U) 1_{\{U\le p\}}$
$ F^{-1}(U) 1_{\{U\le p\}}$
![]() $\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} G^{-1}(U) 1_{\{U\le p\}}$
for
$\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} G^{-1}(U) 1_{\{U\le p\}}$
for
![]() $p\in (0,1)$
, where U is a random variable uniformly distributed on (0,1).
$p\in (0,1)$
, where U is a random variable uniformly distributed on (0,1).
Remark 4.1. When
![]() $\gamma=1$
, the result of Proposition 4.1 was implicitly given by Theorem 4.A.42 of [Reference Shaked and Shanthikumar26] without the constraint of continuity. However, we point out that the condition of continuity is necessary. To see it, we give a counter-example. Define two random variables X and Y with PMFs given by
$\gamma=1$
, the result of Proposition 4.1 was implicitly given by Theorem 4.A.42 of [Reference Shaked and Shanthikumar26] without the constraint of continuity. However, we point out that the condition of continuity is necessary. To see it, we give a counter-example. Define two random variables X and Y with PMFs given by
![]() $\mathbb{P}(X=0)=0.625$
,
$\mathbb{P}(X=0)=0.625$
,
![]() $\mathbb{P}(X=4)=0.375$
and
$\mathbb{P}(X=4)=0.375$
and
![]() $\mathbb{P}(Y=1)=0.7$
,
$\mathbb{P}(Y=1)=0.7$
,
![]() $\mathbb{P}(Y=2)=0.1$
,
$\mathbb{P}(Y=2)=0.1$
,
![]() $\mathbb{P}(Y=3)=0.2$
. It is easy to verify that
$\mathbb{P}(Y=3)=0.2$
. It is easy to verify that
![]() $\mathbb{E}[X]=1.5=\mathbb{E}[Y]$
, and hence
$\mathbb{E}[X]=1.5=\mathbb{E}[Y]$
, and hence
![]() $X\preccurlyeq_{\mathrm{SSD}} Y$
. Let F and G denote the distribution functions of X and Y, respectively. Note that, for
$X\preccurlyeq_{\mathrm{SSD}} Y$
. Let F and G denote the distribution functions of X and Y, respectively. Note that, for
![]() $p=0.7$
,
$p=0.7$
,
and
Thus
![]() $[X\mid X\le F^{-1}(p)] \not \prec_{\mathrm{SSD}} [Y\mid Y\le G^{-1}(p)]$
.
$[X\mid X\le F^{-1}(p)] \not \prec_{\mathrm{SSD}} [Y\mid Y\le G^{-1}(p)]$
.
4.2. Closure under comonotonic sums
Equation (2.5) states that
![]() $(1+\gamma)$
-SD is closed under independent sums. With Theorem 3.1 we can prove that
$(1+\gamma)$
-SD is closed under independent sums. With Theorem 3.1 we can prove that
![]() $(1+\gamma)$
-SD is closed under comonotonic sums.
$(1+\gamma)$
-SD is closed under comonotonic sums.
Proposition 4.2. Let
![]() $X_i$
and
$X_i$
and
![]() $Y_i$
be two random variables such that
$Y_i$
be two random variables such that
![]() $X_i\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}{\rm SD}}} Y_i$
for
$X_i\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}{\rm SD}}} Y_i$
for
![]() $i=1, 2$
and
$i=1, 2$
and
![]() $\gamma\in [0,1]$
. If
$\gamma\in [0,1]$
. If
![]() $X_1$
and
$X_1$
and
![]() $X_2$
are comonotonic and
$X_2$
are comonotonic and
![]() $Y_1$
and
$Y_1$
and
![]() $Y_2$
are comonotonic, then
$Y_2$
are comonotonic, then
![]() $ X_1+X_2\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}{\rm SD}}} Y_1+Y_2$
.
$ X_1+X_2\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}{\rm SD}}} Y_1+Y_2$
.
Proof. Let
![]() $F_i$
and F denote the distribution functions of
$F_i$
and F denote the distribution functions of
![]() $X_i$
and
$X_i$
and
![]() $X_1+X_2$
, respectively. Similarly, let
$X_1+X_2$
, respectively. Similarly, let
![]() $G_i$
and G denote the distribution functions of
$G_i$
and G denote the distribution functions of
![]() $Y_i$
and
$Y_i$
and
![]() $Y_1+Y_2$
, respectively. Since
$Y_1+Y_2$
, respectively. Since
![]() $X_1$
and
$X_1$
and
![]() $X_2$
are comonotonic, it follows from [Reference Dhaene, Denuit, Goovaerts, Kaas and Vyncke8] that
$X_2$
are comonotonic, it follows from [Reference Dhaene, Denuit, Goovaerts, Kaas and Vyncke8] that
![]() $F^{-1}(\alpha) = F_1^{-1}(\alpha) + F_2^{-1}(\alpha)$
for all
$F^{-1}(\alpha) = F_1^{-1}(\alpha) + F_2^{-1}(\alpha)$
for all
![]() $\alpha\in (0,1)$
. Similarly,
$\alpha\in (0,1)$
. Similarly,
![]() $G^{-1}(\alpha) = G_1^{-1}(\alpha) + G_2^{-1}(\alpha)$
for all
$G^{-1}(\alpha) = G_1^{-1}(\alpha) + G_2^{-1}(\alpha)$
for all
![]() $\alpha\in (0,1)$
. By Theorem 3.1 (iii),
$\alpha\in (0,1)$
. By Theorem 3.1 (iii),
![]() $X_i\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} Y_i$
implies that
$X_i\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} Y_i$
implies that
Thus
implying
![]() $X_1+X_2\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} Y_1+Y_2$
by applying Theorem 3.1 (iii) again. This completes the proof of the proposition.
$X_1+X_2\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} Y_1+Y_2$
by applying Theorem 3.1 (iii) again. This completes the proof of the proposition.
4.3. Closure under minima
We first present a general result concerning the preservation of
![]() $(1+\gamma)$
-SD under increasing and concave transforms.
$(1+\gamma)$
-SD under increasing and concave transforms.
Proposition 4.3. Let
![]() $X_1, \ldots, X_n$
be a set of independent random variables, and let
$X_1, \ldots, X_n$
be a set of independent random variables, and let
![]() $Y_1, \ldots, Y_n$
be another set of independent random variables. If
$Y_1, \ldots, Y_n$
be another set of independent random variables. If
![]() $X_i \preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}{\rm SD}}} Y_i$
for
$X_i \preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}{\rm SD}}} Y_i$
for
![]() $i=1, \ldots, n$
and
$i=1, \ldots, n$
and
![]() $\gamma\in [0,1]$
, then
$\gamma\in [0,1]$
, then
for every increasing and component-wise concave function g.
Proof. Without loss of generality, assume that all random variables
![]() $X_i$
and
$X_i$
and
![]() $Y_i$
are independent. The proof is by induction on n. For
$Y_i$
are independent. The proof is by induction on n. For
![]() $n=1$
, the result is just Proposition 2.2. Assume that (4.2) holds true for
$n=1$
, the result is just Proposition 2.2. Assume that (4.2) holds true for
![]() $n=m-1\ge 1$
. Let
$n=m-1\ge 1$
. Let
![]() $g\colon \mathbb{R}^m\to\mathbb{R}$
be an increasing and component-wise concave function, and let
$g\colon \mathbb{R}^m\to\mathbb{R}$
be an increasing and component-wise concave function, and let
![]() $u\in \mathcal{U}_\gamma$
. Then
$u\in \mathcal{U}_\gamma$
. Then
![]() $u(g(x_1,\ldots, x_m))\in\mathcal {U}_\gamma$
with respect to
$u(g(x_1,\ldots, x_m))\in\mathcal {U}_\gamma$
with respect to
![]() $x_j$
with other
$x_j$
with other
![]() $x_i$
fixed, and hence
$x_i$
fixed, and hence
 \begin{align*} \mathbb{E} [u(g(X_1, X_2,\ldots, X_m))\mid X_1=x] & = \mathbb{E} [u(g(x, X_2,\ldots, X_m))]\\ &\le \mathbb{E} [u(g(x, Y_2,\ldots, Y_m))]\\ &= \mathbb{E} [u(g(X_1, Y_2,\ldots, Y_m))\mid X_1=x],\end{align*}
\begin{align*} \mathbb{E} [u(g(X_1, X_2,\ldots, X_m))\mid X_1=x] & = \mathbb{E} [u(g(x, X_2,\ldots, X_m))]\\ &\le \mathbb{E} [u(g(x, Y_2,\ldots, Y_m))]\\ &= \mathbb{E} [u(g(X_1, Y_2,\ldots, Y_m))\mid X_1=x],\end{align*}
where the equality follows from the independence of all random variables, and the inequality follows from the induction assumption. Thus
Similarly, we have
This proves the desired result.
From Proposition 4.3 we obtain the following corollary by observing that
![]() $\min\{x_1, \ldots, x_n\}$
is an increasing and component-wise concave function.
$\min\{x_1, \ldots, x_n\}$
is an increasing and component-wise concave function.
Corollary 4.1. Let
![]() $X_1, \ldots, X_n$
be a set of independent random variables, and let
$X_1, \ldots, X_n$
be a set of independent random variables, and let
![]() $Y_1, \ldots, Y_n$
be another set of independent random variables. If
$Y_1, \ldots, Y_n$
be another set of independent random variables. If
![]() $X_i \preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}{\rm SD}}} Y_i$
for
$X_i \preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}{\rm SD}}} Y_i$
for
![]() $i=1, \ldots, n$
and
$i=1, \ldots, n$
and
![]() $\gamma\in [0,1]$
, then
$\gamma\in [0,1]$
, then
For
![]() $\gamma =1$
, Corollary 4.1 for SSD was implicitly given in [Reference Li, Li and Jing17]; see, for example, the paragraph after Corollary 4.A.16 in [Reference Shaked and Shanthikumar26].
$\gamma =1$
, Corollary 4.1 for SSD was implicitly given in [Reference Li, Li and Jing17]; see, for example, the paragraph after Corollary 4.A.16 in [Reference Shaked and Shanthikumar26].
4.4. Closure under distortion
Under suitable conditions,
![]() $(1+\gamma)$
-SD is preserved under a distortion transformation on the space of distribution functions.
$(1+\gamma)$
-SD is preserved under a distortion transformation on the space of distribution functions.
Proposition 4.4. Let F and G be two distribution functions such that
![]() $F\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}{\rm SD}}} G$
, and right continuous
$F\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}{\rm SD}}} G$
, and right continuous
![]() $h\in \mathcal H_\beta$
with
$h\in \mathcal H_\beta$
with
![]() $\gamma\in [0,1]$
,
$\gamma\in [0,1]$
,
![]() $\beta\in (0,1]$
, and
$\beta\in (0,1]$
, and
![]() $\gamma\le \beta$
. Then
$\gamma\le \beta$
. Then
![]() $h(F)\preccurlyeq_{\mathrm{(1+\gamma/\beta)\hbox{-}{\rm SD}}} h(G)$
.
$h(F)\preccurlyeq_{\mathrm{(1+\gamma/\beta)\hbox{-}{\rm SD}}} h(G)$
.
Proof. Denote
![]() $F_h=h(F)$
and
$F_h=h(F)$
and
![]() $G_h=h(G)$
. Then their left inverse functions are
$G_h=h(G)$
. Then their left inverse functions are
![]() $F_h^{-1}(p)=F^{-1}(h^{-1}(p))$
and
$F_h^{-1}(p)=F^{-1}(h^{-1}(p))$
and
![]() $G_h^{-1}(p)=G^{-1}(h^{-1}(p))$
, where all the inversion functions are left inverse. Then, for any
$G_h^{-1}(p)=G^{-1}(h^{-1}(p))$
, where all the inversion functions are left inverse. Then, for any
![]() $\phi\in \mathcal H_{\gamma/\beta}^\ast$
, we have
$\phi\in \mathcal H_{\gamma/\beta}^\ast$
, we have
Similarly,
Note that for any
![]() $\phi\in \mathcal H_{\gamma/\beta}^\ast$
it can be verified that
$\phi\in \mathcal H_{\gamma/\beta}^\ast$
it can be verified that
![]() $\phi(h)\in \mathcal H_{\gamma}^\ast$
. To see this, for any
$\phi(h)\in \mathcal H_{\gamma}^\ast$
. To see this, for any
![]() $0\le p_1<p_2\le p_3<p_4\le 1$
we have
$0\le p_1<p_2\le p_3<p_4\le 1$
we have
 \begin{align*} \gamma \frac{\phi(h(p_4))-\phi(h(p_3))}{p_4-p_3} & = \frac{\gamma}{\beta} \frac{\phi(h(p_4))-\phi(h(p_3))}{h(p_4)-h(p_3)} \cdot \beta \frac{h(p_4)-h(p_3)}{p_4-p_3} \\ &\le \frac{\phi(h(p_2))-\phi(h(p_1))}{h(p_2)-h(p_1)} \cdot \frac{h(p_2)-h(p_1)}{p_2-p_1} \\ & = \frac{\phi(h(p_2))-\phi(h(p_1))}{p_2-p_1},\end{align*}
\begin{align*} \gamma \frac{\phi(h(p_4))-\phi(h(p_3))}{p_4-p_3} & = \frac{\gamma}{\beta} \frac{\phi(h(p_4))-\phi(h(p_3))}{h(p_4)-h(p_3)} \cdot \beta \frac{h(p_4)-h(p_3)}{p_4-p_3} \\ &\le \frac{\phi(h(p_2))-\phi(h(p_1))}{h(p_2)-h(p_1)} \cdot \frac{h(p_2)-h(p_1)}{p_2-p_1} \\ & = \frac{\phi(h(p_2))-\phi(h(p_1))}{p_2-p_1},\end{align*}
where the inequality follows from the fact that
![]() $\phi\in \mathcal H_{\gamma/\beta}^\ast$
,
$\phi\in \mathcal H_{\gamma/\beta}^\ast$
,
![]() $h\in \mathcal H_\beta^\ast$
, and h is increasing. Then the desired result follows immediately from Theorem 3.1 (iii).
$h\in \mathcal H_\beta^\ast$
, and h is increasing. Then the desired result follows immediately from Theorem 3.1 (iii).
For SSD (
![]() $\gamma=\beta=1$
), Proposition 4.4 was implicitly given in Theorem 4.2 of [Reference Tsukahara29], which was proved by using the fact that any concave
$\gamma=\beta=1$
), Proposition 4.4 was implicitly given in Theorem 4.2 of [Reference Tsukahara29], which was proved by using the fact that any concave
![]() $h\in \mathcal{H}$
can be approximated by a sequence of piecewise linear concave distortion functions of the form
$h\in \mathcal{H}$
can be approximated by a sequence of piecewise linear concave distortion functions of the form
![]() $h_\alpha(t)=\min\{t/\alpha, 1\}$
,
$h_\alpha(t)=\min\{t/\alpha, 1\}$
,
![]() $0<\alpha\le 1$
.
$0<\alpha\le 1$
.
4.5. Equivalence characterization
In the expected utility theory, a decision-maker is risk-averse if she has an increasing and concave utility function. The next proposition states that, for two risks X and Y satisfying
![]() $X\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} Y$
, if a risk-averse decision-maker is indifferent between X and Y, then X and Y are identically distributed.
$X\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} Y$
, if a risk-averse decision-maker is indifferent between X and Y, then X and Y are identically distributed.
Proposition 4.5. Let
![]() $\gamma\in [0,1)$
, and let X and Y be two random variables such that
$\gamma\in [0,1)$
, and let X and Y be two random variables such that
![]() $X\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}{\rm SD}}} Y$
. If
$X\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}{\rm SD}}} Y$
. If
![]() $\mathbb{E}[\phi(X)]=\mathbb{E}[\phi(Y)]$
for some strictly increasing and concave function
$\mathbb{E}[\phi(X)]=\mathbb{E}[\phi(Y)]$
for some strictly increasing and concave function
![]() $\phi$
, then
$\phi$
, then
![]() $X \buildrel \mathrm{d} \over = Y$
.
$X \buildrel \mathrm{d} \over = Y$
.
Proof. By Proposition 4.3, it suffices to show the case when
![]() $\phi(x)=x$
for
$\phi(x)=x$
for
![]() $x\in\mathbb{R}$
, i.e.
$x\in\mathbb{R}$
, i.e.
![]() $\mathbb{E}[X]=\mathbb{E}[Y]$
. Let F and G denote the distribution functions of X and Y, respectively. By Proposition 2.1, we have that
$\mathbb{E}[X]=\mathbb{E}[Y]$
. Let F and G denote the distribution functions of X and Y, respectively. By Proposition 2.1, we have that
![]() $X\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}{\rm SD}}} Y$
if and only if (2.3) holds, that is,
$X\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}{\rm SD}}} Y$
if and only if (2.3) holds, that is,
Note that
Then, taking
![]() $t\to\infty$
in (4.3) yields
$t\to\infty$
in (4.3) yields
which implies that
![]() $(G(x)-F(x))_+=0$
for all
$(G(x)-F(x))_+=0$
for all
![]() $x\in\mathbb{R}$
, i.e.
$x\in\mathbb{R}$
, i.e.
![]() $G(x)\le F(x)$
for all
$G(x)\le F(x)$
for all
![]() $x\in\mathbb{R}$
. Thus we have
$x\in\mathbb{R}$
. Thus we have
![]() $X \preccurlyeq_{\mathrm{st}}Y$
. By
$X \preccurlyeq_{\mathrm{st}}Y$
. By
![]() $\mathbb{E}[X]=\mathbb{E}[Y]$
, it follows from Theorem 1.A.8 of [Reference Shaked and Shanthikumar26] that
$\mathbb{E}[X]=\mathbb{E}[Y]$
, it follows from Theorem 1.A.8 of [Reference Shaked and Shanthikumar26] that
![]() $X \buildrel \mathrm{d} \over = Y$
. This completes the proof.
$X \buildrel \mathrm{d} \over = Y$
. This completes the proof.
In the literature, several authors have investigated conditions under which ordered random variables are equal in distribution; see, for example, [Reference Bhattacharjee3], [Reference Bhattacharjee and Bhattacharya4], [Reference Cheung, Dhaene, Kukush and Linders6], and [Reference Li and Zhu16].
An immediate consequence of Proposition 4.5 is the following corollary.
Corollary 4.2. Let
![]() $X_1,X_2, \ldots, X_n$
and
$X_1,X_2, \ldots, X_n$
and
![]() $Y_1, Y_2, \ldots, Y_n$
be two collections of independent and identically distributed random variables. If
$Y_1, Y_2, \ldots, Y_n$
be two collections of independent and identically distributed random variables. If
![]() $X_1\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}{\rm SD}}} Y_1$
and
$X_1\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}{\rm SD}}} Y_1$
and
then
![]() $X_1 \buildrel \mathrm{d} \over = Y_1$
.
$X_1 \buildrel \mathrm{d} \over = Y_1$
.
Proof. From Corollary 4.1 it follows that
![]() $\min_{1\le i\le n} X_i\}\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} \min_{1\le i\le n} Y_i$
. By Proposition 4.5,
$\min_{1\le i\le n} X_i\}\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} \min_{1\le i\le n} Y_i$
. By Proposition 4.5,
![]() $\mathbb{E}[\min_{1\le i\le n} X_i] = \mathbb{E}[\min_{1\le i\le n} Y_i]$
implies that
$\mathbb{E}[\min_{1\le i\le n} X_i] = \mathbb{E}[\min_{1\le i\le n} Y_i]$
implies that
![]() $\min_{1\le i\le n} X_i \buildrel \mathrm{d} \over = \min_{1\le i\le n} Y_i$
. Therefore, by the relation between the survival functions of
$\min_{1\le i\le n} X_i \buildrel \mathrm{d} \over = \min_{1\le i\le n} Y_i$
. Therefore, by the relation between the survival functions of
![]() $X_1$
and
$X_1$
and
![]() $\min_{1\le i\le n} X_i$
, we have
$\min_{1\le i\le n} X_i$
, we have
![]() $X_1 \buildrel \mathrm{d} \over = Y_1$
.
$X_1 \buildrel \mathrm{d} \over = Y_1$
.
5. Examples
In this section we present several examples of distributions ordered with respect to the order
![]() $\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}}$
except for those given in [Reference Müller, Scarsini and Tsetlin25], and also give some applications of the main results in the previous section.
$\preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}}$
except for those given in [Reference Müller, Scarsini and Tsetlin25], and also give some applications of the main results in the previous section.
Example 5.1. (Binary distribution.) Let X and Y be two binary random variables with PMFs given by
where
![]() $x_1<x_2$
and
$x_1<x_2$
and
![]() $y_1<y_2$
, and assume that
$y_1<y_2$
, and assume that
![]() $X \preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} Y$
for some
$X \preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} Y$
for some
![]() $\gamma\in (0,1]$
. Denote
$\gamma\in (0,1]$
. Denote
![]() $X\sim F$
and
$X\sim F$
and
![]() $Y\sim G$
. From (2.3), it follows that
$Y\sim G$
. From (2.3), it follows that
![]() $x_1\le y_1$
and
$x_1\le y_1$
and
If
![]() $y_2>x_2$
, then define a new random variable
$y_2>x_2$
, then define a new random variable
![]() $Y^\ast$
such that
$Y^\ast$
such that
![]() $\mathbb{P}(Y^\ast=y_1)=q=1-\mathbb{P}(Y^\ast=x_2)$
. Then
$\mathbb{P}(Y^\ast=y_1)=q=1-\mathbb{P}(Y^\ast=x_2)$
. Then
![]() $X \preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} Y^\ast$
if and only if
$X \preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} Y^\ast$
if and only if
![]() $X \preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} Y$
. So, without loss of generality, assume that
$X \preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} Y$
. So, without loss of generality, assume that
![]() $x_1\le y_1<y_2\le x_2$
and (5.1) holds. Then
$x_1\le y_1<y_2\le x_2$
and (5.1) holds. Then
 \begin{equation*} G(x)-F(x) = \begin{cases} -p & \text{for $ x_1\le x<y_1$,}\\ q-p & \text{for $ y_1\le x<y_2$,}\\ 1-p & \text{for $ y_2\le x<x_2$,} \\ 0 & \text{otherwise}. \end{cases}\end{equation*}
\begin{equation*} G(x)-F(x) = \begin{cases} -p & \text{for $ x_1\le x<y_1$,}\\ q-p & \text{for $ y_1\le x<y_2$,}\\ 1-p & \text{for $ y_2\le x<x_2$,} \\ 0 & \text{otherwise}. \end{cases}\end{equation*}
It follows that
![]() $X \preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} Y$
if and only if
$X \preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} Y$
if and only if
or, equivalently,
Example 5.2. (Special transfer.) Let Y be a discrete random variable with PMF given by

where
![]() $x_1<x_2<\cdots<x_n$
. Let
$x_1<x_2<\cdots<x_n$
. Let
![]() $0<\alpha<1$
and
$0<\alpha<1$
and
![]() $P_i=\sum_{j=1}^i p_i$
for each i. There exists a k such that
$P_i=\sum_{j=1}^i p_i$
for each i. There exists a k such that
![]() $P_{k-1}<\alpha\le P_k$
, where
$P_{k-1}<\alpha\le P_k$
, where
![]() $P_0=0$
. Define a random variable X with PMF given by
$P_0=0$
. Define a random variable X with PMF given by

where
![]() $a, b>0$
such that
$a, b>0$
such that
![]() $(1-\alpha)b\le \alpha a$
. Denote
$(1-\alpha)b\le \alpha a$
. Denote
![]() $X\sim F$
and
$X\sim F$
and
![]() $Y\sim G$
. Obviously, F single-crosses G from above at point
$Y\sim G$
. Obviously, F single-crosses G from above at point
![]() $x_k$
. It is easy to see that
$x_k$
. It is easy to see that
and
From Corollary 2.5 in [Reference Müller, Scarsini and Tsetlin25], it follows that
![]() $X \preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} Y$
if and only if
$X \preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} Y$
if and only if
and that
![]() $X \preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}PSD}} Y$
if and only if
$X \preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}PSD}} Y$
if and only if
![]() $\gamma = (1-\alpha)b/(\alpha a)$
.
$\gamma = (1-\alpha)b/(\alpha a)$
.
Example 5.3. (Application of the separation theorem.) Let X be a discrete random variable with PMF given by

and let Y be another random variable with
![]() $\mathbb{P}(Y=2)=\mathbb{P}(Y=4)=1/2$
. We claim that
$\mathbb{P}(Y=2)=\mathbb{P}(Y=4)=1/2$
. We claim that
![]() $X \preccurlyeq_{\mathrm{(1\,+\,1/2)\hbox{-}SD}} Y$
. To verify this assertion, define a discrete random variable
$X \preccurlyeq_{\mathrm{(1\,+\,1/2)\hbox{-}SD}} Y$
. To verify this assertion, define a discrete random variable
![]() $X_1$
with PMF given by
$X_1$
with PMF given by

It can be checked that
![]() $X_1$
is a
$X_1$
is a
![]() $1/2$
-transfer of X, and Y is a
$1/2$
-transfer of X, and Y is a
![]() $1/2$
-transfer of
$1/2$
-transfer of
![]() $X_1$
, and hence
$X_1$
, and hence
![]() $X \preccurlyeq_{\mathrm{(1\,+\,1/2)\hbox{-}PSD}} X_1$
and
$X \preccurlyeq_{\mathrm{(1\,+\,1/2)\hbox{-}PSD}} X_1$
and
![]() $X_1\preccurlyeq_{\mathrm{(1+1/2)\hbox{-}PSD}} Y$
. This implies
$X_1\preccurlyeq_{\mathrm{(1+1/2)\hbox{-}PSD}} Y$
. This implies
![]() $X \preccurlyeq_{\mathrm{(1+1/2)\hbox{-}SD}} Y$
(but
$X \preccurlyeq_{\mathrm{(1+1/2)\hbox{-}SD}} Y$
(but
![]() $X \not\preccurlyeq_{\mathrm{(1+1/2)\hbox{-}PSD}} Y$
). Now we apply the method in the proof of Theorem 3.2 to construct two random variables
$X \not\preccurlyeq_{\mathrm{(1+1/2)\hbox{-}PSD}} Y$
). Now we apply the method in the proof of Theorem 3.2 to construct two random variables
![]() $Z_1$
and
$Z_1$
and
![]() $Z_2$
such that
$Z_2$
such that
Let
![]() $X\sim F$
,
$X\sim F$
,
![]() $Y\sim G$
,
$Y\sim G$
,
![]() $Z_1\sim H_1$
, and
$Z_1\sim H_1$
, and
![]() $Z_2\sim H_2$
, and let
$Z_2\sim H_2$
, and let
![]() $\delta_t(x)$
and
$\delta_t(x)$
and
![]() $\eta_t(x)$
be defined by (3.3) and (3.7), respectively. Then
$\eta_t(x)$
be defined by (3.3) and (3.7), respectively. Then
![]() $t_0=3$
in (3.4) and
$t_0=3$
in (3.4) and
![]() $t_1=2/3$
in (3.8). Hence
$t_1=2/3$
in (3.8). Hence
and
Therefore the PMFs of
![]() $Z_1$
and
$Z_1$
and
![]() $Z_2$
, respectively, are given by
$Z_2$
, respectively, are given by

Example 5.4. (Uniform distribution.) Let X and Y be random variables uniformly distributed over the intervals (a,b) and (c,d), respectively, and assume that
![]() $X \preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} Y$
for some
$X \preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} Y$
for some
![]() $\gamma\in (0,1]$
. From (2.3) it follows that
$\gamma\in (0,1]$
. From (2.3) it follows that
![]() $a\le c$
and
$a\le c$
and
![]() $X\preccurlyeq_{\mathrm{SSD}} Y$
, which implies
$X\preccurlyeq_{\mathrm{SSD}} Y$
, which implies
![]() $\mathbb{E} [X]\le \mathbb{E} [Y]$
(i.e.
$\mathbb{E} [X]\le \mathbb{E} [Y]$
(i.e.
![]() $a+b\le c+d$
). If
$a+b\le c+d$
). If
![]() $d>b$
, then
$d>b$
, then
![]() $X\preccurlyeq_{\mathrm{FSD}} Y$
. Without loss of generality, assume that
$X\preccurlyeq_{\mathrm{FSD}} Y$
. Without loss of generality, assume that
![]() $a< c<d\le b$
and
$a< c<d\le b$
and
![]() $a+b\le c+d$
. Denote
$a+b\le c+d$
. Denote
![]() $X\sim F$
and
$X\sim F$
and
![]() $Y\sim G$
. Then F single-crosses G at
$Y\sim G$
. Then F single-crosses G at
![]() $x_0\in (c,d)$
from above, where
$x_0\in (c,d)$
from above, where
It is easy to check that
and
From Corollary 2.5 in [Reference Müller, Scarsini and Tsetlin25] it follows that
![]() $X \preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} Y$
if and only if
$X \preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} Y$
if and only if
Example 5.5. (Shifted exponential distribution.) Let X and Y be two random variables with respective density functions given by
![]() $f(x)=\lambda {\mathrm{e}}^{-\lambda(x-a)}$
for
$f(x)=\lambda {\mathrm{e}}^{-\lambda(x-a)}$
for
![]() $x>a$
and
$x>a$
and
![]() $g(y)= \mu {\mathrm{e}}^{-\mu (y-b)}$
for
$g(y)= \mu {\mathrm{e}}^{-\mu (y-b)}$
for
![]() $y>b$
, where
$y>b$
, where
![]() $a, b\in\mathbb{R}$
and
$a, b\in\mathbb{R}$
and
![]() $\lambda,\mu>0$
. Assume that
$\lambda,\mu>0$
. Assume that
![]() $X \preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} Y$
for
$X \preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} Y$
for
![]() $\gamma\in (0,1]$
. It is known that
$\gamma\in (0,1]$
. It is known that
![]() $X\preccurlyeq_{\mathrm{SSD}} Y$
if and only if
$X\preccurlyeq_{\mathrm{SSD}} Y$
if and only if
![]() $a\le b$
and
$a\le b$
and
![]() $\delta \;:\!=\; b+1/\mu -a -1/\lambda\ge 0$
. If
$\delta \;:\!=\; b+1/\mu -a -1/\lambda\ge 0$
. If
![]() $a\le b$
and
$a\le b$
and
![]() $\lambda\ge \mu$
, then
$\lambda\ge \mu$
, then
![]() $X\preccurlyeq_{\mathrm{FSD}} Y$
. So, assume without loss of generality that
$X\preccurlyeq_{\mathrm{FSD}} Y$
. So, assume without loss of generality that
![]() $a\le b$
,
$a\le b$
,
![]() $\lambda<\mu$
and
$\lambda<\mu$
and
![]() $\delta \ge 0$
. Then F single-crosses G at
$\delta \ge 0$
. Then F single-crosses G at
![]() $x_0\in (c,d)$
from above, where
$x_0\in (c,d)$
from above, where
It is easy to check that
where
From Corollary 2.5 in [Reference Müller, Scarsini and Tsetlin25] it follows that
![]() $X \preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} Y$
if and only if
$X \preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} Y$
if and only if
Example 5.6. (Application of bivariate characterization.) Choose two real numbers
![]() $a<b$
such that
$a<b$
such that
![]() $2a\ge b$
, and define
$2a\ge b$
, and define
Let
![]() $\psi$
be any differentiable function with
$\psi$
be any differentiable function with
![]() $a\le \psi'(x)\le b$
for all
$a\le \psi'(x)\le b$
for all
![]() $x\in \mathbb{R}$
. Then
$x\in \mathbb{R}$
. Then
![]() $\phi(x,y)\;:\!=\; \psi(2x+y)\in {\mathcal G}_\gamma$
, where
$\phi(x,y)\;:\!=\; \psi(2x+y)\in {\mathcal G}_\gamma$
, where
![]() ${\mathcal G}_\gamma$
is defined by (3.11). If
${\mathcal G}_\gamma$
is defined by (3.11). If
![]() $X \preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} Y$
, and X and Y are independent, then
$X \preccurlyeq_{\mathrm{(1+\gamma)\hbox{-}SD}} Y$
, and X and Y are independent, then
by Proposition 3.4.
Acknowledgements
The authors are grateful to the Associate Editor and two anonymous referees for their comprehensive reviews of an earlier version of this paper.
Funding information
T. Mao was supported by the NNSF of China (no. 71671176). T. Hu was supported by the NNSF of China (no. 71871208) and by the Anhui Center for Applied Mathematics.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.