Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-21T17:44:52.611Z Has data issue: false hasContentIssue false
  • English
  • Français

Extrema of multi-dimensional Gaussian processes over random intervals

Part of: Stochastic processes

Published online by Cambridge University Press:  28 February 2022

Lanpeng Ji  and
Xiaofan Peng Open the ORCID record for Xiaofan Peng [Opens in a new window]
Lanpeng Ji*
Affiliation:
University of Leeds
Xiaofan Peng*
Affiliation:
University of Electronic Science and Technology of China
*
*Postal address: School of Mathematics, University of Leeds, Woodhouse Lane, Leeds LS2 9JT, UK.
**Postal address: School of Mathematical Sciences, University of Electronic Science and Technology of China, Chengdu 611731, China. Corresponding author’s email address: xfpeng@uestc.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

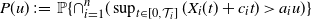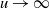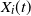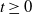This paper studies the joint tail asymptotics of extrema of the multi-dimensional Gaussian process over random intervals defined as $P(u)\;:\!=\; \mathbb{P}\{\cap_{i=1}^n (\sup_{t\in[0,\mathcal{T}_i]} ( X_{i}(t) +c_i t )>a_i u )\}$ , $u\rightarrow\infty$ , where $X_i(t)$ , $t\ge0$ , 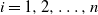$i=1,2,\ldots,n$ , are independent centered Gaussian processes with stationary increments, 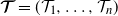$\boldsymbol{\mathcal{T}}=(\mathcal{T}_1, \ldots, \mathcal{T}_n)$ is a regularly varying random vector with positive components, which is independent of the Gaussian processes, and 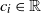$c_i\in \mathbb{R}$ , 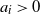$a_i>0$ , 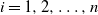$i=1,2,\ldots,n$ . Our result shows that the structure of the asymptotics of P(u) is determined by the signs of the drifts 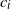$c_i$ . We also discuss a relevant multi-dimensional regenerative model and derive the corresponding ruin probability.

Keywords

Joint tail asymptoticGaussian processperturbed random walkruin probabilityfluid modelfractional Brownian motionregenerative model

MSC classification

Primary: 60G15: Gaussian processes
Secondary: 60G70: Extreme value theory; extremal processes
Type
Original Article
Information
Journal of Applied Probability , Volume 59 , Issue 1 , March 2022 , pp. 81 - 104
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arendarczyk, M. (2017). On the asymptotics of supremum distribution for some iterated processes. Extremes 20, 451–474.CrossRefGoogle Scholar
Arendarczyk, M. and DĘbicki, K. (2011). Asymptotics of supremum distribution of a Gaussian process over a Weibullian time. Bernoulli 17, 194–210.CrossRefGoogle Scholar
Arendarczyk, M. and DĘbicki, K. (2012). Exact asymptotics of supremum of a stationary Gaussian process over a random interval. Statist. Prob. Lett. 82, 645–652.CrossRefGoogle Scholar
Asmussen, S. and Albrecher, H. (2010). Ruin Probabilities, 2nd edn (Advanced Series on Statistical Science & Applied Probability 14). World Scientific, Hackensack, NJ.Google Scholar
Azais, J.-M. and Pham, V. (2019). Geometry of conjunction set of smooth stationary Gaussian fields. Available at arXiv:1909.07090v1.Google Scholar
Barndorff-Nielsen, O. E., Pedersen, J. and Sato, K.-I. (2001). Multivariate subordination, self-decomposability and stability. Adv. Appl. Prob. 33, 160–187.CrossRefGoogle Scholar
Basrak, B., Davis, R. A. and Mikosch, T. (2002). Regular variation of GARCH processes. Stoch. Process. Appl. 99, 95–115.CrossRefGoogle Scholar
Bingham, N., Goldie, C. and Teugels, J. (1989). Regular Variation (Encyclopedia of Mathematics and its Applications 27). Cambridge University Press.Google Scholar
Constantinescu, C., Delsing, G., Mandjes, M. and Rojas Nandayapa, L. (2020). A ruin model with a resampled environment. Scand. Actuarial J. 2020, 323–341.CrossRefGoogle Scholar
DĘbicki, K. and Peng, X. (2020). Sojourns of stationary Gaussian processes over a random interval. Available at arXiv:2004.12290.Google Scholar
DĘbicki, K., Hashorva, E. and Ji, L. (2014). Tail asymptotics of supremum of certain Gaussian processes over threshold dependent random intervals. Extremes 17, 411–429.CrossRefGoogle Scholar
DĘbicki, K., Hashorva, E., Ji, L. and TabiŚ, K. (2015). Extremes of vector-valued Gaussian processes: exact asymptotics. Stoch. Process. Appl. 125, 4039–4065.CrossRefGoogle Scholar
DĘbicki, K., Hashorva, E. and Kriukov, N. (2021). Pandemic-type failures in multivariate Brownian risk models. Available at arXiv:2008.07480.Google Scholar
DĘbicki, K., Hashorva, E. and Krystecki, K. (2020). Finite-time ruin probability for correlated Brownian motions. Available at arXiv:2004.14015.Google Scholar
DĘbicki, K., Hashorva, E. and Wang, L. (2020). Extremes of vector-valued Gaussian processes. Stoch. Process. Appl. 130, 5802–5837.CrossRefGoogle Scholar
DĘbicki, K., Ji, L. and Rolski, T. (2020). Exact asymptotics of component-wise extrema of two-dimensional Brownian motion. Extremes 23, 569–602.CrossRefGoogle Scholar
DĘbicki, K., Kosiński, K., Mandjes, M. and Rolski, T. (2010). Extremes of multi-dimensional Gaussian processes. Stoch. Process. Appl. 120, 2289–2301.CrossRefGoogle Scholar
DĘbicki, K., Zwart, B. and Borst, S. (2004). The supremum of a Gaussian process over a random interval. Statist. Prob. Lett. 68, 221–234.CrossRefGoogle Scholar
Dieker, A. (2005). Extremes of Gaussian processes over an infinite horizon. Stoch. Process. Appl. 115, 207–248.CrossRefGoogle Scholar
He, H., Keirstead, W. P. and Rebholz, J. (1998). Double lookbacks. Math. Finance 8, 201–228.CrossRefGoogle Scholar
Hult, H., Lindskog, F., Mikosch, T. and Samorodnitsky, G. (2006). Functional large deviations for multivariate regularly varying random walks. Ann. Appl. Prob. 15, 2651–2680.Google Scholar
Jessen, A. H. and Mikosch, T. (2006). Regular varying functions. Publ. Inst. Math. 80, 171–192.CrossRefGoogle Scholar
Ji, L. and Robert, S. (2018). Ruin problem of a two-dimensional fractional Brownian motion risk process. Stoch. Models 34, 73–97.CrossRefGoogle Scholar
Kella, O. and Whitt, W. (1992). A storage model with a two-state random environment. Operat. Res. 40, S257–S262.CrossRefGoogle Scholar
Kim, Y. S. (2012). The fractional multivariate normal tempered stable process. Appl. Math. Lett. 25, 2396–2401.CrossRefGoogle Scholar
Luciano, E. and Semeraro, P. (2010). Multivariate time changes for Lévy asset models: characterization and calibration. J. Comput. Appl. Math. 233, 1937–1953.CrossRefGoogle Scholar
Mikosch, T. (1999). Regular Variation, Subexponentiatility and their Applications in Probability Theory (lecture notes for the workshop ‘Heavy tails and queues’). EURANDOM Institute, Eindhoven, The Netherlands.Google Scholar
Palmowski, Z. and Zwart, B. (2007). Tail asymptotics of the supremum of a regenerative process. J. Appl. Prob. 44, 349–365.CrossRefGoogle Scholar
Pham, V.-H. (2020). Conjunction probability of smooth centered Gaussian processes. Acta Math. Vietnam. 45, 865–874.CrossRefGoogle Scholar
Piterbarg, V. (1996). Asymptotic Methods in the Theory of Gaussian Processes and Fields (Translations of Mathematical Monographs 148). American Mathematical Society, Providence, RI.Google Scholar
Piterbarg, V. and Stamatovich, B. (2005). Crude asymptotics of the probability of simultaneous high extrema of two Gaussian processes: the dual action function. Russian Math. Surveys 60, 167–168.CrossRefGoogle Scholar
Ratanov, N. (2020). Kac–Lévy processes. J. Theoret. Prob. 33, 239–267.CrossRefGoogle Scholar
Resnick, S. I. (1987). Extreme Values, Regular variation, and Point Processes. Springer, London.CrossRefGoogle Scholar
Resnick, S. I. (2007). Heavy-Tail Phenomena: Probabilistic and Statistical Modeling. Springer, London.Google Scholar
Samorodnitsky, G. and Taqq, M. S. (1994). Stable Non-Gaussian Random Processes. Chapman & Hall, London.Google Scholar
Tan, Z. and Hashorva, E. (2013). Exact asymptotics and limit theorems for supremum of stationary $\chi$ -processes over a random interval. Stoch. Process. Appl. 123, 2983–2998.CrossRefGoogle Scholar
van der Hofstad, R. and Honnappa, H. (2019). Large deviations of bivariate Gaussian extrema. Queueing Systems 93, 333–349.CrossRefGoogle Scholar
Worsley, K. and Friston, K. (2000). A test for a conjunction. Statist. Prob. Lett. 47, 135–140.CrossRefGoogle Scholar
Zaïdi, N. and Nualart, D. (2003). Smoothness of the law of the supremum of the fractional Brownian motion. Electron. Commun. Prob. 8, 102–111.CrossRefGoogle Scholar
Zwart, B., Borst, S. and DDĘbicki, K. (2005). Subexponential asymptotics of hybrid fluid and ruin models. Ann. Appl. Prob. 15, 500–517.CrossRefGoogle Scholar