Hostname: page-component-76fb5796d-wq484 Total loading time: 0 Render date: 2024-04-25T08:23:33.521Z Has data issue: false hasContentIssue false
  • English
  • Français

A Diffusion Limit for Generalized Correlated Random Walks

Part of: Markov processes Limit theorems

Published online by Cambridge University Press:  14 July 2016

Urs Gruber  and
Martin Schweizer
Urs Gruber*
Affiliation:
Allianz AG
Martin Schweizer*
Affiliation:
ETH Zürich
*
∗ Postal address: Allianz AG, Allianz Global Risks, Königinstrasse 28, D-80802 München, Germany. Email address: ursgruber@gmx.net
∗∗ Postal address: Departement Mathematik, ETH Zürich, ETH-Zentrum, HG G28.2, CH-8092 Zürich, Switzerland. Email address: martin.schweizer@math.ethz.ch
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

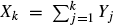A generalized correlated random walk is a process of partial sums such that (X, Y) forms a Markov chain. For a sequence (Xn) of such processes in which each 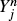takes only two values, we prove weak convergence to a diffusion process whose generator is explicitly described in terms of the limiting behaviour of the transition probabilities for the Yn. Applications include asymptotics of option replication under transaction costs and approximation of a given diffusion by regular recombining binomial trees.

Keywords

Correlated random walkdiffusion limitweak convergencemathematical financelarge investortransaction costbinomial tree

MSC classification

Primary: 60F17: Functional limit theorems; invariance principles 60J60: Diffusion processes
Type
Research Papers
Information
Journal of Applied Probability , Volume 43 , Issue 1 , March 2006 , pp. 60 - 73
Copyright
© Applied Probability Trust 2006 

References

Billingsley, P. (1968). Convergence of Probability Measures. John Wiley, New York.Google Scholar
Boyle, P. P. and Vorst, T. (1992). Option replication in discrete time with transaction costs. J. Finance 47, 271–293.Google Scholar
Chen, A. and Renshaw, E. (1994). The general correlated random walk. J. Appl. Prob. 31, 869–884.Google Scholar
Duffie, D. (1988). Security Markets. Stochastic Models. Academic Press, Boston, MA.Google Scholar
Ethier, S. and Kurtz, T. (1986). Markov Processes. Characterization and Convergence. John Wiley, New York.CrossRefGoogle Scholar
Gruber, U. (2004). Convergence of binomial large investor models and general correlated random walks. , Technical University of Berlin. Available at http://edocs.tu-berlin.de/diss/2004/gruber_urs.htm.Google Scholar
Horváth, L. and Shao, Q.-M. (1998). Limit distributions of directionally reinforced random walks. Adv. Math. 134, 367–383.Google Scholar
Kusuoka, S. (1995). Limit theorem on option replication cost with transaction costs. Ann. Appl. Prob. 5, 198–221.Google Scholar
Mauldin, R. D., Monticino, M. and von Weizsäcker, H. (1996). Directionally reinforced random walks. Adv. Math. 117, 239–252.CrossRefGoogle Scholar
Nelson, D. B. (1990). ARCH models as diffusion approximations. J. Econometrics 45, 7–38.Google Scholar
Nelson, D. B. and Ramaswamy, K. (1990). Simple binomial processes as diffusion approximations in financial models. Rev. Financial Studies 3, 393–430.CrossRefGoogle Scholar
Opitz, A. (1999). Zur Asymptotik der Bewertung von Optionen unter Transaktionskosten im Binomialmodell. , Technical University of Berlin.Google Scholar
Renshaw, E. and Henderson, R. (1981). The correlated random walk. J. Appl. Prob. 18, 403–414.Google Scholar
Stroock, D. W. and Varadhan, S. R. S. (1979). Multidimensional Diffusion Processes. Springer, New York.Google Scholar
Szász, D. and Tóth, B. (1984). Persistent random walks in a one-dimensional random environment. J. Statist. Phys. 37, 27–38.Google Scholar