Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-22T07:06:22.988Z Has data issue: false hasContentIssue false
  • English
  • Français

Clustering in preferential attachment random graphs with edge-step

Part of: Special processes Discrete mathematics in relation to computer science Graph theory

Published online by Cambridge University Press:  22 November 2021

Caio Alves ,
Rodrigo Ribeiro Open the ORCID record for Rodrigo Ribeiro [Opens in a new window]  and
Rémy Sanchis
Caio Alves*
Affiliation:
University of Leipzig
Rodrigo Ribeiro*
Affiliation:
Pontificia Universidad Católica de Chile
Rémy Sanchis*
Affiliation:
Universidade Federal de Minas Gerais
*
*Postal address: Faculty of Mathematics and Computer Science, University of Leipzig, Germany. Email: caio.alves@math.uni-leipzig.de
**Postal address: Pontificia Universidad Católica de Chile, Mathematics, Santiago, Chile. Email: rbotelho@mat.uc.cl
***Postal address: Universidade Federal de Minas Gerais, Belo Horizonte, MG Brazil. Email: rsanchis@mat.ufmg.br
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove concentration inequality results for geometric graph properties of an instance of the Cooper–Frieze [5] preferential attachment model with edge-steps. More precisely, we investigate a random graph model that at each time 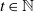$t\in \mathbb{N}$ , with probability p adds a new vertex to the graph (a vertex-step occurs) or with probability 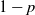$1-p$ an edge connecting two existent vertices is added (an edge-step occurs). We prove concentration results for the global clustering coefficient as well as the clique number. More formally, we prove that the global clustering, with high probability, decays as 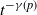$t^{-\gamma(p)}$ for a positive function 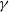$\gamma$ of p, whereas the clique number of these graphs is, up to subpolynomially small factors, of order 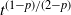$t^{(1-p)/(2-p)}$ .

Keywords

Complex networksclustering coefficientsconcentration boundstransitivityclique number

MSC classification

Primary: 05C82: Small world graphs, complex networks
Secondary: 60K40: Other physical applications of random processes 68R10: Graph theory (including graph drawing)
Type
Original Article
Information
Journal of Applied Probability , Volume 58 , Issue 4 , December 2021 , pp. 890 - 908
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alves, C., Ribeiro, R. and Sanchis, R. (2017). Large communities in a scale-free network. J. Statist. Phys. 166, 137–149.10.1007/s10955-016-1676-8CrossRefGoogle Scholar
Barabási, A.-L. and Albert, R. (1999). Emergence of scaling in random networks. Science 286, 509–512.10.1126/science.286.5439.509CrossRefGoogle ScholarPubMed
Bollobás, B. and Erdös, P. (1976). Cliques in random graphs. Math. Proc. Camb. Phil. Soc. 80, 419–427.10.1017/S0305004100053056CrossRefGoogle Scholar
Bollobás, B. and Riordan, O. (2003). Mathematical results on scale-free random graphs. In Handbook of Graphs And Networks: From the Genome to the Internet, eds. Bronholdt, S. and Schuster, H. G., Wiley, New York, pp. 1–34.Google Scholar
Cooper, C. and Frieze, A. (2003). A general model of web graphs. Random Structures Algorithms 22, 311–335.10.1002/rsa.10084CrossRefGoogle Scholar
Devroye, L., György, A., Lugosi, G. and Udina, F. (2011). High-dimensional random geometric graphs and their clique number. Electron. J. Prob. 16, 2481–2508.Google Scholar
Eggemann, N. and Noble, S. (2011). The clustering coefficient of a scale-free random graph. Discrete Appl. Math. 159, 953–965.10.1016/j.dam.2011.02.003CrossRefGoogle Scholar
Erdös, P. and Renyi, A. (1959). On random graphs i. Publ. Math. Debrecen 6, 290.Google Scholar
Freedman, D. A. (1975). On tail probabilities for martingales. Ann. Prob. 3, 100–118.10.1214/aop/1176996452CrossRefGoogle Scholar
Jacob, E. and Mörters, P. (2015). Spatial preferential attachment networks: Power laws and clustering coefficients. Ann. Appl. Prob. 25, 632–662.10.1214/14-AAP1006CrossRefGoogle Scholar
Janson, S., Luczak, T. and Norros, I. (2010). Large cliques in a power-law random graph. J. Appl. Prob. 47, 1124–1135.10.1239/jap/1294170524CrossRefGoogle Scholar
Oliveira, R. I., Pereira, A. and Ribeiro, R. (2020). Concentration in the generalized Chinese restaurant process. Sankhya A, DOI 10.1007/s13171-020-00210-7.10.1007/s13171-020-00210-7CrossRefGoogle Scholar
Strogatz, S. and Watts, D. J. (1998). Collective dynamics of ‘small-world’ networks. Nature 393, 440–442.Google Scholar
van der Hofstad, R. (2016). Random Graphs and Complex Networks, Vol. 1, 1st edn. Cambridge University Press.Google Scholar
Wang, W.-Q., Zhang, Q.-M. and Zhou, T. (2012). Evaluating network models: A likelihood analysis. Europhys. Lett. 98, 28004.10.1209/0295-5075/98/28004CrossRefGoogle Scholar