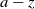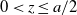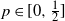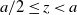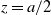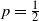1. Introduction and main results
In [Reference Feller4, Chapter XIV], the classical gambler’s ruin problem is studied in detail, in which the gambler plays an adversary with initial capitals z and
![]() $a-z$
, respectively, where
$a-z$
, respectively, where
![]() $a>0$
and
$a>0$
and
![]() $0\le z \le a$
are integers. At each round, the gambler wins or loses a dollar with probabilities p and q (
$0\le z \le a$
are integers. At each round, the gambler wins or loses a dollar with probabilities p and q (
![]() $=1-p$
). The game continues until one of the two players is ruined (and the other player’s capital reaches the maximum value a). We use the symbol
$=1-p$
). The game continues until one of the two players is ruined (and the other player’s capital reaches the maximum value a). We use the symbol
![]() ${\mathbb{P}}_{p,z,a}$
to denote the probability measure with parameters p, z, and a. The duration (total number of rounds) of the game is denoted by N, whose distribution depends on p, z, and a and is denoted by
${\mathbb{P}}_{p,z,a}$
to denote the probability measure with parameters p, z, and a. The duration (total number of rounds) of the game is denoted by N, whose distribution depends on p, z, and a and is denoted by
![]() ${\mathcal{L}}_{p,z,a}(N)$
. We are concerned with stochastic ordering relations for the family of distributions
${\mathcal{L}}_{p,z,a}(N)$
. We are concerned with stochastic ordering relations for the family of distributions
![]() $\{\mathcal{L}_{p,z,a}(N)\colon 0\le p \le 1,\, 0\le z \le a\}$
.
$\{\mathcal{L}_{p,z,a}(N)\colon 0\le p \le 1,\, 0\le z \le a\}$
.
Letting
![]() $I=0$
if the gambler is ruined and
$I=0$
if the gambler is ruined and
![]() $I=1$
otherwise, the generating function for N admits the following explicit expression [Reference Feller4, (4.11) and (4.12), p. 351]:
$I=1$
otherwise, the generating function for N admits the following explicit expression [Reference Feller4, (4.11) and (4.12), p. 351]:
 \begin{align*} \sum_{n=0}^\infty {\mathbb{P}}_{p,z,a}(N=n) s^n & = \sum_{n=0}^\infty {\mathbb{P}}_{p,z,a}(N=n, I=0) s^n+\sum_{n=0}^\infty {\mathbb{P}}_{p,z,a}(N=n, I=1) s^n, \\[5pt] \sum_{n=0}^\infty {\mathbb{P}}_{p,z,a}(N=n, I=0) s^n & = \bigg(\frac{q}{p}\bigg)^z \frac{\lambda_1^{a-z}(s)-\lambda_2^{a-z}(s)}{\lambda_1^a(s)-\lambda_2^a(s)}, \\[5pt] \sum_{n=0}^\infty {\mathbb{P}}_{p,z,a}(N=n, I=1) s^n & = \frac{\lambda_1^z(s)-\lambda_2^z(s)}{\lambda_1^a(s)-\lambda_2^a(s)},\end{align*}
\begin{align*} \sum_{n=0}^\infty {\mathbb{P}}_{p,z,a}(N=n) s^n & = \sum_{n=0}^\infty {\mathbb{P}}_{p,z,a}(N=n, I=0) s^n+\sum_{n=0}^\infty {\mathbb{P}}_{p,z,a}(N=n, I=1) s^n, \\[5pt] \sum_{n=0}^\infty {\mathbb{P}}_{p,z,a}(N=n, I=0) s^n & = \bigg(\frac{q}{p}\bigg)^z \frac{\lambda_1^{a-z}(s)-\lambda_2^{a-z}(s)}{\lambda_1^a(s)-\lambda_2^a(s)}, \\[5pt] \sum_{n=0}^\infty {\mathbb{P}}_{p,z,a}(N=n, I=1) s^n & = \frac{\lambda_1^z(s)-\lambda_2^z(s)}{\lambda_1^a(s)-\lambda_2^a(s)},\end{align*}
where, for
![]() $0<s<1$
,
$0<s<1$
,
Furthermore, for even
![]() $n-z$
and
$n-z$
and
![]() $n>1$
[Reference Feller4, (5.7) and (5.8), pp. 353--354],
$n>1$
[Reference Feller4, (5.7) and (5.8), pp. 353--354],
and
![]() ${\mathbb{P}}_{p,z,a}(N=n, I=0)=0$
for odd
${\mathbb{P}}_{p,z,a}(N=n, I=0)=0$
for odd
![]() $n-z$
. By symmetry, for even
$n-z$
. By symmetry, for even
![]() $n-a+z$
and
$n-a+z$
and
![]() $n>1$
,
$n>1$
,
and
![]() ${\mathbb{P}}_{p,z,a}(N=n, I=1)=0$
for odd
${\mathbb{P}}_{p,z,a}(N=n, I=1)=0$
for odd
![]() $n-a+z$
.
$n-a+z$
.
When a is an even integer, it is shown in [Reference Peköz and Ross8] that
![]() $\mathcal{L}_{{1}/{2}, {a}/{2},a}(N)$
is stochastically larger than
$\mathcal{L}_{{1}/{2}, {a}/{2},a}(N)$
is stochastically larger than
![]() $\mathcal{L}_{p, {a}/{2},a}(N)$
for
$\mathcal{L}_{p, {a}/{2},a}(N)$
for
![]() $p \neq \frac{1}{2}$
. In terms of the likelihood ratio order, which is stronger than the usual stochastic order (see, e.g., [Reference Shaked and Shanthikumar10]), a stronger version of their result may be derived as follows. Let
$p \neq \frac{1}{2}$
. In terms of the likelihood ratio order, which is stronger than the usual stochastic order (see, e.g., [Reference Shaked and Shanthikumar10]), a stronger version of their result may be derived as follows. Let
![]() $X_{n,p}$
,
$X_{n,p}$
,
![]() $n=1,2,\dots$
, be independent and identically distributed (i.i.d.) with
$n=1,2,\dots$
, be independent and identically distributed (i.i.d.) with
For
![]() $0<z<a$
and
$0<z<a$
and
![]() $n \ge 1$
, let
$n \ge 1$
, let
 \begin{align*} {\mathcal{S}}_{z,a}^+(n) & = \{(\omega_1,\dots,\omega_n)\in \{-1,1\}^n \colon 0< z+\omega_1+\cdots+\omega_i<a, i=1,\dots, n-1,\\[5pt] & \qquad z+\omega_1+\dots+\omega_n=a\}, \\[5pt] {\mathcal{S}}_{z,a}^-(n) & = \{(\omega_1,\dots,\omega_n)\in \{-1,1\}^n \colon 0< z+\omega_1+\cdots+\omega_i<a, i=1,\dots, n-1,\\[5pt] & \qquad z+\omega_1+\dots+\omega_n=0\}.\end{align*}
\begin{align*} {\mathcal{S}}_{z,a}^+(n) & = \{(\omega_1,\dots,\omega_n)\in \{-1,1\}^n \colon 0< z+\omega_1+\cdots+\omega_i<a, i=1,\dots, n-1,\\[5pt] & \qquad z+\omega_1+\dots+\omega_n=a\}, \\[5pt] {\mathcal{S}}_{z,a}^-(n) & = \{(\omega_1,\dots,\omega_n)\in \{-1,1\}^n \colon 0< z+\omega_1+\cdots+\omega_i<a, i=1,\dots, n-1,\\[5pt] & \qquad z+\omega_1+\dots+\omega_n=0\}.\end{align*}
For
![]() $z \in \{0,a\}$
and
$z \in \{0,a\}$
and
![]() $n\ge 1$
, let
$n\ge 1$
, let
![]() $\mathcal{S}_{z,a}^+(n)=\mathcal{S}_{z,a}^-(n)=\emptyset$
. Note that
$\mathcal{S}_{z,a}^+(n)=\mathcal{S}_{z,a}^-(n)=\emptyset$
. Note that
![]() $\mathcal{S}_{z,a}^-(n)=\emptyset$
if n and z have opposite parity, while
$\mathcal{S}_{z,a}^-(n)=\emptyset$
if n and z have opposite parity, while
![]() $\mathcal{S}_{z,a}^+(n)=\emptyset$
if n and
$\mathcal{S}_{z,a}^+(n)=\emptyset$
if n and
![]() $a-z$
have opposite parity. Assume a is even and
$a-z$
have opposite parity. Assume a is even and
![]() $0<z<a$
, so that z and
$0<z<a$
, so that z and
![]() $a-z$
are of the same parity. Then we have
$a-z$
are of the same parity. Then we have
![]() ${\mathbb{P}}_{p,z,a}(N=n)=0$
if n and z have opposite parity; and for
${\mathbb{P}}_{p,z,a}(N=n)=0$
if n and z have opposite parity; and for
![]() $n=\min\{z,a-z\}, \min\{z,a-z\}+2,\dots$
,
$n=\min\{z,a-z\}, \min\{z,a-z\}+2,\dots$
,
 \begin{align} {\mathbb{P}}_{p,z,a}(N=n) & = \mathbb{P}((X_{1,p},\dots,X_{n,p}) \in {\mathcal{S}}_{z,a}^+(n)) + \mathbb{P}((X_{1,p},\dots,X_{n,p}) \in {\mathcal{S}}_{z,a}^-(n)) \nonumber \\[5pt] & = p^{({n+a-z})/{2}} q^{({n-a+z})/{2}} |{\mathcal{S}}_{z,a}^+(n)| + p^{({n-z})/{2}} q^{({n+z})/{2}} |{\mathcal{S}}_{z,a}^-(n)| \nonumber \\[5pt] & = (pq)^{{n}/{2}}\bigg[\bigg(\frac{p}{q}\bigg)^{({a-z})/{2}} |{\mathcal{S}}_{z,a}^+(n)| + \bigg(\frac{q}{p}\bigg)^{{z}/{2}} |{\mathcal{S}}_{z,a}^-(n)|\bigg], \end{align}
\begin{align} {\mathbb{P}}_{p,z,a}(N=n) & = \mathbb{P}((X_{1,p},\dots,X_{n,p}) \in {\mathcal{S}}_{z,a}^+(n)) + \mathbb{P}((X_{1,p},\dots,X_{n,p}) \in {\mathcal{S}}_{z,a}^-(n)) \nonumber \\[5pt] & = p^{({n+a-z})/{2}} q^{({n-a+z})/{2}} |{\mathcal{S}}_{z,a}^+(n)| + p^{({n-z})/{2}} q^{({n+z})/{2}} |{\mathcal{S}}_{z,a}^-(n)| \nonumber \\[5pt] & = (pq)^{{n}/{2}}\bigg[\bigg(\frac{p}{q}\bigg)^{({a-z})/{2}} |{\mathcal{S}}_{z,a}^+(n)| + \bigg(\frac{q}{p}\bigg)^{{z}/{2}} |{\mathcal{S}}_{z,a}^-(n)|\bigg], \end{align}
where
![]() $|S|$
denotes the cardinality of the set S. For
$|S|$
denotes the cardinality of the set S. For
![]() $z={a}/{2}$
, we have
$z={a}/{2}$
, we have
![]() $|\mathcal{S}_{{{a}/{2}},a}^+(n)| = |\mathcal{S}_{{{a}/{2}},a}^-(n)|$
by symmetry, which together with (4) implies that
$|\mathcal{S}_{{{a}/{2}},a}^+(n)| = |\mathcal{S}_{{{a}/{2}},a}^-(n)|$
by symmetry, which together with (4) implies that
So, for
![]() $p, p' \in (0,1)$
(with
$p, p' \in (0,1)$
(with
![]() $q'=1-p'$
) and
$q'=1-p'$
) and
![]() $n={a}/{2}, {a}/{2}+2,\dots$
,
$n={a}/{2}, {a}/{2}+2,\dots$
,
which is increasing in n if
![]() $\big|p-{\frac{1}{2}}\big| > \big|p'-{\frac{1}{2}}\big|$
. Consequently, for even a and
$\big|p-{\frac{1}{2}}\big| > \big|p'-{\frac{1}{2}}\big|$
. Consequently, for even a and
![]() $z={a}/{2}$
, if p and
$z={a}/{2}$
, if p and
![]() $ p' \in [0,1]$
satisfy
$ p' \in [0,1]$
satisfy
![]() $\big|p-{\frac{1}{2}}\big| > \big|p'-{\frac{1}{2}}\big|$
, then
$\big|p-{\frac{1}{2}}\big| > \big|p'-{\frac{1}{2}}\big|$
, then
![]() $\mathcal{L}_{p',{{a}/{2}},a}(N)$
is larger than
$\mathcal{L}_{p',{{a}/{2}},a}(N)$
is larger than
![]() $\mathcal{L}_{p,{{a}/{2}},a}(N)$
in the likelihood ratio order. For a family of distributions indexed by
$\mathcal{L}_{p,{{a}/{2}},a}(N)$
in the likelihood ratio order. For a family of distributions indexed by
![]() $\theta \in \mathcal{I}$
(an interval) with probability mass/density functions
$\theta \in \mathcal{I}$
(an interval) with probability mass/density functions
![]() $f_\theta(\cdot)$
on
$f_\theta(\cdot)$
on
![]() $\mathcal{X}$
(a subset of the real line), it is said to have monotone (increasing) likelihood ratio if
$\mathcal{X}$
(a subset of the real line), it is said to have monotone (increasing) likelihood ratio if
whenever
![]() $x,x' \in \mathcal{X}$
and
$x,x' \in \mathcal{X}$
and
![]() $\theta, \theta' \in \mathcal{I}$
satisfy
$\theta, \theta' \in \mathcal{I}$
satisfy
![]() $x<x'$
and
$x<x'$
and
![]() $\theta<\theta'$
, and is said to have monotone (decreasing) likelihood ratio if the inequality (5) is reversed; see [Reference Karlin and Rubin6]. Indeed, we have shown the following result.
$\theta<\theta'$
, and is said to have monotone (decreasing) likelihood ratio if the inequality (5) is reversed; see [Reference Karlin and Rubin6]. Indeed, we have shown the following result.
Theorem 1.
For even
![]() $a\ge 4$
and
$a\ge 4$
and
![]() $z={a}/{2}$
, the family of distributions
$z={a}/{2}$
, the family of distributions
![]() $\big\{\mathcal{L}_{p,{{a}/{2}},a}(N)\colon 0\le p \le {\frac{1}{2}}\big\}$
has monotone (increasing) likelihood ratio, and the family of distributions
$\big\{\mathcal{L}_{p,{{a}/{2}},a}(N)\colon 0\le p \le {\frac{1}{2}}\big\}$
has monotone (increasing) likelihood ratio, and the family of distributions
![]() $\big\{\mathcal{L}_{p,{{a}/{2}},a}(N)\colon {\frac{1}{2}} \le p \le 1\big\}$
has monotone (decreasing) likelihood ratio.
$\big\{\mathcal{L}_{p,{{a}/{2}},a}(N)\colon {\frac{1}{2}} \le p \le 1\big\}$
has monotone (decreasing) likelihood ratio.
By Theorem 1, in terms of the likelihood ratio order, the distribution
![]() $\mathcal{L}_{p, {{a}/{2}},a}(N)$
is maximized over
$\mathcal{L}_{p, {{a}/{2}},a}(N)$
is maximized over
![]() $p \in [0,1]$
by
$p \in [0,1]$
by
![]() $p={\frac{1}{2}}$
, implying the result of [Reference Peköz and Ross8].
$p={\frac{1}{2}}$
, implying the result of [Reference Peköz and Ross8].
We next consider the more general case with a even and
![]() $z \neq {{a}/{2}}$
. We need to establish a crucial monotonicity result for
$z \neq {{a}/{2}}$
. We need to establish a crucial monotonicity result for
![]() $p={\frac{1}{2}}$
, which is of independent interest. For
$p={\frac{1}{2}}$
, which is of independent interest. For
![]() $p={\frac{1}{2}}$
, note that
$p={\frac{1}{2}}$
, note that
Theorem 2.
For
![]() $p={\frac{1}{2}}$
, even
$p={\frac{1}{2}}$
, even
![]() $a\ge 4$
, and
$a\ge 4$
, and
![]() $0<z<{{a}/{2}}$
, as
$0<z<{{a}/{2}}$
, as
![]() $n \in \{z, z+2,\dots\}$
increases to
$n \in \{z, z+2,\dots\}$
increases to
![]() $\infty$
,
$\infty$
,
monotonically increases to
![]() ${\frac{1}{2}}$
. Equivalently, for
${\frac{1}{2}}$
. Equivalently, for
![]() $p={\frac{1}{2}}$
and
$p={\frac{1}{2}}$
and
![]() $0<z<{{a}/{2}}$
,
$0<z<{{a}/{2}}$
,
monotonically increases to 1 as
![]() $n \in \{z, z+2,\dots\}$
increases to
$n \in \{z, z+2,\dots\}$
increases to
![]() $\infty$
.
$\infty$
.
With the help of Theorem 2, the next theorem can be readily shown, which is an extension of Theorem 1 from
![]() $z={{a}/{2}}$
to
$z={{a}/{2}}$
to
![]() $z \neq {{a}/{2}}$
.
$z \neq {{a}/{2}}$
.
Theorem 3.
For even
![]() $a \geq 4$
and
$a \geq 4$
and
![]() $0<z<{{a}/{2}}$
, the family of distributions
$0<z<{{a}/{2}}$
, the family of distributions
![]() $\big\{{\mathcal{L}}_{p,z,a}(N)\colon 0\le p \le {\frac{1}{2}}\big\}$
has monotone (increasing) likelihood ratio, and for
$\big\{{\mathcal{L}}_{p,z,a}(N)\colon 0\le p \le {\frac{1}{2}}\big\}$
has monotone (increasing) likelihood ratio, and for
![]() ${{a}/{2}} <z< a$
, the family of distributions
${{a}/{2}} <z< a$
, the family of distributions
![]() $\big\{{\mathcal{L}}_{p,z,a}(N)\colon {\frac{1}{2}} \le p \le 1\big\}$
has monotone (decreasing) likelihood ratio.
$\big\{{\mathcal{L}}_{p,z,a}(N)\colon {\frac{1}{2}} \le p \le 1\big\}$
has monotone (decreasing) likelihood ratio.
For the case of odd a, analogous results do not hold unless the likelihood ratio order is replaced by a weaker stochastic order. To see this, consider odd
![]() $a\geq 3$
and
$a\geq 3$
and
![]() $0<z<a$
. Then z and
$0<z<a$
. Then z and
![]() $a-z$
have opposite parity. So, for all n, either
$a-z$
have opposite parity. So, for all n, either
![]() ${\mathcal{S}}_{z,a}^-(n)=\emptyset$
or
${\mathcal{S}}_{z,a}^-(n)=\emptyset$
or
![]() ${\mathcal{S}}_{z,a}^+(n)=\emptyset$
. For even
${\mathcal{S}}_{z,a}^+(n)=\emptyset$
. For even
![]() $n-z \geq 0$
,
$n-z \geq 0$
,
while for even
![]() $n-a+z \geq 0$
,
$n-a+z \geq 0$
,
We have
 \begin{equation} \frac{\mathbb{P}_{p',z,a}(N=n)}{{\mathbb{P}}_{p,z,a}(N=n)} = \begin{cases} \bigg(\dfrac{p'q'}{pq}\bigg)^{{n}/{2}}\bigg(\dfrac{p q'}{p' q}\bigg)^{{z}/{2}} & \text{for } n=z, z+2,\dots, \\[5pt] \bigg(\dfrac{p'q'}{pq}\bigg)^{{n}/{2}}\bigg(\dfrac{p'q}{pq'}\bigg)^{({a-z})/{2}} & \text{for } n=a-z,a-z+2,\dots \end{cases}\end{equation}
\begin{equation} \frac{\mathbb{P}_{p',z,a}(N=n)}{{\mathbb{P}}_{p,z,a}(N=n)} = \begin{cases} \bigg(\dfrac{p'q'}{pq}\bigg)^{{n}/{2}}\bigg(\dfrac{p q'}{p' q}\bigg)^{{z}/{2}} & \text{for } n=z, z+2,\dots, \\[5pt] \bigg(\dfrac{p'q'}{pq}\bigg)^{{n}/{2}}\bigg(\dfrac{p'q}{pq'}\bigg)^{({a-z})/{2}} & \text{for } n=a-z,a-z+2,\dots \end{cases}\end{equation}
Consider
![]() $0<p<p'\leq {\frac{1}{2}}$
and
$0<p<p'\leq {\frac{1}{2}}$
and
![]() $0<z<{\frac{a}{2}}$
. By (6), for all
$0<z<{\frac{a}{2}}$
. By (6), for all
![]() $n\geq a-z\ (>z)$
,
$n\geq a-z\ (>z)$
,
i.e. the likelihood ratio
![]() $\mathbb{P}_{p',z,a}(N=n)/{\mathbb{P}}_{p,z,a}(N=n)$
increases by a factor of
$\mathbb{P}_{p',z,a}(N=n)/{\mathbb{P}}_{p,z,a}(N=n)$
increases by a factor of
![]() $p' q'/pq$
when n increases by 2. On the other hand, by (6) again, we have, for
$p' q'/pq$
when n increases by 2. On the other hand, by (6) again, we have, for
![]() $n=a-z,a-z+2,\dots$
,
$n=a-z,a-z+2,\dots$
,
 \begin{align*} & \bigg[\frac{\mathbb{P}_{p',z,a}(N=n+1)}{{\mathbb{P}}_{p,z,a}(N=n+1)}\bigg] \big/ \bigg[\frac{\mathbb{P}_{p',z,a}(N=n)}{{\mathbb{P}}_{p,z,a}(N=n)}\bigg] \\[5pt] & \quad = \bigg[\bigg(\frac{p'q'}{pq}\bigg)^{({n+1})/{2}}\bigg(\frac{p q'}{p' q}\bigg)^{{z}/{2}}\bigg] \big/ \bigg[\bigg(\frac{p'q'}{pq}\bigg)^{{n}/{2}}\bigg(\frac{p'q}{pq'}\bigg)^{({a-z})/{2}}\bigg] \\[5pt] & \quad = \bigg(\frac{p}{p'}\bigg)^{({a-1})/{2}}\bigg(\frac{q'}{q}\bigg)^{({a+1})/{2}}< 1,\end{align*}
\begin{align*} & \bigg[\frac{\mathbb{P}_{p',z,a}(N=n+1)}{{\mathbb{P}}_{p,z,a}(N=n+1)}\bigg] \big/ \bigg[\frac{\mathbb{P}_{p',z,a}(N=n)}{{\mathbb{P}}_{p,z,a}(N=n)}\bigg] \\[5pt] & \quad = \bigg[\bigg(\frac{p'q'}{pq}\bigg)^{({n+1})/{2}}\bigg(\frac{p q'}{p' q}\bigg)^{{z}/{2}}\bigg] \big/ \bigg[\bigg(\frac{p'q'}{pq}\bigg)^{{n}/{2}}\bigg(\frac{p'q}{pq'}\bigg)^{({a-z})/{2}}\bigg] \\[5pt] & \quad = \bigg(\frac{p}{p'}\bigg)^{({a-1})/{2}}\bigg(\frac{q'}{q}\bigg)^{({a+1})/{2}}< 1,\end{align*}
showing that the likelihood ratio
![]() $\mathbb{P}_{p',z,a}(N=n)/{\mathbb{P}}_{p,z,a}(N=n)$
is not monotonically increasing in n. The next theorem gives stochastic ordering results for the odd a case in terms of the usual stochastic order.
$\mathbb{P}_{p',z,a}(N=n)/{\mathbb{P}}_{p,z,a}(N=n)$
is not monotonically increasing in n. The next theorem gives stochastic ordering results for the odd a case in terms of the usual stochastic order.
Theorem 4.
Let
![]() $a\geq 3$
be an odd integer. For
$a\geq 3$
be an odd integer. For
![]() $0<z<{{a}/{2}}$
and
$0<z<{{a}/{2}}$
and
![]() $0\leq p<p' \leq {\frac{1}{2}}$
,
$0\leq p<p' \leq {\frac{1}{2}}$
,
![]() ${\mathcal{L}}_{p,z,a}(N)$
is stochastically smaller than
${\mathcal{L}}_{p,z,a}(N)$
is stochastically smaller than
![]() $\mathcal{L}_{p',z,a}(N)$
, and for
$\mathcal{L}_{p',z,a}(N)$
, and for
![]() ${{a}/{2}}<z<a$
and
${{a}/{2}}<z<a$
and
![]() ${\frac{1}{2}} \leq p<p' \leq 1$
,
${\frac{1}{2}} \leq p<p' \leq 1$
,
![]() ${\mathcal{L}}_{p,z,a}(N)$
is stochastically larger than
${\mathcal{L}}_{p,z,a}(N)$
is stochastically larger than
![]() $\mathcal{L}_{p',z,a}(N)$
.
$\mathcal{L}_{p',z,a}(N)$
.
The long and technical proof of Theorem 2 is given in Section 2, while Sections 3 and 4 present the proofs of Theorems 3 and 4, respectively. We close this section with a number of remarks on some implications of the above results and a conjecture for odd a related to the work of [Reference Peköz and Ross8].
Remark 1. For
![]() $p={\frac{1}{2}}$
, the conditional distributions of N given
$p={\frac{1}{2}}$
, the conditional distributions of N given
![]() $I=0$
and
$I=0$
and
![]() $I=1$
, denoted by
$I=1$
, denoted by
![]() $\mathcal{L}_{{{1}/{2}}, z,a}(N \mid I=0)$
and
$\mathcal{L}_{{{1}/{2}}, z,a}(N \mid I=0)$
and
![]() $\mathcal{L}_{{{1}/{2}}, z,a}(N \mid I=1)$
, have respective probability mass functions
$\mathcal{L}_{{{1}/{2}}, z,a}(N \mid I=1)$
, have respective probability mass functions
 \begin{alignat*}{2} \mathbb{P}_{{{1}/{2}},z,a}(N=n \mid I=0) & = \bigg(\frac{a}{a-z}\bigg) \mathbb{P}_{{{1}/{2}},z,a}(N=n, I=0), \quad & & n=z, z+2, \dots, \\[5pt] \mathbb{P}_{{{1}/{2}},z,a}(N=n \mid I=1) & = \bigg(\frac{a}{z}\bigg) \mathbb{P}_{{{1}/{2}},z,a}(N=n, I=1), & & n=a-z, a-z+2, \dots \end{alignat*}
\begin{alignat*}{2} \mathbb{P}_{{{1}/{2}},z,a}(N=n \mid I=0) & = \bigg(\frac{a}{a-z}\bigg) \mathbb{P}_{{{1}/{2}},z,a}(N=n, I=0), \quad & & n=z, z+2, \dots, \\[5pt] \mathbb{P}_{{{1}/{2}},z,a}(N=n \mid I=1) & = \bigg(\frac{a}{z}\bigg) \mathbb{P}_{{{1}/{2}},z,a}(N=n, I=1), & & n=a-z, a-z+2, \dots \end{alignat*}
So, for even a and
![]() $0<z<{{a}/{2}}$
, Theorem 2 is equivalent to saying that
$0<z<{{a}/{2}}$
, Theorem 2 is equivalent to saying that
![]() $\mathcal{L}_{{{1}/{2}}, z,a}(N \mid I=1)$
is larger than
$\mathcal{L}_{{{1}/{2}}, z,a}(N \mid I=1)$
is larger than
![]() $\mathcal{L}_{{{1}/{2}}, z,a}(N \mid I=0)$
in the likelihood ratio order.
$\mathcal{L}_{{{1}/{2}}, z,a}(N \mid I=0)$
in the likelihood ratio order.
Remark 2. For even a, Theorem 3 does not cover the case
![]() ${{a}/{2}}<z<a$
and
${{a}/{2}}<z<a$
and
![]() $p\le {\frac{1}{2}}$
. In fact, for
$p\le {\frac{1}{2}}$
. In fact, for
![]() ${{a}/{2}} <z<a$
and
${{a}/{2}} <z<a$
and
![]() $0<p<p'\leq {\frac{1}{2}}$
,
$0<p<p'\leq {\frac{1}{2}}$
,
![]() ${\mathcal{L}}_{p,z,a}(N)$
is neither stochastically smaller nor stochastically larger than
${\mathcal{L}}_{p,z,a}(N)$
is neither stochastically smaller nor stochastically larger than
![]() $\mathbb{L}_{p',z,a}(N)$
. To see this, note that
$\mathbb{L}_{p',z,a}(N)$
. To see this, note that
 \begin{align*} {\mathbb{P}}_{p,z,a}(N \leq a-z) &= {\mathbb{P}}_{p,z,a}(N=a-z) = p^{a-z} < (p')^{a-z}=\mathbb{P}_{p',z,a}(N=a-z)\\[5pt] &= \mathbb{P}_{p',z,a}(N \leq a-z). \end{align*}
\begin{align*} {\mathbb{P}}_{p,z,a}(N \leq a-z) &= {\mathbb{P}}_{p,z,a}(N=a-z) = p^{a-z} < (p')^{a-z}=\mathbb{P}_{p',z,a}(N=a-z)\\[5pt] &= \mathbb{P}_{p',z,a}(N \leq a-z). \end{align*}
On the other hand,
![]() ${\mathbb{P}}_{p,z,a}(N \leq n)> \mathbb{P}_{p',z,a}(N \leq n)$
for large n, as shown below. Since
${\mathbb{P}}_{p,z,a}(N \leq n)> \mathbb{P}_{p',z,a}(N \leq n)$
for large n, as shown below. Since
![]() $|{\mathcal{S}}_{z,a}^+(n)|=|\mathcal{S}^-_{a-z,a}(n)|$
and
$|{\mathcal{S}}_{z,a}^+(n)|=|\mathcal{S}^-_{a-z,a}(n)|$
and
![]() $|{\mathcal{S}}_{z,a}^-(n)|=|\mathcal{S}^+_{a-z,a}(n)|$
, it follows from Theorem 2 that
$|{\mathcal{S}}_{z,a}^-(n)|=|\mathcal{S}^+_{a-z,a}(n)|$
, it follows from Theorem 2 that
![]() $|{\mathcal{S}}_{z,a}^-(n)|/|{\mathcal{S}}_{z,a}^+(n)|=|\mathcal{S}^+_{a-z,a}(n)|/|\mathcal{S}^-_{a-z,a}(n)|$
increases to 1 as
$|{\mathcal{S}}_{z,a}^-(n)|/|{\mathcal{S}}_{z,a}^+(n)|=|\mathcal{S}^+_{a-z,a}(n)|/|\mathcal{S}^-_{a-z,a}(n)|$
increases to 1 as
![]() $n\in \{z,z+2,\dots\}$
increases to
$n\in \{z,z+2,\dots\}$
increases to
![]() $\infty$
. By (4), as
$\infty$
. By (4), as
![]() $n \in \{z,z+2,\dots\}$
increases to
$n \in \{z,z+2,\dots\}$
increases to
![]() $\infty$
,
$\infty$
,
Since
![]() $pq<p'q'$
, we have
$pq<p'q'$
, we have
![]() $\lim_{n \to \infty} {\mathbb{P}}_{p,z,a}(N \geq n)/\mathbb{P}_{p',z,a}(N \geq n)=0$
by (7). So
$\lim_{n \to \infty} {\mathbb{P}}_{p,z,a}(N \geq n)/\mathbb{P}_{p',z,a}(N \geq n)=0$
by (7). So
![]() ${\mathbb{P}}_{p,z,a}(N \leq n)> \mathbb{P}_{p',z,a}(N \leq n)$
for large n.
${\mathbb{P}}_{p,z,a}(N \leq n)> \mathbb{P}_{p',z,a}(N \leq n)$
for large n.
Remark 3. In view of (6) and (7), it can be shown that for
![]() $0<z<a$
and
$0<z<a$
and
![]() $p, p' \in (0,1)$
,
$p, p' \in (0,1)$
,
Thus,
![]() ${\mathcal{L}}_{p,z,a}(N)$
has much lighter tails than
${\mathcal{L}}_{p,z,a}(N)$
has much lighter tails than
![]() $\mathcal{L}_{p',z,a}(N)$
for
$\mathcal{L}_{p',z,a}(N)$
for
![]() $\big|p-{\frac{1}{2}}\big| > \big|p'-{\frac{1}{2}}\big|$
.
$\big|p-{\frac{1}{2}}\big| > \big|p'-{\frac{1}{2}}\big|$
.
Remark 4. For even a and
![]() $z={{a}/{2}}$
, it is shown in [Reference Peköz and Ross8] that the distribution
$z={{a}/{2}}$
, it is shown in [Reference Peköz and Ross8] that the distribution
![]() ${\mathcal{L}}_{p,z,a}(N)$
is stochastically maximized over
${\mathcal{L}}_{p,z,a}(N)$
is stochastically maximized over
![]() $p \in [0,1]$
by
$p \in [0,1]$
by
![]() $p={\frac{1}{2}}$
. Can an analogous result hold for odd a? For odd a, it seems natural to consider a random initial state z that takes on the two middle values
$p={\frac{1}{2}}$
. Can an analogous result hold for odd a? For odd a, it seems natural to consider a random initial state z that takes on the two middle values
![]() $({a+1})/{2}$
and
$({a+1})/{2}$
and
![]() $({a-1})/{2}$
with equal probabilities. Then the distribution of the duration N is a mixture of the two distributions
$({a-1})/{2}$
with equal probabilities. Then the distribution of the duration N is a mixture of the two distributions
![]() $\mathcal{L}_{p,({a+1})/{2},a}(N)$
and
$\mathcal{L}_{p,({a+1})/{2},a}(N)$
and
![]() $\mathcal{L}_{p,({a-1})/{2},a}(N)$
with equal weights, denoted by
$\mathcal{L}_{p,({a-1})/{2},a}(N)$
with equal weights, denoted by
![]() ${\frac{1}{2}}\mathcal{L}_{p,({a+1})/{2},a}(N) + {\frac{1}{2}}\mathcal{L}_{p,({a-1})/{2},a}(N)$
. Note that for
${\frac{1}{2}}\mathcal{L}_{p,({a+1})/{2},a}(N) + {\frac{1}{2}}\mathcal{L}_{p,({a-1})/{2},a}(N)$
. Note that for
![]() $p={\frac{1}{2}}$
,
$p={\frac{1}{2}}$
,
![]() $\mathcal{L}_{{{1}/{2}},({a+1})/{2},a}(N)=\mathcal{L}_{{{1}/{2}},({a-1})/{2},a}(N)$
, and for
$\mathcal{L}_{{{1}/{2}},({a+1})/{2},a}(N)=\mathcal{L}_{{{1}/{2}},({a-1})/{2},a}(N)$
, and for
![]() $p+p'=1$
,
$p+p'=1$
,
We conjecture that
![]() ${\frac{1}{2}}\mathcal{L}_{p,({a+1})/{2},a}(N) + {\frac{1}{2}}\mathcal{L}_{p,({a-1})/{2},a}(N)$
is stochastically maximized over
${\frac{1}{2}}\mathcal{L}_{p,({a+1})/{2},a}(N) + {\frac{1}{2}}\mathcal{L}_{p,({a-1})/{2},a}(N)$
is stochastically maximized over
![]() $p \in [0,1]$
by
$p \in [0,1]$
by
![]() $p={\frac{1}{2}}$
, which can be shown to hold for small odd a. Moreover, this conjecture is equivalent to saying that
$p={\frac{1}{2}}$
, which can be shown to hold for small odd a. Moreover, this conjecture is equivalent to saying that
![]() ${\frac{1}{2}}{\mathbb{P}}_{p,(a+1)/2,a}(N \geq n) + {\frac{1}{2}}{\mathbb{P}}_{p,(a-1)/2,a}(N \geq n)$
is maximized over
${\frac{1}{2}}{\mathbb{P}}_{p,(a+1)/2,a}(N \geq n) + {\frac{1}{2}}{\mathbb{P}}_{p,(a-1)/2,a}(N \geq n)$
is maximized over
![]() $p \in [0,1]$
by
$p \in [0,1]$
by
![]() $p={\frac{1}{2}}$
for all n. It may be verified directly for small n.
$p={\frac{1}{2}}$
for all n. It may be verified directly for small n.
Remark 5. [Reference Feller5, II.7] introduces a model of randomized random walks where instead of successive jumps occurring at epochs
![]() $1,2,\dots$
, the time intervals between successive jumps are assumed to be i.i.d. exponential random variables with mean 1. This model is a compound Poisson process
$1,2,\dots$
, the time intervals between successive jumps are assumed to be i.i.d. exponential random variables with mean 1. This model is a compound Poisson process
![]() $Z_t=\sum_{n=1}^{\Pi_t} X_{n,p}$
,
$Z_t=\sum_{n=1}^{\Pi_t} X_{n,p}$
,
![]() $t\geq 0$
, where
$t\geq 0$
, where
![]() $X_{n,p}$
(
$X_{n,p}$
(
![]() $n=1,2,\dots$
) are i.i.d. as defined in (3), and
$n=1,2,\dots$
) are i.i.d. as defined in (3), and
![]() $\Pi_t$
is a Poisson process of constant rate 1 (independent of the
$\Pi_t$
is a Poisson process of constant rate 1 (independent of the
![]() $X_{n,p}$
). (For a discussion of compound Poisson processes, see, e.g., [Reference Karlin and Taylor7, 16.9].) For
$X_{n,p}$
). (For a discussion of compound Poisson processes, see, e.g., [Reference Karlin and Taylor7, 16.9].) For
![]() $0<z<a$
, let
$0<z<a$
, let
![]() $\mathcal{T}\;:\!=\;\inf\{t>0\colon z+Z_t \notin (0,a)\}$
, the first exit time of the process
$\mathcal{T}\;:\!=\;\inf\{t>0\colon z+Z_t \notin (0,a)\}$
, the first exit time of the process
![]() $z+Z_t$
from the interval (0,a). We denote the distribution of
$z+Z_t$
from the interval (0,a). We denote the distribution of
![]() $\mathcal{T}$
by
$\mathcal{T}$
by
![]() $\mathcal{L}_{p,z,a}(\mathcal{T})$
, which is the same as the distribution of
$\mathcal{L}_{p,z,a}(\mathcal{T})$
, which is the same as the distribution of
![]() $\sum_{i=1}^N \mathcal{E}_i$
where N is the duration of the gambler’s ruin game and
$\sum_{i=1}^N \mathcal{E}_i$
where N is the duration of the gambler’s ruin game and
![]() $\mathcal{E}_i$
(
$\mathcal{E}_i$
(
![]() $i=1,2,\dots$
) are i.i.d. exponential with mean 1 (independent of N). We write
$i=1,2,\dots$
) are i.i.d. exponential with mean 1 (independent of N). We write
![]() $\mathcal{L}_{p,z,a}(\mathcal{T}) = \mathcal{L}_{p,z,a}\big(\sum_{i=1}^N \mathcal{E}_i\big)$
. In view of this, if
$\mathcal{L}_{p,z,a}(\mathcal{T}) = \mathcal{L}_{p,z,a}\big(\sum_{i=1}^N \mathcal{E}_i\big)$
. In view of this, if
![]() ${\mathcal{L}}_{p,z,a}(N)$
is stochastically smaller than
${\mathcal{L}}_{p,z,a}(N)$
is stochastically smaller than
![]() $\mathcal{L}_{p',z,a}(N)$
, then
$\mathcal{L}_{p',z,a}(N)$
, then
![]() $\mathcal{L}_{p,z,a}(\mathcal{T})$
is stochastically smaller than
$\mathcal{L}_{p,z,a}(\mathcal{T})$
is stochastically smaller than
![]() $\mathcal{L}_{p',z,a}(\mathcal{T})$
. In other words, the usual stochastic order relation concerning the distribution of N carries over to
$\mathcal{L}_{p',z,a}(\mathcal{T})$
. In other words, the usual stochastic order relation concerning the distribution of N carries over to
![]() $\mathcal{T}$
. However, the likelihood ratio order relation does not carry over. It follows from Theorems 3 and 4 that, for
$\mathcal{T}$
. However, the likelihood ratio order relation does not carry over. It follows from Theorems 3 and 4 that, for
![]() $0<p<p'\le {\frac{1}{2}}$
and
$0<p<p'\le {\frac{1}{2}}$
and
![]() $0<z\leq {{a}/{2}}$
,
$0<z\leq {{a}/{2}}$
,
![]() $\mathcal{L}_{p,z,a}(\mathcal{T})$
is stochastically smaller than
$\mathcal{L}_{p,z,a}(\mathcal{T})$
is stochastically smaller than
![]() $\mathcal{L}_{p',z,a}(\mathcal{T})$
.
$\mathcal{L}_{p',z,a}(\mathcal{T})$
.
Remark 6. [Reference Feller4, XIV.6] discusses the connection of the gambler’s ruin game with Brownian motion as a limit, which is briefly described below. To have Brownian motion as a limit, the time and step size for the random walk in the gambler’s ruin problem may be rescaled such that there are r steps per unit time and each step causes a displacement equal to
![]() $\pm \delta$
. Given real values c and
$\pm \delta$
. Given real values c and
![]() $0<\xi<\alpha$
, let
$0<\xi<\alpha$
, let
in such a way that
Then the duration N of the gambler’s ruin game with initial state z becomes, in the limit, the first exit time
![]() $\tau\;:\!=\;\inf\{t>0\colon \xi+ct+B_t \notin (0,\alpha)\}$
from the interval
$\tau\;:\!=\;\inf\{t>0\colon \xi+ct+B_t \notin (0,\alpha)\}$
from the interval
![]() $(0,\alpha)$
, where
$(0,\alpha)$
, where
![]() $B_t$
is standard Brownian motion and
$B_t$
is standard Brownian motion and
![]() $\xi+ct+B_t$
is Brownian motion with drift parameter c and initial state
$\xi+ct+B_t$
is Brownian motion with drift parameter c and initial state
![]() $\xi$
. Denote the density function of
$\xi$
. Denote the density function of
![]() $\tau$
by
$\tau$
by
![]() $u_{c,\xi,\alpha}(t)$
, which may be decomposed as
$u_{c,\xi,\alpha}(t)$
, which may be decomposed as
![]() $u_{c,\xi,\alpha}(t)=u_{c,\xi,\alpha}^-(t)+u_{c,\xi,\alpha}^+(t)$
. Here,
$u_{c,\xi,\alpha}(t)=u_{c,\xi,\alpha}^-(t)+u_{c,\xi,\alpha}^+(t)$
. Here,
![]() $u_{c,\xi,\alpha}^-(t)$
and
$u_{c,\xi,\alpha}^-(t)$
and
![]() $u_{c,\xi,\alpha}^+(t)$
denote, respectively, the density functions of
$u_{c,\xi,\alpha}^+(t)$
denote, respectively, the density functions of
![]() $\tau$
when the Brownian motion process exits through the lower and upper boundaries, i.e., for
$\tau$
when the Brownian motion process exits through the lower and upper boundaries, i.e., for
![]() $t>0$
,
$t>0$
,
 \begin{align*} \mathbb{P}(\tau \leq t,\, \xi+c \tau+B_\tau=0) & = \int_0^t u_{c,\xi,\alpha}^-(s)\,{\mathrm{d}} s, \\[5pt] \mathbb{P}(\tau \leq t,\, \xi+c \tau+B_\tau=\alpha) & = \int_0^t u_{c,\xi,\alpha}^+(s)\,{\mathrm{d}} s. \end{align*}
\begin{align*} \mathbb{P}(\tau \leq t,\, \xi+c \tau+B_\tau=0) & = \int_0^t u_{c,\xi,\alpha}^-(s)\,{\mathrm{d}} s, \\[5pt] \mathbb{P}(\tau \leq t,\, \xi+c \tau+B_\tau=\alpha) & = \int_0^t u_{c,\xi,\alpha}^+(s)\,{\mathrm{d}} s. \end{align*}
Since
![]() $u_{c,\xi,\alpha}^-(t)$
and
$u_{c,\xi,\alpha}^-(t)$
and
![]() $u_{c,\xi,\alpha}^+(t)$
are the continuous-time counterparts of
$u_{c,\xi,\alpha}^+(t)$
are the continuous-time counterparts of
![]() ${\mathbb{P}}_{p,z,a}(N=n,I=0)$
and
${\mathbb{P}}_{p,z,a}(N=n,I=0)$
and
![]() ${\mathbb{P}}_{p,z,a}(N=n,I=1)$
as given in (1) and (2), applying a standard limiting argument to (1) and (2) yields
${\mathbb{P}}_{p,z,a}(N=n,I=1)$
as given in (1) and (2), applying a standard limiting argument to (1) and (2) yields
where (10) is [Reference Feller4, (6.15) (with
![]() $D=1$
), p. 359] and (11) is due to
$D=1$
), p. 359] and (11) is due to
![]() $u_{c,\xi,\alpha}^+(t)=u_{-c,\alpha-\xi,\alpha}^-(t)$
by symmetry. In [Reference Feller4, Problem 22, p. 370], (10) and (11) are given in the following alternative form:
$u_{c,\xi,\alpha}^+(t)=u_{-c,\alpha-\xi,\alpha}^-(t)$
by symmetry. In [Reference Feller4, Problem 22, p. 370], (10) and (11) are given in the following alternative form:
(See also [Reference Darling and Siegert3] for the Laplace transforms of
![]() $u_{c,\xi,\alpha}^-(t)$
and
$u_{c,\xi,\alpha}^-(t)$
and
![]() $u_{c,\xi,\alpha}^+(t)$
.) Since a can be taken to be an even number as a increases to
$u_{c,\xi,\alpha}^+(t)$
.) Since a can be taken to be an even number as a increases to
![]() $\infty$
in (8) and (9), the monotonicity property of
$\infty$
in (8) and (9), the monotonicity property of
![]() ${\mathbb{P}}_{p,z,a}(N=n,I=1)/{\mathbb{P}}_{p,z,a}(N=n,I=0)$
with
${\mathbb{P}}_{p,z,a}(N=n,I=1)/{\mathbb{P}}_{p,z,a}(N=n,I=0)$
with
![]() $p={\frac{1}{2}}$
and
$p={\frac{1}{2}}$
and
![]() $0<z<{{a}/{2}}$
in Theorem 2 carries over to the continuous-time counterpart
$0<z<{{a}/{2}}$
in Theorem 2 carries over to the continuous-time counterpart
![]() $u_{c,\xi,\alpha}^+(t)/u_{c,\xi,\alpha}^-(t)$
with
$u_{c,\xi,\alpha}^+(t)/u_{c,\xi,\alpha}^-(t)$
with
![]() $c=0$
and
$c=0$
and
![]() $0<\xi<{\alpha}/{2}$
. Moreover, in (10) and (11), the term with
$0<\xi<{\alpha}/{2}$
. Moreover, in (10) and (11), the term with
![]() $\nu=1$
is dominant for large t, so that
$\nu=1$
is dominant for large t, so that
![]() $\lim_{t \to \infty} u_{0,\xi,\alpha}^+(t)/u_{0,\xi,\alpha}^-(t)=1$
. On the other hand, in (12) and (13), the term with
$\lim_{t \to \infty} u_{0,\xi,\alpha}^+(t)/u_{0,\xi,\alpha}^-(t)=1$
. On the other hand, in (12) and (13), the term with
![]() $k=0$
is dominant for small t, so that
$k=0$
is dominant for small t, so that
![]() $\lim_{t \to 0+} u_{0,\xi,\alpha}^+(t)/u_{0,\xi,\alpha}^-(t)=0$
for
$\lim_{t \to 0+} u_{0,\xi,\alpha}^+(t)/u_{0,\xi,\alpha}^-(t)=0$
for
![]() $0<\xi < {\alpha}/{2}$
. Hence, for
$0<\xi < {\alpha}/{2}$
. Hence, for
![]() $0<\xi<{\alpha}/{2}$
, as t increases from 0 to
$0<\xi<{\alpha}/{2}$
, as t increases from 0 to
![]() $\infty$
,
$\infty$
,
![]() $u_{0,\xi,\alpha}^+(t)/u_{0,\xi,\alpha}^-(t)$
monotonically increases from 0 to 1. (Equivalently, for
$u_{0,\xi,\alpha}^+(t)/u_{0,\xi,\alpha}^-(t)$
monotonically increases from 0 to 1. (Equivalently, for
![]() $c=0$
and
$c=0$
and
![]() $0<\xi<{\alpha}/{2}$
, the conditional distribution of
$0<\xi<{\alpha}/{2}$
, the conditional distribution of
![]() $\tau$
given
$\tau$
given
![]() $\xi +B_{\tau}=0$
(which has probability density
$\xi +B_{\tau}=0$
(which has probability density
![]() $({\alpha}/({\alpha-\xi})) u_{0,\xi,\alpha}^-(t)$
) is smaller, in the likelihood ratio order, than the conditional distribution of
$({\alpha}/({\alpha-\xi})) u_{0,\xi,\alpha}^-(t)$
) is smaller, in the likelihood ratio order, than the conditional distribution of
![]() $\tau$
given
$\tau$
given
![]() $\xi+B_{\tau}=\alpha$
(which has probability density
$\xi+B_{\tau}=\alpha$
(which has probability density
![]() $({\alpha}/{\xi}) u_{0,\xi,\alpha}^+(t)$
).) Furthermore, the monotone likelihood ratio property for N in Theorem 3 also carries over to
$({\alpha}/{\xi}) u_{0,\xi,\alpha}^+(t)$
).) Furthermore, the monotone likelihood ratio property for N in Theorem 3 also carries over to
![]() $\tau$
. Specifically, for
$\tau$
. Specifically, for
![]() $0<\xi\leq {\alpha}/{2}$
, the family of distributions
$0<\xi\leq {\alpha}/{2}$
, the family of distributions
![]() $\{\mathcal{L}_{c,\xi,\alpha}(\tau)\colon c \in (\!-\!\infty, 0]\}$
has monotone (increasing) likelihood ratio, while for
$\{\mathcal{L}_{c,\xi,\alpha}(\tau)\colon c \in (\!-\!\infty, 0]\}$
has monotone (increasing) likelihood ratio, while for
![]() ${\alpha}/{2}\leq \xi <\alpha$
, the family of distributions
${\alpha}/{2}\leq \xi <\alpha$
, the family of distributions
![]() $\{\mathcal{L}_{c,\xi,\alpha}(\tau)\colon c \in [0,\infty)\}$
has monotone (decreasing) likelihood ratio. In particular, in terms of the likelihood ratio order, the distribution
$\{\mathcal{L}_{c,\xi,\alpha}(\tau)\colon c \in [0,\infty)\}$
has monotone (decreasing) likelihood ratio. In particular, in terms of the likelihood ratio order, the distribution
![]() $\mathcal{L}_{c,{\alpha}/{2},\alpha}(\tau)$
is maximized over
$\mathcal{L}_{c,{\alpha}/{2},\alpha}(\tau)$
is maximized over
![]() $c \in (\!-\!\infty, \infty)$
by
$c \in (\!-\!\infty, \infty)$
by
![]() $c=0$
. The first exit time
$c=0$
. The first exit time
![]() $\tau$
of Brownian motion is a special case of the two-sided barrier problem in the subject of level-crossing problems for random processes. It is one of a limited number of cases where an explicit solution is available. See the survey articles [Reference Abrahams, Blake, Poor and Springer1, Reference Blake and Lindsey2] for discussion of the related literature.
$\tau$
of Brownian motion is a special case of the two-sided barrier problem in the subject of level-crossing problems for random processes. It is one of a limited number of cases where an explicit solution is available. See the survey articles [Reference Abrahams, Blake, Poor and Springer1, Reference Blake and Lindsey2] for discussion of the related literature.
2. Proof of Theorem 2
To prove Theorem 2, we need to introduce some notation and establish a few lemmas. Let
![]() $a \ge 4$
be an even integer. For
$a \ge 4$
be an even integer. For
![]() $ 0\le z \le a$
and
$ 0\le z \le a$
and
![]() $n\ge 1$
, let
$n\ge 1$
, let
![]() $T_{z,a}^+(n)\;:\!=\;|{\mathcal{S}}_{z,a}^+(n)|$
and
$T_{z,a}^+(n)\;:\!=\;|{\mathcal{S}}_{z,a}^+(n)|$
and
![]() $T_{z,a}^-(n)\;:\!=\;|{\mathcal{S}}_{z,a}^-(n)|$
. For
$T_{z,a}^-(n)\;:\!=\;|{\mathcal{S}}_{z,a}^-(n)|$
. For
![]() $n \ge 2$
and
$n \ge 2$
and
![]() $0<z<a$
, since
$0<z<a$
, since
we have
Let
![]() $T_{z,a}^+(0)=1$
or 0 according as
$T_{z,a}^+(0)=1$
or 0 according as
![]() $z=a$
or
$z=a$
or
![]() $0\le z<a$
. Then (14) also holds for
$0\le z<a$
. Then (14) also holds for
![]() $n=1$
and
$n=1$
and
![]() $0<z<a$
. That is,
$0<z<a$
. That is,
Similarly,
where
![]() $T_{z,a}^-(0)=1$
or 0 according as
$T_{z,a}^-(0)=1$
or 0 according as
![]() $z=0$
or
$z=0$
or
![]() $0<z\le a$
. Let
$0<z\le a$
. Let
![]() $T_{z,a}(n)=T_{z,a}^+(n)+T_{z,a}^-(n)$
for
$T_{z,a}(n)=T_{z,a}^+(n)+T_{z,a}^-(n)$
for
![]() $n\ge 0$
and
$n\ge 0$
and
![]() $0\le z \le a$
. By (15) and (16), we have
$0\le z \le a$
. By (15) and (16), we have
Applying (15) twice yields
 \begin{align} T_{z,a}^+(n) & = T_{z-1,a}^+(n-1) + T_{z+1,a}^+(n-1) \notag \\[5pt] & = T_{z-2,a}^+(n-2)+2 T_{z,a}^+(n-2)+T_{z+2,a}^+(n-2) \quad \mathrm{for}\ n\ge 2\ \mathrm{and}\ 2\le z \le a-2.\end{align}
\begin{align} T_{z,a}^+(n) & = T_{z-1,a}^+(n-1) + T_{z+1,a}^+(n-1) \notag \\[5pt] & = T_{z-2,a}^+(n-2)+2 T_{z,a}^+(n-2)+T_{z+2,a}^+(n-2) \quad \mathrm{for}\ n\ge 2\ \mathrm{and}\ 2\le z \le a-2.\end{align}
Similarly,
We have, by symmetry,
Below we adopt the convention that
![]() ${0}/{0}\;:\!=\;0$
and
${0}/{0}\;:\!=\;0$
and
![]() ${c}/{0}\;:\!=\;\infty$
for
${c}/{0}\;:\!=\;\infty$
for
![]() $c>0$
.
$c>0$
.
We are now ready to state and prove four lemmas. In particular, the inequality (21) given in Lemma 1 is a key observation for the proof of Theorem 2.
Lemma 1.
For even
![]() $a \ge 6$
and
$a \ge 6$
and
![]() $2\le z \le {{a}/{2}}-1$
,
$2\le z \le {{a}/{2}}-1$
,
Proof. By (20),
from which it follows that (21) holds for
![]() $z={{a}/{2}}-1$
.
$z={{a}/{2}}-1$
.
We now prove (21) by induction on n. Since
![]() $T_{z+2,a}(0)=T_{z+2,a}(1)=0$
for
$T_{z+2,a}(0)=T_{z+2,a}(1)=0$
for
![]() $2\le z \le {{a}/{2}}-1$
, (21) holds for
$2\le z \le {{a}/{2}}-1$
, (21) holds for
![]() $n=0$
and
$n=0$
and
![]() $n=1$
. Suppose (21) holds for
$n=1$
. Suppose (21) holds for
![]() $2 \le z \le {{a}/{2}}-1$
and for
$2 \le z \le {{a}/{2}}-1$
and for
![]() $n\le m$
with some
$n\le m$
with some
![]() $m\ge 1$
. We need to show that
$m\ge 1$
. We need to show that
for
![]() $2\le z \le {{a}/{2}}-1$
. By (22), (23) holds for
$2\le z \le {{a}/{2}}-1$
. By (22), (23) holds for
![]() $z={{a}/{2}}-1$
. By (17), for
$z={{a}/{2}}-1$
. By (17), for
![]() $3\le z \le {{a}/{2}}-2$
, (23) is equivalent to
$3\le z \le {{a}/{2}}-2$
, (23) is equivalent to
 \begin{multline} \frac{T_{z-1,a}(m)+T_{z+1,a}(m)}{T_{z-3,a}(m)+T_{z-1,a}(m)+T_{z+1,a}(m)+T_{z+3,a}(m)} \\[5pt] \ge \frac{T_{z+1,a}(m)+T_{z+3,a}(m)}{T_{z-1,a}(m)+T_{z+1,a}(m)+T_{z+3,a}(m)+T_{z+5,a}(m)}. \end{multline}
\begin{multline} \frac{T_{z-1,a}(m)+T_{z+1,a}(m)}{T_{z-3,a}(m)+T_{z-1,a}(m)+T_{z+1,a}(m)+T_{z+3,a}(m)} \\[5pt] \ge \frac{T_{z+1,a}(m)+T_{z+3,a}(m)}{T_{z-1,a}(m)+T_{z+1,a}(m)+T_{z+3,a}(m)+T_{z+5,a}(m)}. \end{multline}
For
![]() $3 \le z \le {{a}/{2}}-2$
, we have, by the induction hypothesis,
$3 \le z \le {{a}/{2}}-2$
, we have, by the induction hypothesis,
Note that the right-hand side of (25) and the left-hand side of (26) are the same. Since for
![]() $c_i, c_i'\ge 0$
$c_i, c_i'\ge 0$
![]() $(i=1,2)$
,
$(i=1,2)$
,
![]() ${c_1}/{c_2} \ge {c'_{\!\!1}}/{c'_{\!\!2}}$
implies
${c_1}/{c_2} \ge {c'_{\!\!1}}/{c'_{\!\!2}}$
implies
it follows from (25) and (26) that the left-hand side of (24) is greater than or equal to the right-hand side of (25) while the right-hand side of (24) is less than or equal to the left-hand side of (26). This establishes (24) (and hence (23)) for
![]() $3 \le z \le {{a}/{2}}-2$
.
$3 \le z \le {{a}/{2}}-2$
.
It remains to prove (23) for
![]() $z=2$
; i.e.,
$z=2$
; i.e.,
Note that
![]() $T_{0,a}(m+1)=0$
and that, for
$T_{0,a}(m+1)=0$
and that, for
![]() $a=6$
, (27) is an equality (since
$a=6$
, (27) is an equality (since
![]() $T_{2,6}(m+1)=T_{4,6}(m+1)$
and
$T_{2,6}(m+1)=T_{4,6}(m+1)$
and
![]() $T_{6,6}(m+1)=0$
). By (19), for (even)
$T_{6,6}(m+1)=0$
). By (19), for (even)
![]() $a \ge 8$
, (27) is equivalent to
$a \ge 8$
, (27) is equivalent to
 \begin{multline} \frac{T_{0,a}(m-1)+2 T_{2,a}(m-1)+T_{4,a}(m-1)}{T_{2,a}(m-1)+2 T_{4,a}(m-1)+T_{6,a}(m-1)} \\[5pt] \ge \frac{T_{2,a}(m-1)+2 T_{4,a}(m-1)+T_{6,a}(m-1)}{T_{0,a}(m-1)+2 T_{2,a}(m-1)+2 T_{4,a}(m-1) + 2 T_{6,a}(m-1)+T_{8,a}(m-1)}. \end{multline}
\begin{multline} \frac{T_{0,a}(m-1)+2 T_{2,a}(m-1)+T_{4,a}(m-1)}{T_{2,a}(m-1)+2 T_{4,a}(m-1)+T_{6,a}(m-1)} \\[5pt] \ge \frac{T_{2,a}(m-1)+2 T_{4,a}(m-1)+T_{6,a}(m-1)}{T_{0,a}(m-1)+2 T_{2,a}(m-1)+2 T_{4,a}(m-1) + 2 T_{6,a}(m-1)+T_{8,a}(m-1)}. \end{multline}
Since
![]() $T_{2,a}(m-1)=T_{4,a}(m-1)=T_{6,a}(m-1)=0$
for
$T_{2,a}(m-1)=T_{4,a}(m-1)=T_{6,a}(m-1)=0$
for
![]() $m=1$
and
$m=1$
and
![]() $a \ge 8$
, (28) holds for
$a \ge 8$
, (28) holds for
![]() $m=1$
. We now assume
$m=1$
. We now assume
![]() $m>1$
(implying that
$m>1$
(implying that
![]() $T_{0,a}(m-1)=T_{a,a}(m-1)=0$
). By (20), for
$T_{0,a}(m-1)=T_{a,a}(m-1)=0$
). By (20), for
![]() $a=8$
, (28) reduces to
$a=8$
, (28) reduces to
The induction hypothesis applied to
![]() $a=8$
and
$a=8$
and
![]() $z=2$
yields
$z=2$
yields
which implies (or more precisely, is equivalent to) (29). To show (28) for (even)
![]() $a\ge 10$
, by the induction hypothesis applied to
$a\ge 10$
, by the induction hypothesis applied to
![]() $a\ge 10$
and
$a\ge 10$
and
![]() $z=2,4$
(
$z=2,4$
(
![]() $\le {{a}/{2}}-1$
), we have
$\le {{a}/{2}}-1$
), we have
![]() $A_1\ge A_2 \ge A_3$
, where
$A_1\ge A_2 \ge A_3$
, where
Note that
If
![]() $T_{2,a}(m-1)=0$
, then necessarily
$T_{2,a}(m-1)=0$
, then necessarily
![]() $m-1$
(
$m-1$
(
![]() $\geq 1$
) is odd and
$\geq 1$
) is odd and
![]() $T_{4,a}(m-1)=T_{6,a}(m-1)=T_{8,a}(m-1)=0$
, so that (28) holds trivially. Suppose
$T_{4,a}(m-1)=T_{6,a}(m-1)=T_{8,a}(m-1)=0$
, so that (28) holds trivially. Suppose
![]() $T_{2,a}(m-1)>0$
. Then each of the two sides of (28) is a weighted average of
$T_{2,a}(m-1)>0$
. Then each of the two sides of (28) is a weighted average of
![]() $A_1$
,
$A_1$
,
![]() $A_2$
, and
$A_2$
, and
![]() $A_3$
. Indeed, the left-hand side of (28) equals
$A_3$
. Indeed, the left-hand side of (28) equals
![]() $c_1 A_1 +c_2 A_2$
with weights
$c_1 A_1 +c_2 A_2$
with weights
 \begin{align*} c_1&=\frac{2T_{4,a}(m-1)}{T_{2,a}(m-1)+2T_{4,a}(m-1)+T_{6,a}(m-1)},\\[5pt] c_2&=\frac{T_{2,a}(m-1)+T_{6,a}(m-1)}{T_{2,a}(m-1)+2T_{4,a}(m-1)+T_{6,a}(m-1)}, \end{align*}
\begin{align*} c_1&=\frac{2T_{4,a}(m-1)}{T_{2,a}(m-1)+2T_{4,a}(m-1)+T_{6,a}(m-1)},\\[5pt] c_2&=\frac{T_{2,a}(m-1)+T_{6,a}(m-1)}{T_{2,a}(m-1)+2T_{4,a}(m-1)+T_{6,a}(m-1)}, \end{align*}
while the right-hand side of (28) equals
![]() $c'_{\!\!1} A_1+c'_{\!\!2} A_2 +c'_{\!\!3} A_3$
with weights
$c'_{\!\!1} A_1+c'_{\!\!2} A_2 +c'_{\!\!3} A_3$
with weights
 \begin{align*} c'_{\!\!1}&=\frac{T_{4,a}(m-1)}{2T_{2,a}(m-1)+2T_{4,a}(m-1)+2T_{6,a}(m-1)+T_{8,a}(m-1)},\\[5pt] c'_{\!\!2}&=\frac{2T_{2,a}(m-1)+2T_{6,a}(m-1)}{2T_{2,a}(m-1)+2T_{4,a}(m-1)+2T_{6,a}(m-1)+T_{8,a}(m-1)},\\[5pt] c'_{\!\!3}&=\frac{T_{4,a}(m-1)+T_{8,a}(m-1)}{2T_{2,a}(m-1)+2T_{4,a}(m-1)+2T_{6,a}(m-1)+T_{8,a}(m-1)}. \end{align*}
\begin{align*} c'_{\!\!1}&=\frac{T_{4,a}(m-1)}{2T_{2,a}(m-1)+2T_{4,a}(m-1)+2T_{6,a}(m-1)+T_{8,a}(m-1)},\\[5pt] c'_{\!\!2}&=\frac{2T_{2,a}(m-1)+2T_{6,a}(m-1)}{2T_{2,a}(m-1)+2T_{4,a}(m-1)+2T_{6,a}(m-1)+T_{8,a}(m-1)},\\[5pt] c'_{\!\!3}&=\frac{T_{4,a}(m-1)+T_{8,a}(m-1)}{2T_{2,a}(m-1)+2T_{4,a}(m-1)+2T_{6,a}(m-1)+T_{8,a}(m-1)}. \end{align*}
Since
![]() $c_1 \ge c'_{\!\!1}$
, it follows from
$c_1 \ge c'_{\!\!1}$
, it follows from
![]() $A_1\ge A_2 \ge A_3$
that
$A_1\ge A_2 \ge A_3$
that
![]() $c_1 A_1+c_2 A_2 \ge c'_{\!\!1} A_1 +c'_{\!\!2} A_2 +c'_{\!\!3} A_3$
. This shows (28) for
$c_1 A_1+c_2 A_2 \ge c'_{\!\!1} A_1 +c'_{\!\!2} A_2 +c'_{\!\!3} A_3$
. This shows (28) for
![]() $a \ge 10$
and completes the induction proof.
$a \ge 10$
and completes the induction proof.
Remark 7. The proof of Lemma 1 makes use of the induction method on n with the help of the recursion (17), which is related to first-step analysis in Markov chains (see, e.g., [Reference Privault9]). After the first step, the initial state z moves either down to
![]() $z-1$
or up to
$z-1$
or up to
![]() $z+1$
. To apply the induction hypothesis, it is necessary to consider the boundary cases
$z+1$
. To apply the induction hypothesis, it is necessary to consider the boundary cases
![]() $z=2$
and
$z=2$
and
![]() $z={{a}/{2}}-1$
separately from
$z={{a}/{2}}-1$
separately from
![]() $3 \leq z \leq {{a}/{2}}-2$
. (The induction hypothesis is applicable neither in the case that
$3 \leq z \leq {{a}/{2}}-2$
. (The induction hypothesis is applicable neither in the case that
![]() $z=2$
moves down to 1 nor in the case that
$z=2$
moves down to 1 nor in the case that
![]() $z={{a}/{2}}-1$
moves up to
$z={{a}/{2}}-1$
moves up to
![]() ${{a}/{2}}$
.) The proofs of Lemmas 2 and 3 and Theorem 2 also make use of the recursions (15), (18), and (19). Again, the boundary cases need to be treated separately.
${{a}/{2}}$
.) The proofs of Lemmas 2 and 3 and Theorem 2 also make use of the recursions (15), (18), and (19). Again, the boundary cases need to be treated separately.
Lemma 2.
For even
![]() $n\ge 2$
,
$n\ge 2$
,
![]() ${T_{z,a}^+(n)}/{T_{z,a}(n)}$
is increasing in
${T_{z,a}^+(n)}/{T_{z,a}(n)}$
is increasing in
![]() $z \in \{2,4,\dots, a-2\}$
. For odd
$z \in \{2,4,\dots, a-2\}$
. For odd
![]() $n\ge 1$
,
$n\ge 1$
,
![]() ${T_{z,a}^+(n)}/{T_{z,a}(n)}$
is increasing in
${T_{z,a}^+(n)}/{T_{z,a}(n)}$
is increasing in
![]() $z \in \{1,3,\dots, a-1\}$
.
$z \in \{1,3,\dots, a-1\}$
.
Proof. Let
![]() $\rho(n)=1$
or 2 according as n is odd or even. We show that, for
$\rho(n)=1$
or 2 according as n is odd or even. We show that, for
![]() $n \ge 1$
,
$n \ge 1$
,
![]() ${T_{z,a}^+(n)}/{T_{z,a}(n)}$
is increasing in
${T_{z,a}^+(n)}/{T_{z,a}(n)}$
is increasing in
![]() $z \in \{\rho(n),\rho(n)+2,\dots, a-\rho(n)\}$
; i.e., for
$z \in \{\rho(n),\rho(n)+2,\dots, a-\rho(n)\}$
; i.e., for
![]() $n\ge 1$
,
$n\ge 1$
,
We proceed by induction on n. Since
![]() ${T_{z,a}^+(1)}/{T_{z,a}(1)}=0$
for
${T_{z,a}^+(1)}/{T_{z,a}(1)}=0$
for
![]() $z<a-1$
, and
$z<a-1$
, and
![]() ${T_{a-1,a}^+(1)}/{T_{a-1,a}(1)}=1$
, (30) holds for
${T_{a-1,a}^+(1)}/{T_{a-1,a}(1)}=1$
, (30) holds for
![]() $n=1$
. Suppose (30) holds for
$n=1$
. Suppose (30) holds for
![]() $n \le m$
with some
$n \le m$
with some
![]() $m\ge 1$
. We need to show that
$m\ge 1$
. We need to show that
Consider the case that m is even. Then
![]() $m\ge 2$
and
$m\ge 2$
and
![]() $\rho(m+1)=1$
. For
$\rho(m+1)=1$
. For
![]() $z=1,3,\dots,a-3$
, we have, by (15) and (17),
$z=1,3,\dots,a-3$
, we have, by (15) and (17),
The right-hand side of (32) equals
![]() ${T_{z+1,a}^+(m)}/{T_{z+1,a}(m)}$
for
${T_{z+1,a}^+(m)}/{T_{z+1,a}(m)}$
for
![]() $z=1$
and is less than or equal to
$z=1$
and is less than or equal to
![]() ${T_{z+1,a}^+(m)}/{T_{z+1,a}(m)}$
for
${T_{z+1,a}^+(m)}/{T_{z+1,a}(m)}$
for
![]() $z>1$
since, by the induction hypothesis, for
$z>1$
since, by the induction hypothesis, for
![]() $z=3,\dots, a-3$
,
$z=3,\dots, a-3$
,
The right-hand side of (33) equals
![]() ${T_{z+1,a}^+(m)}/{T_{z+1,a}(m)}$
for
${T_{z+1,a}^+(m)}/{T_{z+1,a}(m)}$
for
![]() $z=a-3$
and is greater than or equal to
$z=a-3$
and is greater than or equal to
![]() ${T_{z+1,a}^+(m)}/{T_{z+1,a}(m)}$
for
${T_{z+1,a}^+(m)}/{T_{z+1,a}(m)}$
for
![]() $z<a-3$
since, by the induction hypothesis, for
$z<a-3$
since, by the induction hypothesis, for
![]() $z=1,\dots, a-5$
,
$z=1,\dots, a-5$
,
This proves (31) for the case of even m. The case of odd m can be treated similarly.
Lemma 3.
For even
![]() $a\ge 4$
and
$a\ge 4$
and
![]() $n\ge 0$
,
$n\ge 0$
,
Proof. Note that (34) holds trivially for even n since both sides of (34) are
![]() ${0}/{0}$
for even n. We now prove (34) for odd
${0}/{0}$
for even n. We now prove (34) for odd
![]() $n\ge 1$
. By (15),
$n\ge 1$
. By (15),
Similarly, by (17),
![]() $T_{1,a}(n+2)=T_{1,a}(n)+T_{3,a}(n)$
, which together with (36) implies that
$T_{1,a}(n+2)=T_{1,a}(n)+T_{3,a}(n)$
, which together with (36) implies that
where the inequality follows from
![]() ${T_{1,a}^+(n)}/{T_{1,a}(n)} \le {T_{3,a}^+(n)}/{T_{3,a}(n)}$
(by Lemma 2).
${T_{1,a}^+(n)}/{T_{1,a}(n)} \le {T_{3,a}^+(n)}/{T_{3,a}(n)}$
(by Lemma 2).
Next, to prove (35), it suffices to consider the case of even n. For
![]() $n=0$
, the right-hand side of (35) is 0, so (35) holds. For even
$n=0$
, the right-hand side of (35) is 0, so (35) holds. For even
![]() $n\ge 2$
and
$n\ge 2$
and
![]() $a=4$
, both sides of (35) equal
$a=4$
, both sides of (35) equal
![]() ${\frac{1}{2}}$
by symmetry. For even
${\frac{1}{2}}$
by symmetry. For even
![]() $n\geq 2$
and
$n\geq 2$
and
![]() $a\ge 6$
, we have, by (18) and (19),
$a\ge 6$
, we have, by (18) and (19),
 \begin{align*} \frac{T_{2,a}^+(n+2)}{T_{2,a}(n+2)} & = \frac{T_{0,a}^+(n)+2T_{2,a}^+(n)+T_{4,a}^+(n)}{T_{0,a}(n)+2T_{2,a}(n)+T_{4,a}(n)} \\[5pt] & = \frac{2T_{2,a}^+(n)+T_{4,a}^+(n)}{2T_{2,a}(n)+T_{4,a}(n)} \ge \frac{ T_{2,a}^+(n)}{T_{2,a}(n)}, \end{align*}
\begin{align*} \frac{T_{2,a}^+(n+2)}{T_{2,a}(n+2)} & = \frac{T_{0,a}^+(n)+2T_{2,a}^+(n)+T_{4,a}^+(n)}{T_{0,a}(n)+2T_{2,a}(n)+T_{4,a}(n)} \\[5pt] & = \frac{2T_{2,a}^+(n)+T_{4,a}^+(n)}{2T_{2,a}(n)+T_{4,a}(n)} \ge \frac{ T_{2,a}^+(n)}{T_{2,a}(n)}, \end{align*}
where the inequality follows from
![]() ${T_{2,a}^+(n)}/{T_{2,a}(n)} \leq {T_{4,a}^+(n)}/{T_{4,a}(n)}$
(by Lemma 2). The proof is complete.
${T_{2,a}^+(n)}/{T_{2,a}(n)} \leq {T_{4,a}^+(n)}/{T_{4,a}(n)}$
(by Lemma 2). The proof is complete.
Lemma 4.
Let
![]() $\alpha_1>0$
and
$\alpha_1>0$
and
![]() $\alpha_i\geq \beta_i \ge 0$
,
$\alpha_i\geq \beta_i \ge 0$
,
![]() $i=1,2,3,4$
. Suppose
$i=1,2,3,4$
. Suppose
Then
Proof. If
![]() $\alpha_2=0$
then
$\alpha_2=0$
then
![]() $\alpha_3=0$
since
$\alpha_3=0$
since
![]() ${\alpha_2}/({\alpha_1+\alpha_3}) \ge {\alpha_3}/({\alpha_2+\alpha_4})$
. So
${\alpha_2}/({\alpha_1+\alpha_3}) \ge {\alpha_3}/({\alpha_2+\alpha_4})$
. So
If
![]() $\alpha_3=0$
, then
$\alpha_3=0$
, then
implying that
Now suppose
![]() $\alpha_2>0$
and
$\alpha_2>0$
and
![]() $\alpha_3>0$
. We have
$\alpha_3>0$
. We have
 \begin{align*} 0 & \leq \frac{\alpha_2\alpha_3}{\alpha_1+\alpha_3} \bigg[\frac{\beta_2+\beta_4}{\alpha_2+\alpha_4}-\frac{\beta_3}{\alpha_3}\bigg] + \alpha_2\bigg[\frac{\beta_1+\beta_3}{\alpha_1+\alpha_3}-\frac{\beta_2}{\alpha_2}\bigg] \\[5pt] & = \frac{\alpha_2(\alpha_2+\alpha_4)\beta_1+\alpha_2\alpha_3\beta_4 - (\alpha_1\alpha_2+\alpha_1\alpha_4+\alpha_3\alpha_4)\beta_2}{(\alpha_1+\alpha_3)(\alpha_2+\alpha_4)}, \\[5pt] 0 & \leq \frac{\alpha_2\alpha_3}{\alpha_2+\alpha_4} \bigg[\frac{\beta_1+\beta_3}{\alpha_1+\alpha_3}-\frac{\beta_2}{\alpha_2}\bigg] + \alpha_3\bigg[\frac{\beta_2+\beta_4}{\alpha_2+\alpha_4}-\frac{\beta_3}{\alpha_3}\bigg] \\[5pt] & = \frac{\alpha_2\alpha_3\beta_1+\alpha_3(\alpha_1+\alpha_3)\beta_4 - (\alpha_1\alpha_2+\alpha_1\alpha_4+\alpha_3\alpha_4)\beta_3}{(\alpha_1+\alpha_3)(\alpha_2+\alpha_4)}, \end{align*}
\begin{align*} 0 & \leq \frac{\alpha_2\alpha_3}{\alpha_1+\alpha_3} \bigg[\frac{\beta_2+\beta_4}{\alpha_2+\alpha_4}-\frac{\beta_3}{\alpha_3}\bigg] + \alpha_2\bigg[\frac{\beta_1+\beta_3}{\alpha_1+\alpha_3}-\frac{\beta_2}{\alpha_2}\bigg] \\[5pt] & = \frac{\alpha_2(\alpha_2+\alpha_4)\beta_1+\alpha_2\alpha_3\beta_4 - (\alpha_1\alpha_2+\alpha_1\alpha_4+\alpha_3\alpha_4)\beta_2}{(\alpha_1+\alpha_3)(\alpha_2+\alpha_4)}, \\[5pt] 0 & \leq \frac{\alpha_2\alpha_3}{\alpha_2+\alpha_4} \bigg[\frac{\beta_1+\beta_3}{\alpha_1+\alpha_3}-\frac{\beta_2}{\alpha_2}\bigg] + \alpha_3\bigg[\frac{\beta_2+\beta_4}{\alpha_2+\alpha_4}-\frac{\beta_3}{\alpha_3}\bigg] \\[5pt] & = \frac{\alpha_2\alpha_3\beta_1+\alpha_3(\alpha_1+\alpha_3)\beta_4 - (\alpha_1\alpha_2+\alpha_1\alpha_4+\alpha_3\alpha_4)\beta_3}{(\alpha_1+\alpha_3)(\alpha_2+\alpha_4)}, \end{align*}
implying that
So
![]() $C \geq \beta_2+\beta_3$
, where
$C \geq \beta_2+\beta_3$
, where
To show
![]() $({\beta_1+\beta_4})/({\alpha_1+\alpha_4}) \ge ({\beta_2+\beta_3})/({\alpha_2+\alpha_3})$
, since
$({\beta_1+\beta_4})/({\alpha_1+\alpha_4}) \ge ({\beta_2+\beta_3})/({\alpha_2+\alpha_3})$
, since
![]() $C \geq \beta_2+\beta_3$
it suffices to verify that
$C \geq \beta_2+\beta_3$
it suffices to verify that
We have
 \begin{align*} C_1 (\alpha_1 \alpha_2+\alpha_1 \alpha_4 +\alpha_3 \alpha_4) & = \alpha_4[\alpha_3(\alpha_1+\alpha_3)-\alpha_2(\alpha_2+\alpha_4)]\beta_1 \\[5pt] & \quad + \alpha_1[\alpha_2(\alpha_2+\alpha_4)-\alpha_1(\alpha_1+\alpha_3)] \beta_4 \\[5pt] & = [\alpha_2(\alpha_2+\alpha_4)-\alpha_3(\alpha_1+\alpha_3)](\alpha_1\beta_4-\alpha_4\beta_1) \geq 0, \end{align*}
\begin{align*} C_1 (\alpha_1 \alpha_2+\alpha_1 \alpha_4 +\alpha_3 \alpha_4) & = \alpha_4[\alpha_3(\alpha_1+\alpha_3)-\alpha_2(\alpha_2+\alpha_4)]\beta_1 \\[5pt] & \quad + \alpha_1[\alpha_2(\alpha_2+\alpha_4)-\alpha_1(\alpha_1+\alpha_3)] \beta_4 \\[5pt] & = [\alpha_2(\alpha_2+\alpha_4)-\alpha_3(\alpha_1+\alpha_3)](\alpha_1\beta_4-\alpha_4\beta_1) \geq 0, \end{align*}
since
![]() ${\alpha_2}/({\alpha_1+\alpha_3}) \geq {\alpha_3}/({\alpha_2+\alpha_4})$
and
${\alpha_2}/({\alpha_1+\alpha_3}) \geq {\alpha_3}/({\alpha_2+\alpha_4})$
and
![]() ${\beta_4}/{\alpha_4} \geq {\beta_1}/{\alpha_1}$
. This proves (37), and completes the proof.
${\beta_4}/{\alpha_4} \geq {\beta_1}/{\alpha_1}$
. This proves (37), and completes the proof.
Proof of Theorem
2. We claim that, for even
![]() $a\ge 4$
and
$a\ge 4$
and
![]() $0<z<{{a}/{2}}$
,
$0<z<{{a}/{2}}$
,
By Lemma 3, (38) holds for
![]() $z=1$
and
$z=1$
and
![]() $z=2$
. Consequently, (38) holds for
$z=2$
. Consequently, (38) holds for
![]() $a=4$
and
$a=4$
and
![]() $a=6$
. Note also that
$a=6$
. Note also that
(If n and
![]() ${{a}/{2}}$
have opposite parity, both sides of (39) are
${{a}/{2}}$
have opposite parity, both sides of (39) are
![]() ${0}/{0}=0$
. For n and
${0}/{0}=0$
. For n and
![]() ${{a}/{2}}$
of the same parity,
${{a}/{2}}$
of the same parity,
![]() ${T_{{{a}/{2}},a}^+(n)}/{T_{{{a}/{2}},a}(n)}=0$
or
${T_{{{a}/{2}},a}^+(n)}/{T_{{{a}/{2}},a}(n)}=0$
or
![]() ${\frac{1}{2}}$
according as
${\frac{1}{2}}$
according as
![]() $n<{{a}/{2}}$
or
$n<{{a}/{2}}$
or
![]() $\ge {{a}/{2}}$
. This shows (39).)
$\ge {{a}/{2}}$
. This shows (39).)
We now prove (38) for
![]() $a \geq 8$
and
$a \geq 8$
and
![]() $3 \leq z <{{a}/{2}}$
by induction on n. For
$3 \leq z <{{a}/{2}}$
by induction on n. For
![]() $n=0$
and
$n=0$
and
![]() $n=1$
, the right-hand side of (38) equals 0 since
$n=1$
, the right-hand side of (38) equals 0 since
![]() $T_{z,a}^+(0)=T_{z,a}^+(1)=0$
for
$T_{z,a}^+(0)=T_{z,a}^+(1)=0$
for
![]() $0<z<{{a}/{2}}$
. So (38) holds for
$0<z<{{a}/{2}}$
. So (38) holds for
![]() $n\le 1$
. Suppose (38) holds for
$n\le 1$
. Suppose (38) holds for
![]() $n\le m$
with some
$n\le m$
with some
![]() $m \ge 1$
. We need to show that
$m \ge 1$
. We need to show that
By (15) and (17), this is equivalent to
for
![]() $a \ge 8$
and
$a \ge 8$
and
![]() $3\le z <{{a}/{2}}$
. By (18) and (19) applied to the left-hand side of (40), (40) is equivalent to
$3\le z <{{a}/{2}}$
. By (18) and (19) applied to the left-hand side of (40), (40) is equivalent to
for
![]() $a \ge 8$
and
$a \ge 8$
and
![]() $3\le z <{{a}/{2}}$
. Note that (41) holds trivially if z and m are of the same parity. Suppose z and m have opposite parity. If
$3\le z <{{a}/{2}}$
. Note that (41) holds trivially if z and m are of the same parity. Suppose z and m have opposite parity. If
![]() $T_{z-1,a}(m+2)=0$
, then
$T_{z-1,a}(m+2)=0$
, then
![]() $m+2<z-1$
(
$m+2<z-1$
(
![]() $<{{a}/{2}}-1$
), so that both sides of (40) (and hence (41)) are 0.
$<{{a}/{2}}-1$
), so that both sides of (40) (and hence (41)) are 0.
Now suppose
![]() $T_{z-1,a}(m+2)>0$
. We first prove (41) for
$T_{z-1,a}(m+2)>0$
. We first prove (41) for
![]() $z=3$
(and even m), in which case we have
$z=3$
(and even m), in which case we have
![]() $T_{z-3,a}(m)=T_{z-3,a}^+(m)=0$
, so that (41) becomes
$T_{z-3,a}(m)=T_{z-3,a}^+(m)=0$
, so that (41) becomes
This inequality holds since, by Lemma 2,
We now prove (41) for
![]() $4\le z <{{a}/{2}}$
(in which case necessarily
$4\le z <{{a}/{2}}$
(in which case necessarily
![]() $a \ge 10$
). Note that
$a \ge 10$
). Note that
![]() $T_{z-1,a}(m+2)>0$
implies
$T_{z-1,a}(m+2)>0$
implies
![]() $T_{z-3,a}(m)>0$
. By the induction hypothesis together with (39), we have
$T_{z-3,a}(m)>0$
. By the induction hypothesis together with (39), we have
By (18) and (19) applied to the left-hand sides of each of these inequalities, we have
Noting that the left-hand side of (42) equals
where
the inequality in (42) implies that
Similarly, if
![]() $T_{z-1,a}(m)>0$
, then the inequality in (43) implies that
$T_{z-1,a}(m)>0$
, then the inequality in (43) implies that
If
![]() $T_{z-1,a}(m)=0$
, then
$T_{z-1,a}(m)=0$
, then
![]() $T_{z+1,a}(m)=T_{z+3,a}(m)=0$
(since
$T_{z+1,a}(m)=T_{z+3,a}(m)=0$
(since
![]() $z-1 < z+3 \le a-(z-1)$
), so the inequality in (45) holds trivially.
$z-1 < z+3 \le a-(z-1)$
), so the inequality in (45) holds trivially.
Let
 \begin{alignat*}{4} \alpha_1 & = T_{z-3,a}(m), \qquad & \alpha_2 & = T_{z-1,a}(m), \qquad & \alpha_3 & = T_{z+1,a}(m), \qquad & \alpha_4 & = T_{z+3,a}(m), \\[5pt] \beta_1 & = T_{z-3,a}^+(m), & \beta_2 & = T_{z-1,a}^+(m), & \beta_3 & = T_{z+1,a}^+(m), & \beta_4 & = T_{z+3,a}^+(m). \end{alignat*}
\begin{alignat*}{4} \alpha_1 & = T_{z-3,a}(m), \qquad & \alpha_2 & = T_{z-1,a}(m), \qquad & \alpha_3 & = T_{z+1,a}(m), \qquad & \alpha_4 & = T_{z+3,a}(m), \\[5pt] \beta_1 & = T_{z-3,a}^+(m), & \beta_2 & = T_{z-1,a}^+(m), & \beta_3 & = T_{z+1,a}^+(m), & \beta_4 & = T_{z+3,a}^+(m). \end{alignat*}
Since
![]() $T_{z-1,a}(m+2)>0$
, we have
$T_{z-1,a}(m+2)>0$
, we have
![]() $\alpha_1=T_{z-3,a}(m)>0$
. By (44) and (45),
$\alpha_1=T_{z-3,a}(m)>0$
. By (44) and (45),
Furthermore, by Lemma 1,
and by Lemma 2,
It follows from Lemma 4 that
implying that
 \begin{align*} \frac{T_{z-1,a}^+(m)+T_{z+1,a}^+(m)}{T_{z-1,a}(m)+T_{z+1,a}(m)} & = \frac{\beta_2+\beta_3}{\alpha_2+\alpha_3} \\[5pt] & \le \frac{\beta_1+3\beta_2+3\beta_3+\beta_4}{\alpha_1+3\alpha_2+3\alpha_3+\alpha_4} \\[5pt] & = \frac{T_{z-3,a}^+(m)+3T_{z-1,a}^+(m)+3T_{z+1,a}^+(m)+T_{z+3,a}^+(m)} {T_{z-3,a}(m)+3T_{z-1,a}(m)+3T_{z+1,a}(m)+T_{z+3,a}(m)}, \end{align*}
\begin{align*} \frac{T_{z-1,a}^+(m)+T_{z+1,a}^+(m)}{T_{z-1,a}(m)+T_{z+1,a}(m)} & = \frac{\beta_2+\beta_3}{\alpha_2+\alpha_3} \\[5pt] & \le \frac{\beta_1+3\beta_2+3\beta_3+\beta_4}{\alpha_1+3\alpha_2+3\alpha_3+\alpha_4} \\[5pt] & = \frac{T_{z-3,a}^+(m)+3T_{z-1,a}^+(m)+3T_{z+1,a}^+(m)+T_{z+3,a}^+(m)} {T_{z-3,a}(m)+3T_{z-1,a}(m)+3T_{z+1,a}(m)+T_{z+3,a}(m)}, \end{align*}
proving (41) for
![]() $4 \le z <{{a}/{2}}$
. This completes the proof of (38), which implies that
$4 \le z <{{a}/{2}}$
. This completes the proof of (38), which implies that
is increasing as
![]() $n \in \{z,z+2,\dots\}$
increases. Finally, as
$n \in \{z,z+2,\dots\}$
increases. Finally, as
![]() $n \in \{z,z+2,\dots\}$
tends to
$n \in \{z,z+2,\dots\}$
tends to
![]() $\infty$
, it follows from (1) and (2) (with
$\infty$
, it follows from (1) and (2) (with
![]() $p={\frac{1}{2}}$
) that
$p={\frac{1}{2}}$
) that
approaches 1, implying that
![]() ${|{\mathcal{S}}_{z,a}^+(n)|}/({|{\mathcal{S}}_{z,a}^+(n)|+|{\mathcal{S}}_{z,a}^-(n)|})$
increases to
${|{\mathcal{S}}_{z,a}^+(n)|}/({|{\mathcal{S}}_{z,a}^+(n)|+|{\mathcal{S}}_{z,a}^-(n)|})$
increases to
![]() ${\frac{1}{2}}$
in the limit. The proof of Theorem 2 is complete.
${\frac{1}{2}}$
in the limit. The proof of Theorem 2 is complete.
3. Proof of Theorem 3
Theorem 2 plays a key role in the following proof of Theorem 3.
Proof of Theorem
3. By (4), for
![]() $0<z<{{a}/{2}}$
and
$0<z<{{a}/{2}}$
and
![]() $n=z,z+2,\dots$
,
$n=z,z+2,\dots$
,
 \begin{align*} {\mathbb{P}}_{p,z,a}(N=n) & = (pq)^{{n}/{2}}\bigg[\bigg(\frac{p}{q}\bigg)^{({a-z})/{2}}|{\mathcal{S}}_{z,a}^+(n)| + \bigg(\frac{q}{p}\bigg)^{{z}/{2}}|{\mathcal{S}}_{z,a}^-(n)|\bigg] \\[5pt] & = (pq)^{{n}/{2}}\bigg[\bigg(\frac{p}{q}\bigg)^{({a-z})/{2}}\frac{T_{z,a}^+(n)}{T_{z,a}(n)} + \bigg(\frac{q}{p}\bigg)^{{z}/{2}}\bigg(1-\frac{T_{z,a}^+(n)}{T_{z,a}(n)}\bigg)\bigg] T_{z,a}(n) \\[5pt] & = (pq)^{{n}/{2}}\bigg\{\bigg[\bigg(\frac{p}{q}\bigg)^{({a-z})/{2}} - \bigg(\frac{q}{p}\bigg)^{{z}/{2}}\bigg] \frac{T_{z,a}^+(n)}{T_{z,a}(n)} + \bigg(\frac{q}{p}\bigg)^{{z}/{2}}\bigg\} T_{z,a}(n). \end{align*}
\begin{align*} {\mathbb{P}}_{p,z,a}(N=n) & = (pq)^{{n}/{2}}\bigg[\bigg(\frac{p}{q}\bigg)^{({a-z})/{2}}|{\mathcal{S}}_{z,a}^+(n)| + \bigg(\frac{q}{p}\bigg)^{{z}/{2}}|{\mathcal{S}}_{z,a}^-(n)|\bigg] \\[5pt] & = (pq)^{{n}/{2}}\bigg[\bigg(\frac{p}{q}\bigg)^{({a-z})/{2}}\frac{T_{z,a}^+(n)}{T_{z,a}(n)} + \bigg(\frac{q}{p}\bigg)^{{z}/{2}}\bigg(1-\frac{T_{z,a}^+(n)}{T_{z,a}(n)}\bigg)\bigg] T_{z,a}(n) \\[5pt] & = (pq)^{{n}/{2}}\bigg\{\bigg[\bigg(\frac{p}{q}\bigg)^{({a-z})/{2}} - \bigg(\frac{q}{p}\bigg)^{{z}/{2}}\bigg] \frac{T_{z,a}^+(n)}{T_{z,a}(n)} + \bigg(\frac{q}{p}\bigg)^{{z}/{2}}\bigg\} T_{z,a}(n). \end{align*}
So, for
![]() $0<p<p'\leq {\frac{1}{2}}$
,
$0<p<p'\leq {\frac{1}{2}}$
,
![]() $0<z<{{a}/{2}}$
, and
$0<z<{{a}/{2}}$
, and
![]() $n=z,z+2,\dots$
,
$n=z,z+2,\dots$
,
where
Note that
 \begin{align} &\frac{{\mathrm{d}}}{{\mathrm{d}} x}H_{p,p',z,a}(x) \nonumber \\[5pt] & \quad = \bigg\{\bigg[\bigg(\frac{p}{q}\bigg)^{({a-z})/{2}} - \bigg(\frac{q}{p}\bigg)^{{z}/{2}}\bigg]x + \bigg(\frac{q}{p}\bigg)^{{z}/{2}}\bigg\}^{-2} \bigg(\frac{qq'}{pp'}\bigg)^{{z}/{2}}\bigg[\bigg({p'}/{q'}\bigg)^{{{a}/{2}}} - \bigg(\frac{p}{q}\bigg)^{{{a}/{2}}}\bigg] > 0. \end{align}
\begin{align} &\frac{{\mathrm{d}}}{{\mathrm{d}} x}H_{p,p',z,a}(x) \nonumber \\[5pt] & \quad = \bigg\{\bigg[\bigg(\frac{p}{q}\bigg)^{({a-z})/{2}} - \bigg(\frac{q}{p}\bigg)^{{z}/{2}}\bigg]x + \bigg(\frac{q}{p}\bigg)^{{z}/{2}}\bigg\}^{-2} \bigg(\frac{qq'}{pp'}\bigg)^{{z}/{2}}\bigg[\bigg({p'}/{q'}\bigg)^{{{a}/{2}}} - \bigg(\frac{p}{q}\bigg)^{{{a}/{2}}}\bigg] > 0. \end{align}
Since, by Theorem 2,
![]() ${T_{z,a}^+(n)}/{T_{z,a}(n)}$
is increasing in
${T_{z,a}^+(n)}/{T_{z,a}(n)}$
is increasing in
![]() $n \in \{z,z+2,\dots\}$
, it follows from (46) and (47) that
$n \in \{z,z+2,\dots\}$
, it follows from (46) and (47) that
![]() ${\mathbb{P}_{p',z,a}(N=n)}/{{\mathbb{P}}_{p,z,a}(N=n)}$
is increasing in
${\mathbb{P}_{p',z,a}(N=n)}/{{\mathbb{P}}_{p,z,a}(N=n)}$
is increasing in
![]() $n \in \{z,z+2,\dots\}$
. This proves that
$n \in \{z,z+2,\dots\}$
. This proves that
![]() $\{{\mathcal{L}}_{p,z,a}(N)\colon 0\le p \le {\frac{1}{2}}\}$
has monotone (increasing) likelihood ratio. For
$\{{\mathcal{L}}_{p,z,a}(N)\colon 0\le p \le {\frac{1}{2}}\}$
has monotone (increasing) likelihood ratio. For
![]() ${{a}/{2}}<z<a$
, note that
${{a}/{2}}<z<a$
, note that
![]() $\mathcal{L}_{p,z,a}(N)=\mathcal{L}_{p',z',a}(N)$
with
$\mathcal{L}_{p,z,a}(N)=\mathcal{L}_{p',z',a}(N)$
with
![]() $p'=1-p$
and
$p'=1-p$
and
![]() $z'=a-z$
, implying that
$z'=a-z$
, implying that
![]() $\{{\mathcal{L}}_{p,z,a}(N)\colon {\frac{1}{2}} \le p \le 1 \}$
has monotone (decreasing) likelihood ratio, completing the proof.
$\{{\mathcal{L}}_{p,z,a}(N)\colon {\frac{1}{2}} \le p \le 1 \}$
has monotone (decreasing) likelihood ratio, completing the proof.
4. Proof of Theorem 4
Proof of Theorem
4. Fix
![]() $0<z<{{a}/{2}}$
. We claim that, for
$0<z<{{a}/{2}}$
. We claim that, for
![]() $n \geq 0$
,
$n \geq 0$
,
Let
and let
![]() $(\omega_1,\dots,\omega_n)_z\;:\!=\;\big(z,z+\omega_1,z+\omega_1+\omega_2, \dots, z+\sum_{i=1}^n \omega_i\big)$
, which is the sample path starting at z with successive increments
$(\omega_1,\dots,\omega_n)_z\;:\!=\;\big(z,z+\omega_1,z+\omega_1+\omega_2, \dots, z+\sum_{i=1}^n \omega_i\big)$
, which is the sample path starting at z with successive increments
![]() $\omega_1,\dots, \omega_n$
. Since z is fixed, for convenience we may identify
$\omega_1,\dots, \omega_n$
. Since z is fixed, for convenience we may identify
![]() $(\omega_1,\dots,\omega_n)$
with the corresponding sample path
$(\omega_1,\dots,\omega_n)$
with the corresponding sample path
![]() $(\omega_1,\dots,\omega_n)_z$
. In particular, we refer to
$(\omega_1,\dots,\omega_n)_z$
. In particular, we refer to
![]() $S_z(n)$
as the collection of all sample paths starting at z and strictly staying between 0 and a up to time n. (By abusing notation, for
$S_z(n)$
as the collection of all sample paths starting at z and strictly staying between 0 and a up to time n. (By abusing notation, for
![]() $(\omega_1,\dots,\omega_{n}) \in S_{z}(n)$
, we also write
$(\omega_1,\dots,\omega_{n}) \in S_{z}(n)$
, we also write
![]() $(\omega_1,\dots,\omega_{n})_z \in S_{z}(n)$
.)
$(\omega_1,\dots,\omega_{n})_z \in S_{z}(n)$
.)
We now prove (48) by induction on n. Plainly, (48) holds for
![]() $n=0$
. Suppose (48) holds for
$n=0$
. Suppose (48) holds for
![]() $n\leq m$
with some
$n\leq m$
with some
![]() $m\geq 0$
. We need to show that
$m\geq 0$
. We need to show that
By (49),
![]() $f(p,m+1)\;:\!=\;\mathbb{P}_{p,z, a}(N>m+1)=\mathbb{P}\{(X_{1,p},\dots, X_{m+1,p}) \in S_{z}(m+1)\}$
, where the
$f(p,m+1)\;:\!=\;\mathbb{P}_{p,z, a}(N>m+1)=\mathbb{P}\{(X_{1,p},\dots, X_{m+1,p}) \in S_{z}(m+1)\}$
, where the
![]() $X_{i,p}$
are defined as in (3). We partition the sample paths of
$X_{i,p}$
are defined as in (3). We partition the sample paths of
![]() $S_{z}(m+1)$
into subsets
$S_{z}(m+1)$
into subsets
![]() $\Delta_i$
,
$\Delta_i$
,
![]() $i=0,1,\dots, m+1$
, where
$i=0,1,\dots, m+1$
, where
![]() $\Delta_0$
is the subset of those sample paths that always stay below
$\Delta_0$
is the subset of those sample paths that always stay below
![]() $a-1$
, and
$a-1$
, and
![]() $\Delta_i$
(
$\Delta_i$
(
![]() $i=1,\dots, m+1$
) is the subset of those sample paths that visit
$i=1,\dots, m+1$
) is the subset of those sample paths that visit
![]() $a-1$
at time i for the first time. (Note that for
$a-1$
at time i for the first time. (Note that for
![]() $i \geq 1$
,
$i \geq 1$
,
![]() $\Delta_i=\emptyset$
if i and
$\Delta_i=\emptyset$
if i and
![]() $a-z-1$
have opposite parity.) Then
$a-z-1$
have opposite parity.) Then
![]() $f(p,m+1)=\sum_{i=0}^{m+1} g(p,m+1,i)$
, where
$f(p,m+1)=\sum_{i=0}^{m+1} g(p,m+1,i)$
, where
![]() $g(p,m+1,i)\;:\!=\;\mathbb{P}\{(X_{1,p},\dots, X_{m+1,p})_{z} \in \Delta_i\}$
. To prove (50), it suffices to show that, for
$g(p,m+1,i)\;:\!=\;\mathbb{P}\{(X_{1,p},\dots, X_{m+1,p})_{z} \in \Delta_i\}$
. To prove (50), it suffices to show that, for
![]() $i=0,1,\dots,m+1$
,
$i=0,1,\dots,m+1$
,
![]() $g(p,m+1,i)$
is increasing in
$g(p,m+1,i)$
is increasing in
![]() $p \in \big[0,{\frac{1}{2}}\big]$
. To show
$p \in \big[0,{\frac{1}{2}}\big]$
. To show
![]() $g(p,m+1,0)$
is increasing in
$g(p,m+1,0)$
is increasing in
![]() $p \in \big[0,{\frac{1}{2}}\big]$
, we have
$p \in \big[0,{\frac{1}{2}}\big]$
, we have
 \begin{align*} g(p,m+1,0) & = \mathbb{P}\{(X_{1,p},\dots, X_{m+1,p})_{z} \in \Delta_0\} \\[5pt] & = \mathbb{P}\{(X_{1,p},\dots, X_{m+1,p})_{z} \text{ stays strictly between } 0 \text{ and } a-1\} \\[5pt] & = \mathbb{P}_{p,z, a-1}(N>m+1), \end{align*}
\begin{align*} g(p,m+1,0) & = \mathbb{P}\{(X_{1,p},\dots, X_{m+1,p})_{z} \in \Delta_0\} \\[5pt] & = \mathbb{P}\{(X_{1,p},\dots, X_{m+1,p})_{z} \text{ stays strictly between } 0 \text{ and } a-1\} \\[5pt] & = \mathbb{P}_{p,z, a-1}(N>m+1), \end{align*}
which, by Theorems 1 and 3, is increasing in
![]() $p \in \big[0,{\frac{1}{2}}\big]$
.
$p \in \big[0,{\frac{1}{2}}\big]$
.
To show that
![]() $g(p,m+1,i)$
is increasing in
$g(p,m+1,i)$
is increasing in
![]() $p \in \big[0,{\frac{1}{2}}\big]$
for
$p \in \big[0,{\frac{1}{2}}\big]$
for
![]() $i=1,\dots, m+1$
, we further partition the
$i=1,\dots, m+1$
, we further partition the
![]() $\Delta_i$
into
$\Delta_i$
into
![]() $\Delta_{i,j}$
(
$\Delta_{i,j}$
(
![]() $i\leq j\le m+1$
) where
$i\leq j\le m+1$
) where
![]() $\Delta_{i,i}$
is the subset of those sample paths that after time i never revisit z, and
$\Delta_{i,i}$
is the subset of those sample paths that after time i never revisit z, and
![]() $\Delta_{i,j}$
(
$\Delta_{i,j}$
(
![]() $j>i$
) is the subset of those sample paths that after time i revisit z at time j for the first time. Let
$j>i$
) is the subset of those sample paths that after time i revisit z at time j for the first time. Let
![]() $h(p,m+1,i,j)\;:\!=\;\mathbb{P}\{(X_{1,p},\dots, X_{m+1,p})_{z} \in \Delta_{i,j}\}$
. We have
$h(p,m+1,i,j)\;:\!=\;\mathbb{P}\{(X_{1,p},\dots, X_{m+1,p})_{z} \in \Delta_{i,j}\}$
. We have
![]() $g(p,m+1,i)=\sum_{j=i}^{m+1} h(p,m+1,i,j)$
. It suffices to show that each
$g(p,m+1,i)=\sum_{j=i}^{m+1} h(p,m+1,i,j)$
. It suffices to show that each
![]() $h(p,m+1,i,j)$
is increasing in
$h(p,m+1,i,j)$
is increasing in
![]() $p \in \big[0,{\frac{1}{2}}\big]$
.
$p \in \big[0,{\frac{1}{2}}\big]$
.
For
![]() $i<j\leq m+1$
, let
$i<j\leq m+1$
, let
 \begin{align*} A_{i,j}\;:\!=\;\{(\omega_1,\dots,\omega_j) \in \{-1,1\}^j \colon & 0<z+\omega_1+\dots+\omega_\ell<a-1,\ell=1,\dots,i-1; \\[5pt] & z+\omega_1+\cdots+\omega_i=a-1; \\[5pt] & z<a-1+\omega_{i+1}+\cdots+\omega_\ell<a, \ell=i+1,\dots, j-1; \\[5pt] & \omega_{i+1}+\cdots+\omega_j=-(a-z-1)\}, \end{align*}
\begin{align*} A_{i,j}\;:\!=\;\{(\omega_1,\dots,\omega_j) \in \{-1,1\}^j \colon & 0<z+\omega_1+\dots+\omega_\ell<a-1,\ell=1,\dots,i-1; \\[5pt] & z+\omega_1+\cdots+\omega_i=a-1; \\[5pt] & z<a-1+\omega_{i+1}+\cdots+\omega_\ell<a, \ell=i+1,\dots, j-1; \\[5pt] & \omega_{i+1}+\cdots+\omega_j=-(a-z-1)\}, \end{align*}
and
 \begin{align*} S_{z}(m+1-j) & \;:\!=\; \{(\omega_1,\dots, \omega_{m+1-j}) \in \{-1,1\}^{m+1-j} \colon \\[5pt] & \qquad 0<z+\omega_1+\cdots+\omega_\ell<a,\ \ell=1,\dots, m+1-j\} \\[5pt] & = \{(\omega_{j+1},\dots, \omega_{m+1}) \in \{-1,1\}^{m+1-j} \colon \\[5pt] & \qquad 0<z+\omega_{j+1}+\cdots+\omega_\ell<a,\ \ell=j+1,\dots, m+1\}. \end{align*}
\begin{align*} S_{z}(m+1-j) & \;:\!=\; \{(\omega_1,\dots, \omega_{m+1-j}) \in \{-1,1\}^{m+1-j} \colon \\[5pt] & \qquad 0<z+\omega_1+\cdots+\omega_\ell<a,\ \ell=1,\dots, m+1-j\} \\[5pt] & = \{(\omega_{j+1},\dots, \omega_{m+1}) \in \{-1,1\}^{m+1-j} \colon \\[5pt] & \qquad 0<z+\omega_{j+1}+\cdots+\omega_\ell<a,\ \ell=j+1,\dots, m+1\}. \end{align*}
Since
![]() $(\omega_1,\dots, \omega_{m+1})_{z} \in \Delta_{i,j}$
if and only if
$(\omega_1,\dots, \omega_{m+1})_{z} \in \Delta_{i,j}$
if and only if
![]() $(\omega_1,\dots, \omega_{m+1}) \in A_{i,j} \times S_{z}(m+1-j)$
,
$(\omega_1,\dots, \omega_{m+1}) \in A_{i,j} \times S_{z}(m+1-j)$
,
 \begin{align} h(p,m+1,i,j) & = \mathbb{P}\{(X_{1,p},\dots, X_{m+1,p})_{z} \in \Delta_{i,j}\} \notag \\[5pt] & = \mathbb{P}\{(X_{1,p},\dots, X_{m+1,p}) \in A_{i,j} \times S_{z}(m+1-j)\} \notag \\[5pt] & = \mathbb{P}\{(X_{1,p},\dots, X_{j,p}) \in A_{i,j}\} \mathbb{P}\{(X_{j+1,p},\dots, X_{m+1,p}) \in S_{z}(m+1-j)\} \notag \\[5pt] & = \mathbb{P}\{(X_{1,p},\dots, X_{j,p}) \in A_{i,j}\} \mathbb{P}_{p,z,a}(N>m+1-j). \end{align}
\begin{align} h(p,m+1,i,j) & = \mathbb{P}\{(X_{1,p},\dots, X_{m+1,p})_{z} \in \Delta_{i,j}\} \notag \\[5pt] & = \mathbb{P}\{(X_{1,p},\dots, X_{m+1,p}) \in A_{i,j} \times S_{z}(m+1-j)\} \notag \\[5pt] & = \mathbb{P}\{(X_{1,p},\dots, X_{j,p}) \in A_{i,j}\} \mathbb{P}\{(X_{j+1,p},\dots, X_{m+1,p}) \in S_{z}(m+1-j)\} \notag \\[5pt] & = \mathbb{P}\{(X_{1,p},\dots, X_{j,p}) \in A_{i,j}\} \mathbb{P}_{p,z,a}(N>m+1-j). \end{align}
By the induction hypothesis,
![]() $\mathbb{P}_{p,z,a}(N>m+1-j)$
is increasing in
$\mathbb{P}_{p,z,a}(N>m+1-j)$
is increasing in
![]() $p \in \big[0,{\frac{1}{2}}\big]$
. Also,
$p \in \big[0,{\frac{1}{2}}\big]$
. Also,
 \begin{equation*} \mathbb{P}\{(X_{1,p},\dots, X_{j,p}) \in A_{i,j}\} = \begin{cases} (pq)^{j/2} |A_{i,j}| & \text{if } j \text{ is even}, \\[5pt] 0& \text{otherwise}, \end{cases} \end{equation*}
\begin{equation*} \mathbb{P}\{(X_{1,p},\dots, X_{j,p}) \in A_{i,j}\} = \begin{cases} (pq)^{j/2} |A_{i,j}| & \text{if } j \text{ is even}, \\[5pt] 0& \text{otherwise}, \end{cases} \end{equation*}
which is increasing in
![]() $p \in \big[0,{\frac{1}{2}}\big]$
. By (51),
$p \in \big[0,{\frac{1}{2}}\big]$
. By (51),
![]() $h(p,m+1,i,j)$
is increasing in
$h(p,m+1,i,j)$
is increasing in
![]() $p \in \big[0,{\frac{1}{2}}\big]$
.
$p \in \big[0,{\frac{1}{2}}\big]$
.
It remains to show that
![]() $h(p,m+1,i,i)$
is increasing in
$h(p,m+1,i,i)$
is increasing in
![]() $p \in \big[0,{\frac{1}{2}}\big]$
. Observe that each sample path
$p \in \big[0,{\frac{1}{2}}\big]$
. Observe that each sample path
![]() $(\omega_1,\dots, \omega_{m+1})_{z} \in \Delta_{i,i}$
ends above z at time
$(\omega_1,\dots, \omega_{m+1})_{z} \in \Delta_{i,i}$
ends above z at time
![]() $m+1$
, so that there are more
$m+1$
, so that there are more
![]() $+1$
increments than
$+1$
increments than
![]() $-1$
increments. It follows that the probability of each sample path in
$-1$
increments. It follows that the probability of each sample path in
![]() $\Delta_{i,i}$
is increasing in
$\Delta_{i,i}$
is increasing in
![]() $p \in \big[0,{\frac{1}{2}}\big]$
. Consequently,
$p \in \big[0,{\frac{1}{2}}\big]$
. Consequently,
![]() $h(p,m+1,i,i)=\mathbb{P}\{(X_{1,p},\dots, X_{m+1,p})_{z} \in \Delta_{i,i}\}$
is increasing in
$h(p,m+1,i,i)=\mathbb{P}\{(X_{1,p},\dots, X_{m+1,p})_{z} \in \Delta_{i,i}\}$
is increasing in
![]() $p \in \big[0,{\frac{1}{2}}\big]$
. This completes the induction proof of (48).
$p \in \big[0,{\frac{1}{2}}\big]$
. This completes the induction proof of (48).
It follows from (48) that, for
![]() $0<z<{{a}/{2}}$
, the distribution
$0<z<{{a}/{2}}$
, the distribution
![]() ${\mathcal{L}}_{p,z,a}(N)$
is stochastically increasing in
${\mathcal{L}}_{p,z,a}(N)$
is stochastically increasing in
![]() $p \in \big[0,{\frac{1}{2}}\big]$
. Since
$p \in \big[0,{\frac{1}{2}}\big]$
. Since
![]() $\mathcal{L}_{p,z,a}(N)=\mathcal{L}_{p',z',a}(N)$
for
$\mathcal{L}_{p,z,a}(N)=\mathcal{L}_{p',z',a}(N)$
for
![]() $p'=1-p$
and
$p'=1-p$
and
![]() $z'=a-z$
, it follows that
$z'=a-z$
, it follows that
![]() $\mathcal{L}_{p,z,a}(N)$
is stochastically decreasing in
$\mathcal{L}_{p,z,a}(N)$
is stochastically decreasing in
![]() $p \in \big[{\frac{1}{2}},1\big]$
for
$p \in \big[{\frac{1}{2}},1\big]$
for
![]() ${{a}/{2}}<z<a$
. The proof is complete.
${{a}/{2}}<z<a$
. The proof is complete.
Acknowledgement
We wish to thank the editor and three reviewers for their constructive comments leading to an improved presentation.
Funding information
This work was supported in part by the National Science and Technology Council, Taiwan, R.O.C.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.