Hostname: page-component-8448b6f56d-cfpbc Total loading time: 0 Render date: 2024-04-16T23:41:21.172Z Has data issue: false hasContentIssue false
  • English
  • Français

Stochastic approximation for the general epidemic

Published online by Cambridge University Press:  14 July 2016

Donald Ludwig
Donald Ludwig*
Affiliation:
Courant Institute of Mathematical Sciences, New York University
Get access Rights & Permissions [Opens in a new window]

Abstract

A system of equations is introduced whose solutions are remarkably close to corresponding solutions of the “general stochastic epidemic”. If N is the population size, then there are approximately 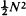equations to be solved for the general stochastic epidemic while the number of equations in the approximating system is proportional to N. An asymptotic approximation to the general stochastic epidemic is also introduced. Numerical comparisons of the stochastic and asymptotic approximations with the exact solution are presented.

Keywords

STOCHASTIC EPIDEMICRELATED STOCHASTIC SYSTEM: NUMERICAL SOLUTIONS OF STOCHASTIC PROCESSESASYMPTOTIC SOLUTIONS FOR STOCHASTIC PROCESSES
Type
Research Papers
Information
Journal of Applied Probability , Volume 10 , Issue 2 , June 1973 , pp. 263 - 276
Copyright
Copyright © Applied Probability Trust 1973 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bailey, N. T. J. (1957) The Mathematical Theory of Epidemics. Griffin, London.Google Scholar
Bharucha-Reid, A. T. (1960) Elements of the Theory of Markov Processes and their Applications. McGraw-Hill, New York.Google Scholar
Cole, J. D. (1968) Perturbation Methods in Applied Mathematics. Blaisdell, Waltham, Mass.Google Scholar
Daniels, H. E. (1967) Distribution of the total size of an epidemic. Proc. 5th Berkeley Symp. Math. Stat. IV, 281–293.Google Scholar
Kendall, D. G. (1956) Deterministic and stochastic epidemics in closed populations. Proc. 3rd Berkeley Symp. Math. Stat. IV, 149–165.Google Scholar
Whittle, P. (1955) The outcome of a stochastic epidemic — a note on Bailey's paper. Biometrika 42, 116–122.Google Scholar