Article contents
Simple conditions for metastability of continuous Markov chains
Published online by Cambridge University Press: 25 February 2021
Abstract
A family 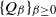 $\{Q_{\beta}\}_{\beta \geq 0}$ of Markov chains is said to exhibit metastable mixing with modes
$\{Q_{\beta}\}_{\beta \geq 0}$ of Markov chains is said to exhibit metastable mixing with modes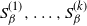 $S_{\beta}^{(1)},\ldots,S_{\beta}^{(k)}$ if its spectral gap (or some other mixing property) is very close to the worst conductance
$S_{\beta}^{(1)},\ldots,S_{\beta}^{(k)}$ if its spectral gap (or some other mixing property) is very close to the worst conductance 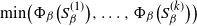 $\min\!\big(\Phi_{\beta}\big(S_{\beta}^{(1)}\big), \ldots, \Phi_{\beta}\big(S_{\beta}^{(k)}\big)\big)$ of its modes for all large values of
$\min\!\big(\Phi_{\beta}\big(S_{\beta}^{(1)}\big), \ldots, \Phi_{\beta}\big(S_{\beta}^{(k)}\big)\big)$ of its modes for all large values of 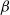 $\beta$. We give simple sufficient conditions for a family of Markov chains to exhibit metastability in this sense, and verify that these conditions hold for a prototypical Metropolis–Hastings chain targeting a mixture distribution. The existing metastability literature is large, and our present work is aimed at filling the following small gap: finding sufficient conditions for metastability that are easy to verify for typical examples from statistics using well-studied methods, while at the same time giving an asymptotically exact formula for the spectral gap (rather than a bound that can be very far from sharp). Our bounds from this paper are used in a companion paper (O. Mangoubi, N. S. Pillai, and A. Smith, arXiv:1808.03230) to compare the mixing times of the Hamiltonian Monte Carlo algorithm and a random walk algorithm for multimodal target distributions.
$\beta$. We give simple sufficient conditions for a family of Markov chains to exhibit metastability in this sense, and verify that these conditions hold for a prototypical Metropolis–Hastings chain targeting a mixture distribution. The existing metastability literature is large, and our present work is aimed at filling the following small gap: finding sufficient conditions for metastability that are easy to verify for typical examples from statistics using well-studied methods, while at the same time giving an asymptotically exact formula for the spectral gap (rather than a bound that can be very far from sharp). Our bounds from this paper are used in a companion paper (O. Mangoubi, N. S. Pillai, and A. Smith, arXiv:1808.03230) to compare the mixing times of the Hamiltonian Monte Carlo algorithm and a random walk algorithm for multimodal target distributions.
MSC classification
- Type
- Research Papers
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press on behalf of Applied Probability Trust
References
- 1
- Cited by



