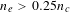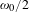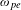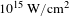1 Introduction
Laser plasma interactions (LPIs) are widely associated with many applications such as inertial confinement fusion (ICF)[Reference Campbell, Goncharov, Sangster, Regan, Radha, Betti, Myatt, Froula, Rosenberg and Igumenshchev1–Reference Myatt, Zhang, Short, Maximov, Seka, Froula, Edgell, Michel, Igumenshchev, Hinkel, Michel and Moody3], radiation sources[Reference Liu, Tripathi and Eliasson4], plasma optics[Reference Lancia, Giribono, Vassura, Chiaramello, Riconda, Weber, Castan, Chatelain, Frank and Gangolf5, Reference Lehmann and Spatschek6] and laboratory astrophysics[Reference Drake7, Reference Falk8]. The concomitant parametric instabilities found in LPI are nonlinear processes, which can greatly affect the outcome[Reference Gibbon9]. Generally, laser plasma instabilities[Reference Kruer10, Reference Montgomery11], especially stimulated Raman scattering (SRS), stimulated Brillouin scattering (SBS) and two-plasmon decay (TPD) instability, have been mainly considered in ICF with the incident laser intensity less than  $10^{15}~\text{W}/\text{cm}^{2}$[Reference Craxton, Anderson, Boehly, Goncharov, Harding, Knauer, McCrory, McKenty, Meyerhofer, Myatt, Schmitt, Sethian, Short, Skupsky, Theobald, Kruer, Tanaka, Betti, Collins, Delettrez, Hu, Marozas, Maximov, Michel, Radha, Regan, Sangster, Seka, Solodov, Soures, Stoeckl and Zuegel12–Reference Moody, MacGowan, Rothenberg, Berger, Divol, Glenzer, Kirkwood, Williams and Young14]. However, the laser intensity may be of the order of
$10^{15}~\text{W}/\text{cm}^{2}$[Reference Craxton, Anderson, Boehly, Goncharov, Harding, Knauer, McCrory, McKenty, Meyerhofer, Myatt, Schmitt, Sethian, Short, Skupsky, Theobald, Kruer, Tanaka, Betti, Collins, Delettrez, Hu, Marozas, Maximov, Michel, Radha, Regan, Sangster, Seka, Solodov, Soures, Stoeckl and Zuegel12–Reference Moody, MacGowan, Rothenberg, Berger, Divol, Glenzer, Kirkwood, Williams and Young14]. However, the laser intensity may be of the order of  $10^{16}$ or even
$10^{16}$ or even  $10^{17}~\text{W}/\text{cm}^{2}$ in shock ignition[Reference Betti and Hurricane15–Reference Gu, Klimo, Nicola, Shekhanov, Weber and Tikhonchuk19], Brillouin amplification[Reference Weber, Riconda and Tikhonchuk20, Reference Lancia, Marques, Nakatsutsumi, Riconda, Weber, Hüller, Mančić, Antici, Tikhonchuk and Héron21] and the interactions of high-power laser with matter[Reference Rethfeld, Ivanov, Garcia and Anisimov22–Reference George, Morrison, Feister, Ngirmang, Smith, Klim, Snyder, Austin, Erbsen, Frische, Nees, Orban, Chowdhury and Roquemore24]. Therefore, the parametric instabilities close to the regime of subrelativistic intensity need to be explored in depth.
$10^{17}~\text{W}/\text{cm}^{2}$ in shock ignition[Reference Betti and Hurricane15–Reference Gu, Klimo, Nicola, Shekhanov, Weber and Tikhonchuk19], Brillouin amplification[Reference Weber, Riconda and Tikhonchuk20, Reference Lancia, Marques, Nakatsutsumi, Riconda, Weber, Hüller, Mančić, Antici, Tikhonchuk and Héron21] and the interactions of high-power laser with matter[Reference Rethfeld, Ivanov, Garcia and Anisimov22–Reference George, Morrison, Feister, Ngirmang, Smith, Klim, Snyder, Austin, Erbsen, Frische, Nees, Orban, Chowdhury and Roquemore24]. Therefore, the parametric instabilities close to the regime of subrelativistic intensity need to be explored in depth.
As well known, SRS usually develops in plasma density not larger than the quarter critical density  $n_{e}\leqslant 0.25n_{c}$ due to the decay of the scattering light in its propagation in the overdense density plasma[Reference Liu, Tripathi and Eliasson4, Reference Kruer10]. In the density region
$n_{e}\leqslant 0.25n_{c}$ due to the decay of the scattering light in its propagation in the overdense density plasma[Reference Liu, Tripathi and Eliasson4, Reference Kruer10]. In the density region  $n_{e}\leqslant 0.25n_{c}$, the electrostatic wave is the eigenmode of the electron plasma wave. Relativistic intensity lasers can reduce the effective electron plasma frequency, and therefore eigenmode SRS may develop at
$n_{e}\leqslant 0.25n_{c}$, the electrostatic wave is the eigenmode of the electron plasma wave. Relativistic intensity lasers can reduce the effective electron plasma frequency, and therefore eigenmode SRS may develop at  $n_{e}>0.25n_{c}$[Reference Zhao, Zheng, Chen, Yu, Weng, Ren, Liu and Sheng25]. In this work, we show the presence of non-eigenmode SRS, which is found at plasma density
$n_{e}>0.25n_{c}$[Reference Zhao, Zheng, Chen, Yu, Weng, Ren, Liu and Sheng25]. In this work, we show the presence of non-eigenmode SRS, which is found at plasma density  $n_{e}>0.25n_{c}$ even without considering the relativistic effect. The development of a non-eigen electrostatic mode is described by the linear perturbations of fluid equations, which may lead to a few subsequent nonlinear phenomena[Reference Weber, Riconda and Tikhonchuk20, Reference Ghizzo, Johnston, Réveillé, Bertrand and Albrecht-Marc26–Reference Riconda, Weber, Tikhonchuk, Adam and Heron28]. This mode develops only when the laser intensity exceeds a certain threshold. The theoretical model is supported by particle-in-cell (PIC) simulations.
$n_{e}>0.25n_{c}$ even without considering the relativistic effect. The development of a non-eigen electrostatic mode is described by the linear perturbations of fluid equations, which may lead to a few subsequent nonlinear phenomena[Reference Weber, Riconda and Tikhonchuk20, Reference Ghizzo, Johnston, Réveillé, Bertrand and Albrecht-Marc26–Reference Riconda, Weber, Tikhonchuk, Adam and Heron28]. This mode develops only when the laser intensity exceeds a certain threshold. The theoretical model is supported by particle-in-cell (PIC) simulations.
2 Theoretical analysis of SRS in the non-eigenmode regime
Generally, SRS is a three-wave instability where a laser decays into an electrostatic wave, with frequency equal to the eigen electron plasma wave, and a light wave. However, the stimulated electrostatic wave is no longer the eigenmode of the electron plasma wave in the SRS non-eigenmode regime, where both the frequencies of scattered light and electrostatic field are nearly half of the incident laser frequency. The mechanism of this instability can be described by the SRS dispersion relation at plasma density  $n_{e}>0.25n_{c}$.
$n_{e}>0.25n_{c}$.

Figure 1. Amplitude thresholds for the development of eigenmode and non-eigenmode SRS in plasma above the quarter critical density. The threshold for the case of eigenmode SRS  $a_{th-e}$ is due to the relativistic effect.
$a_{th-e}$ is due to the relativistic effect.
To investigate the non-eigenmode SRS mechanism in LPI, we first introduce the non-relativistic dispersion relation of SRS in cold plasma[Reference Kruer10]
 $$\begin{eqnarray}\unicode[STIX]{x1D714}_{e}^{2}-\unicode[STIX]{x1D714}_{pe}^{2}=\frac{\unicode[STIX]{x1D714}_{pe}^{2}k_{e}^{2}c^{2}a_{0}^{2}}{4}\left(\frac{1}{D_{e+}}+\frac{1}{D_{e-}}\right),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D714}_{e}^{2}-\unicode[STIX]{x1D714}_{pe}^{2}=\frac{\unicode[STIX]{x1D714}_{pe}^{2}k_{e}^{2}c^{2}a_{0}^{2}}{4}\left(\frac{1}{D_{e+}}+\frac{1}{D_{e-}}\right),\end{eqnarray}$$ where  $D_{e\pm }=\unicode[STIX]{x1D714}_{e}^{2}-k_{e}^{2}c^{2}\mp 2(k_{0}k_{e}c^{2}-\unicode[STIX]{x1D714}_{0}\unicode[STIX]{x1D714}_{e})$ and
$D_{e\pm }=\unicode[STIX]{x1D714}_{e}^{2}-k_{e}^{2}c^{2}\mp 2(k_{0}k_{e}c^{2}-\unicode[STIX]{x1D714}_{0}\unicode[STIX]{x1D714}_{e})$ and  $a_{0}$ is the laser normalized amplitude. The relation between laser intensity
$a_{0}$ is the laser normalized amplitude. The relation between laser intensity  $I$ and
$I$ and  $a_{0}$ is given by
$a_{0}$ is given by  $I(\text{W}/\text{cm}^{2})=1.37\times 10^{18}a_{0}^{2}/[\unicode[STIX]{x1D706}(\unicode[STIX]{x03BC}\text{m})]^{2}$. Furthermore, in Equation (1),
$I(\text{W}/\text{cm}^{2})=1.37\times 10^{18}a_{0}^{2}/[\unicode[STIX]{x1D706}(\unicode[STIX]{x03BC}\text{m})]^{2}$. Furthermore, in Equation (1),  $\unicode[STIX]{x1D714}_{0}$ and
$\unicode[STIX]{x1D714}_{0}$ and  $\unicode[STIX]{x1D714}_{e}$ are the frequencies of the incident laser and the electrostatic wave, respectively.
$\unicode[STIX]{x1D714}_{e}$ are the frequencies of the incident laser and the electrostatic wave, respectively.  $k_{0}$ and
$k_{0}$ and  $k_{e}$ are the wavenumbers of the pump laser and the electrostatic wave, respectively. Generally, we have
$k_{e}$ are the wavenumbers of the pump laser and the electrostatic wave, respectively. Generally, we have  $\text{Re}(\unicode[STIX]{x1D714}_{e})=\unicode[STIX]{x1D714}_{pe}$ in the SRS eigenmode regime
$\text{Re}(\unicode[STIX]{x1D714}_{e})=\unicode[STIX]{x1D714}_{pe}$ in the SRS eigenmode regime  $n_{e}\leqslant 0.25n_{c}$. However, when the amplitude of the incident laser
$n_{e}\leqslant 0.25n_{c}$. However, when the amplitude of the incident laser  $a_{0}$ is larger than a threshold, a stimulated non-eigen electrostatic mode
$a_{0}$ is larger than a threshold, a stimulated non-eigen electrostatic mode  $\text{Re}(\unicode[STIX]{x1D714}_{e})\neq \unicode[STIX]{x1D714}_{pe}$ will be developed at
$\text{Re}(\unicode[STIX]{x1D714}_{e})\neq \unicode[STIX]{x1D714}_{pe}$ will be developed at  $n_{e}>0.25n_{c}$.
$n_{e}>0.25n_{c}$.
Now we analytically solve Equation (1) under  $n_{e}>0.25n_{c}$. Let
$n_{e}>0.25n_{c}$. Let  $\unicode[STIX]{x1D714}_{e}=\unicode[STIX]{x1D714}_{er}+i\unicode[STIX]{x1D714}_{ei}$, where
$\unicode[STIX]{x1D714}_{e}=\unicode[STIX]{x1D714}_{er}+i\unicode[STIX]{x1D714}_{ei}$, where  $\unicode[STIX]{x1D714}_{er}$ and
$\unicode[STIX]{x1D714}_{er}$ and  $\unicode[STIX]{x1D714}_{ei}$ are the real and imaginary parts of
$\unicode[STIX]{x1D714}_{ei}$ are the real and imaginary parts of  $\unicode[STIX]{x1D714}_{e}$, respectively. The wavenumber of scattering light is a real
$\unicode[STIX]{x1D714}_{e}$, respectively. The wavenumber of scattering light is a real  $k_{s}c=0$ in the non-eigenmode regime, i.e., the scattered light is trapped in the plasma. And to keep the phase-matching conditions, we set the electrostatic wavenumber
$k_{s}c=0$ in the non-eigenmode regime, i.e., the scattered light is trapped in the plasma. And to keep the phase-matching conditions, we set the electrostatic wavenumber  $k_{e}c=k_{0}c$. In this case, the imaginary part of Equation (1) can be simplified to
$k_{e}c=k_{0}c$. In this case, the imaginary part of Equation (1) can be simplified to
 $$\begin{eqnarray}\displaystyle & & \displaystyle (\unicode[STIX]{x1D714}_{0}\unicode[STIX]{x1D714}_{ei}-2\unicode[STIX]{x1D714}_{ei}\unicode[STIX]{x1D714}_{er})(\unicode[STIX]{x1D714}_{ei}^{2}-\unicode[STIX]{x1D714}_{er}^{2}-2\unicode[STIX]{x1D714}_{0}\unicode[STIX]{x1D714}_{er}+3\unicode[STIX]{x1D714}_{0}^{2}\nonumber\\ \displaystyle & & \displaystyle \quad -\,3\unicode[STIX]{x1D714}_{pe}^{2} )(\unicode[STIX]{x1D714}_{er}^{2}+\unicode[STIX]{x1D714}_{ei}^{2}-\unicode[STIX]{x1D714}_{er}\unicode[STIX]{x1D714}_{0}-\unicode[STIX]{x1D714}_{pe}^{2})=0.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle (\unicode[STIX]{x1D714}_{0}\unicode[STIX]{x1D714}_{ei}-2\unicode[STIX]{x1D714}_{ei}\unicode[STIX]{x1D714}_{er})(\unicode[STIX]{x1D714}_{ei}^{2}-\unicode[STIX]{x1D714}_{er}^{2}-2\unicode[STIX]{x1D714}_{0}\unicode[STIX]{x1D714}_{er}+3\unicode[STIX]{x1D714}_{0}^{2}\nonumber\\ \displaystyle & & \displaystyle \quad -\,3\unicode[STIX]{x1D714}_{pe}^{2} )(\unicode[STIX]{x1D714}_{er}^{2}+\unicode[STIX]{x1D714}_{ei}^{2}-\unicode[STIX]{x1D714}_{er}\unicode[STIX]{x1D714}_{0}-\unicode[STIX]{x1D714}_{pe}^{2})=0.\end{eqnarray}$$ Equation (2) is satisfied for any  $\unicode[STIX]{x1D714}_{pe}$ when
$\unicode[STIX]{x1D714}_{pe}$ when  $\unicode[STIX]{x1D714}_{er}=\unicode[STIX]{x1D714}_{0}/2$. Therefore, the frequency of the electrostatic wave is a constant, and it is independent of the plasma density. The phase velocity of the electrostatic wave is around
$\unicode[STIX]{x1D714}_{er}=\unicode[STIX]{x1D714}_{0}/2$. Therefore, the frequency of the electrostatic wave is a constant, and it is independent of the plasma density. The phase velocity of the electrostatic wave is around  $v_{ph}=\unicode[STIX]{x1D714}_{er}/k_{e}\gtrsim c/\sqrt{3}\sim 0.58c$.
$v_{ph}=\unicode[STIX]{x1D714}_{er}/k_{e}\gtrsim c/\sqrt{3}\sim 0.58c$.
Substituting  $\unicode[STIX]{x1D714}_{er}=\unicode[STIX]{x1D714}_{0}/2$ into the real part of Equation (1), one obtains the growth rate of the SRS non-eigenmode:
$\unicode[STIX]{x1D714}_{er}=\unicode[STIX]{x1D714}_{0}/2$ into the real part of Equation (1), one obtains the growth rate of the SRS non-eigenmode:
 $$\begin{eqnarray}\unicode[STIX]{x1D714}_{ei}=\frac{1}{2}\sqrt{4\unicode[STIX]{x1D714}_{pe}(\unicode[STIX]{x1D714}_{0}-\unicode[STIX]{x1D714}_{pe})+\unicode[STIX]{x1D714}_{pe}^{2}a_{0}^{2}k_{0}^{2}c^{2}/\unicode[STIX]{x1D714}_{0}^{2}-\unicode[STIX]{x1D714}_{0}^{2}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D714}_{ei}=\frac{1}{2}\sqrt{4\unicode[STIX]{x1D714}_{pe}(\unicode[STIX]{x1D714}_{0}-\unicode[STIX]{x1D714}_{pe})+\unicode[STIX]{x1D714}_{pe}^{2}a_{0}^{2}k_{0}^{2}c^{2}/\unicode[STIX]{x1D714}_{0}^{2}-\unicode[STIX]{x1D714}_{0}^{2}}.\end{eqnarray}$$ The above equation indicates that the growth rate  $\unicode[STIX]{x1D714}_{ei}$ is reduced by the increase in plasma density. The threshold
$\unicode[STIX]{x1D714}_{ei}$ is reduced by the increase in plasma density. The threshold  $a_{th-n}$ for SRS developing in the non-eigenmode regime can be obtained from
$a_{th-n}$ for SRS developing in the non-eigenmode regime can be obtained from  $4\unicode[STIX]{x1D714}_{pe}(\unicode[STIX]{x1D714}_{0}-\unicode[STIX]{x1D714}_{pe})+\unicode[STIX]{x1D714}_{pe}^{2}a_{th-n}^{2}k_{0}^{2}c^{2}/\unicode[STIX]{x1D714}_{0}^{2}-\unicode[STIX]{x1D714}_{0}^{2}\gtrsim 0$, i.e.,
$4\unicode[STIX]{x1D714}_{pe}(\unicode[STIX]{x1D714}_{0}-\unicode[STIX]{x1D714}_{pe})+\unicode[STIX]{x1D714}_{pe}^{2}a_{th-n}^{2}k_{0}^{2}c^{2}/\unicode[STIX]{x1D714}_{0}^{2}-\unicode[STIX]{x1D714}_{0}^{2}\gtrsim 0$, i.e.,
 $$\begin{eqnarray}a_{th-n}\gtrsim \frac{\unicode[STIX]{x1D714}_{0}\sqrt{\unicode[STIX]{x1D714}_{0}^{2}+4(\unicode[STIX]{x1D714}_{pe}^{2}-\unicode[STIX]{x1D714}_{pe}\unicode[STIX]{x1D714}_{0})}}{\unicode[STIX]{x1D714}_{pe}k_{0}c}.\end{eqnarray}$$
$$\begin{eqnarray}a_{th-n}\gtrsim \frac{\unicode[STIX]{x1D714}_{0}\sqrt{\unicode[STIX]{x1D714}_{0}^{2}+4(\unicode[STIX]{x1D714}_{pe}^{2}-\unicode[STIX]{x1D714}_{pe}\unicode[STIX]{x1D714}_{0})}}{\unicode[STIX]{x1D714}_{pe}k_{0}c}.\end{eqnarray}$$ Equation (4) indicates that  $0.25n_{c}$ is the turning point between eigenmode SRS and non-eigenmode SRS, where the threshold
$0.25n_{c}$ is the turning point between eigenmode SRS and non-eigenmode SRS, where the threshold  $a_{th-n}=0$.
$a_{th-n}=0$.
For the density region just near the quarter critical density  $n_{e}\gtrsim 0.25n_{c}$, Equation (4) can be simplified to
$n_{e}\gtrsim 0.25n_{c}$, Equation (4) can be simplified to  $a_{th-n}\gtrsim (8/\sqrt{3})(n_{e}/n_{c}-0.25)$. Therefore, the condition for the excitation of non-eigenmode SRS in a plasma with density
$a_{th-n}\gtrsim (8/\sqrt{3})(n_{e}/n_{c}-0.25)$. Therefore, the condition for the excitation of non-eigenmode SRS in a plasma with density  $n_{e}\gtrsim 0.25n_{c}$ is that the amplitude of pump laser satisfies the above condition, which is almost linearly proportional to the plasma density.
$n_{e}\gtrsim 0.25n_{c}$ is that the amplitude of pump laser satisfies the above condition, which is almost linearly proportional to the plasma density.
In the following, we consider the relativistic modification of the SRS non-eigenmode in hot plasma. The dispersion of SRS under the relativistic intensity laser is[Reference Gibbon9, Reference Zhao, Zheng, Chen, Yu, Weng, Ren, Liu and Sheng25]
 $$\begin{eqnarray}\unicode[STIX]{x1D714}_{e}^{2}-\unicode[STIX]{x1D714}_{L}^{2}=\frac{\unicode[STIX]{x1D714}_{pe}^{\prime 2}k_{e}^{2}c^{2}a_{0}^{2}}{4\unicode[STIX]{x1D6FE}^{2}}\left(\frac{1}{D_{e+}}+\frac{1}{D_{e-}}\right),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D714}_{e}^{2}-\unicode[STIX]{x1D714}_{L}^{2}=\frac{\unicode[STIX]{x1D714}_{pe}^{\prime 2}k_{e}^{2}c^{2}a_{0}^{2}}{4\unicode[STIX]{x1D6FE}^{2}}\left(\frac{1}{D_{e+}}+\frac{1}{D_{e-}}\right),\end{eqnarray}$$ where  $\unicode[STIX]{x1D714}_{L}^{2}=\unicode[STIX]{x1D714}_{pe}^{\prime 2}+3k_{e}^{2}v_{th}^{2}$ with
$\unicode[STIX]{x1D714}_{L}^{2}=\unicode[STIX]{x1D714}_{pe}^{\prime 2}+3k_{e}^{2}v_{th}^{2}$ with  $\unicode[STIX]{x1D714}_{pe}^{\prime }=\unicode[STIX]{x1D714}_{pe}/\sqrt{\unicode[STIX]{x1D6FE}}$, and
$\unicode[STIX]{x1D714}_{pe}^{\prime }=\unicode[STIX]{x1D714}_{pe}/\sqrt{\unicode[STIX]{x1D6FE}}$, and  $\unicode[STIX]{x1D6FE}=(1+a_{0}^{2}/2)^{1/2}$ and
$\unicode[STIX]{x1D6FE}=(1+a_{0}^{2}/2)^{1/2}$ and  $v_{th}$ are the relativistic factor and electron thermal velocity, respectively. Different from non-eigenmode SRS, the threshold for eigenmode SRS developing in cold plasma with
$v_{th}$ are the relativistic factor and electron thermal velocity, respectively. Different from non-eigenmode SRS, the threshold for eigenmode SRS developing in cold plasma with  $n_{e}>0.25n_{c}$ is
$n_{e}>0.25n_{c}$ is  $\unicode[STIX]{x1D714}_{pe}^{\prime }\leqslant 0.5\unicode[STIX]{x1D714}_{0}$, i.e.,
$\unicode[STIX]{x1D714}_{pe}^{\prime }\leqslant 0.5\unicode[STIX]{x1D714}_{0}$, i.e.,  $a_{th-e}\geqslant \sqrt{2(16n_{e}^{2}/n_{c}^{2}-1)}$. As a comparison, the driven amplitudes for non-eigenmode SRS
$a_{th-e}\geqslant \sqrt{2(16n_{e}^{2}/n_{c}^{2}-1)}$. As a comparison, the driven amplitudes for non-eigenmode SRS  $a_{th-n}$ and eigenmode SRS
$a_{th-n}$ and eigenmode SRS  $a_{th-e}$ at different plasma densities are shown in Figure 1. One finds that the amplitude threshold for eigenmode SRS is much larger than for non-eigenmode SRS, i.e.,
$a_{th-e}$ at different plasma densities are shown in Figure 1. One finds that the amplitude threshold for eigenmode SRS is much larger than for non-eigenmode SRS, i.e.,  $a_{th-e}\gg a_{th-n}$. Therefore, the intensity of SRS in
$a_{th-e}\gg a_{th-n}$. Therefore, the intensity of SRS in  $n_{e}>0.25n_{c}$ is underestimated according to the previous eigenmode model. As an example, the threshold for laser driving non-eigenmode SRS at plasma density
$n_{e}>0.25n_{c}$ is underestimated according to the previous eigenmode model. As an example, the threshold for laser driving non-eigenmode SRS at plasma density  $n_{e}=0.26n_{c}$ is around
$n_{e}=0.26n_{c}$ is around  $a_{th-n}=0.045$. A laser with amplitude
$a_{th-n}=0.045$. A laser with amplitude  $a_{0}=0.1$ can develop non-eigenmode SRS in the plasma region with density
$a_{0}=0.1$ can develop non-eigenmode SRS in the plasma region with density  $0.25n_{c}<n_{e}\lesssim 0.273n_{c}$.
$0.25n_{c}<n_{e}\lesssim 0.273n_{c}$.
Following the similar steps of the non-relativistic case, the imaginary part of Equation (5) is simplified to
 $$\begin{eqnarray}\displaystyle & & \displaystyle (\unicode[STIX]{x1D714}_{0}\unicode[STIX]{x1D714}_{ei}-2\unicode[STIX]{x1D714}_{ei}\unicode[STIX]{x1D714}_{er})(\unicode[STIX]{x1D714}_{ei}^{2}-\unicode[STIX]{x1D714}_{er}^{2}-2\unicode[STIX]{x1D714}_{0}\unicode[STIX]{x1D714}_{er}+3\unicode[STIX]{x1D714}_{0}^{2}\nonumber\\ \displaystyle & & \displaystyle \quad -\,3\unicode[STIX]{x1D714}_{pe}^{\prime 2} )(\unicode[STIX]{x1D714}_{er}^{2}+\unicode[STIX]{x1D714}_{ei}^{2}-\unicode[STIX]{x1D714}_{er}\unicode[STIX]{x1D714}_{0}-\unicode[STIX]{x1D714}_{L}^{2})=0.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle (\unicode[STIX]{x1D714}_{0}\unicode[STIX]{x1D714}_{ei}-2\unicode[STIX]{x1D714}_{ei}\unicode[STIX]{x1D714}_{er})(\unicode[STIX]{x1D714}_{ei}^{2}-\unicode[STIX]{x1D714}_{er}^{2}-2\unicode[STIX]{x1D714}_{0}\unicode[STIX]{x1D714}_{er}+3\unicode[STIX]{x1D714}_{0}^{2}\nonumber\\ \displaystyle & & \displaystyle \quad -\,3\unicode[STIX]{x1D714}_{pe}^{\prime 2} )(\unicode[STIX]{x1D714}_{er}^{2}+\unicode[STIX]{x1D714}_{ei}^{2}-\unicode[STIX]{x1D714}_{er}\unicode[STIX]{x1D714}_{0}-\unicode[STIX]{x1D714}_{L}^{2})=0.\end{eqnarray}$$ We obtain the same identical relation for the real part  $\unicode[STIX]{x1D714}_{er}=\unicode[STIX]{x1D714}_{0}/2$ from Equation (6). Note that the relativistic factor and electron temperature have no effect on
$\unicode[STIX]{x1D714}_{er}=\unicode[STIX]{x1D714}_{0}/2$ from Equation (6). Note that the relativistic factor and electron temperature have no effect on  $\unicode[STIX]{x1D714}_{er}$ which is no longer the eigen frequency
$\unicode[STIX]{x1D714}_{er}$ which is no longer the eigen frequency  $\unicode[STIX]{x1D714}_{L}$. The dispersion relation of the non-eigen electrostatic mode satisfies
$\unicode[STIX]{x1D714}_{L}$. The dispersion relation of the non-eigen electrostatic mode satisfies
 $$\begin{eqnarray}\unicode[STIX]{x1D714}_{er}=\frac{\unicode[STIX]{x1D714}_{0}}{2}=\frac{1}{2}\sqrt{k_{e}^{2}c^{2}+\unicode[STIX]{x1D714}_{pe}^{2}}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D714}_{er}=\frac{\unicode[STIX]{x1D714}_{0}}{2}=\frac{1}{2}\sqrt{k_{e}^{2}c^{2}+\unicode[STIX]{x1D714}_{pe}^{2}}.\end{eqnarray}$$ From Equation (7), we know that the group velocity of non-eigen electrostatic wave is  $v_{g}=\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D714}_{er}/\unicode[STIX]{x1D6FF}k_{e}\approx 0$. Therefore, electrostatic wave will be trapped in the plasma.
$v_{g}=\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D714}_{er}/\unicode[STIX]{x1D6FF}k_{e}\approx 0$. Therefore, electrostatic wave will be trapped in the plasma.
The comparisons between the numerical solutions of Equations (1) and (5) are exhibited in Figure 2. One finds that  $\text{Re}(\unicode[STIX]{x1D714}_{e})=\unicode[STIX]{x1D714}_{0}/2$ is a constant even including relativistic and temperature effects. The frequency of electron plasma wave is reduced by the relativistic factor
$\text{Re}(\unicode[STIX]{x1D714}_{e})=\unicode[STIX]{x1D714}_{0}/2$ is a constant even including relativistic and temperature effects. The frequency of electron plasma wave is reduced by the relativistic factor  $\unicode[STIX]{x1D714}_{pe}^{\prime }=\unicode[STIX]{x1D714}_{pe}/\sqrt{\unicode[STIX]{x1D6FE}}$. Therefore, the growth rate
$\unicode[STIX]{x1D714}_{pe}^{\prime }=\unicode[STIX]{x1D714}_{pe}/\sqrt{\unicode[STIX]{x1D6FE}}$. Therefore, the growth rate  $\unicode[STIX]{x1D714}_{ei}$ is increased by the relativistic modification as shown in Figure 2(a). On the contrary, the frequency of electron plasma wave is enhanced by the electron temperature
$\unicode[STIX]{x1D714}_{ei}$ is increased by the relativistic modification as shown in Figure 2(a). On the contrary, the frequency of electron plasma wave is enhanced by the electron temperature  $\unicode[STIX]{x1D714}_{L}=\sqrt{\unicode[STIX]{x1D714}_{pe}^{\prime 2}+3k_{e}^{2}v_{th}^{2}}$, and therefore we find a decrease of the growth rate at higher temperature
$\unicode[STIX]{x1D714}_{L}=\sqrt{\unicode[STIX]{x1D714}_{pe}^{\prime 2}+3k_{e}^{2}v_{th}^{2}}$, and therefore we find a decrease of the growth rate at higher temperature  $T_{e}=1~\text{keV}$ in Figure 2(b). Note that the above studies are discussed in the weak relativistic regime, where the plasma density modulation induced by the laser ponderomotive force is weak.
$T_{e}=1~\text{keV}$ in Figure 2(b). Note that the above studies are discussed in the weak relativistic regime, where the plasma density modulation induced by the laser ponderomotive force is weak.

Figure 2. Numerical solutions of SRS dispersion equation at plasma density  $n_{e}=0.27n_{c}$ with laser amplitude
$n_{e}=0.27n_{c}$ with laser amplitude  $a_{0}=0.1$. (a) The relativistic modification on the non-eigenmode SRS at
$a_{0}=0.1$. (a) The relativistic modification on the non-eigenmode SRS at  $T_{e}=0$. (b) The effect of electron temperature on non-eigenmode SRS. The dotted line and dashed line are the imaginary part and the real part of the solutions, respectively.
$T_{e}=0$. (b) The effect of electron temperature on non-eigenmode SRS. The dotted line and dashed line are the imaginary part and the real part of the solutions, respectively.
Phase-matching conditions are satisfied in the SRS non-eigenmode regime, and therefore the frequency of concomitant light is also  $\text{Re}(\unicode[STIX]{x1D714}_{s})\approx 0.5\unicode[STIX]{x1D714}_{0}$, which can be obtained from the dispersion relation of scattered light
$\text{Re}(\unicode[STIX]{x1D714}_{s})\approx 0.5\unicode[STIX]{x1D714}_{0}$, which can be obtained from the dispersion relation of scattered light
 $$\begin{eqnarray}\unicode[STIX]{x1D714}_{s}^{2}-k_{s}^{2}c^{2}-\unicode[STIX]{x1D714}_{pe}^{2}=D_{s+}+D_{s-},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D714}_{s}^{2}-k_{s}^{2}c^{2}-\unicode[STIX]{x1D714}_{pe}^{2}=D_{s+}+D_{s-},\end{eqnarray}$$ where  $D_{s\pm }=\unicode[STIX]{x1D714}_{pe}^{2}(k_{s}\pm k_{0})^{2}c^{2}a_{0}^{2}/4[(\unicode[STIX]{x1D714}_{s}\pm \unicode[STIX]{x1D714}_{0})^{2}-\unicode[STIX]{x1D714}_{pe}^{2}]$.
$D_{s\pm }=\unicode[STIX]{x1D714}_{pe}^{2}(k_{s}\pm k_{0})^{2}c^{2}a_{0}^{2}/4[(\unicode[STIX]{x1D714}_{s}\pm \unicode[STIX]{x1D714}_{0})^{2}-\unicode[STIX]{x1D714}_{pe}^{2}]$.
According to the linear parametric model of inhomogeneous plasma, the Rosenbluth gain saturation coefficient for convective instability is  $G=2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6E4}^{2}/v_{s}v_{p}K^{\prime }$[Reference Rosenbluth29], where
$G=2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6E4}^{2}/v_{s}v_{p}K^{\prime }$[Reference Rosenbluth29], where  $\unicode[STIX]{x1D6E4}$,
$\unicode[STIX]{x1D6E4}$,  $v_{s}$ and
$v_{s}$ and  $v_{p}$ are the instability growth rate, the group velocity of scattering light and the plasma wave, respectively.
$v_{p}$ are the instability growth rate, the group velocity of scattering light and the plasma wave, respectively.  $K$ is the wavenumber mismatch for incident light, scattering light and plasma wave. As it is known, convective instability transits to absolute instability when
$K$ is the wavenumber mismatch for incident light, scattering light and plasma wave. As it is known, convective instability transits to absolute instability when  $K=0$[Reference Liu, Rosenbluth and White30]. Based on the above discussions, the mismatching term of non-eigenmode SRS is
$K=0$[Reference Liu, Rosenbluth and White30]. Based on the above discussions, the mismatching term of non-eigenmode SRS is  $K_{ne}=k_{0}-k_{e}-k_{s}=0$ due to
$K_{ne}=k_{0}-k_{e}-k_{s}=0$ due to  $k_{e}=k_{0}$ and
$k_{e}=k_{0}$ and  $k_{s}=0$ all the time. Therefore, non-eigenmode SRS is an absolute instability in inhomogeneous plasma.
$k_{s}=0$ all the time. Therefore, non-eigenmode SRS is an absolute instability in inhomogeneous plasma.
In conclusion, different from normal SRS, a new type of non-eigenmode SRS can develop in plasma with density  $n_{e}>0.25n_{c}$. The stimulated electrostatic mode has an almost constant frequency around half of the incident light frequency
$n_{e}>0.25n_{c}$. The stimulated electrostatic mode has an almost constant frequency around half of the incident light frequency  $\unicode[STIX]{x1D714}_{0}/2$, which is no longer the eigenmode of the electron plasma wave
$\unicode[STIX]{x1D714}_{0}/2$, which is no longer the eigenmode of the electron plasma wave  $\unicode[STIX]{x1D714}_{pe}$. The group velocities of concomitant light and electrostatic wave are zero in the non-eigenmode regime. The non-eigenmode SRS develops only when the laser intensity is higher than a certain threshold, which is related to the plasma density.
$\unicode[STIX]{x1D714}_{pe}$. The group velocities of concomitant light and electrostatic wave are zero in the non-eigenmode regime. The non-eigenmode SRS develops only when the laser intensity is higher than a certain threshold, which is related to the plasma density.
3 Simulations for non-eigenmode SRS excitation
3.1 One-dimensional simulations for non-eigenmode SRS in homogeneous plasma
To validate the analytical predictions for non-eigenmode SRS, we have performed several one-dimensional simulations by using the OSIRIS code[Reference Fonseca, Silva, Tsung, Decyk, Lu, Ren, Mori, Deng, Lee, Katsouleas and Dongarra31, Reference Hemker32]. The space and time given in the following are normalized by the laser wavelength in vacuum  $\unicode[STIX]{x1D706}$ and the laser period
$\unicode[STIX]{x1D706}$ and the laser period  $\unicode[STIX]{x1D70F}$. A linearly polarized semi-infinite pump laser with a uniform amplitude is incident from the left boundary of the simulation box. In this subsection, only the fluid property of the instability is considered, and therefore we set electron temperature
$\unicode[STIX]{x1D70F}$. A linearly polarized semi-infinite pump laser with a uniform amplitude is incident from the left boundary of the simulation box. In this subsection, only the fluid property of the instability is considered, and therefore we set electron temperature  $T_{e}=100~\text{eV}$ with immobile ions. The plasma density is
$T_{e}=100~\text{eV}$ with immobile ions. The plasma density is  $n_{e}=0.26n_{c}$.
$n_{e}=0.26n_{c}$.

Figure 3. Distributions of the electrostatic wave in  $(k_{e},\unicode[STIX]{x1D714}_{e})$ space obtained for the time window
$(k_{e},\unicode[STIX]{x1D714}_{e})$ space obtained for the time window  $[100\unicode[STIX]{x1D70F},400\unicode[STIX]{x1D70F}]$ at plasma density
$[100\unicode[STIX]{x1D70F},400\unicode[STIX]{x1D70F}]$ at plasma density  $n_{e}=0.26n_{c}$ under (a) pump laser amplitude
$n_{e}=0.26n_{c}$ under (a) pump laser amplitude  $a_{0}=0.04$ and (b) pump laser amplitude
$a_{0}=0.04$ and (b) pump laser amplitude  $a_{0}=0.046$. (c) Distribution of the electromagnetic wave in
$a_{0}=0.046$. (c) Distribution of the electromagnetic wave in  $(k_{s},\unicode[STIX]{x1D714}_{s})$ space obtained under the same conditions as in (b). (d) Longitudinal phase space distribution of electrons under different laser amplitudes at
$(k_{s},\unicode[STIX]{x1D714}_{s})$ space obtained under the same conditions as in (b). (d) Longitudinal phase space distribution of electrons under different laser amplitudes at  $t=600\unicode[STIX]{x1D70F}$.
$t=600\unicode[STIX]{x1D70F}$.
Based on Equation (4) and Figure 1, we know that the triggering threshold for non-eigenmode SRS is  $a_{th-n}=0.045$ at density
$a_{th-n}=0.045$ at density  $n_{e}=0.26n_{c}$. To validate the theoretical threshold, two simulation examples under different laser intensities are displayed here. Figure 3(a) shows the case when the laser amplitude is less than the threshold (
$n_{e}=0.26n_{c}$. To validate the theoretical threshold, two simulation examples under different laser intensities are displayed here. Figure 3(a) shows the case when the laser amplitude is less than the threshold ( $a_{0}=0.04<0.045$), and no instability mode can be found. When the laser amplitude is increased to
$a_{0}=0.04<0.045$), and no instability mode can be found. When the laser amplitude is increased to  $a_{0}=0.046>0.045$, the non-eigen electrostatic mode can be found at
$a_{0}=0.046>0.045$, the non-eigen electrostatic mode can be found at  $k_{e}c\approx 0.86\unicode[STIX]{x1D714}_{0}$ and
$k_{e}c\approx 0.86\unicode[STIX]{x1D714}_{0}$ and  $\unicode[STIX]{x1D714}_{e}\approx 0.499\unicode[STIX]{x1D714}_{0}$ in Figure 3(b). The corresponding electromagnetic mode with
$\unicode[STIX]{x1D714}_{e}\approx 0.499\unicode[STIX]{x1D714}_{0}$ in Figure 3(b). The corresponding electromagnetic mode with  $k_{s}c\approx 0$ and
$k_{s}c\approx 0$ and  $\unicode[STIX]{x1D714}_{s}\approx 0.5\unicode[STIX]{x1D714}_{0}$ is shown in Figure 3(c). These simulation results agree well with the analytical prediction. As discussed above, the phase velocity of the non-eigen electrostatic wave is around
$\unicode[STIX]{x1D714}_{s}\approx 0.5\unicode[STIX]{x1D714}_{0}$ is shown in Figure 3(c). These simulation results agree well with the analytical prediction. As discussed above, the phase velocity of the non-eigen electrostatic wave is around  $v_{ph}\sim 0.58c$ at
$v_{ph}\sim 0.58c$ at  $n_{e}=0.26n_{c}$. Therefore, numbers of electrons are heated enormously at the nonlinear stage
$n_{e}=0.26n_{c}$. Therefore, numbers of electrons are heated enormously at the nonlinear stage  $t\gtrsim 600\unicode[STIX]{x1D70F}$ in the SRS non-eigenmode regime as compared to the case below the threshold as shown in Figure 3(d).
$t\gtrsim 600\unicode[STIX]{x1D70F}$ in the SRS non-eigenmode regime as compared to the case below the threshold as shown in Figure 3(d).
3.2 Two-dimensional simulations for non-eigenmode SRS in homogeneous plasma
To further validate the linear development and nonlinear evolution of non-eigenmode SRS in high-dimensionality with mobile ions, we have performed several two-dimensional simulations. The plasma occupies a longitudinal region from  $25\unicode[STIX]{x1D706}$ to
$25\unicode[STIX]{x1D706}$ to  $125\unicode[STIX]{x1D706}$ and a transverse region from
$125\unicode[STIX]{x1D706}$ and a transverse region from  $5\unicode[STIX]{x1D706}$ to
$5\unicode[STIX]{x1D706}$ to  $25\unicode[STIX]{x1D706}$ with homogeneous density
$25\unicode[STIX]{x1D706}$ with homogeneous density  $n_{e}=0.26n_{c}$. The initial electron temperature is
$n_{e}=0.26n_{c}$. The initial electron temperature is  $T_{e}=100~\text{eV}$. Ions are movable with mass
$T_{e}=100~\text{eV}$. Ions are movable with mass  $m_{i}=3672m_{e}$ and an effective charge
$m_{i}=3672m_{e}$ and an effective charge  $Z=1$. An s-polarized (electric field of light is perpendicular to the simulation plane) semi-infinite pump laser with a peak amplitude
$Z=1$. An s-polarized (electric field of light is perpendicular to the simulation plane) semi-infinite pump laser with a peak amplitude  $a_{0}=0.05$ at focal plane
$a_{0}=0.05$ at focal plane  $x=75\unicode[STIX]{x1D706}$ is incident from the left boundary of the simulation box.
$x=75\unicode[STIX]{x1D706}$ is incident from the left boundary of the simulation box.

Figure 4. The plasma density is  $n_{e}=0.26n_{c}$ for (a)–(d). (a) Distribution of the electrostatic wave in
$n_{e}=0.26n_{c}$ for (a)–(d). (a) Distribution of the electrostatic wave in  $(k_{e},\unicode[STIX]{x1D714}_{e})$ space obtained for the time window
$(k_{e},\unicode[STIX]{x1D714}_{e})$ space obtained for the time window  $[320\unicode[STIX]{x1D70F},480\unicode[STIX]{x1D70F}]$ and transverse region
$[320\unicode[STIX]{x1D70F},480\unicode[STIX]{x1D70F}]$ and transverse region  $[14.4\unicode[STIX]{x1D706},15.6\unicode[STIX]{x1D706}]$. (b) Spatial distribution of electrostatic wave at
$[14.4\unicode[STIX]{x1D706},15.6\unicode[STIX]{x1D706}]$. (b) Spatial distribution of electrostatic wave at  $t=1850\unicode[STIX]{x1D70F}$. (c) Spatial distribution of electromagnetic wave at
$t=1850\unicode[STIX]{x1D70F}$. (c) Spatial distribution of electromagnetic wave at  $t=1850\unicode[STIX]{x1D70F}$. (d) Spatial distribution of ion density at
$t=1850\unicode[STIX]{x1D70F}$. (d) Spatial distribution of ion density at  $t=1950\unicode[STIX]{x1D70F}$. The plasma density is
$t=1950\unicode[STIX]{x1D70F}$. The plasma density is  $n_{e}=0.265n_{c}$ for (e) and (f). (e) Distribution of the electrostatic wave in
$n_{e}=0.265n_{c}$ for (e) and (f). (e) Distribution of the electrostatic wave in  $(k_{e},\unicode[STIX]{x1D714}_{e})$ space obtained for the time window
$(k_{e},\unicode[STIX]{x1D714}_{e})$ space obtained for the time window  $[320\unicode[STIX]{x1D70F},480\unicode[STIX]{x1D70F}]$ and transverse region
$[320\unicode[STIX]{x1D70F},480\unicode[STIX]{x1D70F}]$ and transverse region  $[14.4\unicode[STIX]{x1D706},15.6\unicode[STIX]{x1D706}]$. (f) Spatial distribution of the ion density at
$[14.4\unicode[STIX]{x1D706},15.6\unicode[STIX]{x1D706}]$. (f) Spatial distribution of the ion density at  $t=1950\unicode[STIX]{x1D70F}$.
$t=1950\unicode[STIX]{x1D70F}$.  $E_{e}$ and
$E_{e}$ and  $E_{z}$ are normalized by
$E_{z}$ are normalized by  $m_{e}\unicode[STIX]{x1D714}_{0}c/e$, where
$m_{e}\unicode[STIX]{x1D714}_{0}c/e$, where  $m_{e}$ and
$m_{e}$ and  $e$ respectively are the electron mass and electron charge.
$e$ respectively are the electron mass and electron charge.  $n_{i}$ is normalized by
$n_{i}$ is normalized by  $n_{c}$.
$n_{c}$.
According to Equation (4), we know that the incident laser with peak amplitude  $a_{0}=0.05$ is sufficient to develop non-eigenmode SRS at plasma density
$a_{0}=0.05$ is sufficient to develop non-eigenmode SRS at plasma density  $n_{e}=0.26n_{c}$. The simulation results for plasma density
$n_{e}=0.26n_{c}$. The simulation results for plasma density  $n_{e}=0.26n_{c}$ are displayed in Figures 4(a)–4(d). Fourier transform of the electrostatic wave is taken for the time window
$n_{e}=0.26n_{c}$ are displayed in Figures 4(a)–4(d). Fourier transform of the electrostatic wave is taken for the time window  $[320\unicode[STIX]{x1D70F},480\unicode[STIX]{x1D70F}]$. We summate the Fourier spectrum along the transverse direction between
$[320\unicode[STIX]{x1D70F},480\unicode[STIX]{x1D70F}]$. We summate the Fourier spectrum along the transverse direction between  $y=14.4\unicode[STIX]{x1D706}$ and
$y=14.4\unicode[STIX]{x1D706}$ and  $y=15.6\unicode[STIX]{x1D706}$, and show the distribution in Figure 4(a). One can find a non-eigen electrostatic mode around
$y=15.6\unicode[STIX]{x1D706}$, and show the distribution in Figure 4(a). One can find a non-eigen electrostatic mode around  $k_{e}c=0.86\unicode[STIX]{x1D714}_{0}$ and
$k_{e}c=0.86\unicode[STIX]{x1D714}_{0}$ and  $\unicode[STIX]{x1D714}_{e}=0.492\unicode[STIX]{x1D714}_{0}$. Note that the growth rate of SBS is about half of the non-eigenmode SRS; therefore, SBS has little effect on the development of non-eigenmode SRS. As discussed in Section 2, the group velocities of the electrostatic wave and electromagnetic wave associated with the non-eigenmode SRS are zero. As a result, they will be trapped in the plasma. This is confirmed in our numerical simulation as shown in Figures 4(b) and 4(c) that the electrostatic wave and the concomitant electromagnetic wave form localized structures. The trapped light and electrostatic wave may cause the laser energy deficit in ICF related experiments[Reference Zhao, Sheng, Weng, Ji and Zhu33]. The trapped waves expel the ions to form density cavity at later time
$\unicode[STIX]{x1D714}_{e}=0.492\unicode[STIX]{x1D714}_{0}$. Note that the growth rate of SBS is about half of the non-eigenmode SRS; therefore, SBS has little effect on the development of non-eigenmode SRS. As discussed in Section 2, the group velocities of the electrostatic wave and electromagnetic wave associated with the non-eigenmode SRS are zero. As a result, they will be trapped in the plasma. This is confirmed in our numerical simulation as shown in Figures 4(b) and 4(c) that the electrostatic wave and the concomitant electromagnetic wave form localized structures. The trapped light and electrostatic wave may cause the laser energy deficit in ICF related experiments[Reference Zhao, Sheng, Weng, Ji and Zhu33]. The trapped waves expel the ions to form density cavity at later time  $t=1950\unicode[STIX]{x1D70F}$ as seen from Figure 4(d). These plasma cavities subsequently affect the evolution of the non-eigenmode SRS and SBS[Reference Weber, Riconda and Tikhonchuk20, Reference Wu, Zhao, Weng, Chen and Sheng27, Reference Riconda, Weber, Tikhonchuk, Adam and Heron28]. Note that this density cavity is formed due to the non-eigenmode SRS, which is different from the solitons generated by relativistic intensity lasers[Reference Esirkepov, Kamenets, Bulanov and Naumova34–Reference Wu, Yu, Fritzsche, Zheng and He38].
$t=1950\unicode[STIX]{x1D70F}$ as seen from Figure 4(d). These plasma cavities subsequently affect the evolution of the non-eigenmode SRS and SBS[Reference Weber, Riconda and Tikhonchuk20, Reference Wu, Zhao, Weng, Chen and Sheng27, Reference Riconda, Weber, Tikhonchuk, Adam and Heron28]. Note that this density cavity is formed due to the non-eigenmode SRS, which is different from the solitons generated by relativistic intensity lasers[Reference Esirkepov, Kamenets, Bulanov and Naumova34–Reference Wu, Yu, Fritzsche, Zheng and He38].

Figure 5. (a) The spatial–temporal distributions of electrostatic wave. (b) Distributions of the electrostatic wave in  $(k_{e},\unicode[STIX]{x1D714}_{e})$ space obtained for the time window
$(k_{e},\unicode[STIX]{x1D714}_{e})$ space obtained for the time window  $[150\unicode[STIX]{x1D70F},200\unicode[STIX]{x1D70F}]$. (c) The spatial–temporal distributions of ion density. (d) Energy distributions of electrons at different times.
$[150\unicode[STIX]{x1D70F},200\unicode[STIX]{x1D70F}]$. (c) The spatial–temporal distributions of ion density. (d) Energy distributions of electrons at different times.  $E_{e}$ and
$E_{e}$ and  $n_{i}$ respectively are normalized by
$n_{i}$ respectively are normalized by  $m_{e}\unicode[STIX]{x1D714}_{0}c/e$ and
$m_{e}\unicode[STIX]{x1D714}_{0}c/e$ and  $n_{c}$.
$n_{c}$.
The laser with peak amplitude  $a_{0}=0.05<a_{th-n}=0.067$ is insufficient to develop non-eigenmode SRS at
$a_{0}=0.05<a_{th-n}=0.067$ is insufficient to develop non-eigenmode SRS at $n_{e}=0.265n_{c}$. The simulation results under plasma density
$n_{e}=0.265n_{c}$. The simulation results under plasma density  $n_{e}=0.265n_{c}$ are displayed in Figures 4(e) and 4(f). The comparison between Figures 4(a) and 4(e) indicates that the pump laser with peak amplitude
$n_{e}=0.265n_{c}$ are displayed in Figures 4(e) and 4(f). The comparison between Figures 4(a) and 4(e) indicates that the pump laser with peak amplitude  $a_{0}=0.05$ fails to drive non-eigenmode SRS at
$a_{0}=0.05$ fails to drive non-eigenmode SRS at  $n_{e}=0.265n_{c}$ when the amplitude threshold is not reached. Only the ion acoustic wave developed by SBS with wavenumber
$n_{e}=0.265n_{c}$ when the amplitude threshold is not reached. Only the ion acoustic wave developed by SBS with wavenumber  $k_{i}c=2k_{0}c=1.72\unicode[STIX]{x1D714}_{0}$ can be found in Figure 4(f). And no density cavities have been formed under the conditions. These results further indicate that non-eigenmode SRS is a seed for the subsequent nonlinear physical phenomena.
$k_{i}c=2k_{0}c=1.72\unicode[STIX]{x1D714}_{0}$ can be found in Figure 4(f). And no density cavities have been formed under the conditions. These results further indicate that non-eigenmode SRS is a seed for the subsequent nonlinear physical phenomena.
3.3 One-dimensional simulations for non-eigenmode SRS in inhomogeneous plasma
To study the non-eigenmode SRS in hot inhomogeneous plasma, we have performed a simulation for the inhomogeneous plasma  $n_{e}=0.26\exp [(x-50)/1000]n_{c}$ with density range
$n_{e}=0.26\exp [(x-50)/1000]n_{c}$ with density range  $[0.26n_{c},0.287n_{c}]$. The plasma locates in
$[0.26n_{c},0.287n_{c}]$. The plasma locates in  $x=[50\unicode[STIX]{x1D706},150\unicode[STIX]{x1D706}]$, and two
$x=[50\unicode[STIX]{x1D706},150\unicode[STIX]{x1D706}]$, and two  $50\unicode[STIX]{x1D706}$ vacuums are left on either side of the plasma. The initial electron temperature is
$50\unicode[STIX]{x1D706}$ vacuums are left on either side of the plasma. The initial electron temperature is  $T_{e}=2~\text{keV}$. Ions are movable with mass
$T_{e}=2~\text{keV}$. Ions are movable with mass  $m_{i}=3672m_{e}$. The ion charge and temperature respectively are
$m_{i}=3672m_{e}$. The ion charge and temperature respectively are  $Z=1$ and
$Z=1$ and  $T_{i}=1~\text{keV}$. The driving laser is a linearly polarized semi-infinite pump laser with a uniform amplitude
$T_{i}=1~\text{keV}$. The driving laser is a linearly polarized semi-infinite pump laser with a uniform amplitude  $a_{0}=0.07$.
$a_{0}=0.07$.
The spatial–temporal evolution of the electrostatic wave is exhibited in Figure 5(a). We find that a strong electrostatic wave has been developed at the front of plasma  $x\lesssim 60\unicode[STIX]{x1D706}$ at
$x\lesssim 60\unicode[STIX]{x1D706}$ at  $t=180\unicode[STIX]{x1D70F}$. The electrostatic wave envelop is found to be stationary due to its group velocity
$t=180\unicode[STIX]{x1D70F}$. The electrostatic wave envelop is found to be stationary due to its group velocity  $v_{g}=0$. Note that the spatial gradient has little effect on the development of non-eigenmode SRS, in that the phase matching of the three waves is always satisfied in inhomogeneous plasma. Therefore, non-eigenmode SRS is an absolute instability. Figure 5(b) shows the distribution of electrostatic wave in
$v_{g}=0$. Note that the spatial gradient has little effect on the development of non-eigenmode SRS, in that the phase matching of the three waves is always satisfied in inhomogeneous plasma. Therefore, non-eigenmode SRS is an absolute instability. Figure 5(b) shows the distribution of electrostatic wave in  $(k_{e},\unicode[STIX]{x1D714}_{e})$ space, where one can find a spectrum around
$(k_{e},\unicode[STIX]{x1D714}_{e})$ space, where one can find a spectrum around  $\unicode[STIX]{x1D714}_{e}=0.499\unicode[STIX]{x1D714}_{0}$. This result further validates that the frequency of non-eigen electrostatic wave is independent of plasma density and electron temperature. The electrostatic and electromagnetic waves trapped in plasma will expel ions. From Figure 5(c), we know that the ion density cavity is gradually formed from
$\unicode[STIX]{x1D714}_{e}=0.499\unicode[STIX]{x1D714}_{0}$. This result further validates that the frequency of non-eigen electrostatic wave is independent of plasma density and electron temperature. The electrostatic and electromagnetic waves trapped in plasma will expel ions. From Figure 5(c), we know that the ion density cavity is gradually formed from  $t=400\unicode[STIX]{x1D70F}$ at the front of plasma. Large numbers of hot electrons are produced by the non-eigen electrostatic field as shown in Figure 5(d). As discussed above, the phase velocity of the non-eigen electrostatic field is around
$t=400\unicode[STIX]{x1D70F}$ at the front of plasma. Large numbers of hot electrons are produced by the non-eigen electrostatic field as shown in Figure 5(d). As discussed above, the phase velocity of the non-eigen electrostatic field is around  $0.58c$. The temperature of the electron hot tail at
$0.58c$. The temperature of the electron hot tail at  $t=2000\unicode[STIX]{x1D70F}$ is around 141 keV. The transmission rate of the pump laser through plasma is about 19.46% at
$t=2000\unicode[STIX]{x1D70F}$ is around 141 keV. The transmission rate of the pump laser through plasma is about 19.46% at  $t=2000\unicode[STIX]{x1D70F}$, which indicates that non-eigenmode SRS is an important pump energy loss mechanism in the LPI as long as the laser intensity is higher than
$t=2000\unicode[STIX]{x1D70F}$, which indicates that non-eigenmode SRS is an important pump energy loss mechanism in the LPI as long as the laser intensity is higher than  $10^{15}~\text{W}/\text{cm}^{2}$.
$10^{15}~\text{W}/\text{cm}^{2}$.
4 Summary
In summary, we have shown theoretically and numerically that the non-eigenmode SRS develops at plasma density  $n_{e}>0.25n_{c}$ when the laser amplitude is larger than a certain threshold. The electrostatic wave produced by the non-eigenmode SRS has a constant frequency
$n_{e}>0.25n_{c}$ when the laser amplitude is larger than a certain threshold. The electrostatic wave produced by the non-eigenmode SRS has a constant frequency  $\unicode[STIX]{x1D714}_{0}/2$, which is no longer the eigen electron plasma wave
$\unicode[STIX]{x1D714}_{0}/2$, which is no longer the eigen electron plasma wave  $\unicode[STIX]{x1D714}_{pe}$. The phase velocity of the non-eigen electrostatic wave is about
$\unicode[STIX]{x1D714}_{pe}$. The phase velocity of the non-eigen electrostatic wave is about  $0.58c$, which corresponds to an electron energy of 175 keV. Therefore, super-hot electrons can be produced via the development of the non-eigenmode SRS. The trapped electromagnetic wave and electrostatic wave associated with this instability can drive density cavities in plasma. Our theoretical model is validated by PIC simulations. The non-eigenmode SRS is an important pump energy loss mechanism in the LPI as long as the laser intensity is higher than
$0.58c$, which corresponds to an electron energy of 175 keV. Therefore, super-hot electrons can be produced via the development of the non-eigenmode SRS. The trapped electromagnetic wave and electrostatic wave associated with this instability can drive density cavities in plasma. Our theoretical model is validated by PIC simulations. The non-eigenmode SRS is an important pump energy loss mechanism in the LPI as long as the laser intensity is higher than  $10^{15}~\text{W}/\text{cm}^{2}$.
$10^{15}~\text{W}/\text{cm}^{2}$.
Acknowledgements
This work was supported by the Natural Science Foundation of Shanghai (No. 19YF1453200), the Strategic Priority Research Program of Chinese Academy of Sciences (Nos. XDA25050800 and XDA25050100), the National Natural Science Foundation of China (Nos. 11775144 and 1172109), and the National Science and Technology Innovation Foundation of the Chinese Academy of Sciences (No. CXJJ-20S015). The authors would like to acknowledge the OSIRIS Consortium, consisting of UCLA and IST (Lisbon, Portugal), for providing access to the OSIRIS 4.0 framework.