1 Introduction
High-power single-frequency upconverted lasers at visible or ultraviolet wavelengths generated by frequency mixing[ Reference Armstrong, Bloembergen, Ducuing and Pershan 1 ], such as sum-frequency generation (SFG) and second-harmonic generation (SHG), are ubiquitous in scientific research and technology development[ Reference Hänsch 2 – Reference Zhang, Jiang, Cui, Hu and Feng 6 ]. Single-pass frequency mixing of near-infrared fiber lasers provides an efficient, compact and robust solution[ Reference Surin, Borisenko and Larin 7 – Reference Ahmadi, Creeden, Aschaffenburg, Mokan, Underwood, Caprara, Shu, Spinelli, Minelly and Nikolov 10 ]. The power of single-frequency upconverted lasers is usually limited by the corresponding fundamental lasers, because single-frequency fiber amplifiers are susceptible to stimulated Brillouin scattering (SBS)[ Reference Jauregui, Limpert and Tünnermann 11 – Reference Zeng, Cui, Cheng, Zhou, Qi and Feng 13 ], especially for Raman fiber amplifiers[ Reference Zhang, Hu, Wang and Feng 14 ]. Phase modulation provides an elegant method to control the spectrum of the laser signal for SBS suppression. It has been widely used and plays a vital role in fiber laser power scaling[ Reference Chu, Shi, Wen, Ouyang, Zhao, Wang, Lin, Jing and Tang 15 , Reference Wang, Sun, Peng, Feng, Wang, Ma, Gao, Zhu and Tang 16 ]. In this way, a kilowatt narrow linewidth green laser was achieved by frequency doubling of a high-power Yb fiber amplifier[ Reference Ahmadi, Creeden, Aschaffenburg, Mokan, Underwood, Caprara, Shu, Spinelli, Minelly and Nikolov 10 ]. However, the phase-modulated laser is not single-frequency any longer, which is undesirable for many precision applications.
We proposed a method of compressing a phase-modulated laser back to single frequency by utilizing the phase-doubling effect in SHG[
Reference Zeng, Cui, Cheng and Feng
17
]. With the method, a robust 20-W continuous-wave single-frequency 589 nm laser was developed for sodium guide star in astronomy[
Reference Cui, Zeng, Jiang, Cheng, Yang, Zhou and Feng
18
]. Nevertheless, the method requires
![]() $\pi$
-depth binary phase modulation, for example, square wave and pseudo random binary sequences. The generation of such ideal modulation needs an infinite bandwidth. The limited bandwidth in practice results in signal distortion, which induces residual phase modulation in the single-frequency SHG output and reduces the spectral purity.
$\pi$
-depth binary phase modulation, for example, square wave and pseudo random binary sequences. The generation of such ideal modulation needs an infinite bandwidth. The limited bandwidth in practice results in signal distortion, which induces residual phase modulation in the single-frequency SHG output and reduces the spectral purity.
In this paper, we introduce a new method avoiding the bandwidth challenge and allowing high spectral purity upconverted single-frequency laser generation, utilizing the phase summation effect in the SFG process. When two fundamental lasers carrying phase modulation of identical amplitude but opposite signs are mixed in a nonlinear crystal, the upconverted laser returns to single frequency because the phase modulations cancel each other out. In the demonstration, sinusoidal modulation of the same frequency and similar amplitude is applied to two fundamental lasers for SBS suppression during fiber amplification. By adjusting the relative phase between the two modulations, a single-frequency upconverted laser is generated.
2 Theory and method
The concept of a single-frequency upconverted laser generated by utilizing the phase summation effect is illustrated in Figure 1. Two single-frequency seed lasers are phase modulated to have a broader spectrum, so as to reduce the spectral density and suppress SBS in the following fiber amplifier. The electric field strength of the two phase-modulated lasers can be expressed as follows[ Reference Boyd 19 ]:
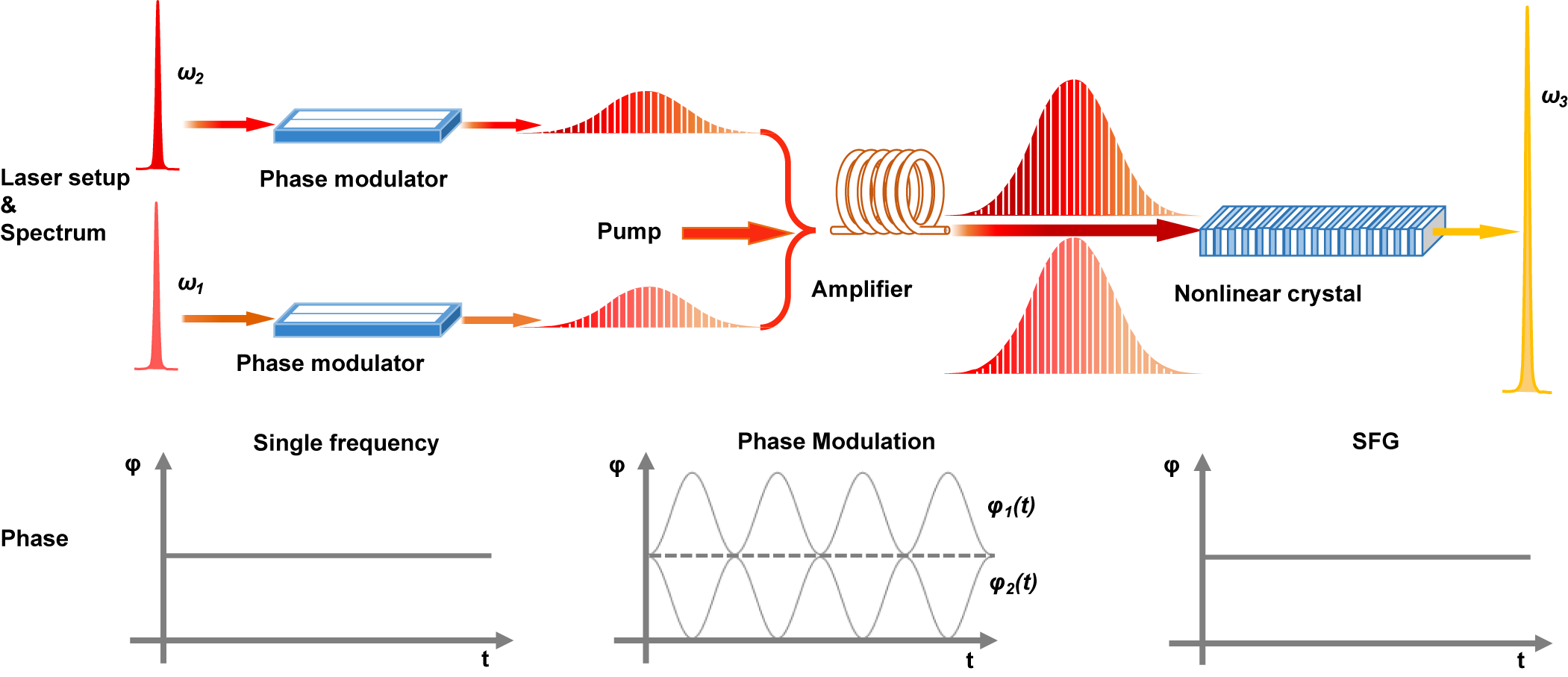
Figure 1 The concept of phase summation in SFG for single-frequency upconverted laser generation. The spectral and phase evolutions at different stages of the laser are schematically illustrated.
where
![]() $n=1,2$
for two lasers, respectively,
$n=1,2$
for two lasers, respectively,
![]() ${E}_n$
represents the field amplitude,
${E}_n$
represents the field amplitude,
![]() ${\omega}_n$
is the laser frequency and
${\omega}_n$
is the laser frequency and
![]() ${\varphi}_n(t)$
is the phase modulation function. The SFG component of the second-order nonlinear polarization is given by the following:
${\varphi}_n(t)$
is the phase modulation function. The SFG component of the second-order nonlinear polarization is given by the following:
 $$\begin{align} {\tilde{P}}^{(2)}\left({\omega}_1+{\omega}_2\right)&=2{\varepsilon}_0{\chi}^{(2)}{E}_1{E}_2\cdot {e}^{-i\left\{\left({\omega}_1+{\omega}_2\right)t+\left[{\varphi}_1(t)+{\varphi}_2(t)\right]\right\}}\nonumber \\ & \quad +\mathrm{c.c.},\end{align}$$
$$\begin{align} {\tilde{P}}^{(2)}\left({\omega}_1+{\omega}_2\right)&=2{\varepsilon}_0{\chi}^{(2)}{E}_1{E}_2\cdot {e}^{-i\left\{\left({\omega}_1+{\omega}_2\right)t+\left[{\varphi}_1(t)+{\varphi}_2(t)\right]\right\}}\nonumber \\ & \quad +\mathrm{c.c.},\end{align}$$
where
![]() ${\varepsilon}_0$
is the permittivity of free space and
${\varepsilon}_0$
is the permittivity of free space and
![]() ${\chi}^{(2)}$
is the second-order nonlinear optical susceptibility. As seen in Equation (2), the generated
${\chi}^{(2)}$
is the second-order nonlinear optical susceptibility. As seen in Equation (2), the generated
![]() ${\omega}_1+{\omega}_2$
field has a phase-modulation term of
${\omega}_1+{\omega}_2$
field has a phase-modulation term of
![]() ${\varphi}_1(t)+{\varphi}_2(t)$
, which is the sum of the phase modulations applied on the two fundamental lasers. Here we are interested in a special case, where
${\varphi}_1(t)+{\varphi}_2(t)$
, which is the sum of the phase modulations applied on the two fundamental lasers. Here we are interested in a special case, where
![]() ${\varphi}_1(t)+{\varphi}_2(t)$
equals a constant value. In this case, the phase modulations on the fundamental lasers are cancelled out during SFG, and thus a single-frequency upconverted laser is generated in spite of broad input lasers.
${\varphi}_1(t)+{\varphi}_2(t)$
equals a constant value. In this case, the phase modulations on the fundamental lasers are cancelled out during SFG, and thus a single-frequency upconverted laser is generated in spite of broad input lasers.
Any modulation functions with opposite signs can be used. Here, sinusoidal modulation is used in the experimental demonstration, because it is the simplest and most basic function. Any periodic functions can be expanded in Fourier series. The phase evolution of lasers with sinusoidal modulation for single-frequency SFG is illustrated in Figure 1. As long as the two sine-wave functions have the same amplitude and are anti-phase, a single-frequency laser can be generated as an SFG output.
3 Results and discussion
3.1 SBS suppression in Raman fiber amplifiers
The experimental setup includes two phase-modulated seed lasers, a two-stage Raman fiber amplifier and a frequency mixing unit, as shown in Figure 2. It has the same configuration as reported in Ref. [Reference Cui, Zeng, Jiang, Cheng, Yang, Zhou and Feng18], except that one seed laser is replaced by two seed lasers. The seed lasers are fiber-pigtailed distributed feedback (DFB) diode lasers around 1180 nm, whose wavelengths are thermally tunable. The linewidths were measured to be 380 and 120 kHz, respectively. Both seed lasers are protected by isolators and phase modulated by electro-optic phase modulators (EOMs) with 10 GHz bandwidth. After that, they are coupled in a two-stage linearly polarized Raman fiber amplifier via a 50:50 coupler.

Figure 2 The experimental setup includes two phase-modulated seed lasers, a two-stage Raman fiber amplifier and a frequency mixing unit. EOM, electro-optic phase modulator; WDM, wavelength division multiplexer.
Two signal lasers could be amplified separately and combined afterwards for sum-frequency mixing. In the experiments, a single Raman fiber amplifier was used, which takes less resources. However, co-amplification in the same amplifier leads to a complication. We observed cascaded four-wave mixing (FWM) of the signal lasers when their wavelengths were close, which significantly broadened the linewidth of the amplified output. The linewidth can easily exceed the acceptance of the nonlinear optical crystal, which is a 30-mm-long periodically poled stoichiometric lithium tantalite (PPSLT) crystal. In order to suppress FWM, the wavelengths of the two seed lasers were tuned apart thermally, but kept within the gain band of the Raman amplifier. At the same time, the amplified output should have similar power at two wavelengths, which is necessary for optimizing the SFG efficiency. The wavelengths were tuned to 1178.3 and 1183.2 nm in the formal experiments.
Turning on the amplifier with the single-frequency seed lasers, SBS quickly limited the performance. The backward SBS light was already 0.38 W when the amplifier output was only 4 W. Sinusoidal modulation of 100 MHz frequency was then applied to the two signal lasers to suppress SBS. The frequency was selected to be higher than the SBS bandwidth, which is about 50 MHz. The sine-waves were generated from a signal generator (Tektronix, AFG3102) with equal frequency, tunable phase offset and adjustable amplitude up to 10 V. Figure 3(a) shows the spectra of the single-frequency and phase-modulated lasers measured by a 4 GHz Fabry–Pérot interferometer (FPI, TOPTICA Photonics). Discrete sidebands are generated at both sides of the carrier frequencies. The separation between the frequency components is the sinusoidal modulation frequency, and the power distribution between the carrier and sidebands is determined by modulation depth. Larger modulation depth means more sidebands, resulting in a lower spectral intensity, which is beneficial for SBS suppression. Two EOMs and their drivers have different responses to the applied radio frequency (RF) signal. The maximum equal modulation depth achieved in the experiments was about 1.93
![]() $\pi$
, whose value is determined by comparison with numerical simulation.
$\pi$
, whose value is determined by comparison with numerical simulation.

Figure 3 Spectra of the fundamental lasers. (a) Spectra of two single-frequency and phase-modulated lasers measured with the FPI. (b) Optical spectra of the seed lasers and main amplifier.
The amplifier was tested firstly with the single phase-modulated seed laser. The SBS-limited outputs at 1178.3 and 1183.2 nm were 16 and 15.4 W, respectively. With both seeds, the SBS-limited output increased to 45.2 W, corresponding to 87.6 W pump power at 1120 nm, where the backward light power was 0.22 W, as shown in Figure 4. Thus, more than 11 times SBS suppression was achieved. The improved SBS suppression in the dual seed case as compared to the single seed case is due to the change of signal power distribution along the amplifier, which determines the exact SBS gain. The spectra of the phase-modulated seed lasers and main amplifier were measured by an optical spectrum analyzer with a resolution of 0.1 nm, as shown in Figure 3(b). It is seen that the spectral intensity difference between the two wavelengths is only about 0.26 dB. In addition, FWM is well suppressed when wavelength separation of the two seed lasers is 4.9 nm. Two FWM-caused lines are still observed at 1173.4 and 1188.1 nm, respectively, but they are 22 dB lower than the 1178.3 and 1183.2 nm laser lines.

Figure 4 Power curves of the fundamental Raman amplifier and upconverted single-frequency laser by sum-frequency generation. (a) The output and backward light power of the Raman fiber amplifier as a function of 1120 nm pump power. (b) The power and conversion efficiency of the single-frequency upconverted laser as a function of the fundamental laser power. Insert: spectrum of the generated 590.3 nm laser.
3.2 Single-frequency upconverted laser generation
According to the analysis above, to get a single-frequency laser after SFG, the depth of phase modulation upon two signal lasers should be the same, and the relative phase between the sine-wave modulations should be
![]() $\pi$
. The fine spectra of the phase-modulated laser and the SFG were simulated numerically. Results of the spectra of the upconverted laser with different phase offset
$\pi$
. The fine spectra of the phase-modulated laser and the SFG were simulated numerically. Results of the spectra of the upconverted laser with different phase offset
![]() $\Delta \phi$
are shown in Figure 5(a), where the modulation depth is set to the experimentally determined
$\Delta \phi$
are shown in Figure 5(a), where the modulation depth is set to the experimentally determined
![]() $1.93\pi$
. In the process of phase-modulated laser SFG, when
$1.93\pi$
. In the process of phase-modulated laser SFG, when
![]() $\Delta \phi$
is close to 0 or an integral multiple of
$\Delta \phi$
is close to 0 or an integral multiple of
![]() $2\pi$
, the resulting upconverted laser has a wider spectrum than the fundamental lasers. When
$2\pi$
, the resulting upconverted laser has a wider spectrum than the fundamental lasers. When
![]() $\Delta \phi$
is
$\Delta \phi$
is
![]() $\pi$
, the upconverted laser becomes single frequency in spite of the multi-line fundamental lasers.
$\pi$
, the upconverted laser becomes single frequency in spite of the multi-line fundamental lasers.

Figure 5 The spectral evolution of upconverted lasers at different phase offsets between sinusoidal signals. (a) The simulated spectra of upconverted lasers. (b) The measured spectra with the FPI. The intensity is normalized by the intensity of the single-frequency case.
The effect of phase offset was investigated experimentally by adjusting the offset between two sine-wave signals and measuring the fine spectra of the SFG output with the FPI. Figure 5(b) shows the measured spectra at different phase offsets. The phase offset contribution due to the optical path difference of the two amplifiers has been deducted. Different from that in the simulated spectrum, the measured spectral lines have finite width owing to the finite resolution of the FPI. With a different phase offset, the SFG output usually has multiple sidebands, but becomes single frequency at specific phase offset of
![]() $\pi$
(or more generally an odd multiple of
$\pi$
(or more generally an odd multiple of
![]() $\pi$
). The spectrum behaves as predicted by the numerical simulation.
$\pi$
). The spectrum behaves as predicted by the numerical simulation.
With the phase offset set as
![]() $\pi$
, the output powers of the Raman fiber amplifier and SFG unit were measured, and the results are plotted in Figure 4. The power and conversion efficiency of the single-frequency upconverted 590.3 nm laser are shown in Figure 4(b). A maximum power of 17.3 W was obtained in the single-pass configuration with a conversion efficiency of 39.3%. The optical spectrum at maximum power is shown in the inset of Figure 4(b). Besides the 590.3 nm SFG line, there are lines at 589.2 and 591.6 nm, which are 39 and 41 dB lower. They are the second harmonics of 1178.3 and 1183.2 nm, respectively, out of the phase matching condition. The phase matching temperature of the 590.3 nm SFG was found to be around
$\pi$
, the output powers of the Raman fiber amplifier and SFG unit were measured, and the results are plotted in Figure 4. The power and conversion efficiency of the single-frequency upconverted 590.3 nm laser are shown in Figure 4(b). A maximum power of 17.3 W was obtained in the single-pass configuration with a conversion efficiency of 39.3%. The optical spectrum at maximum power is shown in the inset of Figure 4(b). Besides the 590.3 nm SFG line, there are lines at 589.2 and 591.6 nm, which are 39 and 41 dB lower. They are the second harmonics of 1178.3 and 1183.2 nm, respectively, out of the phase matching condition. The phase matching temperature of the 590.3 nm SFG was found to be around
![]() ${74}^{\circ}\mathrm{C}$
, while the temperature for the 1178.3 and 1183.2 nm SHG was 74°C and 100°C, respectively.
${74}^{\circ}\mathrm{C}$
, while the temperature for the 1178.3 and 1183.2 nm SHG was 74°C and 100°C, respectively.
The fine spectrum of the single-frequency upconverted laser at 590.3 nm with phase-modulated fundamental lasers was compared with that without phase modulation. As shown in Figure 6, both have a clean profile and are undistinguishable. The linewidth of the former is measured to be 27 MHz at the maximum power of 17.3 W, while the latter is 28 MHz with a maximum output of about 0.14 W. The difference is within the measurement error, limited by the FPI resolution. The true linewidth should be around a few hundred kHz. Notably, the upconverted laser is sideband-free, which is difficult to achieve in the SHG-based phase-doubling approach[ Reference Zeng, Cui, Cheng and Feng 17 , Reference Cui, Zeng, Jiang, Cheng, Yang, Zhou and Feng 18 ]. The phase-doubling approach requires modulation functions of infinite bandwidth in principle, while the present phase summation approach only requires an identical function with the opposite sign. In the case of sinusoidal modulation, a single-frequency electronic signal is applied. Therefore, as long as the signal amplitude is within the linear range of the devices, complete phase demodulation can be achieved by finely adjusting the signal amplitude and phase offset.
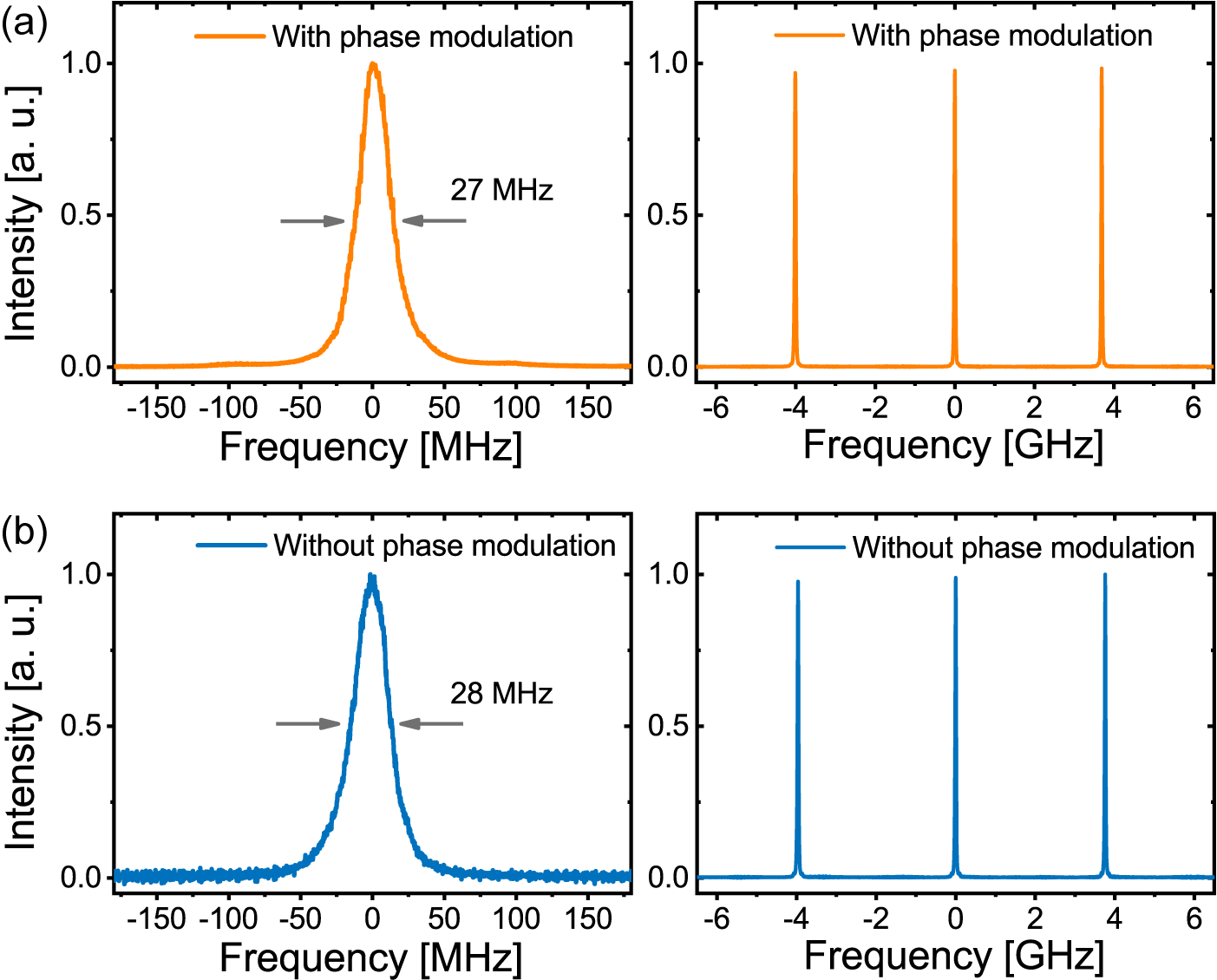
Figure 6 Spectra of upconverted output. (a) The fine spectrum and FPI scan signal of the single-frequency upconverted laser with phase-modulated fundamental lasers at output power of 17.3 W. (b) The fine spectrum and FPI scan signal of the upconverted single-frequency laser without phase modulation.
The output power of the single-frequency upconverted laser was limited by the phase modulation depth, which is required to be identical on both signal lasers. If a higher phase modulation is applied, the SBS-limited fundamental lasers can be further increased and a higher single-frequency upconverted laser can be generated. In the experiments, we tried tuning up both RF signals to maximum regardless of the identical depth requirement. Then the fiber amplifier output increased to 50 W under the SBS limit. The SFG output increased to 21.4 W with a conversion efficiency of 43.3%, corresponding to 101.3 W pump laser power at 1120 nm. Therefore, we believe power scaling of a single-frequency upconverted laser can be readily done with dedicated electronics, which achieves higher phase modulation. Another obvious extension to the technique is to use multi-tone phase modulation, which can also obtain higher SBS suppression and is beneficial for power scaling.
4 Conclusions
In conclusion, we have proposed and demonstrated a new method to achieve high-power single-frequency upconverted laser generation utilizing the phase summation effect in the sum-frequency mixing process. Two single-frequency fundamental lasers are phase modulated to suppress SBS and achieve higher amplified output. By adjusting the phase modulations on the two lasers to have a similar amplitude but opposite signs, the sum-frequency mixed laser returns to single frequency. Such a phase modulation demodulation approach for high-power single-frequency laser generation is analogous to the chirped pulse amplification approach for ultrafast pulsed lasers proposed by Strickland and Mourou[ Reference Strickland and Mourou 20 ], where the optical pulses are expanded before amplification to avoid nonlinear optical damage and are compressed afterwards. The method was experimentally proved in a Raman fiber amplifier-based yellow laser system with sinusoidal phase modulation, which generated a 20-W-level single-frequency 590 nm laser. Compared with the SHG-based method[ Reference Cui, Zeng, Jiang, Cheng, Yang, Zhou and Feng 18 ], the present SFG-based method overcomes the bandwidth difficulty, and allows sideband-free upconverted single-frequency laser generation. It shows great advantage in generating high-power high-spectral-quality single-frequency visible or ultraviolet lasers for high-precision applications.
Acknowledgement
The work was partly supported by the National Natural Science Foundation of China (No. 62075226).









