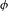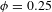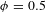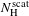1 Introduction
High-resolution X-ray spectra from stellar objects are an important tool to infer their plasma structures[Reference Smith, Brickhouse, Liedahl and Raymond1], physical conditions[Reference Porquet and Dubau2, Reference Porquet, Dubau and Grosso3], wind speed in X-ray binary systems[Reference Watanabe, Sako, Ishida, Ishisaki, Kahn, Kohmura, Nagase, Paerels and Takahashi4] (hereafter W06), coronal abundances (e.g., Blondin et al. 1990[Reference Blondin, Kallman, Fryxell and Taam5]) and other important physical information about astrophysical objects.
Conventionally, the fitting of X-ray spectra is based on reduced
![]() $\unicode[STIX]{x1D712}^{2}$
method (e.g., Sako et al. 1999[Reference Sako, Liedahl, Kahn and Paerels6], Goldenstein et al. 2004[Reference Goldstein, Huenemoerder and Blank7], hereafter S99 and G04) or maximum likelihood (e.g., W06). Among those studies, most continuum models (e.g., power-law and black body) of X-ray spectra are nonlinear with a large number of free parameters (
$\unicode[STIX]{x1D712}^{2}$
method (e.g., Sako et al. 1999[Reference Sako, Liedahl, Kahn and Paerels6], Goldenstein et al. 2004[Reference Goldstein, Huenemoerder and Blank7], hereafter S99 and G04) or maximum likelihood (e.g., W06). Among those studies, most continuum models (e.g., power-law and black body) of X-ray spectra are nonlinear with a large number of free parameters (
![]() ${>}3$
). As to the spectral lines, the effects of satellite lines have not been considered during the fitting of He-like triplets. For the fitting of both continua and lines, it includes many free parameters, which makes the fitting nonlinear and parameters degenerate. In order to decrease the number of free parameters, some parameters were kept fixed during the fitting process, e.g., G04, based on assumptions and previous understanding. In such cases, pitfalls may exist in the estimate of number of degrees of freedom as well as the corresponding error estimates[Reference Andrae8, Reference Andrae, Schulze-Hartung and Melchior9]. In Figure 1, we show an example of reduced
${>}3$
). As to the spectral lines, the effects of satellite lines have not been considered during the fitting of He-like triplets. For the fitting of both continua and lines, it includes many free parameters, which makes the fitting nonlinear and parameters degenerate. In order to decrease the number of free parameters, some parameters were kept fixed during the fitting process, e.g., G04, based on assumptions and previous understanding. In such cases, pitfalls may exist in the estimate of number of degrees of freedom as well as the corresponding error estimates[Reference Andrae8, Reference Andrae, Schulze-Hartung and Melchior9]. In Figure 1, we show an example of reduced
![]() $\unicode[STIX]{x1D712}^{2}$
fit for He-triplets. It can be seen that the model can fit
$\unicode[STIX]{x1D712}^{2}$
fit for He-triplets. It can be seen that the model can fit
![]() $r$
and
$r$
and
![]() $f$
lines (see Section 3.2.2) but hard to find signals of
$f$
lines (see Section 3.2.2) but hard to find signals of
![]() $i$
if a three-Gaussian model was used to fit the three lines simultaneously. Besides, the error bars resulting from the fit were rather large. If the satellite lines are taken into account, i.e., a five/six-Gaussian model is taken to find satellite lines, this method fails to find any line signals.
$i$
if a three-Gaussian model was used to fit the three lines simultaneously. Besides, the error bars resulting from the fit were rather large. If the satellite lines are taken into account, i.e., a five/six-Gaussian model is taken to find satellite lines, this method fails to find any line signals.

Figure 1. Reduced
![]() $\unicode[STIX]{x1D712}^{2}$
fit for He-triplets with a three-Gaussian model, taking Si xiii of Vela X-1 with
$\unicode[STIX]{x1D712}^{2}$
fit for He-triplets with a three-Gaussian model, taking Si xiii of Vela X-1 with
![]() $\unicode[STIX]{x1D719}=0.5$
as an example. Best fitting result and its error range are shown in red thick line and red shadow, respectively. The observed spectrum and its error bars are shown in black steps.
$\unicode[STIX]{x1D719}=0.5$
as an example. Best fitting result and its error range are shown in red thick line and red shadow, respectively. The observed spectrum and its error bars are shown in black steps.
In recent years, modern Bayesian inference, a method of statistical inference in which Bayes’ theorem is used to update our knowledge of a physical parameter, was introduced in astrophysical studies to fit complex models and to interpret observations (e.g., Reichart et al. 1999[Reference Reichart, Castander and Nichol10], Benítez 2000[Reference Benítez11], Buchner et al. 2014[Reference Buchner, Georgakakis, Nandra, Hsu, Rangel, Brightman, Merloni, Salvato, Donley and Kocevski12], Walker et al. 2015[Reference Walker, Olszewski and Mateo13]). Moreover, Buchner et al. [Reference Buchner, Georgakakis, Nandra, Hsu, Rangel, Brightman, Merloni, Salvato, Donley and Kocevski12] adopted the Bayesian analysis for X-ray spectra of deep field Active Galactic Nuclei (AGN), and proved its efficiency. For a Bayesian parameter estimate, Markov Chain Monte Carlo (MCMC) is commonly used in numerical applications. In particular, the method is efficient in probing model-based parameters, estimating uncertainties and describing the nonlinear dependencies among the parameters in cases of a large number of model parameters and low signal-to-noise observations[Reference Foreman-Mackey, Hogg, Lang and Goodman14]. The advantages of Bayesian analysis over previously used methods are the inclusion of prior information of data, providing possible values and confidence intervals for each parameter. In the present paper we apply an MCMC method to estimate the physical parameters of X-ray spectra, taking the observations of the X-ray binary Vela X-1 as an example.
This paper is organized as follows. Section 2 presents how we determine the parameters of continuum and line emission model through the Bayesian approach. In Section 3, we apply this method to parameterized continuum and He-like triplets’ models to the three different phases for Vela X-1, in order to get the posterior probability density functions (PDFs) of each parameter, to probe the degeneracies among parameters, and hence to get continua and He-like triplets with reasonable fitting error bars. The fitting results are shown and discussed in Section 4, with a summary in Section 5.
2 Bayesian inference for X-ray spectrum
In the present paper, we aim to marginalize the posterior PDFs to derive the uncertainties for the parameters of a model fitted to a high-resolution X-ray spectrum. In the Bayesian approach, the posterior PDFs of the model parameters for a given observed spectra,
![]() $F_{\text{obs}}(E)$
, is[Reference MacKay15]
$F_{\text{obs}}(E)$
, is[Reference MacKay15]
where
![]() $\mathbf{p}$
is a vector of parameters of a spectral model,
$\mathbf{p}$
is a vector of parameters of a spectral model,
![]() $b$
represents the background noise of an X-ray spectrum and
$b$
represents the background noise of an X-ray spectrum and
![]() ${\mathcal{L}}[F_{\text{obs}}(E)]$
is the normalization independent of all the parameters, which means that we could sample
${\mathcal{L}}[F_{\text{obs}}(E)]$
is the normalization independent of all the parameters, which means that we could sample
![]() $P[\mathbf{p},b\mid F_{\text{obs}}(E)]$
without computing
$P[\mathbf{p},b\mid F_{\text{obs}}(E)]$
without computing
![]() ${\mathcal{L}}[F_{\text{obs}}(E)]$
[Reference Foreman-Mackey, Hogg, Lang and Goodman14].
${\mathcal{L}}[F_{\text{obs}}(E)]$
[Reference Foreman-Mackey, Hogg, Lang and Goodman14].
![]() ${\mathcal{L}}[F_{\text{obs}}(E)\mid \mathbf{p},b]$
is the likelihood function of
${\mathcal{L}}[F_{\text{obs}}(E)\mid \mathbf{p},b]$
is the likelihood function of
![]() $F_{\text{obs}}(E)$
given the parameters
$F_{\text{obs}}(E)$
given the parameters
![]() $[\mathbf{p},b]$
, whose logarithm form can be written as
$[\mathbf{p},b]$
, whose logarithm form can be written as
 $$\begin{eqnarray}\displaystyle & & \displaystyle \ln {\mathcal{L}}[F_{\text{obs}}(E)\mid \mathbf{p},b]=-\mathop{\sum }_{m=1}^{M}\ln (2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FF}_{m}^{2})\nonumber\\ \displaystyle & & \displaystyle \quad -\,\mathop{\sum }_{m=1}^{M}\frac{1}{2}\left[\frac{F_{\text{mod}}(E_{m}\mid \mathbf{p})-F_{\text{obs}}(E_{m})}{\unicode[STIX]{x1D6FF}_{m}}\right]^{2},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \ln {\mathcal{L}}[F_{\text{obs}}(E)\mid \mathbf{p},b]=-\mathop{\sum }_{m=1}^{M}\ln (2\unicode[STIX]{x1D70B}\unicode[STIX]{x1D6FF}_{m}^{2})\nonumber\\ \displaystyle & & \displaystyle \quad -\,\mathop{\sum }_{m=1}^{M}\frac{1}{2}\left[\frac{F_{\text{mod}}(E_{m}\mid \mathbf{p})-F_{\text{obs}}(E_{m})}{\unicode[STIX]{x1D6FF}_{m}}\right]^{2},\end{eqnarray}$$
where
![]() $F_{\text{mod}}(E_{m}\mid \mathbf{p})$
is parameterized spectral model,
$F_{\text{mod}}(E_{m}\mid \mathbf{p})$
is parameterized spectral model,
![]() $M$
is the total data number used in spectral fitting, and
$M$
is the total data number used in spectral fitting, and
![]() $\unicode[STIX]{x1D716}_{\text{obs}}(E_{m})$
is the error of the observed spectrum.
$\unicode[STIX]{x1D716}_{\text{obs}}(E_{m})$
is the error of the observed spectrum.
![]() $p(\mathbf{p},b)$
is the prior function. Normally, it represents previous knowledge from other experiments and physical limiting conditions, or any other prior beliefs. Here we use a step function over each parameter
$p(\mathbf{p},b)$
is the prior function. Normally, it represents previous knowledge from other experiments and physical limiting conditions, or any other prior beliefs. Here we use a step function over each parameter
 $$\begin{eqnarray}\displaystyle \begin{array}{@{}l@{}}p(\mathbf{p})=\left\{\begin{array}{@{}cl@{}}\frac{1}{\mathbf{p}_{\text{upper}}-\mathbf{p}_{\text{lower}}}, & \text{if}\,\mathbf{p}\in [\mathbf{p}_{\text{lower}},\mathbf{p}_{\text{upper}}],\\[2.0pt] 0, & \text{otherwise},\end{array}\right.\\[12.0pt] p(b)=\left\{\begin{array}{@{}cl@{}}\frac{1}{b_{\text{upper}}}, & \text{if}\,b\in (0,b_{\text{upper}}),\\[2.0pt] 0, & \text{otherwise}.\end{array}\right.\end{array} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \begin{array}{@{}l@{}}p(\mathbf{p})=\left\{\begin{array}{@{}cl@{}}\frac{1}{\mathbf{p}_{\text{upper}}-\mathbf{p}_{\text{lower}}}, & \text{if}\,\mathbf{p}\in [\mathbf{p}_{\text{lower}},\mathbf{p}_{\text{upper}}],\\[2.0pt] 0, & \text{otherwise},\end{array}\right.\\[12.0pt] p(b)=\left\{\begin{array}{@{}cl@{}}\frac{1}{b_{\text{upper}}}, & \text{if}\,b\in (0,b_{\text{upper}}),\\[2.0pt] 0, & \text{otherwise}.\end{array}\right.\end{array} & & \displaystyle\end{eqnarray}$$
Selecting the
![]() $[\mathbf{p}_{\text{lower}},\mathbf{p}_{\text{upper}}]$
and
$[\mathbf{p}_{\text{lower}},\mathbf{p}_{\text{upper}}]$
and
![]() $b_{\text{upper}}$
is different from case to case.
$b_{\text{upper}}$
is different from case to case.
To approach our propose, we adopt a stable, well-tested MCMC algorithm, emcee proposed by Foreman-Mackey et al.
[Reference Foreman-Mackey, Hogg, Lang and Goodman14]. The algorithm is based on the Metropolis–Hasting method (Section 15.8 in Ref. [Reference Press16]) and an affine-invariant ensemble sampling algorithm called the ‘stretch move’[Reference Goodman and Weare17]. The key feature of emcee is that it makes an affine transformation to probability density of parameter during the sampling, which makes it insensitive to covariances among parameters. Therefore, emcee requires hand-turning of only one or two parameters, while the tuning of parameters scales as
![]() $N(N+1)/2$
in an
$N(N+1)/2$
in an
![]() $N$
-dimensional space for traditional algorithms. It thus reduces computational costs during the fitting procedure. A complete discussion of the MCMC methods and the algorithms can be found in Ref. [Reference Foreman-Mackey, Hogg, Lang and Goodman14] and references therein.
$N$
-dimensional space for traditional algorithms. It thus reduces computational costs during the fitting procedure. A complete discussion of the MCMC methods and the algorithms can be found in Ref. [Reference Foreman-Mackey, Hogg, Lang and Goodman14] and references therein.
3 Application to the spectra of Vela X-1
In this section, our method is applied to the spectral study of Vela X-1. Vela X-1 is a well-studied X-ray binary, with extensive astronomical simulations of observations[Reference Watanabe, Sako, Ishida, Ishisaki, Kahn, Kohmura, Nagase, Paerels and Takahashi4, Reference Sako, Liedahl, Kahn and Paerels6, Reference Goldstein, Huenemoerder and Blank7], several linked laboratory experiments[Reference Fujioka, Takabe, Yamamoto, Salzmann, Wang, Nishimura, Li, Dong, Wang, Zhang, Rhee, Lee, Han, Tanabe, Fujiwara, Nakabayashi, Zhao, Zhang and Mima18] and related theoretical modeling[Reference Chung, Chen, Morgan, Ralchenko and Lee19, Reference Han, Wang, Salzmann and Zhao20], which provides a chance to test the performance of this method through a thorough comparison. Vela X-1 is a pulsing, eclipsing high mass X-ray binary (HMXB) system with highly ionized gases, which was first identified by Ulmer et al.
[Reference Ulmer, Baity, Wheaton and Peterson21]. Previous observations and theoretical studies have given a reasonably complete description of the system properties. The global structure of the stellar wind in the system was first modeled by S99 using the spectra in the Eclipse phase observed by
![]() $ASCA$
Solid-State Image Spectrometer. Other physical properties of Vela X-1 were provided by the high-resolution X-ray spectra during different phases observed with the Chandra High-Energy Transmission Grating Spectrometer (HETGS)[Reference Sako, Kahn, Paerels, Liedahl, Watanabe, Nagase and Takahashi22, Reference Schulz, Canizares, Lee and Sako23]. G04 first presented the variation of spectra in three orbital phases: Eclipse,
$ASCA$
Solid-State Image Spectrometer. Other physical properties of Vela X-1 were provided by the high-resolution X-ray spectra during different phases observed with the Chandra High-Energy Transmission Grating Spectrometer (HETGS)[Reference Sako, Kahn, Paerels, Liedahl, Watanabe, Nagase and Takahashi22, Reference Schulz, Canizares, Lee and Sako23]. G04 first presented the variation of spectra in three orbital phases: Eclipse,
![]() $\unicode[STIX]{x1D719}=0.25$
, and
$\unicode[STIX]{x1D719}=0.25$
, and
![]() $\unicode[STIX]{x1D719}=0.5$
. In addition, W06 probed the stellar wind dynamics and ionization structures by a quantitative analysis of Doppler shift and line intensities with the same X-ray spectra. The previous literature studies are considered to be sufficiently convincing to be used as benchmarks. With the results of these studies, it is possible for us to verify our analysis method.
$\unicode[STIX]{x1D719}=0.5$
. In addition, W06 probed the stellar wind dynamics and ionization structures by a quantitative analysis of Doppler shift and line intensities with the same X-ray spectra. The previous literature studies are considered to be sufficiently convincing to be used as benchmarks. With the results of these studies, it is possible for us to verify our analysis method.
3.1 Observations
The datasets of Vela X-1 used in our analysis were observed with the Chandra HETG/ACIS-S – the High-Energy Transmission Grating/Advanced Imaging Spectrometer, during three different orbital phases centered on Eclipse,
![]() $\unicode[STIX]{x1D719}=0.25$
and
$\unicode[STIX]{x1D719}=0.25$
and
![]() $\unicode[STIX]{x1D719}=0.5$
in 2001, with Chandra ObsIDs 1926, 1928 and 1927, respectively. The observation and instrument details can be found in Ref. [Reference Paul, Dewangan, Sako, Kahn, Paerels, Liedahl, Wojdowski, Nagase, Ikeuchi, Hearnshaw and Hanawa24], Ref. [Reference Sako, Kahn, Paerels, Liedahl, Watanabe, Nagase and Takahashi22] and G04. Table 1 summarizes the observation dates and exposure times. The full datasets including counts spectra, ancillary response files (ARFs), and redistribution matrix file (RMFs) are all obtained from public archive Transmission Grating Catalog and Archive (TGCat)Footnote
1
. Only the first-order events of the high-energy grating (HEG) data are used in our analysis. The data of positive and negative spectral orders are combined to decrease the error bars of observation. Flux correction was done with the Interactive Spectral Interpretation System (ISIS, version 1.6.2-30)Footnote
2
for the observed data to have the same dimensions as the models and to improve the agreement with physical predictions. The background for the observations is not measured independently, which is difficult to be resolved from the source of interest. Practically, the background could be subtracted from the observation signals, as was done in W06. But it is treated as a correction of observation error in the present work because subtracting the background could cause loss of useful signals.
$\unicode[STIX]{x1D719}=0.5$
in 2001, with Chandra ObsIDs 1926, 1928 and 1927, respectively. The observation and instrument details can be found in Ref. [Reference Paul, Dewangan, Sako, Kahn, Paerels, Liedahl, Wojdowski, Nagase, Ikeuchi, Hearnshaw and Hanawa24], Ref. [Reference Sako, Kahn, Paerels, Liedahl, Watanabe, Nagase and Takahashi22] and G04. Table 1 summarizes the observation dates and exposure times. The full datasets including counts spectra, ancillary response files (ARFs), and redistribution matrix file (RMFs) are all obtained from public archive Transmission Grating Catalog and Archive (TGCat)Footnote
1
. Only the first-order events of the high-energy grating (HEG) data are used in our analysis. The data of positive and negative spectral orders are combined to decrease the error bars of observation. Flux correction was done with the Interactive Spectral Interpretation System (ISIS, version 1.6.2-30)Footnote
2
for the observed data to have the same dimensions as the models and to improve the agreement with physical predictions. The background for the observations is not measured independently, which is difficult to be resolved from the source of interest. Practically, the background could be subtracted from the observation signals, as was done in W06. But it is treated as a correction of observation error in the present work because subtracting the background could cause loss of useful signals.
Table 1. A summary of observation information taken from Chandra data archive a .

3.2 Model
The spectra of Vela X-1 are considered to be composed of continuum and line emission (W06). Therefore, in the present work, for the likelihood function Equation (2), a linear sum of parameterized continuum (
![]() $F_{\text{cont}}$
) and line (
$F_{\text{cont}}$
) and line (
![]() $F_{\text{line}}$
), that is,
$F_{\text{line}}$
), that is,
![]() $F_{\text{mod}}=F_{\text{cont}}+F_{\text{line}}$
, is used to model the spectra of Vela X-1. For
$F_{\text{mod}}=F_{\text{cont}}+F_{\text{line}}$
, is used to model the spectra of Vela X-1. For
![]() $F_{\text{line}}$
, we mainly focus on He-like triplets which have relatively high
$F_{\text{line}}$
, we mainly focus on He-like triplets which have relatively high
![]() $S/N$
-ratio and are commonly used in photoionization plasma diagnostics.
$S/N$
-ratio and are commonly used in photoionization plasma diagnostics.
3.2.1 Continuum
As to the continuum emissions of Vela X-1, we adopt a two-component model (S99), having the form
 $$\begin{eqnarray}\displaystyle F_{\text{cont}}(E) & = & \displaystyle A^{\text{scat}}\exp \left[-\unicode[STIX]{x1D70E}(E)N_{\text{H}}^{\text{scat}}\right]E_{\text{keV}}^{-\unicode[STIX]{x1D6E4}^{\text{scat}}}\nonumber\\ \displaystyle & & \displaystyle +\,A^{\text{dir}}\exp \left[-\unicode[STIX]{x1D70E}(E)N_{\text{H}}^{\text{dir}}\right]E_{\text{keV}}^{-\unicode[STIX]{x1D6E4}^{\text{dir}}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F_{\text{cont}}(E) & = & \displaystyle A^{\text{scat}}\exp \left[-\unicode[STIX]{x1D70E}(E)N_{\text{H}}^{\text{scat}}\right]E_{\text{keV}}^{-\unicode[STIX]{x1D6E4}^{\text{scat}}}\nonumber\\ \displaystyle & & \displaystyle +\,A^{\text{dir}}\exp \left[-\unicode[STIX]{x1D70E}(E)N_{\text{H}}^{\text{dir}}\right]E_{\text{keV}}^{-\unicode[STIX]{x1D6E4}^{\text{dir}}},\end{eqnarray}$$
where
![]() $F_{\text{cont}}$
is the energy-resolved photon flux (
$F_{\text{cont}}$
is the energy-resolved photon flux (
![]() $\text{photon}\,\cdot \,\text{cm}^{-2}\,\cdot \,\text{s}^{-1}\,\cdot \,\text{keV}^{-1}$
). Equation (5) indicates that the intrinsic continuum radiation of Vela X-1 consisted of two components: (1) the first term (labeled with ‘scat’) represents the intrinsic continuum radiation, which is strongly absorbed when the neutron star passes through the surrounding stellar wind; (2) the second term (labeled with ‘dir’) is the direct continuum which is blocked by the companion.
$\text{photon}\,\cdot \,\text{cm}^{-2}\,\cdot \,\text{s}^{-1}\,\cdot \,\text{keV}^{-1}$
). Equation (5) indicates that the intrinsic continuum radiation of Vela X-1 consisted of two components: (1) the first term (labeled with ‘scat’) represents the intrinsic continuum radiation, which is strongly absorbed when the neutron star passes through the surrounding stellar wind; (2) the second term (labeled with ‘dir’) is the direct continuum which is blocked by the companion.
![]() $A^{\text{scat}}$
and
$A^{\text{scat}}$
and
![]() $A^{\text{dir}}$
, (units:
$A^{\text{dir}}$
, (units:
![]() $\text{photon}\,\cdot \,\text{cm}^{-2}\,\cdot \,\text{s}^{-1}\,\cdot \,\text{keV}^{-1}$
), are normalizations corresponding to the two components.
$\text{photon}\,\cdot \,\text{cm}^{-2}\,\cdot \,\text{s}^{-1}\,\cdot \,\text{keV}^{-1}$
), are normalizations corresponding to the two components.
![]() $\unicode[STIX]{x1D70E}(E)$
is the photoelectric absorption cross-sections taken from Morrison and McCammon[Reference Morrison and McCammon25], which assumes solar abundances for the absorbing medium.
$\unicode[STIX]{x1D70E}(E)$
is the photoelectric absorption cross-sections taken from Morrison and McCammon[Reference Morrison and McCammon25], which assumes solar abundances for the absorbing medium.
![]() $\unicode[STIX]{x1D6E4}^{\text{scat}}$
and
$\unicode[STIX]{x1D6E4}^{\text{scat}}$
and
![]() $\unicode[STIX]{x1D6E4}^{\text{dir}}$
are the photon indices of each component. In previous literature studies, one power-law model was also used (W06), but such a kind of model could barely fit the continuum of
$\unicode[STIX]{x1D6E4}^{\text{dir}}$
are the photon indices of each component. In previous literature studies, one power-law model was also used (W06), but such a kind of model could barely fit the continuum of
![]() $\unicode[STIX]{x1D719}=0.5$
below 3 keV. In the present work, we are interested in the He-like triplets which gather below 3 keV. Therefore, we take the two-component model to get more accurate and precise continua.
$\unicode[STIX]{x1D719}=0.5$
below 3 keV. In the present work, we are interested in the He-like triplets which gather below 3 keV. Therefore, we take the two-component model to get more accurate and precise continua.
3.2.2 Lines
Each set of He-like triplets is described by a multi-Gaussian model, that is,
where
![]() $F_{\text{line}}(E)$
is the energy-resolved photon flux, which has the same dimensionality as
$F_{\text{line}}(E)$
is the energy-resolved photon flux, which has the same dimensionality as
![]() $F_{\text{cont}}(E)$
, and
$F_{\text{cont}}(E)$
, and
![]() $n$
is the total number of lines fitted in each set of He-like line emission. As we know, photoionized plasma shows robust satellite lines[Reference Liedahl and Paerels26], so that in our fitting, satellite lines are also included in order to derive accurate and reliable line ratios and shifts. Commonly used diagnostic for photoionized plasma is He-like triplets[Reference Porquet and Dubau2], including the resonance line (
$n$
is the total number of lines fitted in each set of He-like line emission. As we know, photoionized plasma shows robust satellite lines[Reference Liedahl and Paerels26], so that in our fitting, satellite lines are also included in order to derive accurate and reliable line ratios and shifts. Commonly used diagnostic for photoionized plasma is He-like triplets[Reference Porquet and Dubau2], including the resonance line (
![]() $r$
:
$r$
:
![]() $1{\text{s}^{2}\,}^{1}\text{S}_{0}$
–
$1{\text{s}^{2}\,}^{1}\text{S}_{0}$
–
![]() $1\text{s}2\text{p}\,\text{}^{1}\text{P}_{1}$
), the intercombination lines (
$1\text{s}2\text{p}\,\text{}^{1}\text{P}_{1}$
), the intercombination lines (
![]() $i_{x}$
,
$i_{x}$
,
![]() $i_{y}$
:
$i_{y}$
:
![]() $1\text{s}^{2}\,\text{}^{1}\text{S}_{0}$
–
$1\text{s}^{2}\,\text{}^{1}\text{S}_{0}$
–
![]() $1\text{s}2\text{p}\,^{3}\text{P}_{2,1}$
, respectively) and the forbidden line (
$1\text{s}2\text{p}\,^{3}\text{P}_{2,1}$
, respectively) and the forbidden line (
![]() $f$
:
$f$
:
![]() $1{\text{s}^{2}\,}^{1}\text{S}_{0}$
–
$1{\text{s}^{2}\,}^{1}\text{S}_{0}$
–
![]() $1\text{s}2\text{s}\,^{3}\text{S}1$
).
$1\text{s}2\text{s}\,^{3}\text{S}1$
).
![]() $A_{j}$
,
$A_{j}$
,
![]() $E_{j}$
and
$E_{j}$
and
![]() $\unicode[STIX]{x1D716}_{j}$
represent intensity, central energy and line width of each line, respectively, which are parameters we intend to marginalize simultaneously.
$\unicode[STIX]{x1D716}_{j}$
represent intensity, central energy and line width of each line, respectively, which are parameters we intend to marginalize simultaneously.
3.3 Parameters and prior functions
In the continuum fittings of S99 for the Eclipse phase, the photon indices of the two components were set equal because they assumed that photon scattering is elastic, so that it does not alter the spectral shape. In G04, the photon index was fixed to 1.7 in both power laws in the Eclipse phase, while in other phases
![]() $\unicode[STIX]{x1D6E4}^{\text{scat}}=1.7$
and
$\unicode[STIX]{x1D6E4}^{\text{scat}}=1.7$
and
![]() $\unicode[STIX]{x1D6E4}^{\text{dir}}$
was varied. However, the stellar wind is not strictly spherical because of the wake structures including accretion and photoionized wake (see Figure 8 of Ref. [Reference Kaper, Hammerschlag-Hensberge and Zuiderwijk27], a sketch of the different structures in the stellar wind of Vela X-1). The works of Blondin et al.
[Reference Blondin, Kallman, Fryxell and Taam5, Reference Blondin, Stevens and Kallman28] showed that line-of-sight column density,
$\unicode[STIX]{x1D6E4}^{\text{dir}}$
was varied. However, the stellar wind is not strictly spherical because of the wake structures including accretion and photoionized wake (see Figure 8 of Ref. [Reference Kaper, Hammerschlag-Hensberge and Zuiderwijk27], a sketch of the different structures in the stellar wind of Vela X-1). The works of Blondin et al.
[Reference Blondin, Kallman, Fryxell and Taam5, Reference Blondin, Stevens and Kallman28] showed that line-of-sight column density,
![]() $N_{\text{H}}$
of the stellar wind, is a function of orbital phase (from phase 0.1 to 0.9). That means the indices
$N_{\text{H}}$
of the stellar wind, is a function of orbital phase (from phase 0.1 to 0.9). That means the indices
![]() $\unicode[STIX]{x1D6E4}^{\text{scat}}$
and
$\unicode[STIX]{x1D6E4}^{\text{scat}}$
and
![]() $\unicode[STIX]{x1D6E4}^{\text{dir}}$
may change in different phases. Thus, in our analysis we set
$\unicode[STIX]{x1D6E4}^{\text{dir}}$
may change in different phases. Thus, in our analysis we set
![]() $\unicode[STIX]{x1D6E4}^{\text{scat}}$
and
$\unicode[STIX]{x1D6E4}^{\text{scat}}$
and
![]() $\unicode[STIX]{x1D6E4}^{\text{dir}}$
as free parameters in the data-model fitting. In Equation (1), we introduce a parameter
$\unicode[STIX]{x1D6E4}^{\text{dir}}$
as free parameters in the data-model fitting. In Equation (1), we introduce a parameter
![]() $b$
which could be considered as an adjustment for the observation error to take the background into account. Therefore, the predictions for
$b$
which could be considered as an adjustment for the observation error to take the background into account. Therefore, the predictions for
![]() $F_{\text{cont}}(E)$
are based on seven parameters
$F_{\text{cont}}(E)$
are based on seven parameters
![]() $[\mathbf{p}_{\text{cont}},b_{\text{cont}}]$
for each phase, where
$[\mathbf{p}_{\text{cont}},b_{\text{cont}}]$
for each phase, where
![]() $\mathbf{p}_{\text{cont}}=[A^{\text{scat}},A^{\text{dir}},N_{\text{H}}^{\text{scat}},N_{\text{H}}^{\text{dir}},\unicode[STIX]{x1D6E4}^{\text{scat}},\unicode[STIX]{x1D6E4}^{\text{dir}}]$
.
$\mathbf{p}_{\text{cont}}=[A^{\text{scat}},A^{\text{dir}},N_{\text{H}}^{\text{scat}},N_{\text{H}}^{\text{dir}},\unicode[STIX]{x1D6E4}^{\text{scat}},\unicode[STIX]{x1D6E4}^{\text{dir}}]$
.
He-like triplets can be detected in the phases of Eclipse and
![]() $\unicode[STIX]{x1D719}=0.5$
. Therefore, we only fit He-like triplets for the two phases. Among these emission lines, Mg xi and Si xiii with high
$\unicode[STIX]{x1D719}=0.5$
. Therefore, we only fit He-like triplets for the two phases. Among these emission lines, Mg xi and Si xiii with high
![]() $S/N$
ratio are adopted as the fitting sample in the present work. In our analysis, the main and satellite lines are fitted simultaneously by multi-Gaussian components for each set of He-like emission lines. Here we describe them as follows.
$S/N$
ratio are adopted as the fitting sample in the present work. In our analysis, the main and satellite lines are fitted simultaneously by multi-Gaussian components for each set of He-like emission lines. Here we describe them as follows.
∙ Mg xi From the observed spectra, two groups of satellite lines can be seen around
 $f$
and
$f$
and
 $r$
lines. Two Gaussians with different widths are used to represent them. In principle, four Gaussians with the same line width should be adopted to model the main lines of Mg xi He-like triplets because the lines correspond to transitions between the
$r$
lines. Two Gaussians with different widths are used to represent them. In principle, four Gaussians with the same line width should be adopted to model the main lines of Mg xi He-like triplets because the lines correspond to transitions between the
 $n=2$
shell and the
$n=2$
shell and the
 $n=1$
ground state shell. However, the theoretical central energies of
$n=1$
ground state shell. However, the theoretical central energies of
 $i_{x}$
and
$i_{x}$
and
 $i_{y}$
are closed, i.e.,
$i_{y}$
are closed, i.e.,
 $|h\unicode[STIX]{x1D708}_{i_{x}}-h\unicode[STIX]{x1D708}_{i_{y}}|<0.5$
eV, while the observed full widths at half maximum of the two lines are larger than 1 eV. In this situation, the two lines cannot be resolved. Therefore, three Gaussians with two different line widths are used to represent main lines, that is, the line widths of
$|h\unicode[STIX]{x1D708}_{i_{x}}-h\unicode[STIX]{x1D708}_{i_{y}}|<0.5$
eV, while the observed full widths at half maximum of the two lines are larger than 1 eV. In this situation, the two lines cannot be resolved. Therefore, three Gaussians with two different line widths are used to represent main lines, that is, the line widths of
 $f$
and
$f$
and
 $r$
are equal. And the line shifts of
$r$
are equal. And the line shifts of
 $i_{x}$
and
$i_{x}$
and
 $i_{y}$
lines will not be adopted in the following stellar wind velocity calculation. Finally, the predictions for
$i_{y}$
lines will not be adopted in the following stellar wind velocity calculation. Finally, the predictions for
 $F_{\text{line}}(E)$
(Mg xi) are based on 15 parameters
$F_{\text{line}}(E)$
(Mg xi) are based on 15 parameters
 $[\mathbf{p}_{\text{line}_{Mg}},b_{\text{line}_{Mg}}]$
.
$[\mathbf{p}_{\text{line}_{Mg}},b_{\text{line}_{Mg}}]$
.∙ Si xiii Only one group of satellite lines which are located around the main
 $f$
line can be seen from the observed spectra. For
$f$
line can be seen from the observed spectra. For
 $r$
,
$r$
,
 $i_{x}$
,
$i_{x}$
,
 $i_{y}$
, and
$i_{y}$
, and
 $f$
lines, they also share the same line width. Finally, five Gaussians with 13 parameters
$f$
lines, they also share the same line width. Finally, five Gaussians with 13 parameters
 $[\mathbf{p}_{\text{line}_{Si}},b_{\text{line}_{Si}}]$
need to be marginalized for Si xiii He-like lines.
$[\mathbf{p}_{\text{line}_{Si}},b_{\text{line}_{Si}}]$
need to be marginalized for Si xiii He-like lines.
Selecting suitable upper limits for each parameter in prior functions is based on previous studies (e.g., S99, G04, W06) and observations for Vela X-1. Considering the observed flux and previous studies and experiments, the upper limits of each parameter are listed in Table 2 for each phase. In the estimate of W06, the background event contributions were found to be
![]() ${\sim}5\%$
for the observed flux; thus, the upper limit of
${\sim}5\%$
for the observed flux; thus, the upper limit of
![]() $b$
is set to
$b$
is set to
![]() $10^{-4}$
for the Eclipse phase and
$10^{-4}$
for the Eclipse phase and
![]() $10^{-2}$
for other phases.
$10^{-2}$
for other phases.
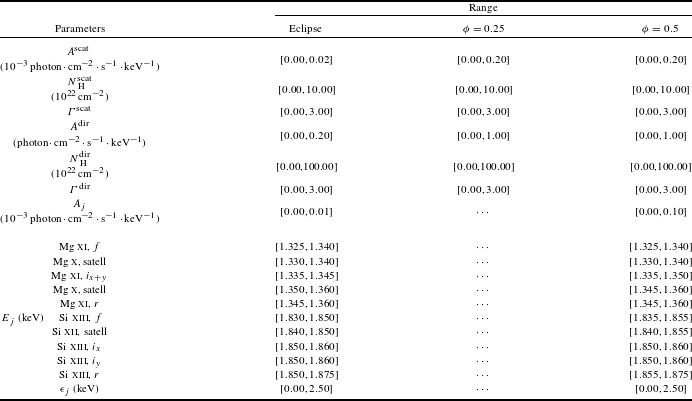
Table 2. The range of each parameter which needs to be marginalized in prior functions.
4 Results and discussion
The best-fit parameters and their uncertainties of
![]() $F_{\text{cont}}$
and
$F_{\text{cont}}$
and
![]() $F_{\text{line}}$
are listed in Tables 3–5. Figures 2, 3 and 4 show
$F_{\text{line}}$
are listed in Tables 3–5. Figures 2, 3 and 4 show
![]() $F_{\text{cont}}$
and
$F_{\text{cont}}$
and
![]() $F_{\text{line}}$
implied by our fits using the models of Equations (5) and (6), respectively. The black lines and gray shadows are the observed flux-corrected spectra and observation errors, respectively. The red thick lines show
$F_{\text{line}}$
implied by our fits using the models of Equations (5) and (6), respectively. The black lines and gray shadows are the observed flux-corrected spectra and observation errors, respectively. The red thick lines show
![]() $F_{\text{cont}}$
and
$F_{\text{cont}}$
and
![]() $F_{\text{line}}$
for the most likely parameters, and the band of light red lines shows a
$F_{\text{line}}$
for the most likely parameters, and the band of light red lines shows a
![]() $1-\unicode[STIX]{x1D70E}$
sampling of the posterior PDFs returned by emcee for
$1-\unicode[STIX]{x1D70E}$
sampling of the posterior PDFs returned by emcee for
![]() $F_{\text{cont}}$
and
$F_{\text{cont}}$
and
![]() $F_{\text{line}}$
. For
$F_{\text{line}}$
. For
![]() $F_{\text{cont}}$
, the contributions from scatter and direct components are individually shown in blue and purple dashed lines, respectively. Error regions of parameters are directly derived from 68% confidence interval of the posterior PDFs of fitted parameters. It can be seen that the residuals between models and observations scatter around zero, which proves the fits are unbiased.
$F_{\text{cont}}$
, the contributions from scatter and direct components are individually shown in blue and purple dashed lines, respectively. Error regions of parameters are directly derived from 68% confidence interval of the posterior PDFs of fitted parameters. It can be seen that the residuals between models and observations scatter around zero, which proves the fits are unbiased.
Table 3. The best fitted continuum parameters in three different phases.
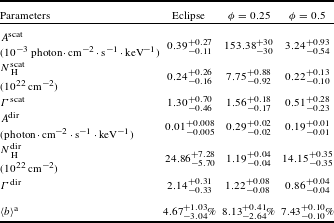
a It is an average relative value over the whole spectrum for each phase.

Figure 2. The best model-predicted continuum shown in red thick lines for three phases. The scatter and direct components are shown separately. Shadows are the 68.3% errors in the recovered value of parameters. The observed spectrum and its error bars are shown in black steps and gray shadow. The large residual values are caused by emission lines.
Table 4. The best fitted parameters for Mg xi and Si xiii He-like lines in phase of Eclipse.

a Errors correspond to 68% confidence level.
b Errors correspond to 90% confidence level.

Figure 3. The best model-predicted He-like Mg xi shown in red thick line for both (a) the Eclipse phase and (b)
![]() $\unicode[STIX]{x1D719}=0.5$
. Red shadows are the 68.3% errors in the recovered value of parameters list in Table 4. The observed spectrum and its error bars are shown in black steps.
$\unicode[STIX]{x1D719}=0.5$
. Red shadows are the 68.3% errors in the recovered value of parameters list in Table 4. The observed spectrum and its error bars are shown in black steps.
Table 5. The best fitted parameters for Mg XI and Si XIII He-like lines for phase of
![]() $\unicode[STIX]{x1D719}=0.5$
.
$\unicode[STIX]{x1D719}=0.5$
.

a Errors correspond to 68% confidence level.
b Errors correspond to 90% confidence level.

Figure 4. The best model-predicted He-like Si XIII shown in red thick line for both (a) the Eclipse phase and (b)
![]() $\unicode[STIX]{x1D719}=0.5$
. Red shadows are the 68.3% errors in the recovered value of parameters list in Table 4. The observed spectrum and its error bars are shown in black steps.
$\unicode[STIX]{x1D719}=0.5$
. Red shadows are the 68.3% errors in the recovered value of parameters list in Table 4. The observed spectrum and its error bars are shown in black steps.
4.1 Comparison with previous studies
The results of previous studies are listed in Table 6 and the last two columns of Tables 4 and 5. We note that the errors of the Eclipse phase are larger than those of the other two phases, because the count of this phase is low and of the same order of magnitude of the observation error.
4.1.1
 $F_{\text{cont}}$
$F_{\text{cont}}$
Our best-fit continua are systematically lower (
![]() ${\sim}5\%{-}20\%$
) than those of G04 probably due to exclusion of emission lines in our fitting and 28% larger than the ones of W06. For the Eclipse phase, our derived flux is 8% higher than that of S02, but 132% lower than the one of S99. Figure 5 puts the
${\sim}5\%{-}20\%$
) than those of G04 probably due to exclusion of emission lines in our fitting and 28% larger than the ones of W06. For the Eclipse phase, our derived flux is 8% higher than that of S02, but 132% lower than the one of S99. Figure 5 puts the
![]() $F_{\text{cont}}$
with the parameters from literatures into context.
$F_{\text{cont}}$
with the parameters from literatures into context.

Figure 5. Comparisons with previous works. Red thick lines and their shadows are our present best-fit results. Aqua, blue, and purple dash lines are the results with parameters determined by S99, G04, and W06, respectively.
Considering the confidence ranges of our fitting, our
![]() $F_{\text{cont}}$
results are in good agreements with previous literature studies (i.e., S99, G04, and W06). For Eclipse, both the results of S99 and G04 fall in our
$F_{\text{cont}}$
results are in good agreements with previous literature studies (i.e., S99, G04, and W06). For Eclipse, both the results of S99 and G04 fall in our
![]() $1-\unicode[STIX]{x1D70E}$
fitting error range in which observed uncertainties are concluded, but our result is systematically lower and the shapes of the continua are different especially in the energy range of 2–4 keV where some He-like triplets such as Si and Mg occur. Our lower results are mainly caused by excluding emission lines during the continuum fitting process. The shape of continuum is determined by photon indices
$1-\unicode[STIX]{x1D70E}$
fitting error range in which observed uncertainties are concluded, but our result is systematically lower and the shapes of the continua are different especially in the energy range of 2–4 keV where some He-like triplets such as Si and Mg occur. Our lower results are mainly caused by excluding emission lines during the continuum fitting process. The shape of continuum is determined by photon indices
![]() $\unicode[STIX]{x1D6E4}^{\text{scat}}$
and
$\unicode[STIX]{x1D6E4}^{\text{scat}}$
and
![]() $\unicode[STIX]{x1D6E4}^{\text{dir}}$
which are both set as free parameters in the present study. In S99, both of
$\unicode[STIX]{x1D6E4}^{\text{dir}}$
which are both set as free parameters in the present study. In S99, both of
![]() $\unicode[STIX]{x1D6E4}^{\text{scat}}$
and
$\unicode[STIX]{x1D6E4}^{\text{scat}}$
and
![]() $\unicode[STIX]{x1D6E4}^{\text{dir}}$
were fixed to 1.7, and G04 set
$\unicode[STIX]{x1D6E4}^{\text{dir}}$
were fixed to 1.7, and G04 set
![]() $\unicode[STIX]{x1D6E4}^{\text{dir}}$
as free for convenient reason. This is a main cause for such a difference. We adopt Bayesian inference to probe all possible values of photon indices, which help us well in understanding the shape of continua and even the structure of the stellar wind of the HMBX system. For
$\unicode[STIX]{x1D6E4}^{\text{dir}}$
as free for convenient reason. This is a main cause for such a difference. We adopt Bayesian inference to probe all possible values of photon indices, which help us well in understanding the shape of continua and even the structure of the stellar wind of the HMBX system. For
![]() $\unicode[STIX]{x1D719}=0.25$
and
$\unicode[STIX]{x1D719}=0.25$
and
![]() $\unicode[STIX]{x1D719}=0.5$
, in the energy range of 3–10 keV the continua are in very good agreements with those of G04 and W06. But in the range below 3 keV the results are much higher than that in W06. It may be because they used a one-power-law model in their studies. Similarly, excluding emission lines is the main reason why the result of G04 is larger than ours in lower energy range for
$\unicode[STIX]{x1D719}=0.5$
, in the energy range of 3–10 keV the continua are in very good agreements with those of G04 and W06. But in the range below 3 keV the results are much higher than that in W06. It may be because they used a one-power-law model in their studies. Similarly, excluding emission lines is the main reason why the result of G04 is larger than ours in lower energy range for
![]() $\unicode[STIX]{x1D719}=0.5$
. The fitted continuum of G04 in
$\unicode[STIX]{x1D719}=0.5$
. The fitted continuum of G04 in
![]() $\unicode[STIX]{x1D719}=0.25$
is lower than lower limit given by our analysis, and it may be caused by fixing the photon-index value during the fitting process. As we discuss in Section 4.2, when the photon index and other parameters are degenerate, fixing one parameter may cause inaccuracy of parameters. For
$\unicode[STIX]{x1D719}=0.25$
is lower than lower limit given by our analysis, and it may be caused by fixing the photon-index value during the fitting process. As we discuss in Section 4.2, when the photon index and other parameters are degenerate, fixing one parameter may cause inaccuracy of parameters. For
![]() $\unicode[STIX]{x1D719}=0.25$
, all modeled continua cannot fit the observed ones in the range of 8–10 keV. From Figure 2(b), one can see that in this energy range the continuum should be dominated by
$\unicode[STIX]{x1D719}=0.25$
, all modeled continua cannot fit the observed ones in the range of 8–10 keV. From Figure 2(b), one can see that in this energy range the continuum should be dominated by
![]() $F^{\text{scat}}$
. However, the models predict a larger contribution from
$F^{\text{scat}}$
. However, the models predict a larger contribution from
![]() $F^{\text{dir}}$
. That is why there is a gap between models and observation in the 8–10 keV range for
$F^{\text{dir}}$
. That is why there is a gap between models and observation in the 8–10 keV range for
![]() $\unicode[STIX]{x1D719}=0.25$
. Fortunately, as there are no emission lines detected there, the gap would not affect our final results.
$\unicode[STIX]{x1D719}=0.25$
. Fortunately, as there are no emission lines detected there, the gap would not affect our final results.
![]() $N_{\text{H}}^{\text{scat}}$
for the three phases are all equal to
$N_{\text{H}}^{\text{scat}}$
for the three phases are all equal to
![]() $0.5\times 10^{22}~\text{cm}^{-2}$
in G04 which implies a spherical stellar wind. In our present fitting,
$0.5\times 10^{22}~\text{cm}^{-2}$
in G04 which implies a spherical stellar wind. In our present fitting,
![]() $N_{\text{H}}^{\text{scat}}$
varies from phase to phase, e.g.,
$N_{\text{H}}^{\text{scat}}$
varies from phase to phase, e.g.,
![]() $0.24_{-0.16}^{+0.26}\times 10^{22}$
,
$0.24_{-0.16}^{+0.26}\times 10^{22}$
,
![]() $7.75_{-0.92}^{+0.88}\times 10^{22}$
and
$7.75_{-0.92}^{+0.88}\times 10^{22}$
and
![]() $0.22_{-0.10}^{+0.13}\times 10^{22}~\text{cm}^{-2}$
for Eclipse,
$0.22_{-0.10}^{+0.13}\times 10^{22}~\text{cm}^{-2}$
for Eclipse,
![]() $\unicode[STIX]{x1D719}=0.25$
and
$\unicode[STIX]{x1D719}=0.25$
and
![]() $\unicode[STIX]{x1D719}=0.5$
, respectively. It implies a non-spherical structure of the stellar wind, which agrees with the simulation in Ref. [Reference Blondin, Stevens and Kallman28].
$\unicode[STIX]{x1D719}=0.5$
, respectively. It implies a non-spherical structure of the stellar wind, which agrees with the simulation in Ref. [Reference Blondin, Stevens and Kallman28].
Table 6. The flux comparison with previous studies for
![]() $F_{\text{cont}}$
.
$F_{\text{cont}}$
.

a Flux is calculated in the energy range of 0.5–10 keV.
b Z17 represents the results of the present work.
4.1.2
 $F_{\text{line}}$
$F_{\text{line}}$
As shown in Tables 4 and 5, line flux derived in the present work is systematically lower than that in W06. This is mainly due to two reasons. (1) W06 considered the corrections of interstellar gas absorption in the flux calculation by assuming a hydrogen column density of
![]() $6\times 10^{21}$
cm
$6\times 10^{21}$
cm
![]() $^{-2}$
which corresponds to the density of
$^{-2}$
which corresponds to the density of
![]() $1~\text{H}~\text{cm}^{-3}$
and the distance of 1.9 kpc. The flux values listed in W06 were compensated by absorption values, which shower higher values. (2) The contributions of satellite lines are subtracted during our flux calculation. Although there is a systematic difference in absolute line flux between the calculations of W06 and ours, after calculating the
$1~\text{H}~\text{cm}^{-3}$
and the distance of 1.9 kpc. The flux values listed in W06 were compensated by absorption values, which shower higher values. (2) The contributions of satellite lines are subtracted during our flux calculation. Although there is a systematic difference in absolute line flux between the calculations of W06 and ours, after calculating the
![]() $G$
-ratio[Reference Porquet and Dubau2] which is used to estimate the plasma temperature with
$G$
-ratio[Reference Porquet and Dubau2] which is used to estimate the plasma temperature with
our values of
![]() $G$
-ratio still have good agreements with the ones of W06 in 90% confidence region, which proves the validity of the present method. With the X-ray photoionized plasma diagnostics[Reference Wang, Han, Salzmann and Zhao29], both of
$G$
-ratio still have good agreements with the ones of W06 in 90% confidence region, which proves the validity of the present method. With the X-ray photoionized plasma diagnostics[Reference Wang, Han, Salzmann and Zhao29], both of
![]() $G$
-ratios of W06 and ours derive the same plasma temperature.
$G$
-ratios of W06 and ours derive the same plasma temperature.
Also shown in Tables 4 and 5, the velocity stellar wind derived from the line shift shows better self-consistency, that is,
![]() $f$
,
$f$
,
![]() $i$
and
$i$
and
![]() $r$
lines of each set of He-like triplets show consistent velocity results in
$r$
lines of each set of He-like triplets show consistent velocity results in
![]() $1-\unicode[STIX]{x1D70E}$
error region, compared with the calculations in W06. The main reason is the inclusion of the satellites during our fitting process. Using Si xiii as an example (see Figures 4(a) and 4(b)), satellite lines gather around 1.845 keV and locate in the blue side of
$1-\unicode[STIX]{x1D70E}$
error region, compared with the calculations in W06. The main reason is the inclusion of the satellites during our fitting process. Using Si xiii as an example (see Figures 4(a) and 4(b)), satellite lines gather around 1.845 keV and locate in the blue side of
![]() $f$
line. In this situation, the derived velocity would be reduced in the Eclipse phase and increased in
$f$
line. In this situation, the derived velocity would be reduced in the Eclipse phase and increased in
![]() $\unicode[STIX]{x1D719}=0.5$
if satellite lines were not separated from main He-like triplets during the fitting.
$\unicode[STIX]{x1D719}=0.5$
if satellite lines were not separated from main He-like triplets during the fitting.

Figure 6. Posterior PDFs of parameters and their correlations. Using the parameters of continuum for
![]() $\unicode[STIX]{x1D719}=0.5$
as an example. Red lines represent values used in best-fit
$\unicode[STIX]{x1D719}=0.5$
as an example. Red lines represent values used in best-fit
![]() $F_{\text{cont}}$
for
$F_{\text{cont}}$
for
![]() $\unicode[STIX]{x1D719}=0.5$
, and dashed lines correspond to 1-
$\unicode[STIX]{x1D719}=0.5$
, and dashed lines correspond to 1-
![]() $\unicode[STIX]{x1D70E}$
error. The plot is made by a Python module corner
[Reference Foreman-Mackey30].
$\unicode[STIX]{x1D70E}$
error. The plot is made by a Python module corner
[Reference Foreman-Mackey30].
Table 7. The comparison with previous studies for
![]() $G$
-ratios.
$G$
-ratios.

4.2 Backgrounds and posterior PDFs
Next we estimate the background effects. As we stated before, we did not subtract the background because their source is not well understood. Any inaccuracy in their subtraction would seriously affect the line intensity determination. We treat it as a correction for the observation error.
Its effect, thereby, results in relatively larger uncertainties of parameters compared with previous literature results. From the posterior PDFs (Figure 6, which is made by Python module corner
[Reference Foreman-Mackey30]) of
![]() $\ln b$
, using the case of
$\ln b$
, using the case of
![]() $\unicode[STIX]{x1D719}=0.5$
as an example, it is possible for us to estimate the average contributions of the backgrounds. The value is
$\unicode[STIX]{x1D719}=0.5$
as an example, it is possible for us to estimate the average contributions of the backgrounds. The value is
![]() $7.41_{-0.46}^{+0.50}\%$
for the
$7.41_{-0.46}^{+0.50}\%$
for the
![]() $\unicode[STIX]{x1D719}=0.5$
and
$\unicode[STIX]{x1D719}=0.5$
and
![]() $8.13_{-2.64}^{+0.41}\%$
for the
$8.13_{-2.64}^{+0.41}\%$
for the
![]() $\unicode[STIX]{x1D719}=0.25$
, which are larger than the estimates of 3% in W06. The value for the Eclipse phase is
$\unicode[STIX]{x1D719}=0.25$
, which are larger than the estimates of 3% in W06. The value for the Eclipse phase is
![]() $4.67_{-3.04}^{+1.03}\%$
. It is in agreement with the maximum of 5% in W06, in which they derive this value from the adjacent region to the dispersed event region of the observed spectrum.
$4.67_{-3.04}^{+1.03}\%$
. It is in agreement with the maximum of 5% in W06, in which they derive this value from the adjacent region to the dispersed event region of the observed spectrum.
From Figure 6, one can see that all the parameters except the background show degeneracy. It would lead to the exclusion of some reasonable values for the free parameters that are degenerate with the fixed parameters. For instance, in the case of Vela X-1, as Figure 6 shows, the parameters
![]() $\unicode[STIX]{x1D6E4}^{\text{scat}}$
and
$\unicode[STIX]{x1D6E4}^{\text{scat}}$
and
![]() $N_{\text{H}}^{\text{scat}}$
are degenerate. Setting
$N_{\text{H}}^{\text{scat}}$
are degenerate. Setting
![]() $\unicode[STIX]{x1D6E4}^{\text{scat}}$
to be same for all the phases results in the same values of
$\unicode[STIX]{x1D6E4}^{\text{scat}}$
to be same for all the phases results in the same values of
![]() $N_{\text{H}}^{\text{scat}}$
for all the phases, which consequently implies a spherical stellar wind. In the present work, we set all parameters free and find the most likely values in parameter space. The fitted
$N_{\text{H}}^{\text{scat}}$
for all the phases, which consequently implies a spherical stellar wind. In the present work, we set all parameters free and find the most likely values in parameter space. The fitted
![]() $N_{\text{H}}^{\text{scat}}$
varies from phase to phase due to setting
$N_{\text{H}}^{\text{scat}}$
varies from phase to phase due to setting
![]() $\unicode[STIX]{x1D6E4}^{\text{scat}}$
as free. For the photoionized plasma in other astronomical objects, non-fixing any parameters would provide a general approach to deal with their X-ray observed spectra.
$\unicode[STIX]{x1D6E4}^{\text{scat}}$
as free. For the photoionized plasma in other astronomical objects, non-fixing any parameters would provide a general approach to deal with their X-ray observed spectra.
5 Summary
In this paper, we introduce the Bayesian approach, which is applied to the archive spectra of Vela X-1 with three different phases: Eclipse,
![]() $\unicode[STIX]{x1D719}=0.25$
and
$\unicode[STIX]{x1D719}=0.25$
and
![]() $\unicode[STIX]{x1D719}=0.5$
. We adopt a parameterized two-component power-law model of
$\unicode[STIX]{x1D719}=0.5$
. We adopt a parameterized two-component power-law model of
![]() $F_{\text{cont}}$
and a multi-Gaussian model of
$F_{\text{cont}}$
and a multi-Gaussian model of
![]() $F_{\text{line}}$
to predict the continua and He-like triplets, respectively, for all three phases, by setting all parameters as free. Then we fit the observed continua and He-like triplets of Mg xi and Si xiii, by using an MCMC algorithm, emcee to recover the posterior PDFs of all parameters of
$F_{\text{line}}$
to predict the continua and He-like triplets, respectively, for all three phases, by setting all parameters as free. Then we fit the observed continua and He-like triplets of Mg xi and Si xiii, by using an MCMC algorithm, emcee to recover the posterior PDFs of all parameters of
![]() $F_{\text{cont}}$
,
$F_{\text{cont}}$
,
![]() $F_{\text{line}}$
and the background. Then we derive best-fit parameters and associated uncertainties for which propagation from the observational errors, uncertainty in the background and the errors from fitting process are all considered. In our results, the column density of scatter component
$F_{\text{line}}$
and the background. Then we derive best-fit parameters and associated uncertainties for which propagation from the observational errors, uncertainty in the background and the errors from fitting process are all considered. In our results, the column density of scatter component
![]() $N_{\text{H}}^{\text{scat}}$
varies from phase to phase, which implies a non-spherical structure of stellar wind. Moreover, our measured wind velocities show very good self-consistency, which provides a reliable approach for the diagnostics of photoionized plasma in the future.
$N_{\text{H}}^{\text{scat}}$
varies from phase to phase, which implies a non-spherical structure of stellar wind. Moreover, our measured wind velocities show very good self-consistency, which provides a reliable approach for the diagnostics of photoionized plasma in the future.
Acknowledgements
This work is supported by the Science Challenge Project (No. TZ2016005) and the National Natural Science Foundation of China (NSFC) (Nos. 11573040, 11773033, 11390371/2, and 11233004). X. X. Xue acknowledges the support from the Recruitment Program of Global Youth Experts of China.