1. Introduction
After the invention of laser, scientists began to study laser fusion for simulation of hydrogen bombs and as a long-term option to generate electric energy. Preliminary calculations suggested that a laser pulse of at least 100 kJ of energy and at most 10 ns duration would be required. However, recent experiments with NIF in United States implied that even 2 MJ might be still not enough by using the method of indirect drive[Reference Lindl1].
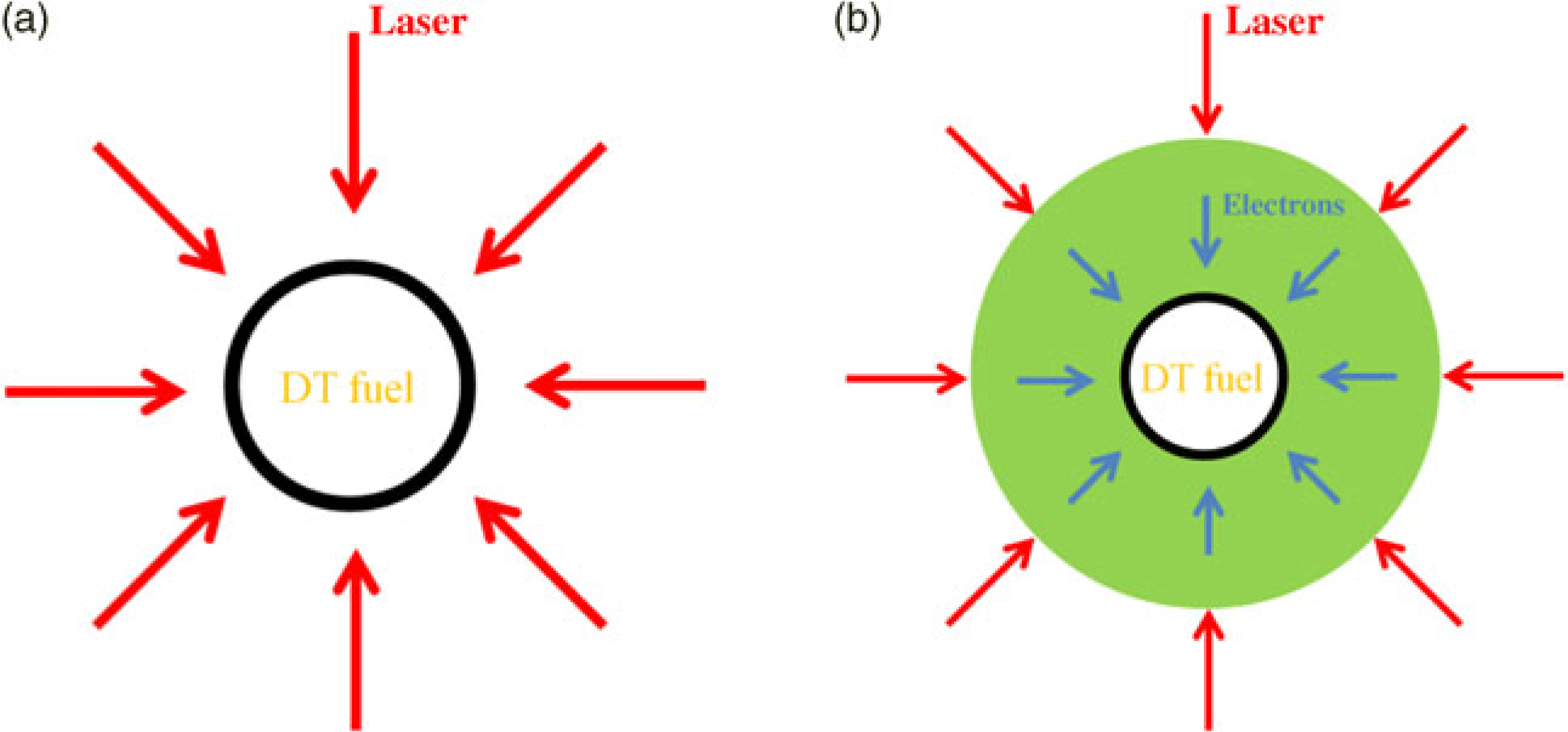
One of the main problems is the hydrodynamic instabilities during the shell implosion. For inertial confinement fusion, in order to burn a substantial part of the fuel in a very short time, extremely high plasma densities have to be realized to achieve high reaction rates, since the confinement time is very short, typically 0.1 ns. To achieve such a high plasma density, one has to compress the fuel with very high pressure and design special targets as illustrated in Figure 1a. The targets consist of a hollow shell capsule with an outer ablator layer and a fuel layer of cryogenic DT.
Laser pulses, x-rays, or particle beams were proposed to heat the ablator to generate the required high pressure. The ignition threshold factor (ITF) is[Reference Lindl1]
 $$\begin {eqnarray*} {\rm ITF} &=& I_0 \left (\frac {M_{{\rm DT}}}{M_0}\right ) \left (\frac {v}{v_0}\right )^8 \left (\frac {\alpha }{\alpha _0} \right )^{-4}\left (1-1.2\frac {\Delta R^{{\rm K}\text {-}{\rm wtd}}_{{\rm hotstspot}}} {R_{{\rm hotstspot}}}\right )^4 \\ && \times \left (\frac {M_{{\rm clean}}}{M_{{\rm DT}}}\right )^{0.5} \left (1-P_{{\rm HS}}\right ), \end {eqnarray*}$$
$$\begin {eqnarray*} {\rm ITF} &=& I_0 \left (\frac {M_{{\rm DT}}}{M_0}\right ) \left (\frac {v}{v_0}\right )^8 \left (\frac {\alpha }{\alpha _0} \right )^{-4}\left (1-1.2\frac {\Delta R^{{\rm K}\text {-}{\rm wtd}}_{{\rm hotstspot}}} {R_{{\rm hotstspot}}}\right )^4 \\ && \times \left (\frac {M_{{\rm clean}}}{M_{{\rm DT}}}\right )^{0.5} \left (1-P_{{\rm HS}}\right ), \end {eqnarray*}$$ where ![]() $I_0$ is the overall multiplier,
$I_0$ is the overall multiplier, ![]() $M_{DT}$ is the fuel mass,
$M_{DT}$ is the fuel mass, ![]() $v$ is the implosion velocity,
$v$ is the implosion velocity, ![]() $\alpha $ is the adiabat,
$\alpha $ is the adiabat, ![]() $\Delta R^{{\rm K}\text {-}{\rm wtd}}_{{\rm hotstspot}}$ is the hot spot perturbation,
$\Delta R^{{\rm K}\text {-}{\rm wtd}}_{{\rm hotstspot}}$ is the hot spot perturbation, ![]() $M_{\rm clean}$ is the clean fuel mass and
$M_{\rm clean}$ is the clean fuel mass and ![]() $P_{{\rm HS}}$ is the hot spot purity factor. From this, we know that the fuel implosion velocity
$P_{{\rm HS}}$ is the hot spot purity factor. From this, we know that the fuel implosion velocity ![]() $v$ is a critical parameter if the shell is not destroyed during the compression and the fuel mixture is not serious. The strong dependence of the minimum energy on the achievable implosion velocity means that only a factor of about 4 increase in the implosion velocity is required to go from a minimum energy of about 1 MJ to a minimum energy of 1 kJ[Reference Lindl1]. However hydrodynamic instabilities prevent high implosion velocity while low entropy is kept.
$v$ is a critical parameter if the shell is not destroyed during the compression and the fuel mixture is not serious. The strong dependence of the minimum energy on the achievable implosion velocity means that only a factor of about 4 increase in the implosion velocity is required to go from a minimum energy of about 1 MJ to a minimum energy of 1 kJ[Reference Lindl1]. However hydrodynamic instabilities prevent high implosion velocity while low entropy is kept.
The growth rate of the instabilities ![]() $\sigma $ is represented by[Reference Lindl1, Reference Atzeni and Meyer-ter-Vehn2]
$\sigma $ is represented by[Reference Lindl1, Reference Atzeni and Meyer-ter-Vehn2]
where ![]() $L$ is a characteristic density scale length at the ablation front,
$L$ is a characteristic density scale length at the ablation front, ![]() $\beta $ is the coefficient in the range 1–3,
$\beta $ is the coefficient in the range 1–3, ![]() $k$ is the wave number of the perturbation,
$k$ is the wave number of the perturbation, ![]() $a$ is the acceleration, and
$a$ is the acceleration, and ![]() $u_a$ is the ablation velocity that is given by the mass ablation rate per unit surface area
$u_a$ is the ablation velocity that is given by the mass ablation rate per unit surface area ![]() $m$ divided by the ablation density,
$m$ divided by the ablation density,
It is clear that large ![]() $u_a$ means small
$u_a$ means small ![]() $\sigma $. In the indirect-drive approach[Reference Lindl1], once laser energy is converted into x-ray radiation in a hohlraum, the mass ablation rate is generally much larger than that in the direct-drive approach. So, the requirement on laser-beam uniformity is relaxed and sensitivity to hydrodynamic instabilities is reduced. Therefore, the ICF programs around the world have concentrated most of their effort on the x-ray or indirect-drive approach.
$\sigma $. In the indirect-drive approach[Reference Lindl1], once laser energy is converted into x-ray radiation in a hohlraum, the mass ablation rate is generally much larger than that in the direct-drive approach. So, the requirement on laser-beam uniformity is relaxed and sensitivity to hydrodynamic instabilities is reduced. Therefore, the ICF programs around the world have concentrated most of their effort on the x-ray or indirect-drive approach.

Figure 1. (Color online) Sketch map of fusion targets designed for (a) normal ICF Programs and (b) in our scheme.
But for inertial fusion energy (IFE), after the demonstration of ignition and energy gain, the overall efficiency from input electricity to output electricity must be considered[Reference Bodner, Schmitt and Sethian3]. At present, the efficiency from electricity to driving glass laser is only about 1%, although the efficiency may be increased to more than 10% in the future. Indirect-drive targets can further reduce the coupling efficiency from laser energy to the DT fuel.
Based on the above discussions, here we propose a new concept of inertial fusion by using powerful long wavelength electromagnetic pulses (EMPs), such as ![]() ${\rm CO}_{2}$ laser pulses or high power microwave pulses, which can be efficiently generated. Special targets are designed to suppress the hydrodynamic instabilities.
${\rm CO}_{2}$ laser pulses or high power microwave pulses, which can be efficiently generated. Special targets are designed to suppress the hydrodynamic instabilities.
2. Main concept
The main concept is illustrated in Figure 1b. A normal fusion target is surrounded by a gas layer of specially designed density and size. Many long wavelength EMPs illuminate it symmetrically from all directions.
The long wavelength EMPs could be ![]() ${\rm CO}_{2}$ laser pulses or high power microwave pulses. The main reason to choose such pulses is that they can be very efficiently generated. For electricity power, it is very important, because the requirement for the energy gain from driver to fusion energy can be greatly reduced.
${\rm CO}_{2}$ laser pulses or high power microwave pulses. The main reason to choose such pulses is that they can be very efficiently generated. For electricity power, it is very important, because the requirement for the energy gain from driver to fusion energy can be greatly reduced.
The problem is that the hydrodynamic instabilities can be easily developed, if we simply replace the ![]() $1\ \mathrm {\mu} {\rm m}$ laser pulses (or their third harmonics) with long wavelength EMPs. Normal indirect drive with long wavelength EMPs is also not a good choice, since larger holes are needed to permit the pulses to penetrate into the hohlraum and the low density plasma in the hohlraum would prevent the transportation of the pulses of long wavelength (the critical density
$1\ \mathrm {\mu} {\rm m}$ laser pulses (or their third harmonics) with long wavelength EMPs. Normal indirect drive with long wavelength EMPs is also not a good choice, since larger holes are needed to permit the pulses to penetrate into the hohlraum and the low density plasma in the hohlraum would prevent the transportation of the pulses of long wavelength (the critical density ![]() $n_c$ becomes lower). Our solution is to use two-step driving, something like indirect drive but without a hohlraum. First, EMPs accelerate (not heat) electrons to about 2 MeV or less inside the low density gas layer just outside the normal fusion target. Second, the energetic electrons heat the ablator to produce high pressure to compress the fuel to high density and form a hot spot in the center of the fusion capsule.
$n_c$ becomes lower). Our solution is to use two-step driving, something like indirect drive but without a hohlraum. First, EMPs accelerate (not heat) electrons to about 2 MeV or less inside the low density gas layer just outside the normal fusion target. Second, the energetic electrons heat the ablator to produce high pressure to compress the fuel to high density and form a hot spot in the center of the fusion capsule.
In order to confirm the validity of the method, several main problems have to be solved. First, we should make sure electrons can truly be efficiently accelerated forward to about 1 MeV. The electron energy should not be too large, or too small. Second, since the current of the electron bunches is much larger than the Alfven limit in vacuum, we should make sure that such energetic beams of intense current can transport in plasmas. As a primarily concept design, we will discuss the two problems in Sections 3–5, although there are certainly many other problems.
3. Electron acceleration
Both x-rays and particle beams can penetrate into plasma of high density to produce large ablation velocity ![]() $u_a$. For indirect-drive fusion, x-rays of black body are used. For simpler direct-drive fusion, x-rays can also be generated if a high Z material is added at the outside of the capsule shell[Reference Fujioka4]. We may discuss this option in other publications. One defect of this method is that the x-rays go in all directions so that only half of the x-rays go inward, leading to low efficiency. Here we consider converting the energy of EMPs to inward moving energetic electron beams.
$u_a$. For indirect-drive fusion, x-rays of black body are used. For simpler direct-drive fusion, x-rays can also be generated if a high Z material is added at the outside of the capsule shell[Reference Fujioka4]. We may discuss this option in other publications. One defect of this method is that the x-rays go in all directions so that only half of the x-rays go inward, leading to low efficiency. Here we consider converting the energy of EMPs to inward moving energetic electron beams.

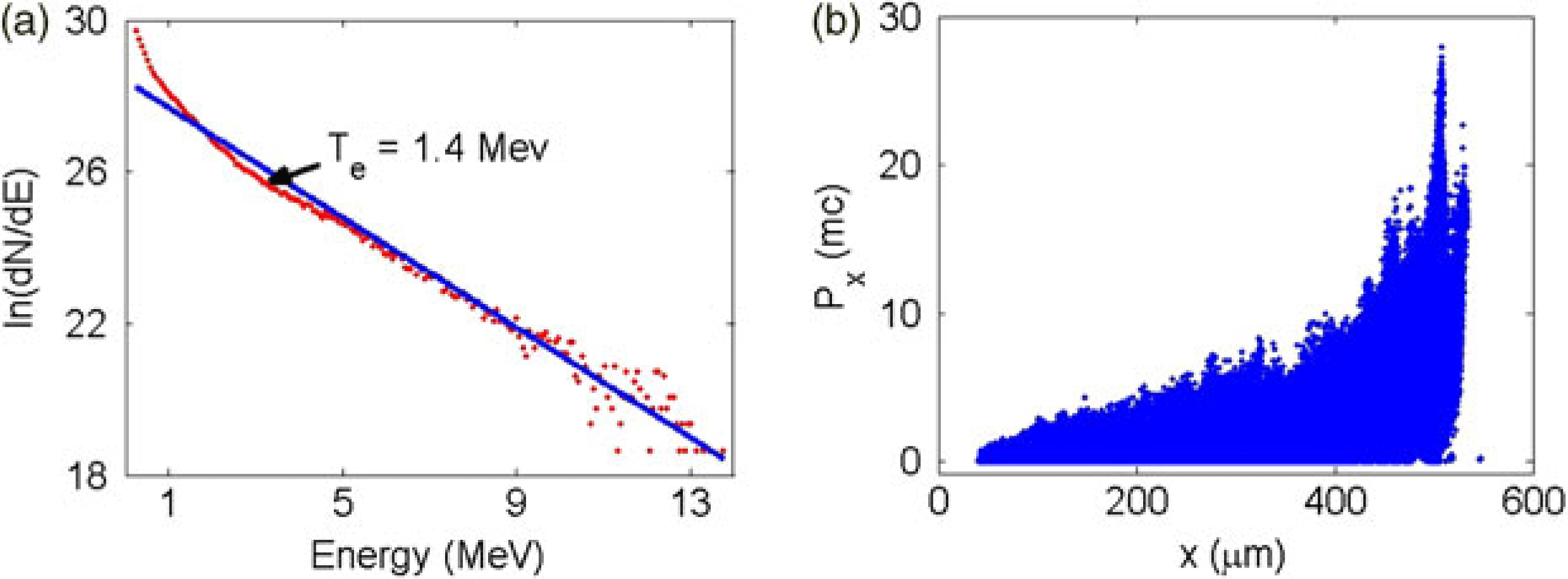
Figure 2. (Color online) Energy spectra (a) and longitudinal phase space distribution (b) of the energetic electrons generated by a ![]() ${\rm CO}_{2}$ laser pulse (only electrons with energy larger than 500 keV are presented). The blue fitting line in (a) gives an electron temperature of 1.4 MeV.
${\rm CO}_{2}$ laser pulse (only electrons with energy larger than 500 keV are presented). The blue fitting line in (a) gives an electron temperature of 1.4 MeV.
From the research of laser acceleration, we know that electrons can not only be heated but also be efficiently accelerated with the plasma wake and other mechanism driven by 800 nm laser pulses[Reference Esarey, Schroeder and Leemans5]. The laser wavelength should certainly not be restricted to 800 nm. Electrons should also be efficiently accelerated by long wavelength EMPs such as ![]() ${\rm CO}_{2}$ laser pulses or high power microwave pulses, if the normalized amplitude of the laser field remains about
${\rm CO}_{2}$ laser pulses or high power microwave pulses, if the normalized amplitude of the laser field remains about ![]() $a = 1$ (the intensity is much lower than in the case of 800 nm laser pulses) and the plasma density decreases accordingly.
$a = 1$ (the intensity is much lower than in the case of 800 nm laser pulses) and the plasma density decreases accordingly.
For the research of laser acceleration, the emphasis is usually put on the high energy and high quality of the energetic electron beams. Here for inertial fusion, the electron energy cannot substantially exceed one MeV, as we will discuss in Section 4. Therefore, a high plasma density near to the critical density is used so that the acceleration length is limited. At the same time, in this way the number of energetic electrons increases greatly[Reference Shen, Wu, Dong, Zhu, Gu, Ji, Jiao, Teng, Hong, Zhao, Cao, Wang and Yu6].
Here as an example, particle in cell (PIC) simulation is carried out to show the generation of energetic electrons driven by a ![]() ${\rm CO}_{2}$ laser pulse of wavelength
${\rm CO}_{2}$ laser pulse of wavelength ![]() $10.6\ \mathrm {\mu} {\rm m}$, duration 200 fs, focal size
$10.6\ \mathrm {\mu} {\rm m}$, duration 200 fs, focal size ![]() $120\ \mathrm {\mu} {\rm m}$, intensity
$120\ \mathrm {\mu} {\rm m}$, intensity ![]() $7.6 \times 10^{16}\ {\rm W}/{\rm cm}^{2}$ and normalized amplitude
$7.6 \times 10^{16}\ {\rm W}/{\rm cm}^{2}$ and normalized amplitude ![]() $a = 2.5$. The total laser energy is about 29 J. The plasma density is
$a = 2.5$. The total laser energy is about 29 J. The plasma density is ![]() $2 \times 10^{18}\ {\rm cm}^{-3}$ which is
$2 \times 10^{18}\ {\rm cm}^{-3}$ which is ![]() $0.2\, n_c$.
$0.2\, n_c$.
After acceleration in a 0.5 mm long plasma, a bulk of energetic electrons is produced. Figure 2a indicates the energy spectrum exhibits typical property of Maxwell distribution with a temperature of 1.4 MeV. The longitudinal phase space distribution of the electrons with energy larger than 500 keV is shown in Figure 2b. The total charge of the hot electrons is ![]() $6\ \mathrm {\mu} {\rm C}$ and the efficiency from laser to energetic electron in this case is 31.9%, which is sufficient for potential fusion applications in future. It should be mentioned that for the laser and plasma parameters used here acceleration mechanism is complicated. Stochastic acceleration, self modulated wake acceleration and direct laser acceleration may all play important roles[Reference Gahn and Sheng7] while other instabilities such as stimulated Raman scattering is not found to be important.
$6\ \mathrm {\mu} {\rm C}$ and the efficiency from laser to energetic electron in this case is 31.9%, which is sufficient for potential fusion applications in future. It should be mentioned that for the laser and plasma parameters used here acceleration mechanism is complicated. Stochastic acceleration, self modulated wake acceleration and direct laser acceleration may all play important roles[Reference Gahn and Sheng7] while other instabilities such as stimulated Raman scattering is not found to be important.
It should be noted that the method works as well for ns laser pulse required for actual fusion experiment which is much longer than in our simulation, which is limited by computer resource.
The initial part of the laser pulse should be of lower intensity than used in the above example so that the electron energy should be lower than 1 MeV. In this way the energetic electron can be stopped within a short distance, since in the initial phase of compression, the ![]() $\rho r$ of the shell is still very small.
$\rho r$ of the shell is still very small.
If high power microwave pulses are used, lower gas density and larger gas size should be chosen, since the wavelength becomes even larger.

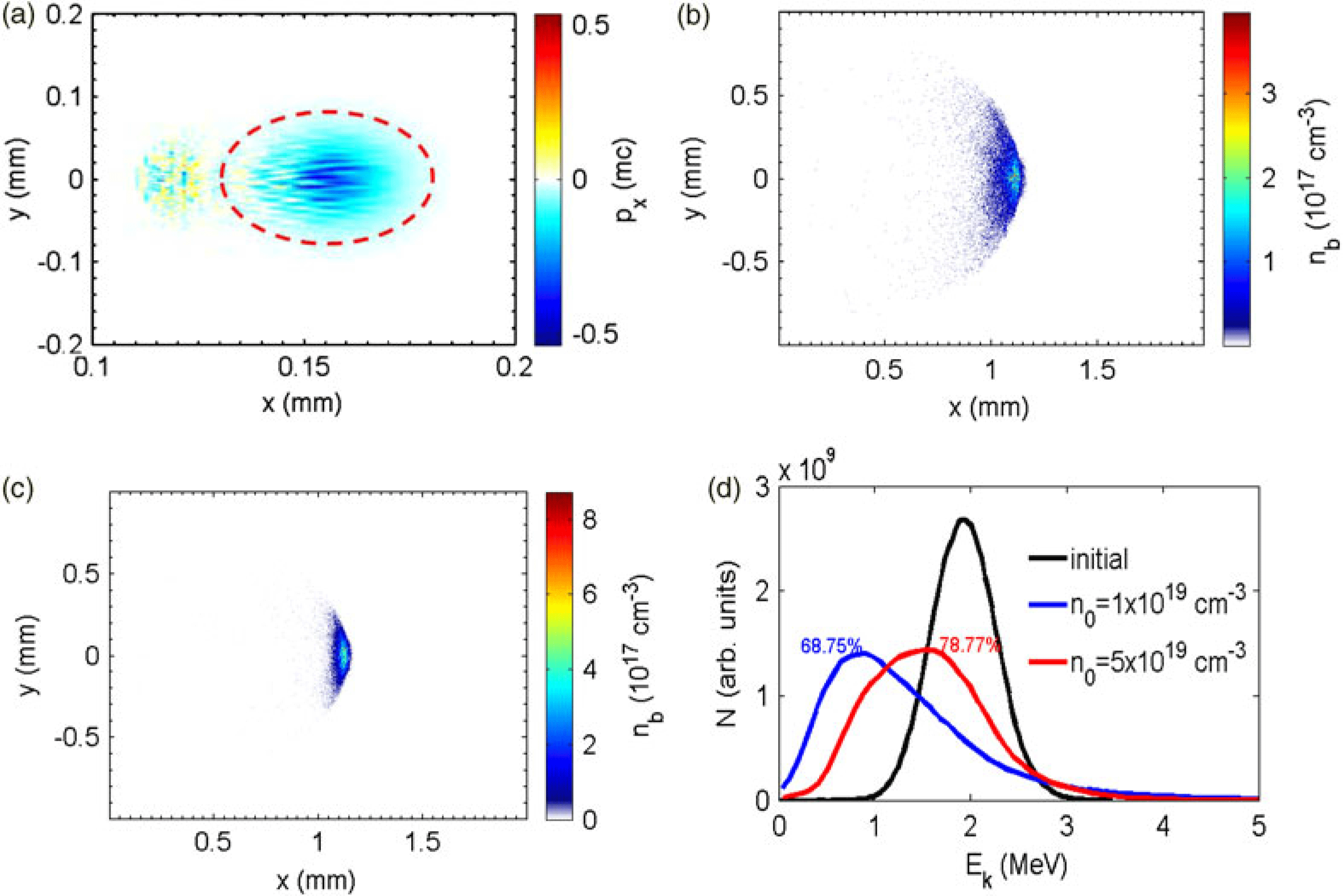
Figure 3. (Color online) Longitudinal momentum of background plasma electrons at the beam position (marked by the red dashed curve) (a). Density distribution of electron beam after propagating 1 mm in the plasma of density ![]() $1 \times 10^{19}\ {\rm cm}^{-3}$ (b) and
$1 \times 10^{19}\ {\rm cm}^{-3}$ (b) and ![]() $5 \times 10^{19}\ {\rm cm}^{-3}$ (c). The energy spectrum of electron beam at propagating distance
$5 \times 10^{19}\ {\rm cm}^{-3}$ (c). The energy spectrum of electron beam at propagating distance ![]() $x =0$ mm (black curve),
$x =0$ mm (black curve), ![]() $x = 1$ mm in the
$x = 1$ mm in the ![]() $1 \times 10^{19}\ {\rm cm}^{-3}$ plasma (blue curve), and
$1 \times 10^{19}\ {\rm cm}^{-3}$ plasma (blue curve), and ![]() $x = 1$ mm in the
$x = 1$ mm in the ![]() $5 \times 10^{19}\ {\rm cm}^{-3}$ plasma (red curve) (d).
$5 \times 10^{19}\ {\rm cm}^{-3}$ plasma (red curve) (d).
4. Electron beam driven fusion
Electron beam driven fusion has been studied since 1970s, because electrons can be efficiently accelerated with conventional accelerators[Reference Yonas8, Reference Clauser9]. It was estimated that an electron beam of energy 1 MJ, duration 10 ns and power 100 TW is required for inertial fusion[Reference Yonas8, Reference Clauser9]. Similar to x-rays, energetic electrons can easily penetrate into the fuel. It is good to increase the ablation rate to overcome the hydrodynamic instabilities. The electron energy cannot be too large, although the fuel shell in our approach should be thicker than the one in conventional target design. If only classical singleparticle beam stopping is considered, electron energy cannot substantially exceed one MeV. The mechanisms responsible for energy loss by the beam electrons in the target plasma are generally binary coulomb collisions with the target electrons and ions, and excitation of plasma oscillations. In addition, some evidence of enhanced deposition due to beam-plasma instabilities has been reported[Reference Nakai10], but the practical effect needs more investigation. The burn material may consist of two layers. The outer layer consists of middle Z ablators to help effectively stop the electrons while low Z ablators should be used for the inner layer to reduce the generation of bremsstrahlung which could preheat the cold fuel.
For electron driven fusion, similar to the well known fast ignition[Reference Tabak11, Reference Deutsch, Furukawa, Mima, Murakami and Nishihara12], one of the main difficulties is the propagation of the high current electron beams. For beam energy of about 1 MeV and beam power of ![]() $1^{14}$ W, the beam current would be
$1^{14}$ W, the beam current would be ![]() $10^{8}$ A. We know that the Alfven current in vacuum is
$10^{8}$ A. We know that the Alfven current in vacuum is ![]() $I_A = 17\beta \gamma $ kA. For 1 MeV electrons
$I_A = 17\beta \gamma $ kA. For 1 MeV electrons ![]() $\beta \sim 1$ and
$\beta \sim 1$ and ![]() $\gamma \sim 3$, and one finds that
$\gamma \sim 3$, and one finds that ![]() $I_A\sim 50$ kA. This is far below the required current of
$I_A\sim 50$ kA. This is far below the required current of ![]() $10^{8}$ A. We know that NIF has 192 laser beams. Similarly many electron beams bombarding the target from several sides can be used to significantly decrease the required current for each beam. But even for one hundred bunches, the current of each beam would be
$10^{8}$ A. We know that NIF has 192 laser beams. Similarly many electron beams bombarding the target from several sides can be used to significantly decrease the required current for each beam. But even for one hundred bunches, the current of each beam would be ![]() ${{\sim }}10^{6}$ A and thus well above the Alfven limit. Anyway it should be noted that this current is much lower than the current required for fast ignition.
${{\sim }}10^{6}$ A and thus well above the Alfven limit. Anyway it should be noted that this current is much lower than the current required for fast ignition.
Another problem with conventional accelerators is that the facility size is too large. There is always a long distance between the accelerators and the tiny fusion capsule. Since the current of each beam is still much larger than the Alfven limit in vacuum, the electron beam was hardly focused to the pellet due to the space-charge effect and that the current cannot propagate in vacuum. Fortunately, preformed current-carrying plasma discharge channels can be used to transport these beams. The efficiency of beam transportation and overlapping can be measured with the current density gain, which is the ratio of beam current density at the target surface to that of the individual beams. The problem of transportation is not completely solved so that light ion beams and heavy ion beams were proposed to replace the electron beams and laser pulses were chosen to be the most favorable driver for inertial fusion.
Now, in our case, many EMPs of long wavelength can be easily focused to the underdense plasma surrounding the fusion capsule, since photons are bosons. Inside the underdense plasma, electrons are accelerated inward directly to the capsule. There is no additional vacuum gap for the energetic electrons to go through.
In order to check how the energetic electron beams propagate in plasma, PIC simulations are performed. We suppose 100 electron beams are used to generate total power of 100 TW which is required for inertial fusion. If pulse duration is 5 ns and the efficiency from laser to electron is about 30% as estimated above, the total required laser energy is about 1.6 MJ, similar to the one provided by NIF. Therefore, the power of each beam is 1 TW. The intensity is ![]() $2\times 10^{16 }\ {\rm W}/{\rm cm}^{2}$ and the mean electron energy is 2 MeV. Therefore the current is
$2\times 10^{16 }\ {\rm W}/{\rm cm}^{2}$ and the mean electron energy is 2 MeV. Therefore the current is ![]() $5 \times 10^{4}$ A, which is about 10
$5 \times 10^{4}$ A, which is about 10 ![]() $I_A$. In the coronal area of fuel, the plasma density is usually larger than where the electrons are accelerated so that an energetic electron beam can more easily propagate. We consider two typical cases of background plasma density where the electron beam propagates
$I_A$. In the coronal area of fuel, the plasma density is usually larger than where the electrons are accelerated so that an energetic electron beam can more easily propagate. We consider two typical cases of background plasma density where the electron beam propagates ![]() $n_0=1 \times 10^{19}\ {\rm cm}^{-3}$ and
$n_0=1 \times 10^{19}\ {\rm cm}^{-3}$ and ![]() $5 \times 10^{19 }\ {\rm cm}^{-3}$ for comparison. Due to the limitation of PIC codes, the beam length is
$5 \times 10^{19 }\ {\rm cm}^{-3}$ for comparison. Due to the limitation of PIC codes, the beam length is ![]() $50\ \mathrm {\mu} {\rm m}$. Because collisions are not included in the PIC code, here we only consider the collective effects.
$50\ \mathrm {\mu} {\rm m}$. Because collisions are not included in the PIC code, here we only consider the collective effects.
As shown in Figure 3a, when a dense electron beam with current larger than Alfven limit propagates in plasma, the beam charge induces collective shifting of background electrons, which forms a backward current within the incident electron beam. This induced current neutralizes the incident beam current and therefore permits its propagation in plasma. At the same time, comparing Figure 3a with Figure 3b–c, one can see that the electron beam is dispersed due to the repulsive space-charge force of all the electrons in the beam. This beam dispersion can be moderated by increasing the plasma density for the remaining plasma ions neutralize part of the space-charge force within the beam.
Apparently, the efficiency of energy transport is related to the density of background plasma as shown in Figure 3d. Usually in plasmas of higher density more intense induced backward current is formed to ensure better transportation of the energetic electrons. As a result, about 68.7% of the total electron energy remains over after 1-mm-propagation in the plasma with density of ![]() $1\times 10^{19}\ {\rm cm}^{-3}$, while the proportion is 78.8% in the
$1\times 10^{19}\ {\rm cm}^{-3}$, while the proportion is 78.8% in the ![]() $5 \times 10^{19}\ {\rm cm}^{-3}$ plasma. So comparing to electron driven fusion scheme based on conventional accelerators, in our case, the electrons can propagate more efficiently through the dense plasmas in the coronal area of fuel to heat the ablator and generate the required high pressure. The beam energy is converted to implosion kinetic energy with efficiency typically of order 20%[Reference Clauser9].
$5 \times 10^{19}\ {\rm cm}^{-3}$ plasma. So comparing to electron driven fusion scheme based on conventional accelerators, in our case, the electrons can propagate more efficiently through the dense plasmas in the coronal area of fuel to heat the ablator and generate the required high pressure. The beam energy is converted to implosion kinetic energy with efficiency typically of order 20%[Reference Clauser9].
5. Discussion
There are certainly many other challenges to be overcome to realize this new fusion concept. One problem is that the stopping range of the electron is usually much larger than soft x-ray for indirect-drive fusion. For an electron of 2 MeV, the collisional stopping power is about ![]() $1.5\ \text {MeV cm}^{2}/{\rm g}$. Therefore, a special fusion capsule of thick burn layer should be used. The electron energy of the front part of the electron beams can be designed to be smaller than the electron energy of the back part, since after compression, the
$1.5\ \text {MeV cm}^{2}/{\rm g}$. Therefore, a special fusion capsule of thick burn layer should be used. The electron energy of the front part of the electron beams can be designed to be smaller than the electron energy of the back part, since after compression, the ![]() $\rho r$ of the fusion target would become much larger.
$\rho r$ of the fusion target would become much larger.
For laser fusion, the laser wavelength is fixed during one shot. Only the laser power can change with time. For laser electron beam fusion, the electron energy is determined by the intensity of each laser pulse and the total beam energy is determined by the total laser power. Therefore, the time evolution of both the penetration depth and the burn pressure can be controlled.
Another problem is the filaments formed during the propagation which would easily excite the hydrodynamic instabilities. It was shown that the electron beam filaments are formed when ![]() $n_p/n_b = 10$[Reference Honda, Meyer-ter-Vehn and Pukhov13]. Fortunately the density of the energetic electron beams is about
$n_p/n_b = 10$[Reference Honda, Meyer-ter-Vehn and Pukhov13]. Fortunately the density of the energetic electron beams is about ![]() $10^{18}/{\rm cm}^{3}$ in our case and the deposit plasma density for the beams is larger than
$10^{18}/{\rm cm}^{3}$ in our case and the deposit plasma density for the beams is larger than ![]() $10^{22}/{\rm cm}^{3}$. Therefore, the ratio
$10^{22}/{\rm cm}^{3}$. Therefore, the ratio ![]() $n_b/n_p < 10^{-4}$ at the deposition layer, where collision will dominate compared to self-collimation due to self generated magnetic field[Reference Deutsch, Furukawa, Mima, Murakami and Nishihara12]. Based on the above discussion, we expect plasma heating at the deposition layer by the electron beams might be transversely smooth.
$n_b/n_p < 10^{-4}$ at the deposition layer, where collision will dominate compared to self-collimation due to self generated magnetic field[Reference Deutsch, Furukawa, Mima, Murakami and Nishihara12]. Based on the above discussion, we expect plasma heating at the deposition layer by the electron beams might be transversely smooth.
Ions can also be accelerated by a light pressure driven electrostatic field in the plasma of density slightly larger than critical density. The energetic electron beams in our proposal may be replaced by energetic light ions.
6. Conclusions
In conclusion, a new two-step scheme for inertial confinement fusion is proposed in this paper. Powerful long wavelength EMPs, which can be efficiently produced, accelerate large amounts of hot electrons in plasmas close to the critical density just outside the normal fusion target. Then energetic electrons heat the ablator to produce high pressure to compress the fuel to high density and form a hot spot in the center of the fusion capsule. The energy of the accelerated electrons follows Maxwell distribution. The temperature can be controlled to be around 1–2 MeV to ensure the electrons can easily penetrate into the fuel shell but without penetrating through it. PIC simulations indicate these hot electrons can be produced by ![]() ${\rm CO}_{2}$ lasers with a relatively high efficiency of 31.9%. On the other hand, the problem that propagation of the high current (above Alfven limit) electron beams in our scheme can be overcome by special design of fuel targets. The high current electron beams can easily propagate in the dense plasmas in the coronal area of fuel because the current is offset by the collective backward shifting of the plasma electrons.
${\rm CO}_{2}$ lasers with a relatively high efficiency of 31.9%. On the other hand, the problem that propagation of the high current (above Alfven limit) electron beams in our scheme can be overcome by special design of fuel targets. The high current electron beams can easily propagate in the dense plasmas in the coronal area of fuel because the current is offset by the collective backward shifting of the plasma electrons.