1 Introduction
High-power laser system plays an important role in many fields, such as inertial confinement fusion (ICF)[Reference Lindl1], industrial processing, optical information processing, clinical application of laser medicine and scientific research[Reference Brown, Ekberg, Feldman, Seely, Richardson, Marshall and Behring2, Reference Remo and Adams3]. On large laser systems[Reference Miller, Moses and Wuest4–Reference Dai, Hu, Zhou, Zhao, Jing, Yang, Zhang, Jiang, Deng, Zhao, Peng and Feng14], there is an ongoing effort to continuously improve various aspects of system performance. Some new problems appear in the process of development of the large solid-state laser system, such as laser-induced optics damage[Reference Liao, Abdulla, Negres, Cross and Carr15–Reference Cai, Lu, Li, Wang, Zhu, Lin and He19], nonlinear effects after long-range transport of the laser[Reference Henesian, Swift and Murray20, Reference Lin, Kessler and Lawrence21] and self-focussing in high-energy Nd:glass laser[Reference Potemkin, Khazanov, Martyanov and Kochetkova22]. In order to study these problems, relatively medium-scale solid-state laser systems are needed to set up for physics experiments, which have the similar fluence to the huge laser system, and operate more flexibly with high spatiotemporal beam quality.
In the past few decades, a series of medium-scale laser systems were established worldwide in many famous labs, such as the Optical Sciences Laser (OSL) in Lawrence Livermore National Lab (LLNL)[Reference Nostrand, Weiland, Luthi, Vickers, Sell, Stanley, Honig, Auerbach, Hackel and Wegner23], the ALISE facility in CEA-CESTA, France[Reference Lamaignere, Dupuy, Bourgeade, Benoist, Roques and Courchinoux24], the HERCULES facility in University of Michigan, United States[Reference Yanovsky, Alinchenko, Rousseau, Chvykov, Mourou and Krushelnick25], the J-KAREN system in Japan Atomic Energy Agency[Reference Kiriyama, Michiaki, Nakai, Shimomura, Sasao, Tanaka, Ochi, Tanoue, Okada, Kondo, Kanazawa, Sagisaka, Daito, Wakai, Sasao, Suzuki, Kotakai, Kondo, Sugiyama, Bulanov, Bolton, Daido, Kawanishi, Collier, Hernandez-Gomez, Hooker, Ertel, Kimura and Tajima26], the Nd:glass laser with the pulse energy of several hundred Joules in the Institute of Applied Physics of the Russian Academy of Sciences[Reference Kuzmin, Khazanov, Kulagin and Shaykin27–Reference Poteomkin, Khazanov, Martyanov, Kirsanov and Shaykin30], the HELEN system at the Atomic Weapons Establishment (AWE), UK[Reference Norman, Andrew, Bett, Clifford, England, Hopps, Parker, Porter and Stevenson31], the two-arm Nd:glass laser system in Raja Ramanna Centre for Advanced Technology (RRCAT), India[Reference Kamath, Tripathi, Kulkarni, Chandra, Joshi, Navathe and Gupta32], the Sinmyung I system in the Korea Advanced Institute of Science and Technology[Reference Kong, Lee, Kim, Han, Kim, Um, Park and Lee33] and the HiLASE system in development at the Institute of Physics ASCR, Czech Republic[Reference Divoky, Smrz, Chyla, Sikocinski, Severova, Novak, Huynh, Nagisetty, Miura and Pilař34–Reference Pilar, Slezak, Sikocinski, Divoky, Sawicka, Bonora, Lucianetti, Mocek and Jelinkova36]. These lasers are used for many emerging applications such as shock hardening of materials, laser-induced damage threshold testing[Reference Nostrand, Weiland, Luthi, Vickers, Sell, Stanley, Honig, Auerbach, Hackel and Wegner23, Reference Lamaignere, Dupuy, Bourgeade, Benoist, Roques and Courchinoux24], pumping of Ti:Sa lasers[Reference Yanovsky, Alinchenko, Rousseau, Chvykov, Mourou and Krushelnick25–Reference Kuzmin, Kulagin, Khazanov and Shaykin28], high-energy physics experiments[Reference Norman, Andrew, Bett, Clifford, England, Hopps, Parker, Porter and Stevenson31, Reference Kamath, Tripathi, Kulkarni, Chandra, Joshi, Navathe and Gupta32] and many more potential applications[Reference Kong, Lee, Kim, Han, Kim, Um, Park and Lee33].
All these medium-scale lasers use master-oscillator, power-amplifier (MOPA) architecture, which generally includes a pulse generation stage (i.e., front-end system), a preamplification stage and a main amplifier stage. In the front-end system, some lasers use ![]() $Q$-switched Nd:YAG or Nd:YLF crystal master oscillators, which generate several tens to hundreds of millijoule level pulses with a duration of tens of nanoseconds (full width at half maximum)[Reference Nostrand, Weiland, Luthi, Vickers, Sell, Stanley, Honig, Auerbach, Hackel and Wegner23, Reference Yanovsky, Alinchenko, Rousseau, Chvykov, Mourou and Krushelnick25–Reference Kuzmin, Kulagin, Khazanov and Shaykin28, Reference Kamath, Tripathi, Kulkarni, Chandra, Joshi, Navathe and Gupta32]. However, such master oscillators make it difficult to control the pulse shape and spectrum. Nowadays the fiber oscillator is used as the front end in some medium-scale solid-state lasers[Reference Norman, Andrew, Bett, Clifford, England, Hopps, Parker, Porter and Stevenson31, Reference Divoky, Smrz, Chyla, Sikocinski, Severova, Novak, Huynh, Nagisetty, Miura and Pilař34–Reference Pilar, Slezak, Sikocinski, Divoky, Sawicka, Bonora, Lucianetti, Mocek and Jelinkova36] because of its robustness, flexibility of performance and pulse shaping capability. Therefore, we will use an all-fiber front end in the laser system.
$Q$-switched Nd:YAG or Nd:YLF crystal master oscillators, which generate several tens to hundreds of millijoule level pulses with a duration of tens of nanoseconds (full width at half maximum)[Reference Nostrand, Weiland, Luthi, Vickers, Sell, Stanley, Honig, Auerbach, Hackel and Wegner23, Reference Yanovsky, Alinchenko, Rousseau, Chvykov, Mourou and Krushelnick25–Reference Kuzmin, Kulagin, Khazanov and Shaykin28, Reference Kamath, Tripathi, Kulkarni, Chandra, Joshi, Navathe and Gupta32]. However, such master oscillators make it difficult to control the pulse shape and spectrum. Nowadays the fiber oscillator is used as the front end in some medium-scale solid-state lasers[Reference Norman, Andrew, Bett, Clifford, England, Hopps, Parker, Porter and Stevenson31, Reference Divoky, Smrz, Chyla, Sikocinski, Severova, Novak, Huynh, Nagisetty, Miura and Pilař34–Reference Pilar, Slezak, Sikocinski, Divoky, Sawicka, Bonora, Lucianetti, Mocek and Jelinkova36] because of its robustness, flexibility of performance and pulse shaping capability. Therefore, we will use an all-fiber front end in the laser system.
Among the preamplifier systems, many of these medium-scale lasers use single-pass or multi-pass amplifier structure except Helen facility, where a regenerative amplifier structure is adopted[Reference Norman, Andrew, Bett, Clifford, England, Hopps, Parker, Porter and Stevenson31]. To our knowledge, the regenerative amplifier is widely used in large high-power laser systems[Reference Bowers, Burkhart, Cohen, Erbert, Heebner, Hermann and Jedlovec37–Reference Rambo, Smith, Porter, Hurst, Speas, Adams, Garcia, Dawson, Thurston, Wakefield, Kellogg, Slattery, Ives, Broyles, Caird, Erlandson, Murray, Behrendt, Neilsen and Narduzzi40] because of its significant reductions in both initial construction costs and subsequent operation costs as a result of a decrease in the number of components for a given output energy. It has a good short-term stability, but its long-term stability is a big challenge because the output energy of the regenerative amplifier is very sensitive to the gain of the amplifier and the loss of its inner optics elements which will change as time past. The long-term stability of the regenerative amplifier is difficult to guarantee during the operation in engineering practice without a big advanced team. On the other hand, the regenerative amplifier requires higher quality of optics elements than the simple MOPA structure does. The benefit of single-pass or multi-pass structure for the preamplifier is its long-term stability compared to using a regenerative amplifier. Considering our laser system is a facility for users and it is required to operate stably for a long time without maintenance, we choose single-pass and two-pass structures in the preamplifier system.
Among the main amplifier systems, most of these medium-scale lasers use Nd:glass rod amplification cascade[Reference Yanovsky, Alinchenko, Rousseau, Chvykov, Mourou and Krushelnick25–Reference Kuzmin, Kulagin, Khazanov and Shaykin28, Reference Kong, Lee, Kim, Han, Kim, Um, Park and Lee33] and a few of them use a combination of rod and disk amplifiers[Reference Nostrand, Weiland, Luthi, Vickers, Sell, Stanley, Honig, Auerbach, Hackel and Wegner23, Reference Kamath, Tripathi, Kulkarni, Chandra, Joshi, Navathe and Gupta32] or pure multi-slab amplifiers[Reference Divoky, Smrz, Chyla, Sikocinski, Severova, Novak, Huynh, Nagisetty, Miura and Pilař34–Reference Pilar, Slezak, Sikocinski, Divoky, Sawicka, Bonora, Lucianetti, Mocek and Jelinkova36]. In our opinion, rod active elements also have good prospects. The optical quality of rods is generally much higher than that of slabs. For 100-J-level Nd:glass lasers, the rod amplifier is more available thanks to its compact character, easy adjustment and benefits in terms of reduced costs of operation and maintenance and increased system availability. Therefore, the rod amplifier is determined in our system at the level of hundred Joules per pulse.
In these medium-scale laser systems, spatial beam-shaping methods generating flat-top fluence distributions in the output near field have been investigated, such as image relaying with spatial filtering[Reference Nostrand, Weiland, Luthi, Vickers, Sell, Stanley, Honig, Auerbach, Hackel and Wegner23–Reference Kuzmin, Kulagin, Khazanov and Shaykin28, Reference Norman, Andrew, Bett, Clifford, England, Hopps, Parker, Porter and Stevenson31–Reference Kong, Lee, Kim, Han, Kim, Um, Park and Lee33], stimulated Brillouin scattering phase conjugation mirrors (SBS-PCMs)[Reference Kuzmin, Khazanov, Kulagin and Shaykin27], Gaussian mirror output coupler in the oscillator[Reference Yanovsky, Alinchenko, Rousseau, Chvykov, Mourou and Krushelnick25], circular aperture selecting the quasi-uniform intensity region at the center of the expanded beam[Reference Norman, Andrew, Bett, Clifford, England, Hopps, Parker, Porter and Stevenson31] and diffractive optical element (DOE)[Reference Kiriyama, Michiaki, Nakai, Shimomura, Sasao, Tanaka, Ochi, Tanoue, Okada, Kondo, Kanazawa, Sagisaka, Daito, Wakai, Sasao, Suzuki, Kotakai, Kondo, Sugiyama, Bulanov, Bolton, Daido, Kawanishi, Collier, Hernandez-Gomez, Hooker, Ertel, Kimura and Tajima26]. However, these are all passive shaping methods used for particular laser system, which is not suitable for achieving high spatial beam quality in complex high-power lasers applied in accurate physics experiments. In recent years, programmable liquid-crystal spatial light modulator (SLM) has been used for adaptive spatial beam shaping and it has been installed onto some large laser systems, such as the National Ignition Facility (NIF)[Reference Awwal, Orth, Tse, Matone, Paul, Hardy, Brunton, Hermann, Yang, DiNicola, Rever, Dixit and Heebner41] and the OMEGA EP laser[Reference Barczys, Bahk, Spilatro, Coppenbarger, Hill, Hinterman, Kidder, Puth, Touris and Zuegel42]. However, there have been only a limited number of reports on spatial beam shaping for high-power lasers using an SLM, especially for medium-scale 100-J lasers[Reference Bahk, Begishev and Zuegel43].
The uniform wavefront is an important part of the beam quality for high-power lasers. Two wavefront shaping methods have been employed in these medium-scale laser systems, including SBS-PCMs[Reference Kuzmin, Khazanov, Kulagin and Shaykin27, Reference Kuzmin, Kulagin, Khazanov and Shaykin28] and photo-controlled deformable mirror (DM) in HiLASE recently. However, SBS-PCM is a passive method for wavefront shaping and it is used as a cavity-end mirror which can only compensate the wavefront aberration of the elements in the two-pass beamline. Deformable mirror is an active device for wavefront shaping and it can give arbitrary wavefront distribution of the output in the adaptive optics systems. Therefore, DM is chosen in our system for adaptive wavefront shaping.
The goal of this work was the creation of a 100-J-level Nd:glass laser system with good beam quality. The laser is integrated with high flexibility of performance, including arbitrary pulse time-domain shaping in the all-fiber front end, generation of single-mode laser (spectral width less than 0.02 nm) or small broadband laser (spectral width less than 0.3 nm) by phase modulation, adaptive spatial beam shaping by using SLM, adaptive wavefront shaping by using DM, the capacity of operating at three wavelengths – 1053 nm ![]() $(1{\it\omega})$, 527 nm
$(1{\it\omega})$, 527 nm ![]() $(2{\it\omega})$ and 351 nm
$(2{\it\omega})$ and 351 nm ![]() $(3{\it\omega})$ – and easy operation and maintainability thanks to its two-side beamline surrounding a vertical steel truss. This 100-J-level laser system has recently been constructed to perform a standard source of high-energy-density science experiments at National Key Laboratory of Science and Technology on Tunable Laser, Harbin. This laser system is ideally suited for a wide variety of high-energy-density science experiments, including laser-induced damage mechanism for UV optics research[Reference Liu, Huang, Wang, Zhou, Ye, Zhou, Sun, Jiang, Sui and Zheng44], SBS[Reference Wang, Lu, Li, Wu, Fan, Zheng and He45–Reference Yuan, Lu, Wang, Zheng and Chen47] and stimulated Raman scattering (SRS)[Reference Fan, Lu, Lin, Yang, Liu, Dong, Zhu and Hasi48]. This is designed as one beam with an aperture of 60 mm and the whole size of the laser system is about 7 m length, 2 m height and 1.5 m width. To mitigate laser damage from particulate contamination at sensitive optics, this lab affords class 1000 clean-room conditions throughout with the capability of bringing class 100 conditions to the location of the laser system. The laser system has localized 0.5-m-thick concrete slab foundations helping to alleviate the general effects of surrounding vibrations. Figures 1 and 2 show the 3D drawings and the photograph of the laser system in the lab. The laser system is supported by a vertical truss, and the beam path is on both sides. Laser components with relatively high weight are seated in the bottom of the support frame, such as 100-mm-diameter Faraday isolators and 70-mm-diameter rod amplifiers. The truss posture maintains balance, as the result of the double-side arrangement of the beam path and both sides have a considerable weight of components.
$(3{\it\omega})$ – and easy operation and maintainability thanks to its two-side beamline surrounding a vertical steel truss. This 100-J-level laser system has recently been constructed to perform a standard source of high-energy-density science experiments at National Key Laboratory of Science and Technology on Tunable Laser, Harbin. This laser system is ideally suited for a wide variety of high-energy-density science experiments, including laser-induced damage mechanism for UV optics research[Reference Liu, Huang, Wang, Zhou, Ye, Zhou, Sun, Jiang, Sui and Zheng44], SBS[Reference Wang, Lu, Li, Wu, Fan, Zheng and He45–Reference Yuan, Lu, Wang, Zheng and Chen47] and stimulated Raman scattering (SRS)[Reference Fan, Lu, Lin, Yang, Liu, Dong, Zhu and Hasi48]. This is designed as one beam with an aperture of 60 mm and the whole size of the laser system is about 7 m length, 2 m height and 1.5 m width. To mitigate laser damage from particulate contamination at sensitive optics, this lab affords class 1000 clean-room conditions throughout with the capability of bringing class 100 conditions to the location of the laser system. The laser system has localized 0.5-m-thick concrete slab foundations helping to alleviate the general effects of surrounding vibrations. Figures 1 and 2 show the 3D drawings and the photograph of the laser system in the lab. The laser system is supported by a vertical truss, and the beam path is on both sides. Laser components with relatively high weight are seated in the bottom of the support frame, such as 100-mm-diameter Faraday isolators and 70-mm-diameter rod amplifiers. The truss posture maintains balance, as the result of the double-side arrangement of the beam path and both sides have a considerable weight of components.

Figure 1. The 3D drawings of the main part of the 100-J-level laser system.

Figure 2. Photograph of the 100-J-level laser system.
In this paper, we provide a stage-by-stage explanation of the laser system and how it achieves its performance capabilities with high beam quality. The laser has four main sections: the front-end system, the preamplifier system, the main amplifier system and the frequency converter. The front end provides a 10-nJ-scale seed pulse at 1 Hz. The latter amplifiers grow progressively larger in size and the preamplifier can amplify to millijoule-scale energies at 1 Hz. Then the laser pulse passes through the main amplifier with the four-stage rod amplifier which can amplify 100-J level of energy at 1053 nm with a repetition rate of approximately two shots per hour, and finally to the frequency converter which can generate 50-J level of energy at 351 nm. An overall schematic of the laser system is shown in Figure 3. There is an arbitrary waveform generator (AWG) in the front-end system, and it has the capacity of precompensation of the amplified waveform distortion and achieving a square pulse output. A beam-shaping system with a liquid-crystal SLM is placed after the preamplifier system. It has the capacity of precompensation of the gain distribution of the amplifiers to achieve a flat-top spatial intensity distribution of the output laser. A DM is placed at the end of the two-pass ![]() ${\it\Phi}20$ rod amplifier beamline to precompensate the wavefront aberration in the following laser system for achieving a flat-top wavefront distribution of the output laser.
${\it\Phi}20$ rod amplifier beamline to precompensate the wavefront aberration in the following laser system for achieving a flat-top wavefront distribution of the output laser.

Figure 3. The overall schematic of the 100-J-level laser system. The blue two-direction arrow real lines refer to the relay image plane. P1–P7, polarizer; FR1–FR3, Faraday rotator; HWP, half-wave plate; CSF, cavity spatial filter in the main amplifier system; TSF, transport spatial filter; THG, third-harmonic generator; ![]() ${\it\Phi}$20,
${\it\Phi}$20, ![]() ${\it\Phi}$40 and
${\it\Phi}$40 and ![]() ${\it\Phi}$70 rod Amp, 20, 40 and 70-mm-diameter Nd:phosphate glass rod amplifiers;
${\it\Phi}$70 rod Amp, 20, 40 and 70-mm-diameter Nd:phosphate glass rod amplifiers; ![]() $1{\it\omega}$ and
$1{\it\omega}$ and ![]() $3{\it\omega}$ Diagrams refer to the respective beam diagnostic units.
$3{\it\omega}$ Diagrams refer to the respective beam diagnostic units.
2 Front-end system
A design with fiber-based technology was adopted in the front-end system. This front-end system has a more reliable master oscillator requiring less maintenance than the Nd:YLF crystal oscillator. This system is composed of four subsystems: a continuous-wave (CW) oscillator, intensity and phase modulators, two Yb:fiber amplifiers and a polarize controller (see Figure 4).

Figure 4. Schematic of the front-end system. The four main sections are the CW oscillator, the AWG, the Yb-doped fiber amplifiers (YDFA) and the polarize controller. IM, intensity modulator; PM, phase modulator; AOM, acousto-optic modulator used for chopping and isolating.
The front end begins with a 100-mW CW oscillator with linear polarization. The fiber oscillator output then proceeds into a fiber intensity modulator, which chops the CW beam into packets of 3 ns (although the size can range from 0.2 to 100 ns). The waveform is controlled by an AWG. The intensity modulator is driven electronically by an RF driver at 1 Hz. Pulse-shape distortion is the primary concern that drives operation of the laser to the small-signal gain regime. Saturated amplification would be more stable energetically but would lead to pulse-shape distortions[Reference Frantz and Nodvik49]. Pulse shaping can precompensate the saturation-related distortions when an AWG is used to drive the intensity modulator in the front-end system. The laser pulse is single mode without the working of the phase modulator. When small broadband is needed, the phase modulator is driven electronically by an RF driver with a sine signal.
After passing through the phase modulator, the beam enters into the amplifier region. There are two Yb amplifiers in this section, and after each amplifier, there is an RF-driven acousto-optic modulator (AOM, 90 ns width). The AOM’s major role is in two aspects: first, filtering ASE of the fiber amplifier to enhance the contrast of the laser pulse; second, isolating the reflected laser to protect the front-end system. The AOM switching gate time and the AWG rigger signal are from a synchronization controller.
The output of the amplifier–chopper section is injected into the polarization controller. After the pulse traverses the polarization controller, the laser has linear polarization, and the output energy is 10 nJ at 3 ns in a single pulse. The output energy stability of the front end is affected by the YDFA pump and the temperature. When the pump power is low, the output energy is relatively stable. The temperature affects the refractive index of the fiber, in particular the birefringence of the polarization maintaining fiber. So when the surrounding temperature changes, the polarization state will change in the fiber, leading directly to the pulse energy fluctuation after the polarization controller in the end. Results show that, the peak-to-valley (PV) value [(max–min)![]() $/$mean] of the output energy stability in the front-end system is less than 5%. The stability of the front-end output provides a guarantee to subsequent amplification of the laser system.
$/$mean] of the output energy stability in the front-end system is less than 5%. The stability of the front-end output provides a guarantee to subsequent amplification of the laser system.
3 Preamplifier
The master-oscillator output propagates through a fiber-optic interconnect to the front-end section of the laser system. The fiber output is collimated into a freely propagating beam that is then injected into the preamplifier system. The preamplifier system constitutes one LD-pumped ![]() ${\it\Phi}$2, two LD-pumped
${\it\Phi}$2, two LD-pumped ![]() ${\it\Phi}$3, and two flash-lamp-pumped
${\it\Phi}$3, and two flash-lamp-pumped ![]() ${\it\Phi}$6 Nd:phosphate glass amplifier rods with the whole small-signal gain of nearly
${\it\Phi}$6 Nd:phosphate glass amplifier rods with the whole small-signal gain of nearly ![]() $10^{6}$ (with small-signal gain nearly
$10^{6}$ (with small-signal gain nearly ![]() $10^{3}$ in two-pass
$10^{3}$ in two-pass ![]() ${\it\Phi}$2 rod, nearly
${\it\Phi}$2 rod, nearly ![]() $10^{3}$ in two-pass double
$10^{3}$ in two-pass double ![]() ${\it\Phi}$3 rods and nearly 5 in
${\it\Phi}$3 rods and nearly 5 in ![]() ${\it\Phi}$6 rod) which can amplify the pulse energy from 10-nJ to 5-mJ level. In the case of the laser system, the preamplifier (see Figure 5) is an MOPA configuration design. Because it is polarized horizontally (or p-polarized relative to the optical elements), the injected pulse transmits through the first half-wave plate and polarizer, and then is rotated to vertical or s polarization with a Faraday rotator, and then transmits through the second half-wave plate and polarizer. Then the pulse transmits though a focal lens and a Pockels cell, and sees gain in the first two-pass amplifier head Amp1. The pulse polarization changes
${\it\Phi}$6 rod) which can amplify the pulse energy from 10-nJ to 5-mJ level. In the case of the laser system, the preamplifier (see Figure 5) is an MOPA configuration design. Because it is polarized horizontally (or p-polarized relative to the optical elements), the injected pulse transmits through the first half-wave plate and polarizer, and then is rotated to vertical or s polarization with a Faraday rotator, and then transmits through the second half-wave plate and polarizer. Then the pulse transmits though a focal lens and a Pockels cell, and sees gain in the first two-pass amplifier head Amp1. The pulse polarization changes ![]() $90^{\circ }$ by a quarter-wave plate in the back pass and then it reflects off from the third polarizer P3. Then the pulse transmits through a passive
$90^{\circ }$ by a quarter-wave plate in the back pass and then it reflects off from the third polarizer P3. Then the pulse transmits through a passive ![]() $45^{\circ }$ quartz polarization rotator, a polarizer and a Faraday rotator, and this causes the pulse to be p-polarized after crossing the passive rotator, leading to transmission at the last polarizer. Then the pulse injects into another two-pass amplifier heads Amp2 and Amp3 which are connected together. As the same case above, the pulse reflects off from the fifth polarizer. After passing through a polarizer and a Faraday rotator, the pulse then injects into the last single-pass amplifier heads Amp4 and Amp5. When transmitting through a half-wave plate and a polarizer in the end of the preamplifier system, the pulse has typically been amplified to energies up to a few millijoules with the beam diameter of 6 mm.
$45^{\circ }$ quartz polarization rotator, a polarizer and a Faraday rotator, and this causes the pulse to be p-polarized after crossing the passive rotator, leading to transmission at the last polarizer. Then the pulse injects into another two-pass amplifier heads Amp2 and Amp3 which are connected together. As the same case above, the pulse reflects off from the fifth polarizer. After passing through a polarizer and a Faraday rotator, the pulse then injects into the last single-pass amplifier heads Amp4 and Amp5. When transmitting through a half-wave plate and a polarizer in the end of the preamplifier system, the pulse has typically been amplified to energies up to a few millijoules with the beam diameter of 6 mm.

Figure 5. Schematic of the preamplifier. ![]() ${\it\lambda}/2$, half-wave plate;
${\it\lambda}/2$, half-wave plate; ![]() ${\it\lambda}/4$, quarter-wave plate; P01–P07, polarizers; FR01–FR03, Faraday rotator; L1, long-focal-length lens; PC, Pockels cells; Amp1, 2-mm-diameter Nd:phosphate glass rod amplifier heads; Amp2 and Amp3, 3-mm-diameter rod amplifier heads; Amp4 and Amp5, 6-mm-diameter rod amplifier heads; R1,
${\it\lambda}/4$, quarter-wave plate; P01–P07, polarizers; FR01–FR03, Faraday rotator; L1, long-focal-length lens; PC, Pockels cells; Amp1, 2-mm-diameter Nd:phosphate glass rod amplifier heads; Amp2 and Amp3, 3-mm-diameter rod amplifier heads; Amp4 and Amp5, 6-mm-diameter rod amplifier heads; R1, ![]() $45^{\circ }$ quartz polarization rotator; R2,
$45^{\circ }$ quartz polarization rotator; R2, ![]() $90^{\circ }$ quartz polarization rotator.
$90^{\circ }$ quartz polarization rotator.
There are a few key details about the design of the preamplifier system. First, the repetition rate is kept low such that the rods have a full thermal recovery time, avoiding any thermal lensing associated with the accumulated heat from repetition-rated operation. This limits the operational rate to 1 Hz. Second, placing the ![]() $90^{\circ }$ quartz polarization rotator R2 between Amp4 and Amp5 (6-mm-diameter amplifier) can reduce thermal birefringence effects in the amplifiers[Reference Scott and De Wit50]. In the absence of
$90^{\circ }$ quartz polarization rotator R2 between Amp4 and Amp5 (6-mm-diameter amplifier) can reduce thermal birefringence effects in the amplifiers[Reference Scott and De Wit50]. In the absence of ![]() $90^{\circ }$ quartz polarization rotator R2, thermal birefringence can occur because of the rod pumped by two flash lamps symmetrically placed around it. Third, the long-focal-length lens L1 can reduce the beam diffraction effect and leads the beam to the 2-mm-diameter amplifier. Fourth, a half-wave plate and a polarizer located in the end of the preamplifier allow variable pulse energies, with typical settings in the 2 mJ at 3 ns pulse duration. Fifth, the Faraday isolator with polarizer can isolate reverse laser from residual reflection of the subsequent optical components. Because the preamplifier gain is relatively high, the reflected residual laser will damage the preamplifier system. Finally, the Pockels cell can improve the pulse-to-background contrast by chopping off prepulses and postpulses as well as any pedestal that may exist outside of its 100 ns window.
$90^{\circ }$ quartz polarization rotator R2, thermal birefringence can occur because of the rod pumped by two flash lamps symmetrically placed around it. Third, the long-focal-length lens L1 can reduce the beam diffraction effect and leads the beam to the 2-mm-diameter amplifier. Fourth, a half-wave plate and a polarizer located in the end of the preamplifier allow variable pulse energies, with typical settings in the 2 mJ at 3 ns pulse duration. Fifth, the Faraday isolator with polarizer can isolate reverse laser from residual reflection of the subsequent optical components. Because the preamplifier gain is relatively high, the reflected residual laser will damage the preamplifier system. Finally, the Pockels cell can improve the pulse-to-background contrast by chopping off prepulses and postpulses as well as any pedestal that may exist outside of its 100 ns window.
When the injection energy is 10 nJ achieving from the front-end system, the preamplifier output energy is roughly 2.5 mJ. The stability in 20 minutes of the preamplifier output is shown in Figure 6. The PV value of the output is 6.8%, and the root mean square (RMS) value is 1.5%.

Figure 6. The energy stability of the preamplifier.
4 Spatial beam-shaping module
After the preamplifier, the beam transmits to the spatial beam-shaping module (see Figure 7). The main component of the beam-shaping module is the liquid-crystal SLM[Reference Bahk, Fess, Kruschwitz and Zuegel51–Reference Li, Wang, Lu, Ding, Du, Chen, Zheng, Ba, Dong, Yuan, Bai, Liu and Cui53]. This element is chosen as the object plane that is the relayed image at various elements further along in the laser system, providing the best beam quality at these locations. The spatial beam-shaping module consists of three main sections: the ![]() $5\times$ telescope, the liquid-crystal SLM and the spatial filter. First, the telescope magnifies the Gaussian-shaped spatial beam to uniformly fill the apodizer, and the apodizer can chop the central region, creating a flat intensity region with the beam diameter of 13 mm. Second, the laser beam transmits through a polarizer to be p-polarized. And the local polarization will change a certain angle through the SLM depending on the load voltage on the liquid crystal. After the second polarizer, the laser beam spatial intensity modulation can be achieved. The programmable SLM enables spatial shaping of the beam profile to precompensate for the spatial gain distortions in the remaining amplifiers. Finally, the beam passes through a spatial filter with a 1:1 reduction ratio, as the result that high spatial frequencies are removed, and the image plane is relayed to the main amplifier system. The output beam has a soft edge to reduce hard-edged diffractive effects. The output energy after the spatial beam-shaping module is roughly 200
$5\times$ telescope, the liquid-crystal SLM and the spatial filter. First, the telescope magnifies the Gaussian-shaped spatial beam to uniformly fill the apodizer, and the apodizer can chop the central region, creating a flat intensity region with the beam diameter of 13 mm. Second, the laser beam transmits through a polarizer to be p-polarized. And the local polarization will change a certain angle through the SLM depending on the load voltage on the liquid crystal. After the second polarizer, the laser beam spatial intensity modulation can be achieved. The programmable SLM enables spatial shaping of the beam profile to precompensate for the spatial gain distortions in the remaining amplifiers. Finally, the beam passes through a spatial filter with a 1:1 reduction ratio, as the result that high spatial frequencies are removed, and the image plane is relayed to the main amplifier system. The output beam has a soft edge to reduce hard-edged diffractive effects. The output energy after the spatial beam-shaping module is roughly 200 ![]() ${\rm\mu}$J with the diameter of 13 mm and with the desired shape injected into the main amplifier system.
${\rm\mu}$J with the diameter of 13 mm and with the desired shape injected into the main amplifier system.

Figure 7. Schematic of the beam shaper of the laser system.
As mentioned above, in the spatial beam-shaping module, the downstream polarizer enables the polarization modulation to be manifested as an amplitude modulation. The SLM is an active spatial optical modulator with high contrast ratio and high resolution. The electrically addressable SLM (Holoeye LC2002) operates in a transmissive scheme with ![]() $600\times 800$ pixels; size of each pixel is 32
$600\times 800$ pixels; size of each pixel is 32 ![]() ${\rm\mu}$m. The phase retardation in each pixel, and hence the transmittance of the SLM, is controlled by an 8-bit command gray map. The programmable spatial beam-shaping module based on liquid-crystal SLM was designed to introduce arbitrarily shaped beam profile, which is the desired condition on the SLM.
${\rm\mu}$m. The phase retardation in each pixel, and hence the transmittance of the SLM, is controlled by an 8-bit command gray map. The programmable spatial beam-shaping module based on liquid-crystal SLM was designed to introduce arbitrarily shaped beam profile, which is the desired condition on the SLM.
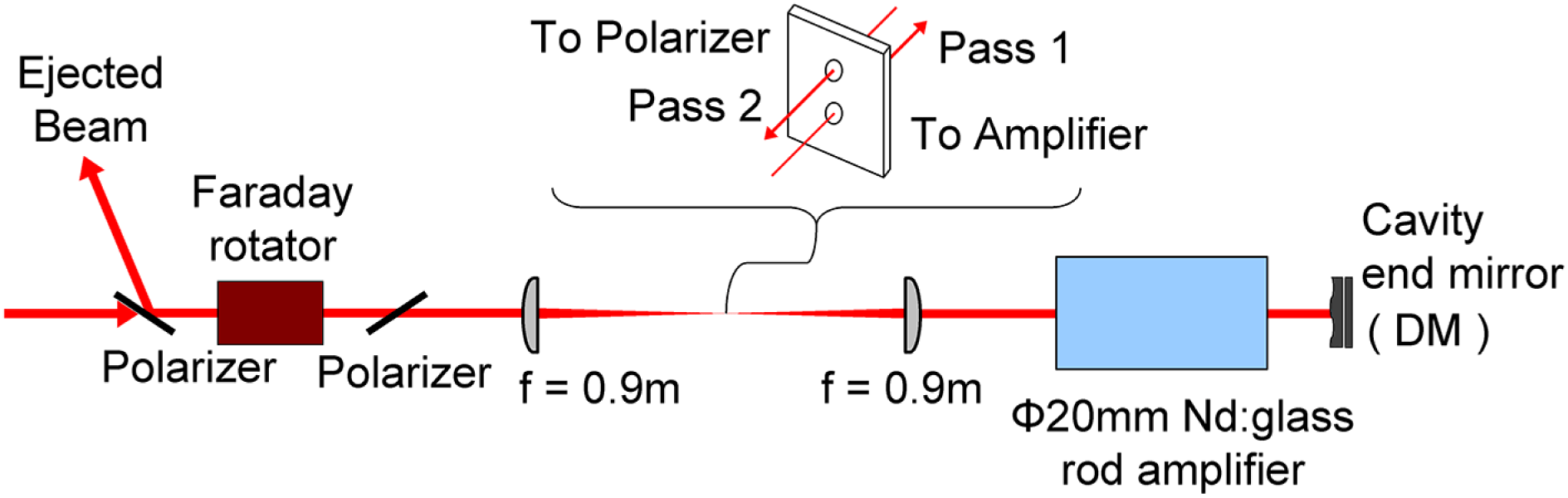
Figure 8. Two-pass 20-mm-diameter rod amplifier.

Figure 9. Photographs of the rod amplifiers.
5 Main amplifier
After the spatial beam-shaping module, the beam passes through a mirror pair (used to point and center the beam) and then it is transported to the main amplifier section (see Figure 3) by a polarizer that transmits the p-polarized incident beam. A Faraday rotator shifts the polarization by ![]() $45^{\circ }$ (half s and half p polarization relative to its input) such that the subsequent polarizer must be oriented at
$45^{\circ }$ (half s and half p polarization relative to its input) such that the subsequent polarizer must be oriented at ![]() $45^{\circ }$ from the horizontal plane to transmit the beam. After passing through this polarizer the beam enters a vacuum spatial filter with a 1:1 reduction ratio and an angled off-axis design. As shown in Figure 8, two pinholes in this design permit the beam to pass any pinhole only once. This approach maintains beam quality by avoiding undesired backreflections and plasma-shutter effects that might be present in a single pinhole design[Reference Celliers, Estabrook, Wallace, Murray, Silva, Gowan, Wonterghem and Manes54, Reference Murray, Milam, Boley, Estabrook and Caird55]. The pinhole used under shot conditions is a conical stainless-steel aperture developed to reduce pinhole closure effects. The downcollimated beam enters the 20-mm-diameter, 360-mm-long Nd:phosphate glass amplifier rod (pass 1) and turns back from an end mirror. After the return beam passes back through the gain medium (pass 2), the spatial filter, the
$45^{\circ }$ from the horizontal plane to transmit the beam. After passing through this polarizer the beam enters a vacuum spatial filter with a 1:1 reduction ratio and an angled off-axis design. As shown in Figure 8, two pinholes in this design permit the beam to pass any pinhole only once. This approach maintains beam quality by avoiding undesired backreflections and plasma-shutter effects that might be present in a single pinhole design[Reference Celliers, Estabrook, Wallace, Murray, Silva, Gowan, Wonterghem and Manes54, Reference Murray, Milam, Boley, Estabrook and Caird55]. The pinhole used under shot conditions is a conical stainless-steel aperture developed to reduce pinhole closure effects. The downcollimated beam enters the 20-mm-diameter, 360-mm-long Nd:phosphate glass amplifier rod (pass 1) and turns back from an end mirror. After the return beam passes back through the gain medium (pass 2), the spatial filter, the ![]() $45^{\circ }$ polarizer and the Faraday rotator, its polarization will be linear and orthogonal to that of the amplifier input beam (i.e., orthogonal to the linear polarization of the beam in pass 1). In the same way, this pass 2 beam will reflect off from the polarizer. Retroreflecting the beam at this point with a mirror pair (used to point and center the beam) will send it to a half-wave plate–transport spatial filter for expanding the beam diameter to 30 mm in the second line. The half-wave plate changes the pulse to p-polarization beam and it allows transmission for the 40-mm-diameter, 380-mm-long Nd:phosphate glass amplifier rod in the third line. As in the round trip in the
$45^{\circ }$ polarizer and the Faraday rotator, its polarization will be linear and orthogonal to that of the amplifier input beam (i.e., orthogonal to the linear polarization of the beam in pass 1). In the same way, this pass 2 beam will reflect off from the polarizer. Retroreflecting the beam at this point with a mirror pair (used to point and center the beam) will send it to a half-wave plate–transport spatial filter for expanding the beam diameter to 30 mm in the second line. The half-wave plate changes the pulse to p-polarization beam and it allows transmission for the 40-mm-diameter, 380-mm-long Nd:phosphate glass amplifier rod in the third line. As in the round trip in the ![]() ${\it\Phi}$20 rod amplifier cavity, the beam transmits for two passes through the
${\it\Phi}$20 rod amplifier cavity, the beam transmits for two passes through the ![]() ${\it\Phi}$40 rod gain medium, a spatial filter, a Faraday rotator and a
${\it\Phi}$40 rod gain medium, a spatial filter, a Faraday rotator and a ![]() $45^{\circ }$ polarizer. As the beam returned from a cavity-end mirror, it would have attained the same polarization as the
$45^{\circ }$ polarizer. As the beam returned from a cavity-end mirror, it would have attained the same polarization as the ![]() ${\it\Phi}$40 rod amplifier input. Then the beam diameter will be expanded from 30 to 60 mm through a spatial filter in the fourth line. This state allows reflection at the polarizer in the fifth line through a mirror pair. The beam will have made a total of two passes through the 70-mm-diameter, 380-mm-long Nd:phosphate glass amplifier rod as same as the first two amplifiers. In the second pass, the Faraday rotator that follows will convert the outgoing beam polarization to horizontal (or p polarization), causing the injection polarizer now to transmit the beam. Then the pulse transmits through another
${\it\Phi}$40 rod amplifier input. Then the beam diameter will be expanded from 30 to 60 mm through a spatial filter in the fourth line. This state allows reflection at the polarizer in the fifth line through a mirror pair. The beam will have made a total of two passes through the 70-mm-diameter, 380-mm-long Nd:phosphate glass amplifier rod as same as the first two amplifiers. In the second pass, the Faraday rotator that follows will convert the outgoing beam polarization to horizontal (or p polarization), causing the injection polarizer now to transmit the beam. Then the pulse transmits through another ![]() ${\it\Phi}$70 rod as a single-pass booster. After the booster section, the
${\it\Phi}$70 rod as a single-pass booster. After the booster section, the ![]() $1{\it\omega}$ laser beam is folded toward a spatial filter with a 1:1 reduction ratio, which is framed by two lenses of 1.9 m focal length. In the end, the 1
$1{\it\omega}$ laser beam is folded toward a spatial filter with a 1:1 reduction ratio, which is framed by two lenses of 1.9 m focal length. In the end, the 1![]() ${\it\omega}$ laser passes through a polarizer. The small-signal gain of the four amplifiers is about 2000 in the two-pass
${\it\omega}$ laser passes through a polarizer. The small-signal gain of the four amplifiers is about 2000 in the two-pass ![]() ${\it\Phi}$20 rod, about 50 in the two-pass
${\it\Phi}$20 rod, about 50 in the two-pass ![]() ${\it\Phi}$40 rod, about 6.3 in the two-pass
${\it\Phi}$40 rod, about 6.3 in the two-pass ![]() ${\it\Phi}$70 rod and about 2.2 in the single-pass
${\it\Phi}$70 rod and about 2.2 in the single-pass ![]() ${\it\Phi}$70 rod. The main amplifier system provides a whole gain of about
${\it\Phi}$70 rod. The main amplifier system provides a whole gain of about ![]() $5\times 10^{5}$ with the beam diameter of 60 mm injecting into the frequency conversion system. Depending on the setting of the preamplifier energy output, the main amplifier output energy can reach 100-J level for pulses of 3–5 ns. The main amplifier system has a total of six lines with a spatial filter at each line, causing the laser system as a full image relay system.
$5\times 10^{5}$ with the beam diameter of 60 mm injecting into the frequency conversion system. Depending on the setting of the preamplifier energy output, the main amplifier output energy can reach 100-J level for pulses of 3–5 ns. The main amplifier system has a total of six lines with a spatial filter at each line, causing the laser system as a full image relay system.
The main amplifier is comprised of four Nd:phosphate glass amplifier rods. There is a ![]() $2^{\circ }$ or
$2^{\circ }$ or ![]() $4^{\circ }$ oblique angle to the rod axis cutting at each rod ends, and the design minimizes undesired beam backreflections. In the current configuration, each amplifier is held in a gold-coated modular mount (see Figure 9). The flash lamps (each of 51-cm length and 2-cm diameter) are placed around a given amplifier module to pump the gain medium. The pulsed power on the main amplifier consists of six individual 220-
$4^{\circ }$ oblique angle to the rod axis cutting at each rod ends, and the design minimizes undesired beam backreflections. In the current configuration, each amplifier is held in a gold-coated modular mount (see Figure 9). The flash lamps (each of 51-cm length and 2-cm diameter) are placed around a given amplifier module to pump the gain medium. The pulsed power on the main amplifier consists of six individual 220-![]() ${\rm\mu}$F capacitors (one for
${\rm\mu}$F capacitors (one for ![]() ${\it\Phi}$20, one for
${\it\Phi}$20, one for ![]() ${\it\Phi}$40 and four for the two
${\it\Phi}$40 and four for the two ![]() ${\it\Phi}$70 rods) charged typically to 9, 16, 13 and 13 kV, respectively. At this level, the total discharged electrical energy is roughly 110 kJ. The flash lamp and the Nd:glass rod will generate a lot of waste heat in the rods and lamps. In order to achieve high repetition operating rate and high stability, circulating water is used for cooling the four rod amplifiers. The main amplifier is able to return to its initial state (i.e., the same birefringence) in about 30 min by a 1.4 kW water-cooled machine. Thus the laser system operates at a repetition rate of approximately two shots per hour.
${\it\Phi}$70 rods) charged typically to 9, 16, 13 and 13 kV, respectively. At this level, the total discharged electrical energy is roughly 110 kJ. The flash lamp and the Nd:glass rod will generate a lot of waste heat in the rods and lamps. In order to achieve high repetition operating rate and high stability, circulating water is used for cooling the four rod amplifiers. The main amplifier is able to return to its initial state (i.e., the same birefringence) in about 30 min by a 1.4 kW water-cooled machine. Thus the laser system operates at a repetition rate of approximately two shots per hour.
The output energy of the main amplifier against the input energy is shown in Figure 10. It has been noted that the data are clearly in the small saturation when the output energy is large. The gain is dependent on the electric voltage of the pump pulsed power. Four operating states are given, including pulse width of 3 ns and 5 ns. The pulsed power of the four amplifiers (![]() ${\it\Phi}$20,
${\it\Phi}$20, ![]() ${\it\Phi}$40 and two
${\it\Phi}$40 and two ![]() ${\it\Phi}$70 amplifiers) is charged in different states [9, 15, 13, 12 kV (5 ns); 9.5, 16, 13, 13 kV (5 ns); 10, 16, 13, 13 kV (3 ns) and 11, 16, 13, 13 kV (3 ns)].
${\it\Phi}$70 amplifiers) is charged in different states [9, 15, 13, 12 kV (5 ns); 9.5, 16, 13, 13 kV (5 ns); 10, 16, 13, 13 kV (3 ns) and 11, 16, 13, 13 kV (3 ns)].

Figure 10. Main amplifier gain data of optical output versus optical input energies.
Since the laser fluence in the main amplifier chain is relatively high, a proper isolation is necessary. In the beam path arrangement, the amplification, spatial filtering and isolation are distributing alternatively. The Faraday rotator placed between polarizers forms the proper isolation. Especially in the two-pass amplification cavity, the pulse transmits off-axis in the spatial filter and this action prevents any spontaneous emission in the main amplifiers from getting amplified by the rod amplifier.
6 Wavefront shaping module
When the beam injects into the main amplifier, the wavefront of the laser can be shaped in wavefront shaping module. The main component of the wavefront shaping module is the electromagnetic DM (Imagine eyes Mirao 52-e). As shown in Figures 3 and 8, the DM is placed in the first beam path of the main amplifier as the cavity-end mirror of the two-pass ![]() ${\it\Phi}$20 amplifier. When the laser beam finishes the first pass through the
${\it\Phi}$20 amplifier. When the laser beam finishes the first pass through the ![]() ${\it\Phi}$20 amplifier, it is reflected by the DM and the wavefront is shaped at the same time. The position of the DM is the relayed image plane of the laser system. After the laser beam passes through the whole laser system, the wavefront of the output laser can be measured by the Shack–Hartmann wavefront sensor (Thorlabs, WFS150-5C) at the relayed image plane in the 1
${\it\Phi}$20 amplifier, it is reflected by the DM and the wavefront is shaped at the same time. The position of the DM is the relayed image plane of the laser system. After the laser beam passes through the whole laser system, the wavefront of the output laser can be measured by the Shack–Hartmann wavefront sensor (Thorlabs, WFS150-5C) at the relayed image plane in the 1![]() ${\it\omega}$ diagnostic system. The key elements of the wavefront shaping module are DM, Shack–Hartmann wavefront sensor as well as the spatial-filtered image relay system. The surface shape of the DM is set to compensate for the wavefront aberrations which are mainly the static aberrations of optical elements and thermal aberrations of active media in the whole laser system.
${\it\omega}$ diagnostic system. The key elements of the wavefront shaping module are DM, Shack–Hartmann wavefront sensor as well as the spatial-filtered image relay system. The surface shape of the DM is set to compensate for the wavefront aberrations which are mainly the static aberrations of optical elements and thermal aberrations of active media in the whole laser system.
In the wavefront shaping module, the DM works in closed loop with the Shack–Hartmann wavefront sensor. The laser energy injected on the DM is about 10 mJ and the corresponding laser fluence is less than 10 mJ cm![]() $^{-2}$. The surface of the DM is coated with silver film with the laser damage threshold nearly 400 mJ cm
$^{-2}$. The surface of the DM is coated with silver film with the laser damage threshold nearly 400 mJ cm![]() $^{-2}$. Obviously, the DM is in safe condition as the cavity-end mirror of the former amplifier (
$^{-2}$. Obviously, the DM is in safe condition as the cavity-end mirror of the former amplifier (![]() ${\it\Phi}$20). There are 52 actuators in the DM with the effective diameter of 15 mm. The maximum of the generated wavefront PV is 50
${\it\Phi}$20). There are 52 actuators in the DM with the effective diameter of 15 mm. The maximum of the generated wavefront PV is 50 ![]() ${\rm\mu}$m, which is enough to correct the wavefront aberrations in the laser system.
${\rm\mu}$m, which is enough to correct the wavefront aberrations in the laser system.
7 Frequency converter
The beam ejected from the main amplifier system is then propagated to the frequency converter section. The frequency converter system consists of two ![]() $100\times 100\times 14~(\text{mm})$ KDP crystals, using Type-II
$100\times 100\times 14~(\text{mm})$ KDP crystals, using Type-II![]() $/$Type-II polarization-mismatch scheme[Reference Craxton56, Reference Wegner, Henesian, Speck, Bibeau, Ehrlich, Laumann, Lawson and Weiland57], because it is easier to adjust the two crystals in this scheme than in Type-I
$/$Type-II polarization-mismatch scheme[Reference Craxton56, Reference Wegner, Henesian, Speck, Bibeau, Ehrlich, Laumann, Lawson and Weiland57], because it is easier to adjust the two crystals in this scheme than in Type-I![]() $/$Type-II angle-detuned scheme. As shown in Figure 11, the beam undergoes second-harmonic generation in the first KDP crystal as a doubler to yield the 527-nm light and third-harmonic generation in the second KDP crystal as a tripler to yield the 351-nm light. The
$/$Type-II angle-detuned scheme. As shown in Figure 11, the beam undergoes second-harmonic generation in the first KDP crystal as a doubler to yield the 527-nm light and third-harmonic generation in the second KDP crystal as a tripler to yield the 351-nm light. The ![]() $3{\it\omega}$ laser is mixed with the
$3{\it\omega}$ laser is mixed with the ![]() $1{\it\omega}$ and
$1{\it\omega}$ and ![]() $2{\it\omega}$ lasers, and it is separated from them by two spectral mirrors (CS1 and CS2) with special coating layer [
$2{\it\omega}$ lasers, and it is separated from them by two spectral mirrors (CS1 and CS2) with special coating layer [![]() $R(3{\it\omega})>99\%$,
$R(3{\it\omega})>99\%$, ![]() $R(1{\it\omega})<10\%$,
$R(1{\it\omega})<10\%$, ![]() $R(2{\it\omega})<10\%$]. After folded by the mirror pair, the
$R(2{\it\omega})<10\%$]. After folded by the mirror pair, the ![]() $3{\it\omega}$ laser enters the transport spatial filter, which is a vacuum spatial filter framed by two lenses of 2.35 m focal length. Then the
$3{\it\omega}$ laser enters the transport spatial filter, which is a vacuum spatial filter framed by two lenses of 2.35 m focal length. Then the ![]() $3{\it\omega}$ laser outputs after filtering the high spatial frequency, and at the same time, the image plane is relayed to 2 m away from the shot exit. The remaining
$3{\it\omega}$ laser outputs after filtering the high spatial frequency, and at the same time, the image plane is relayed to 2 m away from the shot exit. The remaining ![]() $1{\it\omega}$ and
$1{\it\omega}$ and ![]() $2{\it\omega}$ lasers can be rejected to absorbed dump, and the
$2{\it\omega}$ lasers can be rejected to absorbed dump, and the ![]() $2{\it\omega}$ laser also can be extracted by two spectral mirrors [
$2{\it\omega}$ laser also can be extracted by two spectral mirrors [![]() $R(2{\it\omega})>99\%$,
$R(2{\it\omega})>99\%$, ![]() $R(1{\it\omega})<5\%$].
$R(1{\it\omega})<5\%$].

Figure 11. The frequency converter system layout. CS1–CS4, spectral mirrors with special coating layer.
The KDP crystals are in a better clean-room and airtight environment with two ![]() $3^{\circ }$ oblique windows on each side. There are three electric motors controlling the two crystals on three directions. The stability of the crystals is observed by the optical grating ruler. The temperature is stabilized at
$3^{\circ }$ oblique windows on each side. There are three electric motors controlling the two crystals on three directions. The stability of the crystals is observed by the optical grating ruler. The temperature is stabilized at ![]() $20\pm 0.7\,^{\circ }\text{C}$ by circulated cooling water near the KDP. There is desiccant in the frequency converter system to avoid the KDP crystals’ deliquescence.
$20\pm 0.7\,^{\circ }\text{C}$ by circulated cooling water near the KDP. There is desiccant in the frequency converter system to avoid the KDP crystals’ deliquescence.
The third-harmonic diagnostics data can be used to establish conversion efficiencies. When high beam intensities are used, the conversion efficiencies of more than 50% are attained (see Figure 12). Note that the diameter of the ![]() $1{\it\omega}$ input laser beam is about
$1{\it\omega}$ input laser beam is about ![]() ${\it\Phi}$58 mm and the pulse width is 5 ns. The near-field modulation (
${\it\Phi}$58 mm and the pulse width is 5 ns. The near-field modulation (![]() $F_{\text{max}}/F_{\text{avg}}$, where
$F_{\text{max}}/F_{\text{avg}}$, where ![]() $F_{\text{max}}$ means the maximal fluence and
$F_{\text{max}}$ means the maximal fluence and ![]() $F_{\text{avg}}$ means the average fluence of the laser beam profile[Reference Speck, Bliss, Glaze, Herris, Holloway, Hunt, Johnson, Kuizenga, Ozarski, Patton, Rupert, Suski, Swift and Thompson58]) of the
$F_{\text{avg}}$ means the average fluence of the laser beam profile[Reference Speck, Bliss, Glaze, Herris, Holloway, Hunt, Johnson, Kuizenga, Ozarski, Patton, Rupert, Suski, Swift and Thompson58]) of the ![]() $1{\it\omega}$ input laser beam is about 1.3:1. The data obtained in the experiment account for the local beam distortions (such as hot spots or an intensity roll-off across the beam profile), pulse-shape and pulse-width issues (that might be inherently present in the seed or might occur during the increment from 1
$1{\it\omega}$ input laser beam is about 1.3:1. The data obtained in the experiment account for the local beam distortions (such as hot spots or an intensity roll-off across the beam profile), pulse-shape and pulse-width issues (that might be inherently present in the seed or might occur during the increment from 1![]() ${\it\omega}$ to 3
${\it\omega}$ to 3![]() ${\it\omega}$), leading to slight disagreements with the ideal data.
${\it\omega}$), leading to slight disagreements with the ideal data.

Figure 12. Conversion efficiency to third harmonic. The data are for a 5 ns input 1![]() ${\it\omega}$ pulse width and for a
${\it\omega}$ pulse width and for a ![]() ${\it\Phi}$58 mm beam.
${\it\Phi}$58 mm beam.

Figure 13. The output energy stability in six shots.

Figure 14. The ![]() $1{\it\omega}$ and
$1{\it\omega}$ and ![]() $3{\it\omega}$ output 3 and 5 ns temporal pulses.
$3{\it\omega}$ output 3 and 5 ns temporal pulses.
8 Output results
Critical beam information is gathered in two diagnostic systems: the ![]() $1{\it\omega}$ diagnostic system, which uses a weak reflection from a
$1{\it\omega}$ diagnostic system, which uses a weak reflection from a ![]() $1{\it\omega}$ pickoff beam splitter (
$1{\it\omega}$ pickoff beam splitter (![]() $R=0.86\%$) before the KDP crystals and the
$R=0.86\%$) before the KDP crystals and the ![]() $3{\it\omega}$ diagnostic system, which uses a leakage beam transmitted (
$3{\it\omega}$ diagnostic system, which uses a leakage beam transmitted (![]() $T=0.3\%$) through the last folding mirror before the
$T=0.3\%$) through the last folding mirror before the ![]() $3{\it\omega}$ output side. Both diagnostic systems have large downcollimating telescopes to reduce the beam to a reasonable size for measurement. Each of these diagnostic systems includes full-energy shot near-field cameras, a fast photodiode to provide temporal measurements and a calorimeter for energy information.
$3{\it\omega}$ output side. Both diagnostic systems have large downcollimating telescopes to reduce the beam to a reasonable size for measurement. Each of these diagnostic systems includes full-energy shot near-field cameras, a fast photodiode to provide temporal measurements and a calorimeter for energy information.
The maximum ![]() $1{\it\omega}$ output energy is 137 J in the operation record of the laser system. For 5 ns operation, the
$1{\it\omega}$ output energy is 137 J in the operation record of the laser system. For 5 ns operation, the ![]() $3{\it\omega}$ output energy of 47.7 J has been successfully achieved with the frequency conversion efficiency of 51.8%. The energy stability is measured and the results show that the average
$3{\it\omega}$ output energy of 47.7 J has been successfully achieved with the frequency conversion efficiency of 51.8%. The energy stability is measured and the results show that the average ![]() $1{\it\omega}$ input energy is 63.5 J in six shots with the RMS value of 2.8%. At this case, the average
$1{\it\omega}$ input energy is 63.5 J in six shots with the RMS value of 2.8%. At this case, the average ![]() $3{\it\omega}$ output energy is 29.2 J with the conversion efficiency of 46%, and the RMS value is 4.4% (see Figure 13). Such energy stability of the laser output can meet the application for many science experiments.
$3{\it\omega}$ output energy is 29.2 J with the conversion efficiency of 46%, and the RMS value is 4.4% (see Figure 13). Such energy stability of the laser output can meet the application for many science experiments.
The ![]() $1{\it\omega}$ and
$1{\it\omega}$ and ![]() $3{\it\omega}$ temporal laser pulses are measured by fast photodiodes (InGaAs material, Ultrafast Photodetectors UPD-40-UVIR-P and UPD-40-UVIR-D) with the rise time less than 40 ps, and the beam diameter is reduced to
$3{\it\omega}$ temporal laser pulses are measured by fast photodiodes (InGaAs material, Ultrafast Photodetectors UPD-40-UVIR-P and UPD-40-UVIR-D) with the rise time less than 40 ps, and the beam diameter is reduced to ![]() ${\it\Phi}$10 mm on their surface. The AWG in the front-end system has the ability of generating arbitrary pulse shape to precompensate pulse-shape distortions caused by the following amplifiers. In the end, the laser system can give the output
${\it\Phi}$10 mm on their surface. The AWG in the front-end system has the ability of generating arbitrary pulse shape to precompensate pulse-shape distortions caused by the following amplifiers. In the end, the laser system can give the output ![]() $1{\it\omega}$ and
$1{\it\omega}$ and ![]() $3{\it\omega}$ pulse with a square shape. For the front-end system giving the output of 3 ns
$3{\it\omega}$ pulse with a square shape. For the front-end system giving the output of 3 ns![]() $/$10 nJ and 5 ns
$/$10 nJ and 5 ns![]() $/$15 nJ with this pulse shape, the
$/$15 nJ with this pulse shape, the ![]() $1{\it\omega}$ output temporal pulses at 3 and 5 ns are shown in Figure 14. It also shows the
$1{\it\omega}$ output temporal pulses at 3 and 5 ns are shown in Figure 14. It also shows the ![]() $3{\it\omega}$ output temporal pulses at 3 ns and 5 ns, respectively. Besides the square pulse, any other uniform pulse waveform can also be achieved in the laser system such as the Gaussian pulse and the triangle pulse.
$3{\it\omega}$ output temporal pulses at 3 ns and 5 ns, respectively. Besides the square pulse, any other uniform pulse waveform can also be achieved in the laser system such as the Gaussian pulse and the triangle pulse.

Figure 15. The ![]() $1{\it\omega}$ and
$1{\it\omega}$ and ![]() $3{\it\omega}$ output near field by spatial beam shaping. The
$3{\it\omega}$ output near field by spatial beam shaping. The ![]() $1{\it\omega}$ near field (a) and the lineout gray distribution (b), the
$1{\it\omega}$ near field (a) and the lineout gray distribution (b), the ![]() $3{\it\omega}$ near field (c) and the lineout gray distribution (d).
$3{\it\omega}$ near field (c) and the lineout gray distribution (d).
After entering into the diagnostics system, the laser beam passes through a 4F system with a 10:1 reduction ratio, and the image plan is relayed on the scientific grade CCD camera with ![]() $1024\times 1024$ pixels and each pixel is of size 13
$1024\times 1024$ pixels and each pixel is of size 13 ![]() ${\rm\mu}$m, which is used to measure the near field. There are some bandpass filters and attenuators in front of the CCD that can reduce the interference of stray light and make the laser pulse decay to the affordable energy of the CCD. The image measured by the CCD can indicate the spatial intensity distribution of the image plane of the laser beam. The SLM placed after the preamplifier has the ability to precompensate the spatial gain distortions in the main amplifiers and the nonuniformity in the frequency converter system (see Section 4). After spatial beam shaping, the output laser with high near-field beam quality is achieved. Results show that the
${\rm\mu}$m, which is used to measure the near field. There are some bandpass filters and attenuators in front of the CCD that can reduce the interference of stray light and make the laser pulse decay to the affordable energy of the CCD. The image measured by the CCD can indicate the spatial intensity distribution of the image plane of the laser beam. The SLM placed after the preamplifier has the ability to precompensate the spatial gain distortions in the main amplifiers and the nonuniformity in the frequency converter system (see Section 4). After spatial beam shaping, the output laser with high near-field beam quality is achieved. Results show that the ![]() $1{\it\omega}$ output near-field modulation is 1.26:1, and the fluence contrast (RMS value) is 9% [see Figure 15(a) and (b)]. After spatial beam shaping, the
$1{\it\omega}$ output near-field modulation is 1.26:1, and the fluence contrast (RMS value) is 9% [see Figure 15(a) and (b)]. After spatial beam shaping, the ![]() $3{\it\omega}$ output near-field modulation is 1.42:1[Reference Li, Wang, Lu, Ding, Cui, Chen, Du, Ba, Zheng, Yuan, Shi, Bai, Liu, Zhu, Dong and Zhou59], and the fluence contrast is 15.4% [see Figure 15(c) and (d)]. There is a degree of large-scale asymmetry in the
$3{\it\omega}$ output near-field modulation is 1.42:1[Reference Li, Wang, Lu, Ding, Cui, Chen, Du, Ba, Zheng, Yuan, Shi, Bai, Liu, Zhu, Dong and Zhou59], and the fluence contrast is 15.4% [see Figure 15(c) and (d)]. There is a degree of large-scale asymmetry in the ![]() $3{\it\omega}$ output near-field profile, which is thought to derive in part from frequency conversion efficiency variations in the KDP crystals. In spite of this, the output laser with such perfect near-field beam quality is of great significance to the application of the laser system.
$3{\it\omega}$ output near-field profile, which is thought to derive in part from frequency conversion efficiency variations in the KDP crystals. In spite of this, the output laser with such perfect near-field beam quality is of great significance to the application of the laser system.
In the diagnostics system, the laser wavefront is measured by a Shack–Hartmann wavefront sensor. The laser beam passes through a 4F system with a 20:1 reduction ratio, and the image plane is relayed on the wavefront sensor with ![]() $39\times 31$ lenslets with each lenslet focal length of 5.2 mm and pitch of 150
$39\times 31$ lenslets with each lenslet focal length of 5.2 mm and pitch of 150 ![]() ${\rm\mu}$m. There are also some bandpass filters and attenuators in front of the wavefront sensor, which can reduce the interference of stray light and make the laser pulse attenuated to the affordable energy of the wavefront sensor. The DM placed at the position of the cavity-end mirror of the
${\rm\mu}$m. There are also some bandpass filters and attenuators in front of the wavefront sensor, which can reduce the interference of stray light and make the laser pulse attenuated to the affordable energy of the wavefront sensor. The DM placed at the position of the cavity-end mirror of the ![]() ${\it\Phi}$20 amplifier has the ability to compensate the wavefront aberrations in the laser system (see Section 6). The
${\it\Phi}$20 amplifier has the ability to compensate the wavefront aberrations in the laser system (see Section 6). The ![]() $1{\it\omega}$ output wavefront and far field without DM are shown in Figure 16(a) and (b). The calculated PV value of the wavefront is 3.56 waves and the RMS value is 0.77 waves. The output far field is also measured by a scientific grade CCD camera which is the same type with the near-field CCD camera. To measure the output far field of the laser pulse, the sampling laser beam transmits through a focal lens (
$1{\it\omega}$ output wavefront and far field without DM are shown in Figure 16(a) and (b). The calculated PV value of the wavefront is 3.56 waves and the RMS value is 0.77 waves. The output far field is also measured by a scientific grade CCD camera which is the same type with the near-field CCD camera. To measure the output far field of the laser pulse, the sampling laser beam transmits through a focal lens (![]() $f=1200$ mm) and is focussed on the far-field CCD. Without DM, the calculated far-field divergence angle is 311
$f=1200$ mm) and is focussed on the far-field CCD. Without DM, the calculated far-field divergence angle is 311 ![]() ${\rm\mu}$rad (approximately 7.3 DL, i.e., diffraction limit). After wavefront shaping, the output laser with high wavefront beam quality is achieved. Results show that the
${\rm\mu}$rad (approximately 7.3 DL, i.e., diffraction limit). After wavefront shaping, the output laser with high wavefront beam quality is achieved. Results show that the ![]() $1{\it\omega}$ output laser beam has a PV value of 0.29 waves and an RMS value of 0.06 waves [see Figure 16(c)]. Figure 16(d) shows the
$1{\it\omega}$ output laser beam has a PV value of 0.29 waves and an RMS value of 0.06 waves [see Figure 16(c)]. Figure 16(d) shows the ![]() $1{\it\omega}$ output far-field profile and the calculated far-field divergence angle is 221
$1{\it\omega}$ output far-field profile and the calculated far-field divergence angle is 221 ![]() ${\rm\mu}$rad (approximately 5.2 DL). A small far-field divergence angle means a good beam transmission direction. After the far-field distribution of the laser beam is tested in the high-power laser system by the scientific grade CCD, the long-term far-field stability is analyzed by calculating the geometric center of the far-field spots. In the 6-h tests, the RMS value of the angle drift is less than 17
${\rm\mu}$rad (approximately 5.2 DL). A small far-field divergence angle means a good beam transmission direction. After the far-field distribution of the laser beam is tested in the high-power laser system by the scientific grade CCD, the long-term far-field stability is analyzed by calculating the geometric center of the far-field spots. In the 6-h tests, the RMS value of the angle drift is less than 17 ![]() ${\rm\mu}$rad. This fully meets the requirements for laser transmission and injection into the frequency converter system.
${\rm\mu}$rad. This fully meets the requirements for laser transmission and injection into the frequency converter system.

Figure 16. The ![]() $1{\it\omega}$ output wavefront (a) and the far field (b) without DM, and
$1{\it\omega}$ output wavefront (a) and the far field (b) without DM, and ![]() $1{\it\omega}$ output wavefront (c) and the far field (d) after wavefront shaping.
$1{\it\omega}$ output wavefront (c) and the far field (d) after wavefront shaping.
9 Conclusion
The 100-J-level Nd:glass laser system with MOPA configuration can produce energies of 100-J level at 1053 nm and roughly 50 J at 351 nm in a ![]() ${\it\Phi}$60 mm beam size with high beam quality. The excellent performance of the laser is that it is integrated with arbitrary pulse shaping in the all-fiber front end and adaptive spatial beam shaping by using SLM. It has the capacity to shape pulse lengths which are variable from 0.2 to 100 ns and achieves
${\it\Phi}$60 mm beam size with high beam quality. The excellent performance of the laser is that it is integrated with arbitrary pulse shaping in the all-fiber front end and adaptive spatial beam shaping by using SLM. It has the capacity to shape pulse lengths which are variable from 0.2 to 100 ns and achieves ![]() $1{\it\omega}$ and
$1{\it\omega}$ and ![]() $3{\it\omega}$ output pulses with a square shape. The excellent
$3{\it\omega}$ output pulses with a square shape. The excellent ![]() $1{\it\omega}$ near-field modulation of 1.26:1 is successfully achieved by spatial beam shaping in experiment. After frequency conversion, the output
$1{\it\omega}$ near-field modulation of 1.26:1 is successfully achieved by spatial beam shaping in experiment. After frequency conversion, the output ![]() $3{\it\omega}$ near-field modulation is about 1.42:1. The
$3{\it\omega}$ near-field modulation is about 1.42:1. The ![]() $1{\it\omega}$ output laser beam has a flat-top wavefront with a PV value of 0.29 waves and RMS value of 0.06 waves. The
$1{\it\omega}$ output laser beam has a flat-top wavefront with a PV value of 0.29 waves and RMS value of 0.06 waves. The ![]() $1{\it\omega}$ output far-field divergence angle is approximately 5.2 DL. The system has proven to be reliable and flexible, and it can be used as the standard source of science experiments.
$1{\it\omega}$ output far-field divergence angle is approximately 5.2 DL. The system has proven to be reliable and flexible, and it can be used as the standard source of science experiments.
Acknowledgments
The authors appreciate the efforts of the following students at the Harbin Institute of Technology who have been instrumental in the success of this project: Lei Shi, Jianhui Zhang, Penghua Zhao, Mengzhi Sun, Ze Cheng, Meihui Yang, Linpeng Yu, Xiaoyan Liu, Fang Yang, XinMin Fan, Baoshen Jia, Zhaoming Zhong, Ying Liu, Xingbo Han, Xiang Lin, Qilin Gao, Yuefei Cai and Luoxian Zhou. The authors also appreciate the efforts of the following staff members within the Research Center of Laser Fusion who have contributed to the success of this project. These include Xiaofeng Wei, Xiaomin Zhang, Feng Jing, Mingzhong Li, Qihua Zhu, Bing Feng, Xiaodong Yuan, Xudong Xie, Wenyi Wang, Qiang Yuan, Keyu Li, Fang Wang and Wei Han. This work is supported by the project of the National Natural Science Foundation of China (grant numbers 61378007 and 61138005).


















