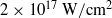1. Introduction
Electron wakefield acceleration by intense subpicosecond laser radiation[Reference Esarey, Schroeder and Leemans1,Reference Tajima and Dawson2] is a promising field of research in high-energy physics. High accelerating fields, several orders of magnitude higher than in conventional radio frequency accelerators, open up a way to designing compact particle accelerators for many applications in fundamental science, diagnostics, and treatment in medicine.
Trapping of electrons by a plasma wake is one of the key problems for laser–plasma acceleration. The initial momentum of the electrons has to be sufficient for them to stay in an accelerating phase of the plasma wave traveling with speed close to the speed of light[Reference Esarey, Schroeder and Leemans1]. Many solutions have been proposed to solve the problem of electron trapping, such as external injection[Reference Stragier, Luiten, van der Geer, van der Wiel and Brussaard3,Reference Nakajima, Fisher, Kawakubo, Nakanishi, Ogata, Kato, Kitagawa, Kodama, Mima and Shiraga4] , self-injection by a nonlinear plasma wave in the so-called bubble regime[Reference Pukhov and Meyer-ter-Vehn5–Reference Ma, Kawata, Yu, Gu, Sheng, Yu, Zhuo, Liu, Yin, Takahashi, Xie, Liu, Tian and Shao7], counter-propagating laser pulses[Reference Faure, Rechatin, Norlin, Lifschitz, Glinec and Malka8], using a mixture of gases, one of which has a high ionization threshold[Reference Pollock, Clayton, Ralph, Albert, Davidson, Divol, Filip, Glenzer, Herpoldt, Lu, Marsh, Meinecke, Mori, Pak, Rensink, Ross, Shaw, Tynan, Joshi and Froula9–Reference Ho, Hung, Yen, Chen, Chu, Lin, Wang and Chou11], or plasma density gradients (downramp)[Reference Faure, Rechatin, Lundh, Ammoura and Malka12]. But the problem still persists.
In the regime of linear plasma wave excitation which produces a stable plasma wave but with low amplitude, the problem of electron injection is especially acute. Although the excitation of weakly linear plasma waves at long paths, which are necessary to accelerate particles to several hundreds of MeV, was demonstrated in Refs. [Reference Eremin, Malkov, Korolikhin, Kiselev, Skobelev, Stepanov and Andreev13,Reference Wojda, Cassou, Genoud, Burza, Glinec, Lundh, Persson, Vieux, Brunetti, Shanks, Jaroszynski, Andreev, Wahlström and Cros14], there are only a few results on synchronous (with the laser pulse) electron injection into the wave.
In some studies, attempts were made to inject electrons using an external high-frequency accelerator. However, this scheme has difficulties with synchronizing the electron beam and the laser pulse, and a relatively large length of the electron bunches. Currently, an injector based on a radio frequency (RF) accelerator, the photocathode of which is irradiated by a femtosecond pulse exactly synchronized with the strong pulse exciting a plasma wave[Reference Stragier, Luiten, van der Geer, van der Wiel and Brussaard3], is being actively developed. However, practical results have not been published yet.
An alternative way to realize a synchronized electron injection is to focus high-intensity radiation on a solid target. The emission of electron beams in the specular direction at focusing laser radiation on the solid was observed in Refs. [Reference Bastiani, Rousse, Geindre, Audebert, Quoix, Hamoniaux, Antonetti and Gauthier15–Reference Wang, Liu, Cai, Wang, Liu, Xia, Deng, Xu, Leng, Li and Xu18]. In some experiments, the energy spectrum of the electrons emitted from the plasma at a large angle of incidence of the laser beam on the solid target surface contained quasi-monoenergetic bunches of accelerated electrons, Refs. [Reference Mordovanakis, Easter, Naumova, Popov, Masson-Laborde, Hou, Sokolov, Mourou, Glazyrin, Rozmus, Bychenkov, Nees and Krushelnick19,Reference Mao, Chen, Ge, Zhang, Yan, Li, Liao, Ma, Huang, Li, Lu, Dong, Wei, Sheng and Zhang20]. It was shown that a critically important factor in this case is the existence of preplasma, which is induced by the relatively low contrast of the laser pulse.
The goal of the present paper is theoretical and experimental investigation of the generation of collimated quasi-monoenergetic beams of accelerated electrons in plasma with sharp spatial gradients by intense laser radiation. To achieve this goal in experiments, laser radiation was focused on the edge of an aluminum foil perpendicular to its plane, so that half of the laser beam bypassed the foil. We observed generation of highly collimated electron beams propagating in the direction of the laser pulse and characterized by a narrow energy distribution peaking in the 0.2–0.8 MeV range. The electron-beam charge ranges from 1 to 10 pC. In the theoretical consideration, 1D and 2D PIC simulations were performed on the propagation of laser pulses with different envelopes in inhomogeneous plasma, which revealed plasma wave excitation as a result of self-modulation laser pulse instability with consecutive electron acceleration due to self-injection into the wakefield plasma wave on longitudinal plasma inhomogeneities. The role of the transverse plasma inhomogeneity is discussed on the base of the obtained 2D modeling results.
2. Theoretical description
One of the possible mechanisms of formation of accelerated electrons with a quasi-monochromatic spectrum is acceleration in the field of the plasma wave generated in the prepulse-induced dense plasma due to the self-modulation instability of the laser pulse[Reference Andreev, Gorbunov, Kirsanov, Pogosova and Ramazashvili21]. Let us assume that the prepulse arriving approximately 10 ns before the main pulse with intensity ![]() $I\sim 1{0}^{13} ~\mathrm{W} \cdot {\mathrm{cm} }^{- 2} $ ionizes the metal target at the skin depth, after which the formed plasma spreads with ion sound velocity. Then the plasma density is estimated to be
$I\sim 1{0}^{13} ~\mathrm{W} \cdot {\mathrm{cm} }^{- 2} $ ionizes the metal target at the skin depth, after which the formed plasma spreads with ion sound velocity. Then the plasma density is estimated to be ![]() $1{0}^{19} {\unicode{x2013}} 1{0}^{20} ~{\mathrm{cm} }^{- 3} $, and the characteristic plasma size at the time of the main pulse arrival is
$1{0}^{19} {\unicode{x2013}} 1{0}^{20} ~{\mathrm{cm} }^{- 3} $, and the characteristic plasma size at the time of the main pulse arrival is ![]() ${\sim }100~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $. When a laser pulse propagates in this dense plasma, the length of the wake plasma wave,
${\sim }100~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $. When a laser pulse propagates in this dense plasma, the length of the wake plasma wave, ![]() ${\lambda }_{p} = 2\mathrm{\pi} c/ {\omega }_{p} $, is much shorter than that of the femtosecond pulse (
${\lambda }_{p} = 2\mathrm{\pi} c/ {\omega }_{p} $, is much shorter than that of the femtosecond pulse (![]() $L= c{t}_{L} $), which may lead to its self-modulation and effective generation of an accelerating wake field. It should be emphasized that the development of self-modulation instability and generation of a wake field by a relatively long laser pulse
$L= c{t}_{L} $), which may lead to its self-modulation and effective generation of an accelerating wake field. It should be emphasized that the development of self-modulation instability and generation of a wake field by a relatively long laser pulse ![]() $(L\gg {\lambda }_{p} )$ demands a sufficiently large initial amplitude of the ‘seed’ plasma wave and propagation of the laser pulse over a rather long distance[Reference Andreev, Kirsanov and Gorbunov22].
$(L\gg {\lambda }_{p} )$ demands a sufficiently large initial amplitude of the ‘seed’ plasma wave and propagation of the laser pulse over a rather long distance[Reference Andreev, Kirsanov and Gorbunov22].
To analyze the wakefield acceleration of electron bunches, we first performed a pilot PIC simulation in one-dimensional inhomogeneous (1D3V) plasma. The simulation was done using the 1D version of the VLPL code[Reference Pukhov23]. A laser pulse with duration ![]() ${t}_{L} = 66~\mathrm{fs} $ propagated along the
${t}_{L} = 66~\mathrm{fs} $ propagated along the ![]() $x$-axis. The pulse had a transverse linear polarization along the
$x$-axis. The pulse had a transverse linear polarization along the ![]() $y$-axis. We considered the laser pulse wavelength
$y$-axis. We considered the laser pulse wavelength ![]() $\lambda = 1~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $ and the dimensionless amplitude
$\lambda = 1~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $ and the dimensionless amplitude ![]() ${a}_{0} = eE/ ({m}_{e} c\omega )= 0. 468$ (
${a}_{0} = eE/ ({m}_{e} c\omega )= 0. 468$ (![]() $e$ is the elementary charge,
$e$ is the elementary charge, ![]() ${m}_{e} $ is the electron mass,
${m}_{e} $ is the electron mass, ![]() $c$ is the speed of light, and
$c$ is the speed of light, and ![]() $\omega $ is the laser frequency). These parameters corresponded to the intensity
$\omega $ is the laser frequency). These parameters corresponded to the intensity ![]() ${I}_{0} = 3\times 1{0}^{17} ~\mathrm{W} \cdot {\mathrm{cm} }^{- 2} $. The size of the simulation region was
${I}_{0} = 3\times 1{0}^{17} ~\mathrm{W} \cdot {\mathrm{cm} }^{- 2} $. The size of the simulation region was ![]() $L= 160~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $. At the initial instant the laser pulse center was set at
$L= 160~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $. At the initial instant the laser pulse center was set at ![]() $x= 0$. In the region
$x= 0$. In the region ![]() $0\leqslant x\lt 40~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $, the plasma had an increasing (Gaussian or linear) density profile with characteristic inhomogeneity scale
$0\leqslant x\lt 40~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $, the plasma had an increasing (Gaussian or linear) density profile with characteristic inhomogeneity scale ![]() $l= 15~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $. At
$l= 15~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $. At ![]() $40~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} \lt x\leqslant 160~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $, the plasma was homogeneous with density
$40~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} \lt x\leqslant 160~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $, the plasma was homogeneous with density ![]() ${n}_{0} = 0. 045{n}_{cr} = 5\times 1{0}^{19} ~{\mathrm{cm} }^{- 3} $, where
${n}_{0} = 0. 045{n}_{cr} = 5\times 1{0}^{19} ~{\mathrm{cm} }^{- 3} $, where ![]() ${n}_{cr} = {m}_{e} {\omega }^{2} / (4\mathrm{\pi} {e}^{2} )$. The cell size was
${n}_{cr} = {m}_{e} {\omega }^{2} / (4\mathrm{\pi} {e}^{2} )$. The cell size was ![]() ${D}_{x} = 0. 01~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $ and the number of particles per cell was 500. The ions were assumed to be immobile, and they formed a neutralizing background. At the initial instant, the plasma was considered to be cold.
${D}_{x} = 0. 01~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $ and the number of particles per cell was 500. The ions were assumed to be immobile, and they formed a neutralizing background. At the initial instant, the plasma was considered to be cold.
The calculations performed with a Gaussian time profile of the laser pulse showed the following: for the plasma and pulse parameters under consideration, when the pulse had a smooth envelope and relatively low intensity, the ‘seed’ plasma wave amplitude (generated by a smooth Gaussian front of the laser pulse, which is longer than the plasma wavelength) is insufficiently large to develop a self-modulation instability and generate an accelerating wake field.
The situation was different in the case of a sharp leading edge of a laser pulse (rectangular or hyper-Gaussian), when there occurred generation of a wake wave and acceleration of electrons. Note that the pulse leading edge may be sharpened under experimental conditions due to the ionization nonlinearity[Reference Andreev, Chegotov and Pogosova24]. The principal mechanism that sharpens the pulse leading edge is a pulse front refraction on the radially inhomogeneous electron plasma density produced by the optical field ionization of the not fully ionized plasma formed by the prepulse. This mechanism does not require relativistic intensities, but a laser field strength strong enough for the inner shell’s ionization that is just the case of our experimental conditions with the intensity ![]() ${I}_{0} = 3\times 1{0}^{17} ~\mathrm{W} \cdot {\mathrm{cm} }^{- 2} $ and aluminum target. For a sharp leading edge, as the laser pulse was propagating in the plasma layer, the processes of the pulse self-modulation and generation of a wake were developed independent of the plasma density profile at the layer input. The evolution of self-modulation instability, shown in Figure 1, did not depend on the initial density gradient and looked identical in both cases of linear and Gaussian input density profiles (dashed lines in Figures 1(a) and 1(c)).
${I}_{0} = 3\times 1{0}^{17} ~\mathrm{W} \cdot {\mathrm{cm} }^{- 2} $ and aluminum target. For a sharp leading edge, as the laser pulse was propagating in the plasma layer, the processes of the pulse self-modulation and generation of a wake were developed independent of the plasma density profile at the layer input. The evolution of self-modulation instability, shown in Figure 1, did not depend on the initial density gradient and looked identical in both cases of linear and Gaussian input density profiles (dashed lines in Figures 1(a) and 1(c)).

Figure 1. Dimensionless projections of the electric field vector at ![]() $t= 233~\mathrm{fs} $ (
$t= 233~\mathrm{fs} $ (![]() $ct= 70~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $) (a, c) and
$ct= 70~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $) (a, c) and ![]() $t= 433~\mathrm{fs} $ (
$t= 433~\mathrm{fs} $ (![]() $ct= 130~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $) (b, d) for linear (a, b) and Gaussian (c, d) input plasma density profiles. The plasma density profiles are shown by dashed curves in parts a and c.
$ct= 130~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $) (b, d) for linear (a, b) and Gaussian (c, d) input plasma density profiles. The plasma density profiles are shown by dashed curves in parts a and c.
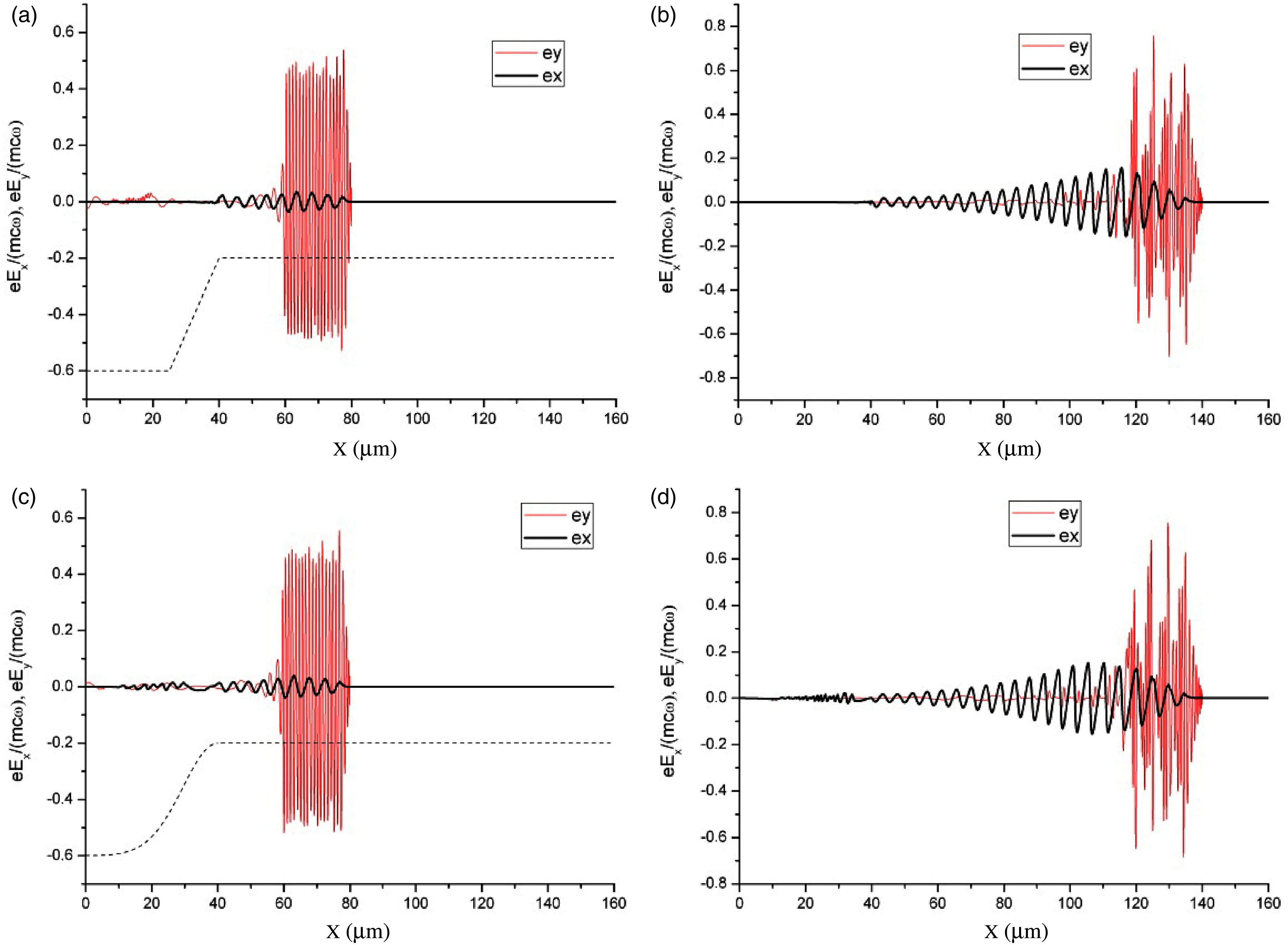
However, the phase space images showed that the dynamics of a small part of the electrons in the region of the sharp change in the spatial distribution of the plasma density at the layer input (in the case of a linear profile) radically differed from the case of a smooth Gaussian density profile passing to a homogeneous layer without jumps in the derivative. For a smooth Gaussian density profile, no electrons were injected into the wakefield and accelerated (Figures 2(c) and 2(d)). In the case of a linear input density profile, due to the sharp change in the wave phase velocity[Reference Bulanov, Inovenkov, Naumova and Sakharov25], a small part of the electrons captured by the wake wave at the boundary of the homogeneous plasma layer (Figure 2(a)) acquired a rather high energy as a result of acceleration in the rising (during the development of laser pulse self-modulation) wake wave (Figure 2(b)). For ultra-relativistic laser intensities, the mechanism of injection using the up-ramp density transition was investigated recently in Ref. Ref. [Reference Li, Sheng, Liu, Meyer-ter-Vehn, Mori, Lu and Zhang26].

Figure 2. Phase plane of electrons at ![]() $t= 233~\mathrm{fs} $ (
$t= 233~\mathrm{fs} $ (![]() $ct= 70~\unicode[.5,0][STIXGeneral,Times]{x03BC} m$) (a, c) and
$ct= 70~\unicode[.5,0][STIXGeneral,Times]{x03BC} m$) (a, c) and ![]() $t= 433~\mathrm{fs} $ (
$t= 433~\mathrm{fs} $ (![]() $ct= 130~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $) (b, d) for linear (a, b) and Gaussian (c, d) plasma density profile at the layer input.
$ct= 130~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $) (b, d) for linear (a, b) and Gaussian (c, d) plasma density profile at the layer input.
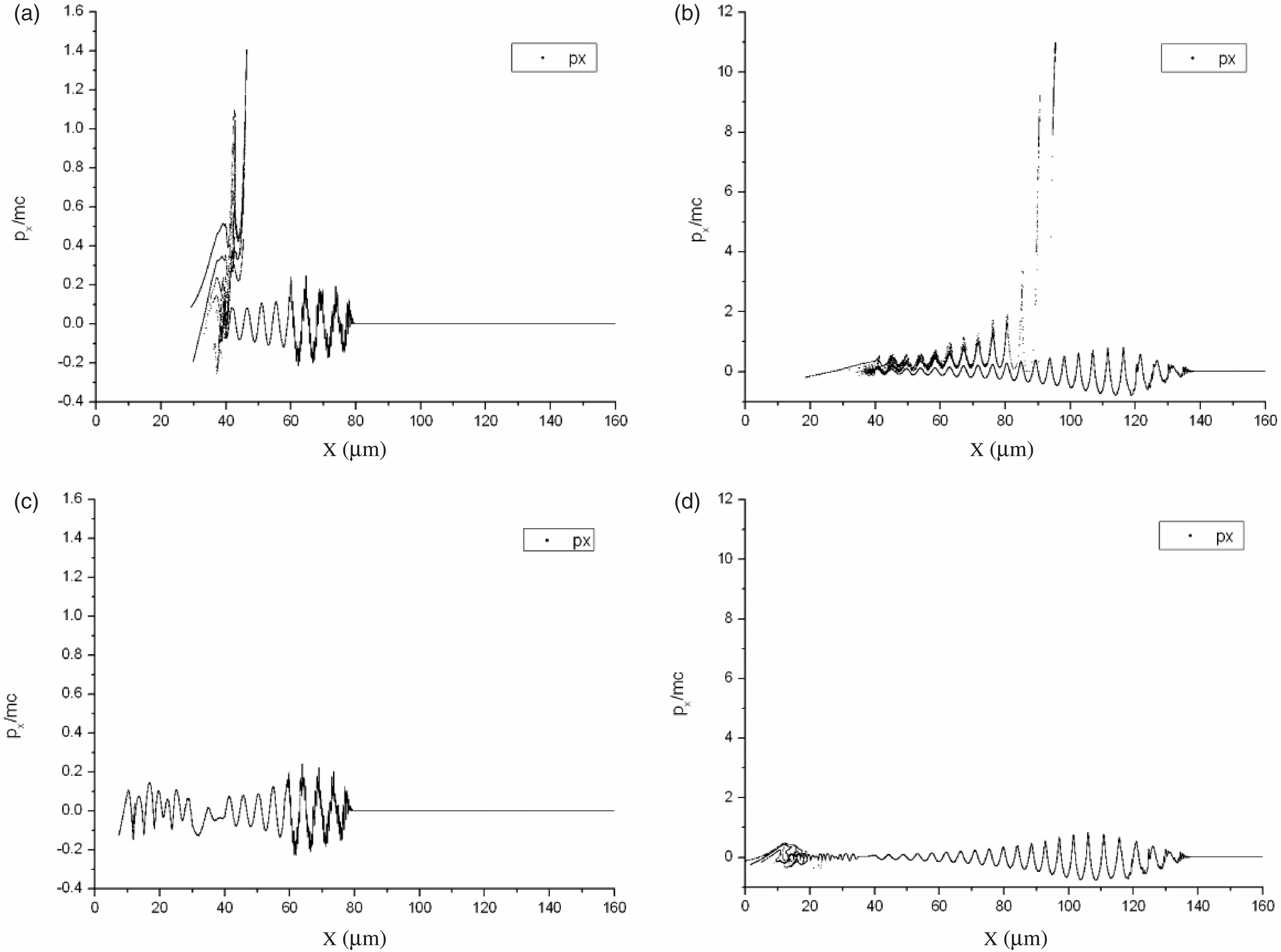
The corresponding electron energy spectrum is shown in Figure 3 on logarithmic (up to energy of ![]() ${\sim }5~\mathrm{MeV} $) and linear (up to energy of 1 MeV) scales. Figure 3(a) shows the electron spectrum in the entire range of acceleration energies (about 5 MeV; see Figure 2(b)). Several groups of accelerated electrons are observed. However, the number of accelerated electrons with energies exceeding 0.6 MeV is much smaller than the number of electrons in the main maximum of the distribution of accelerated electrons with energies from 0.5 to 0.6 MeV. This can be clearly seen in Figure 3(b), which also demonstrates another pronounced peak near
${\sim }5~\mathrm{MeV} $) and linear (up to energy of 1 MeV) scales. Figure 3(a) shows the electron spectrum in the entire range of acceleration energies (about 5 MeV; see Figure 2(b)). Several groups of accelerated electrons are observed. However, the number of accelerated electrons with energies exceeding 0.6 MeV is much smaller than the number of electrons in the main maximum of the distribution of accelerated electrons with energies from 0.5 to 0.6 MeV. This can be clearly seen in Figure 3(b), which also demonstrates another pronounced peak near ![]() ${\sim }0. 3~\mathrm{MeV} $. The formation of several groups of accelerated electrons is due to the capture and acceleration of electrons in different periods of the wake plasma wave (Figure 2(b)).
${\sim }0. 3~\mathrm{MeV} $. The formation of several groups of accelerated electrons is due to the capture and acceleration of electrons in different periods of the wake plasma wave (Figure 2(b)).
The simulation results (Figures 2 and 3) indicate that the wakefield mechanism of acceleration and formation of directed high-energy electron bunches can be implemented under our experimental conditions described below (see Figures 6 and 8). The necessary condition is the presence of a steep profile of plasma density at the input of the plasma layer formed by the laser prepulse and a sufficiently sharp leading edge of the laser pulse, which may arise as a result of ionization nonlinearity when the main femtosecond laser pulse propagates in the incompletely ionized plasma formed by the prepulse. The charge of accelerated electrons in the quasi-monoenergetic bunch with energies from 0.5 to 0.6 MeV (Figure 3(b)) emitted from the area determined by the laser beam focal spot with radius ![]() ${r}_{0} \approx 25~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $ is 5 pC; i.e., it is in the range of experimentally measured values.
${r}_{0} \approx 25~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $ is 5 pC; i.e., it is in the range of experimentally measured values.
The reason for our pilot 1D PIC simulation is the fact that under experimental conditions we expect a relatively large transverse length of plasma inhomogeneity in comparison with the radius of the laser beam (which determines the characteristic transverse size of the plasma wave responsible for electron acceleration). Note that the applicability of this approach needs further investigation. Moreover, the discussed mechanism based on the laser pulse self-modulation is not the only mechanism that can lead to collimated electron acceleration. A direct laser acceleration mechanism based on a steep perpendicular density gradient was considered in some publications, but usually it requires relativistic[Reference Li, Yuan, Xu, Zheng, Sheng, Chen, Ma, Liang, Yu, Zhang, Liu, Wang, Wei, Zhao, Jin and Zhang27] or ultra-relativistic[Reference Chen, Sheng, Zheng, Ma, Bari, Li and Zhang28] laser intensities, and also angles of incidence about ![]() $7{0}^{\circ } {\unicode{x2013}} 7{5}^{\circ } $[Reference Nakamura, Mima, Sakagami and Johzaki29], which is not the case of our experiments at intensity
$7{0}^{\circ } {\unicode{x2013}} 7{5}^{\circ } $[Reference Nakamura, Mima, Sakagami and Johzaki29], which is not the case of our experiments at intensity ![]() ${I}_{0} = 3\times 1{0}^{17} ~\mathrm{W} \cdot {\mathrm{cm} }^{- 2} $ and with a laser propagating along the target surface (see also the 2D modeling results below, Figures 4 and 5).
${I}_{0} = 3\times 1{0}^{17} ~\mathrm{W} \cdot {\mathrm{cm} }^{- 2} $ and with a laser propagating along the target surface (see also the 2D modeling results below, Figures 4 and 5).

Figure 3. Energy spectra of electrons at ![]() $t= 433~\mathrm{fs} $ (
$t= 433~\mathrm{fs} $ (![]() $ct= 130~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $) on (a) logarithmic and (b) linear scales for a linear plasma density profile at the layer input. The number of electrons per transverse (with respect to the
$ct= 130~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $) on (a) logarithmic and (b) linear scales for a linear plasma density profile at the layer input. The number of electrons per transverse (with respect to the ![]() $x$-axis) cross section with area
$x$-axis) cross section with area ![]() ${\lambda }^{2} = 1~\unicode[.5,0][STIXGeneral,Times]{x03BC} {\mathrm{m} }^{2} $ per unit energy (in MeV) is plotted on the vertical axes.
${\lambda }^{2} = 1~\unicode[.5,0][STIXGeneral,Times]{x03BC} {\mathrm{m} }^{2} $ per unit energy (in MeV) is plotted on the vertical axes.
To analyze the role of 2D plasma density inhomogeneity and finite laser pulse spot size, modeling was performed by a modified LSP 2D PIC code[Reference Kemp and Ruhl30]. To simulate the interaction, we considered the propagation of a laser pulse with duration 60 fs, different time envelopes (Gaussian and super-Gaussian), beam radius (FWHM) ![]() $60~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $, wavelength 815 nm, and intensity
$60~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $, wavelength 815 nm, and intensity ![]() ${I}_{0} = 3\times 1{0}^{17} ~\mathrm{W} / {\mathrm{cm} }^{2} $. The size of the simulation box was
${I}_{0} = 3\times 1{0}^{17} ~\mathrm{W} / {\mathrm{cm} }^{2} $. The size of the simulation box was ![]() $150\times 150~\unicode[.5,0][STIXGeneral,Times]{x03BC} {\mathrm{m} }^{2} $ with grid size 60 nm and time step 0.1 fs. The number of quasiparticles was chosen to be
$150\times 150~\unicode[.5,0][STIXGeneral,Times]{x03BC} {\mathrm{m} }^{2} $ with grid size 60 nm and time step 0.1 fs. The number of quasiparticles was chosen to be ![]() $2500\times 2500= \text{6250,000} $, 20 particles per cell.
$2500\times 2500= \text{6250,000} $, 20 particles per cell.
For the above-described 1D inhomogeneous plasma density with linear profile at the layer input (the dashed line in Figure 1(a)), 2D modeling confirmed the main findings of 1D3V modeling: a laser pulse with smooth Gaussian time envelope does not generate a wakefield and does not accelerate electrons, while for a steep leading laser pulse profile (hyper-Gaussian with power 20) acceleration of electrons takes place in much the same way as shown in Figures 1–3.
To investigate the influence of transversal (relative to the direction of laser pulse propagation, ![]() $x$-axis) inhomogeneity of plasma (along the
$x$-axis) inhomogeneity of plasma (along the ![]() $y$-axis), the ion density profile was described as
$y$-axis), the ion density profile was described as
for ![]() $y\geqslant {y}_{0} $, with maximum density
$y\geqslant {y}_{0} $, with maximum density ![]() ${n}_{0} = 1. 5\times 1{0}^{20} ~{\mathrm{cm} }^{- 3} $ at
${n}_{0} = 1. 5\times 1{0}^{20} ~{\mathrm{cm} }^{- 3} $ at ![]() ${y}_{0} = 75~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $ and density that did not grow for
${y}_{0} = 75~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $ and density that did not grow for ![]() $y\leqslant {y}_{0} $. In the above equation,
$y\leqslant {y}_{0} $. In the above equation, ![]() ${x}_{0} = 75~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $,
${x}_{0} = 75~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $, ![]() ${L}_{x} = 50~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $, and two different transverse density gradients
${L}_{x} = 50~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $, and two different transverse density gradients ![]() ${L}_{y} = 26~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $ and
${L}_{y} = 26~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $ and ![]() $13~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $ were used in the calculations. The laser pulse propagates along the
$13~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $ were used in the calculations. The laser pulse propagates along the ![]() $x$-direction with the beam axis at
$x$-direction with the beam axis at ![]() $y= 75~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $ and a Gaussian time envelope. With this smooth pulse envelope and long enough transverse plasma density scale length,
$y= 75~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $ and a Gaussian time envelope. With this smooth pulse envelope and long enough transverse plasma density scale length, ![]() ${L}_{y} = 26~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $, no accelerated electrons were detected. In the case of smaller transverse density scale length,
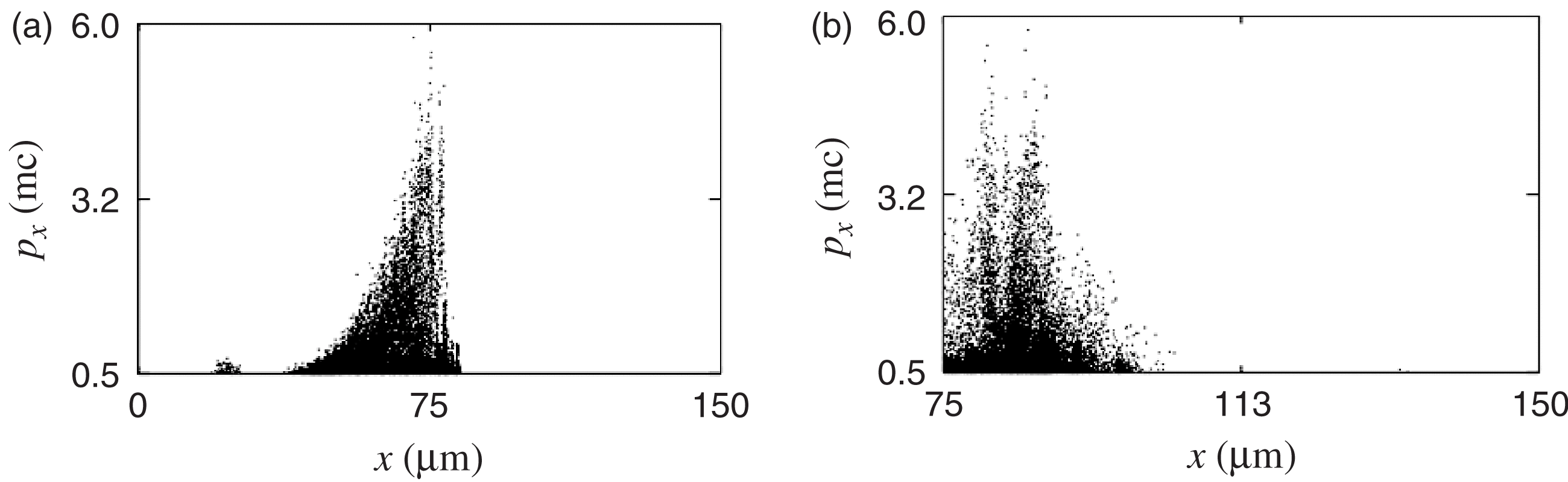
${L}_{y} = 26~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $, no accelerated electrons were detected. In the case of smaller transverse density scale length, ![]() ${L}_{y} = 13~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $, the results of simulations for longitudinal normalized momentum of electrons along the propagation axis (Figure 4(a)) and in the transversal direction (Figure 4(b)) are presented at
${L}_{y} = 13~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $, the results of simulations for longitudinal normalized momentum of electrons along the propagation axis (Figure 4(a)) and in the transversal direction (Figure 4(b)) are presented at ![]() $t= 325~\mathrm{fs} $. Near the axis of a laser beam in a region limited by plasma density
$t= 325~\mathrm{fs} $. Near the axis of a laser beam in a region limited by plasma density ![]() $1{0}^{19} {\unicode{x2013}} 1{0}^{20} ~{\mathrm{cm} }^{3} $, the presence of accelerated electrons with energy up to
$1{0}^{19} {\unicode{x2013}} 1{0}^{20} ~{\mathrm{cm} }^{3} $, the presence of accelerated electrons with energy up to ![]() ${\sim }3~\mathrm{MeV} $ is clearly seen (Figure 4(b)). Analysis of optimal parameters of laser pulses and plasma densities is the subject of further investigations.
${\sim }3~\mathrm{MeV} $ is clearly seen (Figure 4(b)). Analysis of optimal parameters of laser pulses and plasma densities is the subject of further investigations.

Figure 4. Phase diagrams (![]() $x, {p}_{x} $) (a) and (
$x, {p}_{x} $) (a) and (![]() $y, {p}_{x} $) (b) at
$y, {p}_{x} $) (b) at ![]() $t= 325~\mathrm{fs} $ for sharp density gradient.
$t= 325~\mathrm{fs} $ for sharp density gradient.
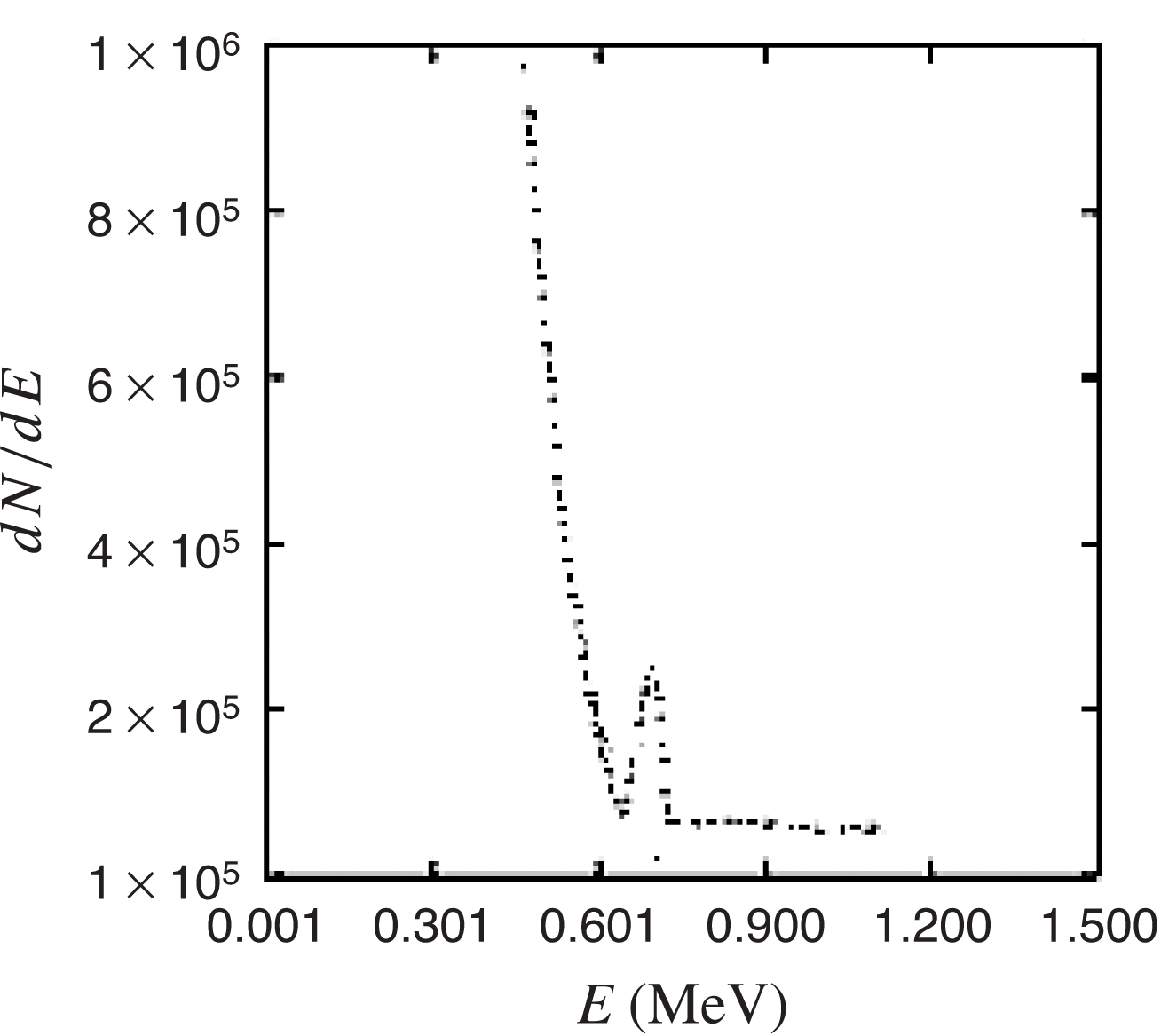
The electron energy distribution for the electrons moving in the forward direction (angle to the ![]() $x$-axis
$x$-axis ![]() $\theta = 0{\unicode{x2013}} 2{0}^{\circ } $) is presented in Figure 5 for the case of small transverse scale length, demonstrating the appearance of electron bunches with energies 0.5–1.0 MeV.
$\theta = 0{\unicode{x2013}} 2{0}^{\circ } $) is presented in Figure 5 for the case of small transverse scale length, demonstrating the appearance of electron bunches with energies 0.5–1.0 MeV.

Figure 5. Electron energy distribution at ![]() $t= 435~\mathrm{fs} $, the angle of observation is
$t= 435~\mathrm{fs} $, the angle of observation is ![]() $\mathop{[0{\unicode{x2013}} 20] }\nolimits ^{\circ } $.
$\mathop{[0{\unicode{x2013}} 20] }\nolimits ^{\circ } $.
Thus, from our 2D simulations, we can conclude that significant electron acceleration is determined by three scales of inhomogeneity: plasma density gradients along two axes and laser pulse steepness. In the case of a smooth density gradient in the transversal direction, a sharp gradient along the laser propagation axis and steep laser pulse time envelope for acceleration of electrons are demanded. For acceleration by a smooth (Gaussian) laser pulse time envelope, a sharp density gradient in the transversal direction in respect to laser beam propagation is required. The mechanism of laser electron acceleration in plasma with sharp transverse density gradients will be a subject of future investigations.
3. Experimental technique
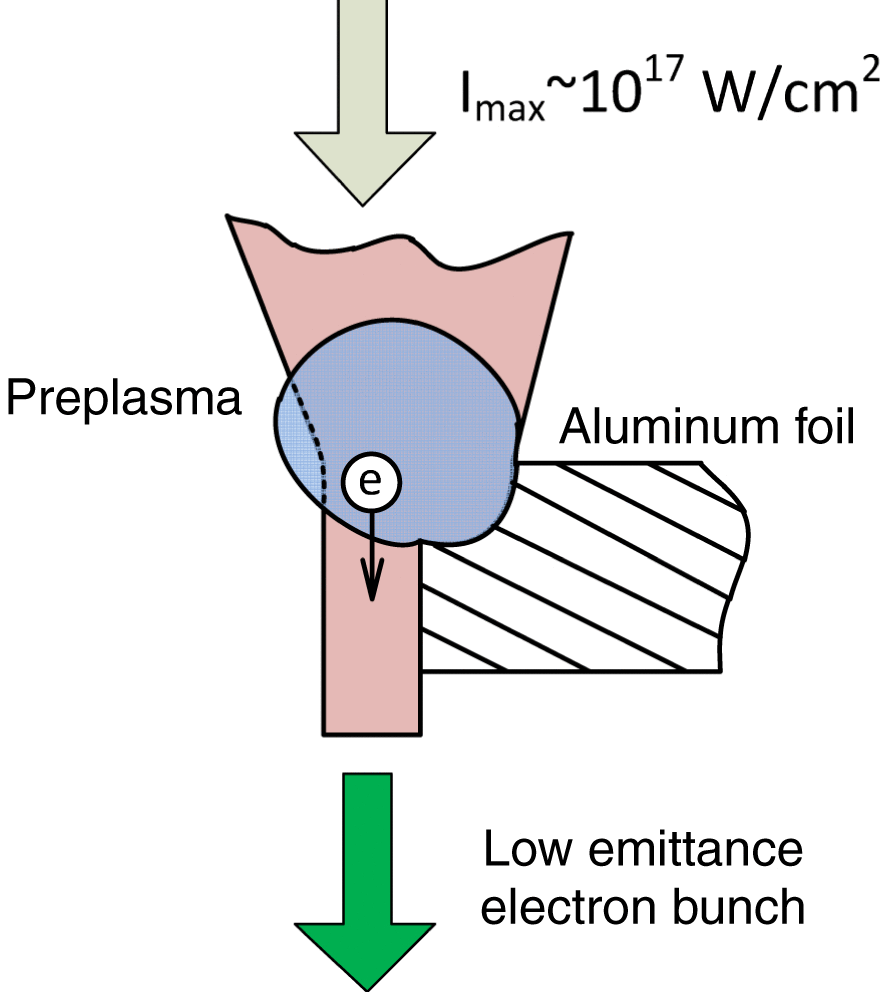
A Ti:sapphire laser generating 60 fs pulses with maximum energy up to 100 mJ and central wavelength 800 nm was used in the experiment. A spherical mirror with focal length ![]() $F= 50~\mathrm{cm} $ focused the laser beam on the edge of an aluminum foil (
$F= 50~\mathrm{cm} $ focused the laser beam on the edge of an aluminum foil (![]() $200~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $ thick), normally to its surface, placed in a vacuum camera (Figure 6). The maximum intensity in focus (
$200~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $ thick), normally to its surface, placed in a vacuum camera (Figure 6). The maximum intensity in focus (![]() $1/ {e}^{2} $ beam radius
$1/ {e}^{2} $ beam radius ![]() ${r}_{0} = 25~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $, pulse energy 100 mJ) was
${r}_{0} = 25~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $, pulse energy 100 mJ) was ![]() ${I}_{\mathrm{max} } = 2\times 1{0}^{17} ~\mathrm{W} / {\mathrm{cm} }^{2} $. The main intense pulse was preceded by a femtosecond prepulse, 12 ns ahead of the main pulse, with energy
${I}_{\mathrm{max} } = 2\times 1{0}^{17} ~\mathrm{W} / {\mathrm{cm} }^{2} $. The main intense pulse was preceded by a femtosecond prepulse, 12 ns ahead of the main pulse, with energy ![]() $1{0}^{- 4} $ of the main pulse energy. As a result, when focused on the target, the prepulse laser intensity exceeded the ionization threshold for the target material, and the main laser pulse interacted not only with the metal target but also with the plasma formed by the prepulse (Figure 6).
$1{0}^{- 4} $ of the main pulse energy. As a result, when focused on the target, the prepulse laser intensity exceeded the ionization threshold for the target material, and the main laser pulse interacted not only with the metal target but also with the plasma formed by the prepulse (Figure 6).

Figure 6. The geometry of interaction of the laser pulse and foil.
To diagnose accelerated electrons, we recorded the luminescence of a Lanex scintillation screen with known sensitivity[Reference Glinec, Faure, Guemnie-Tafo, Malka, Monard, Larbre, De Waele, Marignier and Mostafavi31] with a Hamamatsu C8484 digital camera. The scintillation screen was set about 12 cm behind the target foil. The screen was isolated from optical radiation using a ![]() $10~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $ thick aluminum film placed close to the screen surface. The minimum measurable electron energy (cutoff energy), with allowance for the scintillation screen sensitivity and the transmittance of the aluminum film, was about 140 keV.
$10~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $ thick aluminum film placed close to the screen surface. The minimum measurable electron energy (cutoff energy), with allowance for the scintillation screen sensitivity and the transmittance of the aluminum film, was about 140 keV.
The laser beam passed through the interaction region was monitored by another CCD camera. The electron energy was measured using a magnetic spectrometer 5 cm in diameter based on a pair of NdFeB magnets that provided a 0.2 kG uniform magnetic field. A metal slit was placed at the spectrometer input to collimate the electron beam. The electron energy spectra were reconstructed by luminescence data from the luminescence screen.
A laser pulse was focused by a spherical mirror on the aluminum foil edge so that approximately half of the laser beam fell on the foil and the other half passed by. The foil plane was oriented normally to the laser beam direction. A pair of motorized translators was used to adjust the transverse foil position.
4. Experimental results
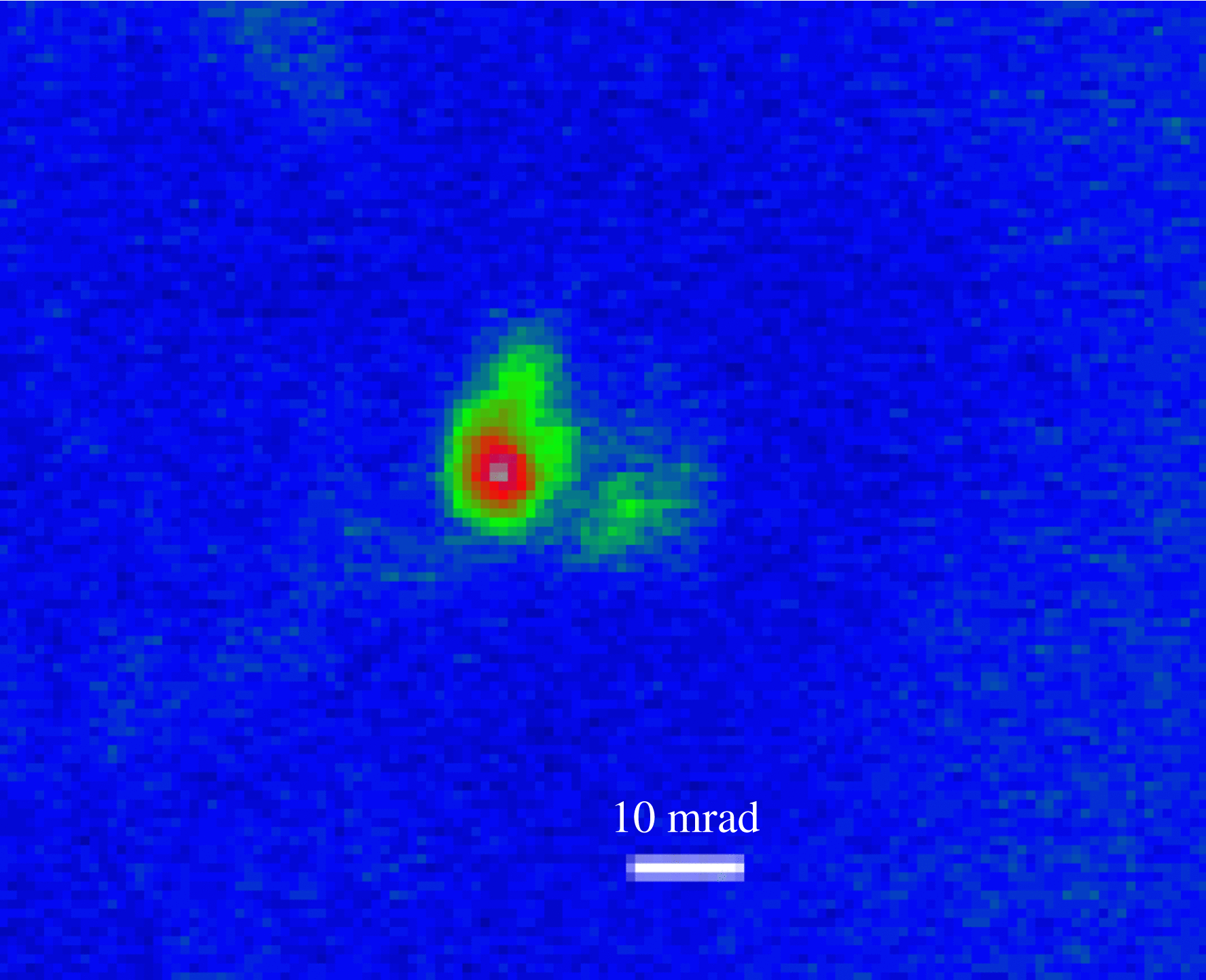
The spatial distribution of accelerated electrons was studied in the absence of the magnetic spectrometer. The same area of the foil was successively irradiated by several laser pulses. The spatial distribution of luminescence on the scintillation screen was controlled in each laser pulse. After four or five laser pulses, the screen luminescence disappeared. Visual analysis by means of an optical microscope showed the formation of a ![]() $100~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $ diameter hole in a foil at the interaction point, as a result of which the laser beam passed through without distortions. Then the foil was shifted to a new place and the procedure was repeated. The spatial distribution of luminescence for the majority of the laser pulses revealed the formation of highly collimated electron beams with an angular divergence of about 10–20 mrad propagating close to the laser beam direction (Figure 7). The beams were surrounded by a weak uniform background. The typical beam charge was within 1–10 pC estimated from the Lanex sensitivity[Reference Glinec, Faure, Guemnie-Tafo, Malka, Monard, Larbre, De Waele, Marignier and Mostafavi31], fast electron transmission through elements of diagnostics, etc.
$100~\unicode[.5,0][STIXGeneral,Times]{x03BC} \mathrm{m} $ diameter hole in a foil at the interaction point, as a result of which the laser beam passed through without distortions. Then the foil was shifted to a new place and the procedure was repeated. The spatial distribution of luminescence for the majority of the laser pulses revealed the formation of highly collimated electron beams with an angular divergence of about 10–20 mrad propagating close to the laser beam direction (Figure 7). The beams were surrounded by a weak uniform background. The typical beam charge was within 1–10 pC estimated from the Lanex sensitivity[Reference Glinec, Faure, Guemnie-Tafo, Malka, Monard, Larbre, De Waele, Marignier and Mostafavi31], fast electron transmission through elements of diagnostics, etc.

Figure 7. Angular distribution of electron beam formed by focusing laser radiation onto the foil edge.
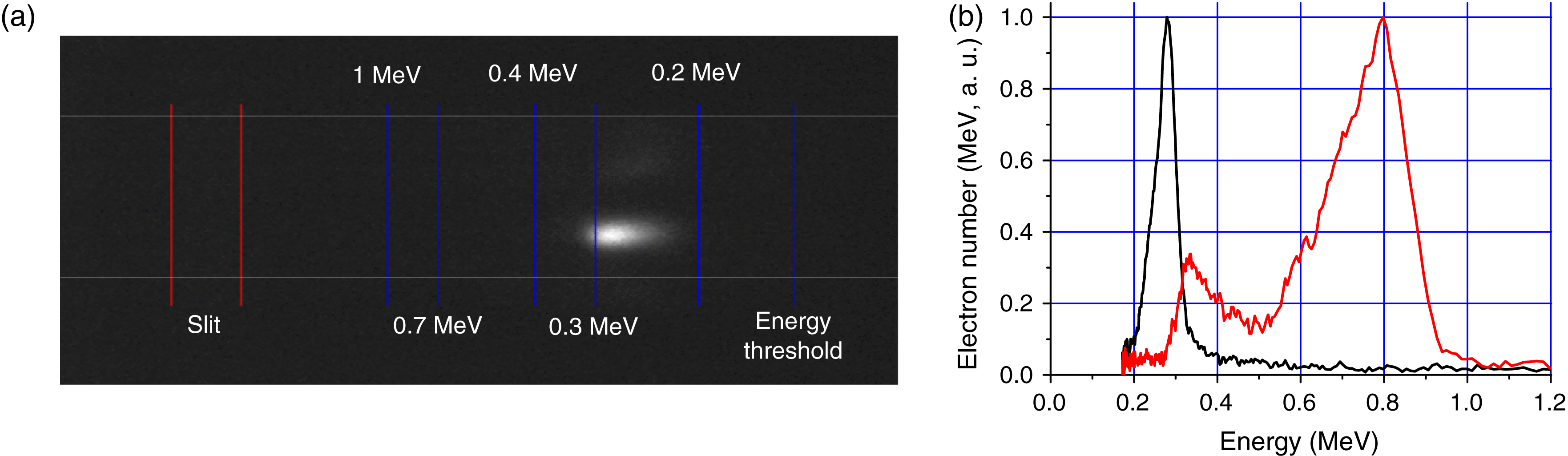
To measure the energy spectrum of spatially collimated beams, we place a magnetic spectrometer with an input slit in front of the scintillation screen. An example of the Lanex screen luminescence after the spectrometer for a single laser pulse is presented in Figure 8(a). The energy spectrum was found to have a nonmonotonic energy distribution with one or several peaks. Energy distribution with a single energy peak with width (FWHM) less than 20% of the energy at maximum was observed for some laser pulses. An example of such a spectrum is shown in Figure 8(b), black line. In other laser pulses, the energy spectra demonstrated several peaks Figure 8(b), red lines. The spectra presented correspond to laser pulse energies in the 60–80 mJ range. Typically the electron energy peaks lie within 0.2–0.8 MeV. Note that the energy spread in the case of narrow peaks was determined by the resolution of our diagnostics, and it may be even narrower in real conditions.

Figure 8. Typical distribution of scintillation screen luminescence (a) and experimental electron energy spectra (b) with a single peak (black) and with two peaks (red). The blue lines in (a) correspond to different electron energies. The red lines correspond to projections of the slit on the scintillator screen.
5. Conclusions
In this paper, we report the results of experimental and theoretical studies of a source of accelerated electrons that can be used for injection in schemes of laser–plasma acceleration of electrons in a plasma wave[Reference Eremin, Malkov, Korolikhin, Kiselev, Skobelev, Stepanov and Andreev13,Reference Wojda, Cassou, Genoud, Burza, Glinec, Lundh, Persson, Vieux, Brunetti, Shanks, Jaroszynski, Andreev, Wahlström and Cros14] .
The experiment on irradiation of an aluminum foil edge by a focused high-intensity femtosecond laser pulse showed generation of highly collimated quasi-monochromatic electron beams whose direction coincided with the laser beam propagation direction. The electron energy in the energy distribution peak was 0.2–0.8 MeV, with peak width smaller than 20%; the beam divergence was ![]() $0. 5{\unicode{x2013}} {1}^{\circ } $. The high directionality of the electron beam and its narrow energy spectrum can be explained by the acceleration of electrons in the plasma wave generated as a result of self-modulation instability of an intense laser pulse in the plasma formed by the prepulse arriving at the target about 10 ns before the main pulse.
$0. 5{\unicode{x2013}} {1}^{\circ } $. The high directionality of the electron beam and its narrow energy spectrum can be explained by the acceleration of electrons in the plasma wave generated as a result of self-modulation instability of an intense laser pulse in the plasma formed by the prepulse arriving at the target about 10 ns before the main pulse.
The results of one (1D3V) and two (LSP 2D) PIC code simulations of the interaction of femtosecond laser radiation with dense plasma showed that effective excitation of a plasma wave as well as trapping and acceleration of electron beams to the energies of about 1 MeV may occur in the presence of plasma inhomogeneities at the plasma boundary, sharp transversal density gradients, and laser pulse time envelope steepness. Under our experimental conditions, the inhomogeneities in the temporal envelope of the laser pulse may be caused by ionization nonlinearity of the plasma formed by the prepulse, and the spatial density inhomogeneities may be due to the sharp boundaries of the foil and the complex configuration of the plasma spread.
Acknowledgements
This work was supported by the programme ‘Extreme Light Fields and Their Applications’ of the Presidium of the Russian Academy of Sciences.