1 Introduction
Over recent decades, fiber lasers and amplifiers have attracted great interest owing to their advantages of high slope efficiency, high beam quality, superior thermal management property, and compactness[Reference Tünnermann, Schreiber, Röser, Liem, Höfer, Zellmer, Nolte and Limpert1]. Fiber lasers and amplifiers are widely used in the field of laser marking, material processing[Reference Ikoma, Nguyen, Kashiwagi, Uchiyama, Shima and Tanaka2], and many other industrial applications. Although the power of single-mode fiber laser system has already reached a high level of 10 kW[Reference Jauregui, Limpert and Tünnermann3], scientific and industrial applications seek much higher laser power and light beam quality[Reference Limpert, Roser, Klingebiel, Schreiber, Wirth, Peschel, Eberhardt and Tiinnermann4]. However, nonlinear effects induced by high laser power limit further scaling of the output power. For example, single-frequency or narrow-linewidth fiber lasers' power scaling is limited by stimulated Brillouin scattering (SBS), and power scaling for ultrashort pulsed fiber laser systems is limited by stimulated Raman scattering (SRS). Therefore, suppressing nonlinear effects is particularly critical for further scaling of the output power from high-power fiber lasers and amplifiers[Reference Liu, Liu, Zhang, Hou, Qi, Feng and Wang5, Reference Nodop, Jauregui, Jansen, Limpert and Tünnermann6]. The most direct and effective approach to increase the threshold of nonlinear effects is to increase the effective mode area (A eff), and the simplest and most obvious way of increasing A eff is to increase the core diameter (D) and decrease numerical aperture (NA). Fibers that achieve large mode area (LMA) by increasing the core diameter and decreasing NA are widely applied in high-power fiber laser system[Reference Richardson, Offerhaus and Broderick7]. Such LMA fibers can effectively mitigate nonlinear effects[Reference Morandotti, Jäger, Ruda, Caplette, Verville, Yao and Villeneuve8], but there are two emerging problems in practical applications. One is that they support high-order modes (HOMs) owing to the larger core diameter and lower NA, which results in transverse mode instability (TMI) at high average power levels[Reference Huang, Yao, Leng, Guo, Tao, Zhou and Cheng9]; the other is that such fibers become highly sensitive to bending, which results in high bending loss and severe mode area compression. Therefore, it is important for LMA fibers to suppress nonlinear effects and ensure transverse mode stability simultaneously.
Over the past decade, varieties of LMA fibers have been proposed to scale output power and ensure high beam quality in high-power fiber laser and amplifier systems. The novel LMA fibers include photonic crystal fiber (PCF)[Reference Kumar, Saini, Naik and Sinha10], leakage channel fiber (LCF)[Reference Gu, Kong, Hawkins, Foy, Wei, Samson and Dong11], rod-type fiber[Reference Jain, Baskiotis and Sahu12], low-NA step index fiber (SIF)[Reference Jain, Jung, Barua, Alam and Sahu13], segmented cladding fiber (SCF)[Reference Rastogi and Chiang14, Reference Ma, Ning, Lu, Zheng, Li and Pei15], and other promising LMA fibers[Reference Jain, Baskiotis, May-Smith, Kim and Sahu16, Reference Dawson, Messerly, Heebner, Pax and Dubinskii17]. Much effort has been directed towards developing novel fiber designs that offer LMA and single-mode operation. For example, SIF obtains LMA by increasing core radius and decreasing NA, and single-mode propagation by bend-induced HOMs filtering. PCF and LCF with special fiber structures show good potential for mode area scaling and single-mode operation, but their performances become worse under bending. SCF, first reported by Rastogi and Chiang in 2001[Reference Rastogi and Chiang14], is characterized by its cladding that has periodic distribution of high and low refractive indices in the angular direction, and it can have both large core and high NA. In 2004, the large-core SCFs made from polymer material were first demonstrated by Yeung et al.[Reference Yeung, Chiang, Rastogi, Chu and Peng18], and the large-core four-segment and eight-segment SCFs were fabricated by the cladding-segment-in-tube technique and cladding-core-segment-in-tube technique, respectively. In 2015, Hooda et al.[Reference Hooda, Pal, Rastogi, Sen, Gandhi and Kobelke19] demonstrated fabrication of a silica-based SCF by using the stack-and-draw technique, and the fabricated SCF showed efficient HOMs filtering. HOMs propagating in SCF can be stripped off by taking advantage of high leakage loss difference between fundamental mode and them. Therefore, large-core SCF can simultaneously support LMA and single-mode operation, which is attractive for high-power fiber lasers and amplifiers.
In addition to these longitudinal uniform LMA fibers, a novel promising tapered fiber design has been developed in recent years. Different from the longitudinal uniform fibers, core and cladding diameters of tapered fibers vary along the fiber length. In high-power fiber laser and amplifier systems, tapered LMA fibers exhibit numerous unique advantages compared with regular LMA fibers, such as higher absorption per unit length, intrinsic built-in mechanism for amplified spontaneous emission (ASE) suppression, and a high factor of brightness. In 2015, a polarization-maintaining Yb-doped tapered fiber was applied to an ultrashort pulse fiber laser system[Reference Koptev, Anashkina, Bobkov, Likhachev, Levchenko, Aleshkina, Semjonov, Denisov, Bubnov, Lipatov, Laptev, Gur'yanov, Andrianov, Muravyev and Kim20]. The tapered fiber with a single-mode input end (core and cladding diameters of 10 and 80 Ҽm) and a multimode output end (core and cladding diameters of 45 and 430 Ҽm) was used as the output amplifier stage to reach the megawatt output power. In 2016, a tapered double-clad fiber (T-DCF) was demonstrated and used as gain fiber in the continuous wave (CW) high-power amplifier system, actively Q-switched fiber laser, and picosecond pulsed fiber laser system.[Reference Ballato, Filippov, Chamorovskii, Golant, Vorotynskii and Okhotnikov21] In 2017, LMA Yb-doped tapered fiber fabricated by a non-stationary fiber drawing process was employed in a high-power fiber amplifier system, which ensured a low ASE level and realized a high peak power of 22 MW[Reference Bobkov, Andrianov, Koptev, Muravyev, Levchenko, Velmiskin, Aleshkina, Semjonov, Lipatov, Guryanov, Kim and Likhachev22]. In 2018, a birefringent Yb-doped tapered fiber was demonstrated for linearly polarized CW and pulsed high-power amplifiers.[Reference Fedotov, Noronen, Gumenyuk, Ustimchik, Chamorovskii, Golant, Odnoblyudov, Rissanen, Niemi and Filippov23] In 2019, the double cladding tapered Yb-doped fiber was used in a high-power monolithic fiber laser oscillator, which obtained the maximum average power of 1720 W when employing 975 nm pump source,[Reference Yang, Zhang, Shi, Wang, Pan, Wang, Zhou and Xu24] but the TMI effect occurred at the output power of 1350 W when employing 915 nm pump.
In this paper, a tapered segmented cladding fiber (T-SCF) is proposed. Modal loss, effective mode area, power evolution, and heat load density of T-SCFs with concave, linear, and convex tapered structures are theoretically investigated based on a finite-element method (FEM) and few-mode steady-state rate equation. The simulation consists of three parts. In the first part, mode characteristics of straight and bent T-SCFs with different parabolic shape factors (b) are investigated by the FEM. In the second part, we set the small end of the T-SCF as the pump and signal input end, and simulate the amplification characteristics of T-SCFs based on a simple amplifier model and a few-mode steady-state rate equation. In addition, we compare laser performance of the amplifier based on T-SCF with that of the amplifier based on tapered step index fiber (T-SIF). In the third part, we choose the large end of the T-SCF as the pump and signal input end, and study the laser performances of the amplifier based on T-SCF. Results show that the concave tapered structure can provide high modal loss for HOMs, whereas the convex tapered structure presents large effective mode area. Thus, concave T-SCF has advantages on stripping off HOMs but convex T-SCF can mitigate nonlinear effects more effectively. Single-mode operation is easier to achieve for T-SCF under small-to-large amplification scheme, whereas heat load density of T-SCF under large-to-small amplification scheme is much lower than that under small-to-large amplification scheme. These results suggest that the tapered structure and amplification scheme have an effect on the mode characteristics and laser performance, which provides theoretical foundations for developing compact high-power fiber lasers and amplifiers.
2 Theory and model
The schematic of the SCF is displayed in Figure 1. Parameters a and b are the core and cladding radii, respectively, and φ is the azimuth angle between the x-axis and bending orientation. The fiber comprises a uniform core region (0 < r < a) with high refractive index (n 1) and a segmented cladding region (a < r < b). The low-index (n 2) segments and high-index (n 1) segments alternate periodically and angularly, and their angular widths are θ 1 and θ 2. The period of the segment cladding is defined as Λ = θ 1 + θ 2, and N is the number of the fiber cladding segments. The refractive index difference between n 1 and n 2 is characterized by Δ = (n 12−n 22)/2n 12 and we assume Δ![]() $\ll$1, so the SCF can be considered as weakly guiding fiber. The transverse component of the electromagnetic field of the weakly guiding fiber satisfies the scalar wave equation. The scalar wave equation for SCF can be solved by the radial effective-index method (REIM) and FEM[Reference Al-Alimi, Bakar, Abidin, Abas, Alresheedi and Mahdi26] and the transverse mode characteristics are simulated by FEM in this paper.
$\ll$1, so the SCF can be considered as weakly guiding fiber. The transverse component of the electromagnetic field of the weakly guiding fiber satisfies the scalar wave equation. The scalar wave equation for SCF can be solved by the radial effective-index method (REIM) and FEM[Reference Al-Alimi, Bakar, Abidin, Abas, Alresheedi and Mahdi26] and the transverse mode characteristics are simulated by FEM in this paper.

Figure 1 Schematic diagram of the SCF, N = 6[Reference Ma, Ning, Li, Zheng, Wen and Pei25].
Tapered fibers include the fast-varying tapered fiber and slowly varying tapered fiber. The length of fast varying tapered fibers is generally short (even in the millimeter range)[Reference Al-Alimi, Bakar, Abidin, Abas, Alresheedi and Mahdi26], while the length of slowly varying tapered fiber ranges from several to hundreds of meters, and Figure 2 displays three novel tapered structures[Reference Okhotnikov27, Reference Tian, Chen, Leng, Yao, Zhou and Chen28]. In this paper, our numerical simulation concerns on the long T-SCF that has a longitudinally varying core/cladding radius along the fiber length, and the core radius profile of the T-SCF can be given by[Reference Shi, Wang, Zhou, Xu and Lu29]
 $$\begin{align}\rho (z)=\frac{b_0-{b}_{\mathrm{f}}}{2L}{z}^2+\frac{b_{\mathrm{f}}}{2}z+\frac{1}{2}{D}_1,\end{align}$$
$$\begin{align}\rho (z)=\frac{b_0-{b}_{\mathrm{f}}}{2L}{z}^2+\frac{b_{\mathrm{f}}}{2}z+\frac{1}{2}{D}_1,\end{align}$$where D 1 and D 2 are the core diameters of the small and large end, respectively, L is the length of T-SCF, b f is the parabolic shape factor, and b 0 = (D 2 – D 1)/L is average taper angle. According to the difference between b f and b 0, the radius profile can be divided into three categories shown in Figure 3, which include b f < b 0, b f = b 0, and b f > b 0 corresponding to concave, linear, and convex radius profile.

Figure 2 Three major tapered categories: (a) concave tapered fiber, (b) linear tapered fiber, and (c) convex tapered fiber.

Figure 3 Effects of different parabolic shape factors on the core radius profile (from the small end to the large end).
Longitudinal stretching along the fiber length results in elasto-optical effect when the fiber is curved, which makes the refractive index change. We take into account refractive index perturbations induced by bending, and employ coordinate transformation that allows the bent fiber to be represented by an equivalent, straight fiber with modified refractive index distribution. Considering the non-circular symmetry and tapered structure of SCF, the bend-induced refractive index should be φ-dependent and z-dependent, and it takes the form[Reference Ma, Ning, Lu, Zheng, Li and Pei15]
 $$\begin{align}{n}_{\mathrm{bent}}\left(x,y,z\right)={n}_{\mathrm{straight}}\left(x,y,z\right)\left(1+\frac{\overrightarrow{x}\cos \varphi +\overrightarrow{y}\sin \varphi }{\rho R}\right),\end{align}$$
$$\begin{align}{n}_{\mathrm{bent}}\left(x,y,z\right)={n}_{\mathrm{straight}}\left(x,y,z\right)\left(1+\frac{\overrightarrow{x}\cos \varphi +\overrightarrow{y}\sin \varphi }{\rho R}\right),\end{align}$$where n straight(x, y, z) is the index profile of the straight fiber, R is the bending radius, and ![]() $\overrightarrow{x}$ and
$\overrightarrow{x}$ and ![]() $\overrightarrow{y}$ denote the orientation of Cartesian coordinates. Note that ρ is fixed to 1.25 when taking account of the stress factor for the silica-based fiber.[Reference Ma, Ning, Lu, Zheng, Li and Pei15]
$\overrightarrow{y}$ denote the orientation of Cartesian coordinates. Note that ρ is fixed to 1.25 when taking account of the stress factor for the silica-based fiber.[Reference Ma, Ning, Lu, Zheng, Li and Pei15]
In optical fibers, the modal field actually distributes both in the core and in cladding. The leakage structure of SCF suggests that modal fields may have more distribution in cladding, and thus modal fields would experience greater leakage loss. In addition, bend-induced stress can have a significant effect on leakage loss. In high-power laser and amplifier systems, it can achieve single-mode operation by taking advantages of leakage loss characteristics. In this paper, we focus on the modal leakage loss aiming at achieving HOMs filtering by coiling fiber. Based on Equations (1) and (2), we can determine the LP modes of SCF and simulate their bend-induced characteristics by FEM. The effective index of the ith mode (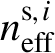 ${n}_{\mathrm{eff}}^{{\rm s},i}$) becomes complex with the real part and the imaginary part under FEM, and the imaginary part is related to the modal loss that can be expressed as[Reference Han, Gao, Zhao and Hou30]
${n}_{\mathrm{eff}}^{{\rm s},i}$) becomes complex with the real part and the imaginary part under FEM, and the imaginary part is related to the modal loss that can be expressed as[Reference Han, Gao, Zhao and Hou30]
 $$\begin{align}{\alpha}_{\text{\rm s},i}(Z)=\frac{20}{\mathrm{In}10}\frac{2\pi }{\lambda}\operatorname{Im}\left({n}_{\text{\rm eff}}^{\text{\rm s},i}\right).\end{align}$$
$$\begin{align}{\alpha}_{\text{\rm s},i}(Z)=\frac{20}{\mathrm{In}10}\frac{2\pi }{\lambda}\operatorname{Im}\left({n}_{\text{\rm eff}}^{\text{\rm s},i}\right).\end{align}$$As in the previous work[Reference Jain, Nunez-Velazquez and Sahu31], we assume an additional layer known as a perfectly matched layer (PML) in the outer boundary region to absorb the leakage light from the cladding when simulating mode loss. In reality, high absorption for leakage light in the cladding can be ensured by employing the cladding light stripper.
We propose a simple amplifier model based on the T-SCF, and then there are two amplification schemes owing to the different signal input end. A large-to-small amplification scheme denotes that the large end of the T-SCF is the signal input end, whereas a small-to-large amplification scheme means that the small end of the T-SCF is the signal input end. Based on the z-dependent transverse mode parameters calculated by FEM, then amplification characteristics can be simulated by the few-mode steady-state rate equation:
 $$\begin{align}\frac{N_2(z)}{N_{\mathrm{Yb}}}&=\bigg\{\displaystyle \frac{\left[{P}_{\mathrm{p}}^{+}(z)+{P}_{\mathrm{p}}^{-}(z)\right]{\sigma}_{\mathrm{ap}}{{\it \Gamma}}_{\mathrm{p}}(z)}{h{\nu}_{\mathrm{p}}{A}_{\mathrm{dope}}(z)}\nonumber\\[4pt]&\quad+\sum \displaystyle\frac{\left[{P}_{\mathrm{s},i}^{+}(z)+{P}_{\mathrm{s},i}^{-}(z)\right]{\sigma}_{\mathrm{as}}{\it \Gamma}_{\mathrm{s},i}(z)}{h{\nu}_{\mathrm s}{A}_{\mathrm{dope}}(z)}\bigg\}\nonumber\\[4pt]&\times\bigg\{\displaystyle\frac{\left[{P}_{\mathrm{p}}^{+}(z)+{P}_{\mathrm{p}}^{-}(z)\right]\left({\sigma}_{\mathrm{ap}}+{\sigma}_{\mathrm{ep}}\right){\it \Gamma}_{\mathrm{p}}(z)} {h{\nu}_{\mathrm p}{A}_{\mathrm{dope}}(z)}\nonumber\\[4pt]&\quad+\sum \displaystyle\frac{\left[{P}_{\mathrm{s},i}^{+}(z)+{P}_{\mathrm{s},i}^{-}(z)\right]\left({\sigma}_{\mathrm{as}}+{\sigma}_{\mathrm{es}}\right){\it \Gamma}_{\mathrm{s},i}(z)}{h{\nu}_{\mathrm s}{A}_{\mathrm{dope}}(z)} +\displaystyle\frac{1}{\tau }\bigg\}^{-1}, \end{align}$$
$$\begin{align}\frac{N_2(z)}{N_{\mathrm{Yb}}}&=\bigg\{\displaystyle \frac{\left[{P}_{\mathrm{p}}^{+}(z)+{P}_{\mathrm{p}}^{-}(z)\right]{\sigma}_{\mathrm{ap}}{{\it \Gamma}}_{\mathrm{p}}(z)}{h{\nu}_{\mathrm{p}}{A}_{\mathrm{dope}}(z)}\nonumber\\[4pt]&\quad+\sum \displaystyle\frac{\left[{P}_{\mathrm{s},i}^{+}(z)+{P}_{\mathrm{s},i}^{-}(z)\right]{\sigma}_{\mathrm{as}}{\it \Gamma}_{\mathrm{s},i}(z)}{h{\nu}_{\mathrm s}{A}_{\mathrm{dope}}(z)}\bigg\}\nonumber\\[4pt]&\times\bigg\{\displaystyle\frac{\left[{P}_{\mathrm{p}}^{+}(z)+{P}_{\mathrm{p}}^{-}(z)\right]\left({\sigma}_{\mathrm{ap}}+{\sigma}_{\mathrm{ep}}\right){\it \Gamma}_{\mathrm{p}}(z)} {h{\nu}_{\mathrm p}{A}_{\mathrm{dope}}(z)}\nonumber\\[4pt]&\quad+\sum \displaystyle\frac{\left[{P}_{\mathrm{s},i}^{+}(z)+{P}_{\mathrm{s},i}^{-}(z)\right]\left({\sigma}_{\mathrm{as}}+{\sigma}_{\mathrm{es}}\right){\it \Gamma}_{\mathrm{s},i}(z)}{h{\nu}_{\mathrm s}{A}_{\mathrm{dope}}(z)} +\displaystyle\frac{1}{\tau }\bigg\}^{-1}, \end{align}$$ $$\begin{align}\pm \frac{{\mathrm{d}P}_{\mathrm{p}}^{\pm }(z)}{\mathrm{d}z}&={\it \Gamma}_{\mathrm{p}}(z)\left[{\sigma}_{\mathrm{ep}}{N}_2(z)-{\sigma}_{\mathrm{ap}}{N}_1(z)\right]{P}_{\mathrm{p}}^{\pm }(z)\notag\\&\quad{}-\frac{\ln 10}{10}{\alpha}_{\mathrm{p}}(z){P}_{\mathrm{p}}^{\pm }(z),\end{align}$$
$$\begin{align}\pm \frac{{\mathrm{d}P}_{\mathrm{p}}^{\pm }(z)}{\mathrm{d}z}&={\it \Gamma}_{\mathrm{p}}(z)\left[{\sigma}_{\mathrm{ep}}{N}_2(z)-{\sigma}_{\mathrm{ap}}{N}_1(z)\right]{P}_{\mathrm{p}}^{\pm }(z)\notag\\&\quad{}-\frac{\ln 10}{10}{\alpha}_{\mathrm{p}}(z){P}_{\mathrm{p}}^{\pm }(z),\end{align}$$ $$\begin{align}\pm \frac{{\mathrm{d}P}_{\mathrm{s},i}^{\pm }(z)}{\mathrm{d}z}&=\left[{\sigma}_{\mathrm{es}}{N}_2(z)-{\sigma}_{\mathrm{as}}{N}_1(z)\right]{\it \Gamma}_{\mathrm{s},i}(z){P}_{\mathrm{s},i}^{\pm }(z)\notag\\&\quad{}-\frac{\ln 10}{10}{\alpha}_{\mathrm{s},i}(z){P}_{\mathrm{s},i}^{\pm }(z),\end{align}$$
$$\begin{align}\pm \frac{{\mathrm{d}P}_{\mathrm{s},i}^{\pm }(z)}{\mathrm{d}z}&=\left[{\sigma}_{\mathrm{es}}{N}_2(z)-{\sigma}_{\mathrm{as}}{N}_1(z)\right]{\it \Gamma}_{\mathrm{s},i}(z){P}_{\mathrm{s},i}^{\pm }(z)\notag\\&\quad{}-\frac{\ln 10}{10}{\alpha}_{\mathrm{s},i}(z){P}_{\mathrm{s},i}^{\pm }(z),\end{align}$$where N 1/N 2 and N Yb are the lower/upper state population and Yb3+ ion concentration, respectively; 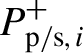 ${P}_{\mathrm{p}/\mathrm{s},i}^{+}$ and
${P}_{\mathrm{p}/\mathrm{s},i}^{+}$ and ![]() ${P}_{\mathrm{p}/ \mathrm{s},i}^{-}$ represent the forward and backward pump/ith modal power; σ ap/σ ep and σ as/σ es are the absorption/emission cross-sections at the pump and signal wavelengths; α p(z) and α s,i(z) are the pump loss and ith mode loss that can be calculated according to Equation (3), and the units for those losses are dB/m; the pump and ith mode power fill factor are denoted by
${P}_{\mathrm{p}/ \mathrm{s},i}^{-}$ represent the forward and backward pump/ith modal power; σ ap/σ ep and σ as/σ es are the absorption/emission cross-sections at the pump and signal wavelengths; α p(z) and α s,i(z) are the pump loss and ith mode loss that can be calculated according to Equation (3), and the units for those losses are dB/m; the pump and ith mode power fill factor are denoted by ![]() ${\it \Gamma}$p(z) and
${\it \Gamma}$p(z) and ![]() ${\it \Gamma}$s,i(z); and A dope(z) is the effective ion-doped area that is mainly dependent on Equation (1).
${\it \Gamma}$s,i(z); and A dope(z) is the effective ion-doped area that is mainly dependent on Equation (1).
The rare-earth-doped core can act as a heat source under a high-power pump[Reference Jauregui, Stihler and Limpert32], and thus the longitudinally varying core radius of T-SCF results in longitudinally varying heat load density that is
 $$\begin{align}q=\frac{Q(z)}{A_{\mathrm{dope}}(z)}=\frac{\left(\frac{{\mathrm{d}P}_{\mathrm{p}}^{-}}{\mathrm{d}z}-\frac{{\mathrm{d}P}_{\mathrm{p}}^{+}}{\mathrm{d}z}\right)\times \left(1-\frac{\lambda_{\mathrm{p}}}{\lambda_\mathrm{s}}\right)}{A_{\mathrm{dope}}(z)},\end{align}$$
$$\begin{align}q=\frac{Q(z)}{A_{\mathrm{dope}}(z)}=\frac{\left(\frac{{\mathrm{d}P}_{\mathrm{p}}^{-}}{\mathrm{d}z}-\frac{{\mathrm{d}P}_{\mathrm{p}}^{+}}{\mathrm{d}z}\right)\times \left(1-\frac{\lambda_{\mathrm{p}}}{\lambda_\mathrm{s}}\right)}{A_{\mathrm{dope}}(z)},\end{align}$$where q and Q are the heat load density and heat load.
Both fiber radius profile and refractive index distribution are z-dependent that can induce the mode characteristics to evolve along the T-SCF, and thus laser performance can present evolution behaviors. In the following section, we analyze the mode and laser evolution characteristics of SCF with different tapered structures.
3 Results and discussion
This section consists of three parts. In the first part, we simulate fiber core radius and modal loss characteristics that change along T-SCF according to Equations (1)–(3). In the second part, the laser characteristics of the T-SCF under a large-to-small amplification scheme are analyzed by substituting the mode parameters calculated in the first part into Equations (4)–(7), and are compared with that of the T-SIF under a large-to-small amplification scheme. In the third part, laser characteristics of the T-SCF under a small-to-large amplification scheme are discussed. Assuming the T-SCF is doped with ytterbium ions, we choose the cladding radius in the small end of the fiber b 1 = 62.5 Ҽm and keep the cladding–core radius ratio as 6.25. Then we preliminarily optimize the fiber parameters to ensure that the loss of LP01 of T-SCF is lower than 0.1 dB/m[Reference Li, Liu, Gray, Wang, Walton and Zenteno33] and to ensure saturation amplification for LP01 mode. The initial simulation parameters are listed in Table 1.
Table 1 The initial simulation parameters.

3.1 Mode characteristics of T-SCF
Figure 3 clearly demonstrates the core radius profile for different tapered structures. Note that the legends in the figure mean the proportional relationship between the parabolic shape factor b f and the average taper angle b 0. For example, 0.1b 0 represents the relational expression b f = 0.1b 0. It is obvious that T-SCF with a larger parabolic shape factor has a larger core radius at the same fiber position. Therefore, T-SCF with a larger parabolic shape factor would be better for enlarging mode area. These characteristics of the fiber structure may have an effect on the T-SCF-based laser and amplifier performance. On the one hand, LMA is helpful for mitigating nonlinear effects. On the other hand, the large core radius may reduce HOMs loss that has a negative effect on single-mode operation. In the following, we analyze the mode loss, amplification characteristics, and single-mode propagation for T-SCF with different parabolic shape factor. We choose 0.1b 0, 1b 0, and 1.9b 0 to denote the concave, linear, and convex T-SCF, respectively.
Based on initial parameters and keeping the clad-to-core ratio as a constant of 6.25, we simulate the mode loss of straight and bent T-SCF using FEM. Simulation results show that mode losses of LP11 (LP11o and LP11e) and LP31e are lower than the losses of other HOMs, where the subscripts ‘e’ or ‘o’ added to the LP modal labels denote that the mode is even or odd with respect to the y-axis. For example, the minimum losses of LP11o and LP31e are 0.346 and 0.247 dB/m, respectively, whereas the minimum loss of LP21 is as high as 38.6 dB/m along the T-SCF. Such high mode losses can make those HOMs be stripped off easily. Therefore, we focus on the mode and amplification characteristics of LP01, LP11, and LP31e in the following analyses. Figure 4 displays the mode loss evolution for LP01, LP11o, and LP31e. Significantly, the reason why only mode loss of LP11o is shown in the figure of the LP11 mode is that mode losses of LP11o and LP11e are almost the same. According to Figure 4, mode losses of LP01, LP11o, and LP31e gradually drop from the small end to the large end of T-SCF, and a larger parabolic shape factor results in lower modal loss. The mode loss of LP11o decreases from 104.88 dB/m at the small end of T-SCF to 0.28 dB/m at the large end, showing great decline. The mode loss of LP31e drops from 2.03 to 0.27 dB/m, representing a slight decrease. More importantly, the loss of LP31e is lower than that of LP11 owing to the symmetry between six modal lobes and six low-index cladding segments. These results suggest that losses of lower-order modes are more sensitive to enlarging core radius than those of the higher-order modes.

Figure 4 Comparison of modal loss of straight T-SCF from the small end to the large end: (a) mode losses of LP01 and LP31e; (b) mode loss of LP11o.
Coiling fiber is a successful strategy to achieve effective single-mode operation for few-mode fibers because it introduces high losses for HOMs. Assuming the T-SCF is curved in the x-axis, we investigate mode loss under a bending radius of 32 cm. Figure 5 illustrates the modal loss of the bent T-SCF; it is obvious that bending operation induces mode losses to increase significantly, especially loss of LP31e. Furthermore, bend-induced modal loss evolutions of LP01, LP11o, and LP31e are different from each other. From the small end to the large end, loss of LP01 decreases to the minimum value and then increases gradually. Loss of LP31e increases from 9.81 to 70.77 dB/m, which indicates that the total loss of LP31e is higher than 64.75 dB for the 6.6 m long T-SCF. In contrast to loss of LP31e, loss of LP11o decreases from 113.01 to 3.51 dB/m. Based on these modal losses of the straight and bent T-SCF, we can simulate the amplification characteristics for the based T-SCF amplifier and analyze the laser performance.

Figure 5 Comparison of modal loss of T-SCF with a bending radius of 32 cm: (a) mode losses of LP01 and LP31e; (b) mode loss of LP11o.
Equations (2) and (3) suggest that bending azimuth angle may have an effect on mode characteristics. The elasto-optical effect of the bent fiber is mainly induced by longitudinal stretching, and thus we can analyze the bending modal loss and mode area for a given z. Mode performance under bending azimuth angle in the range of [0°, 60°] can fully represent overall performance of the fiber because the segment cladding period of the proposed SCF is π/3. Figure 6 displays the effects of bending orientation on the mode performance at R = 32 cm and z = 3.3 m. Loss of LP01 remains lower than 0.1 dB/m, not shown in the figure. Figure 6 clearly illustrates that the fiber performance is insensitive to the bending azimuth angle, which makes it more flexible and convenient when coiling fiber to achieve single-mode operation in actual applications.

Figure 6 (a) Modal loss and (b) effective mode area of LP01 for T-SCF under various bending azimuth angles, R = 32 cm, and z = 3.3 m.
3.2 Amplification characteristics based on the small-to-large scheme
In this section, a simple amplifier model is proposed to investigate laser characteristics under a small-to-large amplification scheme, as shown in Figure 7. We assume that the input pump power and signal power of LP01 are 1000 W and 10 W, respectively, while those of LP11 (LP11o and LP11e) and LP31e are all 1 W. Results show that the output powers of LP01 in the large end of the concave, linear, and convex T-SCF are 881.48, 875.66, and 872.42 W, respectively. Thus, the larger parabolic shape factor may degrade the laser efficiency of LP01 mode. Figure 8(a) demonstrates output power of LP11. For concave and linear T-SCF, the output power of LP11 is lower than 1 × 10−4 W, which is extremely low when compared with the output power of LP01. Therefore, it can be considered that the LP11 mode in concave and linear T-SCF is stripped off successfully. The power of LP11 mode in convex T-SCF remains at around 0.1 W so can be considered as a noise signal. In addition to LP01 mode, LP31e mode gets effective amplification owing to its low loss, as displayed in Figure 8(b). Moreover, the output power of LP31e increases with the increasing parabolic shape factor, and is 24.69, 31.29, and 37.02 W for concave, linear, and convex T-SCF, respectively. These simulated results indicate that the concave T-SCF presents excellent HOMs filtering effect, but its effective mode area and thermal performance are inferior to that of linear and convex T-SCF, as illustrated in Figure 9. For a given fiber position z, for example, z = 4.0 m, A eff of LP01 and the heat load density in concave T-SCF are 486.49 Ҽm2 and 7.98 × 1010 W/m3, whereas those in the convex T-SCF are 904.45 Ҽm2 and 1.57 × 109 W/m3. These comparisons indicate that convex T-SCF can help to mitigate nonlinear effects and thermal effects in high-power fiber lasers and amplifiers owing to its LMA and low heat load density.

Figure 7 The amplifier model based on T-SCF under the small-to-large amplification scheme (the doped region colored red).

Figure 8 Modal power evolution of (a) LP11 mode and (b) LP31e mode for concave, linear, and convex T-SCF based on the small-to-large amplification scheme.

Figure 9 (a) Effective mode area of LP01 and (b) heat load density evolution along T-SCF.
We investigate modal power evolution of the linear T-SIF to make comparisons with that of T-SCF. Mode losses of the guided modes in straight linear T-SIF are lower than 1 × 10−10 dB/m. Thus, those guided modes are effectively amplified owing to the low losses. The output power of LP01 in linear T-SIF is 725.0 W, which is much lower than the 875.66 W of linear T-SCF. Although the output power of HOMs in linear T-SIF is higher than that in linear T-SCF, and Figure 10(a) displays the power evolution of four HOMs, it is clear that those HOMs are amplified effectively, and thus the T-SIF supports few-modes amplification. Figure 10(b) compares the heat load density and mode area in straight T-SIF and T-SCF. The effective mode area of LP01 in T-SIF is smaller by 23.05–72.5 Ҽm2 than that of T-SCF, whereas the heat load density in the front-end of straight T-SIF is slightly higher than that in T-SCF.

Figure 10 (a) Modal power evolution of four HOMs in linear T-SIF and (b) comparison of heat load density and effective mode area of LP01 between linear T-SCF and T-SIF.
To demonstrate the single-mode operation by coiling fiber, we simulate the bending-induced amplification characteristics for the T-SCF under a bending radius of 32 cm by keeping the input pump and signal power unchanged. The output powers of LP01 from the concave, linear, and convex T-SCF are 882.84, 878.18, and 861.02 W. The output power of LP11 from the concave T-SCF is lower than 1.0×10−6 W, which suggests that LP11 mode is filtered out effectively, as shown in Figure 11(a). As the output power of LP11 from linear and convex T-SCF still remains at the milliwatt level, the LP11 mode can thus work as noise. Figure 11(b) demonstrates that the signal power of LP31e drops from 1 W to lower than the level of 10−6 W, indicating that LP31e mode is effectively stripped off. These results indicate that single-mode operation can be achieved by coiling T-SCF.

Figure 11 Power evolution of (a) LP11 mode and (b) LP31e mode in the T-SCF under a bending radius of 32 cm.
Comparison of heat load density between straight T-SCF and bent T-SCF is presented in Figure 12. It is clear that the bending operation (R = 32 cm) has a minor effect on the heat load density. As illustrated in Equation (7), heat load density is directly dependent on the effective ion-doped area and state rate equation, but the effective ion-doped area and the state rate equation are hardly influenced by the loose bending radius. This is why heat load density has no significant difference between the straight and bent T-SCF.

Figure 12 Comparison of heat load density between straight T-SCF and bent T-SCF of R = 32 cm.
3.3 Amplification characteristics based on the large-to-small scheme
The signal of HOMs may be effectively amplified owing to their low mode losses. We set the large end of the fiber as the input end to investigate the laser characteristics of the straight and bent T-SCF, as illustrated in Figure 13. The output powers of LP01 from the concave, linear, and convex T-SCF are 848.53, 842.66, and 841.76 W, respectively, which suggests the concave structure can help to maintain high amplification efficiency for LP01 mode. Signal of LP11 mode under the large-to-small scheme is effectively amplified in the middle section of the fiber, as displayed in Figure 14(a). The low loss in the front segment of T-SCF under the large-to-small scheme results in high gain for the signal of LP11, but LP11 gradually leaks out when propagating to the rear end of T-SCF because of the high loss. The output powers of LP11 from the concave, linear, and convex T-SCF are 1.471.68×10−9, 0.00016, and 0.083 W. Amplification characteristics of LP31e are given in Figure 14(b). Signal of LP31e is amplified to several tens of watts and then shows a slight decline. The power content of HOMs is relatively high under the large-to-small amplification scheme when considering both LP11 and LP31e. Comparing Figure 8 with Figure 14, it can be concluded that the small-to-large scheme is better at filtering out HOMs.

Figure 13 The amplifier model based on T-SCF under the large-to-small amplification scheme (the doped region colored red).

Figure 14 Modal power evolution of (a) LP11 mode and (b) LP31e mode for concave, linear, and convex T-SCF under the large-to-small amplification scheme.
Figure 15 compares the heat load density of the concave T-SCF between the two amplification schemes. The maximum heat load density of the concave T-SCF under the large-to-small scheme is 1.355×1010 W/m3, whereas that under the small-to-large scheme is four times higher. This comparison clearly shows that the large-to-small amplification scheme can mitigate the heat density.

Figure 15 Comparison of heat load density between the two amplification schemes.
Keeping the bending radius as 32 cm, we investigate the bending-induced HOMs filtering effects under the large-to-small pumping scheme. As illustrated in Figure 16(a), LP11 still is effectively amplified in the middle section of T-SCF. The maximum power of LP11 in concave, linear, and convex T-SCF is 7.55, 9.88, and 12.36 W, respectively, keeping the power content high. However, the power of LP11 gradually decreases in the rear section of the T-SCF owing to its high loss. The output power of LP11 in concave, linear, and convex T-SCF is 7.69×10−10, 2.54×10−10, 0.00557 W. The LP11 mode can be considered to be effectively stripped off because the output power of LP11 is extremely low, but the effective amplification of LP11 in the middle section of T-SCF may degrade the amplification efficiency of LP01. Figure 16(b) indicates that the LP31e mode can be filtered out under the large-to-small scheme. According to the analyses above, it can be shown that the large-to-small scheme can decrease the heat load density and maintain HOMs filtering effect when compared with the small-to-large scheme.

Figure 16 Power of (a) LP11 and (b) LP31e of the T-SCF under a bending radius of 32 cm.
4 Conclusion
In conclusion, we have proposed a potential T-SCF with LMA. Mode and amplification characteristics of the T-SCF with different tapered structures have been investigated by FEM and few-mode steady-state rate equation. Simulation results suggest that the concave tapered structure has advantages in stripping off HOMs, whereas the convex tapered structure provides LMA and low heat load density. In addition to tapered structures, the bending operation and amplification scheme have effects on the laser and thermal performance. The 6.6 m long T-SCF under a bending radius of 32 cm can achieve single-mode operation when choosing the small end of the fiber as the signal input end, but it keeps relatively high content of LP11 power when choosing the large end of the fiber as the signal input end. Moreover, heat load density under the large-to-small amplification scheme is four times lower than that under the small-to-large amplification scheme. These results suggest that different tapered structures and amplification schemes present different advantages on achieving single-mode operation and mitigating nonlinear effects as well as thermal effects, which provides theoretical suggestions for designing high-power fiber lasers and amplifiers.
Acknowledgments
This work was jointly supported by the National Key R&D Program of China (No. 2020YFB1805802), National Natural Science Foundation of China (Nos. 62005012 and 61827817), State Key Laboratory of Rail Traffic Control and Safety (No. RCS2019ZZ007), Beijing Jiaotong University, and Shandong Province Higher Educational Science and Technology Program (No. J18KA368).




















