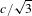1 Introduction
Stimulated Raman scattering (SRS), the decay of incident laser into scattered light and electron plasma wave[Reference Kruer1–Reference Montgomery3], remains to be one of the major obstacles to direct-drive, indirect-drive and possible hybrid-drive schemes[Reference Betti and Hurricane4–Reference He, Li, Fan, Wang, Liu, Lan, Wu and Ye9]. SRS generates a large amount of hot electrons[Reference Smalyuk, Shvarts, Betti, Delettrez, Edgell, Glebov, Goncharov, McCrory, Meyerhofer, Radha, Regan, Sangster, Seka, Skupsky, Stoeckl, Yaakobi, Frenje, Li, Petrasso and Séguin10–Reference Batani, Baton, Casner, Depierreux, Hohenberger, Klimo, Koenig, Labaune, Ribeyre, Rousseaux, Schurtz, Theobald and Tikhonchuk12], which can preheat the capsule. This has significant impacts on the implosion and ignition processes[Reference Dewald, Thomas, Hunter, Divol, Meezan, Glenzer, Suter, Bond, Kline, Celeste, Bradley, Bell, Kauffman, Kilkenny and Landen13, Reference Regan, Meezan, Suter, Strozzi, Kruer, Meeker, Glenzer, Seka, Stoeckl and Glebov14]. Even though there have been tremendous studies on the problem of hot electron production via SRS both in theory and experiments[Reference Montgomery3, Reference Strozzi, Williams, Hinkel, Froula, London and Callahan15], the generation mechanisms of hot electrons at nonlinear stages involving multiple driving waves are not yet fully understood.
Rescattering of SRS has been reported both theoretically and experimentally in different parametric conditions[Reference Winjum, Fahlen, Tsung and Mori16–Reference Klimo, Weber, Tikhonchuk and Limpouch20]. Some previous works have discussed about the effects of SRS rescattering on the nonlinear scattering spectrum and saturation mechanism of instabilities in the regime where backward SRS is heavily damped[Reference Kruer, Estabrook, Lasinski and Langdon17, Reference Hinkel, Haan, Langdon, Dittrich, Still and Marinak18]. Anomalously hot electrons due to rescattering of SRS have been studied recently[Reference Winjum, Fahlen, Tsung and Mori16]. However, this work mainly studied the rescattering of SRS in homogeneous plasma, i.e., the absolute instabilities induced by rescattering in inhomogeneous plasma not yet been sufficiently discussed. Generally, the absolute instability mode is the most significant instability in inhomogeneous plasma with the smallest threshold[Reference Liu, Rosenbluth and White2]. In addition, the phase velocity of the Langmuir wave excited by the absolute SRS is larger than that of other rescattering instability modes. In our work, we present a mechanism of hot electron production via the absolute instabilities in a large nonuniform plasma due to rescattering of SRS. It is well known that parametric instabilities in inhomogeneous plasma are convective in one-dimensional (1D) geometry except near the quarter-critical density, where both SRS and two plasmon decay (TPD) become absolute instabilities[Reference Liu, Rosenbluth and White2]. For the indirect-drive scheme, even though there is a large underdense plasma region, the absolute instability is usually ignored since the maximum density of the plasma is typically less than
![]() $0.2n_{c}$
[Reference Myatt, Zhang, Short, Maximov, Seka, Froula, Edgell, Michel, Igumenshchev, Hinkel, Michel and Moody21]. In this work, we investigate the generation mechanism and associate conditions for the absolute instabilities. Our work suggests that the absolute instability modes induced via rescattering of SRS are the important mechanisms for hot electron production for long time interactions between laser and large scale inhomogeneous plasma, even if the maximum plasma density is less than
$0.2n_{c}$
[Reference Myatt, Zhang, Short, Maximov, Seka, Froula, Edgell, Michel, Igumenshchev, Hinkel, Michel and Moody21]. In this work, we investigate the generation mechanism and associate conditions for the absolute instabilities. Our work suggests that the absolute instability modes induced via rescattering of SRS are the important mechanisms for hot electron production for long time interactions between laser and large scale inhomogeneous plasma, even if the maximum plasma density is less than
![]() $0.2n_{c}$
. Our theoretical model is supported by particle-in-cell (PIC) simulations.
$0.2n_{c}$
. Our theoretical model is supported by particle-in-cell (PIC) simulations.
2 Theoretical analysis of the absolute instability modes via rescattering of SRS
Here we consider cascaded scattering of SRS in an inhomogeneous plasma, including the first-order scattering occurring at the plasma electron density
![]() $n_{1}$
, the subsequent second-order scattering at the density
$n_{1}$
, the subsequent second-order scattering at the density
![]() $n_{2}$
and the third-order scattering at the density
$n_{2}$
and the third-order scattering at the density
![]() $n_{3}$
. The plasma has a positive density gradient along the laser propagation direction with an electron density range
$n_{3}$
. The plasma has a positive density gradient along the laser propagation direction with an electron density range
![]() $[n_{\text{min}},n_{\text{max}}]$
, where
$[n_{\text{min}},n_{\text{max}}]$
, where
![]() $n_{\text{min}}$
and
$n_{\text{min}}$
and
![]() $n_{\text{max}}$
are the minimum and maximum densities, respectively. Assume that the corresponding electron plasma wave frequencies are given by
$n_{\text{max}}$
are the minimum and maximum densities, respectively. Assume that the corresponding electron plasma wave frequencies are given by
![]() $\unicode[STIX]{x1D714}_{p1}=\sqrt{4\unicode[STIX]{x1D70B}n_{1}e^{2}/m_{e}}$
,
$\unicode[STIX]{x1D714}_{p1}=\sqrt{4\unicode[STIX]{x1D70B}n_{1}e^{2}/m_{e}}$
,
![]() $\unicode[STIX]{x1D714}_{p2}=\sqrt{4\unicode[STIX]{x1D70B}n_{2}e^{2}/m_{e}}$
and
$\unicode[STIX]{x1D714}_{p2}=\sqrt{4\unicode[STIX]{x1D70B}n_{2}e^{2}/m_{e}}$
and
![]() $\unicode[STIX]{x1D714}_{p3}=\sqrt{4\unicode[STIX]{x1D70B}n_{3}e^{2}/m_{e}}$
. According to the frequency match conditions for three wave coupling, the scattered light frequencies via the first-order scattering, second-order scattering and third-order scattering are given by
$\unicode[STIX]{x1D714}_{p3}=\sqrt{4\unicode[STIX]{x1D70B}n_{3}e^{2}/m_{e}}$
. According to the frequency match conditions for three wave coupling, the scattered light frequencies via the first-order scattering, second-order scattering and third-order scattering are given by
![]() $\unicode[STIX]{x1D714}_{s1}=\unicode[STIX]{x1D714}_{0}-\unicode[STIX]{x1D714}_{p1}$
(the corresponding wavenumber
$\unicode[STIX]{x1D714}_{s1}=\unicode[STIX]{x1D714}_{0}-\unicode[STIX]{x1D714}_{p1}$
(the corresponding wavenumber
![]() $k_{s1}\leqslant 0$
),
$k_{s1}\leqslant 0$
),
![]() $\unicode[STIX]{x1D714}_{s2}=\unicode[STIX]{x1D714}_{0}-\unicode[STIX]{x1D714}_{p1}-\unicode[STIX]{x1D714}_{p2}$
(the corresponding wavenumber
$\unicode[STIX]{x1D714}_{s2}=\unicode[STIX]{x1D714}_{0}-\unicode[STIX]{x1D714}_{p1}-\unicode[STIX]{x1D714}_{p2}$
(the corresponding wavenumber
![]() $k_{s2}\geqslant 0$
) and
$k_{s2}\geqslant 0$
) and
![]() $\unicode[STIX]{x1D714}_{s3}=\unicode[STIX]{x1D714}_{0}-\unicode[STIX]{x1D714}_{p1}-\unicode[STIX]{x1D714}_{p2}-\unicode[STIX]{x1D714}_{p3}$
(the corresponding wavenumber
$\unicode[STIX]{x1D714}_{s3}=\unicode[STIX]{x1D714}_{0}-\unicode[STIX]{x1D714}_{p1}-\unicode[STIX]{x1D714}_{p2}-\unicode[STIX]{x1D714}_{p3}$
(the corresponding wavenumber
![]() $k_{s3}\leqslant 0$
). The absolute instabilities in inhomogeneous plasma are found at the quarter-critical density of the incident electromagnetic wave. This can occur in certain regions in plasma via multiple SRS processes. Via multiple-order scattering, the incident laser energy is dissipated to plasma wave excitation and hot electron production.
$k_{s3}\leqslant 0$
). The absolute instabilities in inhomogeneous plasma are found at the quarter-critical density of the incident electromagnetic wave. This can occur in certain regions in plasma via multiple SRS processes. Via multiple-order scattering, the incident laser energy is dissipated to plasma wave excitation and hot electron production.
In the following, we examine the absolute instabilities via the second-order and third-order scattering. With the first-order backward SRS developed at
![]() $n_{1}$
and the second-order scattering at
$n_{1}$
and the second-order scattering at
![]() $n_{2}$
, the second-order scattering becomes the absolute instability when it is developed at the quarter-critical density of the first-order scattered light, i.e.,
$n_{2}$
, the second-order scattering becomes the absolute instability when it is developed at the quarter-critical density of the first-order scattered light, i.e.,
where
![]() $\unicode[STIX]{x1D714}_{L2}=\sqrt{\unicode[STIX]{x1D714}_{p2}^{2}+3k_{L2}^{2}v_{e}^{2}}$
with
$\unicode[STIX]{x1D714}_{L2}=\sqrt{\unicode[STIX]{x1D714}_{p2}^{2}+3k_{L2}^{2}v_{e}^{2}}$
with
![]() $v_{e}$
the electron thermal velocity. In the following, we take
$v_{e}$
the electron thermal velocity. In the following, we take
![]() $\unicode[STIX]{x1D714}_{L2}=\unicode[STIX]{x1D714}_{p2}$
for simplicity by ignoring the plasma electron temperature. Since
$\unicode[STIX]{x1D714}_{L2}=\unicode[STIX]{x1D714}_{p2}$
for simplicity by ignoring the plasma electron temperature. Since
![]() $n_{2}\leqslant n_{1}$
, one finds that
$n_{2}\leqslant n_{1}$
, one finds that
![]() $n_{1}\geqslant n_{c}/9$
and
$n_{1}\geqslant n_{c}/9$
and
![]() $n_{2}\leqslant n_{c}/9$
from Equation (1). This indicates that the backscattering light from the region
$n_{2}\leqslant n_{c}/9$
from Equation (1). This indicates that the backscattering light from the region
![]() $n_{1}\geqslant n_{c}/9\approx 0.11n_{c}$
can trigger absolute instabilities in the density area
$n_{1}\geqslant n_{c}/9\approx 0.11n_{c}$
can trigger absolute instabilities in the density area
![]() $n_{2}\leqslant n_{c}/9$
. One may note that the first-order forward SRS light from
$n_{2}\leqslant n_{c}/9$
. One may note that the first-order forward SRS light from
![]() $n_{1}\leqslant n_{c}/9$
can induce absolute modes in the region
$n_{1}\leqslant n_{c}/9$
can induce absolute modes in the region
![]() $n_{2}\geqslant n_{c}/9$
. Therefore, the major difference between rescattering of forward and backward scattering lights is the density region for absolute instability. Without loss of generality, we mainly consider the rescattering of backward SRS in this paper.
$n_{2}\geqslant n_{c}/9$
. Therefore, the major difference between rescattering of forward and backward scattering lights is the density region for absolute instability. Without loss of generality, we mainly consider the rescattering of backward SRS in this paper.
With the condition
![]() $\unicode[STIX]{x1D714}_{s1}=2\unicode[STIX]{x1D714}_{p2}$
or
$\unicode[STIX]{x1D714}_{s1}=2\unicode[STIX]{x1D714}_{p2}$
or
![]() $1-\sqrt{n_{1}/n_{c}}=2\sqrt{n_{2}/n_{c}}$
for the development of absolute instabilities, it is obvious that backscattered lights from different plasma density
$1-\sqrt{n_{1}/n_{c}}=2\sqrt{n_{2}/n_{c}}$
for the development of absolute instabilities, it is obvious that backscattered lights from different plasma density
![]() $n_{1}$
develop absolute modes at different density
$n_{1}$
develop absolute modes at different density
![]() $n_{2}$
. When the minimum quarter-critical density for the backscattering light
$n_{2}$
. When the minimum quarter-critical density for the backscattering light
![]() $n_{2}^{\text{min}}$
is within
$n_{2}^{\text{min}}$
is within
![]() $[n_{\text{min}},n_{\text{max}}]$
, the absolute instability region is simply
$[n_{\text{min}},n_{\text{max}}]$
, the absolute instability region is simply
![]() $[(1-\sqrt{n_{\text{max}}/n_{c}})^{2}/4,1/9]n_{c}$
. In this linear analysis, we ignored the coupling of backscattering lights from different plasma density between
$[(1-\sqrt{n_{\text{max}}/n_{c}})^{2}/4,1/9]n_{c}$
. In this linear analysis, we ignored the coupling of backscattering lights from different plasma density between
![]() $n_{c}/9$
and
$n_{c}/9$
and
![]() $n_{\text{max}}$
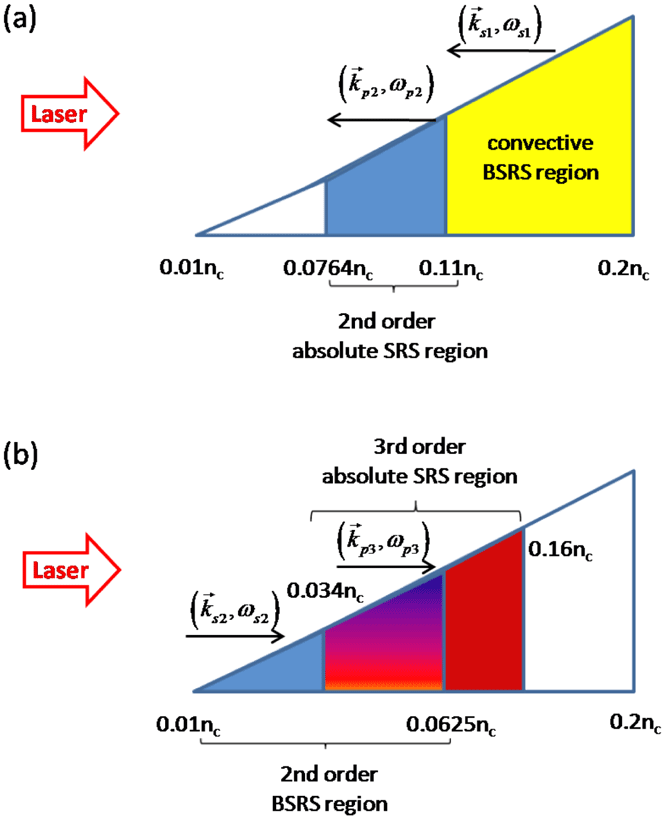
. As shown in Figure 1(a), for example, the initial plasma electron density is
$n_{\text{max}}$
. As shown in Figure 1(a), for example, the initial plasma electron density is
![]() $[0.01,0.2]n_{c}$
, and the minimum density for absolute SRS
$[0.01,0.2]n_{c}$
, and the minimum density for absolute SRS
![]() $n_{2}^{\text{min}}=0.0764n_{c}$
is found for backscattering from the density at
$n_{2}^{\text{min}}=0.0764n_{c}$
is found for backscattering from the density at
![]() $0.2n_{c}$
. The first-order convective SRS occurs in
$0.2n_{c}$
. The first-order convective SRS occurs in
![]() $[0.11,0.2]n_{c}$
, and its backscattering light can induce absolute instabilities by second-order rescattering of SRS within
$[0.11,0.2]n_{c}$
, and its backscattering light can induce absolute instabilities by second-order rescattering of SRS within
![]() $[0.0764,0.11]n_{c}$
.
$[0.0764,0.11]n_{c}$
.
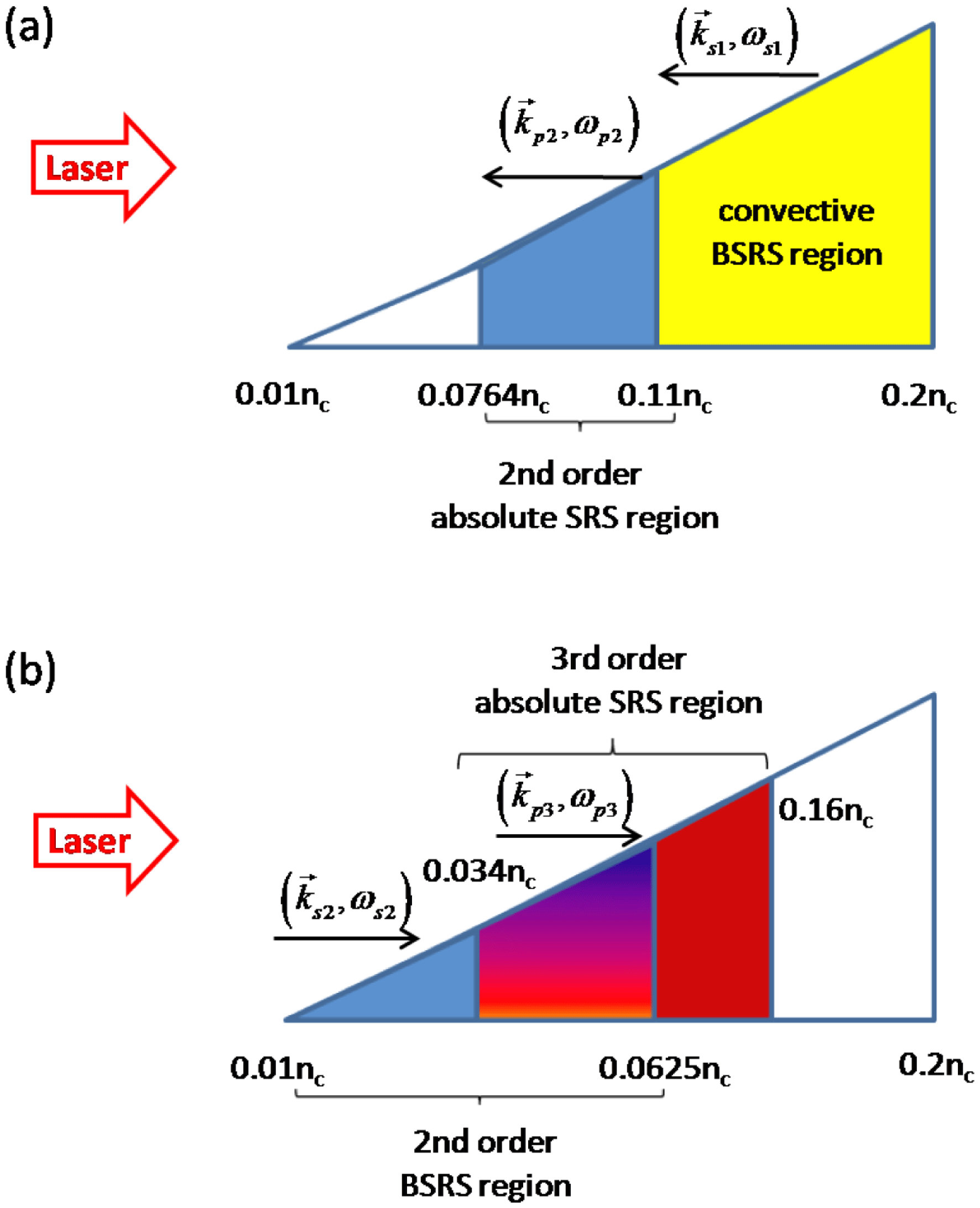
Figure 1. Schematic diagram for absolute instability regions due to (a) the second-order rescattering of SRS and (b) the third-order rescattering of SRS in a linearly inhomogeneous plasma with density
![]() $[0.01,0.2]n_{c}$
. BSRS means backscattering of SRS.
$[0.01,0.2]n_{c}$
. BSRS means backscattering of SRS.
Analogously, assume that the first-order backward SRS develops at
![]() $n_{1}$
, the second-order backward SRS develops at
$n_{1}$
, the second-order backward SRS develops at
![]() $n_{2}$
, and the third-order backward SRS develops at
$n_{2}$
, and the third-order backward SRS develops at
![]() $n_{3}$
. If the third-order scattering is absolute, it is required that it is developed at its corresponding quarter-critical density, i.e.,
$n_{3}$
. If the third-order scattering is absolute, it is required that it is developed at its corresponding quarter-critical density, i.e.,
Since
![]() $n_{1}\geqslant n_{2}$
and
$n_{1}\geqslant n_{2}$
and
![]() $n_{3}\geqslant n_{2}$
, one finds that
$n_{3}\geqslant n_{2}$
, one finds that
![]() $n_{2}\leqslant n_{c}/16=0.0625n_{c}$
according to Equation (2). Therefore, the second-order backward SRS developed in
$n_{2}\leqslant n_{c}/16=0.0625n_{c}$
according to Equation (2). Therefore, the second-order backward SRS developed in
![]() $[n_{\text{min}},0.0625]n_{c}$
can induce the third-order absolute instability modes in a slightly higher density region. Note that
$[n_{\text{min}},0.0625]n_{c}$
can induce the third-order absolute instability modes in a slightly higher density region. Note that
![]() $\unicode[STIX]{x1D714}_{0}=\unicode[STIX]{x1D714}_{p1}+\unicode[STIX]{x1D714}_{p2}+2\unicode[STIX]{x1D714}_{p3}\leqslant \unicode[STIX]{x1D714}_{p1}+3\unicode[STIX]{x1D714}_{p3}$
and that
$\unicode[STIX]{x1D714}_{0}=\unicode[STIX]{x1D714}_{p1}+\unicode[STIX]{x1D714}_{p2}+2\unicode[STIX]{x1D714}_{p3}\leqslant \unicode[STIX]{x1D714}_{p1}+3\unicode[STIX]{x1D714}_{p3}$
and that
![]() $\unicode[STIX]{x1D714}_{0}=\unicode[STIX]{x1D714}_{p1}+\unicode[STIX]{x1D714}_{p2}+2\unicode[STIX]{x1D714}_{p3}\geqslant 2\unicode[STIX]{x1D714}_{p2}+2\unicode[STIX]{x1D714}_{p3}$
. One finds the absolute instability range of the third-order rescattering
$\unicode[STIX]{x1D714}_{0}=\unicode[STIX]{x1D714}_{p1}+\unicode[STIX]{x1D714}_{p2}+2\unicode[STIX]{x1D714}_{p3}\geqslant 2\unicode[STIX]{x1D714}_{p2}+2\unicode[STIX]{x1D714}_{p3}$
. One finds the absolute instability range of the third-order rescattering
![]() $[(1-\sqrt{n_{\text{max}}/n_{c}})^{2}/9,(1-2\sqrt{n_{\text{min}}/n_{c}})^{2}/4]n_{c}$
. The absolute instability region may be reduced by the upper or lower limits of the plasma density profile. As an example, for the given plasma electron density shown in Figure 1(b), the secondary backward SRS is developed in
$[(1-\sqrt{n_{\text{max}}/n_{c}})^{2}/9,(1-2\sqrt{n_{\text{min}}/n_{c}})^{2}/4]n_{c}$
. The absolute instability region may be reduced by the upper or lower limits of the plasma density profile. As an example, for the given plasma electron density shown in Figure 1(b), the secondary backward SRS is developed in
![]() $[0.01,0.0625]n_{c}$
, which can induce the third-order absolute instabilities in
$[0.01,0.0625]n_{c}$
, which can induce the third-order absolute instabilities in
![]() $[0.034,0.16]n_{c}$
. Note that even though the absolute instability region via the third-order scattering is relatively larger than that via the second-order scattering, its intensity is much weaker. One finds a common region
$[0.034,0.16]n_{c}$
. Note that even though the absolute instability region via the third-order scattering is relatively larger than that via the second-order scattering, its intensity is much weaker. One finds a common region
![]() $[0.0764,0.11]n_{c}$
for both the second-order and third-order absolute instability modes.
$[0.0764,0.11]n_{c}$
for both the second-order and third-order absolute instability modes.
It is worthwhile to check with the phase velocity of the excited electron plasma wave, which determines the energy of trapped electrons. Without loss of generality, the wavenumber match condition for the second-order absolute SRS is
![]() $k_{p2}=k_{s1}-k_{s2}$
. Since
$k_{p2}=k_{s1}-k_{s2}$
. Since
![]() $k_{s2}\approx 0$
for the absolute SRS, one obtains
$k_{s2}\approx 0$
for the absolute SRS, one obtains
![]() $k_{p2}\approx k_{s1}=-\left.\sqrt{\unicode[STIX]{x1D714}_{s1}^{2}-\unicode[STIX]{x1D714}_{p2}^{2}}\right/c$
. With the help of Equation (1), one finds the phase velocity of the electron plasma wave is simply
$k_{p2}\approx k_{s1}=-\left.\sqrt{\unicode[STIX]{x1D714}_{s1}^{2}-\unicode[STIX]{x1D714}_{p2}^{2}}\right/c$
. With the help of Equation (1), one finds the phase velocity of the electron plasma wave is simply
The negative sign means that the phase velocity is opposite to the incident laser propagation as shown in Figure 1(a). Corresponding to this phase velocity, the electron energy is about 170 keV. Similarly one can find the phase velocity of the electron plasma wave excited via third-order absolute SRS
![]() $v_{ph3}=\unicode[STIX]{x1D714}_{p3}/k_{p3}\approx c/\sqrt{3}$
.
$v_{ph3}=\unicode[STIX]{x1D714}_{p3}/k_{p3}\approx c/\sqrt{3}$
.
Now we discuss the qualitatively necessary conditions for the development of absolute modes besides the density scale. Generally backward SRS is much stronger than forward SRS due to its larger growth rate. However, when the backward SRS is heavily Landau damped in a very hot plasma, the absolute instabilities will be mainly induced via the rescattering of forward scattering[Reference Hinkel, Haan, Langdon, Dittrich, Still and Marinak18, Reference Langdon and Hinkel22], which may play a role in the direct-drive scheme. Here we consider a plasma with a few keV where the backscattering SRS has not been heavily damped. The Landau damping of absolute SRS is weak due to the high phase velocity of the Langmuir wave. For example, assume the electron temperature is 2 keV, i.e., thermal velocity
![]() $v_{th}=0.0626c$
, which is one ninth of the Langmuir wave phase velocity
$v_{th}=0.0626c$
, which is one ninth of the Langmuir wave phase velocity
![]() $v_{ph}=0.58c$
. The high temperature mainly reduces the saturation level of backscattering light, which acts as a damping of pump wave to develop absolute SRS. Therefore, the threshold for the development of absolute SRS induced via rescattering is mainly determined by the density scale length
$v_{ph}=0.58c$
. The high temperature mainly reduces the saturation level of backscattering light, which acts as a damping of pump wave to develop absolute SRS. Therefore, the threshold for the development of absolute SRS induced via rescattering is mainly determined by the density scale length
![]() $L$
and incident laser intensity. As we know, the threshold for the first-order absolute SRS in inhomogeneous plasma is
$L$
and incident laser intensity. As we know, the threshold for the first-order absolute SRS in inhomogeneous plasma is
![]() $a_{0}\gtrsim (k_{0}L)^{-2/3}$
[Reference Liu, Rosenbluth and White2]. We treat the backscattering light as a pump wave, and then we have
$a_{0}\gtrsim (k_{0}L)^{-2/3}$
[Reference Liu, Rosenbluth and White2]. We treat the backscattering light as a pump wave, and then we have
![]() $a_{s0}\gtrsim (k_{s0}L_{s})^{-2/3}$
where
$a_{s0}\gtrsim (k_{s0}L_{s})^{-2/3}$
where
![]() $L_{s}=L\unicode[STIX]{x1D714}_{s}^{2}/\unicode[STIX]{x1D714}_{0}^{2}$
and
$L_{s}=L\unicode[STIX]{x1D714}_{s}^{2}/\unicode[STIX]{x1D714}_{0}^{2}$
and
![]() $k_{s0}$
is the wavenumber of the first-order incident light, i.e.,
$k_{s0}$
is the wavenumber of the first-order incident light, i.e.,
![]() $k_{s0}=k_{0}$
. By normalizing
$k_{s0}=k_{0}$
. By normalizing
![]() $a_{s0}$
back to the frequency of incident laser, we obtain the threshold for absolute SRS induced via second-order SRS rescattering
$a_{s0}$
back to the frequency of incident laser, we obtain the threshold for absolute SRS induced via second-order SRS rescattering
The above linear analysis only considers individual scattering at local plasma density. When considering the absolute SRS instability, waves scattered at different plasma densities with different frequencies can be strongly coupled. Let us consider the bandwidth effects of backscattering light at the near-quarter-critical density, where the mismatch of wave numbers becomes so weak. Considering that the mismatch of wave numbers approximates to zero for absolute instabilities, we can do the Fourier transform of the propagation equations of the scattered light and electron plasma wave similar to the homogeneous case. The width of the instability region in the plasma wave vector
![]() $\unicode[STIX]{x0394}k$
is proved to be a critical factor for the modes coupling[Reference Zhao, Weng, Chen, Zheng, Zhuo, Ren, Sheng and Zhang23]. The dispersion for SRS in homogeneous plasma is given by[Reference Kruer1]
$\unicode[STIX]{x0394}k$
is proved to be a critical factor for the modes coupling[Reference Zhao, Weng, Chen, Zheng, Zhuo, Ren, Sheng and Zhang23]. The dispersion for SRS in homogeneous plasma is given by[Reference Kruer1]
where
![]() $D_{e}=\unicode[STIX]{x1D714}^{2}-\unicode[STIX]{x1D714}_{p}^{2}$
,
$D_{e}=\unicode[STIX]{x1D714}^{2}-\unicode[STIX]{x1D714}_{p}^{2}$
,
![]() $D_{\pm }=\unicode[STIX]{x1D714}^{2}-k^{2}c^{2}\pm 2(\unicode[STIX]{x1D714}_{0}\unicode[STIX]{x1D714}-k_{0}kc^{2})$
. Numerical solutions of Equation (5) at different densities with the normalized laser amplitude
$D_{\pm }=\unicode[STIX]{x1D714}^{2}-k^{2}c^{2}\pm 2(\unicode[STIX]{x1D714}_{0}\unicode[STIX]{x1D714}-k_{0}kc^{2})$
. Numerical solutions of Equation (5) at different densities with the normalized laser amplitude
![]() $a_{0}=0.01$
are plotted in Figure 2. The relation between
$a_{0}=0.01$
are plotted in Figure 2. The relation between
![]() $a_{0}$
and laser intensity
$a_{0}$
and laser intensity
![]() $I_{0}$
is given by
$I_{0}$
is given by
![]() $a_{0}=\sqrt{I_{0}(\text{W}/\text{cm}^{2})[\unicode[STIX]{x1D706}(\unicode[STIX]{x03BC}\text{m})]^{2}/1.37\times 10^{18}}$
. As show in Figure 2, at
$a_{0}=\sqrt{I_{0}(\text{W}/\text{cm}^{2})[\unicode[STIX]{x1D706}(\unicode[STIX]{x03BC}\text{m})]^{2}/1.37\times 10^{18}}$
. As show in Figure 2, at
![]() $n_{e}=0.24n_{c}$
, the instability regions of forward and backward SRS are well-separated in their wave vectors with almost equal width. However, when the plasma density increases to very near the quarter-critical density
$n_{e}=0.24n_{c}$
, the instability regions of forward and backward SRS are well-separated in their wave vectors with almost equal width. However, when the plasma density increases to very near the quarter-critical density
![]() $n_{e}=0.2485n_{c}$
, one finds the forward and backward SRS sharing a common plasma wave. The width of the coupling instability region can be estimated as twice of the backward instability region at
$n_{e}=0.2485n_{c}$
, one finds the forward and backward SRS sharing a common plasma wave. The width of the coupling instability region can be estimated as twice of the backward instability region at
![]() $n_{e}=0.2485n_{c}$
, i.e.,
$n_{e}=0.2485n_{c}$
, i.e.,
![]() $\unicode[STIX]{x0394}kc\approx 16.8a_{0}\unicode[STIX]{x1D714}_{0}=0.168\unicode[STIX]{x1D714}_{0}$
. Such a large instability region can greatly increase the coupling of light beams with different frequencies for the development of absolute SRS instabilities[Reference Zhao, Weng, Chen, Zheng, Zhuo, Ren, Sheng and Zhang23]. Therefore, in inhomogeneous plasma, even if the first-order backscattering light may have broad bandwidth, they can be strongly coupled in their subsequent scattering for absolute SRS. Note that when the absolute SRS is developed, the scattered light waves have the wave number
$\unicode[STIX]{x0394}kc\approx 16.8a_{0}\unicode[STIX]{x1D714}_{0}=0.168\unicode[STIX]{x1D714}_{0}$
. Such a large instability region can greatly increase the coupling of light beams with different frequencies for the development of absolute SRS instabilities[Reference Zhao, Weng, Chen, Zheng, Zhuo, Ren, Sheng and Zhang23]. Therefore, in inhomogeneous plasma, even if the first-order backscattering light may have broad bandwidth, they can be strongly coupled in their subsequent scattering for absolute SRS. Note that when the absolute SRS is developed, the scattered light waves have the wave number
![]() $k_{s}\approx 0$
. The scattering light at the quarter-critical density can be described by near-zero refractive index photonics, which contains rich physics and extensive applications[Reference Liberal and Engheta24, Reference Ahmed and Nader25]. The trapped light with
$k_{s}\approx 0$
. The scattering light at the quarter-critical density can be described by near-zero refractive index photonics, which contains rich physics and extensive applications[Reference Liberal and Engheta24, Reference Ahmed and Nader25]. The trapped light with
![]() $k_{s}=0$
may be one of the reasons for laser energy deficit in inertial confinement fusion[Reference Klimo, Weber, Tikhonchuk and Limpouch20]. One notes that the broad width of
$k_{s}=0$
may be one of the reasons for laser energy deficit in inertial confinement fusion[Reference Klimo, Weber, Tikhonchuk and Limpouch20]. One notes that the broad width of
![]() $k$
spectrum also indicates a wide range of the Langmuir wave phase velocity, the median of which is given by Equation (3). A large range of phase velocity leads to a staged acceleration of electrons.
$k$
spectrum also indicates a wide range of the Langmuir wave phase velocity, the median of which is given by Equation (3). A large range of phase velocity leads to a staged acceleration of electrons.

Figure 2. Numerical solutions of SRS dispersion equation at the plasma density
![]() $n_{e}=0.24n_{c}$
and
$n_{e}=0.24n_{c}$
and
![]() $n_{e}=0.2485n_{c}$
, where
$n_{e}=0.2485n_{c}$
, where
![]() $a_{0}=0.01$
. The dotted line and continuous line are the imaginary part and the real part of the solutions, respectively.
$a_{0}=0.01$
. The dotted line and continuous line are the imaginary part and the real part of the solutions, respectively.
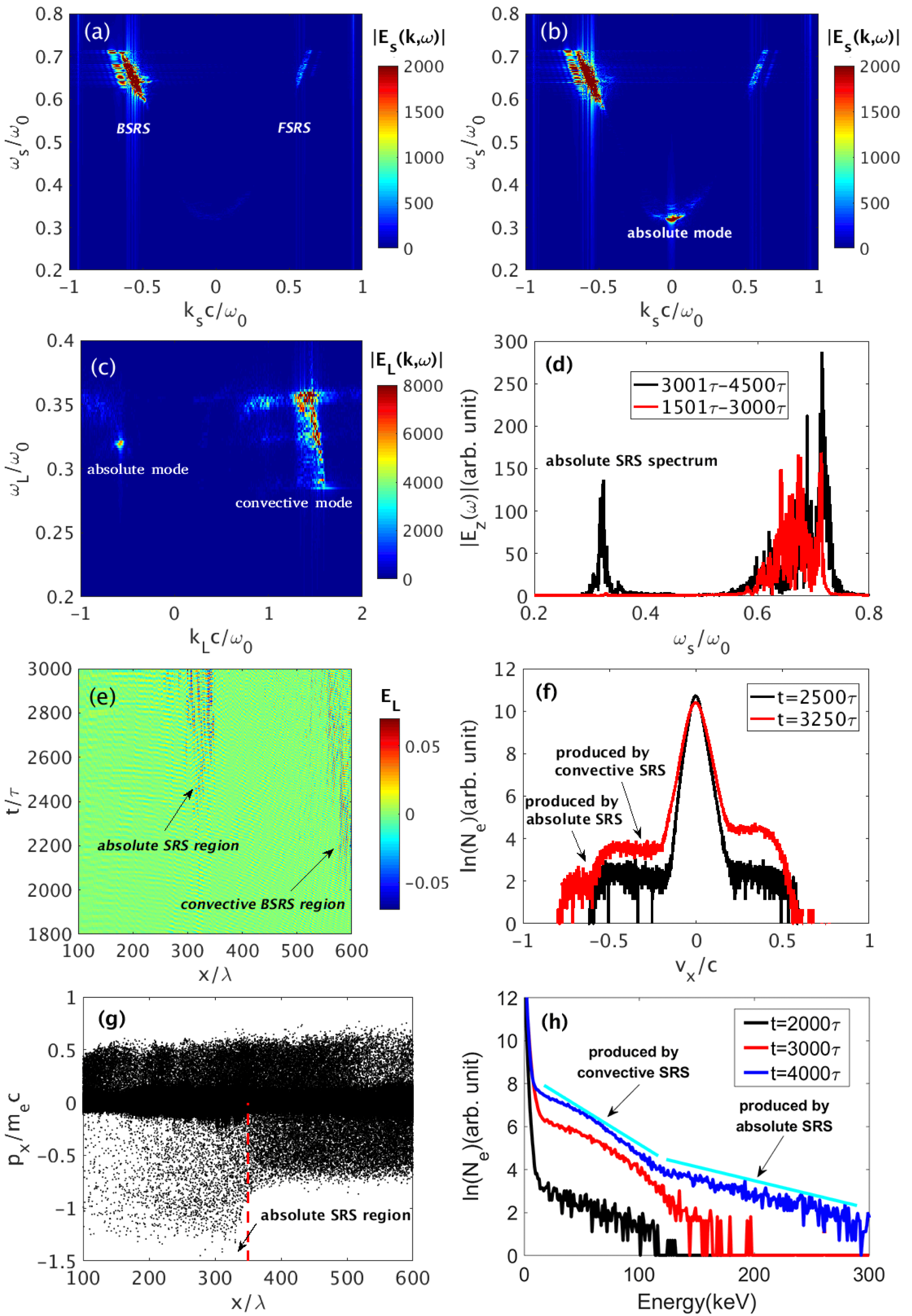
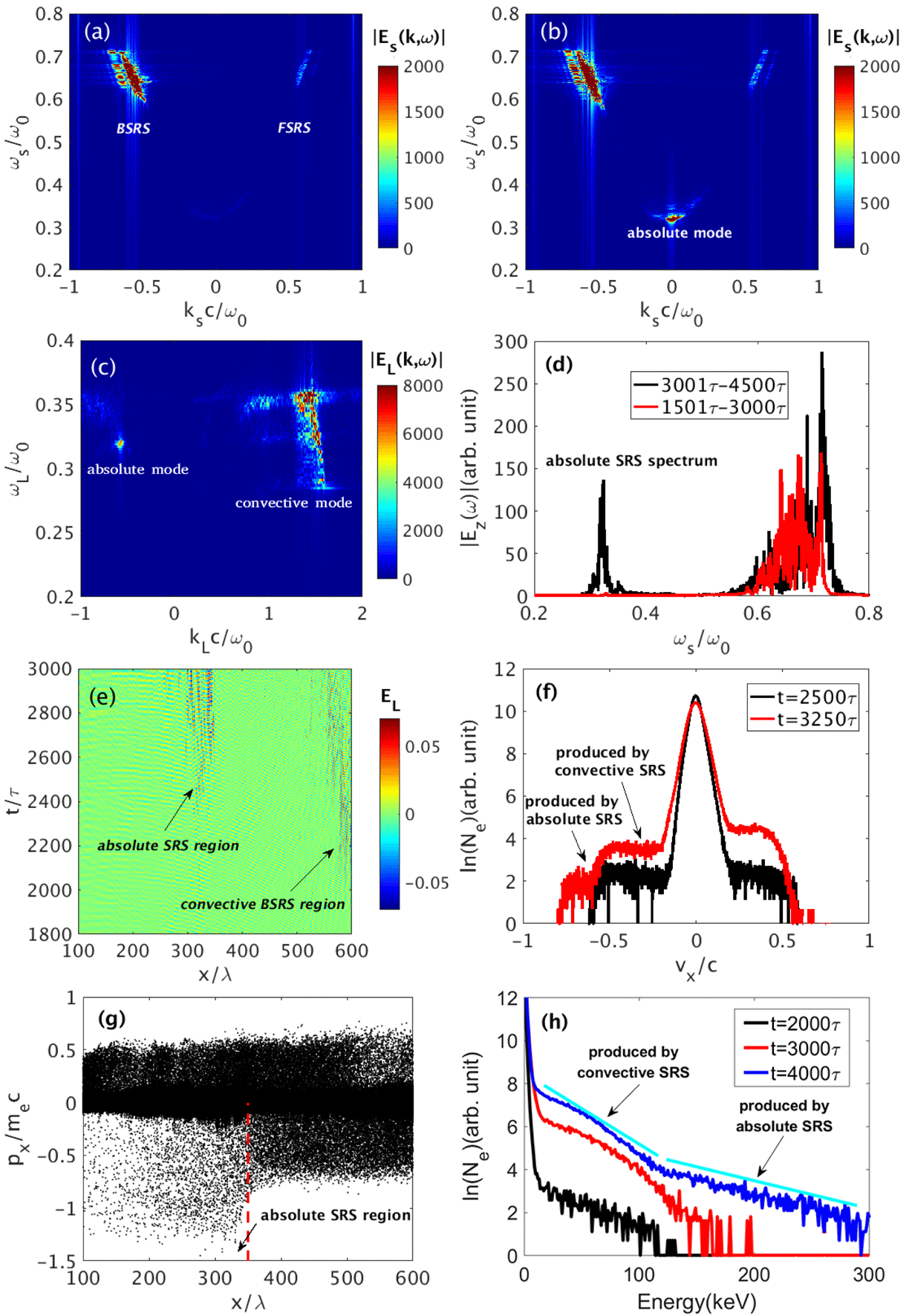
Figure 3. PIC simulation results for the development of the absolute SRS via the second-order scattering. (a) and (b) Wavenumber–frequency distributions of the scattered light in the time windows
![]() $[1501,2000]\unicode[STIX]{x1D70F}$
and
$[1501,2000]\unicode[STIX]{x1D70F}$
and
![]() $[2001,2500]\unicode[STIX]{x1D70F}$
, respectively. FSRS means forward scattering of SRS. (c) 2D Fourier transform
$[2001,2500]\unicode[STIX]{x1D70F}$
, respectively. FSRS means forward scattering of SRS. (c) 2D Fourier transform
![]() $|E_{L}(k,\unicode[STIX]{x1D714})|$
of the electric field in the time window
$|E_{L}(k,\unicode[STIX]{x1D714})|$
of the electric field in the time window
![]() $[2001,2500]\unicode[STIX]{x1D70F}$
. (d) Fourier spectra of backscattered light diagnosed at
$[2001,2500]\unicode[STIX]{x1D70F}$
. (d) Fourier spectra of backscattered light diagnosed at
![]() $x=10\unicode[STIX]{x1D706}$
. (e) Time–space distributions of Langmuir waves, where
$x=10\unicode[STIX]{x1D706}$
. (e) Time–space distributions of Langmuir waves, where
![]() $E_{L}$
is the longitudinal electric field normalized by
$E_{L}$
is the longitudinal electric field normalized by
![]() $m_{e}\unicode[STIX]{x1D714}_{0}c/e$
,
$m_{e}\unicode[STIX]{x1D714}_{0}c/e$
,
![]() $m_{e}$
,
$m_{e}$
,
![]() $c$
and
$c$
and
![]() $e$
are electron mass, light speed in vacuum and electron charge, respectively. (f) Longitudinal velocity distributions of electron at different time. (g) Longitudinal phase space distribution of electrons near the region of the absolute SRS instability at
$e$
are electron mass, light speed in vacuum and electron charge, respectively. (f) Longitudinal velocity distributions of electron at different time. (g) Longitudinal phase space distribution of electrons near the region of the absolute SRS instability at
![]() $t=3250\unicode[STIX]{x1D70F}$
. (h) Energy distributions of electrons at different time, where
$t=3250\unicode[STIX]{x1D70F}$
. (h) Energy distributions of electrons at different time, where
![]() $N_{e}$
is the relative electron number.
$N_{e}$
is the relative electron number.
In conclusion, the linear analysis suggests that a laser propagating in large inhomogeneous plasma can generate a large region of absolute instabilities by cascaded scattering and coupling of different frequency components of scattering light. Both the second- and third-order rescattering of SRS contributes to the development of absolute instabilities. Even though the intensity of the third-order scattering is relatively weak, it can still be strong enough to heat abundant electrons in a long time interaction.
3 Simulations for absolute instabilities due to the second-order rescattering of SRS
3.1 1D simulations for absolute SRS mode

Figure 4. The case when the absolute SRS is absent provided
![]() $n_{\text{min}}>n_{c}/9$
. (a) Wavenumber–frequency distributions of the scattered light in the time window
$n_{\text{min}}>n_{c}/9$
. (a) Wavenumber–frequency distributions of the scattered light in the time window
![]() $[2001,2500]\unicode[STIX]{x1D70F}$
. (b) Energy distributions of electrons at different time.
$[2001,2500]\unicode[STIX]{x1D70F}$
. (b) Energy distributions of electrons at different time.
To validate the above theoretical prediction, a series of PIC simulations has been performed in different plasma density regions by using the KLAP code[Reference Chen, Sheng, Zheng, Ma and Zhang26]. First, one-dimensional (1D) PIC simulations have been carried out, which avoid mixing up of various instabilities and enable one to identify the development of the multiple SRS rescattering instabilities more clearly. The space and time given in the following are normalized by the laser wavelength in vacuum
![]() $\unicode[STIX]{x1D706}$
and the laser period
$\unicode[STIX]{x1D706}$
and the laser period
![]() $\unicode[STIX]{x1D70F}$
. The length of the simulation box is
$\unicode[STIX]{x1D70F}$
. The length of the simulation box is
![]() $700\unicode[STIX]{x1D706}$
, where the plasma occupies a region from
$700\unicode[STIX]{x1D706}$
, where the plasma occupies a region from
![]() $25\unicode[STIX]{x1D706}$
to
$25\unicode[STIX]{x1D706}$
to
![]() $650\unicode[STIX]{x1D706}$
with density profile
$650\unicode[STIX]{x1D706}$
with density profile
![]() $n_{e}(x)=0.08[1+(x-25)/1000]n_{c}$
, with
$n_{e}(x)=0.08[1+(x-25)/1000]n_{c}$
, with
![]() $x$
the longitudinal axis. To exclude the third-order absolute mode, the minimum plasma density is set at
$x$
the longitudinal axis. To exclude the third-order absolute mode, the minimum plasma density is set at
![]() $0.08n_{c}$
, and the maximum density is
$0.08n_{c}$
, and the maximum density is
![]() $0.13n_{c}$
. The initial electron temperature is
$0.13n_{c}$
. The initial electron temperature is
![]() $T_{e0}=100$
eV. The ions are immobile with a charge
$T_{e0}=100$
eV. The ions are immobile with a charge
![]() $Z=1$
. A linearly polarized semi-infinite pump laser with a uniform amplitude
$Z=1$
. A linearly polarized semi-infinite pump laser with a uniform amplitude
![]() $a_{0}=0.02$
(the corresponding intensity is
$a_{0}=0.02$
(the corresponding intensity is
![]() $I_{0}=5.48\times 10^{14}~\text{W}/\text{cm}^{2}$
with
$I_{0}=5.48\times 10^{14}~\text{W}/\text{cm}^{2}$
with
![]() $\unicode[STIX]{x1D706}=1~\unicode[STIX]{x03BC}\text{m}$
) is incident from the left boundary of the simulation box. We have taken 100 cells per wavelength and 50 particles per cell.
$\unicode[STIX]{x1D706}=1~\unicode[STIX]{x03BC}\text{m}$
) is incident from the left boundary of the simulation box. We have taken 100 cells per wavelength and 50 particles per cell.
Based on the discussion in Section 2, a strong convective backward SRS develops in relatively high density region
![]() $n_{e}\geqslant n_{c}/9$
due to the large growth rate, and then the produced backscattering light induces absolute SRS mode in the region
$n_{e}\geqslant n_{c}/9$
due to the large growth rate, and then the produced backscattering light induces absolute SRS mode in the region
![]() $n_{e}\leqslant n_{c}/9$
. Figure 3 illustrates the development of SRS in different stages. A strong convective backscattering SRS is developed in the time window of
$n_{e}\leqslant n_{c}/9$
. Figure 3 illustrates the development of SRS in different stages. A strong convective backscattering SRS is developed in the time window of
![]() $[1501,2000]\unicode[STIX]{x1D70F}$
as shown in Figure 3(a), which is mainly caused by the first-order SRS scattering. The frequency of backscattering light ranges from
$[1501,2000]\unicode[STIX]{x1D70F}$
as shown in Figure 3(a), which is mainly caused by the first-order SRS scattering. The frequency of backscattering light ranges from
![]() $0.64\unicode[STIX]{x1D714}_{0}$
(corresponding to
$0.64\unicode[STIX]{x1D714}_{0}$
(corresponding to
![]() $n_{1}=0.13n_{c}$
) to
$n_{1}=0.13n_{c}$
) to
![]() $0.72\unicode[STIX]{x1D714}_{0}$
(corresponding to
$0.72\unicode[STIX]{x1D714}_{0}$
(corresponding to
![]() $n_{1}=0.08n_{c}$
). Note that the forward scattering mode is much weaker than the backward mode due to its relatively smaller growth rate, and therefore will not be discussed in the following. From Figure 3(b), we find that an absolute SRS mode has been generated during
$n_{1}=0.08n_{c}$
). Note that the forward scattering mode is much weaker than the backward mode due to its relatively smaller growth rate, and therefore will not be discussed in the following. From Figure 3(b), we find that an absolute SRS mode has been generated during
![]() $[2001,2500]\unicode[STIX]{x1D70F}$
. The absolute mode is identified due to
$[2001,2500]\unicode[STIX]{x1D70F}$
. The absolute mode is identified due to
![]() $k_{s}\approx 0$
as discussed above. The central frequency of the absolute SRS mode is around
$k_{s}\approx 0$
as discussed above. The central frequency of the absolute SRS mode is around
![]() $0.32\unicode[STIX]{x1D714}_{0}$
, which is expected according to Equation (1). The wavenumber–frequency distribution of Langmuir wave is shown in Figure 3(c). The absolute mode is found at
$0.32\unicode[STIX]{x1D714}_{0}$
, which is expected according to Equation (1). The wavenumber–frequency distribution of Langmuir wave is shown in Figure 3(c). The absolute mode is found at
![]() $k_{L}c=-0.56\unicode[STIX]{x1D714}_{0}$
which is consistent with the deduction from Figure 3(b) and in agreement with Equation (3). The backscattered light (propagates from right to left) is diagnosed at
$k_{L}c=-0.56\unicode[STIX]{x1D714}_{0}$
which is consistent with the deduction from Figure 3(b) and in agreement with Equation (3). The backscattered light (propagates from right to left) is diagnosed at
![]() $x=10\unicode[STIX]{x1D706}$
with its Fourier spectrum shown in Figure 3(d). A strong spectrum around
$x=10\unicode[STIX]{x1D706}$
with its Fourier spectrum shown in Figure 3(d). A strong spectrum around
![]() $\unicode[STIX]{x1D714}_{s}=0.36\unicode[STIX]{x1D714}_{0}$
is formed during
$\unicode[STIX]{x1D714}_{s}=0.36\unicode[STIX]{x1D714}_{0}$
is formed during
![]() $3001\unicode[STIX]{x1D70F}$
–
$3001\unicode[STIX]{x1D70F}$
–
![]() $4500\unicode[STIX]{x1D70F}$
, which is produced via forward scattering of absolute SRS. The scattering spectrum can help us to identify the development of absolute SRS mode.
$4500\unicode[STIX]{x1D70F}$
, which is produced via forward scattering of absolute SRS. The scattering spectrum can help us to identify the development of absolute SRS mode.
The generation mechanism for the absolute SRS mode can be well demonstrated in Figure 3(e). One finds a strong convective mode developed at
![]() $x=580\unicode[STIX]{x1D706}$
around
$x=580\unicode[STIX]{x1D706}$
around
![]() $t=1900\unicode[STIX]{x1D70F}$
, and then it gradually spread out of the resonant region. A simple calculation indicates that the quarter-critical density for the backscattering light is around
$t=1900\unicode[STIX]{x1D70F}$
, and then it gradually spread out of the resonant region. A simple calculation indicates that the quarter-critical density for the backscattering light is around
![]() $n_{e}=0.105n_{c}$
. At
$n_{e}=0.105n_{c}$
. At
![]() $t=2350\unicode[STIX]{x1D70F}$
, the backscattering light induces an intense absolute SRS mode near
$t=2350\unicode[STIX]{x1D70F}$
, the backscattering light induces an intense absolute SRS mode near
![]() $x=320\unicode[STIX]{x1D706}$
where the plasma density is
$x=320\unicode[STIX]{x1D706}$
where the plasma density is
![]() $n_{e}=0.104n_{c}$
. For the absolute SRS instability, the resonant region is stationary. One finds that the absolute instability region gradually widens to
$n_{e}=0.104n_{c}$
. For the absolute SRS instability, the resonant region is stationary. One finds that the absolute instability region gradually widens to
![]() $[300,345]\unicode[STIX]{x1D706}$
, due to the enhanced bandwidth of the backscattering light. As mentioned above, a broad instability region near the quarter-critical density can greatly reduce the suppression effects of finite bandwidth of the backscattering light. After
$[300,345]\unicode[STIX]{x1D706}$
, due to the enhanced bandwidth of the backscattering light. As mentioned above, a broad instability region near the quarter-critical density can greatly reduce the suppression effects of finite bandwidth of the backscattering light. After
![]() $t=2800\unicode[STIX]{x1D70F}$
, the absolute SRS becomes the dominant instability mode.
$t=2800\unicode[STIX]{x1D70F}$
, the absolute SRS becomes the dominant instability mode.
According to Equation (3), the phase velocity of the Langmuir wave excited by the absolute SRS is very high. In linear stage, the temperatures of most electrons are much lower than 170 keV. Therefore, the absolute SRS mode can grow without Landau damping. The main damping for the growth of absolute SRS mode comes from the backscattering light developed via backward SRS. In our simulation, the phase velocity of the Langmuir wave developed by convective SRS is around
![]() $0.26c$
. From Figure 3(f), we find that the electron energy distribution is flattened around
$0.26c$
. From Figure 3(f), we find that the electron energy distribution is flattened around
![]() $v_{x}=-0.27c$
by trapped electrons at
$v_{x}=-0.27c$
by trapped electrons at
![]() $t=2500\unicode[STIX]{x1D70F}$
. Note that the velocity of most electrons is less than
$t=2500\unicode[STIX]{x1D70F}$
. Note that the velocity of most electrons is less than
![]() $0.58c$
. Therefore, this time period is the linear stage for the absolute SRS instability. At
$0.58c$
. Therefore, this time period is the linear stage for the absolute SRS instability. At
![]() $t=3250\unicode[STIX]{x1D70F}$
, the absolute SRS mode has started evolving into the nonlinear regime, and another flattened region near
$t=3250\unicode[STIX]{x1D70F}$
, the absolute SRS mode has started evolving into the nonlinear regime, and another flattened region near
![]() $v_{x}=-0.6c$
is formed. Figure 3(g) presents a clear physical picture of electrons accelerated in the absolute SRS region. The maximum electron momentums are below
$v_{x}=-0.6c$
is formed. Figure 3(g) presents a clear physical picture of electrons accelerated in the absolute SRS region. The maximum electron momentums are below
![]() $|p_{x}|\sim 0.7m_{e}c$
at
$|p_{x}|\sim 0.7m_{e}c$
at
![]() $x>350\unicode[STIX]{x1D706}$
. When the electrons propagate into the absolute SRS region, they are accelerated up to even
$x>350\unicode[STIX]{x1D706}$
. When the electrons propagate into the absolute SRS region, they are accelerated up to even
![]() $|p_{x}|\sim 1.5m_{e}c$
.
$|p_{x}|\sim 1.5m_{e}c$
.
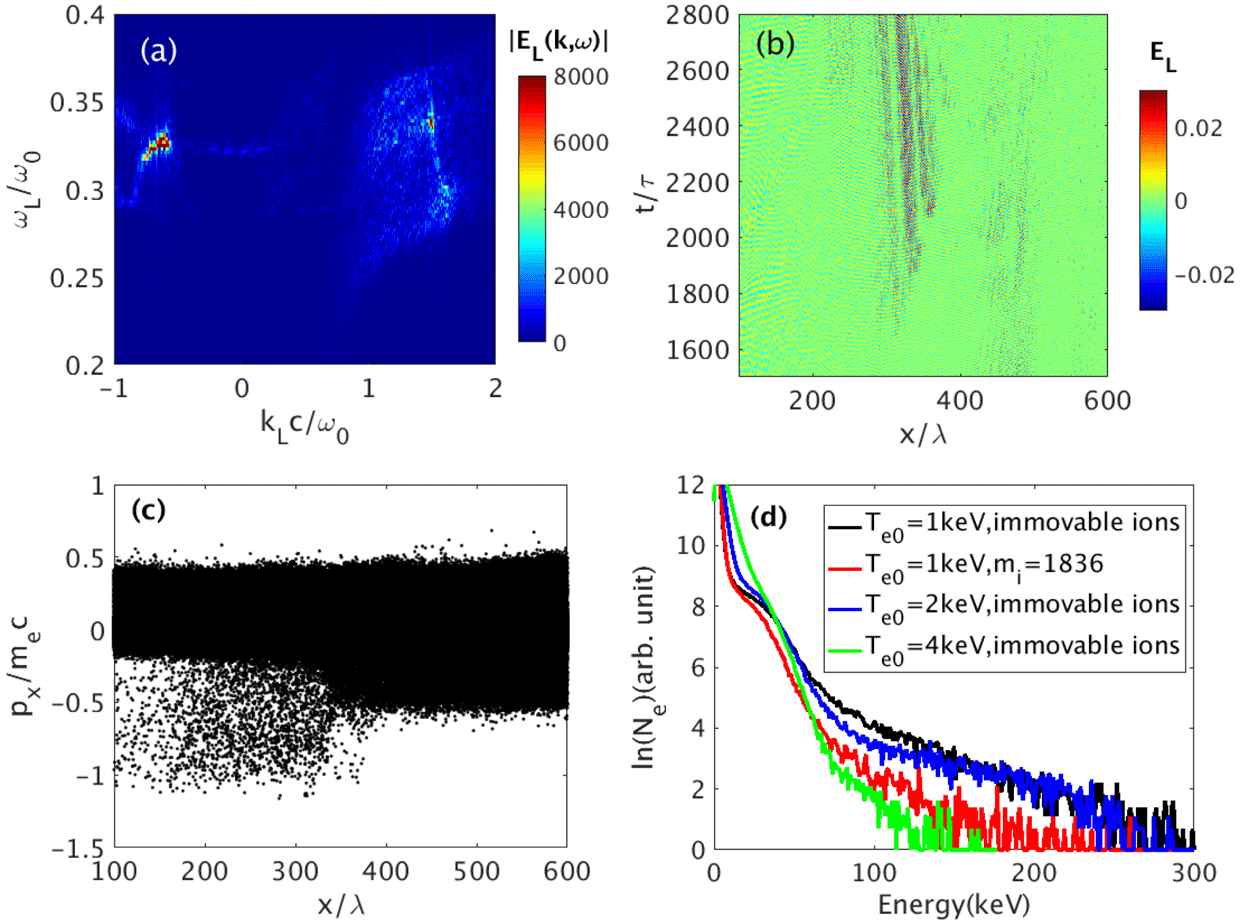
Figure 5. (a)–(c) PIC simulation results for a plasma at
![]() $T_{e0}=1$
keV with immovable ions. (a) 2D Fourier transform
$T_{e0}=1$
keV with immovable ions. (a) 2D Fourier transform
![]() $|E_{L}(k,\unicode[STIX]{x1D714})|$
of the electric field in the time window
$|E_{L}(k,\unicode[STIX]{x1D714})|$
of the electric field in the time window
![]() $[2001,2500]\unicode[STIX]{x1D70F}$
. (b) Time–space distributions of Langmuir waves. (c) Longitudinal phase space distribution of electrons at
$[2001,2500]\unicode[STIX]{x1D70F}$
. (b) Time–space distributions of Langmuir waves. (c) Longitudinal phase space distribution of electrons at
![]() $t=2800\unicode[STIX]{x1D70F}$
. (d) Energy distributions of electrons with different temperatures or different ions at
$t=2800\unicode[STIX]{x1D70F}$
. (d) Energy distributions of electrons with different temperatures or different ions at
![]() $t=4000\unicode[STIX]{x1D70F}$
.
$t=4000\unicode[STIX]{x1D70F}$
.
The overall electron energy distribution has been diagnosed as shown in Figure 3(h). Before the development of the absolute SRS, electron heating is weak at
![]() $t=2000\unicode[STIX]{x1D70F}$
. During
$t=2000\unicode[STIX]{x1D70F}$
. During
![]() $2000\unicode[STIX]{x1D70F}$
to
$2000\unicode[STIX]{x1D70F}$
to
![]() $3000\unicode[STIX]{x1D70F}$
, however, a large number of hot electrons start to be heated up to above 100 keV. Afterwards when the process evolves into the nonlinear regime, lots of hot electrons can be trapped by the Langmuir wave and heated even up to 300 keV, where a hot electron tail with temperature around
$3000\unicode[STIX]{x1D70F}$
, however, a large number of hot electrons start to be heated up to above 100 keV. Afterwards when the process evolves into the nonlinear regime, lots of hot electrons can be trapped by the Langmuir wave and heated even up to 300 keV, where a hot electron tail with temperature around
![]() $T_{e}=78$
keV is generated by the absolute SRS mode at
$T_{e}=78$
keV is generated by the absolute SRS mode at
![]() $t=4000\unicode[STIX]{x1D70F}$
. One finds that absolute SRS plays a leading role in the heating process after
$t=4000\unicode[STIX]{x1D70F}$
. One finds that absolute SRS plays a leading role in the heating process after
![]() $t=2600\unicode[STIX]{x1D70F}$
. It has been reported that experiments in NIF demonstrate that the electrons with temperature
$t=2600\unicode[STIX]{x1D70F}$
. It has been reported that experiments in NIF demonstrate that the electrons with temperature
![]() $T_{e}>170$
keV can cause ignition capsule preheat[Reference Dewald, Thomas, Hunter, Divol, Meezan, Glenzer, Suter, Bond, Kline, Celeste, Bradley, Bell, Kauffman, Kilkenny and Landen13]. Therefore, the absolute SRS instability induced by convective backward SRS could be a crucial factor in the long time interactions.
$T_{e}>170$
keV can cause ignition capsule preheat[Reference Dewald, Thomas, Hunter, Divol, Meezan, Glenzer, Suter, Bond, Kline, Celeste, Bradley, Bell, Kauffman, Kilkenny and Landen13]. Therefore, the absolute SRS instability induced by convective backward SRS could be a crucial factor in the long time interactions.
To further validate the theoretical predictions on the condition of absolute SRS instability, we have performed a simulation with plasma density profile
![]() $n_{e}(x)=0.12[1+(x-525)/1500]n_{c}$
with plasma region
$n_{e}(x)=0.12[1+(x-525)/1500]n_{c}$
with plasma region
![]() $[525,650]\unicode[STIX]{x1D706}$
, where the minimum density is larger than
$[525,650]\unicode[STIX]{x1D706}$
, where the minimum density is larger than
![]() $n_{c}/9$
. The other parameters are the same as the above simulation. As discussed in Section 2, under this plasma condition, the second-order absolute SRS mode would not be triggered. As shown in Figure 4(a), only convective SRS mode can be found in the phase distribution of scattered light in the same time window with Figure 3(b), i.e., no absolute SRS is developed. The absolute SRS mode is thought to be a mechanism for the production of hot electrons. As shown in Figure 4(b), the electron energy distribution tends to be saturated after
$n_{c}/9$
. The other parameters are the same as the above simulation. As discussed in Section 2, under this plasma condition, the second-order absolute SRS mode would not be triggered. As shown in Figure 4(a), only convective SRS mode can be found in the phase distribution of scattered light in the same time window with Figure 3(b), i.e., no absolute SRS is developed. The absolute SRS mode is thought to be a mechanism for the production of hot electrons. As shown in Figure 4(b), the electron energy distribution tends to be saturated after
![]() $t=3000\unicode[STIX]{x1D70F}$
, and the maximum electron energy is still less than 200 keV at
$t=3000\unicode[STIX]{x1D70F}$
, and the maximum electron energy is still less than 200 keV at
![]() $t=4000\unicode[STIX]{x1D70F}$
. This simulation result further proves that hot electron production is considerably reduced if no absolute SRS mode is developed.
$t=4000\unicode[STIX]{x1D70F}$
. This simulation result further proves that hot electron production is considerably reduced if no absolute SRS mode is developed.
Based upon the above two simulations as well as the simulation with density range
![]() $[0.08,0.1]n_{c}$
, we calculate the energy ratio of electrons heated by absolute SRS to the whole electrons with energy
$[0.08,0.1]n_{c}$
, we calculate the energy ratio of electrons heated by absolute SRS to the whole electrons with energy
![]() ${>}60$
keV when the electron temperatures are saturated, and the result is
${>}60$
keV when the electron temperatures are saturated, and the result is
![]() ${\sim}30\%$
. This calculation indicates that absolute instabilities in inhomogeneous plasma have a crucial effect on the production of hot electrons.
${\sim}30\%$
. This calculation indicates that absolute instabilities in inhomogeneous plasma have a crucial effect on the production of hot electrons.
Now we study the absolute SRS developed in a plasma at temperature
![]() $T_{e0}\sim \text{keV}$
. First, the simulation has been performed at
$T_{e0}\sim \text{keV}$
. First, the simulation has been performed at
![]() $T_{e0}=1$
keV. The other parameters are the same as in the first simulation example. An absolute SRS mode with finite bandwidth can be found around
$T_{e0}=1$
keV. The other parameters are the same as in the first simulation example. An absolute SRS mode with finite bandwidth can be found around
![]() $k_{L}c=-0.6\unicode[STIX]{x1D714}_{0}$
and
$k_{L}c=-0.6\unicode[STIX]{x1D714}_{0}$
and
![]() $\unicode[STIX]{x1D714}_{L}=0.33\unicode[STIX]{x1D714}_{0}$
in the time window
$\unicode[STIX]{x1D714}_{L}=0.33\unicode[STIX]{x1D714}_{0}$
in the time window
![]() $[2001,2500]\unicode[STIX]{x1D70F}$
as shown in Figure 5(a). The low-frequency convective mode is much weaker than the case with
$[2001,2500]\unicode[STIX]{x1D70F}$
as shown in Figure 5(a). The low-frequency convective mode is much weaker than the case with
![]() $T_{e0}=100$
eV, due to the heavy Landau damping. Note that the characteristic collision time for 1 keV plasma is larger than
$T_{e0}=100$
eV, due to the heavy Landau damping. Note that the characteristic collision time for 1 keV plasma is larger than
![]() $10^{4}\unicode[STIX]{x1D70F}$
; therefore, the collisions have weak effects on the absolute SRS. Figure 5(b) provides the time–space distributions of Langmuir waves. The absolute SRS mode develops around
$10^{4}\unicode[STIX]{x1D70F}$
; therefore, the collisions have weak effects on the absolute SRS. Figure 5(b) provides the time–space distributions of Langmuir waves. The absolute SRS mode develops around
![]() $x\sim 330\unicode[STIX]{x1D706}$
at
$x\sim 330\unicode[STIX]{x1D706}$
at
![]() $t=1900\unicode[STIX]{x1D70F}$
, and its intensity is much stronger than the convective backward SRS mode. The longitudinal momentum distributions displayed in Figure 5(c) indicate that the hot electrons can be accelerated up to
$t=1900\unicode[STIX]{x1D70F}$
, and its intensity is much stronger than the convective backward SRS mode. The longitudinal momentum distributions displayed in Figure 5(c) indicate that the hot electrons can be accelerated up to
![]() $|p_{x}|\sim 1m_{e}c$
when they transport into absolute instability region
$|p_{x}|\sim 1m_{e}c$
when they transport into absolute instability region
![]() ${\sim}330\unicode[STIX]{x1D706}$
. The above results demonstrate that the absolute SRS can be developed even at keV plasma.
${\sim}330\unicode[STIX]{x1D706}$
. The above results demonstrate that the absolute SRS can be developed even at keV plasma.
To investigate the effects of electron temperature and ion acoustic wave on the absolute SRS, we performed other three simulations as shown in Figure 5(d). The hot tail is barely reduced when the electron temperature increases from 1 keV to 2 keV. Considerable suppression is found when
![]() $T_{e0}=4$
keV; however, the hot tail still exists. The hot tail with movable ions
$T_{e0}=4$
keV; however, the hot tail still exists. The hot tail with movable ions
![]() $m_{i}=1836$
at electron temperature
$m_{i}=1836$
at electron temperature
![]() $T_{e0}=1$
keV and ion temperature
$T_{e0}=1$
keV and ion temperature
![]() $T_{i0}=0.76$
keV is obviously reduced as compared to the case with stationary ions. Ion acoustic wave always weakens the strength of convective SRS by triggering stimulated Brillouin scattering (SBS), Langmuir decay instability (LDI) and plasma density modulations[Reference Hinkel, Haan, Langdon, Dittrich, Still and Marinak18]. However, the ion effects are weakened at keV plasmas, due to the reduction of ion acoustic wave[Reference Weber and Riconda8, Reference Weber, Riconda and Tikhonchuk27, Reference Zhao, Yu, Weng, Ren, Liu and Sheng28]. In conclusion, we can find a relatively weak absolute SRS mode in the plasma with keV electron temperature and movable ions.
$T_{i0}=0.76$
keV is obviously reduced as compared to the case with stationary ions. Ion acoustic wave always weakens the strength of convective SRS by triggering stimulated Brillouin scattering (SBS), Langmuir decay instability (LDI) and plasma density modulations[Reference Hinkel, Haan, Langdon, Dittrich, Still and Marinak18]. However, the ion effects are weakened at keV plasmas, due to the reduction of ion acoustic wave[Reference Weber and Riconda8, Reference Weber, Riconda and Tikhonchuk27, Reference Zhao, Yu, Weng, Ren, Liu and Sheng28]. In conclusion, we can find a relatively weak absolute SRS mode in the plasma with keV electron temperature and movable ions.
Figure 6. Development of absolute SRS instability as seen from 2D PIC simulation with
![]() $a_{0}=0.02$
and
$a_{0}=0.02$
and
![]() $T_{e0}=2$
keV. The incident laser is p-polarized. (a) Spatial Fourier transform
$T_{e0}=2$
keV. The incident laser is p-polarized. (a) Spatial Fourier transform
![]() $|E_{L}(k_{x},k_{y})|$
of the electric field at
$|E_{L}(k_{x},k_{y})|$
of the electric field at
![]() $t=2300\unicode[STIX]{x1D70F}$
. (b) Energy distributions of electrons at different time.
$t=2300\unicode[STIX]{x1D70F}$
. (b) Energy distributions of electrons at different time.
3.2 2D simulations for absolute instability modes
To further validate the absolute instabilities induced via the rescattering of SRS in high dimension, we performed a 2D PIC simulation. The length of the simulation box is
![]() $550\unicode[STIX]{x1D706}$
, where the plasma occupies a region from
$550\unicode[STIX]{x1D706}$
, where the plasma occupies a region from
![]() $25\unicode[STIX]{x1D706}$
to
$25\unicode[STIX]{x1D706}$
to
![]() $525\unicode[STIX]{x1D706}$
with density profile
$525\unicode[STIX]{x1D706}$
with density profile
![]() $n_{e}(x)=0.0998[1+(x-25)/2000]n_{c}$
. The width of the plasma is
$n_{e}(x)=0.0998[1+(x-25)/2000]n_{c}$
. The width of the plasma is
![]() $20\unicode[STIX]{x1D706}$
. The initial electron temperature is
$20\unicode[STIX]{x1D706}$
. The initial electron temperature is
![]() $T_{e0}=2$
keV. The ions are immovable with a charge
$T_{e0}=2$
keV. The ions are immovable with a charge
![]() $Z=1$
. A p-polarized (electric field of light is parallel to the simulation plane) semi-infinite pump laser with a uniform amplitude
$Z=1$
. A p-polarized (electric field of light is parallel to the simulation plane) semi-infinite pump laser with a uniform amplitude
![]() $a_{0}=0.02$
(the corresponding intensity is
$a_{0}=0.02$
(the corresponding intensity is
![]() $I_{0}=5.48\times 10^{14}~\text{W}/\text{cm}^{2}$
with
$I_{0}=5.48\times 10^{14}~\text{W}/\text{cm}^{2}$
with
![]() $\unicode[STIX]{x1D706}=1~\unicode[STIX]{x03BC}\text{m}$
) is incident from the left boundary of the simulation box. We have taken 50 cells per wavelength in both transverse and longitudinal directions.
$\unicode[STIX]{x1D706}=1~\unicode[STIX]{x03BC}\text{m}$
) is incident from the left boundary of the simulation box. We have taken 50 cells per wavelength in both transverse and longitudinal directions.
Figure 6(a) exhibits the spatial Fourier spectra of longitudinal electric field. An intense absolute SRS mode has been developed near
![]() $k_{x}c=0.58\unicode[STIX]{x1D714}_{0}$
at
$k_{x}c=0.58\unicode[STIX]{x1D714}_{0}$
at
![]() $t=2300\unicode[STIX]{x1D70F}$
, which confirms that the absolute SRS is not only a one-dimensional effect. The TPD mode has not been found in this region due to high electron temperature. As known, the ratio between the thresholds for SRS and TPD is roughly
$t=2300\unicode[STIX]{x1D70F}$
, which confirms that the absolute SRS is not only a one-dimensional effect. The TPD mode has not been found in this region due to high electron temperature. As known, the ratio between the thresholds for SRS and TPD is roughly
![]() $(24/T_{e0})/L^{1/3}$
; therefore SRS-dominated regime can be separated from TPD-dominant regime via increasing electron temperature in a finite-size inhomogeneous plasma[Reference Weber and Riconda8]. The energy spectrum of hot electrons is shown in Figure 6(b), where a hot electron tail is formed at
$(24/T_{e0})/L^{1/3}$
; therefore SRS-dominated regime can be separated from TPD-dominant regime via increasing electron temperature in a finite-size inhomogeneous plasma[Reference Weber and Riconda8]. The energy spectrum of hot electrons is shown in Figure 6(b), where a hot electron tail is formed at
![]() $t=2300\unicode[STIX]{x1D70F}$
. This further proves that the absolute instabilities induced via SRS rescattering do contribute significantly to the hot electron productions.
$t=2300\unicode[STIX]{x1D70F}$
. This further proves that the absolute instabilities induced via SRS rescattering do contribute significantly to the hot electron productions.
4 Simulations for absolute SRS mode via the third-order rescattering of SRS
The above simulations are calculated for absolute SRS mode via the second-order rescattering of SRS. It is possible that absolute SRS mode via the third-order scattering can be found in a large scale plasma according to our theoretical analysis. In this section we show 1D simulation results to demonstrate this. An inhomogeneous plasma with density profile
![]() $n_{e}(x)=0.04[1+(x-25)/1000]n_{c}$
occupies a region from
$n_{e}(x)=0.04[1+(x-25)/1000]n_{c}$
occupies a region from
![]() $x=25\unicode[STIX]{x1D706}$
to
$x=25\unicode[STIX]{x1D706}$
to
![]() $x=1275\unicode[STIX]{x1D706}$
. Note that the plasma density range covers
$x=1275\unicode[STIX]{x1D706}$
. Note that the plasma density range covers
![]() $n_{e}=0.0625n_{c}$
, and the maximum plasma density is
$n_{e}=0.0625n_{c}$
, and the maximum plasma density is
![]() $n_{\text{max}}=0.09n_{c}<n_{c}/9$
. The initial electron temperature is
$n_{\text{max}}=0.09n_{c}<n_{c}/9$
. The initial electron temperature is
![]() $T_{e0}=100$
eV. The ions are stationary with a charge
$T_{e0}=100$
eV. The ions are stationary with a charge
![]() $Z=1$
. The incident laser amplitude is
$Z=1$
. The incident laser amplitude is
![]() $a_{0}=0.02$
.
$a_{0}=0.02$
.
Figure 7 illustrates the evolution of the scattering waves and Langmuir waves in the wavenumber–frequency space. Figure 7(a) shows clearly the cascaded scattering has developed, including the first-order scattering, the second-order scattering and even the third-order scattering. It also suggests that the third-order scattering is the convective backward SRS mode, which is generated around
![]() $t=4000\unicode[STIX]{x1D70F}$
at a very low intensity. Some time later, a relatively strong absolute mode can be found in the time window
$t=4000\unicode[STIX]{x1D70F}$
at a very low intensity. Some time later, a relatively strong absolute mode can be found in the time window
![]() $[4001,5000]\unicode[STIX]{x1D70F}$
as shown in Figure 7(b). The absolute instability mode can be clearly distinguished from the convective one in the spectrum distribution. One notes that the absolute mode is developed in the density region ranging from
$[4001,5000]\unicode[STIX]{x1D70F}$
as shown in Figure 7(b). The absolute instability mode can be clearly distinguished from the convective one in the spectrum distribution. One notes that the absolute mode is developed in the density region ranging from
![]() $0.066n_{c}$
to
$0.066n_{c}$
to
![]() $0.077n_{c}$
in this period.
$0.077n_{c}$
in this period.

Figure 7. PIC simulation results for the development of the absolute SRS via the third-order scattering. (a)–(c) Simulation results for the plasma with the inhomogeneous plasma density range
![]() $[0.04,0.09]n_{c}$
. (a) and (b) show the 2D Fourier transform
$[0.04,0.09]n_{c}$
. (a) and (b) show the 2D Fourier transform
![]() $|E_{s}(k,\unicode[STIX]{x1D714})|$
of the scattered light
$|E_{s}(k,\unicode[STIX]{x1D714})|$
of the scattered light
![]() $E_{s}(x,t)$
in the time windows
$E_{s}(x,t)$
in the time windows
![]() $[3001,4000]\unicode[STIX]{x1D70F}$
and
$[3001,4000]\unicode[STIX]{x1D70F}$
and
![]() $[4001,5000]\unicode[STIX]{x1D70F}$
, respectively. (c) 2D Fourier transform
$[4001,5000]\unicode[STIX]{x1D70F}$
, respectively. (c) 2D Fourier transform
![]() $|E_{L}(k,\unicode[STIX]{x1D714})|$
of the electric field in the time window
$|E_{L}(k,\unicode[STIX]{x1D714})|$
of the electric field in the time window
![]() $[5001,6000]\unicode[STIX]{x1D70F}$
. The white line denotes the linear resonant region for convective backscattering SRS. (d) 2D Fourier transform
$[5001,6000]\unicode[STIX]{x1D70F}$
. The white line denotes the linear resonant region for convective backscattering SRS. (d) 2D Fourier transform
![]() $|E_{L}(k,\unicode[STIX]{x1D714})|$
of the electric field in the time window
$|E_{L}(k,\unicode[STIX]{x1D714})|$
of the electric field in the time window
![]() $[5001,6000]\unicode[STIX]{x1D70F}$
, when the plasma density profile is limited to the range of
$[5001,6000]\unicode[STIX]{x1D70F}$
, when the plasma density profile is limited to the range of
![]() $[0.0625,0.09]n_{c}$
.
$[0.0625,0.09]n_{c}$
.
Figure 7(c) shows the distribution of the Langmuir wave in
![]() $(k_{L},\unicode[STIX]{x1D714}_{L})$
space. The white line marks the linear resonant region for the convective backward SRS obtained from
$(k_{L},\unicode[STIX]{x1D714}_{L})$
space. The white line marks the linear resonant region for the convective backward SRS obtained from
![]() $k_{L}c=\sqrt{\unicode[STIX]{x1D714}_{0}^{2}-\unicode[STIX]{x1D714}_{L}^{2}}+\sqrt{\unicode[STIX]{x1D714}_{0}^{2}-2\unicode[STIX]{x1D714}_{0}\unicode[STIX]{x1D714}_{L}}$
. Broad wave number spectrum indicates that the convective modes spread in space with strong frequency shift[Reference Winjum, Fahlen and Mori29]. Moreover, the generation of the third-order backward SRS and the increasing of electron temperature can also lead to the wave number shift. The absolute mode around
$k_{L}c=\sqrt{\unicode[STIX]{x1D714}_{0}^{2}-\unicode[STIX]{x1D714}_{L}^{2}}+\sqrt{\unicode[STIX]{x1D714}_{0}^{2}-2\unicode[STIX]{x1D714}_{0}\unicode[STIX]{x1D714}_{L}}$
. Broad wave number spectrum indicates that the convective modes spread in space with strong frequency shift[Reference Winjum, Fahlen and Mori29]. Moreover, the generation of the third-order backward SRS and the increasing of electron temperature can also lead to the wave number shift. The absolute mode around
![]() $k_{L}=0.4\unicode[STIX]{x1D714}_{0}/c$
with bandwidth
$k_{L}=0.4\unicode[STIX]{x1D714}_{0}/c$
with bandwidth
![]() $0.022\unicode[STIX]{x1D714}_{0}$
demonstrates that the absolute SRS instability region is
$0.022\unicode[STIX]{x1D714}_{0}$
demonstrates that the absolute SRS instability region is
![]() $[0.067,0.079]n_{c}$
, which is the same as the range inferred from Figure 7(b). One notes that the intensity of the absolute SRS mode becomes comparable to the first-order backward SRS at
$[0.067,0.079]n_{c}$
, which is the same as the range inferred from Figure 7(b). One notes that the intensity of the absolute SRS mode becomes comparable to the first-order backward SRS at
![]() $6000\unicode[STIX]{x1D70F}$
. When the absolute SRS mode induced by third-order rescattering of SRS suffers Landau damping, then the Langmuir wave will transfer energy to the hot electrons.
$6000\unicode[STIX]{x1D70F}$
. When the absolute SRS mode induced by third-order rescattering of SRS suffers Landau damping, then the Langmuir wave will transfer energy to the hot electrons.
As comparison, we have performed another set of simulation with a plasma density profile limited to the range
![]() $[0.0625,0.09]n_{c}$
and other parameters unchanged. Based on the discussion in Section 2, the development of the absolute SRS mode via the third-order scattering needs a second-order backward SRS region
$[0.0625,0.09]n_{c}$
and other parameters unchanged. Based on the discussion in Section 2, the development of the absolute SRS mode via the third-order scattering needs a second-order backward SRS region
![]() $n_{e}<0.0625n_{c}$
to generate backscattering lights. Without this density region, only a convective mode can be found and no third-order absolute SRS can be developed. This is verified in Figure 7(d).
$n_{e}<0.0625n_{c}$
to generate backscattering lights. Without this density region, only a convective mode can be found and no third-order absolute SRS can be developed. This is verified in Figure 7(d).
5 Summary
In summary, we have theoretically and numerically studied the mechanism of the absolute instabilities induced by cascading SRS processes in a large scale nonuniform plasma. Theoretical analysis indicates that the backscattering light from convective SRS can generate strong absolute instabilities in a plasma within
![]() $n_{e}<1/9n_{c}$
via the second-order SRS rescattering. The absolute SRS mode develops a Langmuir wave with a high phase velocity of about
$n_{e}<1/9n_{c}$
via the second-order SRS rescattering. The absolute SRS mode develops a Langmuir wave with a high phase velocity of about
![]() $0.58c$
, corresponding to hot electron energy around 170 keV. In the linear stage of the absolute SRS instability, the absolute SRS mode can grow without Landau damping, where the hot electron energy is well below 100 keV. When the interactions evolve into the nonlinear regime, due to the rescattering processes, a large number of electrons are trapped by the Langmuir wave and are heated up to 300 keV. It is further demonstrated that the absolute SRS instability can be developed via the third-order backward SRS when the inhomogeneous plasma is even larger and the interaction time is long over a few picoseconds. The absolute instabilities due to rescattering of SRS may play a significant role for the capsule preheating in inertial confinement fusion, where a large inhomogeneous plasma is often involved.
$0.58c$
, corresponding to hot electron energy around 170 keV. In the linear stage of the absolute SRS instability, the absolute SRS mode can grow without Landau damping, where the hot electron energy is well below 100 keV. When the interactions evolve into the nonlinear regime, due to the rescattering processes, a large number of electrons are trapped by the Langmuir wave and are heated up to 300 keV. It is further demonstrated that the absolute SRS instability can be developed via the third-order backward SRS when the inhomogeneous plasma is even larger and the interaction time is long over a few picoseconds. The absolute instabilities due to rescattering of SRS may play a significant role for the capsule preheating in inertial confinement fusion, where a large inhomogeneous plasma is often involved.
Acknowledgements
The authors acknowledge useful discussions with C. Z. Xiao, R. Yan and C. Ren. This work was supported by the National Natural Science Foundation of China (Nos. 11775144 and 1172109) and the Natural Science Foundation of Shanghai (No. 19YF1453200).