No CrossRef data available.
Article contents
Existence of solution for a class of activator–inhibitor systems
Published online by Cambridge University Press: 12 April 2022
Abstract
We prove the existence of a solution for a class of activator–inhibitor system of type
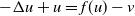 $- \Delta u +u = f(u) -v$
,
$- \Delta u +u = f(u) -v$
,
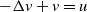 $-\Delta v+ v=u$
in
$-\Delta v+ v=u$
in
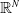 $\mathbb{R}^{N}$
. The function f is a general nonlinearity which can grow polynomially in dimension
$\mathbb{R}^{N}$
. The function f is a general nonlinearity which can grow polynomially in dimension
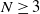 $N\geq 3$
or exponentiallly if
$N\geq 3$
or exponentiallly if
 $N=2$
. We are able to treat f when it has critical growth corresponding to the Sobolev space we work with. We transform the system into an equation with a nonlocal term. We find a critical point of the corresponding energy functional defined in the space of functions with norm endowed by a scalar product that takes into account such nonlocal term. For that matter, and due to the lack of compactness, we deal with weak convergent minimizing sequences and sequences of Lagrange multipliers of an action minima problem.
$N=2$
. We are able to treat f when it has critical growth corresponding to the Sobolev space we work with. We transform the system into an equation with a nonlocal term. We find a critical point of the corresponding energy functional defined in the space of functions with norm endowed by a scalar product that takes into account such nonlocal term. For that matter, and due to the lack of compactness, we deal with weak convergent minimizing sequences and sequences of Lagrange multipliers of an action minima problem.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Glasgow Mathematical Journal Trust





