Hostname: page-component-848d4c4894-2xdlg Total loading time: 0 Render date: 2024-06-21T14:43:19.714Z Has data issue: false hasContentIssue false
  • English
  • Français

Deciding if an automorphism of an infinite soluble group is inner

Published online by Cambridge University Press:  18 May 2009

Derek J. S. Robinson
Derek J. S. Robinson
Affiliation:
Department of Mathematics, University of Illinoisin Urbana-Champaign, Urbana, Illinois, USA
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G be a group with a finite set of generators x1, x2,…,xn and a recursive set of defining relators in the generators. Then an endomorphism η of G is completely determined by the images of the generators 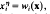, and hence by the n-tuple of words in x, (w1,…,wn). This allows the formulation of algorithmic problems about endomorphisms and automorphisms. For example, can one decide if a given n-tuple of words represents an endomorphism, and if so, an automorphism? Some results on these questions may be found in [2] and [12]. Here we shall be concerned with a similar problem: given that an n-tuple of words represents an automorphism of the group G, does there exist an algorithm which decides if the automorphism is inner?

Type
Research Article
Information
Glasgow Mathematical Journal , Volume 32 , Issue 3 , September 1990 , pp. 265 - 272
Copyright
Copyright © Glasgow Mathematical Journal Trust 1990

References

REFERENCES

1.Baumslag, G. and Bieri, R., Constructable soluble group, Math. Z. 151 (1976), 249–257.CrossRefGoogle Scholar
2.Baumslag, G., Cannonito, F. B. and Miller, C. F. III, Infinitely generated subgroups of finitely presented groups I, Math. Z. 153 (1977), 117–134.CrossRefGoogle Scholar
3.Baumslag, G., Cannonito, F. B. and Miller, C. F. III, Some recognizable properties of solvable groups, Math. Z. 178 (1981), 289–295.CrossRefGoogle Scholar
4.Baumslag, G., Cannonito, F. B. and Miller, C. F. III, Computable algebra and group embeddings, J. Algebra 69 (1981), 186–212.CrossRefGoogle Scholar
5.Baumslag, G., Cannonito, F. B., Robinson, D. J. S. and Segal, D., The algorithmic theory of polycyclic-by-finite groups, J. Algebra, to appear.Google Scholar
6.Baumslag, G., Gildenhuys, D. and Strebel, R., Algorithmically insoluble problems about finitely presented solvable groups, Lie and associative algebras, I, II, J. Pure Appl. Algebra 39 (1986), 53–94, J. Algebra 97 (1985), 278–285.CrossRefGoogle Scholar
7.Cannonito, F. B. and Robinson, D. J. S., The word problem for finitely generated soluble groups of finite rank, Bull. London Math. Soc. 16 (1984), 43–46.CrossRefGoogle Scholar
8.Lewin, J., A finitely presented group whose group of automorphisms is infinitely generated, J. London Math. Soc. 42 (1967), 610–613.CrossRefGoogle Scholar
9.Noskov, G. A., On conjugacy in metabelian groups, Mat. Zametki 31 (1982), 495–507.Google Scholar
10.Robinson, D. J. S., Finiteness conditions and generalized soluble groups, Part 2 (Springer, 1972).CrossRefGoogle Scholar
11.Robinson, D. J. S., Decision problems for soluble groups of finite rank, Illinois J. Math. 30 (1986), 197–213.CrossRefGoogle Scholar
12.Robinson, D. J. S., Algorithmic problems for automorphisms and endomorphisms of infinite soluble groups, in Proceedings of the Hong Kong Conference on Algebras and their Applications, to appear.Google Scholar
13.Romanovskñ, N. S., The occurrence problem for extensions of abelian groups by nilpotent groups, Sibirsk. Mat. Ž. 21 (1980), 170–174.Google Scholar
14.Samuel, P., À propos du theorème des unités, Bull. Sci. Math. 90 (1966), 89–96.Google Scholar