No CrossRef data available.
Article contents
CO-UNIVERSAL C*-ALGEBRAS ASSOCIATED TO APERIODIC k-GRAPHS
Published online by Cambridge University Press: 13 August 2013
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
We construct a representation of each finitely aligned aperiodic k-graph Λ on the Hilbert space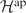 
$\mathcal{H}^{\rm ap}$ with basis indexed by aperiodic boundary paths in Λ. We show that the canonical expectation on 
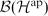$\mathcal{B}(\mathcal{H}^{\rm ap})$ restricts to an expectation of the image of this representation onto the subalgebra spanned by the final projections of the generating partial isometries. We then show that every quotient of the Toeplitz algebra of the k-graph admits an expectation compatible with this one. Using this, we prove that the image of our representation, which is canonically isomorphic to the Cuntz–Krieger algebra, is co-universal for Toeplitz–Cuntz–Krieger families consisting of non-zero partial isometries.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 2013
References
REFERENCES
1.Bates, T., Pask, D., Raeburn, I. and Szymański, W., The C*-algebras of row-finite graphs, New York J. Math. 6 (2000), 307–324.Google Scholar
3.Cuntz, J., Simple C*-algebras generated by isometries, Comm. Math. Phys. 57 (1977), 173–185.Google Scholar
4.Farthing, C., Muhly, P. and Yeend, T., Higher-rank graph C*-algebras: An inverse semigroup and groupoid approach, Semigroup Forum 71 (2005), 159–187.CrossRefGoogle Scholar
5.Fowler, N. J. and Sims, A., Product systems over right-angled Artin semigroups, Trans. Amer. Math. Soc. 354 (2002), 1487–1509.Google Scholar
6.Hong, J. H. and Szymański, W., The primitive ideal space of the C*-algebras of infinite graphs, J. Math. Soc. Japan 56 (2004), 45–64.Google Scholar
7.Katsura, T., A class of C*-algebras generalizing both graph algebras and homeomorphism C*-algebras I. Fundamental results, Trans. Amer. Math. Soc. 356 (2004), 4287–4322.Google Scholar
8.Katsura, T., A class of C*-algebras generalizing both graph algebras and homeomorphism C*-algebras. III. Ideal structures, Ergodic Theory Dynam. Syst. 26 (2006), 1805–1854.Google Scholar
9.Katsura, T., Ideal structure of C*-algebras associated with C*-correspondences, Pacific J. Math. 230 (2007), 107–146.CrossRefGoogle Scholar
10.Kumjian, A. and Pask, D., Higher rank graph C*-algebras, New York J. Math. 6 (2000), 1–20.Google Scholar
11.Kumjian, A., Pask, D. and Raeburn, I., Cuntz–Krieger algebras of directed graphs, Pacific J. Math. 184 (1998), 161–174.Google Scholar
12.Kumjian, A., Pask, D., Raeburn, I. and Renault, J., Graphs, groupoids, and Cuntz–Krieger algebras, J. Funct. Anal. 144 (1997), 505–541.Google Scholar
13.Lewin, P. and Sims, A., Aperiodicity and cofinality for finitely aligned higher-rank graphs, Math. Proc. Cambridge Philos. Soc. 149 (2010), 333–350.Google Scholar
14.Raeburn, I., Graph algebras. CBMS Regional Conference Series in Mathematics, vol. 103. Published for the Conference Board of the Mathematical Sciences, Washington, DC. (American Mathematical Society, Providence, RI, 2005).CrossRefGoogle Scholar
15.Raeburn, I. and Sims, A., Product systems of graphs and the Toeplitz algebras of higher-rank graphs, J. Operator Theory 53 (2005), 399–429.Google Scholar
16.Raeburn, I., Sims, A. and Yeend, T., The C*-algebras of finitely aligned higher-rank graphs, J. Funct. Anal. 213 (2004), 206–240.Google Scholar
17.Robertson, D. I. and Sims, A., Simplicity of C*-algebras associated to higher-rank graphs, Bull. London Math. Soc. 39 (2007), 337–344.Google Scholar
18.Sims, A., Relative Cuntz–Krieger algebras of finitely aligned higher-rank graphs, Indiana Univ. Math. J. 55 (2006), 849–868.CrossRefGoogle Scholar
19.Sims, A. and Webster, S. B. G., A direct approach to co-universal algebras associated to directed graphs, Bull. Malays. Math. Sci. Soc. 33 (2) (2010), 211–220.Google Scholar
You have
Access