Article contents
ON THE ARITHMETIC OF MORI MONOIDS AND DOMAINS
Published online by Cambridge University Press: 08 April 2019
Abstract
Let R be a Mori domain with complete integral closure 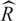 $\widehat R$, nonzero conductor
$\widehat R$, nonzero conductor 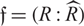 $\mathfrak f = (R: \widehat R)$, and suppose that both v-class groups
$\mathfrak f = (R: \widehat R)$, and suppose that both v-class groups 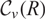 ${{\cal C}_v}(R)$ and
${{\cal C}_v}(R)$ and 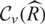 ${{\cal C}_v}(3\widehat R)$ are finite. If
${{\cal C}_v}(3\widehat R)$ are finite. If 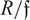 $R \mathfrak f$ is finite, then the elasticity of R is either rational or infinite. If
$R \mathfrak f$ is finite, then the elasticity of R is either rational or infinite. If 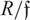 $R \mathfrak f$ is artinian, then unions of sets of lengths of R are almost arithmetical progressions with the same difference and global bound. We derive our results in the setting of v-noetherian monoids.
$R \mathfrak f$ is artinian, then unions of sets of lengths of R are almost arithmetical progressions with the same difference and global bound. We derive our results in the setting of v-noetherian monoids.
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 2019
References
- 3
- Cited by


