Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-27T00:36:41.804Z Has data issue: false hasContentIssue false
  • English
  • Français

Development of associative overdominance through linkage disequilibrium in finite populations*

Published online by Cambridge University Press:  14 April 2009

Tomoko Ohta  and
Motoo Kimura
Tomoko Ohta
Affiliation:
National Institute of Genetics, Mishima, Japan
Motoo Kimura
Affiliation:
National Institute of Genetics, Mishima, Japan
Rights & Permissions [Opens in a new window]

Summary

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Associative overdominance arises at an intrinsically neutral locus through its non-random association with overdominant loci. In finite populations, even if fitness is additive between loci, non-random association will be created by random genetic drift.

The magnitude of such associative overdominance is roughly proportional to the sum of 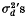between the neutral and the surrounding over-dominant loci, where 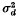is the squared standard linkage deviation, defined between any two loci by the relation

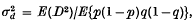
in which p and 1 – p are frequencies of alleles A1 and A2 in the first locus, q and 1 – q are frequencies of alleles B1 and B2 in the second locus, and D is the coefficient of linkage disequilibrium. A theory was developed based on diffusion models which enables us to obtain formulae for 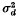under various conditions, and Monte Carlo experiments were performed to check the validity of those formulae.

It was shown that if A1 and A2 are strongly overdominant while B1 and B2 are selectively neutral, we have approximately

provided that 4Nec ≫ 1, where Ne is the effective population size and c is the recombination fraction between the two loci. This approximation formula is also valid between two strongly overdominant as well as weakly overdominant loci, if 4Nec ≫ 1.

The significance of associative overdominance for the maintenance of genetic variability in natural populations was discussed, and it was shown that Nes′, that is, the product between effective population size and the coefficient of associative overdominance, remanis constant with varying Ne, if the total segregational (overdominant) load is kept constant.

The amount of linkage disequilibrium expected due to random drift in experimental populations was also discussed, and it was shown that 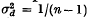in the first generation, if it is produced by extracting n chromosomes from a large parental population in which D = 0.

Type
Research Article
Information
Genetics Research , Volume 16 , Issue 2 , October 1970 , pp. 165 - 177
Copyright
Copyright © Cambridge University Press 1970

References

REFERENCES

Bodmer, W. F. & Felsenstein, J. (1967). Linkage and selection: Theoretical analysis of the deterministic two locus random mating model. Genetics 57, 237–265.CrossRefGoogle ScholarPubMed
Chigusa, S. & Mukai, T. (1964). Linkage disequilibrium and heterosis in experimental populations of Drosophila melanogaster with particular reference to the sepia gene. Japanese Journal of Genetica 39, 289–306.Google Scholar
Comstock, R. E. & Robinson, H. F. (1952). Estimation of average dominance of genes. In Heterosis, pp. 494–516. Ames: Iowa State College Press.Google Scholar
Frydenberg, O. (1963). Population studies of a lethal mutant in Drosophila melanogaster. I. Behaviour in populations with discrete generations. Hereditas 50, 89–116.CrossRefGoogle Scholar
Hill, W. G. & Robertson, A. (1968). Linkage disequilibrium in finite populations. Theoretical and Applied Genetics 38, 226–231.CrossRefGoogle ScholarPubMed
Maruyama, T. & Kimura, M. (1968). Development of temporary overdominance associated with neutral alieles. Proceedings of XII International Congress of Genetics, Tokyo, vol. 1, p. 229.Google Scholar
Ohta, T. (1968). Effect of initial linkage disequilibrium and epistasis on fixation probability in a small population, with two segregating loci. Theoretical and Applied Genetics 38, 243–248.CrossRefGoogle Scholar
Ohta, T. & Kimura, M. (1969 a). Linkage disequilibrium due to random genetic drift. Genetical Research 13, 47–55.CrossRefGoogle Scholar
Ohta, T. & Kimura, M. (1969 b). Linkage disequilibrium at steady state determined by random genetic drift and recurrent mutation. Genetics 63, 229–238.CrossRefGoogle ScholarPubMed
Sved, J. A. (1968). The stability of linked systems of loci with a small population size. Genetics 59, 543–563.CrossRefGoogle ScholarPubMed