Hostname: page-component-8448b6f56d-xtgtn Total loading time: 0 Render date: 2024-04-24T16:34:01.605Z Has data issue: false hasContentIssue false
  • English
  • Français

SINGULARITY OF RANDOM SYMMETRIC MATRICES—A COMBINATORIAL APPROACH TO IMPROVED BOUNDS

Part of: Probability theory on algebraic and topological structures

Published online by Cambridge University Press:  02 August 2019

ASAF FERBER  and
VISHESH JAIN
ASAF FERBER
Affiliation:
Massachusetts Institute of Technology, Department of Mathematics, USA; ferbera@mit.edu, visheshj@mit.edu
VISHESH JAIN
Affiliation:
Massachusetts Institute of Technology, Department of Mathematics, USA; ferbera@mit.edu, visheshj@mit.edu

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 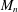$M_{n}$ denote a random symmetric 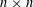$n\times n$ matrix whose upper-diagonal entries are independent and identically distributed Bernoulli random variables (which take values 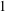$1$ and 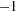$-1$ with probability 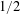$1/2$ each). It is widely conjectured that 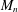$M_{n}$ is singular with probability at most 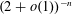$(2+o(1))^{-n}$. On the other hand, the best known upper bound on the singularity probability of 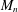$M_{n}$, due to Vershynin (2011), is 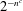$2^{-n^{c}}$, for some unspecified small constant 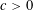$c>0$. This improves on a polynomial singularity bound due to Costello, Tao, and Vu (2005), and a bound of Nguyen (2011) showing that the singularity probability decays faster than any polynomial. In this paper, improving on all previous results, we show that the probability of singularity of 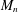$M_{n}$ is at most 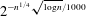$2^{-n^{1/4}\sqrt{\log n}/1000}$ for all sufficiently large $n$. The proof utilizes and extends a novel combinatorial approach to discrete random matrix theory, which has been recently introduced by the authors together with Luh and Samotij.

MSC classification

Primary: 60B20: Random matrices (probabilistic aspects; for algebraic aspects see )
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 7 , 2019 , e22
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2019

References

Bourgain, J., Vu, V. H. and Wood, P. M., ‘On the singularity probability of discrete random matrices’, J. Funct. Anal. 258(2) (2010), 559–603.Google Scholar
Costello, K. P., Tao, T. and Vu, V. H., ‘Random symmetric matrices are almost surely nonsingular’, Duke Math. J. 135(2) (2006), 395–413.Google Scholar
Ferber, A., Jain, V., Luh, K. and Samotij, W., ‘On the counting problem in inverse Littlewood–Offord theory’, Preprint, 2019, arXiv:1904.10425.Google Scholar
Halász, G., ‘Estimates for the concentration function of combinatorial number theory and probability’, Period. Math. Hungar. 8(3-4) (1977), 197–211.Google Scholar
Jain, V., ‘Approximate Spielman–Teng theorems for random matrices with heavy tailed entries: a combinatorial view’, Preprint, 2019, arXiv:1904.11108.Google Scholar
Jain, V., ‘Approximate Spielman–Teng theorems for the least singular value of random combinatorial matrices’, Preprint, 2019, arXiv:1904.10592.Google Scholar
Kahn, J., Komlós, J. and Szemerédi, E., ‘On the probability that a random ± 1-matrix is singular’, J. Amer. Math. Soc. 8(1) (1995), 223–240.Google Scholar
Komlós, J., ‘On determinant of (0, 1) matrices’, Studia Sci. Math. Hungar. 2 (1967), 7–21.Google Scholar
Nguyen, H. H., ‘Inverse Littlewood–Offord problems and the singularity of random symmetric matrices’, Duke Math. J. 161(4) (2012), 545–586.Google Scholar
Nguyen, H. H. and Vu, V. H., ‘Optimal inverse Littlewood–Offord theorems’, Adv. Math. 226(6) (2011), 5298–5319.Google Scholar
Nguyen, H. H. and Vu, V. H., ‘Small ball probability, inverse theorems, and applications’, inErdős Centennial (Springer, Berlin, Heidelberg, 2013), 409–463.Google Scholar
Odlyzko, A. M., ‘On subspaces spanned by random selections of {±}-1 vectors’, J. Combin. Theory Ser. A 47(1) (1988), 124–133.Google Scholar
Rudelson, M. and Vershynin, R., ‘The Littlewood–Offord problem and invertibility of random matrices’, Adv. Math. 218(2) (2008), 600–633.Google Scholar
Rudelson, M. and Vershynin, R., ‘Non-asymptotic theory of random matrices: extreme singular values’, inProceedings of the International Congress of Mathematicians 2010 (ICM 2010) (In 4 Volumes), Vol. I: Plenary Lectures and Ceremonies Vols. II–IV: Invited Lectures (Hindustan Book Agency, New Delhi, 2010), 1576–1602.Google Scholar
Tao, T. and Vu, V. H., ‘On the singularity probability of random Bernoulli matrices’, J. Amer. Math. Soc. 20(3) (2007), 603–628.Google Scholar
Tao, T. and Vu, V. H., ‘John-type theorems for generalized arithmetic progressions and iterated sumsets’, Adv. Math. 219(2) (2008), 428–449.Google Scholar
Tikhomirov, K., ‘Singularity of random Bernoulli matrices’, Preprint, 2018,arXiv:1812.09016.Google Scholar
Vershynin, R., ‘Invertibility of symmetric random matrices’, Random Structures Algorithms 44(2) (2014), 135–182.Google Scholar
Vu, V. H., ‘Random discrete matrices’, inHorizons of Combinatorics (Springer, Berlin, Heidelberg, 2008), 257–280.Google Scholar