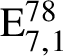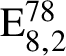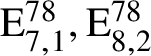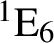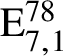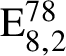1. Introduction
The primary aim of this article is to prove the long standing Tits–Weiss conjecture on U-operators in Albert algebras and the Kneser–Tits conjecture for algebraic groups of type
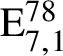 $\mathrm {E}^{78}_{7,1}$
and
$\mathrm {E}^{78}_{7,1}$
and
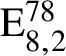 $\mathrm {E}^{78}_{8,2}$
.
$\mathrm {E}^{78}_{8,2}$
.
The Tits–Weiss conjecture asserts that the structure group
![]() ${\mathrm{Str}}(A)$
of an arbitrary Albert algebra A is generated by the inner structure group, formed by the so-called U-operators, and the central homotheties. This problem was raised by Tits and Weiss in their 2002 book [Reference Springer and Veldkamp26], where they studied spherical buildings and the corresponding generalised polygons attached to isotropic groups of relative rank
${\mathrm{Str}}(A)$
of an arbitrary Albert algebra A is generated by the inner structure group, formed by the so-called U-operators, and the central homotheties. This problem was raised by Tits and Weiss in their 2002 book [Reference Springer and Veldkamp26], where they studied spherical buildings and the corresponding generalised polygons attached to isotropic groups of relative rank
![]() $2$
. Despite many efforts, this problem has remained unsolved.
$2$
. Despite many efforts, this problem has remained unsolved.
If
![]() $\mathbf{G}$
is an isotropic simple simply connected group over a field K of relative rank
$\mathbf{G}$
is an isotropic simple simply connected group over a field K of relative rank
![]() $\geq 2$
, then by [Reference Prasad and Raghunathan18] the group
$\geq 2$
, then by [Reference Prasad and Raghunathan18] the group
![]() ${\mathbf{G}}(K)$
is generated by the K-points of isotropic subgroups of
${\mathbf{G}}(K)$
is generated by the K-points of isotropic subgroups of
![]() ${\mathbf{G}}$
of relative rank
${\mathbf{G}}$
of relative rank
![]() $1$
. This result allows one to reduce many problems for
$1$
. This result allows one to reduce many problems for
![]() ${\mathbf{G}}(K)$
to groups of relative rank
${\mathbf{G}}(K)$
to groups of relative rank
![]() $1$
. For instance, this is the case for the Kneser–Tits problem (see the paragraph below). Note also that isotropic groups of relative rank
$1$
. For instance, this is the case for the Kneser–Tits problem (see the paragraph below). Note also that isotropic groups of relative rank
![]() $1$
give rise to important examples of more general groups of rank 1. The latter were introduced by Tits in the early 1990s, who called them Moufang sets. They have proved to be important in the classification of simple groups, incidence geometry, the theory of buildings and other areas. Further still, rank 1 groups are useful in studying isotropic groups of exceptional types, where algebraic groups and their associated root subgroups are typically parametrised by a nonassociative structure and, as emphasised in [Reference Garibaldi and Petersson6], a rich interplay emerges between rank 1 groups, nonassociative algebras and linear algebraic groups.
$1$
give rise to important examples of more general groups of rank 1. The latter were introduced by Tits in the early 1990s, who called them Moufang sets. They have proved to be important in the classification of simple groups, incidence geometry, the theory of buildings and other areas. Further still, rank 1 groups are useful in studying isotropic groups of exceptional types, where algebraic groups and their associated root subgroups are typically parametrised by a nonassociative structure and, as emphasised in [Reference Garibaldi and Petersson6], a rich interplay emerges between rank 1 groups, nonassociative algebras and linear algebraic groups.
The Kneser–Tits conjecture for a simple simply connected isotropic group
![]() ${\mathbf{G}}$
over a field K asserts that the abstract group
${\mathbf{G}}$
over a field K asserts that the abstract group
![]() ${\mathbf{G}}(K)$
of K-points of
${\mathbf{G}}(K)$
of K-points of
![]() ${\mathbf{G}}$
coincides with its normal subgroup
${\mathbf{G}}$
coincides with its normal subgroup
![]() ${\mathbf{G}}(K)^+$
generated by the unipotent radicals of the minimal parabolic K-subgroups of
${\mathbf{G}}(K)^+$
generated by the unipotent radicals of the minimal parabolic K-subgroups of
![]() ${\mathbf{G}}$
. We refer to [Reference Gille9] for a survey of the history and recent results on this conjecture. Its importance comes from the fact that the group
${\mathbf{G}}$
. We refer to [Reference Gille9] for a survey of the history and recent results on this conjecture. Its importance comes from the fact that the group
![]() ${\mathbf{G}}(K)^+$
has a natural
${\mathbf{G}}(K)^+$
has a natural
![]() $BN$
-pair structure and hence is projectively simple (i.e., simple modulo its centre) by a celebrated theorem of Tits. So if
$BN$
-pair structure and hence is projectively simple (i.e., simple modulo its centre) by a celebrated theorem of Tits. So if
![]() ${\mathbf{G}}(K)={\mathbf{G}}(K)^+$
, we would have many more new examples of projectively simple abstract groups. In this way, we would obtain analogues of finite simple groups of Lie type in the case of infinite fields. It is also worth mentioning that the information about the normal subgroup structure of
${\mathbf{G}}(K)={\mathbf{G}}(K)^+$
, we would have many more new examples of projectively simple abstract groups. In this way, we would obtain analogues of finite simple groups of Lie type in the case of infinite fields. It is also worth mentioning that the information about the normal subgroup structure of
![]() ${\mathbf{G}}(K)$
is crucial in the arithmetic of algebraic groups for studying, among other things, congruence subgroups, discrete subgroups, lattices and locally symmetric spaces. In general, the Kneser–Tits conjecture does not hold and the first counterexample was constructed by V. Platonov in 1975 [Reference Platonov17]. However, specialists believe that the conjecture does hold for many isotropic groups of exceptional type, including those of type
${\mathbf{G}}(K)$
is crucial in the arithmetic of algebraic groups for studying, among other things, congruence subgroups, discrete subgroups, lattices and locally symmetric spaces. In general, the Kneser–Tits conjecture does not hold and the first counterexample was constructed by V. Platonov in 1975 [Reference Platonov17]. However, specialists believe that the conjecture does hold for many isotropic groups of exceptional type, including those of type
 $\mathrm {E}_{7,1}^{78}$
and
$\mathrm {E}_{7,1}^{78}$
and
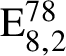 $\mathrm {E}_{8,2}^{78}$
.
$\mathrm {E}_{8,2}^{78}$
.
The bridge connecting the Tits–Weiss conjecture and the Kneser–Tits conjecture for the abovementioned forms of type
![]() $\mathrm {E}_7$
and
$\mathrm {E}_7$
and
![]() $\mathrm {E}_8$
is provided by a theorem of Tits and Weiss (see the Appendix), which states that the two conjectures are equivalent.Footnote
1
It is interesting to mention that the proof in the Appendix is characteristic free. Furthermore, using P. Gille’s results on Whitehead groups [Reference Gille9], one can easily see that
$\mathrm {E}_8$
is provided by a theorem of Tits and Weiss (see the Appendix), which states that the two conjectures are equivalent.Footnote
1
It is interesting to mention that the proof in the Appendix is characteristic free. Furthermore, using P. Gille’s results on Whitehead groups [Reference Gille9], one can easily see that
-
1. the Kneser–Tits conjecture for the abovementioned groups reduces to the R-triviality of structure groups of Albert algebras and
-
2. the conjecture holds in arbitrary characteristic once it is established in characteristic zero.
Our main result is the following.
Theorem. Let A be an Albert algebra over a field K. Then the structure group
![]() ${\mathbf{Str}}(A)$
of A is R-trivial; that is, for any field extension
${\mathbf{Str}}(A)$
of A is R-trivial; that is, for any field extension
![]() $F/K$
the group of R-equivalence classes
$F/K$
the group of R-equivalence classes
![]() ${\mathbf{Str}}(A)(F)/R$
is trivial.
${\mathbf{Str}}(A)(F)/R$
is trivial.
As explained above, this implies that the Tits–Weiss conjecture on U-operators holds for Albert algebras over any field and that the same is true for the Kneser–Tits conjecture for groups of type
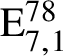 $\mathrm {E}^{78}_{7,1}$
and
$\mathrm {E}^{78}_{7,1}$
and
 $\mathrm {E}^{78}_{8,2}$
. Our proof is geometric in nature. We carefully analyse the properties of the natural action of the structure group
$\mathrm {E}^{78}_{8,2}$
. Our proof is geometric in nature. We carefully analyse the properties of the natural action of the structure group
![]() ${\mathbf{Str}}(A)$
on the corresponding Albert algebra A. The information that we need is encoded in the Galois cohomology of the stabilisers of subalgebras of A. We compute the Galois cohomology of all these stabilisers and, using this information, we explicitly construct a system of generators of
${\mathbf{Str}}(A)$
on the corresponding Albert algebra A. The information that we need is encoded in the Galois cohomology of the stabilisers of subalgebras of A. We compute the Galois cohomology of all these stabilisers and, using this information, we explicitly construct a system of generators of
![]() ${\mathbf{Str}}(A)(K)$
, which we prove are R-trivial.
${\mathbf{Str}}(A)(K)$
, which we prove are R-trivial.
An important step of the proof of our main result is the weak Skolem–Noether theorem for isomorphic embeddings due to S. Garibaldi and H. Petersson (for the terminology, definitions and the precise statement we refer to [Reference Gille7]). In Section 5 we prove Theorem 5.3, which can be viewed as a weaker version of S. Garibaldi and H. Petersson’s result.
We would also like to mention that it follows directly from our main theorem that two standard conjectures hold for simple simply connected strongly inner forms of type
![]() $\mathrm {E}_6$
: the abelian nature of the group of R-equivalence classes and the existence of transfers for the functor of R-equivalence classes. For these groups, the norm principle holds as well. For details we refer to the last section of the article.
$\mathrm {E}_6$
: the abelian nature of the group of R-equivalence classes and the existence of transfers for the functor of R-equivalence classes. For these groups, the norm principle holds as well. For details we refer to the last section of the article.
Lastly, we mention that our results were proved independently by M. Thakur [Reference Thakur24]. His proof differs from ours and is based on some explicit formulas for automorphisms of subalgebras of Albert algebras and extensions of these automorphisms.
Conventions and Notation
Throughout, K will denote a fixed field. A K-ring is a morphism
![]() $K \to R$
in the category of unital commutative associative rings. As is customary, by an abuse of language, the target R of such a morphism is also referred to as a K-ring.
$K \to R$
in the category of unital commutative associative rings. As is customary, by an abuse of language, the target R of such a morphism is also referred to as a K-ring.
By an algebraic K-group, or simply a K-group for convenience, we will understand a group scheme
![]() ${\mathbf{G}}$
of finite type over
${\mathbf{G}}$
of finite type over
![]() ${\textrm {Spec}}(K).$
Footnote
2
The connected component of the identity of an algebraic K-group
${\textrm {Spec}}(K).$
Footnote
2
The connected component of the identity of an algebraic K-group
![]() ${\mathbf{G}}$
will be denoted by
${\mathbf{G}}$
will be denoted by
![]() ${\mathbf{G}}^\circ .$
${\mathbf{G}}^\circ .$
Let A be a finite-dimensional algebra over K (not assumed associative or commutative). For any K-ring R the R-module
![]() $A \otimes _K R$
has a natural R-algebra structure. We denote by
$A \otimes _K R$
has a natural R-algebra structure. We denote by
![]() ${\mathbf {Aut}}(A)$
the algebraic K-group whose functor of points is given by
${\mathbf {Aut}}(A)$
the algebraic K-group whose functor of points is given by
Let V be a K-subspace of
![]() $A.$
We let
$A.$
We let
![]() ${\mathbf {Aut}}(A,V)$
and
${\mathbf {Aut}}(A,V)$
and
![]() ${\mathbf {Aut}}(A/V)$
be the closed algebraic subgroups of
${\mathbf {Aut}}(A/V)$
be the closed algebraic subgroups of
![]() ${\mathbf {Aut}}(A)$
whose functor of points are given by
${\mathbf {Aut}}(A)$
whose functor of points are given by
and
respectively.
If
![]() $\bf G$
is an algebraic K-group, we will denote
$\bf G$
is an algebraic K-group, we will denote
 $H_{\textrm {fppf}}^1(K, {\mathbf{G}})$
simply by
$H_{\textrm {fppf}}^1(K, {\mathbf{G}})$
simply by
![]() $H^1(K, {\mathbf{G}}).$
Whenever
$H^1(K, {\mathbf{G}}).$
Whenever
![]() ${\mathbf{G}}$
is smooth, one knows that
${\mathbf{G}}$
is smooth, one knows that
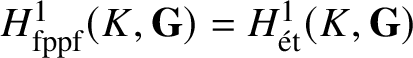 $H_{\textrm {fppf}}^1(K, {\mathbf{G}}) = H_{\acute{e}t}^1(K, {\mathbf{G}})$
and that this last is nothing but the usual (nonabelian) Galois cohomology.
$H_{\textrm {fppf}}^1(K, {\mathbf{G}}) = H_{\acute{e}t}^1(K, {\mathbf{G}})$
and that this last is nothing but the usual (nonabelian) Galois cohomology.
In view of point (2) above, in order to prove our main results we may assume that K is of characteristic zero. That said, many of the preliminary results are of independent interest and hold with less restrictions on the nature of the base field. For this reason, we will henceforth assume, unless specifically stated otherwise, that K of characteristic different from 2 and 3.
2. Preliminaries
For later use we record some facts about Albert algebras and algebraic groups.
2.1. Albert Algebras
A Jordan algebra over K is a unital, commutative, not necessarily associative K-algebra A in which the Jordan identity
is satisfied. In particular, A is power associative. Given an associative algebra B with multiplication
![]() $\cdot $
, the anticommutator
$\cdot $
, the anticommutator
 $\frac {1}{2}(x\cdot y+y\cdot x)$
defines on B the structure of a Jordan algebra, denoted by
$\frac {1}{2}(x\cdot y+y\cdot x)$
defines on B the structure of a Jordan algebra, denoted by
![]() $B^+$
. A Jordan algebra A is said to be special if it is isomorphic to a Jordan subalgebra of
$B^+$
. A Jordan algebra A is said to be special if it is isomorphic to a Jordan subalgebra of
![]() $B^+$
for an associative algebra B and exceptional otherwise. An Albert algebra is by definition a simple, exceptional Jordan algebra. It is known that any Albert algebra has dimension 27 and that, if the field K is separably closed, then all Albert algebras over K are isomorphic, as follows from [Reference De Medts, Mühlherr and Stavrova13, Proposition 37.11]. Thus, all Albert algebras over K are twisted forms of each other.
$B^+$
for an associative algebra B and exceptional otherwise. An Albert algebra is by definition a simple, exceptional Jordan algebra. It is known that any Albert algebra has dimension 27 and that, if the field K is separably closed, then all Albert algebras over K are isomorphic, as follows from [Reference De Medts, Mühlherr and Stavrova13, Proposition 37.11]. Thus, all Albert algebras over K are twisted forms of each other.
If A is an Albert algebra over
![]() $K,$
then
$K,$
then
![]() ${\mathbf{H}}={\mathbf {Aut}}(A)$
is a simple K-group of type
${\mathbf{H}}={\mathbf {Aut}}(A)$
is a simple K-group of type
![]() ${\textrm {F}}_4$
. It is known that any such group arises in this fashion and that two Albert algebras are isomorphic if and only if their automorphism groups are. Moreover, A is equipped with a cubic form
${\textrm {F}}_4$
. It is known that any such group arises in this fashion and that two Albert algebras are isomorphic if and only if their automorphism groups are. Moreover, A is equipped with a cubic form
![]() $N:A\to K$
, called the norm of A. Our main object of study is the structure group
$N:A\to K$
, called the norm of A. Our main object of study is the structure group
![]() ${\mathbf{Str}}(A)$
of A. This is the algebraic K-group whose functor of points is as follows: if R is a K-ring,
${\mathbf{Str}}(A)$
of A. This is the algebraic K-group whose functor of points is as follows: if R is a K-ring,
where
![]() $N_R$
is the base change of N to
$N_R$
is the base change of N to
![]() $A\otimes _K R$
and the multiplier
$A\otimes _K R$
and the multiplier
![]() $\nu (x)\in R^\times $
.
$\nu (x)\in R^\times $
.
The derived subgroup
of
![]() ${\mathbf{Str}}(A)$
is known to be a strongly inner form of a split simple simply connected K-group of type
${\mathbf{Str}}(A)$
is known to be a strongly inner form of a split simple simply connected K-group of type
![]() ${\mathrm{E}}_6$
. Moreover,
${\mathrm{E}}_6$
. Moreover,
![]() ${\mathbf{Str}}(A)$
is an almost direct product of
${\mathbf{Str}}(A)$
is an almost direct product of
![]() ${\mathbf{G}}_m$
and
${\mathbf{G}}_m$
and
![]() ${\mathbf{G}}$
(the intersection being the centre of
${\mathbf{G}}$
(the intersection being the centre of
![]() $\bf {G}$
). Hence,
$\bf {G}$
). Hence,
is an adjoint K-group of type
![]() ${\mathrm{E}}_6$
. Since in the split and even isotropic case,
${\mathrm{E}}_6$
. Since in the split and even isotropic case,
![]() ${\mathbf{G}}$
and
${\mathbf{G}}$
and
![]() ${\mathbf{Str}}(A)$
are R-trivial (see [Reference Chernousov and Platonov5]), we may, in the proof of the main theorem, assume that
${\mathbf{Str}}(A)$
are R-trivial (see [Reference Chernousov and Platonov5]), we may, in the proof of the main theorem, assume that
![]() $\bf G$
is K-anisotropic. This amounts to the Albert algebra A being a division algebra, which is equivalent to the norm map N being anisotropic; that is, the equation
$\bf G$
is K-anisotropic. This amounts to the Albert algebra A being a division algebra, which is equivalent to the norm map N being anisotropic; that is, the equation
![]() $N(a)=0$
having no nonzero solutions over K.
$N(a)=0$
having no nonzero solutions over K.
We denote the group of K-points of
![]() ${\mathbf{Str}}(A)$
(respectively
${\mathbf{Str}}(A)$
(respectively
![]() ${\mathbf{G}},\, {\overline {\mathbf{G}}},\, {\mathbf{H}}$
) by
${\mathbf{G}},\, {\overline {\mathbf{G}}},\, {\mathbf{H}}$
) by
![]() ${\mathrm{Str}}(A)$
(respectively
${\mathrm{Str}}(A)$
(respectively
![]() $G,\,\overline {G},\,H$
). The group
$G,\,\overline {G},\,H$
). The group
![]() ${\mathbf{H}}$
coincides with the stabiliser in
${\mathbf{H}}$
coincides with the stabiliser in
![]() ${\mathbf{Str}}(A)$
of
${\mathbf{Str}}(A)$
of
![]() $1\in A$
; see e.g. [Reference Steinberg20, 5.9.4].
$1\in A$
; see e.g. [Reference Steinberg20, 5.9.4].
2.2. R-equivalence in Algebraic Groups
Let
![]() ${\mathbf{G}}$
be an affine algebraic K-group. Two K-points
${\mathbf{G}}$
be an affine algebraic K-group. Two K-points
![]() $x,y\in {\mathbf{G}}(K)$
are called R-equivalent if there is a path from x to y; that is, if there exists a rational map
$x,y\in {\mathbf{G}}(K)$
are called R-equivalent if there is a path from x to y; that is, if there exists a rational map
 $f:\mathbb A_K^1\dashrightarrow {\mathbf{G}}$
defined at
$f:\mathbb A_K^1\dashrightarrow {\mathbf{G}}$
defined at
![]() $0,1$
and mapping
$0,1$
and mapping
![]() $0$
to x and
$0$
to x and
![]() $1$
to y. One can easily verify that this is indeed an equivalence relation on
$1$
to y. One can easily verify that this is indeed an equivalence relation on
![]() ${\mathbf{G}}(K)$
and that, moreover,
${\mathbf{G}}(K)$
and that, moreover,
![]() ${\mathbf{G}}$
induces a group structure on the set
${\mathbf{G}}$
induces a group structure on the set
![]() ${\mathbf{G}}(K)/R$
of all R-equivalence classes. We will denote the set of elements in
${\mathbf{G}}(K)/R$
of all R-equivalence classes. We will denote the set of elements in
![]() ${\mathbf{G}}(K)$
equivalent to
${\mathbf{G}}(K)$
equivalent to
![]() $1$
by
$1$
by
![]() $R{\mathbf{G}}(K)$
.
$R{\mathbf{G}}(K)$
.
2.3. R-triviality of Cohomology Classes and the Norm Principle
Let
![]() ${\mathbf{G}}$
be a semisimple K-group,
${\mathbf{G}}$
be a semisimple K-group,
![]() ${\mathbf{Z}}\subset {\mathbf{G}}$
a central subgroup and let
${\mathbf{Z}}\subset {\mathbf{G}}$
a central subgroup and let
Definition. We say that
![]() $[\xi ]$
is R-trivial if there exists
$[\xi ]$
is R-trivial if there exists
 $$ \begin{align*}c(t)=[\xi(t)]\in {\textrm{Ker}}\,[H^1(K(t),{\textbf{Z}}_{K(t)})\longrightarrow H^1(K(t),{\mathbf{G}}_{K(t)})], \end{align*} $$
$$ \begin{align*}c(t)=[\xi(t)]\in {\textrm{Ker}}\,[H^1(K(t),{\textbf{Z}}_{K(t)})\longrightarrow H^1(K(t),{\mathbf{G}}_{K(t)})], \end{align*} $$
with
![]() $K(t)$
a purely transcendental extension of K, such that
$K(t)$
a purely transcendental extension of K, such that
![]() $c(t)$
is defined at
$c(t)$
is defined at
![]() $t=0, 1$
and
$t=0, 1$
and
![]() $c(0)=1$
and
$c(0)=1$
and
![]() $c(1)=[\xi ]$
.
$c(1)=[\xi ]$
.
Remark 2.1. The above definition requires some clarification. Here and below, if
![]() ${\mathbf{G}}$
is an algebraic K-group, then an element in
${\mathbf{G}}$
is an algebraic K-group, then an element in
![]() ${\mathbf{G}}(K(t))$
(respectively a class in
${\mathbf{G}}(K(t))$
(respectively a class in
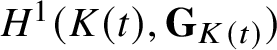 $H^1(K(t),{\mathbf{G}}_{K(t)})$
), where t is a variable over K, is said to be defined at 0 and 1 if it is in the image of
$H^1(K(t),{\mathbf{G}}_{K(t)})$
), where t is a variable over K, is said to be defined at 0 and 1 if it is in the image of
![]() ${\mathbf{G}}(\mathcal O)$
(respectively
${\mathbf{G}}(\mathcal O)$
(respectively
![]() $H^1(\mathcal O,{\mathbf{G}}_{\mathcal O})$
), where
$H^1(\mathcal O,{\mathbf{G}}_{\mathcal O})$
), where
![]() $\mathcal O$
is the intersection in
$\mathcal O$
is the intersection in
![]() $K(t)$
of the localisations
$K(t)$
of the localisations
![]() $K[t]_{(t)}$
and
$K[t]_{(t)}$
and
![]() $K[t]_{(t-1)}$
. In particular, via the evaluation maps
$K[t]_{(t-1)}$
. In particular, via the evaluation maps
![]() $\varepsilon _0,\varepsilon _1:\mathcal O\to K$
, we can evaluate such an element or a class at 0 and at 1.
$\varepsilon _0,\varepsilon _1:\mathcal O\to K$
, we can evaluate such an element or a class at 0 and at 1.
Example 2.2. Let D be a central simple algebra of degree n over K and set
![]() ${\mathbf{G}}={\mathbf{SL}}(1,D)$
. The centre
${\mathbf{G}}={\mathbf{SL}}(1,D)$
. The centre
![]() ${\mathbf{Z}}$
of
${\mathbf{Z}}$
of
![]() ${\mathbf{G}}$
is isomorphic to
${\mathbf{G}}$
is isomorphic to
![]() $\boldsymbol {\mu }_n$
and thus
$\boldsymbol {\mu }_n$
and thus
![]() $H^1(K,{\mathbf{Z}})\simeq K^\times /K^{\times n}$
. Moreover,
$H^1(K,{\mathbf{Z}})\simeq K^\times /K^{\times n}$
. Moreover,
![]() $H^1(K,{\mathbf{G}})\simeq K^\times /{\textrm {Nrd}}\,(D^\times )$
. Hence,
$H^1(K,{\mathbf{G}})\simeq K^\times /{\textrm {Nrd}}\,(D^\times )$
. Hence,
and as D is the affine space
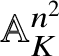 ${\mathbb A}_K^{n^2}$
, any element of the above kernel is R-trivial.
${\mathbb A}_K^{n^2}$
, any element of the above kernel is R-trivial.
Example 2.3. Let f be a Pfister form over K, set
![]() ${\mathbf{G}}={\mathbf{Spin}}(f)$
and let again
${\mathbf{G}}={\mathbf{Spin}}(f)$
and let again
![]() ${\mathbf{Z}}\subset {\mathbf{G}}$
be its centre. Then all cohomology classes in (1) are R-trivial; indeed, by [Reference Merkurjev14, Proposition 7] the group
${\mathbf{Z}}\subset {\mathbf{G}}$
be its centre. Then all cohomology classes in (1) are R-trivial; indeed, by [Reference Merkurjev14, Proposition 7] the group
![]() ${\mathbf{G}}/{\mathbf{Z}}={\mathbf{PGO}}^+(f)$
is stably rational, and hence R-trivial, and since the canonical map
${\mathbf{G}}/{\mathbf{Z}}={\mathbf{PGO}}^+(f)$
is stably rational, and hence R-trivial, and since the canonical map
is surjective, any element in the kernel is R-trivial.
Example 2.4. Let f be an n-fold Pfister form over K, and let g be a nondegenerate subform of
![]() $f\oplus \mathbb H$
of codimension
$f\oplus \mathbb H$
of codimension
![]() $2$
, where
$2$
, where
![]() $\mathbb H$
is the hyperbolic plane. If d is the determinant of g, then we have a decomposition
$\mathbb H$
is the hyperbolic plane. If d is the determinant of g, then we have a decomposition
for some scalar
![]() $a\in K^\times $
. We claim that the group
$a\in K^\times $
. We claim that the group
![]() ${\mathbf{PGO}}^+(g)$
is R-trivial or, equivalently (see [Reference Merkurjev14]), that the multiplier of any similitude with respect to g is R-trivial. In particular, if
${\mathbf{PGO}}^+(g)$
is R-trivial or, equivalently (see [Reference Merkurjev14]), that the multiplier of any similitude with respect to g is R-trivial. In particular, if
![]() ${\mathbf{G}}={\mathbf{Spin}}(g)$
and
${\mathbf{G}}={\mathbf{Spin}}(g)$
and
![]() $\bf {Z}$
is its centre, then arguing as in the previous example, one finds that every element in the kernel (1) is R-trivial.
$\bf {Z}$
is its centre, then arguing as in the previous example, one finds that every element in the kernel (1) is R-trivial.
To compute the group of multipliers of g we first recall that every multiplier of g is contained in the set
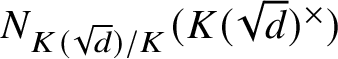 $N_{K(\sqrt {d})/K}(K(\sqrt {d})^\times )$
(see [Reference De Medts, Mühlherr and Stavrova13, Theorem 13.38]). Therefore, it follows from (2) that a multiplier m with respect to g is a multiplier with respect to f as well and hence is contained in the value group
$N_{K(\sqrt {d})/K}(K(\sqrt {d})^\times )$
(see [Reference De Medts, Mühlherr and Stavrova13, Theorem 13.38]). Therefore, it follows from (2) that a multiplier m with respect to g is a multiplier with respect to f as well and hence is contained in the value group
![]() $D(f)$
of f. Conversely, (2) implies that every element
$D(f)$
of f. Conversely, (2) implies that every element
 $$ \begin{align*}m\in N_{K(\sqrt{d})/K}(K(\sqrt{d})^\times)\cap D(f)\end{align*} $$
$$ \begin{align*}m\in N_{K(\sqrt{d})/K}(K(\sqrt{d})^\times)\cap D(f)\end{align*} $$
is a multiplier of g. Let now
![]() $U\subset K(\sqrt {d})$
be the open subvariety consisting of all elements with nonzero norm and let
$U\subset K(\sqrt {d})$
be the open subvariety consisting of all elements with nonzero norm and let
 $X\subset U\times \mathbb {A}_K^{2^n}$
be the K-variety consisting of the elements
$X\subset U\times \mathbb {A}_K^{2^n}$
be the K-variety consisting of the elements
![]() $(x,y)$
satisfying
$(x,y)$
satisfying
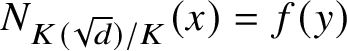 $N_{K(\sqrt {d})/K}(x)=f(y)$
. Consider the map
$N_{K(\sqrt {d})/K}(x)=f(y)$
. Consider the map
![]() $X\to {\mathbf{G}}_m$
given by
$X\to {\mathbf{G}}_m$
given by
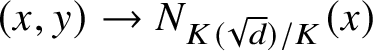 $(x,y) \to N_{K(\sqrt {d})/K}(x)$
. Then the group of multipliers of g is the image of the K-points of X. Since X is K-rational, the group of multipliers of g is R-trivial.
$(x,y) \to N_{K(\sqrt {d})/K}(x)$
. Then the group of multipliers of g is the image of the K-points of X. Since X is K-rational, the group of multipliers of g is R-trivial.
Let
![]() ${\mathbf{G}}$
be a semisimple K-group and let
${\mathbf{G}}$
be a semisimple K-group and let
![]() ${\mathbf{Z}}\subset {\mathbf{G}}$
be a central subgroup. For any finite extension
${\mathbf{Z}}\subset {\mathbf{G}}$
be a central subgroup. For any finite extension
![]() $L/K$
we have the restriction map
$L/K$
we have the restriction map
 $$ \begin{align*}res^L_K: H^1(K,{\textbf{Z}}) \to H^1(L,{\textbf{Z}}) \end{align*} $$
$$ \begin{align*}res^L_K: H^1(K,{\textbf{Z}}) \to H^1(L,{\textbf{Z}}) \end{align*} $$
and the corestriction map
 $$ \begin{align*}cor^L_K: H^1(L,{\textbf{Z}})\to H^1(K,{\textbf{Z}}). \end{align*} $$
$$ \begin{align*}cor^L_K: H^1(L,{\textbf{Z}})\to H^1(K,{\textbf{Z}}). \end{align*} $$
Definition. Let
![]() $L/K$
be a finite field extension. We say that the norm principle holds for a cohomology class
$L/K$
be a finite field extension. We say that the norm principle holds for a cohomology class
if
 $$ \begin{align*}cor^L_K([\eta]) \in {\textrm{Ker}}\,[H^1(K,{\textbf{Z}}) \longrightarrow H^1(K,{\mathbf{G}})]. \end{align*} $$
$$ \begin{align*}cor^L_K([\eta]) \in {\textrm{Ker}}\,[H^1(K,{\textbf{Z}}) \longrightarrow H^1(K,{\mathbf{G}})]. \end{align*} $$
We also say that the norm principle holds for the pair
![]() $({\mathbf{Z}},{\mathbf{G}})$
if it holds for every
$({\mathbf{Z}},{\mathbf{G}})$
if it holds for every
![]() $[\eta ]\in {\textrm {Ker}}\,[H^1(L, {\mathbf{Z}})\longrightarrow H^1(L,{\mathbf{G}})]$
whenever
$[\eta ]\in {\textrm {Ker}}\,[H^1(L, {\mathbf{Z}})\longrightarrow H^1(L,{\mathbf{G}})]$
whenever
![]() $L/K$
is a finite extension.
$L/K$
is a finite extension.
Theorem 2.5 P. Gille [Reference Gille and Quéguiner-Mathieu8]
Let K be a field of arbitrary characteristic and let
![]() $L/K$
be a finite field extension. The norm principle holds for all R-trivial elements
$L/K$
be a finite field extension. The norm principle holds for all R-trivial elements
![]() $[\eta ]\in {\textrm {Ker}}\,[H^1(L, {\mathbf{Z}})\longrightarrow H^1(L,{\mathbf{G}})]$
. Moreover,
$[\eta ]\in {\textrm {Ker}}\,[H^1(L, {\mathbf{Z}})\longrightarrow H^1(L,{\mathbf{G}})]$
. Moreover,
![]() $cor^L_K([\eta ])$
is R-trivial.
$cor^L_K([\eta ])$
is R-trivial.
2.4. Groups of Type
 $\mathrm D_4$
$\mathrm D_4$
First we recall a statement about groups of type
![]() $\mathrm D_4$
inside split groups of type
$\mathrm D_4$
inside split groups of type
![]() $\mathrm {F}_4$
, proved in [Reference Alsaody, Chernousov and Pianzola1].
$\mathrm {F}_4$
, proved in [Reference Alsaody, Chernousov and Pianzola1].
Proposition 2.6. Let
![]() ${\mathbf{F}}$
be a split K-group of type
${\mathbf{F}}$
be a split K-group of type
![]() $\mathrm {F}_4$
. Then any K-subgroup
$\mathrm {F}_4$
. Then any K-subgroup
![]() ${\mathbf{M}}\subset {\mathbf{F}}$
of type
${\mathbf{M}}\subset {\mathbf{F}}$
of type
![]() $\mathrm {D}_4$
is quasi-split.
$\mathrm {D}_4$
is quasi-split.
For later use we need one more fact about groups of type
![]() $^{3,6}\mathrm {D}_4$
inside
$^{3,6}\mathrm {D}_4$
inside
![]() $\mathrm {F}_4$
. Let thus
$\mathrm {F}_4$
. Let thus
![]() ${\mathbf{M}}\subset {\mathbf{F}}$
be a split subgroup of type
${\mathbf{M}}\subset {\mathbf{F}}$
be a split subgroup of type
![]() $\mathrm {D}_4$
and consider its normaliser
$\mathrm {D}_4$
and consider its normaliser
![]() ${\mathbf{N}}=N_{\mathbf{F}}({\mathbf{M}})$
. The quotient group
${\mathbf{N}}=N_{\mathbf{F}}({\mathbf{M}})$
. The quotient group
![]() ${\mathbf{N}}/{\mathbf{M}}$
is isomorphic to the group of outer automorphisms
${\mathbf{N}}/{\mathbf{M}}$
is isomorphic to the group of outer automorphisms
![]() ${\mathbf{Out}}({\mathbf{M}})$
of
${\mathbf{Out}}({\mathbf{M}})$
of
![]() ${\mathbf{M}}$
. This is the symmetric group
${\mathbf{M}}$
. This is the symmetric group
![]() $S_3$
, which we view as a constant finite group scheme over K.
$S_3$
, which we view as a constant finite group scheme over K.
Let
![]() $ [\xi ]\in H^1(K,{\mathbf{N}})$
be an arbitrary cohomology class and consider its image
$ [\xi ]\in H^1(K,{\mathbf{N}})$
be an arbitrary cohomology class and consider its image
![]() $[\overline {\xi }]\in H^1 (K,{\mathbf{Out}}({\mathbf{M}}))$
. Since
$[\overline {\xi }]\in H^1 (K,{\mathbf{Out}}({\mathbf{M}}))$
. Since
![]() ${\mathbf{Out}}({\mathbf{M}})$
is a constant group scheme, any cocycle
${\mathbf{Out}}({\mathbf{M}})$
is a constant group scheme, any cocycle
![]() $\overline {\xi }$
representing it corresponds to a homomorphism
$\overline {\xi }$
representing it corresponds to a homomorphism
![]() $\phi _{\xi }:{\textrm {Gal}}(K^{sep}/K) \to S_3$
. The image
$\phi _{\xi }:{\textrm {Gal}}(K^{sep}/K) \to S_3$
. The image
![]() ${\textrm {Im}}\,\phi _{\xi }$
is then isomorphic to the Galois group of the minimal Galois extension
${\textrm {Im}}\,\phi _{\xi }$
is then isomorphic to the Galois group of the minimal Galois extension
![]() $F/K$
over which the twisted group
$F/K$
over which the twisted group
![]() $^{\xi }{\mathbf{M}}$
becomes a group of inner type. It follows that
$^{\xi }{\mathbf{M}}$
becomes a group of inner type. It follows that
![]() ${\textrm {Im}}\,\phi _{\xi }$
is generated by the cycle
${\textrm {Im}}\,\phi _{\xi }$
is generated by the cycle
![]() $(123)$
if
$(123)$
if
![]() $^{\xi }{\mathbf{M}}$
has type
$^{\xi }{\mathbf{M}}$
has type
![]() $^3\mathrm {D}_4$
and is equal to
$^3\mathrm {D}_4$
and is equal to
![]() $S_3$
if
$S_3$
if
![]() $^{\xi }{\mathbf{M}}$
has type
$^{\xi }{\mathbf{M}}$
has type
![]() $^6\mathrm {D}_4$
.
$^6\mathrm {D}_4$
.
Lemma 2.7. Assume that
![]() $^{\xi }{\mathbf{M}}$
has type
$^{\xi }{\mathbf{M}}$
has type
![]() $^{3,6}{\mathrm {D}}_4$
. Then the natural map
$^{3,6}{\mathrm {D}}_4$
. Then the natural map
 $\phi :{\mathbf {}^{\xi }\mathbf{N}}(K) \to {^{\overline {\xi }}(S_3)(K)}$
is surjective.
$\phi :{\mathbf {}^{\xi }\mathbf{N}}(K) \to {^{\overline {\xi }}(S_3)(K)}$
is surjective.
Proof. If
![]() ${\textrm {Im}}\,\phi _{\xi }=S_3$
, we have
${\textrm {Im}}\,\phi _{\xi }=S_3$
, we have
 $^{\overline {\xi }}(S_3)(K)=1$
and there is nothing to prove. Assume next that
$^{\overline {\xi }}(S_3)(K)=1$
and there is nothing to prove. Assume next that
![]() ${\textrm {Im}}\,\phi _{\xi }=\langle (123)\rangle $
. In this case
${\textrm {Im}}\,\phi _{\xi }=\langle (123)\rangle $
. In this case
 ${^{\overline {\xi }}(S_3)(K)} $
consists of three elements. Note that
${^{\overline {\xi }}(S_3)(K)} $
consists of three elements. Note that
![]() $\phi $
is the composition of the two natural maps
$\phi $
is the composition of the two natural maps
![]() ${\mathbf {}^{\xi }\mathbf {N}}(K) \to {\mathbf {Aut}}({^\xi }{\mathbf{M}})(K)$
and
${\mathbf {}^{\xi }\mathbf {N}}(K) \to {\mathbf {Aut}}({^\xi }{\mathbf{M}})(K)$
and
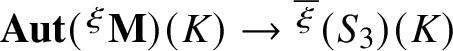 ${\mathbf {Aut}}({^\xi }{\mathbf{M}})(K)\to {^{\overline {\xi }}(S_3)(K)}$
. By [Reference Gille7], the group
${\mathbf {Aut}}({^\xi }{\mathbf{M}})(K)\to {^{\overline {\xi }}(S_3)(K)}$
. By [Reference Gille7], the group
![]() ${\mathbf {Aut}}({^\xi }{\mathbf{M}} )(K)$
contains an outer automorphism, say a, and it suffices to lift it modulo inner automorphisms to
${\mathbf {Aut}}({^\xi }{\mathbf{M}} )(K)$
contains an outer automorphism, say a, and it suffices to lift it modulo inner automorphisms to
![]() ${\mathbf {}^{\xi }\mathbf {N}}(K)$
.
${\mathbf {}^{\xi }\mathbf {N}}(K)$
.
The exact sequence
where
![]() ${\mathbf{Z}}$
is the centre of
${\mathbf{Z}}$
is the centre of
![]() ${\mathbf {}^{\xi }\mathbf {N}} $
, induces the connecting map
${\mathbf {}^{\xi }\mathbf {N}} $
, induces the connecting map
Let
![]() $\eta :=\psi (a)$
. Let
$\eta :=\psi (a)$
. Let
![]() $L/K$
be the cubic field extension over which
$L/K$
be the cubic field extension over which
![]() $^\xi {\mathbf{M}}$
becomes an inner form. By construction, we can say even more: it is a strongly inner form of type
$^\xi {\mathbf{M}}$
becomes an inner form. By construction, we can say even more: it is a strongly inner form of type
![]() ${\textrm {D}}_4$
; hence,
${\textrm {D}}_4$
; hence,
![]() $^\xi {\mathbf{M}}_L\simeq {\textrm {Spin}}(f_L)$
where
$^\xi {\mathbf{M}}_L\simeq {\textrm {Spin}}(f_L)$
where
![]() $f_L$
is a
$f_L$
is a
![]() $3$
-fold Pfister form. Therefore, a viewed over L can be lifted modulo inner automorphisms to an element of
$3$
-fold Pfister form. Therefore, a viewed over L can be lifted modulo inner automorphisms to an element of
![]() $^\xi {\mathbf{N}}(L)$
. In other words, there is an element
$^\xi {\mathbf{N}}(L)$
. In other words, there is an element
![]() $a'\in ({\mathbf {Aut}}({^\xi }{\mathbf{M}}))^\circ (L)$
such that its image under the connecting map
$a'\in ({\mathbf {Aut}}({^\xi }{\mathbf{M}}))^\circ (L)$
such that its image under the connecting map
![]() $\psi _L$
is
$\psi _L$
is
![]() $\eta _L$
.
$\eta _L$
.
According to Example 2.3,
![]() $\eta _L$
is R-trivial. This means that if t is a variable over K, then there exists a class
$\eta _L$
is R-trivial. This means that if t is a variable over K, then there exists a class
such that
![]() $\eta (t)$
is defined at
$\eta (t)$
is defined at
![]() $t=0,1$
and
$t=0,1$
and
![]() $\eta (0)=1, \eta (1)=\eta _L$
. We now pass to
$\eta (0)=1, \eta (1)=\eta _L$
. We now pass to
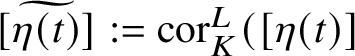 $[\widetilde {\eta (t)}]:={\textrm {cor}}^L_K([\eta (t)]$
. By a result of P. Gille (see Theorem 2.5), the class
$[\widetilde {\eta (t)}]:={\textrm {cor}}^L_K([\eta (t)]$
. By a result of P. Gille (see Theorem 2.5), the class
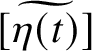 $[\widetilde {\eta (t)}]$
belongs to
$[\widetilde {\eta (t)}]$
belongs to
and can be specialised at
![]() $t=0,1$
. Since
$t=0,1$
. Since
![]() $L/K$
has degree
$L/K$
has degree
![]() $3$
and since
$3$
and since
![]() $H^1(K,{\mathbf{Z}})$
is a
$H^1(K,{\mathbf{Z}})$
is a
![]() $2$
-group, we have
$2$
-group, we have
 $\widetilde {\eta (t)}(1)=\eta $
.
$\widetilde {\eta (t)}(1)=\eta $
.
Choose an element
![]() $b(t)\in ({\mathbf {Aut}}({^\xi }{\mathbf{M}}))^\circ (K(t))$
which maps to
$b(t)\in ({\mathbf {Aut}}({^\xi }{\mathbf{M}}))^\circ (K(t))$
which maps to
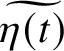 $\widetilde {\eta (t)}$
under
$\widetilde {\eta (t)}$
under
![]() $\psi _{K(t)}$
and which can be specialised at
$\psi _{K(t)}$
and which can be specialised at
![]() $t=0,1$
. By construction,
$t=0,1$
. By construction,
![]() $\psi (b(1))=[\eta ]$
. This implies that
$\psi (b(1))=[\eta ]$
. This implies that
![]() $\psi (ab(1)^{-1})=1$
. In other words,
$\psi (ab(1)^{-1})=1$
. In other words,
![]() $ab(1)^{-1}$
has a lifting to
$ab(1)^{-1}$
has a lifting to
![]() $^\xi {\mathbf{N}}(K)$
, as required.
$^\xi {\mathbf{N}}(K)$
, as required.
2.5. Conjugacy of Maximal Tori
Let
![]() ${\mathbf{G}}$
be an absolutely simple semisimple K-group. Let
${\mathbf{G}}$
be an absolutely simple semisimple K-group. Let
![]() ${\mathbf{T}}$
and
${\mathbf{T}}$
and
![]() ${\mathbf{T}}'$
be maximal tori in
${\mathbf{T}}'$
be maximal tori in
![]() ${\mathbf{G}}.$
Since all maximal tori become conjugate upon extension to
${\mathbf{G}}.$
Since all maximal tori become conjugate upon extension to
![]() $K^{sep}$
, there exists
$K^{sep}$
, there exists
![]() $g\in {\mathbf{G}}(K^{sep})$
such that
$g\in {\mathbf{G}}(K^{sep})$
such that
![]() ${\mathbf{T}}'=g{\mathbf{T}}g^{-1}$
. Since
${\mathbf{T}}'=g{\mathbf{T}}g^{-1}$
. Since
![]() ${\mathbf{T}}$
and
${\mathbf{T}}$
and
![]() ${\mathbf{T}}'$
are K-subgroups, we have
${\mathbf{T}}'$
are K-subgroups, we have
![]() $(g^{-1})^\tau g\in N_{\mathbf{G}}({\mathbf{T}})(K^{sep})$
for all
$(g^{-1})^\tau g\in N_{\mathbf{G}}({\mathbf{T}})(K^{sep})$
for all
![]() $\tau \in {\textrm {Gal}}(K^{sep}/K)$
. Thus, the class of the cocycle
$\tau \in {\textrm {Gal}}(K^{sep}/K)$
. Thus, the class of the cocycle
![]() $(\xi _\tau )=((g^{-1})^\tau g)$
with coefficients in
$(\xi _\tau )=((g^{-1})^\tau g)$
with coefficients in
![]() $N_{\mathbf{G}}({\mathbf{T}})$
is a cohomological obstruction to the conjugacy of
$N_{\mathbf{G}}({\mathbf{T}})$
is a cohomological obstruction to the conjugacy of
![]() ${\mathbf{T}}$
and
${\mathbf{T}}$
and
![]() ${\mathbf{T}}'$
. Note that since
${\mathbf{T}}'$
. Note that since
![]() ${\mathbf{T}}'=g{\mathbf{T}}g^{-1}$
, the twisted tori
${\mathbf{T}}'=g{\mathbf{T}}g^{-1}$
, the twisted tori
![]() $^{(\xi _\tau )}{\mathbf{T}}$
and
$^{(\xi _\tau )}{\mathbf{T}}$
and
![]() ${\mathbf{T}}'$
are isomorphic K-groups.
${\mathbf{T}}'$
are isomorphic K-groups.
Next we will show that under some additional assumptions, one can choose g such that the cocycle
![]() $(\xi _\tau )$
takes values in
$(\xi _\tau )$
takes values in
![]() ${\mathbf{T}}(K^{sep})\subset N_{\mathbf{G}}({\mathbf{T}})(K^{sep})$
. Note that for such a choice of g we have
${\mathbf{T}}(K^{sep})\subset N_{\mathbf{G}}({\mathbf{T}})(K^{sep})$
. Note that for such a choice of g we have
![]() $^{(\xi _\tau )}{\mathbf{T}}\simeq {\mathbf{T}}$
. Therefore, a necessary condition for this is that
$^{(\xi _\tau )}{\mathbf{T}}\simeq {\mathbf{T}}$
. Therefore, a necessary condition for this is that
![]() ${\mathbf{T}}$
and
${\mathbf{T}}$
and
![]() ${\mathbf{T}}'$
be isomorphic over K, since
${\mathbf{T}}'$
be isomorphic over K, since
![]() $^{(\xi _\tau )}{\mathbf{T}}\simeq {\mathbf{T}}'$
. Furthermore, our claim will hold true in
$^{(\xi _\tau )}{\mathbf{T}}\simeq {\mathbf{T}}'$
. Furthermore, our claim will hold true in
![]() ${\mathbf{G}}$
if it does in
${\mathbf{G}}$
if it does in
![]() ${\mathbf{G}}/{\mathbf{Z}}$
for some central subgroup
${\mathbf{G}}/{\mathbf{Z}}$
for some central subgroup
![]() ${\mathbf{Z}}$
(because
${\mathbf{Z}}$
(because
![]() ${\mathbf{Z}}$
is contained in
${\mathbf{Z}}$
is contained in
![]() ${\mathbf{T}}$
). This reduces the problem to the adjoint case.
${\mathbf{T}}$
). This reduces the problem to the adjoint case.
Assume thus that
![]() ${\mathbf{T}}\simeq {\mathbf{T}}'$
and that
${\mathbf{T}}\simeq {\mathbf{T}}'$
and that
![]() ${\mathbf{G}}$
is adjoint. Let
${\mathbf{G}}$
is adjoint. Let
![]() $F/K$
be the minimal splitting field of
$F/K$
be the minimal splitting field of
![]() ${\mathbf{T}}$
(and hence of
${\mathbf{T}}$
(and hence of
![]() ${\mathbf{T}}'$
) and let
${\mathbf{T}}'$
) and let
![]() $\Gamma ={\textrm {Gal}}(F/K)$
. The group
$\Gamma ={\textrm {Gal}}(F/K)$
. The group
![]() $\Gamma $
acts naturally on the character lattices
$\Gamma $
acts naturally on the character lattices
![]() $X({\mathbf{T}})_{\ast }$
and
$X({\mathbf{T}})_{\ast }$
and
![]() $X({\mathbf{T}}')_{\ast }$
and these actions preserve the root systems
$X({\mathbf{T}}')_{\ast }$
and these actions preserve the root systems
![]() $\Sigma =\Sigma (G,{\mathbf{T}})$
and
$\Sigma =\Sigma (G,{\mathbf{T}})$
and
![]() $\Sigma '=\Sigma (G,{\mathbf{T}}')$
. Thus, we have two canonical embeddings
$\Sigma '=\Sigma (G,{\mathbf{T}}')$
. Thus, we have two canonical embeddings
![]() $\rho _1:\Gamma \hookrightarrow {\mathrm{Aut}}(\Sigma )$
and
$\rho _1:\Gamma \hookrightarrow {\mathrm{Aut}}(\Sigma )$
and
![]() $\rho _2:\Gamma \hookrightarrow {\mathrm{Aut}}(\Sigma ')$
. Since
$\rho _2:\Gamma \hookrightarrow {\mathrm{Aut}}(\Sigma ')$
. Since
![]() ${\mathbf{G}}$
is adjoint,
${\mathbf{G}}$
is adjoint,
![]() $\Sigma $
and
$\Sigma $
and
![]() $\Sigma '$
generate
$\Sigma '$
generate
![]() $X({\mathbf{T}})_{\ast }$
and
$X({\mathbf{T}})_{\ast }$
and
![]() $X({\mathbf{T}}')_{\ast }$
, respectively. Since
$X({\mathbf{T}}')_{\ast }$
, respectively. Since
![]() $\Sigma $
and
$\Sigma $
and
![]() $\Sigma '$
are root systems of the same type we may identify them, which in turn gives rise to an identification
$\Sigma '$
are root systems of the same type we may identify them, which in turn gives rise to an identification
![]() $X({\mathbf{T}})_{\ast }=X({\mathbf{T}}')_{\ast }$
. After all of these identifications we obtain two actions of
$X({\mathbf{T}})_{\ast }=X({\mathbf{T}}')_{\ast }$
. After all of these identifications we obtain two actions of
![]() $\Gamma $
on each of
$\Gamma $
on each of
![]() $\Sigma $
and
$\Sigma $
and
![]() $X({\mathbf{T}})_{\ast }$
through
$X({\mathbf{T}})_{\ast }$
through
![]() $\rho _1$
and
$\rho _1$
and
![]() $\rho _2$
.
$\rho _2$
.
Lemma 2.8. Assume that there is an inner automorphism
![]() $\rho : {\mathrm{Aut}}(\Sigma )\to {\mathrm{Aut}}(\Sigma )$
such that
$\rho : {\mathrm{Aut}}(\Sigma )\to {\mathrm{Aut}}(\Sigma )$
such that
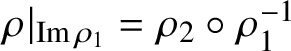 $\rho |_{{\textrm {Im}}\,\rho _1}=\rho _2\circ \rho _1^{-1}$
. Then there is a
$\rho |_{{\textrm {Im}}\,\rho _1}=\rho _2\circ \rho _1^{-1}$
. Then there is a
![]() $\Gamma $
-equivariant automorphism
$\Gamma $
-equivariant automorphism
![]() $X({\mathbf{T}})_{\ast }\to X({\mathbf{T}})_{\ast }$
preserving the root system
$X({\mathbf{T}})_{\ast }\to X({\mathbf{T}})_{\ast }$
preserving the root system
![]() $\Sigma $
, where
$\Sigma $
, where
![]() $\Gamma $
acts on the domain through
$\Gamma $
acts on the domain through
![]() $\rho _1$
and on the codomain through
$\rho _1$
and on the codomain through
![]() $\rho _2$
.
$\rho _2$
.
Proof. Let
![]() $\rho ={\textrm {Int}}(a)$
where
$\rho ={\textrm {Int}}(a)$
where
![]() $a\in {\mathrm{Aut}}(\Sigma )$
. The map
$a\in {\mathrm{Aut}}(\Sigma )$
. The map
![]() $a:\Sigma \to \Sigma $
can be extended uniquely to an automorphism
$a:\Sigma \to \Sigma $
can be extended uniquely to an automorphism
![]() $a_{X({\mathbf{T}})_\ast }:X({\mathbf{T}})_\ast \to X({\mathbf{T}})_\ast $
preserving roots. It is straightforward to check that it is
$a_{X({\mathbf{T}})_\ast }:X({\mathbf{T}})_\ast \to X({\mathbf{T}})_\ast $
preserving roots. It is straightforward to check that it is
![]() $\Gamma $
-equivariant.
$\Gamma $
-equivariant.
We are now ready to conclude this section with the following theorem. Since we will mainly be concerned with outer forms of type
![]() $\mathrm A_2$
, it is stated for groups of outer type.
$\mathrm A_2$
, it is stated for groups of outer type.
Theorem 2.9. Let
![]() ${\mathbf{G}}$
be an absolutely simple semisimple K-group of outer type with
${\mathbf{G}}$
be an absolutely simple semisimple K-group of outer type with
![]() $|{\textrm {Out}}({\mathbf{G}})|=2$
and let
$|{\textrm {Out}}({\mathbf{G}})|=2$
and let
![]() ${\mathbf{T}}$
and
${\mathbf{T}}$
and
![]() ${\mathbf{T}}'$
be two isomorphic maximal tori in
${\mathbf{T}}'$
be two isomorphic maximal tori in
![]() ${\mathbf{G}}$
, with corresponding root systems
${\mathbf{G}}$
, with corresponding root systems
![]() $\Sigma $
and
$\Sigma $
and
![]() $\Sigma '$
, respectively. Assume that there is an inner automorphism
$\Sigma '$
, respectively. Assume that there is an inner automorphism
![]() $\rho : {\mathrm{Aut}}(\Sigma )\to {\mathrm{Aut}}(\Sigma )$
such that
$\rho : {\mathrm{Aut}}(\Sigma )\to {\mathrm{Aut}}(\Sigma )$
such that
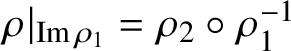 $\rho |_{{\textrm {Im}}\,\rho _1}=\rho _2\circ \rho _1^{-1}$
, where
$\rho |_{{\textrm {Im}}\,\rho _1}=\rho _2\circ \rho _1^{-1}$
, where
![]() $\rho _1$
and
$\rho _1$
and
![]() $\rho _2$
are the above embeddings of
$\rho _2$
are the above embeddings of
![]() $\Gamma $
into
$\Gamma $
into
![]() ${\mathrm{Aut}}(\Sigma )$
. If there is
${\mathrm{Aut}}(\Sigma )$
. If there is
![]() $f\in {\mathrm{Aut}}({\mathbf{G}})(K)\setminus {\textrm {Int}}({\mathbf{G}})(K)$
such that
$f\in {\mathrm{Aut}}({\mathbf{G}})(K)\setminus {\textrm {Int}}({\mathbf{G}})(K)$
such that
![]() $f({\mathbf{T}})={\mathbf{T}}$
, then there is
$f({\mathbf{T}})={\mathbf{T}}$
, then there is
![]() $g\in {\mathbf{G}}(K^{sep})$
such that
$g\in {\mathbf{G}}(K^{sep})$
such that
![]() $g{\mathbf{T}}g^{-1}={\mathbf{T}}'$
and
$g{\mathbf{T}}g^{-1}={\mathbf{T}}'$
and
![]() $(g^{-1})^\tau g\in {\mathbf{T}}(K^{sep})$
for all
$(g^{-1})^\tau g\in {\mathbf{T}}(K^{sep})$
for all
![]() $\tau \in {\textrm {Gal}}(K^{sep}/K)$
.
$\tau \in {\textrm {Gal}}(K^{sep}/K)$
.
Proof. Without loss of generality, we may assume that
![]() ${\mathbf{G}}$
is adjoint. The assumptions of Lemma 2.8 are satisfied. Let thus
${\mathbf{G}}$
is adjoint. The assumptions of Lemma 2.8 are satisfied. Let thus
be the
![]() $\Gamma $
-equivariant map constructed in that lemma. Using the identification of
$\Gamma $
-equivariant map constructed in that lemma. Using the identification of
![]() $X({\mathbf{T}})_\ast $
and
$X({\mathbf{T}})_\ast $
and
![]() $X({\mathbf{T}}')_\ast $
, we obtain a
$X({\mathbf{T}}')_\ast $
, we obtain a
![]() $\Gamma $
-equivariant map
$\Gamma $
-equivariant map
![]() $X({\mathbf{T}})_\ast \to X({\mathbf{T}}')_\ast $
, which can be extended to a K-group isomorphism
$X({\mathbf{T}})_\ast \to X({\mathbf{T}}')_\ast $
, which can be extended to a K-group isomorphism
![]() $a:{\mathbf{T}}\to {\mathbf{T}}'$
that induces an isomorphism between
$a:{\mathbf{T}}\to {\mathbf{T}}'$
that induces an isomorphism between
![]() $\Sigma $
and
$\Sigma $
and
![]() $\Sigma '$
. By [Reference Jacobson11, Theorem 32.1] the map
$\Sigma '$
. By [Reference Jacobson11, Theorem 32.1] the map
![]() $a_{\mathbf{T}}$
can be further extended to an automorphism
$a_{\mathbf{T}}$
can be further extended to an automorphism
![]() $a_{\mathbf{G}}:{\mathbf{G}} \to {\mathbf{G}}$
. Replacing
$a_{\mathbf{G}}:{\mathbf{G}} \to {\mathbf{G}}$
. Replacing
![]() $a_{\mathbf{G}}$
with
$a_{\mathbf{G}}$
with
![]() $a_{\mathbf{G}}\circ f$
, if necessary, we may assume that
$a_{\mathbf{G}}\circ f$
, if necessary, we may assume that
![]() $a_{\mathbf{G}}$
is inner, say
$a_{\mathbf{G}}$
is inner, say
![]() $a_{\mathbf{G}}={\textrm {Int}}(g)$
, where
$a_{\mathbf{G}}={\textrm {Int}}(g)$
, where
![]() $g\in {\mathbf{G}}(K^{sep})$
. Since
$g\in {\mathbf{G}}(K^{sep})$
. Since
![]() ${\textrm {Int}}(g)|_{\mathbf{T}}: {\mathbf{T}} \to {\mathbf{T}}'$
is a K-group isomorphism and
${\textrm {Int}}(g)|_{\mathbf{T}}: {\mathbf{T}} \to {\mathbf{T}}'$
is a K-group isomorphism and
![]() ${\textrm {Int}}((g^{-1})^\tau g)$
fixes
${\textrm {Int}}((g^{-1})^\tau g)$
fixes
![]() $\Sigma $
, it follows that
$\Sigma $
, it follows that
![]() $(g^{-1})^\tau g\in {\mathbf{T}}(K^{sep})$
for all
$(g^{-1})^\tau g\in {\mathbf{T}}(K^{sep})$
for all
![]() $\tau \in {\textrm {Gal}}(K^{sep}/K)$
.
$\tau \in {\textrm {Gal}}(K^{sep}/K)$
.
Example 2.10. We keep the above notation. Let
![]() $E/K$
be a quadratic étale extension and let B be a central simple algebra of degree
$E/K$
be a quadratic étale extension and let B be a central simple algebra of degree
![]() $3$
over E equipped with an involution
$3$
over E equipped with an involution
![]() $\sigma $
of the second kind. Consider two isomorphic cubic subfields
$\sigma $
of the second kind. Consider two isomorphic cubic subfields
![]() $L,L'\subset B_\sigma $
where
$L,L'\subset B_\sigma $
where
![]() $B_\sigma \subset B$
is the subset consisting of all
$B_\sigma \subset B$
is the subset consisting of all
![]() $\sigma $
-invariant elements. Since the maximal subfields
$\sigma $
-invariant elements. Since the maximal subfields
![]() $L\cdot E$
and
$L\cdot E$
and
![]() $L'\cdot E$
of B are
$L'\cdot E$
of B are
![]() $\sigma $
-stable, they give rise to two maximal K-tori
$\sigma $
-stable, they give rise to two maximal K-tori
![]() ${\mathbf{T}}$
and
${\mathbf{T}}$
and
![]() ${\mathbf{T}}'$
in
${\mathbf{T}}'$
in
![]() ${\mathbf{G}}={\mathbf{SU}}(B,\sigma )$
, given by
${\mathbf{G}}={\mathbf{SU}}(B,\sigma )$
, given by
Clearly,
![]() ${\mathbf{T}}\simeq {\mathbf{T}}'$
and the Galois group
${\mathbf{T}}\simeq {\mathbf{T}}'$
and the Galois group
![]() $\Gamma $
of the minimal splitting field of
$\Gamma $
of the minimal splitting field of
![]() ${\mathbf{T}}$
(and hence of
${\mathbf{T}}$
(and hence of
![]() ${\mathbf{T}}'$
) are of order divisible by
${\mathbf{T}}'$
) are of order divisible by
![]() $6$
. Now
$6$
. Now
![]() ${\mathbf{SU}}(B,\sigma )$
is of type
${\mathbf{SU}}(B,\sigma )$
is of type
![]() $\mathrm {A}_2$
, with
$\mathrm {A}_2$
, with
![]() $W(\mathrm {A}_2)\simeq S_3$
and the automorphism group of its root system
$W(\mathrm {A}_2)\simeq S_3$
and the automorphism group of its root system
![]() $\Sigma $
,
$\Sigma $
,
is of order
![]() $12$
. Thus,
$12$
. Thus,
![]() $\Gamma $
has order
$\Gamma $
has order
![]() $6$
or
$6$
or
![]() $12$
.
$12$
.
Case
![]() $1$
:
$1$
:
![]() $|\Gamma |=12$
. Then
$|\Gamma |=12$
. Then
![]() ${\textrm {Im}}\,\rho _1$
and
${\textrm {Im}}\,\rho _1$
and
![]() ${\textrm {Im}}\,\rho _2$
coincide with
${\textrm {Im}}\,\rho _2$
coincide with
![]() ${\mathrm{Aut}}(\Sigma )$
. Note that
${\mathrm{Aut}}(\Sigma )$
. Note that
 $$ \begin{align*}\rho_2\circ \rho_1^{-1}:{\textrm{Aut}}(\Sigma)\to {\textrm{Aut}}(\Sigma)\end{align*} $$
$$ \begin{align*}\rho_2\circ \rho_1^{-1}:{\textrm{Aut}}(\Sigma)\to {\textrm{Aut}}(\Sigma)\end{align*} $$
preserves the Weyl group
![]() $W(\mathrm {A}_2)$
since
$W(\mathrm {A}_2)$
since
 $\rho ^{-1}_1(W(\mathrm {A}_2))$
(respectively
$\rho ^{-1}_1(W(\mathrm {A}_2))$
(respectively
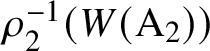 $\rho _2^{-1}(W(\mathrm {A}_2))$
) coincides with
$\rho _2^{-1}(W(\mathrm {A}_2))$
) coincides with
![]() ${\textrm {Gal}}(F/E) < {\textrm {Gal}}(F/K)$
, where
${\textrm {Gal}}(F/E) < {\textrm {Gal}}(F/K)$
, where
![]() $F/K$
is the Galois closure of
$F/K$
is the Galois closure of
![]() $L\cdot E/K$
. Hence,
$L\cdot E/K$
. Hence,
 $\rho _2\circ \rho _1^{-1}$
obviously satisfies all of the assumptions in Theorem 2.9 and the map
$\rho _2\circ \rho _1^{-1}$
obviously satisfies all of the assumptions in Theorem 2.9 and the map
![]() $f(x)=\sigma (x)^{-1}$
is an outer automorphism of
$f(x)=\sigma (x)^{-1}$
is an outer automorphism of
![]() ${\mathbf{G}}$
preserving
${\mathbf{G}}$
preserving
![]() ${\mathbf{T}}$
.
${\mathbf{T}}$
.
Case
![]() $2$
:
$2$
:
![]() $|\Gamma |=6$
. The automorphism group
$|\Gamma |=6$
. The automorphism group
![]() ${\mathrm{Aut}}(\Sigma )$
has 3 subgroups of order
${\mathrm{Aut}}(\Sigma )$
has 3 subgroups of order
![]() $6$
, namely,
$6$
, namely,
![]() $\Gamma _1=W(\mathrm {A}_2)=S_3\times 0$
, the subgroup
$\Gamma _1=W(\mathrm {A}_2)=S_3\times 0$
, the subgroup
![]() $\Gamma _2\subset S_3\times \mathbb {Z}/2$
generated by the two elements
$\Gamma _2\subset S_3\times \mathbb {Z}/2$
generated by the two elements
![]() $((123),0)$
and
$((123),0)$
and
![]() $((12),1)$
, where
$((12),1)$
, where
![]() $(123)$
and
$(123)$
and
![]() $(12)$
are standard cycles in
$(12)$
are standard cycles in
![]() $S_3$
and the cyclic subgroup
$S_3$
and the cyclic subgroup
![]() $\Gamma _3\subset S_3\times \mathbb {Z}/2$
of order
$\Gamma _3\subset S_3\times \mathbb {Z}/2$
of order
![]() $6$
generated by the two elements
$6$
generated by the two elements
![]() $((123),0)$
and
$((123),0)$
and
![]() $({\textrm {Id}},1)$
.
$({\textrm {Id}},1)$
.
Since
![]() ${\mathbf{G}}$
has outer type, we know from [Reference Prasad and Rapinchuk19, Lemma 4.1] that
${\mathbf{G}}$
has outer type, we know from [Reference Prasad and Rapinchuk19, Lemma 4.1] that
![]() $\Gamma $
does not embed into
$\Gamma $
does not embed into
![]() $\Gamma _1=W(\mathrm {A}_2)\simeq S_3$
. If
$\Gamma _1=W(\mathrm {A}_2)\simeq S_3$
. If
![]() $\rho _1(\Gamma )= \Gamma _2\simeq S_3$
, then
$\rho _1(\Gamma )= \Gamma _2\simeq S_3$
, then
![]() ${\textrm {Im}}\,\rho _1={\textrm {Im}}\,\rho _2$
and since every automorphism of
${\textrm {Im}}\,\rho _1={\textrm {Im}}\,\rho _2$
and since every automorphism of
![]() $\Gamma _2$
is obviously inner, the automorphism
$\Gamma _2$
is obviously inner, the automorphism
 $\rho _2\circ \rho _1^{-1}$
of
$\rho _2\circ \rho _1^{-1}$
of
![]() $\Gamma _2$
can be extended to an inner automorphism of
$\Gamma _2$
can be extended to an inner automorphism of
![]() ${\mathrm{Aut}}(\Sigma )$
. If instead
${\mathrm{Aut}}(\Sigma )$
. If instead
![]() $\rho _1(\Gamma )= \Gamma _3\simeq \mathbb {Z}/3\times \mathbb {Z}/2$
, then again
$\rho _1(\Gamma )= \Gamma _3\simeq \mathbb {Z}/3\times \mathbb {Z}/2$
, then again
![]() ${\textrm {Im}}\,\rho _1={\textrm {Im}}\,\rho _2$
. The group
${\textrm {Im}}\,\rho _1={\textrm {Im}}\,\rho _2$
. The group
![]() $\Gamma _3$
has a unique nontrivial automorphism given by
$\Gamma _3$
has a unique nontrivial automorphism given by
![]() $x\mapsto x^{-1}$
and one easily checks that it is the restriction of an inner automorphism of
$x\mapsto x^{-1}$
and one easily checks that it is the restriction of an inner automorphism of
![]() ${\mathrm{Aut}}(\Sigma )$
.
${\mathrm{Aut}}(\Sigma )$
.
Thus, in all cases, the hypothesis of Theorem 2.9 is satisfied.
3. Subgroups of the Automorphism Group of an Albert Algebra
In this section, we will study automorphisms of Albert algebras related to 9-dimensional subalgebras. Recall that for our purposes it suffices to consider Albert algebras that are division algebras. Therefore, throughout this section, A is an arbitrary division Albert algebra over K. The main result of this section is the rationality, hence R-triviality, of the group of all automorphisms stabilising a 9-dimensional subalgebra.
3.1.
 $9$
-dimensional Subalgebras and Their Automorphisms
$9$
-dimensional Subalgebras and Their Automorphisms
By [Reference De Medts, Mühlherr and Stavrova13, Theorem 37.12 (2)], any proper nontrivial subalgebra of A is either a cubic field extension
![]() $K\subset L\subset A$
or a
$K\subset L\subset A$
or a
![]() $9$
-dimensional subalgebra
$9$
-dimensional subalgebra
![]() $K\subset S \subset A$
. Furthermore, S is of the form
$K\subset S \subset A$
. Furthermore, S is of the form
![]() $S=D^+$
where D is a central simple algebra of degree
$S=D^+$
where D is a central simple algebra of degree
![]() $3$
over K or
$3$
over K or
![]() $S=B_\sigma ^+$
where B is a central division algebra of degree
$S=B_\sigma ^+$
where B is a central division algebra of degree
![]() $3$
over a quadratic field extension
$3$
over a quadratic field extension
![]() $E/K$
equipped with an involution
$E/K$
equipped with an involution
![]() $\sigma $
of the second kind. For later use we record some facts related to automorphism groups of
$\sigma $
of the second kind. For later use we record some facts related to automorphism groups of
![]() $D^+,B_\sigma ^+$
and their extensions to automorphisms of A.
$D^+,B_\sigma ^+$
and their extensions to automorphisms of A.
First, let
![]() $S=D^+$
. By [Reference De Medts, Mühlherr and Stavrova13, Theorem 39.14 (2)], the algebra A has a presentation
$S=D^+$
. By [Reference De Medts, Mühlherr and Stavrova13, Theorem 39.14 (2)], the algebra A has a presentation
![]() $A=D\oplus D\oplus D$
(as a vector space) where the subalgebra S coincides with the first component. By [Reference De Medts, Mühlherr and Stavrova13, formula (37.7)], we have an exact sequence
$A=D\oplus D\oplus D$
(as a vector space) where the subalgebra S coincides with the first component. By [Reference De Medts, Mühlherr and Stavrova13, formula (37.7)], we have an exact sequence
This sequence is split if and only if D is split. Since D is a division algebra, any K-automorphism of
![]() $D^+$
thus comes from
$D^+$
thus comes from
![]() ${\mathbf {Aut}}(D)(K)={\mathrm{Aut}}(D)$
; that is, is given by conjugation
${\mathbf {Aut}}(D)(K)={\mathrm{Aut}}(D)$
; that is, is given by conjugation
![]() $x\mapsto dxd^{-1}$
for some
$x\mapsto dxd^{-1}$
for some
![]() $d\in D^\times $
. Moreover, such an automorphism can be extended to A by the formula
$d\in D^\times $
. Moreover, such an automorphism can be extended to A by the formula
Thus, the sequence implies that
Note that
![]() ${\mathbf{PGL}}(1,D)$
is rational and hence, in particular, R-trivial.
${\mathbf{PGL}}(1,D)$
is rational and hence, in particular, R-trivial.
Next, let
![]() $S=B_\sigma ^+$
. Here the situation is completely analogous to that of
$S=B_\sigma ^+$
. Here the situation is completely analogous to that of
![]() $S=D^+$
. Namely, by [Reference De Medts, Mühlherr and Stavrova13, Theorem 39.18 (2)], the algebra A admits the presentation
$S=D^+$
. Namely, by [Reference De Medts, Mühlherr and Stavrova13, Theorem 39.18 (2)], the algebra A admits the presentation
![]() $A=B_\sigma ^+\oplus B$
as a vector space, with the first component a subalgebra. By [Reference De Medts, Mühlherr and Stavrova13, Section 37.B], the algebraic K-group
$A=B_\sigma ^+\oplus B$
as a vector space, with the first component a subalgebra. By [Reference De Medts, Mühlherr and Stavrova13, Section 37.B], the algebraic K-group
![]() ${\mathbf {Aut}}(B^+_\sigma )$
is smooth and
${\mathbf {Aut}}(B^+_\sigma )$
is smooth and
Passing to the quadratic field extension
![]() $E/K$
, we conclude that
$E/K$
, we conclude that
Thus, any K-automorphism of
![]() $B_\sigma ^+$
is given by conjugation
$B_\sigma ^+$
is given by conjugation
![]() $x\mapsto bxb^{-1}$
for some
$x\mapsto bxb^{-1}$
for some
![]() $b\in B^\times $
satisfying
$b\in B^\times $
satisfying
![]() $b\sigma (b)\in K$
. Since
$b\sigma (b)\in K$
. Since
![]() ${\mathbf{PGU}}(B,\sigma )$
has rank
${\mathbf{PGU}}(B,\sigma )$
has rank
![]() $2$
it is rational and hence R-trivial. In Corollary 3.2 we shall see that any K-automorphism of
$2$
it is rational and hence R-trivial. In Corollary 3.2 we shall see that any K-automorphism of
![]() $B_\sigma ^+$
can be extended to a K-automorphism of A.
$B_\sigma ^+$
can be extended to a K-automorphism of A.
3.2. The Group
 ${\mathbf {Aut}}(A/B_\sigma ^+)$
${\mathbf {Aut}}(A/B_\sigma ^+)$
Note that if
![]() $E=K\times K$
and
$E=K\times K$
and
![]() $B=D\otimes _K E$
with the flip involution
$B=D\otimes _K E$
with the flip involution
![]() $\sigma $
, then
$\sigma $
, then
![]() $B_\sigma ^+$
is equal to
$B_\sigma ^+$
is equal to
![]() $D^+$
embedded diagonally into B. This provides a unified treatment of both kinds of 9-dimensional subalgebras. Therefore, here and in what follows in this section, we will let
$D^+$
embedded diagonally into B. This provides a unified treatment of both kinds of 9-dimensional subalgebras. Therefore, here and in what follows in this section, we will let
![]() $E/K$
be a quadratic étale extension, including the possibility of E being split; doing so, any 9-dimensional subalgebra of A is of the form
$E/K$
be a quadratic étale extension, including the possibility of E being split; doing so, any 9-dimensional subalgebra of A is of the form
![]() $B_\sigma ^+$
.
$B_\sigma ^+$
.
As above, let
![]() $A=B_\sigma ^+\oplus B$
. Recall the algebraic K-group
$A=B_\sigma ^+\oplus B$
. Recall the algebraic K-group
(see Introduction). One knows (see [Reference De Medts, Mühlherr and Stavrova13, Section 39.B]) that
![]() ${\mathbf {Aut}}(A/B_\sigma ^+)$
is simple simply connected of type
${\mathbf {Aut}}(A/B_\sigma ^+)$
is simple simply connected of type
![]() $\mathrm {A}_2$
(hence connected). Thus,
$\mathrm {A}_2$
(hence connected). Thus,
where
![]() $\tau $
is some involution of the second kind on B, which in general is different from
$\tau $
is some involution of the second kind on B, which in general is different from
![]() $\sigma $
. Being an algebraic group of rank
$\sigma $
. Being an algebraic group of rank
![]() $2$
, this group is rational and hence R-trivial.
$2$
, this group is rational and hence R-trivial.
3.3. The Group
 ${\mathbf {Aut}}(A,B_\sigma ^+)$
${\mathbf {Aut}}(A,B_\sigma ^+)$
Recall from the Introduction the K-group
By [Reference De Medts, Mühlherr and Stavrova13, Proposition 39.16], we have an exact sequence
Moreover, by [Reference De Medts, Mühlherr and Stavrova13, Corollary 39.12],
Furthermore, the above sequence induces the exact sequence
Thus,
where
![]() ${\mathbf{Z}}\subset {\mathbf{SU}}(B,\sigma )$
is the centre.
${\mathbf{Z}}\subset {\mathbf{SU}}(B,\sigma )$
is the centre.
From the point of view of algebraic groups, (3) implies that the algebraic K-group
![]() ${\mathbf{G}}:={\mathbf {Aut}}(A,B_\sigma ^+)^\circ $
is semisimple and is an almost direct product of two simple simply connected groups of type
${\mathbf{G}}:={\mathbf {Aut}}(A,B_\sigma ^+)^\circ $
is semisimple and is an almost direct product of two simple simply connected groups of type
![]() $\mathrm {A}_2$
: the first is
$\mathrm {A}_2$
: the first is
and the second is isomorphic to
![]() ${\mathbf{G}}_2:={\mathbf{SU}}(B,\sigma )$
. The centres
${\mathbf{G}}_2:={\mathbf{SU}}(B,\sigma )$
. The centres
![]() ${\mathbf{Z}}_1$
and
${\mathbf{Z}}_1$
and
![]() ${\mathbf{Z}}_2$
of
${\mathbf{Z}}_2$
of
![]() ${\mathbf{G}}_1$
and
${\mathbf{G}}_1$
and
![]() ${\mathbf{G}}_2$
, respectively, are both isomorphic to
${\mathbf{G}}_2$
, respectively, are both isomorphic to
 ${\mathbf{Z}}=R_{E/K}^{(1)}(\boldsymbol {\mu }_3)$
and
${\mathbf{Z}}=R_{E/K}^{(1)}(\boldsymbol {\mu }_3)$
and
![]() ${\mathbf{G}}_1\cap {\mathbf{G}}_2={\mathbf{Z}}$
(see [Reference De Medts, Mühlherr and Stavrova13, Corollary 39.12]). Thus, we have the exact sequence
${\mathbf{G}}_1\cap {\mathbf{G}}_2={\mathbf{Z}}$
(see [Reference De Medts, Mühlherr and Stavrova13, Corollary 39.12]). Thus, we have the exact sequence
 $$ \begin{align} 1\longrightarrow {\textbf{Z}} \longrightarrow {\mathbf{G}}_1\times {\mathbf{G}}_2 \stackrel{\phi}{\longrightarrow} {\mathbf{G}} \longrightarrow 1, \end{align} $$
$$ \begin{align} 1\longrightarrow {\textbf{Z}} \longrightarrow {\mathbf{G}}_1\times {\mathbf{G}}_2 \stackrel{\phi}{\longrightarrow} {\mathbf{G}} \longrightarrow 1, \end{align} $$
where
![]() ${\mathbf{Z}}$
is embedded codiagonally; that is, via
${\mathbf{Z}}$
is embedded codiagonally; that is, via
![]() $z\mapsto (z,z^{-1})$
. Identifying the image
$z\mapsto (z,z^{-1})$
. Identifying the image
![]() $\phi ({\mathbf{G}}_1\times 1)\subset {\mathbf{G}}$
with
$\phi ({\mathbf{G}}_1\times 1)\subset {\mathbf{G}}$
with
![]() ${\mathbf{G}}_1$
, we recover the sequence (3) in the form
${\mathbf{G}}_1$
, we recover the sequence (3) in the form
 $$ \begin{align} 1\longrightarrow {\mathbf{G}}_1 \longrightarrow {\mathbf{G}} \stackrel{\psi}{\longrightarrow} {\mathbf{G}}/{\mathbf{G}}_1 \longrightarrow 1. \end{align} $$
$$ \begin{align} 1\longrightarrow {\mathbf{G}}_1 \longrightarrow {\mathbf{G}} \stackrel{\psi}{\longrightarrow} {\mathbf{G}}/{\mathbf{G}}_1 \longrightarrow 1. \end{align} $$
Note that
![]() ${\mathbf{G}}/{\mathbf{G}}_1\simeq {\mathbf{G}}_2/{\mathbf{Z}}$
.
${\mathbf{G}}/{\mathbf{G}}_1\simeq {\mathbf{G}}_2/{\mathbf{Z}}$
.
3.4. Rationality of
 ${\mathbf {Aut}}(A,B_\sigma ^+)^\circ $
${\mathbf {Aut}}(A,B_\sigma ^+)^\circ $
We keep the notation introduced in Subsection 3.3.
Proposition 3.1. The K-group
![]() ${\mathbf{G}}={\mathbf {Aut}}(A,B_\sigma ^+)^\circ $
is rational and hence R-trivial.
${\mathbf{G}}={\mathbf {Aut}}(A,B_\sigma ^+)^\circ $
is rational and hence R-trivial.
Proof. Consider the exact sequences (4) and (5). The two groups
![]() ${\mathbf{G}}_1$
and
${\mathbf{G}}_1$
and
![]() ${\mathbf{G}}_2/{\mathbf{Z}}$
in (5), being groups of rank
${\mathbf{G}}_2/{\mathbf{Z}}$
in (5), being groups of rank
![]() $2$
, are rational over K. Therefore, it suffices to show that
$2$
, are rational over K. Therefore, it suffices to show that
![]() $\psi $
has a rational section. This is equivalent to proving that
$\psi $
has a rational section. This is equivalent to proving that
for all field extensions
![]() $F/K$
.
$F/K$
.
Fix a field extension
![]() $F/K$
and let
$F/K$
and let
![]() $[\xi ]\times 1\in H^1(F,{\mathbf{G}}_1\times 1)$
be a class whose image in
$[\xi ]\times 1\in H^1(F,{\mathbf{G}}_1\times 1)$
be a class whose image in
![]() $H^1(F,{\mathbf{G}})$
is trivial. From (4) it follows that there is
$H^1(F,{\mathbf{G}})$
is trivial. From (4) it follows that there is
![]() $[\lambda ]\in H^1(F,{\mathbf{Z}})$
whose image in
$[\lambda ]\in H^1(F,{\mathbf{Z}})$
whose image in
![]() $H^1(F, {\mathbf{G}}_1\times {\mathbf{G}}_2)$
is
$H^1(F, {\mathbf{G}}_1\times {\mathbf{G}}_2)$
is
![]() $[\xi ]\times 1$
. Since
$[\xi ]\times 1$
. Since
![]() ${\mathbf{Z}}$
is embedded codiagonally into
${\mathbf{Z}}$
is embedded codiagonally into
![]() ${\mathbf{G}}_1\times {\mathbf{G}}_2$
, the image of
${\mathbf{G}}_1\times {\mathbf{G}}_2$
, the image of
![]() $[\lambda ]$
under the natural map
$[\lambda ]$
under the natural map
is trivial. We distinguish two cases.
Case
![]() $1$
: The quadratic étale extension
$1$
: The quadratic étale extension
![]() $E/K$
is split; that is,
$E/K$
is split; that is,
![]() $E=K\times K$
. Then up to K-isomorphism we may assume that
$E=K\times K$
. Then up to K-isomorphism we may assume that
![]() ${\mathbf{G}}_1={\mathbf{SL}}(1,D_1)$
and
${\mathbf{G}}_1={\mathbf{SL}}(1,D_1)$
and
![]() ${\mathbf{G}}_2={\mathbf{SL}}(1,D_2)$
, where
${\mathbf{G}}_2={\mathbf{SL}}(1,D_2)$
, where
![]() $D_1$
and
$D_1$
and
![]() $D_2$
are central simple algebras over K of degree
$D_2$
are central simple algebras over K of degree
![]() $3$
and either
$3$
and either
![]() $D_2=D_1$
or
$D_2=D_1$
or
 $D_2=D_1^{\textrm {op}}$
. In both cases their centres are
$D_2=D_1^{\textrm {op}}$
. In both cases their centres are
![]() $\boldsymbol {\mu }_3$
, whence
$\boldsymbol {\mu }_3$
, whence
![]() $H^1(F,{\mathbf{Z}})\simeq F^\times /F^{\times 3}$
, so that the class
$H^1(F,{\mathbf{Z}})\simeq F^\times /F^{\times 3}$
, so that the class
![]() $[\lambda ]\in H^1(F,{\mathbf{Z}})$
is represented by some
$[\lambda ]\in H^1(F,{\mathbf{Z}})$
is represented by some
![]() $f\in F^\times $
. The fact that
$f\in F^\times $
. The fact that
 $$ \begin{align*}H^1(F,{\mathbf{G}}_2)\simeq F^\times/ {\textrm{Nrd}}(D_2^\times)\end{align*} $$
$$ \begin{align*}H^1(F,{\mathbf{G}}_2)\simeq F^\times/ {\textrm{Nrd}}(D_2^\times)\end{align*} $$
together with the image of
![]() $[\lambda ]$
in
$[\lambda ]$
in
![]() $H^1(F,{\mathbf{G}}_2)$
being trivial then imply that f is a reduced norm in
$H^1(F,{\mathbf{G}}_2)$
being trivial then imply that f is a reduced norm in
![]() $D_2$
, and hence also in
$D_2$
, and hence also in
![]() $D_1$
. This implies that the image
$D_1$
. This implies that the image
![]() $[\xi ]$
of
$[\xi ]$
of
![]() $[\lambda ]$
in
$[\lambda ]$
in
![]() $H^1(F,{\mathbf{G}}_1)$
is trivial, which completes the proof in this case.
$H^1(F,{\mathbf{G}}_1)$
is trivial, which completes the proof in this case.
Case
![]() $2$
:
$2$
:
![]() $E/K$
is a separable field extension. Let
$E/K$
is a separable field extension. Let
![]() $F'=F\cdot E$
and consider the class
$F'=F\cdot E$
and consider the class
![]() $[\lambda ]^2\in H^1(F,{\mathbf{Z}})$
. From Case
$[\lambda ]^2\in H^1(F,{\mathbf{Z}})$
. From Case
![]() $1$
we know that
$1$
we know that
 $res_F^{F'}([\lambda ]^2)$
is contained in
$res_F^{F'}([\lambda ]^2)$
is contained in
![]() ${\textrm {Ker}}\,[H^1(F',{\mathbf{Z}})\to H^1(F',{\mathbf{G}}_1)]$
. It follows from Example 2.2 and the norm principle (Theorem 2.5) that
${\textrm {Ker}}\,[H^1(F',{\mathbf{Z}})\to H^1(F',{\mathbf{G}}_1)]$
. It follows from Example 2.2 and the norm principle (Theorem 2.5) that
 $$ \begin{align*}[\lambda]=[\lambda]^4=cor^{F'}_F(res_F^{F'}([\lambda]^2) \end{align*} $$
$$ \begin{align*}[\lambda]=[\lambda]^4=cor^{F'}_F(res_F^{F'}([\lambda]^2) \end{align*} $$
is contained in
![]() ${\textrm {Ker}}\,[H^1(F,{\mathbf{Z}})\to H^1(F,{\mathbf{G}}_1)]$
and the proof is complete.
${\textrm {Ker}}\,[H^1(F,{\mathbf{Z}})\to H^1(F,{\mathbf{G}}_1)]$
and the proof is complete.
As a direct consequence of our proof, we have the following.
Corollary 3.2. For any field extension
![]() $F/K$
, the canonical map
$F/K$
, the canonical map
![]() ${\mathbf{G}}(F) \to ({\mathbf{G}}_2/{\mathbf{Z}})(F)$
is surjective. Hence, if
${\mathbf{G}}(F) \to ({\mathbf{G}}_2/{\mathbf{Z}})(F)$
is surjective. Hence, if
![]() $A_F$
is a division Albert algebra, then
$A_F$
is a division Albert algebra, then
is surjective.
4. Subgroups of the Structure Group of an Albert Algebra
We now turn to the structure group and consider, along the same lines as in the previous section, subgroups of it related to 9-dimensional subalgebras. Throughout this section, as in the previous, A denotes an arbitrary division Albert algebra over K. We moreover continue using the convention that the quadratic étale algebra E involved in the definition of
![]() $B_\sigma ^+$
may be split.
$B_\sigma ^+$
may be split.
4.1. The Group
 ${\mathbf{Str}}(B_\sigma ^+)$
${\mathbf{Str}}(B_\sigma ^+)$
The structure group
![]() ${\mathbf{Str}}(B_\sigma ^+)$
of the Jordan algebra
${\mathbf{Str}}(B_\sigma ^+)$
of the Jordan algebra
![]() $B_\sigma ^+$
is a closed subgroup of the algebraic K-group
$B_\sigma ^+$
is a closed subgroup of the algebraic K-group
![]() ${\mathbf{GL}}(B_\sigma ^+)$
consisting of all similitudes. More precisely, for any K-ring R,
${\mathbf{GL}}(B_\sigma ^+)$
consisting of all similitudes. More precisely, for any K-ring R,
where
![]() ${\textrm {Nrd}}_R$
is the base change of
${\textrm {Nrd}}_R$
is the base change of
![]() ${\textrm {Nrd}}$
to
${\textrm {Nrd}}$
to
![]() $B\otimes _K R$
and the multiplier
$B\otimes _K R$
and the multiplier
![]() $\nu (x)\in R^\times $
. By [Reference Knus, Merkurjev, Rost and Tignol12, Chap. V, Thm. 5.12.10], the group
$\nu (x)\in R^\times $
. By [Reference Knus, Merkurjev, Rost and Tignol12, Chap. V, Thm. 5.12.10], the group
![]() ${\mathrm{Str}}(B_\sigma ^+)={\mathbf{Str}}(B_\sigma ^+)(K)$
consists of the linear maps of the form
${\mathrm{Str}}(B_\sigma ^+)={\mathbf{Str}}(B_\sigma ^+)(K)$
consists of the linear maps of the form
where
![]() $b\in B^\times $
and
$b\in B^\times $
and
![]() $\lambda \in K^\times $
. It follows that we have a surjective map of algebraic K-groups
$\lambda \in K^\times $
. It follows that we have a surjective map of algebraic K-groups
and that
![]() ${\mathbf{Str}}(B_\sigma ^+)^\circ (K)={\mathbf{Str}}(B_\sigma ^+)(K)$
. The kernel of this map is the torus
${\mathbf{Str}}(B_\sigma ^+)^\circ (K)={\mathbf{Str}}(B_\sigma ^+)(K)$
. The kernel of this map is the torus
![]() $R_{E/K}({\mathbf{G}}_{m,E})$
, where the embedding
$R_{E/K}({\mathbf{G}}_{m,E})$
, where the embedding
is given by
![]() $x\mapsto (N_{E/K}(x^{-1}),x)$
. Thus, we have the exact sequence
$x\mapsto (N_{E/K}(x^{-1}),x)$
. Thus, we have the exact sequence
 $$ \begin{align} 1\longrightarrow R_{E/K}({\mathbf{G}}_{m,E}) \longrightarrow {\mathbf{G}}_m \times R_{E/K}({\textbf{GL}}(1,B)) \stackrel{\phi}{\longrightarrow} {\mathbf{Str}}(B_\sigma^+)^\circ \longrightarrow 1. \end{align} $$
$$ \begin{align} 1\longrightarrow R_{E/K}({\mathbf{G}}_{m,E}) \longrightarrow {\mathbf{G}}_m \times R_{E/K}({\textbf{GL}}(1,B)) \stackrel{\phi}{\longrightarrow} {\mathbf{Str}}(B_\sigma^+)^\circ \longrightarrow 1. \end{align} $$
Lemma 4.1. The algebraic K-group
![]() ${\mathbf{Str}}(B_\sigma ^+)^\circ $
is rational and hence, in particular, R-trivial.
${\mathbf{Str}}(B_\sigma ^+)^\circ $
is rational and hence, in particular, R-trivial.
Proof. We identify
![]() $\phi ({\mathbf{G}}_m\times 1)\subset {\mathbf{Str}}(B_\sigma ^+)^\circ $
with
$\phi ({\mathbf{G}}_m\times 1)\subset {\mathbf{Str}}(B_\sigma ^+)^\circ $
with
![]() ${\mathbf{G}}_m$
. Since for any field extension
${\mathbf{G}}_m$
. Since for any field extension
![]() $F/K$
one has
$F/K$
one has
![]() $H^1(F,{\mathbf{G}}_m)=1$
, the canonical map
$H^1(F,{\mathbf{G}}_m)=1$
, the canonical map
has a rational section. Therefore, it suffices to establish the rationality of
![]() ${\mathbf{Str}}(B_\sigma ^+)^\circ /{\mathbf{G}}_m$
. By (6) we have
${\mathbf{Str}}(B_\sigma ^+)^\circ /{\mathbf{G}}_m$
. By (6) we have
which is clearly rational.
4.2. The Group
 ${\mathbf{Str}}(A,B_\sigma ^+)$
${\mathbf{Str}}(A,B_\sigma ^+)$
Let
![]() ${\mathbf{Str}}(A,B_\sigma ^+)$
(respectively
${\mathbf{Str}}(A,B_\sigma ^+)$
(respectively
![]() ${\mathbf{Str}}(A/B_\sigma ^+)$
) be the closed subgroup of
${\mathbf{Str}}(A/B_\sigma ^+)$
) be the closed subgroup of
![]() ${\mathbf{Str}}(A)$
consisting of those elements stabilising
${\mathbf{Str}}(A)$
consisting of those elements stabilising
![]() $B_\sigma ^+$
(respectively fixing
$B_\sigma ^+$
(respectively fixing
![]() $B_\sigma ^+$
pointwise). Note that since the elements of
$B_\sigma ^+$
pointwise). Note that since the elements of
![]() ${\mathbf{Str}}(A/B_\sigma ^+)$
fix the identity element of A, it follows from [Reference Steinberg20, Proposition 5.9.4] that
${\mathbf{Str}}(A/B_\sigma ^+)$
fix the identity element of A, it follows from [Reference Steinberg20, Proposition 5.9.4] that
![]() ${\mathbf{Str}}(A/B_\sigma ^+)={\mathbf {Aut}}(A/B_\sigma ^+)$
. This group is the kernel of the canonical restriction map
${\mathbf{Str}}(A/B_\sigma ^+)={\mathbf {Aut}}(A/B_\sigma ^+)$
. This group is the kernel of the canonical restriction map
Note that the restriction map is well defined because the restriction to
![]() $B^+_\sigma $
of the norm on A is the norm on
$B^+_\sigma $
of the norm on A is the norm on
![]() $B^+_\sigma $
. Since, by [Reference Gille7, Proposition 7.2.4], this map is surjective on the level of
$B^+_\sigma $
. Since, by [Reference Gille7, Proposition 7.2.4], this map is surjective on the level of
![]() $K^{sep}$
-points, we have the exact sequence
$K^{sep}$
-points, we have the exact sequence
 $$ \begin{align} 1\longrightarrow {\mathbf{Aut}}(A/B_\sigma^+) \longrightarrow {\mathbf{Str}}(A,B_\sigma^+)^\circ \stackrel{\phi}{\longrightarrow} {\mathbf{Str}}(B_\sigma^+)^\circ \longrightarrow 1 \end{align} $$
$$ \begin{align} 1\longrightarrow {\mathbf{Aut}}(A/B_\sigma^+) \longrightarrow {\mathbf{Str}}(A,B_\sigma^+)^\circ \stackrel{\phi}{\longrightarrow} {\mathbf{Str}}(B_\sigma^+)^\circ \longrightarrow 1 \end{align} $$
of algebraic K-groups.
Proposition 4.2. The group
![]() ${\mathbf{Str}}(A,B_\sigma ^+)^\circ $
is rational and hence R-trivial.
${\mathbf{Str}}(A,B_\sigma ^+)^\circ $
is rational and hence R-trivial.
Proof. By [Reference Gille7], for any field extension
![]() $F/K$
the map
$F/K$
the map
 $$ \begin{align*}{\mathbf{Str}}(A,B_\sigma^+)^\circ(F) \stackrel{\phi_F}{\longrightarrow} {\mathbf{Str}}(B_\sigma^+)^\circ(F) \end{align*} $$
$$ \begin{align*}{\mathbf{Str}}(A,B_\sigma^+)^\circ(F) \stackrel{\phi_F}{\longrightarrow} {\mathbf{Str}}(B_\sigma^+)^\circ(F) \end{align*} $$
is surjective, implying that
![]() $\phi $
has a rational section. Thus,
$\phi $
has a rational section. Thus,
![]() ${\mathbf{Str}}(A,B_\sigma ^+)^\circ $
is birationally isomorphic to
${\mathbf{Str}}(A,B_\sigma ^+)^\circ $
is birationally isomorphic to
![]() ${\mathbf {Aut}}(A/B_\sigma ^+) \times {\mathbf{Str}}(B_\sigma ^+)^\circ $
. It remains to be noted that, being a group of rank
${\mathbf {Aut}}(A/B_\sigma ^+) \times {\mathbf{Str}}(B_\sigma ^+)^\circ $
. It remains to be noted that, being a group of rank
![]() $2$
, the group
$2$
, the group
![]() ${\mathbf {Aut}}(A/B_\sigma ^+)$
is rational and by Lemma 4.1 the group
${\mathbf {Aut}}(A/B_\sigma ^+)$
is rational and by Lemma 4.1 the group
![]() ${\mathbf{Str}}(B_\sigma ^+)^\circ $
is rational.
${\mathbf{Str}}(B_\sigma ^+)^\circ $
is rational.
Corollary 4.3. The natural map
![]() ${\mathrm{Str}}(A,B_\sigma ^+)\to {\mathrm{Str}}(B_\sigma ^+)$
is surjective.
${\mathrm{Str}}(A,B_\sigma ^+)\to {\mathrm{Str}}(B_\sigma ^+)$
is surjective.
Proof. From the proof of Proposition 4.2 it follows that the map
is surjective, and from 4.1 we know that
![]() ${\mathbf{Str}}(B_\sigma ^+)(K)={\mathbf{Str}}(B_\sigma ^+)^\circ (K)$
. The assertion follows.
${\mathbf{Str}}(B_\sigma ^+)(K)={\mathbf{Str}}(B_\sigma ^+)^\circ (K)$
. The assertion follows.
5. The Weak Skolem–Noether Property for Isomorphic Embeddings
Let A be an Albert algebra over a field K. Let
![]() $K\subset L\subset A$
and
$K\subset L\subset A$
and
![]() $K\subset L'\subset A$
be two isomorphic separable cubic field extensions; one says that they are weakly equivalent if there exists an element
$K\subset L'\subset A$
be two isomorphic separable cubic field extensions; one says that they are weakly equivalent if there exists an element
![]() $g\in {\mathrm{Str}}(A)$
such that
$g\in {\mathrm{Str}}(A)$
such that
![]() $g(L)=L'$
. That this property holds follows from Theorem B (Skolem–Noether theorem for Albert algebras) due to S. Garibaldi and H. Petersson [Reference Gille7].
$g(L)=L'$
. That this property holds follows from Theorem B (Skolem–Noether theorem for Albert algebras) due to S. Garibaldi and H. Petersson [Reference Gille7].
The goal of this section is to give a self-contained proof of the validity of weak equivalence based on the technique of conjugacy of maximal tori detailed in Section 2.
We start with the intermediate step of a
![]() $9$
-dimensional Jordan algebra
$9$
-dimensional Jordan algebra
![]() $B^+_\sigma $
.
$B^+_\sigma $
.
Proposition 5.1. Let L and
![]() $L'$
be two isomorphic separable cubic field extensions of the base field K contained in the subalgebra
$L'$
be two isomorphic separable cubic field extensions of the base field K contained in the subalgebra
![]() $B_\sigma ^+$
. Then there exists an element
$B_\sigma ^+$
. Then there exists an element
![]() $s\in {\mathrm{Str}}(B_\sigma ^+)$
such that
$s\in {\mathrm{Str}}(B_\sigma ^+)$
such that
![]() $s(L)=L'$
.
$s(L)=L'$
.
Proof. Let
![]() $E/K$
be the étale quadratic extension over which B is defined. The two cubic fields L and
$E/K$
be the étale quadratic extension over which B is defined. The two cubic fields L and
![]() $L'$
give rise to the two
$L'$
give rise to the two
![]() $4$
-dimensional (maximal) tori
$4$
-dimensional (maximal) tori
and
of the algebraic K-group
![]() ${\mathbf{Sim}}(B,\sigma )$
.Footnote
3
From the point of view of algebraic groups,
${\mathbf{Sim}}(B,\sigma )$
.Footnote
3
From the point of view of algebraic groups,
![]() ${\mathbf{Sim}}(B,\sigma )$
is a reductive group which is the almost direct product of the central
${\mathbf{Sim}}(B,\sigma )$
is a reductive group which is the almost direct product of the central
![]() $2$
-dimensional torus
$2$
-dimensional torus
![]() ${\mathbf{P}}=R_{E/K}({\mathbf{G}}_{m,E})$
and the simple simply connected group
${\mathbf{P}}=R_{E/K}({\mathbf{G}}_{m,E})$
and the simple simply connected group
![]() ${\mathbf{SU}}(B,\sigma )$
of outer type
${\mathbf{SU}}(B,\sigma )$
of outer type
![]() $\mathrm {A}_2$
. Note that
$\mathrm {A}_2$
. Note that
![]() ${\mathbf{P}}$
is contained in both
${\mathbf{P}}$
is contained in both
![]() ${\mathbf{T}}$
and
${\mathbf{T}}$
and
![]() ${\mathbf{T}}'$
. Let
${\mathbf{T}}'$
. Let
![]() ${\mathbf{T}}_{ss}={\mathbf{T}}\cap {\mathbf{SU}}(B,\sigma )$
and
${\mathbf{T}}_{ss}={\mathbf{T}}\cap {\mathbf{SU}}(B,\sigma )$
and
![]() ${\mathbf{T}}^{\prime }_{ss}={\mathbf{T}}'\cap {\mathbf{SU}}(B,\sigma )$
. Then
${\mathbf{T}}^{\prime }_{ss}={\mathbf{T}}'\cap {\mathbf{SU}}(B,\sigma )$
. Then
![]() ${\mathbf{T}}={\mathbf{P}}\cdot {\mathbf{T}}_{ss}$
and
${\mathbf{T}}={\mathbf{P}}\cdot {\mathbf{T}}_{ss}$
and
![]() ${\mathbf{T}}'={\mathbf{P}}\cdot {\mathbf{T}}^{\prime }_{ss}$
.
${\mathbf{T}}'={\mathbf{P}}\cdot {\mathbf{T}}^{\prime }_{ss}$
.
By Theorem 2.9 and Example 2.10, there exists
![]() $b\in {\mathbf{SU}}(B,\sigma )(K^{sep})$
such that
$b\in {\mathbf{SU}}(B,\sigma )(K^{sep})$
such that
![]() $b{\mathbf{T}}_{ss}b^{-1}={\mathbf{T}}^{\prime }_{ss}$
and
$b{\mathbf{T}}_{ss}b^{-1}={\mathbf{T}}^{\prime }_{ss}$
and
![]() $b^{-\tau +1} \in {\mathbf{T}}_{ss}(K^{sep})$
for all
$b^{-\tau +1} \in {\mathbf{T}}_{ss}(K^{sep})$
for all
![]() $\tau \in {\textrm {Gal}}(K^{sep}/K)$
. Since
$\tau \in {\textrm {Gal}}(K^{sep}/K)$
. Since
![]() ${\mathbf{P}}\subset {\mathbf{Sim}}(B,\sigma )$
is a central torus, we also have
${\mathbf{P}}\subset {\mathbf{Sim}}(B,\sigma )$
is a central torus, we also have
![]() $b{\mathbf{T}}b^{-1}={\mathbf{T}}'$
.
$b{\mathbf{T}}b^{-1}={\mathbf{T}}'$
.
Consider the following commutative diagram with exact rows:

Here
![]() ${\mathbf{J}}={\mathbf{G}}_{m,K}\times R_{E/K}({\mathbf{GL}}(1,B))$
, so that the lower sequence is the exact sequence (6),
${\mathbf{J}}={\mathbf{G}}_{m,K}\times R_{E/K}({\mathbf{GL}}(1,B))$
, so that the lower sequence is the exact sequence (6),
![]() $\phi _1$
is given by conjugation,
$\phi _1$
is given by conjugation,
and
where
![]() $\nu (x)$
is the multiplier of x. The map
$\nu (x)$
is the multiplier of x. The map
![]() $\lambda _2$
takes
$\lambda _2$
takes
![]() ${\mathbf{T}}$
and
${\mathbf{T}}$
and
![]() ${\mathbf{T}}'$
into the quasi-trivial tori
${\mathbf{T}}'$
into the quasi-trivial tori
 $$ \begin{align*}\widetilde{{\mathbf{T}}}={\mathbf{G}}_{m,K}\times R_{L\cdot E/K}({\mathbf{G}}_{m,L\cdot E}) \end{align*} $$
$$ \begin{align*}\widetilde{{\mathbf{T}}}={\mathbf{G}}_{m,K}\times R_{L\cdot E/K}({\mathbf{G}}_{m,L\cdot E}) \end{align*} $$
and
 $$ \begin{align*}\widetilde{{\mathbf{T}}}'={\mathbf{G}}_{m,K}\times R_{L'\cdot E/K}({\mathbf{G}}_{m,L'\cdot E}), \end{align*} $$
$$ \begin{align*}\widetilde{{\mathbf{T}}}'={\mathbf{G}}_{m,K}\times R_{L'\cdot E/K}({\mathbf{G}}_{m,L'\cdot E}), \end{align*} $$
respectively. Next we need the following.
Lemma 5.2. The torus
![]() $\widetilde {{\mathbf{T}}}$
(respectively
$\widetilde {{\mathbf{T}}}$
(respectively
![]() $\widetilde {{\mathbf{T}}'}$
) is the centraliser of
$\widetilde {{\mathbf{T}}'}$
) is the centraliser of
![]() ${\mathbf{T}}$
(respectively
${\mathbf{T}}$
(respectively
![]() ${\mathbf{T}}'$
) in
${\mathbf{T}}'$
) in
![]() ${\mathbf{G}}_{m,K}\times R_{E/K}({\mathbf{GL}}(1,B))$
.
${\mathbf{G}}_{m,K}\times R_{E/K}({\mathbf{GL}}(1,B))$
.
Proof. We consider the case of the torus
![]() ${\mathbf{T}}$
only. The torus
${\mathbf{T}}$
only. The torus
![]() ${\mathbf{T}}'$
is handled analogously. It suffices to show that
${\mathbf{T}}'$
is handled analogously. It suffices to show that
Without loss of generality, we may assume that the base field K is algebraically closed. Then B may be identified with the algebra
![]() $M_3 \times M_3$
, the involution
$M_3 \times M_3$
, the involution
![]() $\sigma $
switches the components and L with diagonal matrices fixed by
$\sigma $
switches the components and L with diagonal matrices fixed by
![]() $\sigma $
. With this identification we have
$\sigma $
. With this identification we have
and
and, moreover,
It follows that
and we are done.
We now return to proving the proposition. By the above lemma the equality
![]() $b{\mathbf{T}}b^{-1}={\mathbf{T}}'$
implies
$b{\mathbf{T}}b^{-1}={\mathbf{T}}'$
implies
![]() $b\widetilde {{\mathbf{T}}}b^{-1}=\widetilde {{\mathbf{T}}}'$
and
$b\widetilde {{\mathbf{T}}}b^{-1}=\widetilde {{\mathbf{T}}}'$
and
Since
![]() $H^1(K,R_{L\cdot E/K}({\mathbf{G}}_{m,L\cdot E}))=1$
, we can pick an element
$H^1(K,R_{L\cdot E/K}({\mathbf{G}}_{m,L\cdot E}))=1$
, we can pick an element
such that
![]() $b^{-\tau +1}=a^{-\tau +1}$
. Clearly,
$b^{-\tau +1}=a^{-\tau +1}$
. Clearly,
![]() $c:=ba^{-1}$
is
$c:=ba^{-1}$
is
![]() ${\textrm {Gal}}(K^{sep}/K)$
-invariant, hence,
${\textrm {Gal}}(K^{sep}/K)$
-invariant, hence,
![]() $c\in B^\times $
, and, defining s as the map
$c\in B^\times $
, and, defining s as the map
![]() $x\mapsto cx\sigma (c)$
, the following claim completes the proof of the proposition.
$x\mapsto cx\sigma (c)$
, the following claim completes the proof of the proposition.
Claim.
![]() $cL\sigma (c)=L'$
.
$cL\sigma (c)=L'$
.
The claim is equivalent to
![]() $c(L\cdot E)\sigma (c)=L'\cdot E$
. Moreover, it suffices to show that
$c(L\cdot E)\sigma (c)=L'\cdot E$
. Moreover, it suffices to show that
But
![]() $\sigma (c)=\sigma (a^{-1})\sigma (b)$
and both
$\sigma (c)=\sigma (a^{-1})\sigma (b)$
and both
![]() $a^{-1}$
and
$a^{-1}$
and
![]() $\sigma (a^{-1})$
are in
$\sigma (a^{-1})$
are in
![]() $(L\cdot E)\otimes _K K^{sep}$
. Therefore, it suffices to show that
$(L\cdot E)\otimes _K K^{sep}$
. Therefore, it suffices to show that
Recall that, by construction, b is a similitude; hence,
![]() $\sigma (b)=\nu (b)b^{-1}$
, where
$\sigma (b)=\nu (b)b^{-1}$
, where
![]() $\nu (b)$
is the multiplier of b. Since
$\nu (b)$
is the multiplier of b. Since
![]() $b{\mathbf{T}}b^{-1}={\mathbf{T}}'$
, the claim follows upon noting that the centraliser of
$b{\mathbf{T}}b^{-1}={\mathbf{T}}'$
, the claim follows upon noting that the centraliser of
![]() ${\mathbf{T}}$
(respectively
${\mathbf{T}}$
(respectively
![]() ${\mathbf{T}}'$
) in
${\mathbf{T}}'$
) in
![]() $B\otimes _K K^{sep}$
is
$B\otimes _K K^{sep}$
is
![]() $(L\cdot E)\otimes _K K^{sep}$
(respectively
$(L\cdot E)\otimes _K K^{sep}$
(respectively
![]() $(L'\cdot E)\otimes _K K^{sep}$
).
$(L'\cdot E)\otimes _K K^{sep}$
).
The proposition in conjunction with Corollary 4.3 yields the following.
Theorem 5.3. Let A be a division Albert algebra over K and let
![]() $L\subset A$
and
$L\subset A$
and
![]() $L'\subset A$
be isomorphic separable cubic field extensions of K. Then there exists a 9-dimensional subalgebra
$L'\subset A$
be isomorphic separable cubic field extensions of K. Then there exists a 9-dimensional subalgebra
![]() $B_\sigma ^+$
of A and an element
$B_\sigma ^+$
of A and an element
![]() $s\in {\mathrm{Str}}(A,B_\sigma ^+)$
such that
$s\in {\mathrm{Str}}(A,B_\sigma ^+)$
such that
![]() $s(L)=L'=f(L)$
.
$s(L)=L'=f(L)$
.
Proof. If
![]() $L'=L$
, we can take any any
$L'=L$
, we can take any any
![]() $9$
-dimensional subalgebra
$9$
-dimensional subalgebra
![]() $B^+_\sigma $
containing L and choose
$B^+_\sigma $
containing L and choose
![]() $s=\mathrm {Id}$
. Otherwise, the cubic subfields
$s=\mathrm {Id}$
. Otherwise, the cubic subfields
![]() $L,L'$
generate a subalgebra in A of the form
$L,L'$
generate a subalgebra in A of the form
![]() $B_\sigma ^+$
and we can take any lift of the element s constructed in the above proposition.
$B_\sigma ^+$
and we can take any lift of the element s constructed in the above proposition.
Remark 5.4. To be able to approach the Skolem–Noether isomorphic embedding problem using torsor techniques is of independent interest. It seems plausible that this approach can shed some light on the still open and much more difficult Skolem–Noether problem for isotopic embeddings.
6. Reduction to
 $\mathrm {F}_4$
$\mathrm {F}_4$
Throughout this section, we let A be a division Albert algebra over K. We will show that an arbitrary element in
![]() ${\mathrm{Str}}(A)$
can be written as a product of R-trivial elements and elements in
${\mathrm{Str}}(A)$
can be written as a product of R-trivial elements and elements in
![]() ${\mathbf{H}}(K)$
, thereby reducing the problem to subgroups of type
${\mathbf{H}}(K)$
, thereby reducing the problem to subgroups of type
![]() $\mathrm {F}_4$
. To begin with, we recall from [Reference Alsaody, Chernousov and Pianzola1] how to associate, to any
$\mathrm {F}_4$
. To begin with, we recall from [Reference Alsaody, Chernousov and Pianzola1] how to associate, to any
![]() $a\in A^\times $
, a subgroup of type
$a\in A^\times $
, a subgroup of type
![]() $\mathrm {D}_4$
in
$\mathrm {D}_4$
in
![]() ${\mathbf{G}} =[{\mathbf{Str}}(A),{\mathbf{Str}}(A)]$
and a
${\mathbf{G}} =[{\mathbf{Str}}(A),{\mathbf{Str}}(A)]$
and a
![]() $2$
-dimensional torus. Let
$2$
-dimensional torus. Let
![]() $L\subset A$
be the K-subalgebra generated by a if a is not a scalar multiple of the identity of A and by any element that is not such a scalar multiple if a is. Since A is a division algebra, it is known that L is a cubic subfield. Let
$L\subset A$
be the K-subalgebra generated by a if a is not a scalar multiple of the identity of A and by any element that is not such a scalar multiple if a is. Since A is a division algebra, it is known that L is a cubic subfield. Let
![]() ${\mathbf{G}}^L$
be the algebraic K-group whose functor of points is given by
${\mathbf{G}}^L$
be the algebraic K-group whose functor of points is given by
for any K-ring R. Since
![]() ${\mathbf{G}}^L$
stabilises
${\mathbf{G}}^L$
stabilises
![]() $1\in L\subset A$
, we have
$1\in L\subset A$
, we have
![]() ${\mathbf{G}}^L\subset {\mathbf{H}}\subset {\mathbf{G}}$
. It is known that over a separable closure of K the group
${\mathbf{G}}^L\subset {\mathbf{H}}\subset {\mathbf{G}}$
. It is known that over a separable closure of K the group
![]() ${\mathbf{G}}^L$
is conjugate to the standard subgroup in
${\mathbf{G}}^L$
is conjugate to the standard subgroup in
![]() ${\mathbf{G}}$
of type
${\mathbf{G}}$
of type
![]() $\mathrm {D}_4$
generated by roots
$\mathrm {D}_4$
generated by roots
![]() $\alpha _2,\alpha _3,\alpha _4, \alpha _5$
. The lemma below shows that the centraliser
$\alpha _2,\alpha _3,\alpha _4, \alpha _5$
. The lemma below shows that the centraliser
![]() ${\mathbf{S}}^{'L}=C_{\mathbf{G}}({\mathbf{G}}^L)$
of
${\mathbf{S}}^{'L}=C_{\mathbf{G}}({\mathbf{G}}^L)$
of
![]() ${\mathbf{G}}^L$
in
${\mathbf{G}}^L$
in
![]() ${\mathbf{G}}$
is a
${\mathbf{G}}$
is a
![]() $2$
-dimensional torus over K and that
$2$
-dimensional torus over K and that
is the centre of
![]() ${\mathbf{G}}^L$
.
${\mathbf{G}}^L$
.
Lemma 6.1. Let K be an arbitrary field.
![]() ${\mathbf{G}}$
be a split simple simply connected K-group of type
${\mathbf{G}}$
be a split simple simply connected K-group of type
![]() ${\mathrm{E}}_6.$
Let
${\mathrm{E}}_6.$
Let
![]() ${\mathbf{T}}\subset {\mathbf{G}}$
be a maximal split torus. Denote by
${\mathbf{T}}\subset {\mathbf{G}}$
be a maximal split torus. Denote by
![]() $\Pi =\{\alpha _1,\ldots ,\alpha _6\}$
a basis of the root system
$\Pi =\{\alpha _1,\ldots ,\alpha _6\}$
a basis of the root system
![]() $\Sigma ({\mathbf{G}},{\mathbf{T}})$
and by
$\Sigma ({\mathbf{G}},{\mathbf{T}})$
and by
![]() $\Sigma _1$
the root subsystem in
$\Sigma _1$
the root subsystem in
![]() $\Sigma $
generated by
$\Sigma $
generated by
![]() $\alpha _2,\alpha _3,\alpha _4,\alpha _5$
. Then
$\alpha _2,\alpha _3,\alpha _4,\alpha _5$
. Then
![]() ${\mathbf{S}}=C_{\mathbf{G}}({\mathbf{G}}_{\Sigma _1})$
is a
${\mathbf{S}}=C_{\mathbf{G}}({\mathbf{G}}_{\Sigma _1})$
is a
![]() $2$
-dimensional subtorus in
$2$
-dimensional subtorus in
![]() ${\mathbf{T}}$
and
${\mathbf{T}}$
and
![]() ${\mathbf{S}}\cap {\mathbf{G}}_{\Sigma _1}$
is the centre of
${\mathbf{S}}\cap {\mathbf{G}}_{\Sigma _1}$
is the centre of
![]() ${\mathbf{G}}_{\Sigma _1}$
.
${\mathbf{G}}_{\Sigma _1}$
.
Proof. Let
![]() ${\mathbf{T}}_{\Sigma _1}={\mathbf{G}}_{\Sigma _1}\cap {\mathbf{T}}$
. This is a maximal split torus of
${\mathbf{T}}_{\Sigma _1}={\mathbf{G}}_{\Sigma _1}\cap {\mathbf{T}}$
. This is a maximal split torus of
![]() ${\mathbf{G}}_{\Sigma _1}$
. Clearly, one has
${\mathbf{G}}_{\Sigma _1}$
. Clearly, one has
![]() $C_{\mathbf{G}}({\mathbf{G}}_{\Sigma _1})\subset C_{\mathbf{G}}({\mathbf{T}}_{\Sigma _1})$
. By properties of reductive groups,
$C_{\mathbf{G}}({\mathbf{G}}_{\Sigma _1})\subset C_{\mathbf{G}}({\mathbf{T}}_{\Sigma _1})$
. By properties of reductive groups,
![]() $C_{{\mathbf{G}}}({\mathbf{T}}_{\Sigma _1})$
is a reductive group whose derived subgroup
$C_{{\mathbf{G}}}({\mathbf{T}}_{\Sigma _1})$
is a reductive group whose derived subgroup
![]() $[C_{{\mathbf{G}}}({\mathbf{T}}_{\Sigma _1}),C_{{\mathbf{G}}}({\mathbf{T}}_{\Sigma _1})]$
is generated by roots in
$[C_{{\mathbf{G}}}({\mathbf{T}}_{\Sigma _1}),C_{{\mathbf{G}}}({\mathbf{T}}_{\Sigma _1})]$
is generated by roots in
![]() $\Sigma $
orthogonal to
$\Sigma $
orthogonal to
![]() $\alpha _2,\alpha _3,\alpha _4,\alpha _5$
. Since
$\alpha _2,\alpha _3,\alpha _4,\alpha _5$
. Since
![]() $\Sigma $
is of type
$\Sigma $
is of type
![]() ${\mathrm{E}}_6$
there are no such roots, and this implies that
${\mathrm{E}}_6$
there are no such roots, and this implies that
![]() $C_{{\mathbf{G}}}({\mathbf{T}}_{\Sigma _1})={\mathbf{T}}$
. Thus,
$C_{{\mathbf{G}}}({\mathbf{T}}_{\Sigma _1})={\mathbf{T}}$
. Thus,
![]() $S=C_{\mathbf{G}}({\mathbf{G}}_{\Sigma _1})$
is a subtorus in
$S=C_{\mathbf{G}}({\mathbf{G}}_{\Sigma _1})$
is a subtorus in
![]() ${\mathbf{T}}$
. To describe it explicitly we will use the canonical cocharacters
${\mathbf{T}}$
. To describe it explicitly we will use the canonical cocharacters
![]() $\check {\alpha }_i: {\mathbf{G}}_m\to {\mathbf{T}}$
.
$\check {\alpha }_i: {\mathbf{G}}_m\to {\mathbf{T}}$
.
Since
![]() ${\mathbf{G}}$
is simply connected, every element in
${\mathbf{G}}$
is simply connected, every element in
![]() $t\in {\mathbf{T}}(K)$
can be written uniquely in the form
$t\in {\mathbf{T}}(K)$
can be written uniquely in the form
![]() $t=\prod _i \check {\alpha }_i(t_i)$
where
$t=\prod _i \check {\alpha }_i(t_i)$
where
![]() $t_i\in K$
. For a root
$t_i\in K$
. For a root
![]() $\alpha \in \Sigma $
let
$\alpha \in \Sigma $
let
![]() ${\mathbf{U}}_{\alpha }$
be the associated root subgroup in
${\mathbf{U}}_{\alpha }$
be the associated root subgroup in
![]() ${\mathbf{G}}$
. Using Steinberg’s notation (introduced in [Reference Tits and Weiss21]), every element in
${\mathbf{G}}$
. Using Steinberg’s notation (introduced in [Reference Tits and Weiss21]), every element in
![]() ${\mathbf{U}}_{\alpha }$
can be written as
${\mathbf{U}}_{\alpha }$
can be written as
![]() $x_{\alpha }(u)$
where
$x_{\alpha }(u)$
where
![]() $u\in K$
. According to the Steinberg relations [Reference Tits and Weiss21], we have
$u\in K$
. According to the Steinberg relations [Reference Tits and Weiss21], we have
 $$ \begin{align*}\check{\alpha}_i(t_i) x_{\alpha}(u)\check{\alpha}_i(t_i)^{-1}=x_\alpha(t_i^{<\alpha,\alpha_i>}u). \end{align*} $$
$$ \begin{align*}\check{\alpha}_i(t_i) x_{\alpha}(u)\check{\alpha}_i(t_i)^{-1}=x_\alpha(t_i^{<\alpha,\alpha_i>}u). \end{align*} $$
Using this relation, it is straightforward to verify that
![]() ${\mathbf{S}}$
consists of the elements in
${\mathbf{S}}$
consists of the elements in
![]() ${\mathbf{T}}$
of the form
${\mathbf{T}}$
of the form
 $$ \begin{align*}\check{\alpha}_1\left(\frac{b^2}{a^2}\right) \check{\alpha}_3(b) \check{\alpha}_4(a^2) \check{\alpha}_2(a) \check{\alpha}_5\left(\frac{a^3}{b}\right) \check{\alpha}_6\left(\frac{a^4}{b^2}\right) \end{align*} $$
$$ \begin{align*}\check{\alpha}_1\left(\frac{b^2}{a^2}\right) \check{\alpha}_3(b) \check{\alpha}_4(a^2) \check{\alpha}_2(a) \check{\alpha}_5\left(\frac{a^3}{b}\right) \check{\alpha}_6\left(\frac{a^4}{b^2}\right) \end{align*} $$
where
![]() $a,b\in K^\times $
. Lastly, we note that the centre of
$a,b\in K^\times $
. Lastly, we note that the centre of
![]() ${\mathbf{G}}_{\Sigma _1}$
is generated by the two elements
${\mathbf{G}}_{\Sigma _1}$
is generated by the two elements
![]() $\check {\alpha }_3(-1)\check {\alpha }_2(-1)$
and
$\check {\alpha }_3(-1)\check {\alpha }_2(-1)$
and
![]() $\check {\alpha }_5(-1)\check {\alpha }_2(-1)$
which are contained in
$\check {\alpha }_5(-1)\check {\alpha }_2(-1)$
which are contained in
![]() ${\mathbf{S}}$
.
${\mathbf{S}}$
.
Let
![]() ${\mathbf{S}}^L\subset {\mathbf{Str}}(A)$
be the
${\mathbf{S}}^L\subset {\mathbf{Str}}(A)$
be the
![]() $3$
-dimensional torus in
$3$
-dimensional torus in
![]() ${\mathbf{Str}}(A)$
generated by
${\mathbf{Str}}(A)$
generated by
![]() ${\mathbf{S}}^{'L}$
and
${\mathbf{S}}^{'L}$
and
![]() ${\mathbf{G}}_m$
, where the latter is embedded in
${\mathbf{G}}_m$
, where the latter is embedded in
![]() ${\mathbf{Str}}(A)$
as the subgroup of homotheties. The following was proved in [Reference Alsaody, Chernousov and Pianzola1].
${\mathbf{Str}}(A)$
as the subgroup of homotheties. The following was proved in [Reference Alsaody, Chernousov and Pianzola1].
Lemma 6.2. With the notation above,
![]() ${\mathbf{S}}^L\simeq R_{L/K}({\mathbf{G}}_{m,L})$
and
${\mathbf{S}}^L\simeq R_{L/K}({\mathbf{G}}_{m,L})$
and
 ${\mathbf{S}}^{'L}\simeq R_{L/K}^{(1)}({\mathbf{G}}_{m,L})$
. Moreover,
${\mathbf{S}}^{'L}\simeq R_{L/K}^{(1)}({\mathbf{G}}_{m,L})$
. Moreover,
and the natural action of
![]() ${\mathbf{Str}}(A)$
on A induces an action of
${\mathbf{Str}}(A)$
on A induces an action of
![]() ${\mathbf{S}}^L$
on L, which is transitive on the level of the
${\mathbf{S}}^L$
on L, which is transitive on the level of the
![]() $K^{sep}$
-points of the open subset
$K^{sep}$
-points of the open subset
of L and gives rise to an exact sequence
From the exact sequence in cohomology associated to the sequence in the lemma we have a map
![]() $L^\times \to H^1(K,{\mathbf{Z}}^L)$
, which is surjective since
$L^\times \to H^1(K,{\mathbf{Z}}^L)$
, which is surjective since
![]() $H^1(K,{\mathbf{S}}^L)$
is trivial. Using this map we can attach, to any
$H^1(K,{\mathbf{S}}^L)$
is trivial. Using this map we can attach, to any
![]() $a\in L^\times $
, a class
$a\in L^\times $
, a class
![]() $[\xi _a]=(a_\tau )\in H^1(K,{\mathbf{Z}}^L)$
. From [Reference Alsaody, Chernousov and Pianzola1] we moreover know that the image of this class in
$[\xi _a]=(a_\tau )\in H^1(K,{\mathbf{Z}}^L)$
. From [Reference Alsaody, Chernousov and Pianzola1] we moreover know that the image of this class in
![]() $H^1(K,{\mathbf{H}})$
is trivial if a is in the
$H^1(K,{\mathbf{H}})$
is trivial if a is in the
![]() ${\mathrm{Str}}(A)$
-orbit of
${\mathrm{Str}}(A)$
-orbit of
![]() $1$
.
$1$
.
Let now
![]() $g\in {\mathrm{Str}}(A)$
be an arbitrary element and set
$g\in {\mathrm{Str}}(A)$
be an arbitrary element and set
![]() $a:=g(1)$
. As detailed above, we attach to a a subfield L in A and with it the closed subgroups
$a:=g(1)$
. As detailed above, we attach to a a subfield L in A and with it the closed subgroups
![]() ${\mathbf{G}}^L$
,
${\mathbf{G}}^L$
,
![]() ${\mathbf{Z}}^L$
and
${\mathbf{Z}}^L$
and
![]() ${\mathbf{S}}^L$
of
${\mathbf{S}}^L$
of
![]() ${\mathbf{Str}}(A)$
, as well as the class
${\mathbf{Str}}(A)$
, as well as the class
![]() $[\xi _a]=(a_\tau )\in H^1(K,{\mathbf{Z}}^L)$
. Since the image of this class in
$[\xi _a]=(a_\tau )\in H^1(K,{\mathbf{Z}}^L)$
. Since the image of this class in
![]() $H^1(K,{\mathbf{H}})$
is trivial, there exists
$H^1(K,{\mathbf{H}})$
is trivial, there exists
![]() $f\in {\mathbf{H}}(K^{sep})$
such that
$f\in {\mathbf{H}}(K^{sep})$
such that
![]() $a_{\tau }=(f^{-1})^\tau f$
for all
$a_{\tau }=(f^{-1})^\tau f$
for all
![]() $\tau \in {\textrm {Gal}}(K^{sep}/K)$
.
$\tau \in {\textrm {Gal}}(K^{sep}/K)$
.
Lemma 6.3. The subset
![]() $f(L)\subset A_{K^{sep}}=A\otimes _K K^{sep}$
is contained in
$f(L)\subset A_{K^{sep}}=A\otimes _K K^{sep}$
is contained in
![]() $A=A\otimes _K K$
.
$A=A\otimes _K K$
.
Proof. Let
![]() $l\in L$
. We need to show that
$l\in L$
. We need to show that
![]() $f(l)$
is
$f(l)$
is
![]() ${\textrm {Gal}}(K^{sep}/K)$
-invariant. Take any
${\textrm {Gal}}(K^{sep}/K)$
-invariant. Take any
![]() $\tau \in {\textrm {Gal}}(K^{sep}/K)$
. Then
$\tau \in {\textrm {Gal}}(K^{sep}/K)$
. Then
 $$ \begin{align*}\tau(f(l))=(f^\tau)(\tau(l))=f^\tau(l)=f (f^{-1}f^\tau(l))=f a^{-1}_{\tau}(l)=f(l), \end{align*} $$
$$ \begin{align*}\tau(f(l))=(f^\tau)(\tau(l))=f^\tau(l)=f (f^{-1}f^\tau(l))=f a^{-1}_{\tau}(l)=f(l), \end{align*} $$
since
![]() ${\mathbf{Z}}^L\subset {\mathbf{G}}^L$
fixes L pointwise and the statement follows.
${\mathbf{Z}}^L\subset {\mathbf{G}}^L$
fixes L pointwise and the statement follows.
Since
![]() ${\mathbf{H}} = {\mathbf {Aut}}(A)$
, the above lemma implies that the map
${\mathbf{H}} = {\mathbf {Aut}}(A)$
, the above lemma implies that the map
![]() $L\to L'=f(L)$
given by
$L\to L'=f(L)$
given by
![]() $l \mapsto f(l)$
is a field isomorphism over K. Assume that
$l \mapsto f(l)$
is a field isomorphism over K. Assume that
![]() $L\not =L'$
. Let
$L\not =L'$
. Let
![]() $B_\sigma ^+\subset A$
be the
$B_\sigma ^+\subset A$
be the
![]() $9$
-dimensional subalgebra generated by L and
$9$
-dimensional subalgebra generated by L and
![]() $L'$
. Recall from [Reference Alsaody, Chernousov and Pianzola1] that
$L'$
. Recall from [Reference Alsaody, Chernousov and Pianzola1] that
![]() $\xi _a$
is constructed explicitly as follows. Choose
$\xi _a$
is constructed explicitly as follows. Choose
![]() $t\in {\mathbf{S}}^L(K^{sep})$
such that
$t\in {\mathbf{S}}^L(K^{sep})$
such that
![]() $t(1)=a=g(1)$
; this is possible by Lemma 6.2. Then
$t(1)=a=g(1)$
; this is possible by Lemma 6.2. Then
![]() $a_\tau =t^{-\tau +1}$
, from which we conclude that
$a_\tau =t^{-\tau +1}$
, from which we conclude that
![]() $ft^{-1}$
is defined over K and that
$ft^{-1}$
is defined over K and that
which implies that
![]() $ft^{-1}g\in {\mathbf{H}}(K)$
. Thus, modulo
$ft^{-1}g\in {\mathbf{H}}(K)$
. Thus, modulo
![]() ${\mathbf{H}}(K)$
, we may assume that
${\mathbf{H}}(K)$
, we may assume that
![]() $g=ft^{-1}$
.
$g=ft^{-1}$
.
Let now
![]() $s\in {\mathrm{Str}}(A,B_\sigma ^+)$
be the element constructed in Theorem 5.3. It is R-trivial, since so is
$s\in {\mathrm{Str}}(A,B_\sigma ^+)$
be the element constructed in Theorem 5.3. It is R-trivial, since so is
![]() ${\mathbf{Str}}(A,B_\sigma ^+)^\circ $
and it satisfies
${\mathbf{Str}}(A,B_\sigma ^+)^\circ $
and it satisfies
![]() $s(L)=f(L)$
. Furthermore,
$s(L)=f(L)$
. Furthermore,
since
![]() $t(L)=L$
. It follows that modulo R-trivial elements we may assume that
$t(L)=L$
. It follows that modulo R-trivial elements we may assume that
![]() $g(L)=L$
; that is,
$g(L)=L$
; that is,
![]() $g\in {\mathbf{Str}}(A,L)(K)$
, where
$g\in {\mathbf{Str}}(A,L)(K)$
, where
![]() ${\mathbf{Str}}(A,L)\subset {\mathbf{Str}}(A)$
is the subgroup of all elements stabilising L.
${\mathbf{Str}}(A,L)\subset {\mathbf{Str}}(A)$
is the subgroup of all elements stabilising L.
Passing to a separable closure of K one can easily check that the connected component of
![]() ${\mathbf{Str}}(A,L)$
is
${\mathbf{Str}}(A,L)$
is
![]() ${\mathbf{S}}^L\cdot {\mathbf{G}}^L$
. Hence,
${\mathbf{S}}^L\cdot {\mathbf{G}}^L$
. Hence,
 $$ \begin{align*}{\mathbf{Str}}(A,L)=N_{{\mathbf{Str}}(A)}({\textbf{S}}^L\cdot {\mathbf{G}}^L) \end{align*} $$
$$ \begin{align*}{\mathbf{Str}}(A,L)=N_{{\mathbf{Str}}(A)}({\textbf{S}}^L\cdot {\mathbf{G}}^L) \end{align*} $$
and
By Lemma 2.7 we can, if necessary, multiply g by an element from
![]() $N_{\mathbf{H}}({\mathbf{G}}^L)(K)$
to obtain an element
$N_{\mathbf{H}}({\mathbf{G}}^L)(K)$
to obtain an element
![]() $g'\in ({\mathbf{S}}^L\cdot {\mathbf{G}}^L)(K)$
. To complete our reduction to subgroups of type
$g'\in ({\mathbf{S}}^L\cdot {\mathbf{G}}^L)(K)$
. To complete our reduction to subgroups of type
![]() $\mathrm {F}_4$
, it remains to show that
$\mathrm {F}_4$
, it remains to show that
![]() $g'$
is R-trivial modulo elements from
$g'$
is R-trivial modulo elements from
![]() ${\mathbf{H}}(K)$
. This is the content of the following result.
${\mathbf{H}}(K)$
. This is the content of the following result.
Proposition 6.4. Let
![]() $g\in ({\mathbf{S}}^L\cdot {\mathbf{G}}^L)(K)$
. Then there exists an R-trivial element j in
$g\in ({\mathbf{S}}^L\cdot {\mathbf{G}}^L)(K)$
. Then there exists an R-trivial element j in
![]() $({\mathbf{S}}^L\cdot {\mathbf{G}}^L)(K)$
such that
$({\mathbf{S}}^L\cdot {\mathbf{G}}^L)(K)$
such that
![]() $gj\in {\mathbf{G}}^L(K)\subset {\mathbf{H}}(K)$
.
$gj\in {\mathbf{G}}^L(K)\subset {\mathbf{H}}(K)$
.
Proof. Our argument is based on the consideration of the exact sequence
In the corresponding exact sequence in cohomology, the element g is mapped to a class
![]() $[\eta ]$
in
$[\eta ]$
in
![]() $H^1(K,{\mathbf{Z}}^L)$
. Since
$H^1(K,{\mathbf{Z}}^L)$
. Since
![]() $H^1(K,{\mathbf{S}}^L)$
is trivial, this class belongs to
$H^1(K,{\mathbf{S}}^L)$
is trivial, this class belongs to
We first prove that it is R-trivial. Since
![]() ${\mathbf{Z}}^L$
is a group of exponent
${\mathbf{Z}}^L$
is a group of exponent
![]() $2$
, by the norm principle it suffices to prove that
$2$
, by the norm principle it suffices to prove that
![]() $[\eta ]$
becomes R-trivial after extending scalars to
$[\eta ]$
becomes R-trivial after extending scalars to
![]() $L/K$
. Two cases are possible.
$L/K$
. Two cases are possible.
If
![]() $L/K$
is a Galois extension, then
$L/K$
is a Galois extension, then
![]() ${\mathbf{G}}^L_L$
, being a strongly inner form of type
${\mathbf{G}}^L_L$
, being a strongly inner form of type
![]() $^1\mathrm {D}_4$
, is of the form
$^1\mathrm {D}_4$
, is of the form
![]() ${\mathbf{G}}^L_L\simeq {\mathbf{Spin}}(h)$
, where h is a
${\mathbf{G}}^L_L\simeq {\mathbf{Spin}}(h)$
, where h is a
![]() $3$
-fold Pfister form. Hence, by Example 2.3, the class
$3$
-fold Pfister form. Hence, by Example 2.3, the class
![]() ${res}^L_K([\eta ])$
is R-trivial.
${res}^L_K([\eta ])$
is R-trivial.
If
![]() $L/K$
is not a Galois extension, then
$L/K$
is not a Galois extension, then
![]() ${\mathbf{G}}^L_L\simeq {\mathbf{Spin}}(h)$
for some h satisfying all conditions in Example 2.4. Therefore,
${\mathbf{G}}^L_L\simeq {\mathbf{Spin}}(h)$
for some h satisfying all conditions in Example 2.4. Therefore,
![]() ${res}^L_K([\eta ])$
is also R-trivial.
${res}^L_K([\eta ])$
is also R-trivial.
Now the sequence (8) induces the exact sequence
where x is a variable over K. Let
be defined at 0 and 1 and such that
![]() $\eta (0)=1$
and
$\eta (0)=1$
and
![]() $\eta (1)=\eta $
; such an element exists since
$\eta (1)=\eta $
; such an element exists since
![]() $\eta $
is R-trivial. Take any element
$\eta $
is R-trivial. Take any element
![]() $g(x)\in ({\mathbf{S}}^L \cdot {\mathbf{G}}^L)(K(x))$
that is defined at 0 and 1 and whose image in
$g(x)\in ({\mathbf{S}}^L \cdot {\mathbf{G}}^L)(K(x))$
that is defined at 0 and 1 and whose image in
![]() $H^1(K(x), {\mathbf{Z}}^L)$
is
$H^1(K(x), {\mathbf{Z}}^L)$
is
![]() $\eta (x)$
. Note that
$\eta (x)$
. Note that
![]() $g(0)^{-1}g(1)$
is R-trivial in
$g(0)^{-1}g(1)$
is R-trivial in
![]() ${\mathbf{S}}^L \cdot {\mathbf{G}}^L$
. By construction,
${\mathbf{S}}^L \cdot {\mathbf{G}}^L$
. By construction,
![]() $g(0)=u_0$
and
$g(0)=u_0$
and
![]() $g(1)=u_1g$
for some
$g(1)=u_1g$
for some
![]() $u_0,u_1\in ({\mathbf{S}}^L\times {\mathbf{G}}^L)(K)$
. Hence,
$u_0,u_1\in ({\mathbf{S}}^L\times {\mathbf{G}}^L)(K)$
. Hence,
 $$ \begin{align*}g=u_1^{-1}g(1)=u_1^{-1}g(0)\left(g(0)^{-1}g(1)\right)=u_1^{-1}u_0\left(g(0)^{-1}g(1)\right). \end{align*} $$
$$ \begin{align*}g=u_1^{-1}g(1)=u_1^{-1}g(0)\left(g(0)^{-1}g(1)\right)=u_1^{-1}u_0\left(g(0)^{-1}g(1)\right). \end{align*} $$
Writing
 $u_1^{-1}u_0=us$
for some
$u_1^{-1}u_0=us$
for some
![]() $u\in {\mathbf{G}}^L(K)$
and
$u\in {\mathbf{G}}^L(K)$
and
![]() $s\in {\mathbf{S}}^L(K)$
and noting that
$s\in {\mathbf{S}}^L(K)$
and noting that
![]() ${\mathbf{S}}^L$
is a rational torus, the proof is complete upon setting
${\mathbf{S}}^L$
is a rational torus, the proof is complete upon setting
 $j=\left (sg(0)^{-1}g(1)\right )^{-1}$
.
$j=\left (sg(0)^{-1}g(1)\right )^{-1}$
.
We have thus altogether proved the following.
Theorem 6.5. Let
![]() $L\subset A$
be a cubic subfield and let
$L\subset A$
be a cubic subfield and let
![]() $g\in {\mathrm{Str}}(A)$
be such that
$g\in {\mathrm{Str}}(A)$
be such that
![]() $g(L)=L$
. Then modulo R-trivial elements, g can be written as a product
$g(L)=L$
. Then modulo R-trivial elements, g can be written as a product
![]() $g=g_1g_2$
where
$g=g_1g_2$
where
![]() $g_1(L)=g_2(L)=L$
,
$g_1(L)=g_2(L)=L$
,
![]() $g_1\in N_{\mathbf{H}}({\mathbf{G}}^L)(K)$
and
$g_1\in N_{\mathbf{H}}({\mathbf{G}}^L)(K)$
and
![]() $g_2\in {\mathbf{G}}^L(K)$
.
$g_2\in {\mathbf{G}}^L(K)$
.
7. End of the Proof
We now finish the proof that
![]() ${\mathbf{Str}}(A)$
is R-trivial. To begin we recall the following known fact.
${\mathbf{Str}}(A)$
is R-trivial. To begin we recall the following known fact.
Theorem 7.1. Let K be a perfect field. Let
![]() ${\mathbf{G}}$
be a semisimple K-group and
${\mathbf{G}}$
be a semisimple K-group and
![]() $g\in {\mathbf{G}}(K)$
. Then the semisimple and unipotent components
$g\in {\mathbf{G}}(K)$
. Then the semisimple and unipotent components
![]() $g_s,g_u$
of the Jordan decomposition
$g_s,g_u$
of the Jordan decomposition
![]() $g=g_sg_u$
are defined over K. Moreover, if
$g=g_sg_u$
are defined over K. Moreover, if
![]() ${\mathbf{G}}$
is K-anisotropic, then
${\mathbf{G}}$
is K-anisotropic, then
![]() $g_u=1$
.
$g_u=1$
.
Proof. For the first statement see [Reference Borel2, Page 81, Corollary 1] and for the second statement see [Reference Borel and Tits3].
Next we have the following.
Lemma 7.2. Let A be a division Albert algebra over K and let
![]() $g\in {\mathbf{H}}(K)$
. Then g fixes a cubic subfield in A pointwise.
$g\in {\mathbf{H}}(K)$
. Then g fixes a cubic subfield in A pointwise.
Proof. Since
![]() ${\mathbf{H}}$
is K-anisotropic, g is semisimple. Indeed, let
${\mathbf{H}}$
is K-anisotropic, g is semisimple. Indeed, let
![]() $g=g_sg_u$
be its Jordan decomposition over an algebraic closure
$g=g_sg_u$
be its Jordan decomposition over an algebraic closure
![]() $\overline {K}$
of K. Let
$\overline {K}$
of K. Let
![]() $\widetilde {K}=K^{p^{-\infty }}$
. Here p is the characteristic of K. Since
$\widetilde {K}=K^{p^{-\infty }}$
. Here p is the characteristic of K. Since
![]() $p\not =2,3$
, the extension
$p\not =2,3$
, the extension
![]() $\widetilde {K}/K$
cannot kill the cohomological invariant
$\widetilde {K}/K$
cannot kill the cohomological invariant
![]() $g_3$
attached to
$g_3$
attached to
![]() ${\mathbf{H}}$
. By [Reference De Medts, Mühlherr and Stavrova13, Theorem 40.8, part (2)], A is still a division algebra over
${\mathbf{H}}$
. By [Reference De Medts, Mühlherr and Stavrova13, Theorem 40.8, part (2)], A is still a division algebra over
![]() $\widetilde {K}$
, whence
$\widetilde {K}$
, whence
![]() ${\mathbf{H}}_{\widetilde {K}}$
is still anisotropic. It follows from the above theorem that
${\mathbf{H}}_{\widetilde {K}}$
is still anisotropic. It follows from the above theorem that
![]() $g_u=1$
.Footnote
4
$g_u=1$
.Footnote
4
Hence, g is contained in a maximal K-torus
![]() ${\mathbf{T}}\subset {\mathbf{H}}$
. Using an explicit reduced model of the split Albert algebra
${\mathbf{T}}\subset {\mathbf{H}}$
. Using an explicit reduced model of the split Albert algebra
![]() $A\otimes _K K^{sep}$
, one can easily check that over
$A\otimes _K K^{sep}$
, one can easily check that over
![]() $K^{sep}$
, every element in
$K^{sep}$
, every element in
![]() ${\mathbf{T}}$
fixes a commutative subalgebra
${\mathbf{T}}$
fixes a commutative subalgebra
of
![]() $ A\otimes _K K^{sep}$
pointwise. It follows that g fixes a vector
$ A\otimes _K K^{sep}$
pointwise. It follows that g fixes a vector
![]() $v\in A$
which is not a scalar multiple of the identity, whence it fixes the cubic subfield
$v\in A$
which is not a scalar multiple of the identity, whence it fixes the cubic subfield
![]() $K(v)\subset A$
generated by v.
$K(v)\subset A$
generated by v.
In order to finish our proof we need one final ingredient. Let A be an Albert algebra over K and let
![]() $p\in A^\times $
. Recall that this is equivalent to
$p\in A^\times $
. Recall that this is equivalent to
![]() $N(p)\neq 0$
, where N is the cubic norm of A. The isotope
$N(p)\neq 0$
, where N is the cubic norm of A. The isotope
![]() $A^{(p)}$
of A is the algebra with underlying linear space A and multiplication
$A^{(p)}$
of A is the algebra with underlying linear space A and multiplication
where juxtaposition denotes the multiplication of A. It is known that
![]() $A^{(p)}$
is an Albert algebra and that the cubic norm of
$A^{(p)}$
is an Albert algebra and that the cubic norm of
![]() $A^{(p)}$
is
$A^{(p)}$
is
![]() $\nu N$
, where
$\nu N$
, where
![]() $\nu =N(p)$
. From this it follows that
$\nu =N(p)$
. From this it follows that
![]() $A^{(p)}$
is a division algebra if and only if A is and that
$A^{(p)}$
is a division algebra if and only if A is and that
![]() ${\mathbf{Str}}(A)\simeq {\mathbf{Str}}(A^{(p)})$
.
${\mathbf{Str}}(A)\simeq {\mathbf{Str}}(A^{(p)})$
.
Proposition 7.3
[Reference Thakur25]. Let A be a division Albert algebra over K. Then there exists
![]() $p\in A^\times $
such that
$p\in A^\times $
such that
![]() $A^{(p)}$
contains a cubic cyclic subfield.
$A^{(p)}$
contains a cubic cyclic subfield.
Remark 7.4. If the ground field F contains a cubic root of unity, then due to a result of H. Petersson and M. Racine [Reference Petersson and Racine16], one can take
![]() $p=1$
.
$p=1$
.
We are now ready to prove our main result.
Theorem 7.5. Let A be a division Albert algebra over K. Then the algebraic K-group
![]() ${\mathbf{Str}}(A)$
is R-trivial.
${\mathbf{Str}}(A)$
is R-trivial.
Proof. By the above discussion, we may replace A by any isotope
![]() $A^{(p)}$
. Thus, by the preceding proposition we may assume that A contains a cubic cyclic subfield L. Let
$A^{(p)}$
. Thus, by the preceding proposition we may assume that A contains a cubic cyclic subfield L. Let
![]() $g\in {\mathrm{Str}}(A)$
. By the results of Section 6, summarised in Theorem 6.5, we may assume that
$g\in {\mathrm{Str}}(A)$
. By the results of Section 6, summarised in Theorem 6.5, we may assume that
![]() $g\in {\mathbf{H}}(K)$
. Three cases are possible.
$g\in {\mathbf{H}}(K)$
. Three cases are possible.
Case
![]() $1$
: g fixes L but not pointwise. Let
$1$
: g fixes L but not pointwise. Let
![]() $F\subset A$
be a cubic field extension of K pointwise fixed by g; such a field exists by Lemma 7.2. Since
$F\subset A$
be a cubic field extension of K pointwise fixed by g; such a field exists by Lemma 7.2. Since
![]() $F\not =L$
, L and F generate a 9-dimensional subalgebra
$F\not =L$
, L and F generate a 9-dimensional subalgebra
![]() $B_\sigma ^+\subset A$
that is stabilised by g. In the course of the proof of Corollary 4.3 we saw that
$B_\sigma ^+\subset A$
that is stabilised by g. In the course of the proof of Corollary 4.3 we saw that
By Proposition 4.2, the algebraic K-group
![]() ${\mathbf{Str}}(A,B_\sigma ^+)^\circ $
is R-trivial and therefore g is R-trivial.
${\mathbf{Str}}(A,B_\sigma ^+)^\circ $
is R-trivial and therefore g is R-trivial.
Case
![]() $2$
: g fixes L pointwise. Hence, g is in the group of K-points of the algebraic K-group
$2$
: g fixes L pointwise. Hence, g is in the group of K-points of the algebraic K-group
![]() ${\mathbf{Str}}(A/L)$
whose functor of points is as follows: if R is a K-ring,
${\mathbf{Str}}(A/L)$
whose functor of points is as follows: if R is a K-ring,
Since L is cyclic, by Lemma 2.7 there is an element
![]() $h_1\in N_{\mathbf{H}}({\mathbf{G}}^L)(K)$
that stabilises L but does not fix it pointwise. The same is true for
$h_1\in N_{\mathbf{H}}({\mathbf{G}}^L)(K)$
that stabilises L but does not fix it pointwise. The same is true for
 $h_2:=h_1^{-1}g$
, since g fixes L pointwise. From Case (1) we know that
$h_2:=h_1^{-1}g$
, since g fixes L pointwise. From Case (1) we know that
![]() $h_1$
and
$h_1$
and
![]() $h_2$
are R-trivial and hence so is g.
$h_2$
are R-trivial and hence so is g.
Case 3:
![]() $g(L)\not =L$
. Since
$g(L)\not =L$
. Since
![]() $g\in {\mathrm{Aut}}(A)$
, the field
$g\in {\mathrm{Aut}}(A)$
, the field
![]() $g(L)$
is a cubic cyclic subfield of A isomorphic to L. The subfields L and
$g(L)$
is a cubic cyclic subfield of A isomorphic to L. The subfields L and
![]() $g(L)$
generate a 9-dimensional subalgebra
$g(L)$
generate a 9-dimensional subalgebra
![]() $B_\sigma ^+$
of A. By Theorem 5.3 there exists
$B_\sigma ^+$
of A. By Theorem 5.3 there exists
![]() $h_1\in {\mathrm{Str}}(A,B_\sigma ^+)$
such that
$h_1\in {\mathrm{Str}}(A,B_\sigma ^+)$
such that
![]() $h_1(g(L))=L$
and by Proposition 4.2,
$h_1(g(L))=L$
and by Proposition 4.2,
![]() $h_1$
is R-trivial. Let
$h_1$
is R-trivial. Let
![]() $h_2:=h_1g$
. By construction, it belongs to
$h_2:=h_1g$
. By construction, it belongs to
By Theorem 6.5,
![]() $h_2$
can be written, modulo R-trivial elements, as a product
$h_2$
can be written, modulo R-trivial elements, as a product
![]() $h_2=h_3h_4$
with
$h_2=h_3h_4$
with
![]() $h_3\in {\mathbf{G}}^L(K)$
and
$h_3\in {\mathbf{G}}^L(K)$
and
![]() $h_4\in N_{\mathbf{H}}({\mathbf{G}}^L)(K)$
. In particular,
$h_4\in N_{\mathbf{H}}({\mathbf{G}}^L)(K)$
. In particular,
![]() $h_3$
and
$h_3$
and
![]() $h_4$
are in
$h_4$
are in
![]() ${\mathbf{H}}(K)$
and stabilise L. By Cases (1) and (2), the elements
${\mathbf{H}}(K)$
and stabilise L. By Cases (1) and (2), the elements
![]() $h_3$
and
$h_3$
and
![]() $h_4$
are R-trivial and hence so is
$h_4$
are R-trivial and hence so is
![]() $h_2$
and g. This completes the proof.
$h_2$
and g. This completes the proof.
Theorem 7.6. Let
![]() $\overline {\mathbf{G}}$
be an adjoint strongly inner form of type
$\overline {\mathbf{G}}$
be an adjoint strongly inner form of type
![]() ${\mathrm{E}}_6$
. Then
${\mathrm{E}}_6$
. Then
![]() $\overline {\mathbf{G}}$
is R-trivial.
$\overline {\mathbf{G}}$
is R-trivial.
Proof. Indeed, the canonical map
![]() ${\mathbf{Str}}(A) \to \overline {\mathbf{G}}$
has a rational section, since its kernel
${\mathbf{Str}}(A) \to \overline {\mathbf{G}}$
has a rational section, since its kernel
![]() ${\mathbf{G}}_m$
has trivial Galois cohomology in dimension 1. We conclude by the above theorem.
${\mathbf{G}}_m$
has trivial Galois cohomology in dimension 1. We conclude by the above theorem.
8. Applications
8.1. The Kneser–Tits Problem for
 $\mathrm {E}_{7,1}^{78}$
and
$\mathrm {E}_{7,1}^{78}$
and
 $\mathrm {E}_{8,2}^{78}$
$\mathrm {E}_{8,2}^{78}$
Theorem 8.1. Let K be an arbitrary field. Let
![]() ${\mathbf{G}}$
be a simple simply connected K-group of type
${\mathbf{G}}$
be a simple simply connected K-group of type
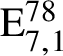 $\mathrm {E}_{7,1}^{78}$
or
$\mathrm {E}_{7,1}^{78}$
or
 $\mathrm {E}_{8,2}^{78}.$
Then the Kneser–Tits conjecture for
$\mathrm {E}_{8,2}^{78}.$
Then the Kneser–Tits conjecture for
![]() ${\mathbf{G}}$
holds.
${\mathbf{G}}$
holds.
Proof. According to [Reference Gille9, Remarque 7.4] we may, without loss of generality, assume that
![]() ${\textrm {char}}(K)=0$
. The Tits index of
${\textrm {char}}(K)=0$
. The Tits index of
![]() ${\mathbf{G}}$
is of the form
${\mathbf{G}}$
is of the form

or

In both cases the semisimple anisotropic kernel
![]() ${\mathbf{H}}$
of
${\mathbf{H}}$
of
![]() ${\mathbf{G}}$
is a strongly inner form of type
${\mathbf{G}}$
is a strongly inner form of type
![]() $\mathrm {E}_6$
. If
$\mathrm {E}_6$
. If
![]() ${\mathbf{S}}\subset {\mathbf{G}}$
is a maximal split torus whose centraliser is
${\mathbf{S}}\subset {\mathbf{G}}$
is a maximal split torus whose centraliser is
![]() ${\mathbf{H}}$
, then arguing as in [Reference Chernousov and Platonov5] one easily verifies that over an algebraic closure of K the intersection
${\mathbf{H}}$
, then arguing as in [Reference Chernousov and Platonov5] one easily verifies that over an algebraic closure of K the intersection
![]() ${\mathbf{S}}\cap {\mathbf{H}}$
is the centre of
${\mathbf{S}}\cap {\mathbf{H}}$
is the centre of
![]() ${\mathbf{H}}$
.
${\mathbf{H}}$
.
Furthermore, by [Reference Gille9, Théorème 7.2], the Kneser–Tits problem has an affirmative answer if and only if
![]() ${\mathbf{G}}(K)/R=1$
. It follows from the Bruhat–Tits decomposition that
${\mathbf{G}}(K)/R=1$
. It follows from the Bruhat–Tits decomposition that
where
![]() $\overline {{\mathbf{H}}}$
is the corresponding adjoint group. It remains to note that by Theorem 7.6, the group
$\overline {{\mathbf{H}}}$
is the corresponding adjoint group. It remains to note that by Theorem 7.6, the group
![]() $\overline {{\mathbf{H}}}$
is R-trivial.
$\overline {{\mathbf{H}}}$
is R-trivial.
8.2. The Tits–Weiss Conjecture
Theorem 8.2. Let A be an Albert algebra defined over an arbitrary field
![]() $K.$
Then the group
$K.$
Then the group
![]() ${\mathbf{Str}}(A)(K)$
is generated by the U-operators
${\mathbf{Str}}(A)(K)$
is generated by the U-operators
![]() $U_a$
with
$U_a$
with
![]() $a\in A^\times $
and the scalar homotheties.
$a\in A^\times $
and the scalar homotheties.
Proof. By the main result of the Appendix, the Tits–Weiss conjecture holds if and only if the Kneser–Tits conjecture holds for groups of type
 $\mathrm {E}_{7,1}^{78}$
and
$\mathrm {E}_{7,1}^{78}$
and
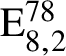 $\mathrm {E}_{8,2}^{78}$
. The result follows.
$\mathrm {E}_{8,2}^{78}$
. The result follows.
Remark 8.3. From this theorem, which we have now established in arbitrary characteristic, the R-triviality of
![]() ${\mathbf{Str}}(A)$
is immediate. Thus, Theorem 7.5 holds in arbitrary characteristic as well.
${\mathbf{Str}}(A)$
is immediate. Thus, Theorem 7.5 holds in arbitrary characteristic as well.
8.3. Properties of the Functor of R-Equivalence Classes for Strongly Inner Forms of Type
 $^1\mathrm {E}_6$
$^1\mathrm {E}_6$
To a reductive K-group
![]() ${\mathbf{G}}$
one can attach the functor of R-equivalence classes
${\mathbf{G}}$
one can attach the functor of R-equivalence classes
where
![]() $Fields/K$
is the category of field extensions of K and
$Fields/K$
is the category of field extensions of K and
![]() $Groups$
is the category of abstract groups. The experts expect that the following conjectures hold:
$Groups$
is the category of abstract groups. The experts expect that the following conjectures hold:
Conjecture 1. The functor
![]() $\mathcal {G}/R$
factors through the subcategory of abelian groups of the category
$\mathcal {G}/R$
factors through the subcategory of abelian groups of the category
![]() $Groups$
; that is, for all field extensions
$Groups$
; that is, for all field extensions
![]() $F/K$
the group
$F/K$
the group
![]() ${\mathbf{G}}(F)/R$
is abelian.
${\mathbf{G}}(F)/R$
is abelian.
Conjecture 2. If F is a finitely generated field over its prime subfield, then
![]() ${\mathbf{G}}(F)/R$
is finite.
${\mathbf{G}}(F)/R$
is finite.
Conjecture 3. The functor
![]() $\mathcal {G}/R$
has transfers; that is, there is a functorial collection of maps
$\mathcal {G}/R$
has transfers; that is, there is a functorial collection of maps
![]() ${\textrm {tr}}^F_K: {\mathbf{G}}(F)/R \to {\mathbf{G}}(K)/R$
for all finite field extensions
${\textrm {tr}}^F_K: {\mathbf{G}}(F)/R \to {\mathbf{G}}(K)/R$
for all finite field extensions
![]() $F/K$
.
$F/K$
.
Furthermore, one expect that the norm principle holds for all semisimple K-groups. Of course, all of these conjectures are obviously true for R-trivial K-groups. In particular, they hold for rational K-groups. For instance, this is the case for groups of type
![]() $\mathrm {G}_2$
. In [Reference Alsaody, Chernousov and Pianzola1] we investigated the case of groups of type
$\mathrm {G}_2$
. In [Reference Alsaody, Chernousov and Pianzola1] we investigated the case of groups of type
![]() $\mathrm {F}_4$
arising from the first Tits construction. Here we consider the next case of simple simply connected strongly inner forms of type
$\mathrm {F}_4$
arising from the first Tits construction. Here we consider the next case of simple simply connected strongly inner forms of type
![]() $\mathrm {E}_6$
.
$\mathrm {E}_6$
.
Theorem 8.4. Let K be an arbitrary field and let
![]() ${\mathbf{G}}$
be a simple simply connected K-group which is a strongly inner form of type
${\mathbf{G}}$
be a simple simply connected K-group which is a strongly inner form of type
![]() $\mathrm {E}_6$
. Then
$\mathrm {E}_6$
. Then
-
(i)
 ${\mathbf{G}}(K)/R$
is an abelian group.
${\mathbf{G}}(K)/R$
is an abelian group. -
(ii) the functor
 $\mathcal {G}/R$
has transfers.
$\mathcal {G}/R$
has transfers. -
(iii) if
 ${\mathbf{Z}}$
is the centre of
${\mathbf{Z}}$
is the centre of
 ${\mathbf{G}}$
, the norm principle holds for
${\mathbf{G}}$
, the norm principle holds for
 $({\mathbf{Z}},{\mathbf{G}})$
.
$({\mathbf{Z}},{\mathbf{G}})$
.
Proof.
-
(i) The group
 ${\mathbf{G}}$
is the derived subgroup of the R-trivial K-group
${\mathbf{G}}$
is the derived subgroup of the R-trivial K-group
 ${\mathbf{Str}}(A)$
for an Albert algebra A. It follows that
${\mathbf{Str}}(A)$
for an Albert algebra A. It follows that
 $[{\mathrm{Str}}(A),{\mathrm{Str}}(A)]\subset R{\mathbf{G}}(K)$
and hence
$[{\mathrm{Str}}(A),{\mathrm{Str}}(A)]\subset R{\mathbf{G}}(K)$
and hence
 ${\mathbf{G}}(K)/R$
is abelian.
${\mathbf{G}}(K)/R$
is abelian. -
(ii) Apply Theorem
 $3.4$
in [Reference Chernousov and Merkurjev4] to
$3.4$
in [Reference Chernousov and Merkurjev4] to
 ${\mathbf{G}}'=R_{F/K}({\mathbf{G}})$
.
${\mathbf{G}}'=R_{F/K}({\mathbf{G}})$
. -
(iii) Since the corresponding adjoint group
 $\overline {\mathbf{G}}$
is R-trivial, the result follows from Theorem 2.5.
$\overline {\mathbf{G}}$
is R-trivial, the result follows from Theorem 2.5.
A. Appendix by Richard M. Weiss
Department of Mathematics
Tufts University
Medford, MA 02155, USA
rweiss@tufts.edu
In this appendix we examine the connection between groups
![]() $G(k)$
with index
$G(k)$
with index

(that is to say,
 $E_{8,2}^{78}$
) and anisotropic exceptional cubic norm structures. Our main goal is show the equivalence of Assertions A.3 and A.4.
$E_{8,2}^{78}$
) and anisotropic exceptional cubic norm structures. Our main goal is show the equivalence of Assertions A.3 and A.4.
Notation A.1. Let k be a field, let G be a semi-simple simply connected algebraic group of absolute type
![]() $E_8$
defined over k such that the index of
$E_8$
defined over k such that the index of
![]() $G(k)$
is
$G(k)$
is
 ${\mathscr I}:=E_{8,2}^{78}$
, let S be a maximal k-split torus of G, let T be a maximal torus containing S and defined over k and let
${\mathscr I}:=E_{8,2}^{78}$
, let S be a maximal k-split torus of G, let T be a maximal torus containing S and defined over k and let
![]() $\Phi $
be the root system of G with respect to T. The nodes of
$\Phi $
be the root system of G with respect to T. The nodes of
![]() ${\mathscr I}$
form a root basis of
${\mathscr I}$
form a root basis of
![]() $\Phi $
. Let
$\Phi $
. Let
![]() $\tilde \alpha $
denote the highest root with respect to this basis.
$\tilde \alpha $
denote the highest root with respect to this basis.
Notation A.2. Let
![]() $\Phi _k$
denote the relative root system of G with respect to S; it is a root system of type
$\Phi _k$
denote the relative root system of G with respect to S; it is a root system of type
![]() $G_2$
. For each
$G_2$
. For each
![]() $\alpha \in \,\Phi _k$
, let
$\alpha \in \,\Phi _k$
, let
![]() $U_{(\alpha )}$
denote the unipotent k-subgroup defined in [Reference Borel and Tits1, Section 5.2]. We call the groups
$U_{(\alpha )}$
denote the unipotent k-subgroup defined in [Reference Borel and Tits1, Section 5.2]. We call the groups
![]() $U_{(\alpha )}$
for
$U_{(\alpha )}$
for
![]() $\alpha \in \,\Phi _k$
the relative root groups of G.
$\alpha \in \,\Phi _k$
the relative root groups of G.
Here now are the two assertions whose equivalence we want to demonstrate.
Assertion A.3.
![]() $G(k)=\langle U_{(\alpha )}(k)\mid \alpha \in \,\Phi _k\rangle $
for all
$G(k)=\langle U_{(\alpha )}(k)\mid \alpha \in \,\Phi _k\rangle $
for all
![]() $G(k)$
as in A.1.
$G(k)$
as in A.1.
Assertion A.4. Let
![]() $\Xi =(J,k,N,\#,T,\times ,1)$
be an exceptional cubic norm structure and suppose that
$\Xi =(J,k,N,\#,T,\times ,1)$
be an exceptional cubic norm structure and suppose that
![]() $\Xi $
is anisotropic. Then the structure group
$\Xi $
is anisotropic. Then the structure group
![]() ${\mathrm{Str}}(\Xi )$
of
${\mathrm{Str}}(\Xi )$
of
![]() $\Xi $
is generated by the set
$\Xi $
is generated by the set
where
![]() $U_a$
is as in [Reference Tits and Weiss4, Section (15.42)].
$U_a$
is as in [Reference Tits and Weiss4, Section (15.42)].
Remark A.5. All anisotropic cubic norm structures arise from one of two constructions of Tits. A proof of this result, due to Racine and Petersson, can be found in [Reference Tits and Weiss4, Chapters 15 and 30 and Section (17.6)].
Let k, G,
![]() ${\mathscr I}$
, S,
${\mathscr I}$
, S,
![]() $\Phi $
and
$\Phi $
and
![]() $\tilde \alpha $
be as in A.1. We begin our demonstration.
$\tilde \alpha $
be as in A.1. We begin our demonstration.
Proposition A.6. The following hold:
-
1. The root group
 $U_{\tilde \alpha }$
of G is defined over k.
$U_{\tilde \alpha }$
of G is defined over k. -
2. The quotient
 $N_{G(k)}(U_{\tilde \alpha }(k))/C_{G(k)}(U_{\tilde \alpha }(k))$
acts freely on the set of nontrivial elements of
$N_{G(k)}(U_{\tilde \alpha }(k))/C_{G(k)}(U_{\tilde \alpha }(k))$
acts freely on the set of nontrivial elements of
 $U_{\tilde \alpha }(k)$
.
$U_{\tilde \alpha }(k)$
.
Proof. The two claims follow from the observation that the root
![]() $\tilde \alpha $
is orthogonal to the subspace spanned by the nodes in the anisotropic part of
$\tilde \alpha $
is orthogonal to the subspace spanned by the nodes in the anisotropic part of
![]() ${\mathscr I}$
.
${\mathscr I}$
.
Remark A.7. Let
![]() $\Phi _k$
and
$\Phi _k$
and
![]() $U_{(\alpha )}$
for
$U_{(\alpha )}$
for
![]() $\alpha \in \Phi _k$
be as in A.2. By A.6(i),
$\alpha \in \Phi _k$
be as in A.2. By A.6(i),
![]() $U_{\tilde \alpha }$
is a relative root group of G for some long root of
$U_{\tilde \alpha }$
is a relative root group of G for some long root of
![]() $\Phi _k$
. Thus, in particular,
$\Phi _k$
. Thus, in particular,
![]() $\dim _kU_{(\alpha )}=1$
for all long roots
$\dim _kU_{(\alpha )}=1$
for all long roots
![]() $\alpha $
of
$\alpha $
of
![]() $\Phi _k$
.
$\Phi _k$
.
Remark A.8. We have
 $$ \begin{align*}\sum_{\alpha\in\Phi_k}\dim_kU_{(\alpha)}=n_8-n_6,\end{align*} $$
$$ \begin{align*}\sum_{\alpha\in\Phi_k}\dim_kU_{(\alpha)}=n_8-n_6,\end{align*} $$
where
![]() $n_\ell $
denotes the cardinality of a root system of type
$n_\ell $
denotes the cardinality of a root system of type
![]() $E_\ell $
for
$E_\ell $
for
![]() $\ell =6$
and 8. It follows that
$\ell =6$
and 8. It follows that
![]() $\dim _kU_{(\alpha )}=27$
for all of the short roots
$\dim _kU_{(\alpha )}=27$
for all of the short roots
![]() $\alpha $
of
$\alpha $
of
![]() $\Phi _k$
.
$\Phi _k$
.
Now let
![]() ${\textrm {BldSc}}(G(k))$
be the spherical building attached to
${\textrm {BldSc}}(G(k))$
be the spherical building attached to
![]() $G(k)$
as described in [Reference Tits and Weiss4, Section 42.3.6] and let X denote the Moufang hexagon associated with
$G(k)$
as described in [Reference Tits and Weiss4, Section 42.3.6] and let X denote the Moufang hexagon associated with
![]() ${\textrm {BldSc}}(G(k))$
. Thus, X is the bipartite graph whose vertices are the nonminimal parabolic subgroups of G defined over k, where two of these parabolic subgroups are adjacent whenever their intersection is also a parabolic subgroup defined over k. Since the cocentre of
${\textrm {BldSc}}(G(k))$
. Thus, X is the bipartite graph whose vertices are the nonminimal parabolic subgroups of G defined over k, where two of these parabolic subgroups are adjacent whenever their intersection is also a parabolic subgroup defined over k. Since the cocentre of
![]() $E_8$
is trivial, the centre of G is trivial. Thus,
$E_8$
is trivial, the centre of G is trivial. Thus,
![]() $G(k)$
acts faithfully on
$G(k)$
acts faithfully on
![]() ${\textrm {BldSc}}(G(k))$
and hence on X. From now on, we identify
${\textrm {BldSc}}(G(k))$
and hence on X. From now on, we identify
![]() $G(k)$
with its image in
$G(k)$
with its image in
![]() ${\mathrm{Aut}}(X)$
. For each
${\mathrm{Aut}}(X)$
. For each
![]() $\alpha \in \Phi _k$
, let
$\alpha \in \Phi _k$
, let
![]() $U_\alpha $
denote the subgroup
$U_\alpha $
denote the subgroup
![]() $U_{(\alpha )}(k)$
of
$U_{(\alpha )}(k)$
of
![]() $G(k)$
.
$G(k)$
.
Let
![]() $\alpha _0,\alpha _1,\ldots ,\alpha _{11}$
be a labelling of the 12 roots in
$\alpha _0,\alpha _1,\ldots ,\alpha _{11}$
be a labelling of the 12 roots in
![]() $\Phi _k$
with subscripts in
$\Phi _k$
with subscripts in
![]() ${\mathbb Z}_{12}$
such that the angle between
${\mathbb Z}_{12}$
such that the angle between
![]() $\alpha _{i-1}$
and
$\alpha _{i-1}$
and
![]() $\alpha _i$
is
$\alpha _i$
is
![]() $\pi /6$
for each i and
$\pi /6$
for each i and
![]() $\alpha _i$
is long if and only if i is even. An apartment of X is a circuit of length
$\alpha _i$
is long if and only if i is even. An apartment of X is a circuit of length
![]() $12$
.
$12$
.
Proposition A.9. There is a unique apartment
![]() $\Sigma $
of X for which there is a labelling
$\Sigma $
of X for which there is a labelling
![]() $x_0,x_1,\ldots ,x_{11}$
of the vertices of
$x_0,x_1,\ldots ,x_{11}$
of the vertices of
![]() $\Sigma $
with subscripts in
$\Sigma $
with subscripts in
![]() ${\mathbb Z}_{12}$
such that for each i,
${\mathbb Z}_{12}$
such that for each i,
![]() $x_{i-1}$
is adjacent to
$x_{i-1}$
is adjacent to
![]() $x_i$
and
$x_i$
and
![]() $U_{\alpha _i}$
is the root group of X corresponding to the root
$U_{\alpha _i}$
is the root group of X corresponding to the root
![]() $(x_i,x_{i+1},\ldots ,x_{i+6})$
of
$(x_i,x_{i+1},\ldots ,x_{i+6})$
of
![]() $\Sigma $
as defined in [Reference Tits and Weiss4, Section (4.1)].
$\Sigma $
as defined in [Reference Tits and Weiss4, Section (4.1)].
Proof. This holds by [Reference Tits and Weiss4, Prop. 42.3.6].
Proposition A.10. Let
![]() $U_i=U_{\alpha _i}$
for each i. Then there exists an anisotropic cubic norm structure
$U_i=U_{\alpha _i}$
for each i. Then there exists an anisotropic cubic norm structure
and isomorphisms
![]() $x_i$
from the additive group of F to
$x_i$
from the additive group of F to
![]() $U_i$
for
$U_i$
for
![]() $i=2$
,
$i=2$
,
![]() $4$
and
$4$
and
![]() $6$
and isomorphisms
$6$
and isomorphisms
![]() $x_i$
from the additive group of J to
$x_i$
from the additive group of J to
![]() $U_i$
for
$U_i$
for
![]() $i=1$
,
$i=1$
,
![]() $3$
and
$3$
and
![]() $5$
such that the commutator relations in [Reference Tits and Weiss4, Section (16.8)] hold and
$5$
such that the commutator relations in [Reference Tits and Weiss4, Section (16.8)] hold and
![]() $[U_i,U_j]=1$
for all index pairs
$[U_i,U_j]=1$
for all index pairs
![]() $(i,j)$
of indices with
$(i,j)$
of indices with
![]() $1\le i<j\le 6$
that do not appear in this list of relations.
$1\le i<j\le 6$
that do not appear in this list of relations.
Proof. This holds by [Reference Tits and Weiss4, Sections (29.1)–(29.35)]. (Note that since
![]() $[U_{(\alpha )},U_{(\beta )}]=1$
for all long roots
$[U_{(\alpha )},U_{(\beta )}]=1$
for all long roots
![]() $\alpha ,\beta $
of
$\alpha ,\beta $
of
![]() $\Phi _k$
at an angle of
$\Phi _k$
at an angle of
![]() $\pi /3$
, the assumption that
$\pi /3$
, the assumption that
![]() $V_i\ne 1$
for all even i at the top of [Reference Tits and Weiss4, page 303] is valid.)
$V_i\ne 1$
for all even i at the top of [Reference Tits and Weiss4, page 303] is valid.)
Remark A.11. By [Reference Tits and Weiss4, Section (7.5)], X is uniquely determined by
![]() $\Xi $
. We can thus set
$\Xi $
. We can thus set
![]() $X={\mathscr H}(\Xi )$
as in [Reference Tits and Weiss4, Section 16.8]. By [Reference Tits and Weiss4, Section (35.13)],
$X={\mathscr H}(\Xi )$
as in [Reference Tits and Weiss4, Section 16.8]. By [Reference Tits and Weiss4, Section (35.13)],
![]() ${\mathscr H}(\Xi )\cong {\mathscr H}(\Xi ')$
for two anisotropic cubic norm structures
${\mathscr H}(\Xi )\cong {\mathscr H}(\Xi ')$
for two anisotropic cubic norm structures
![]() $\Xi $
and
$\Xi $
and
![]() $\Xi '$
if and only if
$\Xi '$
if and only if
![]() $\Xi $
and
$\Xi $
and
![]() $\Xi '$
are isotopes of each other.
$\Xi '$
are isotopes of each other.
Notation A.12. Let
![]() $G_0={\mathrm{Aut}}(X)$
, let
$G_0={\mathrm{Aut}}(X)$
, let
![]() $H_0$
denote the pointwise stabiliser of
$H_0$
denote the pointwise stabiliser of
![]() $\Sigma $
in
$\Sigma $
in
![]() $G_0$
, let
$G_0$
, let
 $G_0^\dagger =\langle U_i\mid i\in {\mathbb Z}_{12}\rangle $
, let
$G_0^\dagger =\langle U_i\mid i\in {\mathbb Z}_{12}\rangle $
, let
 $H_0^\dagger =G_0^\dagger \cap H_0$
and let
$H_0^\dagger =G_0^\dagger \cap H_0$
and let
![]() $J=G(k)\cap H_0$
.
$J=G(k)\cap H_0$
.
Since
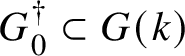 $G_0^\dagger \subset G(k)$
, we have
$G_0^\dagger \subset G(k)$
, we have
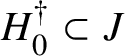 $H_0^\dagger \subset J$
. In fact, we have the following.
$H_0^\dagger \subset J$
. In fact, we have the following.
Proposition A.13.
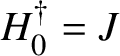 $H_0^\dagger =J$
if and only if
$H_0^\dagger =J$
if and only if
 $G(k)=G_0^\dagger $
.
$G(k)=G_0^\dagger $
.
Proof. Suppose that
 $H_0^\dagger =J$
and let
$H_0^\dagger =J$
and let
![]() $g\in G(k)$
. By [Reference Tits and Weiss4, Section (4.12)], there exists
$g\in G(k)$
. By [Reference Tits and Weiss4, Section (4.12)], there exists
 $a\in G_0^\dagger $
such that
$a\in G_0^\dagger $
such that
![]() $ga$
fixes both
$ga$
fixes both
![]() $\Sigma $
and the edge
$\Sigma $
and the edge
![]() $\{x_0,x_1\}$
. Hence,
$\{x_0,x_1\}$
. Hence,
![]() $ga\in H_0$
. Since
$ga\in H_0$
. Since
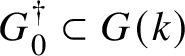 $G_0^\dagger \subset G(k)$
, it follows that
$G_0^\dagger \subset G(k)$
, it follows that
![]() $ga\in J$
. Hence,
$ga\in J$
. Hence,
 $ga\in H_0^\dagger $
and thus
$ga\in H_0^\dagger $
and thus
 $g\in G_0^\dagger $
. Therefore,
$g\in G_0^\dagger $
. Therefore,
 $G(k)=G_0^\dagger $
.
$G(k)=G_0^\dagger $
.
Proposition A.14. Let
![]() $X_i=\langle \mu _i(a)\mu _i(b)\mid a,b\in U_i^*\rangle $
for
$X_i=\langle \mu _i(a)\mu _i(b)\mid a,b\in U_i^*\rangle $
for
![]() $i=1$
and
$i=1$
and
![]() $6$
, where
$6$
, where
![]() $\mu _i$
is as defined in [Reference Tits and Weiss4, Section (6.1)]. Then
$\mu _i$
is as defined in [Reference Tits and Weiss4, Section (6.1)]. Then
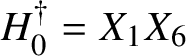 $H_0^\dagger =X_1X_6$
.
$H_0^\dagger =X_1X_6$
.
Proof. This holds by [Reference Tits and Weiss4, Section (33.9)].
Proposition A.15. The image of
![]() $H_0^\dagger $
in
$H_0^\dagger $
in
![]() ${\mathrm{Aut}}(U_6)$
is
${\mathrm{Aut}}(U_6)$
is
![]() $\{x_6(t)\mapsto x_6(st)\mid s\in F^*\}$
, where
$\{x_6(t)\mapsto x_6(st)\mid s\in F^*\}$
, where
![]() $x_6$
is as in A.10. In particular, the derived group of
$x_6$
is as in A.10. In particular, the derived group of
![]() $H^\dagger _0$
centralises
$H^\dagger _0$
centralises
![]() $U_6$
.
$U_6$
.
Proof. This holds by [Reference Tits and Weiss4, Section (33.16)].
Proposition A.16. The groups J and
![]() $H_0^\dagger $
have the same image in
$H_0^\dagger $
have the same image in
![]() ${\mathrm{Aut}}(U_6)$
.
${\mathrm{Aut}}(U_6)$
.
Proof. By A.15,
![]() $H_0^\dagger $
acts transitively on
$H_0^\dagger $
acts transitively on
![]() $U_6^*$
. By A.6(ii) and A.7, the image of J in
$U_6^*$
. By A.6(ii) and A.7, the image of J in
![]() ${\mathrm{Aut}}(U_6)$
acts freely on
${\mathrm{Aut}}(U_6)$
acts freely on
![]() $U_6^*$
. Since
$U_6^*$
. Since
 $H_0^\dagger \subset J$
, the claim follows.
$H_0^\dagger \subset J$
, the claim follows.
Proposition A.17.
 $H_0^\dagger =J$
if and only if
$H_0^\dagger =J$
if and only if
 $C_J(U_6)=C_{H_0^\dagger }(U_6)$
.
$C_J(U_6)=C_{H_0^\dagger }(U_6)$
.
Proof. Suppose that
 $C_J(U_6)=C_{H_0^\dagger }(U_6)$
and let
$C_J(U_6)=C_{H_0^\dagger }(U_6)$
and let
![]() $g\in J$
. By A.16, there exists
$g\in J$
. By A.16, there exists
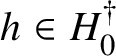 $h\in H_0^\dagger $
such that
$h\in H_0^\dagger $
such that
![]() $gh\in C_J(U_6)$
. Hence,
$gh\in C_J(U_6)$
. Hence,
 $gh\in H_0^\dagger $
and thus
$gh\in H_0^\dagger $
and thus
 $g\in H_0^\dagger $
. Therefore,
$g\in H_0^\dagger $
. Therefore,
 $H_0^\dagger =J$
.
$H_0^\dagger =J$
.
Proposition A.18.
![]() $C_{H_0}(U_6)$
acts faithfully on
$C_{H_0}(U_6)$
acts faithfully on
![]() $U_1$
.
$U_1$
.
Proof. This holds by [Reference Tits and Weiss4, Section (33.5)].
Notation A.19. Let H be the anisotropic kernel of G. Thus, H is the derived group of the centraliser
![]() $C(S)$
.
$C(S)$
.
Proposition A.20.
![]() $H(k)\subset C_J(U_6)$
.
$H(k)\subset C_J(U_6)$
.
Proof. The fixed point set of
![]() $S(k)$
in X is the apartment
$S(k)$
in X is the apartment
![]() $\Sigma $
. Hence,
$\Sigma $
. Hence,
![]() $C(S)(k)\subset J$
. By A.15 and A.16, it follows that
$C(S)(k)\subset J$
. By A.15 and A.16, it follows that
![]() $H(k)\subset C_J(U_6)$
.
$H(k)\subset C_J(U_6)$
.
Proposition A.21.
![]() $F\cong k$
and
$F\cong k$
and
![]() $\dim _FJ=27$
, where F is as in A.10.
$\dim _FJ=27$
, where F is as in A.10.
Proof. We give
![]() $U_1$
the structure of a vector space over F by setting
$U_1$
the structure of a vector space over F by setting
![]() $t\cdot x_1(a)=x_1(ta)$
for all
$t\cdot x_1(a)=x_1(ta)$
for all
![]() $t\in F$
and all
$t\in F$
and all
![]() $a\in J$
. Let
$a\in J$
. Let
![]() $X_6$
be as in A.14. By [Reference Tits and Weiss4, Section (29.20)], the image of
$X_6$
be as in A.14. By [Reference Tits and Weiss4, Section (29.20)], the image of
![]() $X_6$
in
$X_6$
in
![]() ${\mathrm{Aut}}(U_1)$
is
${\mathrm{Aut}}(U_1)$
is
![]() $\{x_1(a)\mapsto t\cdot x_1(a)\mid t\in F^*\}$
. The root groups
$\{x_1(a)\mapsto t\cdot x_1(a)\mid t\in F^*\}$
. The root groups
![]() $U_{\alpha _0}$
and
$U_{\alpha _0}$
and
![]() $U_{\alpha _6}$
of G are opposite and
$U_{\alpha _6}$
of G are opposite and
![]() $X_6=\langle U_0,U_6\rangle \cap S(k)$
. It follows that there exists an isomorphism
$X_6=\langle U_0,U_6\rangle \cap S(k)$
. It follows that there exists an isomorphism
![]() $\psi $
from k to F such that
$\psi $
from k to F such that
![]() $tu=\psi (t)\cdot u$
for all
$tu=\psi (t)\cdot u$
for all
![]() $t\in k$
and all
$t\in k$
and all
![]() $u\in U_1$
. Hence,
$u\in U_1$
. Hence,
![]() $\dim _FJ=\dim _FU_1=27$
by A.8.
$\dim _FJ=\dim _FU_1=27$
by A.8.
Proposition A.22. There is an isomorphism
![]() $\varphi $
from
$\varphi $
from
![]() $C_J(U_6)$
to
$C_J(U_6)$
to
![]() ${\mathrm{Str}}(\Xi )$
and
${\mathrm{Str}}(\Xi )$
and
![]() $\Xi $
is exceptional.
$\Xi $
is exceptional.
Proof. By A.18 and the equation in the third display in [Reference Tits and Weiss4, Section (37.41)], there exists an isomorphism
![]() $\varphi $
from
$\varphi $
from
![]() $C_{H_0}(U_6)$
to
$C_{H_0}(U_6)$
to
![]() ${\mathrm{Str}}(\Xi )$
such that
${\mathrm{Str}}(\Xi )$
such that
![]() $x_1(a)^h=x_1(a^{\varphi (h)})$
for all
$x_1(a)^h=x_1(a^{\varphi (h)})$
for all
![]() $a\in J$
and by A.20, we have
$a\in J$
and by A.20, we have
![]() $H(k)\subset C_J(U_6)\subset C_{H_0}(U_6)$
. By A.21, it follows that
$H(k)\subset C_J(U_6)\subset C_{H_0}(U_6)$
. By A.21, it follows that
![]() $\Xi $
is the Jordan k-algebra in [Reference Tits and Weiss4, Sections 42.5.6(d) and 42.6, Type (8)]. Hence,
$\Xi $
is the Jordan k-algebra in [Reference Tits and Weiss4, Sections 42.5.6(d) and 42.6, Type (8)]. Hence,
![]() $\Xi $
is exceptional and
$\Xi $
is exceptional and
![]() $\varphi $
maps
$\varphi $
maps
![]() $H(k)$
to
$H(k)$
to
![]() ${\mathrm{Str}}(\Xi )$
surjectively. (See also the remarks that follow [Reference Tits3, Section 3.3.1].) It follows that
${\mathrm{Str}}(\Xi )$
surjectively. (See also the remarks that follow [Reference Tits3, Section 3.3.1].) It follows that
![]() $H(k)=C_J(U_6)=C_{H_0}(U_6)$
.
$H(k)=C_J(U_6)=C_{H_0}(U_6)$
.
Proposition A.23.
 $\varphi (C_{H_0^\dagger }(U_6))$
is the subgroup of
$\varphi (C_{H_0^\dagger }(U_6))$
is the subgroup of
![]() ${\mathrm{Str}}(\Xi )$
generated by the set defined in (9), where
${\mathrm{Str}}(\Xi )$
generated by the set defined in (9), where
![]() $\varphi $
is as in A.22.
$\varphi $
is as in A.22.
Proof. This holds by [Reference Tits and Weiss4, Section (33.16)].
Proposition A.24. Every anisotropic exceptional cubic norm structure arises from an application of A.10 to the Moufang hexagon attached to a group
![]() $G(k)$
for some G and some k satisfying the conditions in A.1.
$G(k)$
for some G and some k satisfying the conditions in A.1.
Proof. This holds by [Reference Tits and Weiss4, Section 42.6, Type (8)].
Proof. By A.13 and A.17,
 $G(k)=G_0^\dagger $
if and only if
$G(k)=G_0^\dagger $
if and only if
 $C_{H_0^\dagger }(U_6)=C_J(U_6)$
. By A.22 and A.23,
$C_{H_0^\dagger }(U_6)=C_J(U_6)$
. By A.22 and A.23,
 $C_{H_0^\dagger }(U_6)=C_J(U_6)$
if and only if
$C_{H_0^\dagger }(U_6)=C_J(U_6)$
if and only if
![]() ${\mathrm{Str}}(\Xi )$
is generated by the set defined in (9). The claim holds, therefore, by A.24.
${\mathrm{Str}}(\Xi )$
is generated by the set defined in (9). The claim holds, therefore, by A.24.
Remark A.26. In [Reference Thakur2, Thm. 6.1], Thakur showed that A.3 holds in the case that the cubic norm structure in A.10 is a first Tits construction and in [Reference Thakur2, Thm. 7.2], he showed that the claim in A.4 holds for
![]() $\Xi $
a reduced (rather than anisotropic) exceptional cubic norm structures.
$\Xi $
a reduced (rather than anisotropic) exceptional cubic norm structures.
Acknowledgments
We are grateful to F. Morel, H. Petersson, A. Stavrova and R. Weiss for fruitful discussions and comments. During the preparation of the article, the second author visited the University of Munich; their hospitality and the support of the Alexander von Humboldt Foundation are gratefully acknowledged. S. Alsaody thanks PIMS for their financial support and the Department of Mathematical and Statistical Sciences at the University of Alberta, where he was affiliated during the preparation of the article. V. Chernousov was partially supported by the Alexander von Humboldt Foundation and an NSERC research grant. A. Pianzola thanks NSERC and CONICET for their continuous support.
Conflicts of interest
None.