Article contents
LONG TIME BEHAVIOR OF THE SOLUTIONS OF NLW ON THE 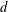 $d$-DIMENSIONAL TORUS
$d$-DIMENSIONAL TORUS
Published online by Cambridge University Press: 06 March 2020
Abstract
We consider the nonlinear wave equation (NLW) on the 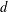 $d$-dimensional torus
$d$-dimensional torus 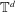 $\mathbb{T}^{d}$ with a smooth nonlinearity of order at least 2 at the origin. We prove that, for almost any mass, small and smooth solutions of high Sobolev indices are stable up to arbitrary long times with respect to the size of the initial data. To prove this result, we use a normal form transformation decomposing the dynamics into low and high frequencies with weak interactions. While the low part of the dynamics can be put under classical Birkhoff normal form, the high modes evolve according to a time-dependent linear Hamiltonian system. We then control the global dynamics by using polynomial growth estimates for high modes and the preservation of Sobolev norms for the low modes. Our general strategy applies to any semilinear Hamiltonian Partial Differential Equations (PDEs) whose linear frequencies satisfy a very general nonresonance condition. The (NLW) equation on
$\mathbb{T}^{d}$ with a smooth nonlinearity of order at least 2 at the origin. We prove that, for almost any mass, small and smooth solutions of high Sobolev indices are stable up to arbitrary long times with respect to the size of the initial data. To prove this result, we use a normal form transformation decomposing the dynamics into low and high frequencies with weak interactions. While the low part of the dynamics can be put under classical Birkhoff normal form, the high modes evolve according to a time-dependent linear Hamiltonian system. We then control the global dynamics by using polynomial growth estimates for high modes and the preservation of Sobolev norms for the low modes. Our general strategy applies to any semilinear Hamiltonian Partial Differential Equations (PDEs) whose linear frequencies satisfy a very general nonresonance condition. The (NLW) equation on 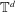 $\mathbb{T}^{d}$ is a good example since the standard Birkhoff normal form applies only when
$\mathbb{T}^{d}$ is a good example since the standard Birkhoff normal form applies only when 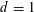 $d=1$ while our strategy applies in any dimension.
$d=1$ while our strategy applies in any dimension.
MSC classification
- Type
- Mathematical Physics
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author(s) 2020
References
- 15
- Cited by


