Hostname: page-component-8448b6f56d-gtxcr Total loading time: 0 Render date: 2024-04-16T06:32:22.869Z Has data issue: false hasContentIssue false
  • English
  • Français

CODIMENSION TWO CYCLES IN IWASAWA THEORY AND ELLIPTIC CURVES WITH SUPERSINGULAR REDUCTION

Part of: Arithmetic algebraic geometry Algebraic number theory: global fields Algebraic number theory: local and $p$-adic fields

Published online by Cambridge University Press:  13 August 2019

ANTONIO LEI Open the ORCID record for ANTONIO LEI [Opens in a new window]  and
BHARATHWAJ PALVANNAN
ANTONIO LEI
Affiliation:
Département de mathématiques et de statistique, Université Laval, Pavillon Alexandre-Vachon, 1045 avenue de la Médecine, Québec, Canada, G1V 0A6; antonio.lei@mat.ulaval.ca
BHARATHWAJ PALVANNAN
Affiliation:
Department of Mathematics, University of Pennsylvania, 4W1 DRL, 209 South 33rd Street, Philadelphia, 19104-6395, USA; pbharath@math.upenn.edu

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A result of Bleher, Chinburg, Greenberg, Kakde, Pappas, Sharifi and Taylor has initiated the topic of higher codimension Iwasawa theory. As a generalization of the classical Iwasawa main conjecture, they prove a relationship between analytic objects (a pair of Katz’s 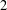$2$-variable 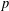$p$-adic 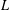$L$-functions) and algebraic objects (two ‘everywhere unramified’ Iwasawa modules) involving codimension two cycles in a 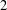$2$-variable Iwasawa algebra. We prove a result by considering the restriction to an imaginary quadratic field 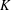$K$ (where an odd prime 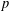$p$ splits) of an elliptic curve 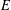$E$, defined over 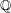$\mathbb{Q}$, with good supersingular reduction at 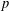$p$. 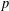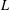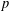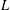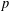On the analytic side, we consider eight pairs of $2$-variable $p$-adic $L$-functions in this setup (four of the $2$-variable $p$-adic $L$-functions have been constructed by Loeffler and a fifth $2$-variable $p$-adic 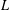$L$-function is due to Hida). On the algebraic side, we consider modifications of fine Selmer groups over the 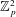$\mathbb{Z}_{p}^{2}$-extension of 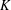$K$. We also provide numerical evidence, using algorithms of Pollack, towards a pseudonullity conjecture of Coates–Sujatha.

MSC classification

Primary: 11R23: Iwasawa theory
Secondary: 11G05: Elliptic curves over global fields 11G07: Elliptic curves over local fields 11R34: Galois cohomology 11S25: Galois cohomology
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 7 , 2019 , e25
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2019

References

Amice, Y. and Vélu, J., ‘Distributions p-adiques associées aux séries de Hecke’, Astérisque 24–25 (1975), 119–131.Google Scholar
Atiyah, M. F. and Macdonald, I. G., Introduction to Commutative Algebra (Addison-Wesley Publishing Co., Reading, Mass.-London-Don Mills, Ont., 1969).Google Scholar
Bleher, F., Chinburg, T., Greenberg, R., Kakde, M., Pappas, G., Sharifi, R. and Taylor, M., ‘Higher Chern classes in Iwasawa theory’, Amer. J. Math., 2019, to appear, available atarXiv:1512.00273.Google Scholar
Bruns, W. and Herzog, J., Cohen–Macaulay Rings, Cambridge Studies in Advanced Mathematics, 39 (Cambridge University Press, Cambridge, 1993).Google Scholar
Büyükboduk, K. and Lei, A., ‘Functional equation for $p$ -adic Rankin–Selberg $L$ -functions’, Ann. Math. Qué., 2019, to appear, available at doi:10.1007/s40316-019-00117-2.Google Scholar
Büyükboduk, K. and Lei, A., ‘Iwasawa theory of elliptic modular forms over imaginary quadratic fields at non-ordinary primes’, Int. Math. Res. Not. IMRN, 2019, to appear, available at arXiv:1605.05310.Google Scholar
Castella, F., Çiperiani, M., Skinner, C. and Sprung, F., ‘On the Iwasawa main conjectures for modular forms at non-ordinary primes’, Preprint, 2018, arXiv:1804.10993.Google Scholar
Castella, F. and Wan, X., ‘Perrin-Riou’s main conjecture for elliptic curves at supersingular primes’, Preprint, 2018, arXiv:1607.02019.Google Scholar
Coates, J. and Greenberg, R., ‘Kummer theory for abelian varieties over local fields’, Invent. Math. 124(1) (1996), 129–174.Google Scholar
Coates, J. and Sujatha, R., ‘Fine Selmer groups of elliptic curves over p-adic Lie extensions’, Math. Ann. 331(4) (2005), 809–839.Google Scholar
Coleman, R. F. and Edixhoven, B., ‘On the semi-simplicity of the U p-operator on modular forms’, Math. Ann. 310(1) (1998), 119–127.Google Scholar
Dion, C. and Lei, A., ‘Plus and minus logarithms and Amice transform’, C. R. Math. Acad. Sci. Paris 355(9) (2017), 942–948.Google Scholar
Edixhoven, B., ‘The weight in Serre’s conjectures on modular forms’, Invent. Math. 109(3) (1992), 563–594.Google Scholar
Greenberg, R., ‘Iwasawa theory and p-adic deformations of motives’, inMotives (Seattle, WA, 1991), Proc. Sympos. Pure Math., 55 (American Mathematical Society, Providence, RI, 1994), 193–223.Google Scholar
Greenberg, R., ‘Iwasawa theory—past and present’, inClass Field Theory—its Centenary and Prospect (Tokyo, 1998), Adv. Stud. Pure Math., 30 (Mathematical Society of Japan, Tokyo, 2001), 335–385.Google Scholar
Greenberg, R., ‘On the structure of certain Galois cohomology groups’, Doc. Math. Extra Vol. (2006), 335–391 (electronic).Google Scholar
Greenberg, R., ‘Surjectivity of the global-to-local map defining a Selmer group’, Kyoto J. Math. 50(4) (2010), 853–888.Google Scholar
Greenberg, R., ‘On the structure of Selmer groups’, inElliptic Curves, Modular Forms and Iwasawa Theory: In Honour of John H. Coates’ 70th Birthday, Cambridge, UK, March 2015 (Springer International Publishing, Switzerland, 2016), 225–252.Google Scholar
Greenberg, R. and Stevens, G., ‘On the conjecture of Mazur, Tate, and Teitelbaum’, in p-adic Monodromy and the Birch and Swinnerton-Dyer Conjecture (Boston, MA, 1991), Contemp. Math., 165 (American Mathematical Society, Providence, RI, 1994), 183–211.Google Scholar
Hartshorne, R., Residues and Duality, Lecture Notes in Mathematics, 20 (Springer, New York, 1966). Lecture notes of a seminar on the work of A. Grothendieck, given at Harvard 1963/64. With an appendix by P. Deligne.Google Scholar
Hida, H., ‘On p-adic L-functions of GL(2) × GL(2) over totally real fields’, Ann. Inst. Fourier (Grenoble) 41(2) (1991), 311–391.Google Scholar
Hida, H., ‘On the search of genuine p-adic modular L-functions for GL(n)’, Mém. Soc. Math. Fr. (N.S.) (67) (1996), vi+110, With a correction to: ‘On $p$ -adic $L$ -functions of $\text{GL}(2)\times \text{GL}(2)$ over totally real fields’ [Ann. Inst. Fourier (Grenoble) 41(2) (1991), 311–391].Google Scholar
Iwasawa, K., ‘On Z l-extensions of algebraic number fields’, Ann. of Math. (2) 98 (1973), 246–326.Google Scholar
Jannsen, U., ‘Iwasawa modules up to isomorphism’, inAlgebraic Number Theory, Adv. Stud. Pure Math., 17 (Academic Press, Boston, MA, 1989), 171–207.Google Scholar
Jannsen, U., ‘A spectral sequence for Iwasawa adjoints’, Münster J. Math. 7(1) (2014), 135–148.Google Scholar
Kim, B. D., ‘Signed-Selmer groups over the ℤp 2 -extension of an imaginary quadratic field’, Canad. J. Math. 66(4) (2014), 826–843.Google Scholar
Kobayashi, S., ‘Iwasawa theory for elliptic curves at supersingular primes’, Invent. Math. 152(1) (2003), 1–36.Google Scholar
Kurihara, M. and Pollack, R., ‘Two p-adic L-functions and rational points on elliptic curves with supersingular reduction’, in L-functions and Galois Representations, London Mathematical Society, Lecture Note Series, 320 (Cambridge University Press, Cambridge, 2007), 300–332.Google Scholar
Lei, A., ‘Factorisation of two-variable p-adic L-functions’, Canad. Math. Bull. 57(4) (2014), 845–852.Google Scholar
Lei, A. and Palvannan, B., ‘Codimension two cycles in Iwasawa theory and tensor product of Hida families’. Preprint, 2019, arXiv:1901.09301.Google Scholar
Lim, M. F., ‘On the pseudo-nullity of the dual fine Selmer groups’, Int. J. Number Theory 11(7) (2015), 2055–2063.Google Scholar
Loeffler, D., ‘ p-adic integration on ray class groups and non-ordinary p-adic L-functions’, inIwasawa theory 2012, Contrib. Math. Comput. Sci., 7 (Springer, Heidelberg, 2014), 357–378.Google Scholar
Loeffler, D. and Zerbes, S. L., ‘Iwasawa theory and p-adic L-functions over ℤp 2 -extensions’, Int. J. Number Theory 10(8) (2014), 2045–2095.Google Scholar
Loeffler, D. and Zerbes, S. L., ‘Rankin–Eisenstein classes in Coleman families’, Res. Math. Sci. 3 (2016), Paper No. 29, 53.Google Scholar
Longo, M. and Vigni, S., ‘Plus/minus Heegner points and Iwasawa theory of elliptic curves at supersingular primes’, Boll. Unione Mat. Ital., 2018, to appear, available at doi:10.1007/s40574-018-0162-4.Google Scholar
Matsumura, H., Commutative Ring Theory, 2nd edn, Cambridge Studies in Advanced Mathematics, 8 (Cambridge University Press, Cambridge, 1989). Translated from the Japanese by M. Reid.Google Scholar
Nekovář, J., ‘Selmer complexes’, Astérisque (310) (2006), viii+559.Google Scholar
Neukirch, J., Schmidt, A. and Wingberg, K., Cohomology of Number Fields, 2nd edn, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], 323 (Springer, Berlin, 2008).Google Scholar
Ochi, Y., ‘A remark on the pseudo-nullity conjecture for fine Selmer groups of elliptic curves’, Comment. Math. Univ. St. Pauli 58(1) (2009), 1–7.Google Scholar
Palvannan, B., ‘On Selmer groups and factoring p -adic L -functions’, Int. Math. Res. Not. IMRN 2018(24) (2018), 7483–7554, 05.Google Scholar
Palvannan, B., ‘Height one specializations of selmer groups’, Ann. Inst. Fourier (Grenoble) 69(1) (2019), 303–334.Google Scholar
Perrin-Riou, B., ‘Théorie d’Iwasawa p-adique locale et globale’, Invent. Math. 99(2) (1990), 247–292.Google Scholar
Perrin-Riou, B., ‘Théorie d’Iwasawa des représentations p-adiques sur un corps local’, Invent. Math. 115(1) (1994), 81–161. With an appendix by Jean-Marc Fontaine.Google Scholar
Pollack, R., ‘On the p-adic L-function of a modular form at a supersingular prime’, Duke Math. J. 118(3) (2003), 523–558.Google Scholar
Pollack, R. and Rubin, K., ‘The main conjecture for CM elliptic curves at supersingular primes’, Ann. of Math. (2) 159(1) (2004), 447–464.Google Scholar
Pollack, R. and Stevens, G., ‘Overconvergent modular symbols and p-adic L-functions’, Ann. Sci. Éc. Norm. Supér. (4) 44(1) (2011), 1–42.Google Scholar
Rubin, K., ‘Elliptic curves and Z p-extensions’, Compos. Math. 56(2) (1985), 237–250.Google Scholar
Rubin, K., ‘Local units, elliptic units, Heegner points and elliptic curves’, Invent. Math. 88(2) (1987), 405–422.Google Scholar
Serre, J.-P., Abelian l-adic Representations and Elliptic Curves (W. A. Benjamin, Inc., New York-Amsterdam, 1968). McGill University lecture notes written with the collaboration of Willem Kuyk and John Labute.Google Scholar
Shekhar, S., ‘Comparing the corank of fine Selmer group and Selmer group of elliptic curves’, J. Ramanujan Math. Soc. 33(2) (2018), 205–217.Google Scholar
Shimura, G., ‘On the periods of modular forms’, Math. Ann. 229(3) (1977), 211–221.Google Scholar
Silverman, J. H., The Arithmetic of Elliptic Curves, Graduate Texts in Mathematics, 106 (Springer, New York, 1986).Google Scholar
Silverman, J. H., Advanced Topics in the Arithmetic of Elliptic Curves, Graduate Texts in Mathematics, 151 (Springer, New York, 1994).Google Scholar
Skinner, C. and Urban, E., ‘The Iwasawa main conjectures for GL2 ’, Invent. Math. 195(1) (2014), 1–277.Google Scholar
Skinner, C. and Zhang, W., ‘Indivisibility of Heegner points in the multiplicative case’, Preprint, 2014, arXiv:1407.1099.Google Scholar
Sprung, F., ‘The Iwasawa Main Conjecture for elliptic curves at odd supersingular primes’, Preprint, 2016, arXiv:1610.10017.Google Scholar
Stevens, G., ‘Rigid analytic modular symbols’, Preprint, 1994.Google Scholar
Tate, J., Algorithm for Determining the Type of a Singular Fiber in an Elliptic Pencil, Lecture Notes in Mathematics, 476 (Springer, Berlin, 1975), 33–52.Google Scholar
The Sage Developers. SageMath, the Sage Mathematics Software System (Version 7.2), 2016, http://www.sagemath.org.Google Scholar
Višik, M. M., ‘Nonarchimedean measures associated with Dirichlet series’, Mat. Sb. (N.S.) 99(141(2)) (1976), 248–260, 296.Google Scholar
Wan, X., ‘Iwasawa main conjecture for non-ordinary modular forms’, Preprint, 2016,arXiv:1607.07729.Google Scholar
Wan., X., ‘Iwasawa main conjecture for supersingular elliptic curves’, Preprint, 2016,arXiv:1411.6352v4.Google Scholar
Weibel, C. A., An Introduction to Homological Algebra, Cambridge Studies in Advanced Mathematics, 38 (Cambridge University Press, Cambridge, 1994).Google Scholar