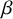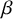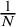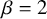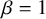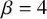1. Introduction
This paper is concerned with the asymptotic expansion for the partition function and the multilinear statistics of
![]() $\beta $
matrix models. These laws represent a generalisation of the joint distribution of the N eigenvalues of the Gaussian Unitary Ensemble [Reference MehtaMeh04]. The convergence of the empirical measure of the eigenvalues is well known (see, for example, [Reference Boutet de Monvel, Pastur and ShcherbinadMPS95]), and we are interested in the all-order finite size corrections to the moments of this empirical measure. Much attention has been paid to this problem in the regime when the eigenvalues condense on a single segment, usually referred to as a one-cut regime. In this case, a central limit theorem for linear statistics was proved by Johansson [Reference JohanssonJoh98], while a full
$\beta $
matrix models. These laws represent a generalisation of the joint distribution of the N eigenvalues of the Gaussian Unitary Ensemble [Reference MehtaMeh04]. The convergence of the empirical measure of the eigenvalues is well known (see, for example, [Reference Boutet de Monvel, Pastur and ShcherbinadMPS95]), and we are interested in the all-order finite size corrections to the moments of this empirical measure. Much attention has been paid to this problem in the regime when the eigenvalues condense on a single segment, usually referred to as a one-cut regime. In this case, a central limit theorem for linear statistics was proved by Johansson [Reference JohanssonJoh98], while a full
![]() $\frac {1}{N}$
expansion was derived first for
$\frac {1}{N}$
expansion was derived first for
![]() $\beta = 2$
[Reference Albeverio, Pastur and ShcherbinaAPS01, Reference Ercolani and McLaughlinEM03, Reference Bleher and ItsBI05] and then for any
$\beta = 2$
[Reference Albeverio, Pastur and ShcherbinaAPS01, Reference Ercolani and McLaughlinEM03, Reference Bleher and ItsBI05] and then for any
![]() $\beta> 0$
in [Reference Borot and GuionnetBG11]. However, the multi-cut regime was, until recently, poorly understood at the rigorous level, except for
$\beta> 0$
in [Reference Borot and GuionnetBG11]. However, the multi-cut regime was, until recently, poorly understood at the rigorous level, except for
![]() $\beta = 2$
, which is related to integrable systems and can be treated with the powerful asymptotic analysis techniques for Riemann–Hilbert problems; see, for example, [Reference Deift, Kriecherbauer, McLaughlin, Venakides and ZhouDKM+99b]. Nevertheless, a heuristic derivation of the asymptotic expansion for the multi-cut regime has been proposed to leading order by Bonnet, David and Eynard [Reference Bonnet, David and EynardBDE00] and extended to all orders in [Reference EynardEyn09], in terms of Theta functions and their derivatives. It features oscillatory behaviour, whose origin lies in the tunneling of eigenvalues between the different connected components of the support. This heuristic, originally written for
$\beta = 2$
, which is related to integrable systems and can be treated with the powerful asymptotic analysis techniques for Riemann–Hilbert problems; see, for example, [Reference Deift, Kriecherbauer, McLaughlin, Venakides and ZhouDKM+99b]. Nevertheless, a heuristic derivation of the asymptotic expansion for the multi-cut regime has been proposed to leading order by Bonnet, David and Eynard [Reference Bonnet, David and EynardBDE00] and extended to all orders in [Reference EynardEyn09], in terms of Theta functions and their derivatives. It features oscillatory behaviour, whose origin lies in the tunneling of eigenvalues between the different connected components of the support. This heuristic, originally written for
![]() $\beta = 2$
, can be trivially extended to
$\beta = 2$
, can be trivially extended to
![]() $\beta> 0$
; see, for example, [Reference BorotBor11].
$\beta> 0$
; see, for example, [Reference BorotBor11].
More recently, M. Shcherbina has established this asymptotic expansion up to terms of order
![]() $1$
[Reference ShcherbinaShc11, Reference ShcherbinaShc12]. This allows us to observe, for instance, that linear statistics do not always satisfy a central limit theorem (this fact was already noticed for
$1$
[Reference ShcherbinaShc11, Reference ShcherbinaShc12]. This allows us to observe, for instance, that linear statistics do not always satisfy a central limit theorem (this fact was already noticed for
![]() $\beta = 2$
in [Reference PasturPas06]). In this work, we go beyond the
$\beta = 2$
in [Reference PasturPas06]). In this work, we go beyond the
![]() $O(1)$
and put the heuristics of [Reference EynardEyn09] to all orders on a firm mathematical ground. Our strategy is to first study the asymptotics in the model with fixed filling fractions and then reconstruct the asymptotics in the original model via a finite-dimensional analysis. As a consequence, we obtain a replacement for the central limit theorem for linear statistics and for filling fractions. Besides, we treat uniformly soft and hard edges, while [Reference ShcherbinaShc12] assumed soft edges.
$O(1)$
and put the heuristics of [Reference EynardEyn09] to all orders on a firm mathematical ground. Our strategy is to first study the asymptotics in the model with fixed filling fractions and then reconstruct the asymptotics in the original model via a finite-dimensional analysis. As a consequence, we obtain a replacement for the central limit theorem for linear statistics and for filling fractions. Besides, we treat uniformly soft and hard edges, while [Reference ShcherbinaShc12] assumed soft edges.
For
![]() $\beta = 2$
, we can establish the full asymptotic expansion outside of the bulk for the orthogonal polynomials with real-analytic potentials and the all-order asymptotic expansion of certain solutions of the Toda lattice in the continuum limit. The same method allows us to rigorously establish the asymptotics of skew-orthogonal polynomials (
$\beta = 2$
, we can establish the full asymptotic expansion outside of the bulk for the orthogonal polynomials with real-analytic potentials and the all-order asymptotic expansion of certain solutions of the Toda lattice in the continuum limit. The same method allows us to rigorously establish the asymptotics of skew-orthogonal polynomials (
![]() $\beta = 1$
and
$\beta = 1$
and
![]() $4$
) away from the bulk, derived heuristically in [Reference EynardEyn01]. To our knowledge, the Riemann–Hilbert analysis of skew-orthogonal polynomials is possible in principle but is cumbersome and has not been done before, so our method provides the first proof of these asymptotics. After this work was released, this method was extended to treat more general Coulomb-like interactions in [Reference Borot, Guionnet and KozlowskiBGK15]. We also note that a proof of the asymptotics up to
$4$
) away from the bulk, derived heuristically in [Reference EynardEyn01]. To our knowledge, the Riemann–Hilbert analysis of skew-orthogonal polynomials is possible in principle but is cumbersome and has not been done before, so our method provides the first proof of these asymptotics. After this work was released, this method was extended to treat more general Coulomb-like interactions in [Reference Borot, Guionnet and KozlowskiBGK15]. We also note that a proof of the asymptotics up to
![]() $o(1)$
with
$o(1)$
with
![]() $\beta = 2$
was obtained by the Riemann–Hilbert approach in the two-cuts situation in [Reference Claeys, Grava and McLaughlinCGMcL15] and in the k-cut situation with
$\beta = 2$
was obtained by the Riemann–Hilbert approach in the two-cuts situation in [Reference Claeys, Grava and McLaughlinCGMcL15] and in the k-cut situation with
![]() $k \geq 2$
in [Reference Charlier, Fahs, Webb and WongCFWW].
$k \geq 2$
in [Reference Charlier, Fahs, Webb and WongCFWW].
Since the first release of this work, several authors have considered asymptotic questions in the multi-cut regime of
![]() $\beta $
-ensembles. A recent approach to central limit theorems inspired by Stein’s method was proposed in [Reference Lambert, Ledoux and WebbLLW19], but it is restricted to the one-cut regime. The transport method introduced in [Reference Bekerman, Guionnet and FigalliBGF15] allowed the rigidity of eigenvalues [Reference LiLi16] and universality [Reference BekermanB18] in the multi-cut regime to be established. In [Reference Bekerman, Leblé and SerfatyBLS18], the validity of central limit theorems for linear fluctuations has also been extended to include test functions with weaker regularity assumptions and to critical cases (and then test functions in the range of the so-called ‘master operator’). Beyond being a source of inspiration for these works, and the first rigorous article where Dyson–Schwinger equations were used to derive central limit theorem in the multi-cut regime, the present article contains results that still did not appear anywhere else, such as the asymptotics of to (skew) orthogonal polynomials and integrable systems (see Section 2), a discussion about the relation with Chekhov–Eynard–Orantin topological recursion (see Section 1.5), and the detailed use of precise estimates of beta ensembles with fixed filling fractions to estimate the free energy in multi-cut models and the reconstruction of the Theta function (see Section 8). Besides, Shcherbina derives in [Reference ShcherbinaShc12] via operator methods and for soft edges an expression of the order N in the free energy in terms of the entropy of the equilibrium measure and a universal constant. Our work proves a similar formula both with soft and hard edges and with a different method based on complex analysis.
$\beta $
-ensembles. A recent approach to central limit theorems inspired by Stein’s method was proposed in [Reference Lambert, Ledoux and WebbLLW19], but it is restricted to the one-cut regime. The transport method introduced in [Reference Bekerman, Guionnet and FigalliBGF15] allowed the rigidity of eigenvalues [Reference LiLi16] and universality [Reference BekermanB18] in the multi-cut regime to be established. In [Reference Bekerman, Leblé and SerfatyBLS18], the validity of central limit theorems for linear fluctuations has also been extended to include test functions with weaker regularity assumptions and to critical cases (and then test functions in the range of the so-called ‘master operator’). Beyond being a source of inspiration for these works, and the first rigorous article where Dyson–Schwinger equations were used to derive central limit theorem in the multi-cut regime, the present article contains results that still did not appear anywhere else, such as the asymptotics of to (skew) orthogonal polynomials and integrable systems (see Section 2), a discussion about the relation with Chekhov–Eynard–Orantin topological recursion (see Section 1.5), and the detailed use of precise estimates of beta ensembles with fixed filling fractions to estimate the free energy in multi-cut models and the reconstruction of the Theta function (see Section 8). Besides, Shcherbina derives in [Reference ShcherbinaShc12] via operator methods and for soft edges an expression of the order N in the free energy in terms of the entropy of the equilibrium measure and a universal constant. Our work proves a similar formula both with soft and hard edges and with a different method based on complex analysis.
Our results on the asymptotics of the partition function have been used (e.g., to study the asymptotics of the determinant of Töplitz matrices in [Reference MarchalMar20, Reference MarchalMar21]). The ideas that we introduce to handle the multi-cut regime are extended in a work in progress [Reference Borot, Guionnet and GorinBGG] to study the fluctuations of discrete
![]() $\beta $
-ensembles appearing in random tiling models in nonsimply connected domains (with holes and/or frozen regions).
$\beta $
-ensembles appearing in random tiling models in nonsimply connected domains (with holes and/or frozen regions).
For Coulomb gases in dimension
![]() $d> 1$
, carrying out the asymptotic analysis when the support of the equilibrium measure has several connected components remains, in general, an open problem. Some specific
$d> 1$
, carrying out the asymptotic analysis when the support of the equilibrium measure has several connected components remains, in general, an open problem. Some specific
![]() $d = 2$
,
$d = 2$
,
![]() $\beta = 2$
situations have been treated in [Reference Ameur, Charlier and CronwallACC, Reference Ameur, Charlier, Cronvall and LenellsACCL] relying on the determinantal structure of these models. In general, probabilistic methods in the spirit of this article that do not rely on integrability, and therefore could address arbitrary
$\beta = 2$
situations have been treated in [Reference Ameur, Charlier and CronwallACC, Reference Ameur, Charlier, Cronvall and LenellsACCL] relying on the determinantal structure of these models. In general, probabilistic methods in the spirit of this article that do not rely on integrability, and therefore could address arbitrary
![]() $\beta> 0$
(where integrability is absent), are still insufficiently developed.
$\beta> 0$
(where integrability is absent), are still insufficiently developed.
1.1. Definitions
1.1.1. Model and empirical measure
We consider the probability measure
![]() $\mu _{N,\beta }^{V;\mathsf {B}}$
on
$\mu _{N,\beta }^{V;\mathsf {B}}$
on
![]() $\mathsf {B}^N$
given by
$\mathsf {B}^N$
given by
 $$ \begin{align} \mathrm{d}\mu_{N,\beta}^{V;\mathsf{B}}(\lambda) = \frac{1}{Z_{N,\beta}^{V;\mathsf{B}}}\prod_{i = 1}^N \mathrm{d}\lambda_i\,\mathbf{1}_{\mathsf{B}}(\lambda_i)\,e^{-\frac{\beta N}{2} \,V(\lambda_i)}\,\prod_{1 \leq i < j \leq N} |\lambda_i - \lambda_j|^{\beta}. \end{align} $$
$$ \begin{align} \mathrm{d}\mu_{N,\beta}^{V;\mathsf{B}}(\lambda) = \frac{1}{Z_{N,\beta}^{V;\mathsf{B}}}\prod_{i = 1}^N \mathrm{d}\lambda_i\,\mathbf{1}_{\mathsf{B}}(\lambda_i)\,e^{-\frac{\beta N}{2} \,V(\lambda_i)}\,\prod_{1 \leq i < j \leq N} |\lambda_i - \lambda_j|^{\beta}. \end{align} $$
![]() $\mathsf {B}$
is a finite disjoint union of closed intervals of
$\mathsf {B}$
is a finite disjoint union of closed intervals of
![]() $\mathbb {R}$
possibly with infinite endpoints,
$\mathbb {R}$
possibly with infinite endpoints,
![]() $\beta $
is a positive number and
$\beta $
is a positive number and
![]() $Z_{N,\beta }^{V;\mathsf {B}}$
is the partition function so that (1.1) has total mass
$Z_{N,\beta }^{V;\mathsf {B}}$
is the partition function so that (1.1) has total mass
![]() $1$
. This model is usually called the
$1$
. This model is usually called the
![]() $\beta $
-ensemble [Reference MehtaMeh04, Reference Dumitriu and EdelmanDE02, Reference ForresterFor10]. We introduce the unnormalised empirical measure
$\beta $
-ensemble [Reference MehtaMeh04, Reference Dumitriu and EdelmanDE02, Reference ForresterFor10]. We introduce the unnormalised empirical measure
![]() $M_N$
of the eigenvalues
$M_N$
of the eigenvalues
 $$ \begin{align*}M_N=\sum_{i=1}^N \delta_{\lambda_i}, \end{align*} $$
$$ \begin{align*}M_N=\sum_{i=1}^N \delta_{\lambda_i}, \end{align*} $$
and we consider several types of statistics for
![]() $M_N$
. We sometimes denote
$M_N$
. We sometimes denote
![]() $\mathbb {L} = \mathrm {diag}(\lambda _1,\ldots ,\lambda _N)$
.
$\mathbb {L} = \mathrm {diag}(\lambda _1,\ldots ,\lambda _N)$
.
1.1.2. Correlators
We introduce the Stieltjes transform of the n-th order moments of the empirical measure, called disconnected correlators:
They are holomorphic functions of
![]() $x_i \in \mathbb {C}\setminus \mathsf {B}$
. It is more convenient to consider the correlators to study large N asymptotics:
$x_i \in \mathbb {C}\setminus \mathsf {B}$
. It is more convenient to consider the correlators to study large N asymptotics:
 $$ \begin{align} \nonumber W_n(x_1,\ldots, x_n) & = \partial_{t_1}\cdots\partial_{t_n}\Big(\ln Z_{N,\beta}^{V-\frac{2}{\beta N}\sum_{i = 1}^n \frac{t_i}{x_i - \bullet};\mathsf{B}}\Big)\Big|_{t_i = 0} \\ & = \mu_{N,\beta}^{V;\mathsf{B}}\Big[\prod_{i = 1}^n {\,\mathrm{Tr}}\:\,\frac{1}{x_j - \mathbb{L}}\Big]_{c}. \end{align} $$
$$ \begin{align} \nonumber W_n(x_1,\ldots, x_n) & = \partial_{t_1}\cdots\partial_{t_n}\Big(\ln Z_{N,\beta}^{V-\frac{2}{\beta N}\sum_{i = 1}^n \frac{t_i}{x_i - \bullet};\mathsf{B}}\Big)\Big|_{t_i = 0} \\ & = \mu_{N,\beta}^{V;\mathsf{B}}\Big[\prod_{i = 1}^n {\,\mathrm{Tr}}\:\,\frac{1}{x_j - \mathbb{L}}\Big]_{c}. \end{align} $$
By construction, the coefficients of their expansions as a Laurent series in the variables
![]() $x_i $
(sufficiently large) give the n-th order cumulants of
$x_i $
(sufficiently large) give the n-th order cumulants of
![]() $M_N$
. If I is a set, we introduce the notation
$M_N$
. If I is a set, we introduce the notation
![]() $x_I = (x_i)_{i \in I}$
for a set of variables indexed by I; their order will not matter as we insert them only in symmetric functions of their variables (like
$x_I = (x_i)_{i \in I}$
for a set of variables indexed by I; their order will not matter as we insert them only in symmetric functions of their variables (like
![]() $W_n$
,
$W_n$
,
![]() $\widetilde {W}_n$
, etc.). The two types of correlators are related by
$\widetilde {W}_n$
, etc.). The two types of correlators are related by

where
![]() $\dot {\cup }$
stands for the disjoint union. If
$\dot {\cup }$
stands for the disjoint union. If
![]() $\varphi _n$
is an analytic (symmetric) function in n variables in a neighbourhood of
$\varphi _n$
is an analytic (symmetric) function in n variables in a neighbourhood of
![]() $\mathsf {B}^n$
, then the n-linear statistics can be deduced as contour integrals of the disconnected correlators:
$\mathsf {B}^n$
, then the n-linear statistics can be deduced as contour integrals of the disconnected correlators:
 $$ \begin{align} \mu_{N,\beta}^{V;\mathsf{B}}\Big[ \sum_{1 \leq i_1,\ldots,i_n \leq N} \varphi_n(\lambda_{i_1},\ldots,\lambda_{i_n})\Big] = \oint_{\mathsf{B}} \frac{\mathrm{d} \xi_1}{2\mathrm{i}\pi} \cdots \oint_{\mathsf{B}} \frac{\mathrm{d} \xi_n}{2\mathrm{i}\pi}\,\varphi_n(\xi_1,\ldots,\xi_n)\,\widetilde{W}_n(\xi_1,\ldots,\xi_n). \end{align} $$
$$ \begin{align} \mu_{N,\beta}^{V;\mathsf{B}}\Big[ \sum_{1 \leq i_1,\ldots,i_n \leq N} \varphi_n(\lambda_{i_1},\ldots,\lambda_{i_n})\Big] = \oint_{\mathsf{B}} \frac{\mathrm{d} \xi_1}{2\mathrm{i}\pi} \cdots \oint_{\mathsf{B}} \frac{\mathrm{d} \xi_n}{2\mathrm{i}\pi}\,\varphi_n(\xi_1,\ldots,\xi_n)\,\widetilde{W}_n(\xi_1,\ldots,\xi_n). \end{align} $$
We remark that the knowledge of the correlators for an analytic family of potentials
![]() $(V_{t})_{t}$
determines the partition function up to an integration constant since
$(V_{t})_{t}$
determines the partition function up to an integration constant since
 $$ \begin{align*}\partial_t \ln Z_{N,\beta}^{V_t;\mathsf{B}} = -\frac{\beta N}{2}\,\mu_{N,\beta}^{V_t;\mathsf{B}}\Big[\sum_{i = 1}^N \partial_t V_t(\lambda_i)\Big] = -\frac{\beta N}{2}\,\oint_{\mathsf{B}} \frac{\mathrm{d}\xi}{2\mathrm{i}\pi}\,\partial_t V_t(\xi)\,W_1^t(\xi), \end{align*} $$
$$ \begin{align*}\partial_t \ln Z_{N,\beta}^{V_t;\mathsf{B}} = -\frac{\beta N}{2}\,\mu_{N,\beta}^{V_t;\mathsf{B}}\Big[\sum_{i = 1}^N \partial_t V_t(\lambda_i)\Big] = -\frac{\beta N}{2}\,\oint_{\mathsf{B}} \frac{\mathrm{d}\xi}{2\mathrm{i}\pi}\,\partial_t V_t(\xi)\,W_1^t(\xi), \end{align*} $$
where
![]() $W_1^{t}$
is the first correlator in the model with potential
$W_1^{t}$
is the first correlator in the model with potential
![]() $V_t$
, and the notation
$V_t$
, and the notation
![]() $\oint _{\mathsf {B}} \mathrm {d} \xi \cdots $
means integration along a contour in
$\oint _{\mathsf {B}} \mathrm {d} \xi \cdots $
means integration along a contour in
![]() $\mathbb {C} \setminus \mathsf {B}$
surrounding
$\mathbb {C} \setminus \mathsf {B}$
surrounding
![]() $\mathsf {B}$
with positive orientation. If the integrand has poles in
$\mathsf {B}$
with positive orientation. If the integrand has poles in
![]() $\mathbb {C} \setminus \mathsf {B}$
(e.g., it depends on extra variables
$\mathbb {C} \setminus \mathsf {B}$
(e.g., it depends on extra variables
![]() $x_i \in \mathbb {C} \setminus \mathsf {B}$
that are not integrated upon and has poles at
$x_i \in \mathbb {C} \setminus \mathsf {B}$
that are not integrated upon and has poles at
![]() $\xi = x_i$
), the contour should be chosen (unless stated otherwise) so that the poles remain outside. The notation should not be confused with
$\xi = x_i$
), the contour should be chosen (unless stated otherwise) so that the poles remain outside. The notation should not be confused with
![]() $\int _{\mathsf {B}} \mathrm {d} \xi \cdots $
, which is the Lebesgue integral on
$\int _{\mathsf {B}} \mathrm {d} \xi \cdots $
, which is the Lebesgue integral on
![]() $\mathsf {B} \subseteq \mathbb {R}$
.
$\mathsf {B} \subseteq \mathbb {R}$
.
1.1.3. Kernels
Let
![]() $\mathbf {c}$
be a n-tuple of nonzero complex numbers. We introduce the n-point kernels:
$\mathbf {c}$
be a n-tuple of nonzero complex numbers. We introduce the n-point kernels:
 $$ \begin{align} \nonumber \mathsf{K}_{n,\mathbf{c}}(x_1,\ldots,x_n) & = \mu_{N,\beta}^{V;\mathsf{B}}\left[\prod_{j = 1}^n \mathrm{det}^{c_j}(x_j - \mathbb{L})\right] \\ & = \frac{Z_{N,\beta}^{V - \frac{2}{\beta N}\sum_{j = 1}^n c_j\ln(x_j - \bullet);\mathsf{B}}}{Z_{N,\beta}^{V;\mathsf{B}}}. \end{align} $$
$$ \begin{align} \nonumber \mathsf{K}_{n,\mathbf{c}}(x_1,\ldots,x_n) & = \mu_{N,\beta}^{V;\mathsf{B}}\left[\prod_{j = 1}^n \mathrm{det}^{c_j}(x_j - \mathbb{L})\right] \\ & = \frac{Z_{N,\beta}^{V - \frac{2}{\beta N}\sum_{j = 1}^n c_j\ln(x_j - \bullet);\mathsf{B}}}{Z_{N,\beta}^{V;\mathsf{B}}}. \end{align} $$
When
![]() $c_j$
are integers, the kernels are holomorphic functions of
$c_j$
are integers, the kernels are holomorphic functions of
![]() $x_j \in \mathbb {C}\setminus \mathsf {B}$
. When
$x_j \in \mathbb {C}\setminus \mathsf {B}$
. When
![]() $c_j$
are not integers, the kernels are multivalued holomorphic functions of
$c_j$
are not integers, the kernels are multivalued holomorphic functions of
![]() $x_j$
in
$x_j$
in
![]() $\mathbb {C}\setminus \mathsf {B}$
, with monodromies around the connected components of
$\mathbb {C}\setminus \mathsf {B}$
, with monodromies around the connected components of
![]() $\mathsf {B}$
and around
$\mathsf {B}$
and around
![]() $\infty $
. The right-hand side of (1.4), where we used
$\infty $
. The right-hand side of (1.4), where we used
![]() $\ln $
, has the same multivalued nature. Alternatively, both sides of (1.4) can be defined as single-valued functions of
$\ln $
, has the same multivalued nature. Alternatively, both sides of (1.4) can be defined as single-valued functions of
![]() $x_1,\ldots ,x_n$
by choosing a determination of the logarithm in a domain
$x_1,\ldots ,x_n$
by choosing a determination of the logarithm in a domain
![]() $\mathsf {D}$
of the form
$\mathsf {D}$
of the form
![]() $\mathbb {C} \setminus \ell $
, where
$\mathbb {C} \setminus \ell $
, where
![]() $\ell $
is a smooth path in
$\ell $
is a smooth path in
![]() $\mathbb {C}$
from
$\mathbb {C}$
from
![]() $0$
to
$0$
to
![]() $\infty $
, and using
$\infty $
, and using
![]() $z^{c} = e^{c \ln z}$
for the left-hand side.
$z^{c} = e^{c \ln z}$
for the left-hand side.
In particular, for
![]() $\beta = 2$
,
$\beta = 2$
,
![]() $\mathsf {K}_{1,(1)}(x)$
is the monic N-th orthogonal polynomial associated to the weight
$\mathsf {K}_{1,(1)}(x)$
is the monic N-th orthogonal polynomial associated to the weight
![]() $\mathbf {1}_{\mathsf {B}}(x)\,e^{-N\,V(x)}\mathrm {d} x$
on the real line, and
$\mathbf {1}_{\mathsf {B}}(x)\,e^{-N\,V(x)}\mathrm {d} x$
on the real line, and
![]() $\mathsf {K}_{2,(1,-1)}(x,y)$
is the N-th Christoffel–Darboux kernel associated to those orthogonal polynomials; see Section 2.
$\mathsf {K}_{2,(1,-1)}(x,y)$
is the N-th Christoffel–Darboux kernel associated to those orthogonal polynomials; see Section 2.
1.2. Equilibrium measure and multi-cut regime
By standard results of potential theory and large deviations – see [Reference JohanssonJoh98, Reference Ben Arous and GuionnetBAG97] or the textbooks [Reference DeiftDei99, Theorem 6] or [Reference Anderson, Guionnet and ZeitouniAGZ10, Theorem 2.6.1 and Corollary 2.6.3] (note there that
![]() $\mathsf {B}=\mathbb R$
, but the generalisation to integration over general sets
$\mathsf {B}=\mathbb R$
, but the generalisation to integration over general sets
![]() $\mathsf {B}$
is straightforward) – we have the following:
$\mathsf {B}$
is straightforward) – we have the following:
Theorem 1.1. Assume that
![]() $V\,:\, \mathsf {B} \rightarrow \mathbb {R}$
is a continuous function, and if V depends on N, assume also that
$V\,:\, \mathsf {B} \rightarrow \mathbb {R}$
is a continuous function, and if V depends on N, assume also that
![]() $V $
converges towards
$V $
converges towards
![]() $V^{\{0\}}$
when N goes to infinity in the space of continuous functions over
$V^{\{0\}}$
when N goes to infinity in the space of continuous functions over
![]() $\mathsf {B}$
for the sup norm. Moreover, for
$\mathsf {B}$
for the sup norm. Moreover, for
![]() $\tau \in \{\pm 1\}$
with
$\tau \in \{\pm 1\}$
with
![]() $\tau \infty \in \mathsf {B}$
, assume that
$\tau \infty \in \mathsf {B}$
, assume that
 $$ \begin{align*}\liminf_{x \rightarrow \tau\infty} \frac{V^{\{0\}}(x)}{2\ln|x|}> 1. \end{align*} $$
$$ \begin{align*}\liminf_{x \rightarrow \tau\infty} \frac{V^{\{0\}}(x)}{2\ln|x|}> 1. \end{align*} $$
We consider the normalised empirical measure
![]() $L_N=N^{-1}\,M_N$
in the space
$L_N=N^{-1}\,M_N$
in the space
![]() $\mathcal {P}(\mathsf {B})$
of probability measures on
$\mathcal {P}(\mathsf {B})$
of probability measures on
![]() $\mathsf {B}$
equipped with its weak topology. Then, the law of
$\mathsf {B}$
equipped with its weak topology. Then, the law of
![]() $L_N$
under
$L_N$
under
![]() $\mu _{N,\beta }^{V;\mathsf {B}}$
satisfies a large deviation principle with scale
$\mu _{N,\beta }^{V;\mathsf {B}}$
satisfies a large deviation principle with scale
![]() $N^2$
and good rate function J given by
$N^2$
and good rate function J given by
 $$ \begin{align} J[\mu]= E[\mu]-\inf_{\nu\in\mathcal{P}(\mathsf{B})} E[\nu],\qquad E[\mu] =\frac{\beta}{2} \iint_{\mathsf{B}^2} \mathrm{d}\mu(\xi)\mathrm{d}\mu(\eta)\Big(\frac{V^{\{0\}}(\xi) + V^{\{0\}}(\eta)}{2} -\ln|\xi-\eta|\Big). \end{align} $$
$$ \begin{align} J[\mu]= E[\mu]-\inf_{\nu\in\mathcal{P}(\mathsf{B})} E[\nu],\qquad E[\mu] =\frac{\beta}{2} \iint_{\mathsf{B}^2} \mathrm{d}\mu(\xi)\mathrm{d}\mu(\eta)\Big(\frac{V^{\{0\}}(\xi) + V^{\{0\}}(\eta)}{2} -\ln|\xi-\eta|\Big). \end{align} $$
As a consequence,
![]() $L_N$
converges almost surely and in expectation to the unique probability measure
$L_N$
converges almost surely and in expectation to the unique probability measure
![]() $\mu _\mathrm{{eq}}^{V}$
on
$\mu _\mathrm{{eq}}^{V}$
on
![]() $\mathsf {B}$
which minimises E.
$\mathsf {B}$
which minimises E.
![]() $\mu _\mathrm{{eq}}^{V}$
has compact support, denoted
$\mu _\mathrm{{eq}}^{V}$
has compact support, denoted
![]() $\mathsf {S}$
. It is characterised by the existence of a constant
$\mathsf {S}$
. It is characterised by the existence of a constant
![]() $C^V$
such that
$C^V$
such that
with equality realised
![]() $\mu _\mathrm{{eq}}^V$
almost surely.
$\mu _\mathrm{{eq}}^V$
almost surely.
The goal of this article is to establish an all-order expansion of the partition function, the correlators and the kernels in all such situations.
1.3. Assumptions
We will refer throughout the text to the following set of assumptions. An integer number
![]() $g\ge 0$
is fixed.
$g\ge 0$
is fixed.
Hypothesis 1.1.
-
○ (Regularity)
 $V\,:\,\mathsf {B} \rightarrow \mathbb {R}$
is continuous, and if V depends on N, it has a limit
$V\,:\,\mathsf {B} \rightarrow \mathbb {R}$
is continuous, and if V depends on N, it has a limit
 $V^{\{0\}}$
in the space of continuous functions on
$V^{\{0\}}$
in the space of continuous functions on
 $\mathsf {B}$
for the sup norm.
$\mathsf {B}$
for the sup norm. -
○ (Confinement) For
 $\tau \in \{\pm 1\}$
so that
$\tau \in \{\pm 1\}$
so that
 $\tau \infty \in \mathsf {B}$
,
$\tau \infty \in \mathsf {B}$
,
 $\liminf _{x \rightarrow \tau \infty } \frac {V(x)}{2\ln |x|}> 1$
. If V depends on N, we require its limit
$\liminf _{x \rightarrow \tau \infty } \frac {V(x)}{2\ln |x|}> 1$
. If V depends on N, we require its limit
 $V^{\{0\}}$
to satisfy this condition.
$V^{\{0\}}$
to satisfy this condition. -
○ (
 $(g + 1)$
-cut regime) The support of
$(g + 1)$
-cut regime) The support of
 $\mu _\mathrm{{eq}}^{V}$
is of the form
$\mu _\mathrm{{eq}}^{V}$
is of the form
 $\mathsf {S} = \bigcup _{h = 0}^{g} \mathsf {S}_h$
, where
$\mathsf {S} = \bigcup _{h = 0}^{g} \mathsf {S}_h$
, where
 $\mathsf {S}_h = [\alpha _{h}^{-},\alpha _{h}^{+}]$
are pairwise disjoint and
$\mathsf {S}_h = [\alpha _{h}^{-},\alpha _{h}^{+}]$
are pairwise disjoint and
 $\alpha _{h}^{-} < \alpha _{h}^+$
for any
$\alpha _{h}^{-} < \alpha _{h}^+$
for any  .
. -
○ (Control of large deviations) The effective potential
 $U^{V;\mathsf {B}}_{\mathrm{eq}}(x) = V(x)- 2\int _{\mathsf {B}} \ln |x-\xi |\mathrm {d}\mu _\mathrm{{eq}}^{V}(\xi )$
for
$U^{V;\mathsf {B}}_{\mathrm{eq}}(x) = V(x)- 2\int _{\mathsf {B}} \ln |x-\xi |\mathrm {d}\mu _\mathrm{{eq}}^{V}(\xi )$
for
 $x \in \mathsf {B}$
achieves its minimum value for
$x \in \mathsf {B}$
achieves its minimum value for
 $x \in \mathsf {S}$
only.
$x \in \mathsf {S}$
only. -
○ (Off-criticality)
 $\mu _\mathrm{{eq}}^{V}$
has a density of the form (1.7)where
$\mu _\mathrm{{eq}}^{V}$
has a density of the form (1.7)where $$ \begin{align} \frac{\mathrm{d}\mu_{\mathrm{eq}}^{V}}{\mathrm{d} x} = \frac{S(x)}{\pi}\,\prod_{h = 0}^{g} (\alpha_h^{+} - x)^{\rho_h^{+}/2}(x - \alpha_h^{-})^{\rho_h^{-}/2}, \end{align} $$
$$ \begin{align} \frac{\mathrm{d}\mu_{\mathrm{eq}}^{V}}{\mathrm{d} x} = \frac{S(x)}{\pi}\,\prod_{h = 0}^{g} (\alpha_h^{+} - x)^{\rho_h^{+}/2}(x - \alpha_h^{-})^{\rho_h^{-}/2}, \end{align} $$
 $\rho _{h}^{\bullet }$
is
$\rho _{h}^{\bullet }$
is
 $+1$
(resp.
$+1$
(resp.
 $-1$
) if the corresponding edge is soft (resp. hard), and
$-1$
) if the corresponding edge is soft (resp. hard), and
 $S(x)> 0$
for
$S(x)> 0$
for
 $x \in \mathsf {S}$
. Hard edges must be boundary points of
$x \in \mathsf {S}$
. Hard edges must be boundary points of
 $\mathsf {B}$
.
$\mathsf {B}$
.
Note that if
![]() $V^{\{0\}}$
is real-analytic in a neighbourhood of
$V^{\{0\}}$
is real-analytic in a neighbourhood of
![]() $\mathsf {B}$
, the
$\mathsf {B}$
, the
![]() $(g + 1)$
-cut regime hypothesis is always satisfied (the support consists of a finite disjoint union of segments) and S is analytic in a neighbourhood of
$(g + 1)$
-cut regime hypothesis is always satisfied (the support consists of a finite disjoint union of segments) and S is analytic in a neighbourhood of
![]() $\mathsf {S}$
. We will hereafter say that V is regular and confining in
$\mathsf {S}$
. We will hereafter say that V is regular and confining in
![]() $\mathsf {B}$
if it satisfies the two first assumptions above. We will also require a stronger regularity for the potential.
$\mathsf {B}$
if it satisfies the two first assumptions above. We will also require a stronger regularity for the potential.
Hypothesis 1.2.
-
○ (Analyticity) V extends to a holomorphic function in some open neighbourhood
 $\mathsf {U}$
of
$\mathsf {U}$
of
 $\mathsf {S}$
.
$\mathsf {S}$
. -
○ (
 $\frac {1}{N}$
expansion of the potential) There exists a sequence
$\frac {1}{N}$
expansion of the potential) There exists a sequence
 $(V^{\{k\}})_{k \geq 0}$
of holomorphic functions in
$(V^{\{k\}})_{k \geq 0}$
of holomorphic functions in
 $\mathsf {U}$
and constants
$\mathsf {U}$
and constants
 $(v^{\{k\}})_{k \geq 1}$
such that, for any
$(v^{\{k\}})_{k \geq 1}$
such that, for any
 $K \geq 0$
, (1.8)
$K \geq 0$
, (1.8) $$ \begin{align} \sup_{\xi \in \mathsf{U}} \Big|V(\xi) - \sum_{k = 0}^{K} N^{-k}\,V^{\{k\}}(\xi)\Big| \leq v^{\{K + 1\}}\,N^{-(K + 1)}. \end{align} $$
$$ \begin{align} \sup_{\xi \in \mathsf{U}} \Big|V(\xi) - \sum_{k = 0}^{K} N^{-k}\,V^{\{k\}}(\xi)\Big| \leq v^{\{K + 1\}}\,N^{-(K + 1)}. \end{align} $$
In Section 6, we shall weaken Hypothesis 1.2 by allowing complex perturbations of order
![]() $\frac {1}{N}$
and harmonic functions instead of analytic functions.
$\frac {1}{N}$
and harmonic functions instead of analytic functions.
Hypothesis 1.3.
![]() $V\,:\,\mathsf {B} \rightarrow \mathbb {C}$
can be decomposed as
$V\,:\,\mathsf {B} \rightarrow \mathbb {C}$
can be decomposed as
![]() $V = \mathcal {V}_1 + \overline {\mathcal {V}_2}$
where:
$V = \mathcal {V}_1 + \overline {\mathcal {V}_2}$
where:
-
○ For
 $j = 1,2$
,
$j = 1,2$
,
 $\mathcal {V}_j$
extends to a holomorphic function in some neighbourhood
$\mathcal {V}_j$
extends to a holomorphic function in some neighbourhood
 $\mathsf {U}$
of
$\mathsf {U}$
of
 $\mathsf {B}$
. There exists a sequence of holomorphic functions
$\mathsf {B}$
. There exists a sequence of holomorphic functions
 $(\mathcal {V}_{j}^{\{k\}})_{k \geq 0}$
and constants
$(\mathcal {V}_{j}^{\{k\}})_{k \geq 0}$
and constants
 $(v_{j}^{\{k\}})_{k \geq 1}$
so that, for any
$(v_{j}^{\{k\}})_{k \geq 1}$
so that, for any
 $K \geq 0$
,
$K \geq 0$
,  $$ \begin{align*}\sup_{\xi \in \mathsf{U}} \Big|\mathcal{V}_j(\xi) - \sum_{k = 0}^{K} N^{-k}\,\mathcal{V}_j^{\{k\}}(\xi)\Big| \leq v_j^{\{K + 1\}}\,N^{-(K + 1)}. \end{align*} $$
$$ \begin{align*}\sup_{\xi \in \mathsf{U}} \Big|\mathcal{V}_j(\xi) - \sum_{k = 0}^{K} N^{-k}\,\mathcal{V}_j^{\{k\}}(\xi)\Big| \leq v_j^{\{K + 1\}}\,N^{-(K + 1)}. \end{align*} $$
-
○
 $V^{\{0\}} = \mathcal {V}_1^{\{0\}} + \overline {\mathcal {V}_2^{\{0\}}}$
is real-valued on
$V^{\{0\}} = \mathcal {V}_1^{\{0\}} + \overline {\mathcal {V}_2^{\{0\}}}$
is real-valued on
 $\mathsf {B}$
.
$\mathsf {B}$
.
The topology for which we study the large N expansion of correlators is described in § 5 and amounts to controlling the (moments of order p)
![]() $\times C^p$
uniformly in p for a constant
$\times C^p$
uniformly in p for a constant
![]() $C> 0$
. We now describe our strategy and announce our results.
$C> 0$
. We now describe our strategy and announce our results.
1.4. Main result with fixed filling fractions: partition function and correlators
Before coming to the multi-cut regime, we analyse a different model where the number of
![]() $\lambda $
s in a small enlargement of
$\lambda $
s in a small enlargement of
![]() $\mathsf {S}_h$
is fixed. Let
$\mathsf {S}_h$
is fixed. Let
![]() $\mathsf {A} = \bigcup _{h = 0}^{g} \mathsf {A}_h$
, where
$\mathsf {A} = \bigcup _{h = 0}^{g} \mathsf {A}_h$
, where
![]() $\mathsf {A}_h = [a_{h}^{-},a_h^{+}]$
are pairwise disjoint segments such that
$\mathsf {A}_h = [a_{h}^{-},a_h^{+}]$
are pairwise disjoint segments such that
![]() $a_{h}^{-} \leq \alpha _{h}^{-} < \alpha _{h}^+ \leq a_{h}^+$
, where the inequalities are equalities if the corresponding edge is hard and are strict if the corresponding edge is soft. We introduce the set
$a_{h}^{-} \leq \alpha _{h}^{-} < \alpha _{h}^+ \leq a_{h}^+$
, where the inequalities are equalities if the corresponding edge is hard and are strict if the corresponding edge is soft. We introduce the set
 $$ \begin{align} \mathcal{E} = \Big\{\boldsymbol{\epsilon} \in (0,1)^{g}\quad\Big| \quad \sum_{h = 1}^{g} \epsilon_h < 1\Big\}. \end{align} $$
$$ \begin{align} \mathcal{E} = \Big\{\boldsymbol{\epsilon} \in (0,1)^{g}\quad\Big| \quad \sum_{h = 1}^{g} \epsilon_h < 1\Big\}. \end{align} $$
If
![]() $\boldsymbol {N}=(N_1,\ldots ,N_g)$
is an integer vector such that
$\boldsymbol {N}=(N_1,\ldots ,N_g)$
is an integer vector such that
![]() $\boldsymbol {\epsilon }=\frac {\boldsymbol {N}}{N} \in \mathcal {E}$
, we denote
$\boldsymbol {\epsilon }=\frac {\boldsymbol {N}}{N} \in \mathcal {E}$
, we denote
![]() $N_0 = N - \sum _{h = 1}^{g} N_h$
and consider the probability measure on
$N_0 = N - \sum _{h = 1}^{g} N_h$
and consider the probability measure on
![]() $\prod _{h = 0}^{g} \mathsf {A}_h^{N_h}$
:
$\prod _{h = 0}^{g} \mathsf {A}_h^{N_h}$
:
 $$ \begin{align} \nonumber \mathrm{d}\mu_{N,\beta;\boldsymbol{\epsilon}}^{V;\mathsf{A}}(\boldsymbol{\lambda}) & = \frac{1}{Z_{N,\beta;\boldsymbol{\epsilon}}^{V;\mathsf{A}}}\prod_{h = 0}^g \Big[\prod_{i = 1}^{N_h} \mathrm{d}\lambda_{h,i}\,\mathbf{1}_{\mathsf{A}_{h}}(\lambda_{h,i})\,e^{-\frac{\beta N}{2}\,V(\lambda_{h,i})}\,\prod_{1 \leq i < j \leq N} |\lambda_{h,i} - \lambda_{h,j}|^{\beta}\Big] \\ & \quad \times \prod_{0 \leq h < h' \leq g} \prod_{\substack{1 \leq i \leq N_h \\ 1 \leq i' \leq N_{h'}}} |\lambda_{h,i} - \lambda_{h',i'}|^{\beta}. \end{align} $$
$$ \begin{align} \nonumber \mathrm{d}\mu_{N,\beta;\boldsymbol{\epsilon}}^{V;\mathsf{A}}(\boldsymbol{\lambda}) & = \frac{1}{Z_{N,\beta;\boldsymbol{\epsilon}}^{V;\mathsf{A}}}\prod_{h = 0}^g \Big[\prod_{i = 1}^{N_h} \mathrm{d}\lambda_{h,i}\,\mathbf{1}_{\mathsf{A}_{h}}(\lambda_{h,i})\,e^{-\frac{\beta N}{2}\,V(\lambda_{h,i})}\,\prod_{1 \leq i < j \leq N} |\lambda_{h,i} - \lambda_{h,j}|^{\beta}\Big] \\ & \quad \times \prod_{0 \leq h < h' \leq g} \prod_{\substack{1 \leq i \leq N_h \\ 1 \leq i' \leq N_{h'}}} |\lambda_{h,i} - \lambda_{h',i'}|^{\beta}. \end{align} $$
The empirical measure
![]() $M_{N}$
and the correlators
$M_{N}$
and the correlators
![]() $W_{n;\boldsymbol {N}/N}(x_1,\ldots ,x_n)$
for this model are defined as in § 1.1 with
$W_{n;\boldsymbol {N}/N}(x_1,\ldots ,x_n)$
for this model are defined as in § 1.1 with
![]() $\mu _{N,\beta }^{V;\mathsf {A}}$
replaced by
$\mu _{N,\beta }^{V;\mathsf {A}}$
replaced by
![]() $\mu _{N,\beta ;\boldsymbol {N}/N}^{V;\mathsf {A}}$
. We call
$\mu _{N,\beta ;\boldsymbol {N}/N}^{V;\mathsf {A}}$
. We call
![]() $\epsilon _h=\frac {N_h}{N}$
the filling fraction of
$\epsilon _h=\frac {N_h}{N}$
the filling fraction of
![]() $\mathsf {A}_h$
. It follows from the definitions that
$\mathsf {A}_h$
. It follows from the definitions that
for
![]() $x_2,\ldots ,x_n \in \mathbb {C} \setminus \mathsf {A}$
. Indeed, from the definition of the correlators (1.2),
$x_2,\ldots ,x_n \in \mathbb {C} \setminus \mathsf {A}$
. Indeed, from the definition of the correlators (1.2),
![]() $W_{n;\boldsymbol {N}/N}(x_{1},x_2,\ldots ,x_n) $
for
$W_{n;\boldsymbol {N}/N}(x_{1},x_2,\ldots ,x_n) $
for
![]() $n \geq 2$
can be expressed as a sum of products of moments of products of the n-tuple of random variables
$n \geq 2$
can be expressed as a sum of products of moments of products of the n-tuple of random variables
![]() $\big (\sum _{i = 1}^{N} \frac {1}{x_j - \lambda _{i}}-\mu _{N,\beta ;\boldsymbol {\epsilon }}^{V;\mathsf {A}}[\sum _{i = 1}^{N} \frac {1}{x_j - \lambda _{i}}] \big )_{j = 1}^{n}$
which are linear in each of these variables. Therefore, we can integrate over the variable
$\big (\sum _{i = 1}^{N} \frac {1}{x_j - \lambda _{i}}-\mu _{N,\beta ;\boldsymbol {\epsilon }}^{V;\mathsf {A}}[\sum _{i = 1}^{N} \frac {1}{x_j - \lambda _{i}}] \big )_{j = 1}^{n}$
which are linear in each of these variables. Therefore, we can integrate over the variable
![]() $x_{1}$
in each of these terms by Fubini’s theorem. The key observation is that
$x_{1}$
in each of these terms by Fubini’s theorem. The key observation is that
![]() $\oint _{\mathsf {A}_h} \sum _{i = 1}^{N} \frac {\mathrm{d} \xi }{2\mathrm{i}\pi }\,\frac {1}{\xi - \lambda _i}$
is the number
$\oint _{\mathsf {A}_h} \sum _{i = 1}^{N} \frac {\mathrm{d} \xi }{2\mathrm{i}\pi }\,\frac {1}{\xi - \lambda _i}$
is the number
![]() $N_{h}$
of
$N_{h}$
of
![]() $\lambda _i$
s belonging to
$\lambda _i$
s belonging to
![]() $\mathsf {A}_h$
. Since
$\mathsf {A}_h$
. Since
![]() $N_h$
is deterministic in the fixed filling fraction model, it is equal to its expectation, and therefore, each of these terms vanish which implies (1.11) for
$N_h$
is deterministic in the fixed filling fraction model, it is equal to its expectation, and therefore, each of these terms vanish which implies (1.11) for
![]() $n\ge 2$
. When
$n\ge 2$
. When
![]() $n=1$
, the cumulant is simply equal to the expectation of
$n=1$
, the cumulant is simply equal to the expectation of
![]() $ \sum _{i = 1}^{N} \frac {1}{\xi - \lambda _i}$
, and the previous remark proves (1.11).
$ \sum _{i = 1}^{N} \frac {1}{\xi - \lambda _i}$
, and the previous remark proves (1.11).
We will refer to (1.1) as the initial model and to (1.10) as the model with fixed filling fractions. Standard results from potential theory or a straightforward generalisation of [Reference Anderson, Guionnet and ZeitouniAGZ10, Theorem 2.6.1 and Corollary 2.6.3] imply the following:
Theorem 1.2. Assume V regular and confining on
![]() $\mathsf {A}$
. We consider the normalised empirical measures
$\mathsf {A}$
. We consider the normalised empirical measures
![]() $L_{N,h}=\frac {1}{N_h}\sum _{i=1}^{N_h} \delta _{\lambda _{h,i}}\in \mathcal {P}(\mathsf {A}_h)$
for
$L_{N,h}=\frac {1}{N_h}\sum _{i=1}^{N_h} \delta _{\lambda _{h,i}}\in \mathcal {P}(\mathsf {A}_h)$
for ![]() . Take a sequence
. Take a sequence
![]() $\boldsymbol {N} = (N_1,\ldots ,N_g)$
of g-tuple of integers, indexed by N, such that
$\boldsymbol {N} = (N_1,\ldots ,N_g)$
of g-tuple of integers, indexed by N, such that
![]() $\sum _{h = 1}^g N_h \leq N$
, and such that
$\sum _{h = 1}^g N_h \leq N$
, and such that
![]() $\boldsymbol {N}/N$
converges to a given
$\boldsymbol {N}/N$
converges to a given
![]() $\boldsymbol {\epsilon }\in \mathcal {E}$
when
$\boldsymbol {\epsilon }\in \mathcal {E}$
when
![]() $N \rightarrow \infty $
. Then, the law of
$N \rightarrow \infty $
. Then, the law of
![]() $(L_{N,h})_{0\le h\le g}$
under
$(L_{N,h})_{0\le h\le g}$
under
![]() $\mu _{N,\beta ;\boldsymbol {N}/N}^{V;\mathsf {A}}$
satisfies a large deviation principle with scale
$\mu _{N,\beta ;\boldsymbol {N}/N}^{V;\mathsf {A}}$
satisfies a large deviation principle with scale
![]() $N^2$
and good rate function
$N^2$
and good rate function
 $$ \begin{align*}J_{\boldsymbol{\epsilon}}[\mu_0,\ldots,\mu_g]=E\Big[\sum_{h=0}^g\epsilon_h \mu_h\Big]-\inf_{\nu_h\in\mathcal{P} (\mathsf{A}_h)} E\Big[\sum_{h=0}^g\epsilon_h \nu_h\Big]\,,\end{align*} $$
$$ \begin{align*}J_{\boldsymbol{\epsilon}}[\mu_0,\ldots,\mu_g]=E\Big[\sum_{h=0}^g\epsilon_h \mu_h\Big]-\inf_{\nu_h\in\mathcal{P} (\mathsf{A}_h)} E\Big[\sum_{h=0}^g\epsilon_h \nu_h\Big]\,,\end{align*} $$
where
![]() $\epsilon _0=1-\sum _{h=1}^g \epsilon _h$
,
$\epsilon _0=1-\sum _{h=1}^g \epsilon _h$
,
![]() $N_0=N-\sum _{h=1}^g N_h$
and E is defined in Equation (1.5). As a consequence, the empirical measure
$N_0=N-\sum _{h=1}^g N_h$
and E is defined in Equation (1.5). As a consequence, the empirical measure
![]() $L_{N;\boldsymbol {\epsilon }}=\sum _{h=0}^g\frac {N_h}{N} L_{N,h}$
converges almost surely and in expectation towards the unique probability measure
$L_{N;\boldsymbol {\epsilon }}=\sum _{h=0}^g\frac {N_h}{N} L_{N,h}$
converges almost surely and in expectation towards the unique probability measure
![]() $\mu _\mathrm{{eq};\boldsymbol {\epsilon }}^{V;\mathsf {A}}$
on
$\mu _\mathrm{{eq};\boldsymbol {\epsilon }}^{V;\mathsf {A}}$
on
![]() $\mathsf {A}$
which minimises E among probability measures with fixed mass
$\mathsf {A}$
which minimises E among probability measures with fixed mass
![]() $\epsilon _h$
on
$\epsilon _h$
on
![]() $\mathsf {A}_h$
for any
$\mathsf {A}_h$
for any ![]() . It is characterised by the existence of constants
. It is characterised by the existence of constants
![]() $C_{\boldsymbol {\epsilon },h}^{V,\mathsf {A}}$
such that
$C_{\boldsymbol {\epsilon },h}^{V,\mathsf {A}}$
such that
with equality realised
![]() $\mu _\mathrm{{eq};\boldsymbol {\epsilon }}^{V;\mathsf {A}}$
almost surely.
$\mu _\mathrm{{eq};\boldsymbol {\epsilon }}^{V;\mathsf {A}}$
almost surely.
![]() $\mu _\mathrm{{eq};\boldsymbol {\epsilon }}^{V;\mathsf {A}}$
can be decomposed as a sum of positive measures
$\mu _\mathrm{{eq};\boldsymbol {\epsilon }}^{V;\mathsf {A}}$
can be decomposed as a sum of positive measures
![]() $\mu _\mathrm{{eq};\boldsymbol {\epsilon },h}^{V}$
having compact support in
$\mu _\mathrm{{eq};\boldsymbol {\epsilon },h}^{V}$
having compact support in
![]() $\mathsf {A}_h$
, denoted
$\mathsf {A}_h$
, denoted
![]() $\mathsf {S}_{\boldsymbol {\epsilon },h}$
. Moreover, if
$\mathsf {S}_{\boldsymbol {\epsilon },h}$
. Moreover, if
![]() $V^{\{0\}}$
is real-analytic in a neighbourhood of
$V^{\{0\}}$
is real-analytic in a neighbourhood of
![]() $\mathsf {A}$
, the support
$\mathsf {A}$
, the support
![]() $\mathsf {S}_{\boldsymbol {\epsilon },h}$
consists of a finite union of segments.
$\mathsf {S}_{\boldsymbol {\epsilon },h}$
consists of a finite union of segments.
Later in the text, we shall consider
![]() $\mu _\mathrm{{eq};\boldsymbol {N}/N}^{V;\mathsf {A}}$
with
$\mu _\mathrm{{eq};\boldsymbol {N}/N}^{V;\mathsf {A}}$
with
![]() $\boldsymbol {N}=(N_1,\ldots ,N_g)$
a vector of positive integers so that
$\boldsymbol {N}=(N_1,\ldots ,N_g)$
a vector of positive integers so that
![]() $\sum _{h = 1}^{g} N_h < N$
: this will denote the unique solution of (1.12) with
$\sum _{h = 1}^{g} N_h < N$
: this will denote the unique solution of (1.12) with
![]() $\boldsymbol {\epsilon }=\boldsymbol {N}/N$
.
$\boldsymbol {\epsilon }=\boldsymbol {N}/N$
.
![]() $\mu _\mathrm{{eq}}^{V;\mathsf {A}}$
appearing in Theorem 1.1 coincides with
$\mu _\mathrm{{eq}}^{V;\mathsf {A}}$
appearing in Theorem 1.1 coincides with
![]() $\mu _\mathrm{{eq};\boldsymbol {\epsilon }_{\star }}^{V}$
for the optimal value
$\mu _\mathrm{{eq};\boldsymbol {\epsilon }_{\star }}^{V}$
for the optimal value
![]() $\boldsymbol {\epsilon }_{\star } = (\mu _\mathrm{{eq}}^{V;\mathsf {A}}(\mathsf {A}_{h}))_{1 \leq h \leq g}$
, and in this case,
$\boldsymbol {\epsilon }_{\star } = (\mu _\mathrm{{eq}}^{V;\mathsf {A}}(\mathsf {A}_{h}))_{1 \leq h \leq g}$
, and in this case,
![]() $\mathsf {S}_{\boldsymbol {\epsilon }_{\star },h}$
is actually the segment
$\mathsf {S}_{\boldsymbol {\epsilon }_{\star },h}$
is actually the segment
![]() $[\alpha ^{-}_h,\alpha _{h}^+]$
. The key point – justified in Appendix 1 – is that, for
$[\alpha ^{-}_h,\alpha _{h}^+]$
. The key point – justified in Appendix 1 – is that, for
![]() $\boldsymbol {\epsilon }$
close enough to
$\boldsymbol {\epsilon }$
close enough to
![]() $\boldsymbol {\epsilon }_{\star }$
, the support
$\boldsymbol {\epsilon }_{\star }$
, the support
![]() $\mathsf {S}_{\boldsymbol {\epsilon },h}$
remains connected, and the model with fixed filling fractions enjoys a
$\mathsf {S}_{\boldsymbol {\epsilon },h}$
remains connected, and the model with fixed filling fractions enjoys a
![]() $\frac {1}{N}$
expansion.
$\frac {1}{N}$
expansion.
Theorem 1.3. If V satisfies Hypotheses 1.1 and 1.3 on
![]() $\mathsf {A}$
, there exists
$\mathsf {A}$
, there exists
![]() $t> 0$
such that, uniformly for integers
$t> 0$
such that, uniformly for integers
![]() $\boldsymbol {N}=(N_1,\ldots ,N_g)$
such that
$\boldsymbol {N}=(N_1,\ldots ,N_g)$
such that
![]() $\boldsymbol {N} /N\in \mathcal {E}$
and
$\boldsymbol {N} /N\in \mathcal {E}$
and
![]() $|\boldsymbol {N}/N- \boldsymbol {\epsilon }_{\star }|_1 < t$
, we have an expansion for the correlators, for any
$|\boldsymbol {N}/N- \boldsymbol {\epsilon }_{\star }|_1 < t$
, we have an expansion for the correlators, for any
![]() $K \geq 0$
,
$K \geq 0$
,
 $$ \begin{align} W_{n;\boldsymbol{N}/N}(x_1,\ldots,x_n) = \sum_{k = n - 2}^{K} N^{-k}\,W_{n;\boldsymbol{N}/N}^{\{k\}}(x_1,\ldots,x_n) + O(N^{-(K + 1)}). \end{align} $$
$$ \begin{align} W_{n;\boldsymbol{N}/N}(x_1,\ldots,x_n) = \sum_{k = n - 2}^{K} N^{-k}\,W_{n;\boldsymbol{N}/N}^{\{k\}}(x_1,\ldots,x_n) + O(N^{-(K + 1)}). \end{align} $$
Up to a fixed
![]() $O(N^{-(K + 1)})$
and for a fixed n, Equation (1.13) holds uniformly for
$O(N^{-(K + 1)})$
and for a fixed n, Equation (1.13) holds uniformly for
![]() $x_1,\ldots ,x_n$
in compact regions of
$x_1,\ldots ,x_n$
in compact regions of
![]() $\mathbb {C}\setminus \mathsf {A}$
. The
$\mathbb {C}\setminus \mathsf {A}$
. The
![]() $W_{n;\boldsymbol {\epsilon }}^{\{k\}}$
can be extended into smooth functions of
$W_{n;\boldsymbol {\epsilon }}^{\{k\}}$
can be extended into smooth functions of
![]() $\boldsymbol {\epsilon }\in \mathcal {E}$
close enough to
$\boldsymbol {\epsilon }\in \mathcal {E}$
close enough to
![]() $\boldsymbol {\epsilon }_{\star }$
.
$\boldsymbol {\epsilon }_{\star }$
.
We prove this theorem, independently of the nature soft/hard of the edges, in Section 5 for real-analytic potential (i.e., Hypothesis 1.2 instead of 1.3). For
![]() $\beta = 2$
and potential V independent of N, the coefficients of expansion
$\beta = 2$
and potential V independent of N, the coefficients of expansion
![]() $W_{n;\boldsymbol {N}/N}^{\{k\}} = 0$
are zero for
$W_{n;\boldsymbol {N}/N}^{\{k\}} = 0$
are zero for
![]() $k = (n + 1) \,\,\mathrm{mod} 2$
, as is well known for hermitian random matrix models (see (1.16) and the remarks on
$k = (n + 1) \,\,\mathrm{mod} 2$
, as is well known for hermitian random matrix models (see (1.16) and the remarks on
![]() $\beta $
-dependence in Section 1.5). The result is extended to harmonic potentials (i.e., Hypothesis 1.3) in Section 6.1. In Proposition 5.6, we provide an explicit control of the errors in terms of the distance of
$\beta $
-dependence in Section 1.5). The result is extended to harmonic potentials (i.e., Hypothesis 1.3) in Section 6.1. In Proposition 5.6, we provide an explicit control of the errors in terms of the distance of
![]() $x_1,\ldots ,x_k$
to
$x_1,\ldots ,x_k$
to
![]() $\mathsf {A}$
, and its proof makes clear that the expansion of the correlators is not expected to be uniform for
$\mathsf {A}$
, and its proof makes clear that the expansion of the correlators is not expected to be uniform for
![]() $x_1,\ldots ,x_n$
chosen in a compact of
$x_1,\ldots ,x_n$
chosen in a compact of
![]() $\mathbb {C}\setminus \mathsf {A}$
independently of n and K (namely, it is uniform only for K fixed). Note that we will sometimes omit to specify the dependence in
$\mathbb {C}\setminus \mathsf {A}$
independently of n and K (namely, it is uniform only for K fixed). Note that we will sometimes omit to specify the dependence in
![]() $\mathsf {A},V$
, etc. in the notations (e.g., for the equilibrium measure, for the correlators and their coefficient of expansions), but we will at least include it when this dependence is of particular importance.
$\mathsf {A},V$
, etc. in the notations (e.g., for the equilibrium measure, for the correlators and their coefficient of expansions), but we will at least include it when this dependence is of particular importance.
We then compute in Section 7 the expansion of the partition function, thanks to the expansion of
![]() $W_{1;\boldsymbol {N}/N}$
and
$W_{1;\boldsymbol {N}/N}$
and
![]() $W_{2;\boldsymbol {N}/N}$
, by an interpolation that reduces the strength of pairwise interactions between eigenvalues in different segments while preserving the equilibrium measure. At the end of the interpolation, we are left with a product of
$W_{2;\boldsymbol {N}/N}$
, by an interpolation that reduces the strength of pairwise interactions between eigenvalues in different segments while preserving the equilibrium measure. At the end of the interpolation, we are left with a product of
![]() $(g + 1)$
partition functions in a one-cut regime, for which the asymptotic expansion was established in [Reference Borot and GuionnetBG11].
$(g + 1)$
partition functions in a one-cut regime, for which the asymptotic expansion was established in [Reference Borot and GuionnetBG11].
Theorem 1.4. If V satisfies Hypotheses 1.1 and 1.3 on
![]() $\mathsf {A}$
, there exists
$\mathsf {A}$
, there exists
![]() $t> 0$
such that, uniformly for g-dimensional vectors of positive integers
$t> 0$
such that, uniformly for g-dimensional vectors of positive integers
![]() $\boldsymbol {N}$
such that
$\boldsymbol {N}$
such that
![]() $\boldsymbol {N} /N\in \mathcal {E}$
and
$\boldsymbol {N} /N\in \mathcal {E}$
and
![]() $|\boldsymbol {N}/N- \boldsymbol {\epsilon }_{\star }|_1 < t$
, we have for any
$|\boldsymbol {N}/N- \boldsymbol {\epsilon }_{\star }|_1 < t$
, we have for any
![]() $K \geq 0$
,
$K \geq 0$
,
 $$ \begin{align} \frac{N!\,Z_{N,\beta;\boldsymbol{N}/N}^{V;\mathsf{A}}}{\prod_{h = 0}^{g} N_h!}= N^{\frac{\beta}{2}N + \varkappa}\exp\Big(\sum_{k = -2}^{K} N^{-k}\,F^{\{k\};V}_{\beta;\boldsymbol{N}/N} + O(N^{-(K + 1)})\Big), \end{align} $$
$$ \begin{align} \frac{N!\,Z_{N,\beta;\boldsymbol{N}/N}^{V;\mathsf{A}}}{\prod_{h = 0}^{g} N_h!}= N^{\frac{\beta}{2}N + \varkappa}\exp\Big(\sum_{k = -2}^{K} N^{-k}\,F^{\{k\};V}_{\beta;\boldsymbol{N}/N} + O(N^{-(K + 1)})\Big), \end{align} $$
with
Besides,
![]() $F^{\{k\};V}_{\beta ;\boldsymbol {\epsilon }}$
extends to a smooth function of
$F^{\{k\};V}_{\beta ;\boldsymbol {\epsilon }}$
extends to a smooth function of
![]() $\boldsymbol {\epsilon }$
close enough to
$\boldsymbol {\epsilon }$
close enough to
![]() $\boldsymbol {\epsilon }_{\star }$
, and at the value
$\boldsymbol {\epsilon }_{\star }$
, and at the value
![]() $\boldsymbol {\epsilon } = \boldsymbol {\epsilon }_{\star }$
, the first derivatives of
$\boldsymbol {\epsilon } = \boldsymbol {\epsilon }_{\star }$
, the first derivatives of
![]() $F^{\{-2\};V}_{\beta ;\boldsymbol {\epsilon }}$
vanish and its Hessian is negative definite.
$F^{\{-2\};V}_{\beta ;\boldsymbol {\epsilon }}$
vanish and its Hessian is negative definite.
We can identify explicitly the following:
 $$ \begin{align} \nonumber F^{\{-2\};V}_{\beta;\boldsymbol{\epsilon}} & = \frac{\beta}{2}\bigg(\iint_{\mathsf{A}^2} \ln|x - y|\,\mathrm{d}\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}(x)\mathrm{d}\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}(y) - \int_{\mathsf{A}} V^{\{0\}}(x)\mathrm{d}\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}(x)\bigg) = -\frac{\beta}{2}\,\inf_{\nu_h \in \mathcal{P}(\mathsf{A}_h)} E\Big[\sum_{h = 0}^{g} \epsilon_h\nu_h\Big], \\ F^{\{-1\};V}_{\beta;\boldsymbol{\epsilon}} & = - \frac{\beta}{2} \int_{\mathsf{A}} V^{\{1\}}(x)\mathrm{d}\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}(x) + \Big(1 - \frac{\beta}{2}\Big)\Big(\mathrm{Ent}[\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}] - \ln\big(\tfrac{\beta}{2}\big)\Big) +\frac{\beta}{2}\ln\big(\tfrac{2\pi}{e}\big) - \ln\Gamma\big(\tfrac{\beta}{2}\big), \end{align} $$
$$ \begin{align} \nonumber F^{\{-2\};V}_{\beta;\boldsymbol{\epsilon}} & = \frac{\beta}{2}\bigg(\iint_{\mathsf{A}^2} \ln|x - y|\,\mathrm{d}\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}(x)\mathrm{d}\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}(y) - \int_{\mathsf{A}} V^{\{0\}}(x)\mathrm{d}\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}(x)\bigg) = -\frac{\beta}{2}\,\inf_{\nu_h \in \mathcal{P}(\mathsf{A}_h)} E\Big[\sum_{h = 0}^{g} \epsilon_h\nu_h\Big], \\ F^{\{-1\};V}_{\beta;\boldsymbol{\epsilon}} & = - \frac{\beta}{2} \int_{\mathsf{A}} V^{\{1\}}(x)\mathrm{d}\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}(x) + \Big(1 - \frac{\beta}{2}\Big)\Big(\mathrm{Ent}[\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}] - \ln\big(\tfrac{\beta}{2}\big)\Big) +\frac{\beta}{2}\ln\big(\tfrac{2\pi}{e}\big) - \ln\Gamma\big(\tfrac{\beta}{2}\big), \end{align} $$
where
is the entropy. The formula for
![]() $F^{\{-2\};V}_{\beta ;\boldsymbol {\epsilon }}$
is obvious from potential theory, while the formula for
$F^{\{-2\};V}_{\beta ;\boldsymbol {\epsilon }}$
is obvious from potential theory, while the formula for
![]() $F^{\{-1\};V}_{\beta ;\boldsymbol {\epsilon }}$
is established in Proposition 7.1 (the first term comes from the fact that we let the potential depend on N). The appearance of the entropy in the term of order N in the free energy is well known in the one-cut case, and here we prove that it appears in the same way for the multi-cut case with fixed filling fractions, and we determine the additional constant. The term
$F^{\{-1\};V}_{\beta ;\boldsymbol {\epsilon }}$
is established in Proposition 7.1 (the first term comes from the fact that we let the potential depend on N). The appearance of the entropy in the term of order N in the free energy is well known in the one-cut case, and here we prove that it appears in the same way for the multi-cut case with fixed filling fractions, and we determine the additional constant. The term
![]() $\frac {\beta }{2} N \ln N$
is universal, while the term
$\frac {\beta }{2} N \ln N$
is universal, while the term
![]() $\varkappa \ln N$
only depends only on the nature of the endpoints of the support. These logarithmic corrections can already be observed in the asymptotic expansion of Selberg integrals for large N computing the partition function of the classical Jacobi, Laguerre or Gaussian
$\varkappa \ln N$
only depends only on the nature of the endpoints of the support. These logarithmic corrections can already be observed in the asymptotic expansion of Selberg integrals for large N computing the partition function of the classical Jacobi, Laguerre or Gaussian
![]() $\beta $
-ensembles, corresponding to a one-cut regime [Reference Borot and GuionnetBG11]. The fact that the coefficient of
$\beta $
-ensembles, corresponding to a one-cut regime [Reference Borot and GuionnetBG11]. The fact that the coefficient of
![]() $\ln N$
shadows in some way the geometry of the support was observed in other contexts (see, for example, [Reference Cardy and PeschelCP88]) and is not specific to two-dimensional Coulomb gases living on a line. Their identification in the multi-cut regime and fixed filling fractions results from an interpolation with a product of one such model for each cut, which changes only the coefficients of powers of N. Up to a given
$\ln N$
shadows in some way the geometry of the support was observed in other contexts (see, for example, [Reference Cardy and PeschelCP88]) and is not specific to two-dimensional Coulomb gases living on a line. Their identification in the multi-cut regime and fixed filling fractions results from an interpolation with a product of one such model for each cut, which changes only the coefficients of powers of N. Up to a given
![]() $O(N^{-K})$
, all expansions are uniform with respect to the parameters of the potential and of
$O(N^{-K})$
, all expansions are uniform with respect to the parameters of the potential and of
![]() $\boldsymbol {\epsilon }$
chosen in a compact set so that the assumptions hold. Theorems 1.3–1.4 are the generalisations to the fixed filling fractions model of our earlier results about existence of the
$\boldsymbol {\epsilon }$
chosen in a compact set so that the assumptions hold. Theorems 1.3–1.4 are the generalisations to the fixed filling fractions model of our earlier results about existence of the
![]() $\frac {1}{N}$
expansion in the one-cut regime [Reference Borot and GuionnetBG11] (see also [Reference JohanssonJoh98, Reference Albeverio, Pastur and ShcherbinaAPS01, Reference Ercolani and McLaughlinEM03, Reference Bleher and ItsBI05, Reference Guionnet and Maurel-SegalaGMS07, Reference Kriecherbauer and ShcherbinaKS10] for earlier results concerning the one-cut regime in
$\frac {1}{N}$
expansion in the one-cut regime [Reference Borot and GuionnetBG11] (see also [Reference JohanssonJoh98, Reference Albeverio, Pastur and ShcherbinaAPS01, Reference Ercolani and McLaughlinEM03, Reference Bleher and ItsBI05, Reference Guionnet and Maurel-SegalaGMS07, Reference Kriecherbauer and ShcherbinaKS10] for earlier results concerning the one-cut regime in
![]() $\beta = 2$
or general
$\beta = 2$
or general
![]() $\beta $
-ensembles).
$\beta $
-ensembles).
1.5. Relation with Chekhov–Eynard–Orantin topological recursion
Once these asymptotic expansions are shown to exist, by consistency, their coefficients
![]() $W_{n;\boldsymbol {\epsilon }}^{\{k\}}$
are computed by the
$W_{n;\boldsymbol {\epsilon }}^{\{k\}}$
are computed by the
![]() $\beta $
topological recursion of Chekhov and Eynard [Reference Chekhov and EynardCE06]. As a matter of fact, the asymptotic expansion
$\beta $
topological recursion of Chekhov and Eynard [Reference Chekhov and EynardCE06]. As a matter of fact, the asymptotic expansion
has a finer structure so that for
![]() $n \geq 1$
and
$n \geq 1$
and
![]() $k \geq -1$
, we can write
$k \geq -1$
, we can write
 $$ \begin{align} W_{n;\boldsymbol{\epsilon}}^{\{k\}}(x_1,\ldots,x_n) = \sum_{G = 0}^{\lfloor \frac{k - n}{2} \rfloor + 1} \Big(\frac{\beta}{2}\Big)^{1 - n - G}\Big(1 - \frac{2}{\beta}\Big)^{k + 2 - 2G - n}\,\mathcal{W}_{n;\boldsymbol{\epsilon}}^{[G,k + 2 - 2G - n]}(x_1,\ldots,x_n), \end{align} $$
$$ \begin{align} W_{n;\boldsymbol{\epsilon}}^{\{k\}}(x_1,\ldots,x_n) = \sum_{G = 0}^{\lfloor \frac{k - n}{2} \rfloor + 1} \Big(\frac{\beta}{2}\Big)^{1 - n - G}\Big(1 - \frac{2}{\beta}\Big)^{k + 2 - 2G - n}\,\mathcal{W}_{n;\boldsymbol{\epsilon}}^{[G,k + 2 - 2G - n]}(x_1,\ldots,x_n), \end{align} $$
where
![]() $\mathcal {W}_{n;\boldsymbol {\epsilon }}^{[G,l]}$
are the quantities computed by the topological recursion of [Reference Chekhov and EynardCE06]. The initial data consists of the nondecaying terms in the correlators – namely,
$\mathcal {W}_{n;\boldsymbol {\epsilon }}^{[G,l]}$
are the quantities computed by the topological recursion of [Reference Chekhov and EynardCE06]. The initial data consists of the nondecaying terms in the correlators – namely,
 $$ \begin{align*} W_{1;\boldsymbol{\epsilon}}^{\{-1\}}(x) & = \mathcal{W}_{1;\boldsymbol{\epsilon}}^{[0,0]}(x) ,\\ W_{1;\boldsymbol{\epsilon}}^{\{0\}}(x) & = \Big(1 - \frac{2}{\beta}\Big)\mathcal{W}_{1;\boldsymbol{\epsilon}}^{[0,1]}(x), \\ W_{2;\boldsymbol{\epsilon}}^{\{0\}}(x_1,x_2) & = \frac{2}{\beta}\,\mathcal{W}_{2;\boldsymbol{\epsilon}}^{[0,0]}(x_1,x_2). \end{align*} $$
$$ \begin{align*} W_{1;\boldsymbol{\epsilon}}^{\{-1\}}(x) & = \mathcal{W}_{1;\boldsymbol{\epsilon}}^{[0,0]}(x) ,\\ W_{1;\boldsymbol{\epsilon}}^{\{0\}}(x) & = \Big(1 - \frac{2}{\beta}\Big)\mathcal{W}_{1;\boldsymbol{\epsilon}}^{[0,1]}(x), \\ W_{2;\boldsymbol{\epsilon}}^{\{0\}}(x_1,x_2) & = \frac{2}{\beta}\,\mathcal{W}_{2;\boldsymbol{\epsilon}}^{[0,0]}(x_1,x_2). \end{align*} $$
All these quantities have an analytic continuation in the variables
![]() $x_i$
on the same Riemann surface
$x_i$
on the same Riemann surface
![]() $\mathcal {C}_{\boldsymbol {\epsilon }}$
called spectral curve. The curve
$\mathcal {C}_{\boldsymbol {\epsilon }}$
called spectral curve. The curve
![]() $\mathcal {C}_{\boldsymbol {\epsilon }}$
can, in fact, be defined as the maximal Riemann surface on which
$\mathcal {C}_{\boldsymbol {\epsilon }}$
can, in fact, be defined as the maximal Riemann surface on which
![]() $W_{1;\boldsymbol {\epsilon }}^{\{-1\}}(x)$
, initially defined for
$W_{1;\boldsymbol {\epsilon }}^{\{-1\}}(x)$
, initially defined for
![]() $x \in \mathbb {C} \setminus \mathsf {A}$
, admits an analytic continuation (cf. Section 1.7 for a continued discussion on geometry of spectral curves). The information carried by the decomposition (1.16) is that, if V is chosen independent of
$x \in \mathbb {C} \setminus \mathsf {A}$
, admits an analytic continuation (cf. Section 1.7 for a continued discussion on geometry of spectral curves). The information carried by the decomposition (1.16) is that, if V is chosen independent of
![]() $\beta $
and N, all the
$\beta $
and N, all the
![]() $\mathcal {W}_{n;\boldsymbol {\epsilon }}^{[G,K]}$
are also independent of
$\mathcal {W}_{n;\boldsymbol {\epsilon }}^{[G,K]}$
are also independent of
![]() $\beta $
and N (except perhaps through the implicit dependence in N of
$\beta $
and N (except perhaps through the implicit dependence in N of
![]() $\boldsymbol {\epsilon }$
), and thus, the coefficients of the expansions of the correlators display a remarkable structure of Laurent polynomial in
$\boldsymbol {\epsilon }$
), and thus, the coefficients of the expansions of the correlators display a remarkable structure of Laurent polynomial in
![]() $\frac {\beta }{2}$
. This property comes from the structure of the Dyson–Schwinger equations.
$\frac {\beta }{2}$
. This property comes from the structure of the Dyson–Schwinger equations.
From the same initial data, Chekhov and Eynard also define numbers
![]() $W_{0;\boldsymbol {\epsilon }}^{[G,K]} = \mathcal {F}_{\boldsymbol {\epsilon }}^{[G,K]}$
, which give the coefficients of the asymptotic expansion of the free energy
$W_{0;\boldsymbol {\epsilon }}^{[G,K]} = \mathcal {F}_{\boldsymbol {\epsilon }}^{[G,K]}$
, which give the coefficients of the asymptotic expansion of the free energy
![]() $\ln Z_{N,\beta ;\boldsymbol {N}/N}^{V;\mathsf {A}}$
up to an integration constant independent of the potential, and which are independent of
$\ln Z_{N,\beta ;\boldsymbol {N}/N}^{V;\mathsf {A}}$
up to an integration constant independent of the potential, and which are independent of
![]() $\beta $
provided V is chosen independent of
$\beta $
provided V is chosen independent of
![]() $\beta $
. More precisely, we mean that for any two potentials V and
$\beta $
. More precisely, we mean that for any two potentials V and
![]() $\tilde {V}$
satisfying the assumptions of Theorem 1.4 and leading to a
$\tilde {V}$
satisfying the assumptions of Theorem 1.4 and leading to a
![]() $(g + 1)$
-cut regime, we must have for
$(g + 1)$
-cut regime, we must have for
![]() $k \geq -2$
, by consistency with [Reference Chekhov and EynardCE06],
$k \geq -2$
, by consistency with [Reference Chekhov and EynardCE06],
 $$ \begin{align*}F^{\{k\};V}_{\beta;\boldsymbol{\epsilon}} - F^{\{k\};\tilde{V}}_{\beta;\boldsymbol{\epsilon}} = \sum_{G = 0}^{\lfloor \frac{k}{2} \rfloor + 1} \Big(\frac{\beta}{2}\Big)^{1 - G}\Big(1 - \frac{2}{\beta}\Big)^{k + 2 - 2G}\,\big(\mathcal{F}^{[G,k + 2 - 2G];V}_{\boldsymbol{\epsilon}} - \mathcal{F}^{[G,k + 2 - 2G];\tilde{V}}_{\boldsymbol{\epsilon}}\big). \end{align*} $$
$$ \begin{align*}F^{\{k\};V}_{\beta;\boldsymbol{\epsilon}} - F^{\{k\};\tilde{V}}_{\beta;\boldsymbol{\epsilon}} = \sum_{G = 0}^{\lfloor \frac{k}{2} \rfloor + 1} \Big(\frac{\beta}{2}\Big)^{1 - G}\Big(1 - \frac{2}{\beta}\Big)^{k + 2 - 2G}\,\big(\mathcal{F}^{[G,k + 2 - 2G];V}_{\boldsymbol{\epsilon}} - \mathcal{F}^{[G,k + 2 - 2G];\tilde{V}}_{\boldsymbol{\epsilon}}\big). \end{align*} $$
In particular, the topological recursion defines
![]() $\mathcal {F}^{[0,0];V}_{\boldsymbol {\epsilon }} = E[\mu _{\mathrm{eq};\boldsymbol {\epsilon }}^V]$
and
$\mathcal {F}^{[0,0];V}_{\boldsymbol {\epsilon }} = E[\mu _{\mathrm{eq};\boldsymbol {\epsilon }}^V]$
and
![]() $\mathcal {F}^{[0,1];V}_{\boldsymbol {\epsilon }} = -\mathrm{Ent}[\mu _{\mathrm{eq};\boldsymbol {\epsilon }}^{V}]$
. By comparison with (1.15), we arrive to an absolute comparison (here, assume the potential to be independent of N – i.e.,
$\mathcal {F}^{[0,1];V}_{\boldsymbol {\epsilon }} = -\mathrm{Ent}[\mu _{\mathrm{eq};\boldsymbol {\epsilon }}^{V}]$
. By comparison with (1.15), we arrive to an absolute comparison (here, assume the potential to be independent of N – i.e.,
![]() $V = V^{\{0\}}$
):
$V = V^{\{0\}}$
):
 $$ \begin{align} \nonumber F^{\{-2\};V}_{\beta;\boldsymbol{\epsilon}} & = \frac{\beta}{2}\,\mathcal{F}^{[0,0];V}_{\boldsymbol{\epsilon}}, \\ F^{\{-1\};V}_{\beta;\boldsymbol{\epsilon}} & = \frac{\beta}{2}\Big(1 - \frac{2}{\beta}\Big)\Big(\mathcal{F}^{[0,1];V}_{\boldsymbol{\epsilon}} + \ln\big(\tfrac{\beta}{2}\big)\Big) + \frac{\beta}{2}\ln\big(\tfrac{2\pi}{e}\big) - \ln \Gamma\big(\tfrac{\beta}{2}\big). \end{align} $$
$$ \begin{align} \nonumber F^{\{-2\};V}_{\beta;\boldsymbol{\epsilon}} & = \frac{\beta}{2}\,\mathcal{F}^{[0,0];V}_{\boldsymbol{\epsilon}}, \\ F^{\{-1\};V}_{\beta;\boldsymbol{\epsilon}} & = \frac{\beta}{2}\Big(1 - \frac{2}{\beta}\Big)\Big(\mathcal{F}^{[0,1];V}_{\boldsymbol{\epsilon}} + \ln\big(\tfrac{\beta}{2}\big)\Big) + \frac{\beta}{2}\ln\big(\tfrac{2\pi}{e}\big) - \ln \Gamma\big(\tfrac{\beta}{2}\big). \end{align} $$
The constant in the second line was not computed in [Reference Chekhov and EynardCE06]. To our knowledge, the absolute – including a
![]() $\beta $
-dependent, possibly g-dependent but otherwise V-independent constant – comparison between the coefficients
$\beta $
-dependent, possibly g-dependent but otherwise V-independent constant – comparison between the coefficients
![]() $F_{\beta ;\boldsymbol {\epsilon }}^{\{k\};V}$
of the asymptotic expansion of the
$F_{\beta ;\boldsymbol {\epsilon }}^{\{k\};V}$
of the asymptotic expansion of the
![]() $\beta $
-ensembles and the invariants
$\beta $
-ensembles and the invariants
![]() $\mathcal {F}^{[G,m]}$
for
$\mathcal {F}^{[G,m]}$
for
![]() $(G,m) \neq (0,0),(0,1)$
produced by the topological recursion has not been performed in full generality. It is only known for
$(G,m) \neq (0,0),(0,1)$
produced by the topological recursion has not been performed in full generality. It is only known for
![]() $\beta = 2$
for all G in the one-cut regime; see [Reference MarchalMar17, Proposition 2.5].
$\beta = 2$
for all G in the one-cut regime; see [Reference MarchalMar17, Proposition 2.5].
When
![]() $\beta = 2$
, only
$\beta = 2$
, only
![]() $\mathcal {W}_{n;\boldsymbol {\epsilon }}^{[G]} = \mathcal {W}_{n;\boldsymbol {\epsilon }}^{[G,0]}$
and
$\mathcal {W}_{n;\boldsymbol {\epsilon }}^{[G]} = \mathcal {W}_{n;\boldsymbol {\epsilon }}^{[G,0]}$
and
![]() $\mathcal {F}_{\boldsymbol {\epsilon }}^{[G]} = \mathcal {F}^{[G,0]}_{\boldsymbol {\epsilon }}$
appear. These are the quantities defined by the Chekhov–Eynard–Orantin topological recursion [Reference Eynard and OrantinEO07], and we retrieve the usual asymptotic expansions
$\mathcal {F}_{\boldsymbol {\epsilon }}^{[G]} = \mathcal {F}^{[G,0]}_{\boldsymbol {\epsilon }}$
appear. These are the quantities defined by the Chekhov–Eynard–Orantin topological recursion [Reference Eynard and OrantinEO07], and we retrieve the usual asymptotic expansions
 $$ \begin{align*} \mathcal{W}_{n;\boldsymbol{\epsilon}}(x_1,\ldots,x_n) & = \sum_{G \geq 0} N^{2 - 2G - n}\,\mathcal{W}_{n;\boldsymbol{\epsilon}}^{[G]}(x_1,\ldots,x_n), \\ \ln\bigg(\frac{Z_{N,\beta;\boldsymbol{\epsilon}}^{V;\mathsf{A}}}{Z_{N,\beta;\boldsymbol{\epsilon}}^{\tilde{V};\mathsf{A}}}\bigg) & = \sum_{G \geq 0} N^{2 - 2G}\big(\mathcal{F}^{[G];V}_{\boldsymbol{\epsilon}} - \mathcal{F}^{[G];\tilde{V}}_{\boldsymbol{\epsilon}}\big), \end{align*} $$
$$ \begin{align*} \mathcal{W}_{n;\boldsymbol{\epsilon}}(x_1,\ldots,x_n) & = \sum_{G \geq 0} N^{2 - 2G - n}\,\mathcal{W}_{n;\boldsymbol{\epsilon}}^{[G]}(x_1,\ldots,x_n), \\ \ln\bigg(\frac{Z_{N,\beta;\boldsymbol{\epsilon}}^{V;\mathsf{A}}}{Z_{N,\beta;\boldsymbol{\epsilon}}^{\tilde{V};\mathsf{A}}}\bigg) & = \sum_{G \geq 0} N^{2 - 2G}\big(\mathcal{F}^{[G];V}_{\boldsymbol{\epsilon}} - \mathcal{F}^{[G];\tilde{V}}_{\boldsymbol{\epsilon}}\big), \end{align*} $$
involving only powers of
![]() $\frac {1}{N}$
with parity
$\frac {1}{N}$
with parity
![]() $(-1)^n$
in the n-point correlators and powers of
$(-1)^n$
in the n-point correlators and powers of
![]() $\frac {1}{N^2}$
in the free energy.
$\frac {1}{N^2}$
in the free energy.
1.6. Main results in the multi-cut regime: partition function
Let us come back to the initial model (1.1). We can always take
![]() $\mathsf {A} = \bigcup _{h = 0}^{g} \mathsf {A}_h \subseteq \mathsf {B}$
to be a small enlargement of the support
$\mathsf {A} = \bigcup _{h = 0}^{g} \mathsf {A}_h \subseteq \mathsf {B}$
to be a small enlargement of the support
![]() $\mathsf {S}$
respecting the setup of § 1.4. It is indeed well known that the partition function
$\mathsf {S}$
respecting the setup of § 1.4. It is indeed well known that the partition function
![]() $Z_{N,\beta }^{V;\mathsf {B}}$
can be replaced by
$Z_{N,\beta }^{V;\mathsf {B}}$
can be replaced by
![]() $Z_{N,\beta }^{V;\mathsf {A}}$
up to exponentially small corrections when N is large (see [Reference Pastur and ShcherbinaPS11, Reference Borot and GuionnetBG11] for results in this direction, and we give a proof for completeness in § 3.1 below). The latter can be decomposed as a sum over all possible ways of distributing the
$Z_{N,\beta }^{V;\mathsf {A}}$
up to exponentially small corrections when N is large (see [Reference Pastur and ShcherbinaPS11, Reference Borot and GuionnetBG11] for results in this direction, and we give a proof for completeness in § 3.1 below). The latter can be decomposed as a sum over all possible ways of distributing the
![]() $\lambda $
s between the segments
$\lambda $
s between the segments
![]() $\mathsf {A}_h$
– namely,
$\mathsf {A}_h$
– namely,
 $$ \begin{align} Z_{N,\beta}^{V;\mathsf{A}} = \sum_{\substack{ N_0,\ldots,N_{g} \geq 0 \\ \sum_{h=0}^g N_h= N}} \frac{N!}{\prod_{h = 0}^{g} N_h!}\,Z_{N,\beta;\boldsymbol{N}/N}^{V;\mathsf{A}}, \end{align} $$
$$ \begin{align} Z_{N,\beta}^{V;\mathsf{A}} = \sum_{\substack{ N_0,\ldots,N_{g} \geq 0 \\ \sum_{h=0}^g N_h= N}} \frac{N!}{\prod_{h = 0}^{g} N_h!}\,Z_{N,\beta;\boldsymbol{N}/N}^{V;\mathsf{A}}, \end{align} $$
where we have denoted
![]() $N_0 = N - \sum _{h = 1}^{g} N_h$
the number of
$N_0 = N - \sum _{h = 1}^{g} N_h$
the number of
![]() $\lambda $
s put in the segment
$\lambda $
s put in the segment
![]() $\mathsf {A}_0$
. So we can use our results for the model with fixed filling fractions to analyse the asymptotic behaviour of each term in the sum and then find the asymptotic expansion of the sum taking into account the interference of all contributions. This is carried out in Section 8.1.
$\mathsf {A}_0$
. So we can use our results for the model with fixed filling fractions to analyse the asymptotic behaviour of each term in the sum and then find the asymptotic expansion of the sum taking into account the interference of all contributions. This is carried out in Section 8.1.
Before stating the results, we need two ingredients. First, we let
![]() $\mathfrak {Z}_{N,\beta ;\boldsymbol {\epsilon }}^{V;\mathsf {A}}$
be the (truncated at an arbitrary order K) asymptotic series depending on a g-dimensional vector with positive entries, at least when its coefficients are defined:
$\mathfrak {Z}_{N,\beta ;\boldsymbol {\epsilon }}^{V;\mathsf {A}}$
be the (truncated at an arbitrary order K) asymptotic series depending on a g-dimensional vector with positive entries, at least when its coefficients are defined:
 $$ \begin{align} \mathfrak{Z}_{N,\beta;\boldsymbol{\epsilon}}^{V;\mathsf{A}}= N^{\frac{\beta}{2}N + \varkappa}\exp\Big(\sum_{k = -2}^{K} N^{-k}\,F^{\{k\};V}_{\beta;\boldsymbol{\epsilon}} + O(N^{-(K + 1)})\Big)\,. \end{align} $$
$$ \begin{align} \mathfrak{Z}_{N,\beta;\boldsymbol{\epsilon}}^{V;\mathsf{A}}= N^{\frac{\beta}{2}N + \varkappa}\exp\Big(\sum_{k = -2}^{K} N^{-k}\,F^{\{k\};V}_{\beta;\boldsymbol{\epsilon}} + O(N^{-(K + 1)})\Big)\,. \end{align} $$
If we substitute
![]() $\boldsymbol {\epsilon } = \boldsymbol {N}/N$
as in Theorem 1.4, it gives the asymptotic expansion of the partition function of the fixed filling fractions model with unordered eigenvalues, and we recall that
$\boldsymbol {\epsilon } = \boldsymbol {N}/N$
as in Theorem 1.4, it gives the asymptotic expansion of the partition function of the fixed filling fractions model with unordered eigenvalues, and we recall that
![]() $F^{\{k\};V}_{\beta ;\boldsymbol {\epsilon }}$
exists as a smooth function of
$F^{\{k\};V}_{\beta ;\boldsymbol {\epsilon }}$
exists as a smooth function of
![]() $\boldsymbol {\epsilon }$
in some non-empty open set. We shall denote
$\boldsymbol {\epsilon }$
in some non-empty open set. We shall denote
![]() $(F^{\{k\};V}_{\beta ;\boldsymbol {\epsilon }})^{(j)}$
the tensor of j-th derivatives with respect to
$(F^{\{k\};V}_{\beta ;\boldsymbol {\epsilon }})^{(j)}$
the tensor of j-th derivatives with respect to
![]() $\boldsymbol {\epsilon }$
.
$\boldsymbol {\epsilon }$
.
Second, we introduce the Siegel Theta function with characteristics
![]() $\boldsymbol {\mu },\boldsymbol {\nu } \in \mathbb {C}^{g}$
. If
$\boldsymbol {\mu },\boldsymbol {\nu } \in \mathbb {C}^{g}$
. If
![]() $\boldsymbol {\tau }$
is a symmetric
$\boldsymbol {\tau }$
is a symmetric
![]() $g \times g$
matrix of complex numbers such that
$g \times g$
matrix of complex numbers such that
![]() $\mathrm {Im}\,\boldsymbol {\tau }> 0$
, the Siegel Theta function is the entire function of
$\mathrm {Im}\,\boldsymbol {\tau }> 0$
, the Siegel Theta function is the entire function of
![]() $\boldsymbol {v} \in \mathbb {C}^{g}$
defined by the exponentially fast converging series
$\boldsymbol {v} \in \mathbb {C}^{g}$
defined by the exponentially fast converging series
 $$ \begin{align} \vartheta\!\left[\begin{array}{@{\hspace{-0.02cm}}l@{\hspace{-0.02cm}}} \boldsymbol{\mu} \\ \boldsymbol{\nu} \end{array}\right]\!\!(\boldsymbol{v}|\boldsymbol{\tau}) = \sum_{\boldsymbol{m} \in \mathbb{Z}^{g}} \exp\Big(\mathrm{i}\pi (\boldsymbol{m} + \boldsymbol{\mu})\cdot\boldsymbol{\tau}\cdot(\boldsymbol{m} + \boldsymbol{\mu}) + 2\mathrm{i}\pi(\boldsymbol{v} + \boldsymbol{\nu})\cdot(\boldsymbol{m} + \boldsymbol{\mu})\Big). \end{align} $$
$$ \begin{align} \vartheta\!\left[\begin{array}{@{\hspace{-0.02cm}}l@{\hspace{-0.02cm}}} \boldsymbol{\mu} \\ \boldsymbol{\nu} \end{array}\right]\!\!(\boldsymbol{v}|\boldsymbol{\tau}) = \sum_{\boldsymbol{m} \in \mathbb{Z}^{g}} \exp\Big(\mathrm{i}\pi (\boldsymbol{m} + \boldsymbol{\mu})\cdot\boldsymbol{\tau}\cdot(\boldsymbol{m} + \boldsymbol{\mu}) + 2\mathrm{i}\pi(\boldsymbol{v} + \boldsymbol{\nu})\cdot(\boldsymbol{m} + \boldsymbol{\mu})\Big). \end{align} $$
Among its essential properties, we mention the following:
-
○ for any characteristics
 $\boldsymbol {\mu },\boldsymbol {\nu }$
, it satisfies the diffusion-like equation
$\boldsymbol {\mu },\boldsymbol {\nu }$
, it satisfies the diffusion-like equation
 $4\mathrm{i}\pi \partial _{\tau _{h,h'}}\vartheta = \partial _{v_h}\partial _{v_{h'}}\vartheta $
.
$4\mathrm{i}\pi \partial _{\tau _{h,h'}}\vartheta = \partial _{v_h}\partial _{v_{h'}}\vartheta $
. -
○ it is a quasi-periodic function with lattice
 $\mathbb {Z}^{g} \oplus \boldsymbol {\tau }(\mathbb {Z}^{g})$
: for any
$\mathbb {Z}^{g} \oplus \boldsymbol {\tau }(\mathbb {Z}^{g})$
: for any
 $\boldsymbol {m}_0,\boldsymbol {n}_0 \in \mathbb {Z}^{g}$
,
$\boldsymbol {m}_0,\boldsymbol {n}_0 \in \mathbb {Z}^{g}$
,  $$ \begin{align*}\vartheta\!\left[\begin{array}{@{\hspace{-0.02cm}}l@{\hspace{-0.02cm}}} \boldsymbol{\mu} \\ \boldsymbol{\nu} \end{array}\right]\!\!(\boldsymbol{v} + \boldsymbol{m}_0 + \boldsymbol{\tau}\cdot\boldsymbol{n}_0|\boldsymbol{\tau}) = \exp\big(2\mathrm{i}\pi\boldsymbol{m}_0\cdot\boldsymbol{\mu} - 2\mathrm{i}\pi \boldsymbol{n_0}\cdot(\boldsymbol{v} + \boldsymbol{\nu}) - \mathrm{i}\pi\boldsymbol{n}_0\cdot\boldsymbol{\tau}\cdot\boldsymbol{n}_0\big)\,\vartheta\!\left[\begin{array}{@{\hspace{-0.02cm}}l@{\hspace{-0.02cm}}} \boldsymbol{\mu} \\ \boldsymbol{\nu} \end{array}\right]\!\!(\boldsymbol{v}|\boldsymbol{\tau}). \end{align*} $$
$$ \begin{align*}\vartheta\!\left[\begin{array}{@{\hspace{-0.02cm}}l@{\hspace{-0.02cm}}} \boldsymbol{\mu} \\ \boldsymbol{\nu} \end{array}\right]\!\!(\boldsymbol{v} + \boldsymbol{m}_0 + \boldsymbol{\tau}\cdot\boldsymbol{n}_0|\boldsymbol{\tau}) = \exp\big(2\mathrm{i}\pi\boldsymbol{m}_0\cdot\boldsymbol{\mu} - 2\mathrm{i}\pi \boldsymbol{n_0}\cdot(\boldsymbol{v} + \boldsymbol{\nu}) - \mathrm{i}\pi\boldsymbol{n}_0\cdot\boldsymbol{\tau}\cdot\boldsymbol{n}_0\big)\,\vartheta\!\left[\begin{array}{@{\hspace{-0.02cm}}l@{\hspace{-0.02cm}}} \boldsymbol{\mu} \\ \boldsymbol{\nu} \end{array}\right]\!\!(\boldsymbol{v}|\boldsymbol{\tau}). \end{align*} $$
-
○ it has a nice transformation law under
 $\boldsymbol {\tau } \rightarrow (\boldsymbol {A\tau } + \boldsymbol {B})(\boldsymbol {C\tau } + \boldsymbol {D})^{-1}$
, where
$\boldsymbol {\tau } \rightarrow (\boldsymbol {A\tau } + \boldsymbol {B})(\boldsymbol {C\tau } + \boldsymbol {D})^{-1}$
, where
 $\boldsymbol {A},\boldsymbol {B},\boldsymbol {C},\boldsymbol {D}$
are the
$\boldsymbol {A},\boldsymbol {B},\boldsymbol {C},\boldsymbol {D}$
are the
 $g \times g$
blocks of a
$g \times g$
blocks of a
 $2g \times 2g$
symplectic matrix [Reference MumfordMum84].
$2g \times 2g$
symplectic matrix [Reference MumfordMum84]. -
○ when
 $\boldsymbol {\tau }$
is the matrix of periods of a genus g Riemann surface, it satisfies the Fay identity [Reference FayFay70].
$\boldsymbol {\tau }$
is the matrix of periods of a genus g Riemann surface, it satisfies the Fay identity [Reference FayFay70].
We define the gradient operator
![]() $\nabla _{\boldsymbol {v}}$
acting on the variable
$\nabla _{\boldsymbol {v}}$
acting on the variable
![]() $\boldsymbol {v}$
of this function. For instance, the diffusion equation takes the form
$\boldsymbol {v}$
of this function. For instance, the diffusion equation takes the form
![]() $4\mathrm{i}\pi \partial _{\boldsymbol {\tau }}\vartheta = \nabla ^{\otimes 2}_{\boldsymbol {v}}\vartheta $
.
$4\mathrm{i}\pi \partial _{\boldsymbol {\tau }}\vartheta = \nabla ^{\otimes 2}_{\boldsymbol {v}}\vartheta $
.
Theorem 1.5. Assume Hypotheses 1.1 and 1.3. Let
![]() $\boldsymbol {\epsilon }_{\star } = (\mu _\mathrm{{eq}}^V[\mathsf {S}_h])_{1 \leq h \leq g}$
– we shall replace all indices
$\boldsymbol {\epsilon }_{\star } = (\mu _\mathrm{{eq}}^V[\mathsf {S}_h])_{1 \leq h \leq g}$
– we shall replace all indices
![]() $\boldsymbol {\epsilon }$
by
$\boldsymbol {\epsilon }$
by
![]() $\star $
in our notations to indicate a specialisation at
$\star $
in our notations to indicate a specialisation at
![]() $\boldsymbol {\epsilon } = \boldsymbol {\epsilon }_\star $
. Then, the partition function has an asymptotic expansion of the form, with
$\boldsymbol {\epsilon } = \boldsymbol {\epsilon }_\star $
. Then, the partition function has an asymptotic expansion of the form, with
![]() $\mathsf {C}=\mathsf {B}$
or
$\mathsf {C}=\mathsf {B}$
or
![]() $\mathsf {A}$
, for any
$\mathsf {A}$
, for any
![]() $K \geq -2$
,
$K \geq -2$
,
 $$ \begin{align} Z_{N,\beta}^{V;\mathsf{C}} = \mathfrak{Z}_{N,\beta;\star}^{V;\mathsf{A}}\left\{\Big(\sum_{k = 0}^{K} N^{-k}\,T_{\beta;\star}^{\{k\}}\big[\tfrac{\nabla_{\boldsymbol v}}{2\mathrm{i}\pi}\big]\Big)\vartheta\!\left[\begin{array}{@{\hspace{-0.03cm}}c@{\hspace{-0.03cm}}} -N\boldsymbol{\epsilon}_{\star}\, \\ \boldsymbol{0} \end{array}\right]\!\!(\boldsymbol{v}_{\beta;\star}|\boldsymbol{\tau}_{\beta;\star}) + O(N^{-(K + 1)})\right\}. \end{align} $$
$$ \begin{align} Z_{N,\beta}^{V;\mathsf{C}} = \mathfrak{Z}_{N,\beta;\star}^{V;\mathsf{A}}\left\{\Big(\sum_{k = 0}^{K} N^{-k}\,T_{\beta;\star}^{\{k\}}\big[\tfrac{\nabla_{\boldsymbol v}}{2\mathrm{i}\pi}\big]\Big)\vartheta\!\left[\begin{array}{@{\hspace{-0.03cm}}c@{\hspace{-0.03cm}}} -N\boldsymbol{\epsilon}_{\star}\, \\ \boldsymbol{0} \end{array}\right]\!\!(\boldsymbol{v}_{\beta;\star}|\boldsymbol{\tau}_{\beta;\star}) + O(N^{-(K + 1)})\right\}. \end{align} $$
In this expression,
![]() $\mathfrak {Z}_{N,\beta ;\star }^{V;\mathsf {A}}$
is the asymptotic series defined in Equation (1.19) and evaluated at
$\mathfrak {Z}_{N,\beta ;\star }^{V;\mathsf {A}}$
is the asymptotic series defined in Equation (1.19) and evaluated at
![]() $\boldsymbol {\epsilon } = \boldsymbol {\epsilon }_{\star }$
. If
$\boldsymbol {\epsilon } = \boldsymbol {\epsilon }_{\star }$
. If
![]() $\boldsymbol {X}$
is a vector with g components, we set
$\boldsymbol {X}$
is a vector with g components, we set
![]() $T^{\{0\}}_{\beta ;\boldsymbol {\epsilon }}[\boldsymbol {X}] = 1$
, and for
$T^{\{0\}}_{\beta ;\boldsymbol {\epsilon }}[\boldsymbol {X}] = 1$
, and for
![]() $k \geq 1$
,
$k \geq 1$
,
 $$ \begin{align} T_{\beta;\boldsymbol{\epsilon}}^{\{k\}}[\boldsymbol{X}] = \sum_{r = 1}^{k} \frac{1}{r!} \sum_{\substack{k_1,\ldots,k_r \geq -2 \\ j_1,\ldots,j_r> 0 \\ k_i + j_i > 0 \\ \sum_{i = 1}^{r} k_i + j_i = k}} \Big(\bigotimes_{i = 1}^{r} \frac{(F_{\beta;\boldsymbol{\epsilon}}^{\{k_i\};V})^{(j_i)}}{j_i!}\Big)\cdot\boldsymbol{X}^{\otimes(\sum_{i = 1}^r j_i)}, \end{align} $$
$$ \begin{align} T_{\beta;\boldsymbol{\epsilon}}^{\{k\}}[\boldsymbol{X}] = \sum_{r = 1}^{k} \frac{1}{r!} \sum_{\substack{k_1,\ldots,k_r \geq -2 \\ j_1,\ldots,j_r> 0 \\ k_i + j_i > 0 \\ \sum_{i = 1}^{r} k_i + j_i = k}} \Big(\bigotimes_{i = 1}^{r} \frac{(F_{\beta;\boldsymbol{\epsilon}}^{\{k_i\};V})^{(j_i)}}{j_i!}\Big)\cdot\boldsymbol{X}^{\otimes(\sum_{i = 1}^r j_i)}, \end{align} $$
where
![]() $\cdot $
denotes the standard scalar product on the tensor space. We have also introduced
$\cdot $
denotes the standard scalar product on the tensor space. We have also introduced
 $$ \begin{align*}\boldsymbol{v}_{\beta;\star} = \frac{(F^{\{-1\};V}_{\beta;\star})'}{2\mathrm{i}\pi},\qquad \boldsymbol{\tau}_{\beta;\star} = \frac{(F^{\{-2\};V}_{\beta;\star})"}{2{\mathrm{i}\pi}}. \end{align*} $$
$$ \begin{align*}\boldsymbol{v}_{\beta;\star} = \frac{(F^{\{-1\};V}_{\beta;\star})'}{2\mathrm{i}\pi},\qquad \boldsymbol{\tau}_{\beta;\star} = \frac{(F^{\{-2\};V}_{\beta;\star})"}{2{\mathrm{i}\pi}}. \end{align*} $$
Being more explicit but less compact, we may rewrite
 $$ \begin{align} \nonumber \quad T_{\beta;\star}^{\{k\}}\big[\tfrac{\nabla_{\boldsymbol{v}}}{2\mathrm{i}\pi}\big]\vartheta\!\left[\begin{array}{@{\hspace{-0.03cm}}c@{\hspace{-0.03cm}}} -N\boldsymbol{\epsilon}_{\star}\, \\ \boldsymbol{0} \end{array}\right]\!\!(\boldsymbol{v}_{\beta;\star}|\boldsymbol{\tau}_{\beta;\star}) & = \sum_{r = 1}^{k} \frac{1}{r!} \sum_{\substack{k_1,\ldots,k_r \geq -2 \\ j_1,\ldots,j_r> 0 \\ k_i + j_i > 0 \\ \sum_{i = 1}^{r} k_i + j_i = k}}\!\!\!\! \Big(\bigotimes_{i = 1}^{r} \frac{(F_{\beta;\star}^{\{k_i\};V})^{(j_i)}}{j_i!}\Big) \\ & \quad \cdot \Big(\sum_{\boldsymbol{m} \in \mathbb{Z}^{g}}(\boldsymbol{m} - N\boldsymbol{\epsilon}_{\star})^{\otimes(\sum_{i = 1}^r j_i)}\,e^{\mathrm{i}\pi \cdot\boldsymbol{\tau_{\beta;\star}}\cdot(\boldsymbol{m} - N\boldsymbol{\epsilon}_{\star})^{\otimes 2} + 2\mathrm{i}\pi \boldsymbol{v}_{\beta;\star}\cdot(\boldsymbol{m} - N\boldsymbol{\epsilon}_{\star})}\Big). \end{align} $$
$$ \begin{align} \nonumber \quad T_{\beta;\star}^{\{k\}}\big[\tfrac{\nabla_{\boldsymbol{v}}}{2\mathrm{i}\pi}\big]\vartheta\!\left[\begin{array}{@{\hspace{-0.03cm}}c@{\hspace{-0.03cm}}} -N\boldsymbol{\epsilon}_{\star}\, \\ \boldsymbol{0} \end{array}\right]\!\!(\boldsymbol{v}_{\beta;\star}|\boldsymbol{\tau}_{\beta;\star}) & = \sum_{r = 1}^{k} \frac{1}{r!} \sum_{\substack{k_1,\ldots,k_r \geq -2 \\ j_1,\ldots,j_r> 0 \\ k_i + j_i > 0 \\ \sum_{i = 1}^{r} k_i + j_i = k}}\!\!\!\! \Big(\bigotimes_{i = 1}^{r} \frac{(F_{\beta;\star}^{\{k_i\};V})^{(j_i)}}{j_i!}\Big) \\ & \quad \cdot \Big(\sum_{\boldsymbol{m} \in \mathbb{Z}^{g}}(\boldsymbol{m} - N\boldsymbol{\epsilon}_{\star})^{\otimes(\sum_{i = 1}^r j_i)}\,e^{\mathrm{i}\pi \cdot\boldsymbol{\tau_{\beta;\star}}\cdot(\boldsymbol{m} - N\boldsymbol{\epsilon}_{\star})^{\otimes 2} + 2\mathrm{i}\pi \boldsymbol{v}_{\beta;\star}\cdot(\boldsymbol{m} - N\boldsymbol{\epsilon}_{\star})}\Big). \end{align} $$
For
![]() $\beta = 2$
, this result has been derived heuristically to leading order in [Reference Bonnet, David and EynardBDE00] and to all orders in [Reference EynardEyn09]. These heuristic arguments can be extended straightforwardly to all values of
$\beta = 2$
, this result has been derived heuristically to leading order in [Reference Bonnet, David and EynardBDE00] and to all orders in [Reference EynardEyn09]. These heuristic arguments can be extended straightforwardly to all values of
![]() $\beta $
; see, for example, [Reference BorotBor11]. Our work justifies their heuristic argument. To prove this result, we exploit the Dyson–Schwinger equations for the
$\beta $
; see, for example, [Reference BorotBor11]. Our work justifies their heuristic argument. To prove this result, we exploit the Dyson–Schwinger equations for the
![]() $\beta $
-ensemble with fixed filling fractions taking advantage of a rough control on the large N behaviour of the correlators. The result of Theorem 1.5 has been derived up to
$\beta $
-ensemble with fixed filling fractions taking advantage of a rough control on the large N behaviour of the correlators. The result of Theorem 1.5 has been derived up to
![]() $o(1)$
by Shcherbina [Reference ShcherbinaShc12] for real-analytic potentials, with different techniques, based on the representation of
$o(1)$
by Shcherbina [Reference ShcherbinaShc12] for real-analytic potentials, with different techniques, based on the representation of
![]() $\prod _{h < h'} \prod _{i,j} |\lambda _{h,i} - \lambda _{h',j}|^{\beta }$
, which is the exponential of a quadratic statistic, as expectation value of a linear statistics coupled to a Brownian motion. The rough a priori controls on the correlators do not allow at present the description of the
$\prod _{h < h'} \prod _{i,j} |\lambda _{h,i} - \lambda _{h',j}|^{\beta }$
, which is the exponential of a quadratic statistic, as expectation value of a linear statistics coupled to a Brownian motion. The rough a priori controls on the correlators do not allow at present the description of the
![]() $o(1)$
by such methods. The results in [Reference ShcherbinaShc12] were also written in a different form:
$o(1)$
by such methods. The results in [Reference ShcherbinaShc12] were also written in a different form:
![]() $F^{\{0\};V}_{\beta ;\boldsymbol {\epsilon }}$
appearing in
$F^{\{0\};V}_{\beta ;\boldsymbol {\epsilon }}$
appearing in
![]() $\mathfrak {Z}$
was identified with a combination of Fredholm determinants (see also the physics paper [Reference Wiegmann and ZabrodinWZ06]), while this representation does not come naturally in our approach. Also, the steps undertaken in Section 8 where we replace the sum over nonnegative integers such that
$\mathfrak {Z}$
was identified with a combination of Fredholm determinants (see also the physics paper [Reference Wiegmann and ZabrodinWZ06]), while this representation does not come naturally in our approach. Also, the steps undertaken in Section 8 where we replace the sum over nonnegative integers such that
![]() $N_0 + \cdots + N_g = N$
in Equation (1.18), by a sum over
$N_0 + \cdots + N_g = N$
in Equation (1.18), by a sum over
![]() $\boldsymbol {N} \in \mathbb {Z}^{g}$
, thus reconstructing the Siegel Theta function, was not performed in [Reference ShcherbinaShc12].
$\boldsymbol {N} \in \mathbb {Z}^{g}$
, thus reconstructing the Siegel Theta function, was not performed in [Reference ShcherbinaShc12].
The
![]() $2\mathrm{i}\pi $
appears because we used the standard definition of the Siegel Theta function,and should not hide the fact that all terms in Equation (1.23) are real-valued. Here, the matrix
$2\mathrm{i}\pi $
appears because we used the standard definition of the Siegel Theta function,and should not hide the fact that all terms in Equation (1.23) are real-valued. Here, the matrix
 $$ \begin{align} \boldsymbol{\tau}_{\beta;\star} = \frac{\mathrm{Hessian}(F^{\{-2\};V}_{\beta;\boldsymbol{\epsilon}})\big|_{\boldsymbol{\epsilon} = \boldsymbol{\epsilon}_{\star}}}{2\mathrm{i}\pi} \end{align} $$
$$ \begin{align} \boldsymbol{\tau}_{\beta;\star} = \frac{\mathrm{Hessian}(F^{\{-2\};V}_{\beta;\boldsymbol{\epsilon}})\big|_{\boldsymbol{\epsilon} = \boldsymbol{\epsilon}_{\star}}}{2\mathrm{i}\pi} \end{align} $$
involved in the Theta function has purely imaginary entries, and
![]() $\mathrm {Im}\,\boldsymbol {\tau }_{\beta ;\star }$
is definite positive according to Theorem 1.4; hence, the Theta function in the right-hand side makes sense. Notice also that for it is
$\mathrm {Im}\,\boldsymbol {\tau }_{\beta ;\star }$
is definite positive according to Theorem 1.4; hence, the Theta function in the right-hand side makes sense. Notice also that for it is
![]() $\mathbb {Z}^g$
-periodic with respect to
$\mathbb {Z}^g$
-periodic with respect to
![]() $\boldsymbol {\mu }$
; hence, we can replace
$\boldsymbol {\mu }$
; hence, we can replace
![]() $-N\boldsymbol {\epsilon }_{\star }$
by
$-N\boldsymbol {\epsilon }_{\star }$
by
![]() $-N\boldsymbol {\epsilon }_{\star } + \lfloor N\boldsymbol {\epsilon }_{\star } \rfloor $
, and this is responsible for modulations in the asymptotic expansion, and thus breakdown of the
$-N\boldsymbol {\epsilon }_{\star } + \lfloor N\boldsymbol {\epsilon }_{\star } \rfloor $
, and this is responsible for modulations in the asymptotic expansion, and thus breakdown of the
![]() $\frac {1}{N}$
expansion. Still, the model has ‘subsequential’ asymptotic expansions in
$\frac {1}{N}$
expansion. Still, the model has ‘subsequential’ asymptotic expansions in
![]() $\frac {1}{N}$
. For instance, for an even potential with two cuts (
$\frac {1}{N}$
. For instance, for an even potential with two cuts (
![]() $g = 1$
) model, we have
$g = 1$
) model, we have
![]() $\epsilon _{\star } = \frac {1}{2}$
, so
$\epsilon _{\star } = \frac {1}{2}$
, so
![]() $(-N\epsilon _{\star }\,\,\mathrm{mod}\,\,\mathbb {Z})$
appearing as characteristic in the Theta function only depends on the parity of N, and for each fixed parity, we get an asymptotic expansion in
$(-N\epsilon _{\star }\,\,\mathrm{mod}\,\,\mathbb {Z})$
appearing as characteristic in the Theta function only depends on the parity of N, and for each fixed parity, we get an asymptotic expansion in
![]() $\frac {1}{N}$
. In fact, having an even potential implies that the fixed-filling fraction model is invariant under
$\frac {1}{N}$
. In fact, having an even potential implies that the fixed-filling fraction model is invariant under
![]() $\epsilon \rightarrow 1 - \epsilon $
, so only the terms with even numbers
$\epsilon \rightarrow 1 - \epsilon $
, so only the terms with even numbers
![]() $j_i$
of derivatives with respect to filling fractions contribute in
$j_i$
of derivatives with respect to filling fractions contribute in
![]() $T^{\{k\}}_{\beta ;\boldsymbol {\epsilon }}$
. If, furthermore,
$T^{\{k\}}_{\beta ;\boldsymbol {\epsilon }}$
. If, furthermore,
![]() $\beta = 2$
, only the
$\beta = 2$
, only the
![]() $(F^{\{k\};V}_{\beta = 2;\star })^{(j)}$
with k even survive, and we deduce that the same is true for
$(F^{\{k\};V}_{\beta = 2;\star })^{(j)}$
with k even survive, and we deduce that the same is true for
![]() $T^{\{k\}}_{\beta =2;\star }$
, so that the logarithm of the partition function has an asymptotic expansion in
$T^{\{k\}}_{\beta =2;\star }$
, so that the logarithm of the partition function has an asymptotic expansion in
![]() $\frac {1}{N^2}$
for N odd and different asymptotic expansion in
$\frac {1}{N^2}$
for N odd and different asymptotic expansion in
![]() $\frac {1}{N^2}$
for N even (of course, up to the universal logarithmic corrections
$\frac {1}{N^2}$
for N even (of course, up to the universal logarithmic corrections
![]() $\frac {\beta }{2}N\ln N + \varkappa \ln N$
).
$\frac {\beta }{2}N\ln N + \varkappa \ln N$
).
Let us give the two first orders of Equation (1.23):
and:
 $$ \begin{align*} T_{\beta;\star}^{\{2\}}[\boldsymbol{X}] & = \frac{1}{72}\,\big[(F_{\beta;\star}^{\{-2\};V})"'\big]^{\otimes 2}\cdot\boldsymbol{X}^{\otimes 6} + \frac{1}{12}\,\big[(F_{\beta;\star}^{\{-2\};V})"'\otimes (F_{\beta;\star}^{\{-1\};V})"\big]\cdot \boldsymbol{X}^{\otimes 5} \\ & \quad + \Big(\frac{1}{6}\,\big[(F_{\beta;\star}^{\{-2\};V})"'\otimes (F_{\beta;\star}^{\{0\};V})'\big] + \frac{1}{8}\,\big[(F_{\beta;\star}^{\{-1\};V})"\big]^{\otimes 2} + \frac{1}{24}\,(F_{\beta;\star}^{\{-2\};V})^{(4)}\Big)\cdot\boldsymbol{X}^{\otimes 4} \\ & \quad + \Big(\frac{1}{2}\,\big[(F_{\beta;\star}^{\{-1\};V})"\otimes(F_{\beta;\star}^{\{0\};V})'\big] + \frac{1}{6}\,(F_{\beta;\star}^{\{-1\};V})"'\Big)\cdot\boldsymbol{X}^{\otimes 3} \\ & \quad + \Big(\frac{1}{2}\,\big[(F_{\beta;\star}^{\{0\};V})'\big]^{\otimes 2} + \frac{1}{2}\,(F_{\beta;\star}^{\{0\};V})"\Big)\cdot\boldsymbol{X}^{\otimes 2} + (F_{\beta;\star}^{\{1\};V})'\cdot \boldsymbol{X}. \end{align*} $$
$$ \begin{align*} T_{\beta;\star}^{\{2\}}[\boldsymbol{X}] & = \frac{1}{72}\,\big[(F_{\beta;\star}^{\{-2\};V})"'\big]^{\otimes 2}\cdot\boldsymbol{X}^{\otimes 6} + \frac{1}{12}\,\big[(F_{\beta;\star}^{\{-2\};V})"'\otimes (F_{\beta;\star}^{\{-1\};V})"\big]\cdot \boldsymbol{X}^{\otimes 5} \\ & \quad + \Big(\frac{1}{6}\,\big[(F_{\beta;\star}^{\{-2\};V})"'\otimes (F_{\beta;\star}^{\{0\};V})'\big] + \frac{1}{8}\,\big[(F_{\beta;\star}^{\{-1\};V})"\big]^{\otimes 2} + \frac{1}{24}\,(F_{\beta;\star}^{\{-2\};V})^{(4)}\Big)\cdot\boldsymbol{X}^{\otimes 4} \\ & \quad + \Big(\frac{1}{2}\,\big[(F_{\beta;\star}^{\{-1\};V})"\otimes(F_{\beta;\star}^{\{0\};V})'\big] + \frac{1}{6}\,(F_{\beta;\star}^{\{-1\};V})"'\Big)\cdot\boldsymbol{X}^{\otimes 3} \\ & \quad + \Big(\frac{1}{2}\,\big[(F_{\beta;\star}^{\{0\};V})'\big]^{\otimes 2} + \frac{1}{2}\,(F_{\beta;\star}^{\{0\};V})"\Big)\cdot\boldsymbol{X}^{\otimes 2} + (F_{\beta;\star}^{\{1\};V})'\cdot \boldsymbol{X}. \end{align*} $$
For
![]() $\beta = 2$
, unlike the one-cut regime where the asymptotic expansion was in
$\beta = 2$
, unlike the one-cut regime where the asymptotic expansion was in
![]() $\frac {1}{N^2}$
up to constants independent of the potential, the multi-cut regime features an asymptotic expansion with nontrivial terms in powers of
$\frac {1}{N^2}$
up to constants independent of the potential, the multi-cut regime features an asymptotic expansion with nontrivial terms in powers of
![]() $\frac {1}{N}$
. For instance, we have a contribution at order
$\frac {1}{N}$
. For instance, we have a contribution at order
![]() $\frac {1}{N}$
of
$\frac {1}{N}$
of
In a two-cuts regime (
![]() $g = 1$
), a sufficient condition for all terms of order
$g = 1$
), a sufficient condition for all terms of order
![]() $N^{-(2k + 1)}$
to vanish (again, up to integration constants already present in
$N^{-(2k + 1)}$
to vanish (again, up to integration constants already present in
![]() $\mathfrak {Z}$
) is that
$\mathfrak {Z}$
) is that
![]() $\epsilon _{\star } = \frac {1}{2}$
and
$\epsilon _{\star } = \frac {1}{2}$
and
![]() $Z_{N,\beta = 2;\epsilon }^{V;\mathsf {A}} = Z_{N,\beta = 2;1 - \epsilon }^{V;\mathsf {A}}$
, for the same reasons that we mentioned for the case of an even potential with two cuts. In such a case, we have an expansion in powers of
$Z_{N,\beta = 2;\epsilon }^{V;\mathsf {A}} = Z_{N,\beta = 2;1 - \epsilon }^{V;\mathsf {A}}$
, for the same reasons that we mentioned for the case of an even potential with two cuts. In such a case, we have an expansion in powers of
![]() $\frac {1}{N^2}$
for the partition function, whose coefficients depend on the parity of N. In general, we also observe that
$\frac {1}{N^2}$
for the partition function, whose coefficients depend on the parity of N. In general, we also observe that
![]() $\boldsymbol {v}_{\beta = 2;\star } = \boldsymbol {0}$
(i.e., Thetanullwerten appear in the expansion).
$\boldsymbol {v}_{\beta = 2;\star } = \boldsymbol {0}$
(i.e., Thetanullwerten appear in the expansion).
Using the fact that the n-th correlator is the n-derivative of the free energy of the partition function for a perturbed potential or order
![]() $1/N$
, and our asymptotic results are uniform for small perturbations of this kind, it is pure algebra to derive from (1.5) an asymptotic expansion for the correlators
$1/N$
, and our asymptotic results are uniform for small perturbations of this kind, it is pure algebra to derive from (1.5) an asymptotic expansion for the correlators
![]() $W_n$
for the initial model in the multi-cut regime. For
$W_n$
for the initial model in the multi-cut regime. For
![]() $\beta = 2$
, the resulting expression can be found, for instance, in [Reference Borot and EynardBE11, Section 6.2] up to
$\beta = 2$
, the resulting expression can be found, for instance, in [Reference Borot and EynardBE11, Section 6.2] up to
![]() $O(\frac {1}{N})$
and a systematic diagrammatic for all orders is given in [Reference Borot and EynardBE12, Appendix A]. This can be straightforwardly extended to the
$O(\frac {1}{N})$
and a systematic diagrammatic for all orders is given in [Reference Borot and EynardBE12, Appendix A]. This can be straightforwardly extended to the
![]() $\beta \neq 2$
case simply by including half-integer genera g (in our conventions, k not having fixed parity).
$\beta \neq 2$
case simply by including half-integer genera g (in our conventions, k not having fixed parity).
1.7. Comments relative to the geometry of the spectral curve
We now stress facts from the theory of the topological recursion [Reference Chekhov and EynardCE06, Reference Eynard and OrantinEO07] which are relevant in the present case – for further details on the geometry compact Riemann surfaces, see, for instance, [Reference EynardEyn18]. When V is a polynomial and
![]() $\boldsymbol {\epsilon }$
is close enough to
$\boldsymbol {\epsilon }$
is close enough to
![]() $\boldsymbol {\epsilon }_{\star }$
, the density of the equilibrium measure can be analytically continued to a hyperelliptic curve of genus g, denoted
$\boldsymbol {\epsilon }_{\star }$
, the density of the equilibrium measure can be analytically continued to a hyperelliptic curve of genus g, denoted
![]() $\mathcal {C}_{\boldsymbol {\epsilon }}$
(the spectral curve). Its equation is
$\mathcal {C}_{\boldsymbol {\epsilon }}$
(the spectral curve). Its equation is
 $$ \begin{align} y^2 = \prod_{h = 0}^{g} (x - \alpha^{-}_{\boldsymbol{\epsilon},h})(x - \alpha^{+}_{\boldsymbol{\epsilon},h}), \end{align} $$
$$ \begin{align} y^2 = \prod_{h = 0}^{g} (x - \alpha^{-}_{\boldsymbol{\epsilon},h})(x - \alpha^{+}_{\boldsymbol{\epsilon},h}), \end{align} $$
and
![]() $\mathcal {C}_{\boldsymbol {\epsilon }}$
is the compactification of the locus of such
$\mathcal {C}_{\boldsymbol {\epsilon }}$
is the compactification of the locus of such
![]() $(x,y)$
obtained by adding the two points at
$(x,y)$
obtained by adding the two points at
![]() $\infty $
, where
$\infty $
, where
![]() $y \sim x^{g +1}$
(first sheet) and
$y \sim x^{g +1}$
(first sheet) and
![]() $y \sim -x^{g+1}$
(second sheet). Let
$y \sim -x^{g+1}$
(second sheet). Let
![]() $\mathcal {A}_h$
be the cycle in
$\mathcal {A}_h$
be the cycle in
![]() $\mathcal {C}_{\boldsymbol {\epsilon }}$
surrounding
$\mathcal {C}_{\boldsymbol {\epsilon }}$
surrounding
![]() $\mathsf {A}_{\boldsymbol {\epsilon },h} = [\alpha ^{-}_{\boldsymbol {\epsilon },h},\alpha ^{+}_{\boldsymbol {\epsilon },h}]$
. The family
$\mathsf {A}_{\boldsymbol {\epsilon },h} = [\alpha ^{-}_{\boldsymbol {\epsilon },h},\alpha ^{+}_{\boldsymbol {\epsilon },h}]$
. The family
![]() $\boldsymbol {\mathcal {A}} = (\mathcal {A}_h)_{1 \leq h \leq g}$
can be completed by a family of cycles
$\boldsymbol {\mathcal {A}} = (\mathcal {A}_h)_{1 \leq h \leq g}$
can be completed by a family of cycles
![]() $\boldsymbol {\mathcal {B}}$
so that
$\boldsymbol {\mathcal {B}}$
so that
![]() $(\boldsymbol {\mathcal {A}},\boldsymbol {\mathcal {B}})$
is a symplectic basis of homology of
$(\boldsymbol {\mathcal {A}},\boldsymbol {\mathcal {B}})$
is a symplectic basis of homology of
![]() $\mathcal {C}_{\boldsymbol {\epsilon }}$
. More precisely, the cycle
$\mathcal {C}_{\boldsymbol {\epsilon }}$
. More precisely, the cycle
![]() $\mathcal {B}_h$
travels from
$\mathcal {B}_h$
travels from
![]() $\alpha _{\boldsymbol {\epsilon },h}^{-}$
to
$\alpha _{\boldsymbol {\epsilon },h}^{-}$
to
![]() $\alpha _{\boldsymbol {\epsilon },h - 1}^+$
in the second sheet and
$\alpha _{\boldsymbol {\epsilon },h - 1}^+$
in the second sheet and
![]() $\alpha _{\boldsymbol {\epsilon },h - 1}^+$
to
$\alpha _{\boldsymbol {\epsilon },h - 1}^+$
to
![]() $\alpha _{\boldsymbol {\epsilon },h}^-$
in the first sheet. The correlators
$\alpha _{\boldsymbol {\epsilon },h}^-$
in the first sheet. The correlators
![]() $W_{n;\boldsymbol {\epsilon }}^{[G,K]}$
are meromorphic functions on
$W_{n;\boldsymbol {\epsilon }}^{[G,K]}$
are meromorphic functions on
![]() $\mathcal {C}^n_{\boldsymbol {\epsilon }}$
, computed recursively by a residue formula on
$\mathcal {C}^n_{\boldsymbol {\epsilon }}$
, computed recursively by a residue formula on
![]() $\mathcal {C}_{\boldsymbol {\epsilon }}$
.
$\mathcal {C}_{\boldsymbol {\epsilon }}$
.
In particular, the analytic continuation of
 $$ \begin{align} \bigg(\frac{\beta}{2} W_{2;\boldsymbol{\epsilon}}^{\{0\}}(x_1,x_2) + \frac{1}{(x_1 - x_2)^2}\bigg)\mathrm{d} x_1\mathrm{d} x_2 = \bigg(\mathcal{W}_{2;\boldsymbol{\epsilon}}^{[0,0]}(x_1,x_2) + \frac{1}{(x_1 - x_2)^2}\bigg)\mathrm{d} x_1\mathrm{d} x_2 \end{align} $$
$$ \begin{align} \bigg(\frac{\beta}{2} W_{2;\boldsymbol{\epsilon}}^{\{0\}}(x_1,x_2) + \frac{1}{(x_1 - x_2)^2}\bigg)\mathrm{d} x_1\mathrm{d} x_2 = \bigg(\mathcal{W}_{2;\boldsymbol{\epsilon}}^{[0,0]}(x_1,x_2) + \frac{1}{(x_1 - x_2)^2}\bigg)\mathrm{d} x_1\mathrm{d} x_2 \end{align} $$
is the unique meromorphic bidifferential, denoted
![]() $\Omega $
, on
$\Omega $
, on
![]() $\mathcal {C}_{\boldsymbol {\epsilon }}$
, which has vanishing
$\mathcal {C}_{\boldsymbol {\epsilon }}$
, which has vanishing
![]() $\boldsymbol {\mathcal {A}}$
-periods and has for only singularity a double pole at coinciding point with leading coefficient
$\boldsymbol {\mathcal {A}}$
-periods and has for only singularity a double pole at coinciding point with leading coefficient
![]() $1$
and without residue. This
$1$
and without residue. This
![]() $\Omega $
plays an important role for the geometry of the spectral curve and is called fundamental bidifferential of the second kind. It sometimes appears under the name of ‘Bergman kernel’, although it does not coincide with (but it is related to) the kernel introduced by Bergman in [Reference Bergman and SchifferBS53]. It can be explicitly computed by the formula
$\Omega $
plays an important role for the geometry of the spectral curve and is called fundamental bidifferential of the second kind. It sometimes appears under the name of ‘Bergman kernel’, although it does not coincide with (but it is related to) the kernel introduced by Bergman in [Reference Bergman and SchifferBS53]. It can be explicitly computed by the formula
 $$ \begin{align} \Omega(z_1,z_2) = \mathrm{d}_{z_1} \mathrm{d}_{z_2} \ln \theta\Big(\int_{z_1}^{z_2} \boldsymbol{\varpi}\mathrm{d} x + \mathbf{c}\,\Big|\,\boldsymbol{\tau}^{\mathcal{C}_{\boldsymbol{\epsilon}}}\Big), \end{align} $$
$$ \begin{align} \Omega(z_1,z_2) = \mathrm{d}_{z_1} \mathrm{d}_{z_2} \ln \theta\Big(\int_{z_1}^{z_2} \boldsymbol{\varpi}\mathrm{d} x + \mathbf{c}\,\Big|\,\boldsymbol{\tau}^{\mathcal{C}_{\boldsymbol{\epsilon}}}\Big), \end{align} $$
where
-
○
 $\theta = \vartheta \big [\begin {smallmatrix} \mathbf {0} \\ \mathbf {0} \end {smallmatrix}\big ]$
is the Riemann Theta function.
$\theta = \vartheta \big [\begin {smallmatrix} \mathbf {0} \\ \mathbf {0} \end {smallmatrix}\big ]$
is the Riemann Theta function. -
○
 $\boldsymbol {\varpi }(z)\mathrm {d} x(z)$
is the basis of holomorphic one-forms dual to the
$\boldsymbol {\varpi }(z)\mathrm {d} x(z)$
is the basis of holomorphic one-forms dual to the
 $\boldsymbol {\mathcal {A}}$
-cycles – that is, characterised by (1.28)
$\boldsymbol {\mathcal {A}}$
-cycles – that is, characterised by (1.28)
-
○
 $\boldsymbol {\tau }^{\mathcal {C}_{\boldsymbol {\epsilon }}}$
is the Riemann matrix of periods of the spectral curve
$\boldsymbol {\tau }^{\mathcal {C}_{\boldsymbol {\epsilon }}}$
is the Riemann matrix of periods of the spectral curve
 $\mathcal {C}_{\boldsymbol {\epsilon }}$
:
$\mathcal {C}_{\boldsymbol {\epsilon }}$
: 
-
○
 $\mathbf {c} = \frac {1}{2}(\mathbf {r} + \boldsymbol {\tau}^{\mathcal{C}_{\boldsymbol{\epsilon}}}(\mathbf {s}))$
with
$\mathbf {c} = \frac {1}{2}(\mathbf {r} + \boldsymbol {\tau}^{\mathcal{C}_{\boldsymbol{\epsilon}}}(\mathbf {s}))$
with
 $\mathbf {r},\mathbf {s} \in \mathbb {Z}^{g}$
such that
$\mathbf {r},\mathbf {s} \in \mathbb {Z}^{g}$
such that
 $\mathbf {r} \cdot \mathbf {s}$
is odd, is a nonsingular characteristic for the Theta function (i.e., such that
$\mathbf {r} \cdot \mathbf {s}$
is odd, is a nonsingular characteristic for the Theta function (i.e., such that
 $\theta \big (\int _{z_1}^{z_2} \boldsymbol {\varpi }\mathrm {d} x + \mathbf {c}\,\big |\,\boldsymbol {\tau}^{\mathcal{C}_{\boldsymbol{\epsilon}}}\big )$
is not identically
$\theta \big (\int _{z_1}^{z_2} \boldsymbol {\varpi }\mathrm {d} x + \mathbf {c}\,\big |\,\boldsymbol {\tau}^{\mathcal{C}_{\boldsymbol{\epsilon}}}\big )$
is not identically
 $0$
when
$0$
when
 $z_1,z_2 \in \mathcal {C}_{\boldsymbol {\epsilon }}$
). Such a
$z_1,z_2 \in \mathcal {C}_{\boldsymbol {\epsilon }}$
). Such a
 $\mathbf {c}$
exists and the result then does not depend on which such
$\mathbf {c}$
exists and the result then does not depend on which such
 $\mathbf {c}$
is chosen.
$\mathbf {c}$
is chosen.
It is a property of the topological recursion that the derivatives of
![]() $F_{\beta ;\boldsymbol {\epsilon }}^{\{k\};V}$
can be computed as
$F_{\beta ;\boldsymbol {\epsilon }}^{\{k\};V}$
can be computed as
![]() $\boldsymbol {\mathcal {B}}$
-cycle integrals of the correlators:
$\boldsymbol {\mathcal {B}}$
-cycle integrals of the correlators:
This relation extends as well to derivatives of correlators:
where it is understood that we differentiate keeping x fixed. In particular,
Besides, the matrix to use in the Theta function appearing in Theorem 1.5 is
This simple dependence in
![]() $\beta $
of
$\beta $
of
![]() $W_{2;\boldsymbol {\epsilon }}^{\{0\}}$
can be traced back to the fact that, as a consequence of the Dyson–Schwinger equations, we have
$W_{2;\boldsymbol {\epsilon }}^{\{0\}}$
can be traced back to the fact that, as a consequence of the Dyson–Schwinger equations, we have
and this equation (together with the properties of the analytic continuation of
![]() $W_{2;\boldsymbol {\epsilon }}^{\{0\}}$
on
$W_{2;\boldsymbol {\epsilon }}^{\{0\}}$
on
![]() $\mathcal {C}_{\boldsymbol {\epsilon }}$
and the constraint of vanishing
$\mathcal {C}_{\boldsymbol {\epsilon }}$
and the constraint of vanishing
![]() $\boldsymbol {\mathcal {A}}$
-periods) fully characterises
$\boldsymbol {\mathcal {A}}$
-periods) fully characterises
![]() $W_{2;\boldsymbol {\epsilon }}^{\{0\}}$
.
$W_{2;\boldsymbol {\epsilon }}^{\{0\}}$
.
This relation has a long history and follows from the identification of
![]() $F^{\{-2\};V}_{\beta ;\boldsymbol {\epsilon }} = \frac {\beta }{2} \mathcal {F}^{[0,0];V}_{\boldsymbol {\epsilon }}$
(cf. Equation (1.17)) with the prepotential of the Hurwitz space associated to the family of curves (1.25) – considered as a Frobenius manifold – computed by Dubrovin [Reference DubrovinDub91], as well as with the tau function of the Whitham hierarchy as shown by Krichever [Reference KricheverKri92]. A derivation in the context of matrix model is, for instance, given in [Reference Chekhov and MironovCM02]. Although a priori differentiability of
$F^{\{-2\};V}_{\beta ;\boldsymbol {\epsilon }} = \frac {\beta }{2} \mathcal {F}^{[0,0];V}_{\boldsymbol {\epsilon }}$
(cf. Equation (1.17)) with the prepotential of the Hurwitz space associated to the family of curves (1.25) – considered as a Frobenius manifold – computed by Dubrovin [Reference DubrovinDub91], as well as with the tau function of the Whitham hierarchy as shown by Krichever [Reference KricheverKri92]. A derivation in the context of matrix model is, for instance, given in [Reference Chekhov and MironovCM02]. Although a priori differentiability of
![]() $F^{\{-2\};V}_{\beta ;\boldsymbol {\epsilon }}$
is not justified in [Reference Chekhov and MironovCM02], it is guaranteed by our results of Section A.2.
$F^{\{-2\};V}_{\beta ;\boldsymbol {\epsilon }}$
is not justified in [Reference Chekhov and MironovCM02], it is guaranteed by our results of Section A.2.
Equation (1.29) at
![]() $\boldsymbol {\epsilon } = \boldsymbol {\epsilon }_{\star }$
can be used to compute
$\boldsymbol {\epsilon } = \boldsymbol {\epsilon }_{\star }$
can be used to compute
![]() $T_{\beta ;\star }^{\{k\}}[\boldsymbol {X}]$
appearing in Equation (1.22). The derivation with respect to
$T_{\beta ;\star }^{\{k\}}[\boldsymbol {X}]$
appearing in Equation (1.22). The derivation with respect to
![]() $\boldsymbol {\epsilon }$
is not a natural operation in the initial model when N is finite since
$\boldsymbol {\epsilon }$
is not a natural operation in the initial model when N is finite since
![]() $N\epsilon _h$
are forced to be integers in Equation (1.10). Yet we show that the coefficients of expansion themselves are smooth functions of
$N\epsilon _h$
are forced to be integers in Equation (1.10). Yet we show that the coefficients of expansion themselves are smooth functions of
![]() $\boldsymbol {\epsilon }$
, and thus,
$\boldsymbol {\epsilon }$
, and thus,
![]() $\partial _{\boldsymbol {\epsilon }}$
makes sense.
$\partial _{\boldsymbol {\epsilon }}$
makes sense.
1.8. Central limit theorems for fluctuations and their breakdown
In Section 8.2, we describe the fluctuation of the number of particles
![]() $N_h$
in each segment
$N_h$
in each segment
![]() $\mathsf {A}_h$
: when
$\mathsf {A}_h$
: when
![]() $N \rightarrow \infty $
, its law is approximated by the law of a Gaussian conditioned to live in a shifted integer lattice. The shift of the lattice oscillates with N by an amount
$N \rightarrow \infty $
, its law is approximated by the law of a Gaussian conditioned to live in a shifted integer lattice. The shift of the lattice oscillates with N by an amount
![]() $\lfloor N\epsilon _{\star ,h} \rfloor $
. Note that since
$\lfloor N\epsilon _{\star ,h} \rfloor $
. Note that since
![]() $N \epsilon _{\star ,h}$
is for general N not an integer, strictly speaking, one cannot say that it converges in law to a discrete Gaussian random variable. This is, however, true along subsequences of N in case
$N \epsilon _{\star ,h}$
is for general N not an integer, strictly speaking, one cannot say that it converges in law to a discrete Gaussian random variable. This is, however, true along subsequences of N in case
![]() $\epsilon _{\star ,h} = \mu _{\mathrm{eq}}^{V}(\mathsf {A}_h)$
is a rational number.
$\epsilon _{\star ,h} = \mu _{\mathrm{eq}}^{V}(\mathsf {A}_h)$
is a rational number.
Theorem 1.6. Assume Hypotheses 1.1 and 1.3, and let
![]() $\boldsymbol {N} = (N_1,\ldots ,N_g)$
be the vector of filling fractions as above. If
$\boldsymbol {N} = (N_1,\ldots ,N_g)$
be the vector of filling fractions as above. If
![]() $\boldsymbol {P}$
is a g-tuple of integers depending on N and such that
$\boldsymbol {P}$
is a g-tuple of integers depending on N and such that
![]() $\boldsymbol {P} - N\boldsymbol {\epsilon }_{\star } = o(N^{\frac {1}{3}})$
when
$\boldsymbol {P} - N\boldsymbol {\epsilon }_{\star } = o(N^{\frac {1}{3}})$
when
![]() $N \rightarrow \infty $
, we have
$N \rightarrow \infty $
, we have
 $$ \begin{align} \mu_{N,\beta}^{V;\mathsf{A}}\big(\boldsymbol{N} = \boldsymbol{P}\big) \sim \frac{e^{\frac{1}{2}\,(F^{\{-2\}}_{\beta;\star})^{"}\cdot(\boldsymbol{P} - N\boldsymbol{\epsilon}_{\star})^{\otimes 2} + (F^{\{-1\}}_{\beta;\star})'\cdot(\boldsymbol{P} - N\boldsymbol{\epsilon}_{\star})}}{\vartheta\big[\begin{smallmatrix} -N\boldsymbol{\epsilon}_{\star}\\ \boldsymbol{0} \end{smallmatrix}\big](\boldsymbol{v}_{\beta;\star}|\boldsymbol{\tau}_{\beta;\star})}. \end{align} $$
$$ \begin{align} \mu_{N,\beta}^{V;\mathsf{A}}\big(\boldsymbol{N} = \boldsymbol{P}\big) \sim \frac{e^{\frac{1}{2}\,(F^{\{-2\}}_{\beta;\star})^{"}\cdot(\boldsymbol{P} - N\boldsymbol{\epsilon}_{\star})^{\otimes 2} + (F^{\{-1\}}_{\beta;\star})'\cdot(\boldsymbol{P} - N\boldsymbol{\epsilon}_{\star})}}{\vartheta\big[\begin{smallmatrix} -N\boldsymbol{\epsilon}_{\star}\\ \boldsymbol{0} \end{smallmatrix}\big](\boldsymbol{v}_{\beta;\star}|\boldsymbol{\tau}_{\beta;\star})}. \end{align} $$
In Section 8.3, we describe the fluctuations of linear statistics in the multi-cut regime.
Theorem 1.7. Assume Hypotheses 1.1 and 1.3. Let
![]() $\varphi $
be an analytic test function in a neighbourhood of
$\varphi $
be an analytic test function in a neighbourhood of
![]() $\mathsf {A}$
, and
$\mathsf {A}$
, and
![]() $s \in \mathbb {R}$
. We have when
$s \in \mathbb {R}$
. We have when
![]() $N \rightarrow \infty $
,
$N \rightarrow \infty $
,
 $$ \begin{align} & \quad \nonumber \mu_{N,\beta}^{V;\mathsf{A}}\big(e^{\mathrm{i}s\big(\sum_{i = 1}^N \varphi(\lambda_i) - N\int_{\mathsf{S}} \varphi(\xi)\mathrm{d}\mu_{\mathrm{eq}}^{V}(\xi)\big)}\big) \\ & \mathop{\sim}_{N \rightarrow \infty} \exp\Big(\mathrm{i}s\,M_{\beta;\star}[\varphi] - \frac{s^2}{2}\,Q_{\beta;\star}[\varphi,\varphi]\Big)\,\frac{\vartheta\!\left[\begin{smallmatrix} -N\boldsymbol{\epsilon}_{\star} \\ \boldsymbol{0} \end{smallmatrix}\right]\!\big(\boldsymbol{v}_{\beta;\star} + \mathrm{i}s\,\boldsymbol{u}_{\beta;\star}[\varphi]\big|\boldsymbol{\tau}_{\beta;\star}\big)}{\vartheta\!\left[\begin{smallmatrix} -N\boldsymbol{\epsilon}_{\star} \\ \boldsymbol{0} \end{smallmatrix}\right]\!\big(\boldsymbol{v}_{\beta;\star}\big|\boldsymbol{\tau}_{\beta;\star}\big)}, \end{align} $$
$$ \begin{align} & \quad \nonumber \mu_{N,\beta}^{V;\mathsf{A}}\big(e^{\mathrm{i}s\big(\sum_{i = 1}^N \varphi(\lambda_i) - N\int_{\mathsf{S}} \varphi(\xi)\mathrm{d}\mu_{\mathrm{eq}}^{V}(\xi)\big)}\big) \\ & \mathop{\sim}_{N \rightarrow \infty} \exp\Big(\mathrm{i}s\,M_{\beta;\star}[\varphi] - \frac{s^2}{2}\,Q_{\beta;\star}[\varphi,\varphi]\Big)\,\frac{\vartheta\!\left[\begin{smallmatrix} -N\boldsymbol{\epsilon}_{\star} \\ \boldsymbol{0} \end{smallmatrix}\right]\!\big(\boldsymbol{v}_{\beta;\star} + \mathrm{i}s\,\boldsymbol{u}_{\beta;\star}[\varphi]\big|\boldsymbol{\tau}_{\beta;\star}\big)}{\vartheta\!\left[\begin{smallmatrix} -N\boldsymbol{\epsilon}_{\star} \\ \boldsymbol{0} \end{smallmatrix}\right]\!\big(\boldsymbol{v}_{\beta;\star}\big|\boldsymbol{\tau}_{\beta;\star}\big)}, \end{align} $$
where

We recall that the
![]() $\varpi _h(x)\mathrm {d} x$
are the holomorphic one-forms from Equations (1.28)–(1.30), while
$\varpi _h(x)\mathrm {d} x$
are the holomorphic one-forms from Equations (1.28)–(1.30), while
![]() $W_{1;\boldsymbol {\epsilon }}^{\{0\}}$
and
$W_{1;\boldsymbol {\epsilon }}^{\{0\}}$
and
![]() $W_{2;\boldsymbol {\epsilon }}^{\{0\}}$
appear in the asymptotic expansion of the correlators in the model with fixed filling fractions (Theorem 1.3), and here they must be specialised at
$W_{2;\boldsymbol {\epsilon }}^{\{0\}}$
appear in the asymptotic expansion of the correlators in the model with fixed filling fractions (Theorem 1.3), and here they must be specialised at
![]() $\boldsymbol {\epsilon } = \boldsymbol {\epsilon }_{\star }$
.
$\boldsymbol {\epsilon } = \boldsymbol {\epsilon }_{\star }$
.
Remark 1.4. In particular,
![]() $\boldsymbol {u}_{\beta ;\star }$
is a linear map associating to a test function
$\boldsymbol {u}_{\beta ;\star }$
is a linear map associating to a test function
![]() $\varphi $
a g-dimensional vector. When
$\varphi $
a g-dimensional vector. When
![]() $\varphi $
is such that
$\varphi $
is such that
![]() $\boldsymbol {u}_{\beta ;\star }[\varphi ] = 0$
, the Theta functions cancel out, and we deduce that the random variable
$\boldsymbol {u}_{\beta ;\star }[\varphi ] = 0$
, the Theta functions cancel out, and we deduce that the random variable
 $$ \begin{align*}\Phi_N[\varphi] := \sum_{i = 1}^N \varphi(\lambda_i) - N\int_{\mathsf{S}} \varphi(\xi)\mathrm{d}\mu_{\mathrm{eq}}^{V}(\xi) \end{align*} $$
$$ \begin{align*}\Phi_N[\varphi] := \sum_{i = 1}^N \varphi(\lambda_i) - N\int_{\mathsf{S}} \varphi(\xi)\mathrm{d}\mu_{\mathrm{eq}}^{V}(\xi) \end{align*} $$
converges in law to a Gaussian random variable with mean
![]() $M_{\beta ;\star }[\varphi ]$
and covariance
$M_{\beta ;\star }[\varphi ]$
and covariance
![]() $Q_{\beta ;\star }[\varphi ,\varphi ]$
. We remark that we have the alternative formula from (8.10):
$Q_{\beta ;\star }[\varphi ,\varphi ]$
. We remark that we have the alternative formula from (8.10):
showing that
![]() $\boldsymbol {u}_{\beta ;\star }[\varphi ] $
vanishes when
$\boldsymbol {u}_{\beta ;\star }[\varphi ] $
vanishes when
![]() $ \boldsymbol {\epsilon }_{\star }$
is a critical point of
$ \boldsymbol {\epsilon }_{\star }$
is a critical point of
![]() $\int _{\mathsf {S}} \varphi (\xi )\,\mathrm {d}\mu _{\mathrm{eq};\boldsymbol {\epsilon }}^V(\xi )$
. Even though our results are obtained for analytic potentials and test functions, this condition clearly makes sense with less regularity. In fact, it is possible to generalise our results and techniques to consider sufficiently smooth potential and test functions instead of analytic ones. We refer the interested reader to [Reference GuionnetG19, Sections 4 and 6] to such a generalisation in the one-cut case.
$\int _{\mathsf {S}} \varphi (\xi )\,\mathrm {d}\mu _{\mathrm{eq};\boldsymbol {\epsilon }}^V(\xi )$
. Even though our results are obtained for analytic potentials and test functions, this condition clearly makes sense with less regularity. In fact, it is possible to generalise our results and techniques to consider sufficiently smooth potential and test functions instead of analytic ones. We refer the interested reader to [Reference GuionnetG19, Sections 4 and 6] to such a generalisation in the one-cut case.
When
![]() $\boldsymbol {u}_{\beta ;\star }[\varphi ] \neq 0$
, the central limit theorem does not hold anymore. Instead, from the shape of the right-hand side,
$\boldsymbol {u}_{\beta ;\star }[\varphi ] \neq 0$
, the central limit theorem does not hold anymore. Instead, from the shape of the right-hand side,
![]() $\Phi _N[\varphi ]$
is approximated when
$\Phi _N[\varphi ]$
is approximated when
![]() $N \rightarrow \infty $
by the sum of two independent random variables: the first one is a Gaussian random variable with mean
$N \rightarrow \infty $
by the sum of two independent random variables: the first one is a Gaussian random variable with mean
![]() $M_{\beta ;\star }[\varphi ]$
and covariance
$M_{\beta ;\star }[\varphi ]$
and covariance
![]() $Q_{\beta ;\star }[\varphi ,\varphi ]$
, and the second one is the scalar product with
$Q_{\beta ;\star }[\varphi ,\varphi ]$
, and the second one is the scalar product with
![]() $2\mathrm{i}\pi \boldsymbol {u}_{\beta ;\star }[\varphi ]$
(which is a vector in
$2\mathrm{i}\pi \boldsymbol {u}_{\beta ;\star }[\varphi ]$
(which is a vector in
![]() $\mathbb {R}^g$
when
$\mathbb {R}^g$
when
![]() $\varphi $
is real-valued) of a random Gaussian vector conditioned to live on the lattice
$\varphi $
is real-valued) of a random Gaussian vector conditioned to live on the lattice
![]() $-\lfloor N\boldsymbol {\epsilon }_{\star } \rfloor + \mathbb {Z}^{g}$
. This also displays N-dependent oscillations. These oscillations can be interpreted in physical terms from tunnelling of particles between different segments. One sees, indeed, than moving a single
$-\lfloor N\boldsymbol {\epsilon }_{\star } \rfloor + \mathbb {Z}^{g}$
. This also displays N-dependent oscillations. These oscillations can be interpreted in physical terms from tunnelling of particles between different segments. One sees, indeed, than moving a single
![]() $\lambda _i$
from
$\lambda _i$
from
![]() $\mathsf {A}_h$
to
$\mathsf {A}_h$
to
![]() $\mathsf {A}_{h'}$
changes
$\mathsf {A}_{h'}$
changes
![]() $\Phi _N[\varphi ]$
by a quantity of order
$\Phi _N[\varphi ]$
by a quantity of order
![]() $1$
, which is already the typical order of fluctuation of linear statistics when filling fractions are fixed.
$1$
, which is already the typical order of fluctuation of linear statistics when filling fractions are fixed.
The next term in the asymptotic expansion of the left-hand side of (1.32) is of relative order
![]() $O(\frac {1}{N})$
, which therefore gives the speed of convergence of the associated linear statistics of the empirical measure.
$O(\frac {1}{N})$
, which therefore gives the speed of convergence of the associated linear statistics of the empirical measure.
1.9. Asymptotic expansion of kernels and correlators
Once the result on large N expansion of the partition function is obtained, we can easily infer the asymptotic expansion of the correlators and the kernels by perturbing the potential by terms of order
![]() $\frac {1}{N}$
, maybe complex-valued, as allowed by Hypothesis 1.3.
$\frac {1}{N}$
, maybe complex-valued, as allowed by Hypothesis 1.3.
1.9.1. Leading behaviour of the correlators
Although we could write down the expansion for the correlators as a corollary of Theorem 1.5, we bound ourselves to point out their leading behaviour. Whereas
![]() $W_n$
behaves as
$W_n$
behaves as
![]() $O(N^{2 - n})$
in the one-cut regime or in the model with fixed filling fractions,
$O(N^{2 - n})$
in the one-cut regime or in the model with fixed filling fractions,
![]() $W_n$
for
$W_n$
for
![]() $n \geq 3$
does not decay when N is large in a
$n \geq 3$
does not decay when N is large in a
![]() $(g + 1)$
-cut regime with
$(g + 1)$
-cut regime with
![]() $g \geq 1$
. More precisely, we have the following.
$g \geq 1$
. More precisely, we have the following.
Theorem 1.8. Assume Hypothesis 1.1 and 1.3 and that the number of cuts
![]() $(g + 1)$
is greater or equal to
$(g + 1)$
is greater or equal to
![]() $2$
. When
$2$
. When
![]() $N \rightarrow \infty $
, we have, uniformly when
$N \rightarrow \infty $
, we have, uniformly when
![]() $x_1,\ldots ,x_n$
belongs to any compact of
$x_1,\ldots ,x_n$
belongs to any compact of
![]() $(\mathbb {C}\setminus \mathsf {A})^n$
,
$(\mathbb {C}\setminus \mathsf {A})^n$
,
 $$ \begin{align*}W_2(x_1,x_2) = W_{2;\star}^{\{0\}}(x_1,x_2) + \Big(\boldsymbol{\varpi}(x_1)\otimes\boldsymbol{\varpi}(x_2)\Big)\cdot\nabla_{\boldsymbol{v}}^{\otimes 2}\ln\vartheta\!\left[\begin{array}{@{\hspace{-0.03cm}}c@{\hspace{-0.03cm}}} -N\boldsymbol{\epsilon}_{\star}\, \\ \boldsymbol{0} \end{array}\right]\!\!\big(\boldsymbol{v}_{\beta;\star}\big|\boldsymbol{\tau}_{\beta;\star}\big) + o(1)\,, \end{align*} $$
$$ \begin{align*}W_2(x_1,x_2) = W_{2;\star}^{\{0\}}(x_1,x_2) + \Big(\boldsymbol{\varpi}(x_1)\otimes\boldsymbol{\varpi}(x_2)\Big)\cdot\nabla_{\boldsymbol{v}}^{\otimes 2}\ln\vartheta\!\left[\begin{array}{@{\hspace{-0.03cm}}c@{\hspace{-0.03cm}}} -N\boldsymbol{\epsilon}_{\star}\, \\ \boldsymbol{0} \end{array}\right]\!\!\big(\boldsymbol{v}_{\beta;\star}\big|\boldsymbol{\tau}_{\beta;\star}\big) + o(1)\,, \end{align*} $$
and for any
![]() $n \geq 3$
,
$n \geq 3$
,
 $$ \begin{align*}W_n(x_1,\ldots,x_n) = \Big(\bigotimes_{i = 1}^n \boldsymbol{\varpi}(x_i)\Big)\cdot\nabla_{\boldsymbol{v}}^{\otimes n}\ln\vartheta\!\left[\begin{array}{@{\hspace{-0.03cm}}c@{\hspace{-0.03cm}}} -N\boldsymbol{\epsilon_{\star}}\, \\ \boldsymbol{0} \end{array}\right]\!\!\big(\boldsymbol{v}_{\beta;\star}\big|\boldsymbol{\tau}_{\beta;\star}\big) + o(1)\,. \end{align*} $$
$$ \begin{align*}W_n(x_1,\ldots,x_n) = \Big(\bigotimes_{i = 1}^n \boldsymbol{\varpi}(x_i)\Big)\cdot\nabla_{\boldsymbol{v}}^{\otimes n}\ln\vartheta\!\left[\begin{array}{@{\hspace{-0.03cm}}c@{\hspace{-0.03cm}}} -N\boldsymbol{\epsilon_{\star}}\, \\ \boldsymbol{0} \end{array}\right]\!\!\big(\boldsymbol{v}_{\beta;\star}\big|\boldsymbol{\tau}_{\beta;\star}\big) + o(1)\,. \end{align*} $$
Integrating this result over
![]() $\boldsymbol {\mathcal {A}}$
-cycles provides the leading order behaviour of n-th order moments of the filling fractions
$\boldsymbol {\mathcal {A}}$
-cycles provides the leading order behaviour of n-th order moments of the filling fractions
![]() $\boldsymbol {N}$
, and the result agrees with Theorem 1.6.
$\boldsymbol {N}$
, and the result agrees with Theorem 1.6.
1.9.2. Kernels
We explain in § 6.3 that the following result concerning the kernel – defined in Equation (1.4) – is a consequence of Theorem 1.3:
Corollary 1.9. Assume Hypothesis 1.1 and 1.3. There exists
![]() $t> 0$
such that, for any sequence of
$t> 0$
such that, for any sequence of
![]() $\boldsymbol {N} = (N_1,\ldots ,N_{g})$
such that
$\boldsymbol {N} = (N_1,\ldots ,N_{g})$
such that
![]() $|\boldsymbol {N}/N - \boldsymbol {\epsilon }_{\star }|_1 < t$
, the n-point kernels in the model with fixed filling fractions have an asymptotic expansion when
$|\boldsymbol {N}/N - \boldsymbol {\epsilon }_{\star }|_1 < t$
, the n-point kernels in the model with fixed filling fractions have an asymptotic expansion when
![]() $N \rightarrow \infty $
of the form, for any
$N \rightarrow \infty $
of the form, for any
![]() $K \geq 0$
,
$K \geq 0$
,
 $$ \begin{align} \mathsf{K}_{n,\boldsymbol{c};\boldsymbol{\epsilon}}(x_1,\ldots,x_n) = \exp\bigg[\sum_{j = 1}^{n} Nc_j\big(\ln(x_j) + 2\mathrm{i}\pi \chi_j\big) + \sum_{k = -1}^{K} N^{-k}\Big(\sum_{r = 1}^{k + 2} \frac{1}{r!}\mathcal{L}_{\boldsymbol{x},\boldsymbol{c}}^{\otimes r}[W_{r;\boldsymbol{\epsilon}}^{\{k\}}]\Big) + O(N^{-(K + 1)})\bigg], \end{align} $$
$$ \begin{align} \mathsf{K}_{n,\boldsymbol{c};\boldsymbol{\epsilon}}(x_1,\ldots,x_n) = \exp\bigg[\sum_{j = 1}^{n} Nc_j\big(\ln(x_j) + 2\mathrm{i}\pi \chi_j\big) + \sum_{k = -1}^{K} N^{-k}\Big(\sum_{r = 1}^{k + 2} \frac{1}{r!}\mathcal{L}_{\boldsymbol{x},\boldsymbol{c}}^{\otimes r}[W_{r;\boldsymbol{\epsilon}}^{\{k\}}]\Big) + O(N^{-(K + 1)})\bigg], \end{align} $$
where
![]() $\mathcal {L}_{\boldsymbol {x},\boldsymbol {c}}$
is the linear form
$\mathcal {L}_{\boldsymbol {x},\boldsymbol {c}}$
is the linear form
 $$ \begin{align} \mathcal{L}_{\boldsymbol{x},\boldsymbol{c}}[f] = \sum_{j = 1}^{n} c_j\int_{\infty}^{x_j} \check{f}(x)\mathrm{d} x,\qquad \mathrm{where}\,\,\check{f}(x) = f(x) + \frac{1}{x} \mathop{\,\mathrm Res\,}_{x = \infty} f(\xi)\mathrm{d} \xi. \end{align} $$
$$ \begin{align} \mathcal{L}_{\boldsymbol{x},\boldsymbol{c}}[f] = \sum_{j = 1}^{n} c_j\int_{\infty}^{x_j} \check{f}(x)\mathrm{d} x,\qquad \mathrm{where}\,\,\check{f}(x) = f(x) + \frac{1}{x} \mathop{\,\mathrm Res\,}_{x = \infty} f(\xi)\mathrm{d} \xi. \end{align} $$
The error terms in this expansion are uniform for
![]() $x_1,\ldots ,x_n$
in any compact of
$x_1,\ldots ,x_n$
in any compact of
![]() $\mathbb {C}\setminus \mathsf {A}$
.
$\mathbb {C}\setminus \mathsf {A}$
.
The
![]() $(r,k) = 1$
term in (1.33) depends on choices for the path of integration from
$(r,k) = 1$
term in (1.33) depends on choices for the path of integration from
![]() $\infty $
to
$\infty $
to
![]() $x_j$
(the other terms do not and are also unaffected by the difference between f and
$x_j$
(the other terms do not and are also unaffected by the difference between f and
![]() $\check {f}$
in (1.34)), and
$\check {f}$
in (1.34)), and
![]() $\chi _j \in \mathbb {Z}$
. These two features are a manifestation of the fact that the definition of the kernel depends on a choice of determination for the complex logarithm; resolving them by the choice of suitable determinations and domain of definition leads to specific integer values for
$\chi _j \in \mathbb {Z}$
. These two features are a manifestation of the fact that the definition of the kernel depends on a choice of determination for the complex logarithm; resolving them by the choice of suitable determinations and domain of definition leads to specific integer values for
![]() $\chi _j$
. These subtleties are explained in details in § 6.3 and can be ignored if all
$\chi _j$
. These subtleties are explained in details in § 6.3 and can be ignored if all
![]() $c_j \in \mathbb {Z}$
(in that case, the definition of the kernel does not depend on choices).
$c_j \in \mathbb {Z}$
(in that case, the definition of the kernel does not depend on choices).
Hereafter, if
![]() $\gamma $
is a smooth path in
$\gamma $
is a smooth path in
![]() $\mathbb {C}\setminus \mathsf {S}_{\boldsymbol {\epsilon }}$
, we set
$\mathbb {C}\setminus \mathsf {S}_{\boldsymbol {\epsilon }}$
, we set
![]() $\mathcal {L}_{\gamma } = \int _{\gamma }$
, and
$\mathcal {L}_{\gamma } = \int _{\gamma }$
, and
![]() $\mathcal {L}_{\gamma }^{\otimes r}$
is given by
$\mathcal {L}_{\gamma }^{\otimes r}$
is given by
 $$ \begin{align*}\mathcal{L}_{\gamma}^{\otimes r}[W_{r;\boldsymbol{\epsilon}}^{\{k\}}] = \int_{\gamma}\mathrm{d} x_1\cdots\int_{\gamma}\mathrm{d} x_r\,W_{r;\boldsymbol{\epsilon}}^{\{k\}}(x_1,\ldots,x_r).\end{align*} $$
$$ \begin{align*}\mathcal{L}_{\gamma}^{\otimes r}[W_{r;\boldsymbol{\epsilon}}^{\{k\}}] = \int_{\gamma}\mathrm{d} x_1\cdots\int_{\gamma}\mathrm{d} x_r\,W_{r;\boldsymbol{\epsilon}}^{\{k\}}(x_1,\ldots,x_r).\end{align*} $$
A priori, the integrals in the right-hand side of Equation (1.33) depend on the relative homology class in
![]() $\mathbb {C}\setminus \mathsf {A}$
of paths between
$\mathbb {C}\setminus \mathsf {A}$
of paths between
![]() $\infty $
to
$\infty $
to
![]() $x_i$
. A basis of homology cycles in
$x_i$
. A basis of homology cycles in
![]() $\mathbb {C}\setminus \mathsf {A}$
is given by
$\mathbb {C}\setminus \mathsf {A}$
is given by
![]() $\overline {\boldsymbol {\mathcal {A}}} = (\mathcal {A}_h)_{0 \leq h \leq g}$
, and we deduce from Equation (1.11) that
$\overline {\boldsymbol {\mathcal {A}}} = (\mathcal {A}_h)_{0 \leq h \leq g}$
, and we deduce from Equation (1.11) that
Therefore, the only multivaluedness of the right-hand side comes from the first term
![]() $N \mathcal {L}_{\boldsymbol {x},\mathbf {c}}[W_{1;\boldsymbol {\epsilon }}^{\{-1\}}]$
, and given Equation (1.35) and observing that
$N \mathcal {L}_{\boldsymbol {x},\mathbf {c}}[W_{1;\boldsymbol {\epsilon }}^{\{-1\}}]$
, and given Equation (1.35) and observing that
![]() $N_h = N\epsilon _h$
are integers, we see that it exactly reproduces the monodromies of the kernels depending on
$N_h = N\epsilon _h$
are integers, we see that it exactly reproduces the monodromies of the kernels depending on
![]() $c_j$
.
$c_j$
.
We now come to the multi-cut regime of the initial model. If
![]() $\boldsymbol {X}$
is a vector with g components, and
$\boldsymbol {X}$
is a vector with g components, and
![]() $\mathcal {L}$
is a linear form on the space of holomorphic functions on
$\mathcal {L}$
is a linear form on the space of holomorphic functions on
![]() $\mathbb {C}\setminus \mathsf {S}_{\boldsymbol {\epsilon }}$
, let us define
$\mathbb {C}\setminus \mathsf {S}_{\boldsymbol {\epsilon }}$
, let us define
 $$ \begin{align*}\tilde{T}^{\{k\}}_{\beta;\boldsymbol{\epsilon}}[\mathcal{L};\boldsymbol{X}] = \sum_{r = 1}^{k} \frac{1}{r!} \sum_{\substack{j_1,\ldots,j_r \geq 1 \\ k_1,\ldots,k_r \geq -2 \\ n_1,\ldots,n_r \geq 0 \\ k_i + j_i + n_i> 0 \\ \sum_{i = 1}^{r} k_i + j_i + n_i = k}} \Big(\bigotimes_{i = 1}^{r} \frac{\mathcal{L}^{\otimes n_i}[(W_{n_i;\boldsymbol{\epsilon}}^{\{k_i\}})^{(j_i)}]}{n_i!\,j_i!}\Big)\cdot\boldsymbol{X}^{\otimes(\sum_{i = 1}^r j_i)}, \end{align*} $$
$$ \begin{align*}\tilde{T}^{\{k\}}_{\beta;\boldsymbol{\epsilon}}[\mathcal{L};\boldsymbol{X}] = \sum_{r = 1}^{k} \frac{1}{r!} \sum_{\substack{j_1,\ldots,j_r \geq 1 \\ k_1,\ldots,k_r \geq -2 \\ n_1,\ldots,n_r \geq 0 \\ k_i + j_i + n_i> 0 \\ \sum_{i = 1}^{r} k_i + j_i + n_i = k}} \Big(\bigotimes_{i = 1}^{r} \frac{\mathcal{L}^{\otimes n_i}[(W_{n_i;\boldsymbol{\epsilon}}^{\{k_i\}})^{(j_i)}]}{n_i!\,j_i!}\Big)\cdot\boldsymbol{X}^{\otimes(\sum_{i = 1}^r j_i)}, \end{align*} $$
where we took as convention
![]() $W_{n = 0;\boldsymbol {\epsilon }}^{\{k\}} = F_{\beta ;\boldsymbol {\epsilon }}^{\{k\}}$
and the derivatives are computed for fixed xs. Then, as a consequence of Theorem 1.5, we have the following.
$W_{n = 0;\boldsymbol {\epsilon }}^{\{k\}} = F_{\beta ;\boldsymbol {\epsilon }}^{\{k\}}$
and the derivatives are computed for fixed xs. Then, as a consequence of Theorem 1.5, we have the following.
Corollary 1.10. Assume Hypothesis 1.1 and 1.3. With the notations of Corollary 1.9, the n-point kernels have an asymptotic expansion, for any
![]() $K \geq 0$
,
$K \geq 0$
,
 $$ \begin{align*} \mathsf{K}_{n,\mathbf{c}}(\boldsymbol{x}) = \mathsf{K}_{n,\mathbf{c};\star}(\boldsymbol{x}) \frac{\Big(\sum_{k = 0}^K N^{-k}\,\tilde{T}_{\beta;\star}^{\{k\}}\big[\mathcal{L}_{\boldsymbol{x},\boldsymbol{c}},\frac{\nabla_{\boldsymbol{v}}}{2{\rm i}\pi}\big]\Big)\vartheta\!\left[\begin{smallmatrix} -N\boldsymbol{\epsilon}_{\star} \\ \boldsymbol{0} \end{smallmatrix}\right]\!\big(\boldsymbol{v}_{\beta;\star} + \mathcal{L}_{\boldsymbol{x},\boldsymbol{c}}[\boldsymbol{\varpi}]\big|\boldsymbol{\tau}_{\beta;\star}\big)}{\Big(\sum_{k = 0}^K N^{-k}\,T_{\beta;\star}^{\{k\}}\big[\frac{\nabla_{\boldsymbol{v}}}{2{\rm i}\pi}\bigr]\Big)\vartheta\!\left[\begin{smallmatrix} -N\boldsymbol{\epsilon}_{\star} \\ \boldsymbol{0} \end{smallmatrix}\right]\!\big(\boldsymbol{v}_{\beta;\star}\big|\boldsymbol{\tau}_{\beta;\star}\big)}\big(1 + O(N^{-(K + 1)})\big). \end{align*} $$
$$ \begin{align*} \mathsf{K}_{n,\mathbf{c}}(\boldsymbol{x}) = \mathsf{K}_{n,\mathbf{c};\star}(\boldsymbol{x}) \frac{\Big(\sum_{k = 0}^K N^{-k}\,\tilde{T}_{\beta;\star}^{\{k\}}\big[\mathcal{L}_{\boldsymbol{x},\boldsymbol{c}},\frac{\nabla_{\boldsymbol{v}}}{2{\rm i}\pi}\big]\Big)\vartheta\!\left[\begin{smallmatrix} -N\boldsymbol{\epsilon}_{\star} \\ \boldsymbol{0} \end{smallmatrix}\right]\!\big(\boldsymbol{v}_{\beta;\star} + \mathcal{L}_{\boldsymbol{x},\boldsymbol{c}}[\boldsymbol{\varpi}]\big|\boldsymbol{\tau}_{\beta;\star}\big)}{\Big(\sum_{k = 0}^K N^{-k}\,T_{\beta;\star}^{\{k\}}\big[\frac{\nabla_{\boldsymbol{v}}}{2{\rm i}\pi}\bigr]\Big)\vartheta\!\left[\begin{smallmatrix} -N\boldsymbol{\epsilon}_{\star} \\ \boldsymbol{0} \end{smallmatrix}\right]\!\big(\boldsymbol{v}_{\beta;\star}\big|\boldsymbol{\tau}_{\beta;\star}\big)}\big(1 + O(N^{-(K + 1)})\big). \end{align*} $$
The first factor comes from evaluation of the right-hand side of Equation (1.33) at
![]() $\boldsymbol {\epsilon } = \boldsymbol {\epsilon }_{\star }$
,
$\boldsymbol {\epsilon } = \boldsymbol {\epsilon }_{\star }$
,
![]() ${\mathcal {L}}_{\boldsymbol {x},\boldsymbol {c}} = \sum _{j = 1}^{n} c_j\int _{\infty }^{x_j}$
and
${\mathcal {L}}_{\boldsymbol {x},\boldsymbol {c}} = \sum _{j = 1}^{n} c_j\int _{\infty }^{x_j}$
and
![]() $\boldsymbol {\varpi }\mathrm{{d}} x$
is the basis of holomorphic one-forms.
$\boldsymbol {\varpi }\mathrm{{d}} x$
is the basis of holomorphic one-forms.
A diagrammatic representation for the terms of such expansion was proposed in [Reference Borot and EynardBE12, Appendix A].
1.10. Strategy of the proof
The key idea of this article is to establish an asymptotic expansion for the partition functions of our models for fixed filling fractions:
 $$ \begin{align} \frac{N!\,Z_{N,\beta;\boldsymbol{N}/N}^{V;{\mathsf{A}}}}{\prod_{h = 0}^{g} N_h!}= N^{\frac{\beta}{2}N + {\varkappa}}\exp\Big(\sum_{k = -2}^{K} N^{-k}\,F^{\{k\};V}_{\beta;\boldsymbol{N}/N} + O(N^{-(K + 1)})\Big), \end{align} $$
$$ \begin{align} \frac{N!\,Z_{N,\beta;\boldsymbol{N}/N}^{V;{\mathsf{A}}}}{\prod_{h = 0}^{g} N_h!}= N^{\frac{\beta}{2}N + {\varkappa}}\exp\Big(\sum_{k = -2}^{K} N^{-k}\,F^{\{k\};V}_{\beta;\boldsymbol{N}/N} + O(N^{-(K + 1)})\Big), \end{align} $$
for any
![]() $K \geq 0$
. Indeed, such an expansion allows to estimate the free energy of the original model
$K \geq 0$
. Indeed, such an expansion allows to estimate the free energy of the original model
![]() $\ln Z_{N,\beta }^{V;\mathsf {A}}$
up to errors of order
$\ln Z_{N,\beta }^{V;\mathsf {A}}$
up to errors of order
![]() $O(N^{-K-1 + \delta })$
; see (1.18) and Theorem 1.5. It also allows to analyse the asymptotic distribution of the filling fractions
$O(N^{-K-1 + \delta })$
; see (1.18) and Theorem 1.5. It also allows to analyse the asymptotic distribution of the filling fractions
![]() $\boldsymbol {\epsilon } = \boldsymbol {N}/N$
(see Theorem 1.6) since this distribution is given as the following ratio of partition functions:
$\boldsymbol {\epsilon } = \boldsymbol {N}/N$
(see Theorem 1.6) since this distribution is given as the following ratio of partition functions:
 $$ \begin{align} \mu_{N,\beta}^{V;\mathsf{A}}\big(\boldsymbol{N} \big)= \frac{N!}{\prod_{h = 0}^g N_h!}\,\frac{Z_{N,\beta;\boldsymbol{N}/N}^{V;\mathsf{A}}}{Z_{N,\beta}^{V;\mathsf{A}}}\,. \end{align} $$
$$ \begin{align} \mu_{N,\beta}^{V;\mathsf{A}}\big(\boldsymbol{N} \big)= \frac{N!}{\prod_{h = 0}^g N_h!}\,\frac{Z_{N,\beta;\boldsymbol{N}/N}^{V;\mathsf{A}}}{Z_{N,\beta}^{V;\mathsf{A}}}\,. \end{align} $$
In particular, if (1.36) is known up to
![]() $o(1)$
, the leading behaviour of (1.37) when
$o(1)$
, the leading behaviour of (1.37) when
![]() $N \rightarrow \infty $
can be computed. This analysis is detailed in Section 8.2.
$N \rightarrow \infty $
can be computed. This analysis is detailed in Section 8.2.
To handle fluctuations of linear statistics, we use the well-known approach of considering the free energy for perturbations of order
![]() $\frac {1}{N}$
of the potential. In fact, if we denote by
$\frac {1}{N}$
of the potential. In fact, if we denote by
![]() $\Phi _N[\varphi ] := \sum _{i = 1}^N \varphi (\lambda _i) - N\int _{\mathsf {S}} \varphi (\xi )\mathrm {d}\mu _{\mathrm{eq}}^{V}(\xi ) $
, as in Remark 1.4, we see that for any real number s,
$\Phi _N[\varphi ] := \sum _{i = 1}^N \varphi (\lambda _i) - N\int _{\mathsf {S}} \varphi (\xi )\mathrm {d}\mu _{\mathrm{eq}}^{V}(\xi ) $
, as in Remark 1.4, we see that for any real number s,
 $$ \begin{align*}\mu_{N,\beta}^{V;\mathsf{A}}\big[e^{s\Phi_{N}[\varphi]}\big] = e^{-sN\int_{\mathsf{S}} \varphi(\xi)\mathrm{d}\mu_{\mathrm{eq}}^{V}(\xi) } \frac{Z_{N,\beta}^{V-\frac{2s}{N\beta}\varphi;\mathsf{A}}}{Z_{N,\beta}^{V;\mathsf{A}}}\,.\end{align*} $$
$$ \begin{align*}\mu_{N,\beta}^{V;\mathsf{A}}\big[e^{s\Phi_{N}[\varphi]}\big] = e^{-sN\int_{\mathsf{S}} \varphi(\xi)\mathrm{d}\mu_{\mathrm{eq}}^{V}(\xi) } \frac{Z_{N,\beta}^{V-\frac{2s}{N\beta}\varphi;\mathsf{A}}}{Z_{N,\beta}^{V;\mathsf{A}}}\,.\end{align*} $$
Again, the expansion of the free energies up to
![]() $o(1)$
allows to derive the asymptotics of the Laplace transform of
$o(1)$
allows to derive the asymptotics of the Laplace transform of
![]() $\Phi _{N}[\varphi ]$
and hence the central limit theorem; see Section 8.3. Note in passing that another way to study these fluctuations is to first condition the law
$\Phi _{N}[\varphi ]$
and hence the central limit theorem; see Section 8.3. Note in passing that another way to study these fluctuations is to first condition the law
![]() $\mu _{N,\beta }^{V;\mathsf {A}}$
by fixing its filling fractions to be equal to some
$\mu _{N,\beta }^{V;\mathsf {A}}$
by fixing its filling fractions to be equal to some
![]() $\boldsymbol {N}$
. Indeed, we can also recover the fluctuations of the linear statistics from those under the conditioned law (that can be deduced from the ratio of the partition functions of Theorem 1.4 and lead to classical central limit theorems with Gaussian limits), together with the fluctuations of the filling fractions. Then, one easily sees that the term
$\boldsymbol {N}$
. Indeed, we can also recover the fluctuations of the linear statistics from those under the conditioned law (that can be deduced from the ratio of the partition functions of Theorem 1.4 and lead to classical central limit theorems with Gaussian limits), together with the fluctuations of the filling fractions. Then, one easily sees that the term
![]() $\boldsymbol {u}_{\beta ;\star }$
comes from the fluctuations of the filling fractions and more precisely from the difference of centerings
$\boldsymbol {u}_{\beta ;\star }$
comes from the fluctuations of the filling fractions and more precisely from the difference of centerings
![]() $N(\int _{\mathsf {S}} \varphi (\xi )\mathrm {d}\mu _{\mathrm{eq}}^{V}(\xi )-\int _{\mathsf {S}} \varphi (\xi )\mathrm {d}\mu _{\mathrm{eq};\boldsymbol {N}/N}^{V}(\xi ))$
for varying
$N(\int _{\mathsf {S}} \varphi (\xi )\mathrm {d}\mu _{\mathrm{eq}}^{V}(\xi )-\int _{\mathsf {S}} \varphi (\xi )\mathrm {d}\mu _{\mathrm{eq};\boldsymbol {N}/N}^{V}(\xi ))$
for varying
![]() $\boldsymbol {N}/N$
.
$\boldsymbol {N}/N$
.
Therefore, the central result of this article is Theorem 1.5. To prove this theorem, we shall as in [Reference Borot and GuionnetBG11] interpolate between the partition functions we are interested in and explicitly computable reference partition functions. For the latter, we take a product of partition functions of one-cut models with Gaussian, Laguerre or Jacobi weight (depending on the nature of edges, soft or hard, of the equilibrium measure one wishes to match) that are evaluated as Selberg integrals. Such reference partition functions were already used in [Reference Borot and GuionnetBG11]. One important new element of the present analysis is the interpolation from a model with several cuts to independent one-cut models. This is realised by considering the s-dependent model
 $$ \begin{align*} & \quad Z_{N,\beta;\boldsymbol{\epsilon}}^{V;\mathsf{A}}(s) \\[7pt] & = \! \int_{\prod_{h = 0}^{g} \mathsf{A}_h^{N_h}} \Bigg[\prod_{h = 0}^{g} \prod_{i = 1}^{N_h} \mathrm{d}\lambda_{h,i}\,e^{-N\frac{\beta}{2}V_h(\lambda_{h,i})}\Bigg] \Bigg[\prod_{0 \leq h < h' \leq g} \prod_{\substack{1 \leq i \leq N_h \\ 1 \leq i' \leq N_{h'}}}\!\! |\lambda_{h,i} - \lambda_{h',i'}|^{s\beta}\Bigg] \Bigg[\prod_{h = 0}^{g} \prod_{1 \leq i < j \leq N_{h}} \!\! |\lambda_{h,i} - \lambda_{h,j}|^{\beta}\Bigg] \end{align*} $$
$$ \begin{align*} & \quad Z_{N,\beta;\boldsymbol{\epsilon}}^{V;\mathsf{A}}(s) \\[7pt] & = \! \int_{\prod_{h = 0}^{g} \mathsf{A}_h^{N_h}} \Bigg[\prod_{h = 0}^{g} \prod_{i = 1}^{N_h} \mathrm{d}\lambda_{h,i}\,e^{-N\frac{\beta}{2}V_h(\lambda_{h,i})}\Bigg] \Bigg[\prod_{0 \leq h < h' \leq g} \prod_{\substack{1 \leq i \leq N_h \\ 1 \leq i' \leq N_{h'}}}\!\! |\lambda_{h,i} - \lambda_{h',i'}|^{s\beta}\Bigg] \Bigg[\prod_{h = 0}^{g} \prod_{1 \leq i < j \leq N_{h}} \!\! |\lambda_{h,i} - \lambda_{h,j}|^{\beta}\Bigg] \end{align*} $$
for
![]() $s \in [0,1]$
. We choose to take the s-dependent potential
$s \in [0,1]$
. We choose to take the s-dependent potential
![]() $V_h(x) = T^s_h(x)$
on the h-segment
$V_h(x) = T^s_h(x)$
on the h-segment
 $$ \begin{align*}T^s_h(x) = V(x) - 2(1 - s)\sum_{h' \neq h} \int_{\mathsf{A}_{h'}} \mathrm{d}\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}(\xi)\,\ln|x - \xi|,\qquad \mathrm{for}\,\,x \in \mathsf{A}_{h}\,, \end{align*} $$
$$ \begin{align*}T^s_h(x) = V(x) - 2(1 - s)\sum_{h' \neq h} \int_{\mathsf{A}_{h'}} \mathrm{d}\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}(\xi)\,\ln|x - \xi|,\qquad \mathrm{for}\,\,x \in \mathsf{A}_{h}\,, \end{align*} $$
where V is the potential of the original model. This choice is such that the equilibrium measure associated with the model
![]() $Z_{N,\beta ;\boldsymbol {\epsilon }}^{T_{s};\mathsf {A}}(s) $
is the equilibrium measure of the original model; see Section 7.4. Moreover,
$Z_{N,\beta ;\boldsymbol {\epsilon }}^{T_{s};\mathsf {A}}(s) $
is the equilibrium measure of the original model; see Section 7.4. Moreover,
![]() $Z_{N,\beta ;\boldsymbol {\epsilon }}^{V;\mathsf {A}}=Z_{N,\beta ;\boldsymbol {\epsilon }}^{T_{1};\mathsf {A}}(1) $
, whereas
$Z_{N,\beta ;\boldsymbol {\epsilon }}^{V;\mathsf {A}}=Z_{N,\beta ;\boldsymbol {\epsilon }}^{T_{1};\mathsf {A}}(1) $
, whereas
![]() $Z_{N,\beta ;\boldsymbol {\epsilon }}^{T_{0};\mathsf {A}}(0)$
is a product of models whose equilibrium measure has only one-cut (they are the restriction of the equilibrium measure of the original model to each of the connected pieces of its support), which we can compute by [Reference Borot and GuionnetBG11] (see Section 7.1). Interpolating along this family yields
$Z_{N,\beta ;\boldsymbol {\epsilon }}^{T_{0};\mathsf {A}}(0)$
is a product of models whose equilibrium measure has only one-cut (they are the restriction of the equilibrium measure of the original model to each of the connected pieces of its support), which we can compute by [Reference Borot and GuionnetBG11] (see Section 7.1). Interpolating along this family yields
 $$ \begin{align} \nonumber & \quad \ln\bigg(\frac{Z_{N,\beta;\boldsymbol{\epsilon}}^{V;\mathsf{A}}}{Z_{N,\beta;\boldsymbol{\epsilon}}^{T_0;\mathsf{A}}(s = 0)}\bigg) =\int_{0}^{1}\partial_{s}\ln Z_{N,\beta;\boldsymbol{\epsilon}}^{T_{s};\mathsf{A}}(s) \mathrm{d} s \\ \nonumber &= \beta \int_{0}^{1} \mathrm{d} s\mu_{N,\beta;\boldsymbol{\epsilon}}^{T_{s};\mathsf{A}}(s) \bigg[\sum_{0 \leq h < h' \leq g}\sum_{{\substack{1 \leq i \leq N_h \\ 1 \leq i' \leq N_{h'}}}}\ln|\lambda_{h,i} - \lambda_{h',i'}| -N\sum_{0 \leq h' \neq h \leq g}\sum_{i = 1}^{N_h} \int_{\mathsf S_{h'}} \ln |\lambda_{h,i}-x| \mathrm{d}\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}(x)\bigg] \\ \nonumber & = -N\beta \sum_{0 \leq h \neq h' \leq g} \oint_{\mathsf{A}_{h}}\oint_{\mathsf{A}_{h'}} \frac{\mathrm{d} x\,\mathrm{d} x'}{(2\mathrm{i}\pi)^2}\,\ln[(x - x')\mathrm{sgn}(h - h')]\,W_{1;\boldsymbol{\epsilon}}^{\{-1\}}(x)\bigg(\int_{0}^{1} \mathrm{d} s\,W_{1;\boldsymbol{\epsilon}}^{s}(x')\bigg) \\ &\quad + \sum_{0 \leq h' \neq h \leq g} \frac{\beta}{2} \oint_{\mathsf{A}_{h}}\oint_{\mathsf{A}_{h'}} \frac{\mathrm{d} x\,\mathrm{d} x'}{(2\mathrm{i}\pi)^2} \ln[(x - x')\mathrm{sgn}(h - h')]\bigg(\int_{0}^{1} \mathrm{d} s \big[W_{2;\boldsymbol{\epsilon}}^{s}(x,x') + W_{1;\boldsymbol{\epsilon}}^{s}(x)W_{1;\boldsymbol{\epsilon}}^{s}(x')\big]\bigg). \end{align} $$
$$ \begin{align} \nonumber & \quad \ln\bigg(\frac{Z_{N,\beta;\boldsymbol{\epsilon}}^{V;\mathsf{A}}}{Z_{N,\beta;\boldsymbol{\epsilon}}^{T_0;\mathsf{A}}(s = 0)}\bigg) =\int_{0}^{1}\partial_{s}\ln Z_{N,\beta;\boldsymbol{\epsilon}}^{T_{s};\mathsf{A}}(s) \mathrm{d} s \\ \nonumber &= \beta \int_{0}^{1} \mathrm{d} s\mu_{N,\beta;\boldsymbol{\epsilon}}^{T_{s};\mathsf{A}}(s) \bigg[\sum_{0 \leq h < h' \leq g}\sum_{{\substack{1 \leq i \leq N_h \\ 1 \leq i' \leq N_{h'}}}}\ln|\lambda_{h,i} - \lambda_{h',i'}| -N\sum_{0 \leq h' \neq h \leq g}\sum_{i = 1}^{N_h} \int_{\mathsf S_{h'}} \ln |\lambda_{h,i}-x| \mathrm{d}\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}(x)\bigg] \\ \nonumber & = -N\beta \sum_{0 \leq h \neq h' \leq g} \oint_{\mathsf{A}_{h}}\oint_{\mathsf{A}_{h'}} \frac{\mathrm{d} x\,\mathrm{d} x'}{(2\mathrm{i}\pi)^2}\,\ln[(x - x')\mathrm{sgn}(h - h')]\,W_{1;\boldsymbol{\epsilon}}^{\{-1\}}(x)\bigg(\int_{0}^{1} \mathrm{d} s\,W_{1;\boldsymbol{\epsilon}}^{s}(x')\bigg) \\ &\quad + \sum_{0 \leq h' \neq h \leq g} \frac{\beta}{2} \oint_{\mathsf{A}_{h}}\oint_{\mathsf{A}_{h'}} \frac{\mathrm{d} x\,\mathrm{d} x'}{(2\mathrm{i}\pi)^2} \ln[(x - x')\mathrm{sgn}(h - h')]\bigg(\int_{0}^{1} \mathrm{d} s \big[W_{2;\boldsymbol{\epsilon}}^{s}(x,x') + W_{1;\boldsymbol{\epsilon}}^{s}(x)W_{1;\boldsymbol{\epsilon}}^{s}(x')\big]\bigg). \end{align} $$
It is important to note that in the first equality, the singularity of the logarithm is away from the range of integration as it involves variables in distinct segments, so we could express (1.38) in terms of analytic linear and quadratic statistics, which, in turn, can be expressed in terms of the correlators
![]() $W_{n;\boldsymbol {\epsilon }}^{s}$
of the model associated with
$W_{n;\boldsymbol {\epsilon }}^{s}$
of the model associated with
![]() $Z_{N,\beta ;\boldsymbol {\epsilon }}^{T_{s};\mathsf {A}}(s)$
. Lemma 7.5 gives the large N expansion of these correlators.
$Z_{N,\beta ;\boldsymbol {\epsilon }}^{T_{s};\mathsf {A}}(s)$
. Lemma 7.5 gives the large N expansion of these correlators.
These expansions are based on the so-called Dyson–Schwinger equations (4.1); see also (7.36) for the correlators of the interpolating models. These equations are exact equations satisfied by the correlators for any fixed N and obtained simply by integration by parts. They are a priori not closed, but the idea is to show that they are asymptotically closed so that if we can show that the correlators have a large N expansion of topological type, their coefficients will satisfy a closed system of equations. The latter is based on the fact that coefficients beyond the leading order satisfy an inhomogeneous linear equation, with inhomogeneous term involving coefficients of lower order only. Hence, solving the linear equation allows to define uniquely and recursively all the coefficients in the expansion of the correlators. The linear equation is described by a linear operator, called the master-operator, that we denote
![]() $\mathcal K$
(see (5.6)) and which is the same for all orders. An inversion of this operator (continuously on some function space) precisely allows to solve the linear equation.
$\mathcal K$
(see (5.6)) and which is the same for all orders. An inversion of this operator (continuously on some function space) precisely allows to solve the linear equation.
The central point of our approach is therefore to invert the operator
![]() $\mathcal K$
. In fact, the operator is not invertible but rather has a kernel of dimension at least g, where
$\mathcal K$
. In fact, the operator is not invertible but rather has a kernel of dimension at least g, where
![]() $(g + 1)$
is the number of cuts (i.e., connected components of the support of the equilibrium measure). However, its extension
$(g + 1)$
is the number of cuts (i.e., connected components of the support of the equilibrium measure). However, its extension
![]() $\hat {\mathcal K}$
, where we also record the periods around the cuts, is invertible in an off-critical situation; see Section 5.2.3. Fixing the filling fractions exactly amounts to use the extended operator
$\hat {\mathcal K}$
, where we also record the periods around the cuts, is invertible in an off-critical situation; see Section 5.2.3. Fixing the filling fractions exactly amounts to use the extended operator
![]() $\widehat {\mathcal {K}}$
instead of
$\widehat {\mathcal {K}}$
instead of
![]() $\mathcal {K}$
, and this is why we first consider the model with fixed filling fractions. The invertibility of the extended operator indeed allows us not only to formally solve the Dyson–Schwinger equations but also to show the existence of this asymptotic expansion to all orders in
$\mathcal {K}$
, and this is why we first consider the model with fixed filling fractions. The invertibility of the extended operator indeed allows us not only to formally solve the Dyson–Schwinger equations but also to show the existence of this asymptotic expansion to all orders in
![]() $\frac {1}{N}$
. To this end, it is necessary to use a priori rough estimates on the correlators, which we obtain by classical methods of concentration of measure and large deviations; see Section 3. These estimates can be improved iteratively with the Dyson–Schwinger equations (see, for example, Section 5.3) to obtain optimal estimates and eventually reach the all-order asymptotic expansion. This bootstrap strategy was first introduced in [Reference Borot and GuionnetBG11] for the one-cut model. We detail these computations in the case where
$\frac {1}{N}$
. To this end, it is necessary to use a priori rough estimates on the correlators, which we obtain by classical methods of concentration of measure and large deviations; see Section 3. These estimates can be improved iteratively with the Dyson–Schwinger equations (see, for example, Section 5.3) to obtain optimal estimates and eventually reach the all-order asymptotic expansion. This bootstrap strategy was first introduced in [Reference Borot and GuionnetBG11] for the one-cut model. We detail these computations in the case where
![]() $s=1$
in Section 5. We also need to carry this out for the interpolating s-dependent model in order to have asymptotic expansions to insert in (1.38). In that case, the extended operator does not have an explicit inverse, but we can nevertheless show by Fredholm arguments that it is invertible. Then we indicate in Section 7 the modifications to take into account the previous bootstrap argument for
$s=1$
in Section 5. We also need to carry this out for the interpolating s-dependent model in order to have asymptotic expansions to insert in (1.38). In that case, the extended operator does not have an explicit inverse, but we can nevertheless show by Fredholm arguments that it is invertible. Then we indicate in Section 7 the modifications to take into account the previous bootstrap argument for
![]() $s\in [0,1]$
.
$s\in [0,1]$
.
We stress again that we cannot use the inversion and bootstrap strategy in the Dyson–Schwinger equations for the correlators of the original model in the multi-cut regime because the relevant master operator is not invertible. This is the reason why we need the detour through the partition function with fixed filling fractions (via (1.36)), from which any desired expansion of the correlators of the original model can be obtained by looking at
![]() $\frac {1}{N}$
-perturbations of the potential.
$\frac {1}{N}$
-perturbations of the potential.
2. Application to (skew) orthogonal polynomials and integrable systems
The one-hermitian matrix model (i.e.,
![]() $\beta = 2$
) is related to the Toda chain and orthogonal polynomials (see, for example, [Reference DeiftDei99]). Similarly, the one-symmetric (resp. quaternionic self-dual) matrix model corresponds to
$\beta = 2$
) is related to the Toda chain and orthogonal polynomials (see, for example, [Reference DeiftDei99]). Similarly, the one-symmetric (resp. quaternionic self-dual) matrix model corresponds to
![]() $\beta = 1$
(resp.
$\beta = 1$
(resp.
![]() $\beta = 4$
) and is related to the Pfaff lattice and skew-orthogonal polynomials [Reference EynardEyn01, Reference Adler and van MoerbekeAvM02, Reference Adler, Horozov and van MoerbekeAHvM02]. Therefore, our results establish the all-order asymptotics of certain solutions (those related to matrix integrals) of the Toda chain and the Pfaff lattice in the continuum limit, and the all-order asymptotics of (skew) orthogonal polynomials away from the bulk. We illustrate it for orthogonal polynomials with respect to an analytic weight defined on the whole real line. It could be applied equally well to orthogonal polynomials with respect to an analytic weight on a finite union of segments of the real axis. We review with fewer details in § 2.4 the definition of skew-orthogonal polynomials and the way to obtain them from Corollary 1.10.
$\beta = 4$
) and is related to the Pfaff lattice and skew-orthogonal polynomials [Reference EynardEyn01, Reference Adler and van MoerbekeAvM02, Reference Adler, Horozov and van MoerbekeAHvM02]. Therefore, our results establish the all-order asymptotics of certain solutions (those related to matrix integrals) of the Toda chain and the Pfaff lattice in the continuum limit, and the all-order asymptotics of (skew) orthogonal polynomials away from the bulk. We illustrate it for orthogonal polynomials with respect to an analytic weight defined on the whole real line. It could be applied equally well to orthogonal polynomials with respect to an analytic weight on a finite union of segments of the real axis. We review with fewer details in § 2.4 the definition of skew-orthogonal polynomials and the way to obtain them from Corollary 1.10.
The leading order asymptotic of orthogonal polynomials is well known since the work of Deift et al. [Reference Deift, Kriecherbauer, McLaughlin, Venakides and ZhouDKM+97, Reference Deift, Kriecherbauer, McLaughlin, Venakides and ZhouDKM+99b, Reference Deift, Kriecherbauer, McLaughlin, Venakides and ZhouDKM+99a], using the asymptotic analysis of Riemann–Hilbert problems which was pioneered in [Reference Deift and ZhouDZ95]. In principle, it is possible to push the Riemann–Hilbert analysis beyond leading order, but because this approach is very cumbersome, it has not been performed yet to our knowledge. Notwithstanding, the all-order expansion has a nice structure and was heuristically derived by Eynard [Reference Eynard, Brézin, Kazakov, Serban, Wiegmann and ZabrodinEyn06] based on the general works [Reference Bonnet, David and EynardBDE00, Reference EynardEyn09]. In this article, we provide a proof of those heuristics.
Unlike the Riemann–Hilbert technique, which becomes cumbersome to study the asymptotics of skew-orthogonal polynomials (i.e.,
![]() $\beta = 1$
and
$\beta = 1$
and
![]() $4$
) and thus has not been performed up to now, our method could be applied without difficulty to those values of
$4$
) and thus has not been performed up to now, our method could be applied without difficulty to those values of
![]() $\beta $
and would allow to justify the heuristics of Eynard [Reference EynardEyn01] formulated for the leading order and describe all subleading orders. In other words, it provides a purely probabilistic approach to address asymptotic problems in integrable systems. It also suggests that the appearance of Theta functions is not intrinsically related to integrability. In particular, we see in Theorem 2.2 that for
$\beta $
and would allow to justify the heuristics of Eynard [Reference EynardEyn01] formulated for the leading order and describe all subleading orders. In other words, it provides a purely probabilistic approach to address asymptotic problems in integrable systems. It also suggests that the appearance of Theta functions is not intrinsically related to integrability. In particular, we see in Theorem 2.2 that for
![]() $\beta = 2$
, the Theta function appearing in the leading order is associated to the matrix of periods of the hyperelliptic curve
$\beta = 2$
, the Theta function appearing in the leading order is associated to the matrix of periods of the hyperelliptic curve
![]() $\mathcal {C}_{\boldsymbol {\epsilon }_{\star }}$
defined by the equilibrium measure. Actually, the Theta function is just the basic block to construct analytic functions on this curve, and this is the reason why it pops up in the Riemann–Hilbert analysis. However, for
$\mathcal {C}_{\boldsymbol {\epsilon }_{\star }}$
defined by the equilibrium measure. Actually, the Theta function is just the basic block to construct analytic functions on this curve, and this is the reason why it pops up in the Riemann–Hilbert analysis. However, for
![]() $\beta \neq 2$
, the Theta function is associated to
$\beta \neq 2$
, the Theta function is associated to
![]() $\frac {\beta }{2}$
times the matrix of periods of
$\frac {\beta }{2}$
times the matrix of periods of
![]() $\mathcal {C}_{\boldsymbol {\epsilon }_{\star }}$
, which might or might not be the matrix of period of a curve, and anyway is not that of
$\mathcal {C}_{\boldsymbol {\epsilon }_{\star }}$
, which might or might not be the matrix of period of a curve, and anyway is not that of
![]() $\mathcal {C}_{\boldsymbol {\epsilon }_{\star }}$
. So the monodromy problem solved by this Theta function is not directly related to the equilibrium measure, which makes, for instance, for
$\mathcal {C}_{\boldsymbol {\epsilon }_{\star }}$
. So the monodromy problem solved by this Theta function is not directly related to the equilibrium measure, which makes, for instance, for
![]() $\beta = 1$
or
$\beta = 1$
or
![]() $4$
, its construction via Riemann–Hilbert techniques a priori more involved.
$4$
, its construction via Riemann–Hilbert techniques a priori more involved.
Contrary to Riemann–Hilbert techniques, however, we are not yet in position within our method to consider the asymptotic in the bulk or at the edges, or the double-scaling limit for varying weights close to a critical point, or the case of complex-values weights which has been studied in [Reference Bertola and MoBM09]. It would be very interesting to find a way out of these technical restrictions within our method.
2.1. Setting
We first review the standard relations between orthogonal polynomials on the real line, random matrices and integrable systems see, for example, [Reference Claeys and GravaCG12, Section 5]. In this section,
![]() $\beta = 2$
, and we omit to precise it in the notations. Let
$\beta = 2$
, and we omit to precise it in the notations. Let
![]() $V_{\mathbf {t}}(\lambda ) = V(\lambda ) + \sum _{k = 1}^{d} t_k\lambda ^{k}$
. Let
$V_{\mathbf {t}}(\lambda ) = V(\lambda ) + \sum _{k = 1}^{d} t_k\lambda ^{k}$
. Let
![]() $(P_{n,N}(x))_{n \geq 0}$
be the monic orthogonal polynomials associated to the weight
$(P_{n,N}(x))_{n \geq 0}$
be the monic orthogonal polynomials associated to the weight
![]() $\mathrm {d} w(x) = \mathrm {d} x\,e^{-NV_{\mathbf {t}}(x)}$
on
$\mathrm {d} w(x) = \mathrm {d} x\,e^{-NV_{\mathbf {t}}(x)}$
on
![]() $\mathsf {B} = \mathbb {R}$
. We choose V and restrict in consequence
$\mathsf {B} = \mathbb {R}$
. We choose V and restrict in consequence
![]() $t_k$
so that the weight increases quickly at
$t_k$
so that the weight increases quickly at
![]() $\pm \infty $
. If we denote
$\pm \infty $
. If we denote
![]() $h_{n,N}$
the
$h_{n,N}$
the
![]() $L^2(\mathrm {d} w)$
norm of
$L^2(\mathrm {d} w)$
norm of
![]() $P_{n,N}$
, the polynomials
$P_{n,N}$
, the polynomials
![]() $\hat {P}_{n,N} = P_{n,N}/\sqrt {h_{n,N}}$
are orthonormal. They satisfy a three-term recurrence relation:
$\hat {P}_{n,N} = P_{n,N}/\sqrt {h_{n,N}}$
are orthonormal. They satisfy a three-term recurrence relation:
The recurrence coefficients are solutions of a Toda chain: if we set
we have
and the coefficients
![]() $t_{k}$
generate higher Toda flows. The recurrence coefficients also satisfy the string equations
$t_{k}$
generate higher Toda flows. The recurrence coefficients also satisfy the string equations
where
![]() $\mathbf {Q}_N$
is the semi-infinite matrix:
$\mathbf {Q}_N$
is the semi-infinite matrix:
 $$ \begin{align*}\mathbf{Q}_N = \left(\begin{array}{ccccc} \sqrt{h_{1,N}} & \beta_{1,N} & & & \\ \beta_{1,N} & \sqrt{h_{2,N}} & \beta_{2,N} & & \\ & \beta_{2,N} & \sqrt{h_{3,N}} & \beta_{3,N} & \\ & \ddots & \ddots & \ddots & \\ & & & & \end{array}\right). \end{align*} $$
$$ \begin{align*}\mathbf{Q}_N = \left(\begin{array}{ccccc} \sqrt{h_{1,N}} & \beta_{1,N} & & & \\ \beta_{1,N} & \sqrt{h_{2,N}} & \beta_{2,N} & & \\ & \beta_{2,N} & \sqrt{h_{3,N}} & \beta_{3,N} & \\ & \ddots & \ddots & \ddots & \\ & & & & \end{array}\right). \end{align*} $$
The equations 2.2 determine in terms of V the initial condition for the system (2.1). The partition function
![]() $\mathcal {T}(\mathbf {t}) = Z_{N}^{V_{\mathbf {t}};\mathbb {R}}$
is the Tau function associated to the solution
$\mathcal {T}(\mathbf {t}) = Z_{N}^{V_{\mathbf {t}};\mathbb {R}}$
is the Tau function associated to the solution
![]() $(u_{n,N}(\mathbf {t}),v_{n,N}(\mathbf {t}))_{n \geq 1}$
of Equation (2.1). The partition function itself can be computed as [Reference MehtaMeh04, Reference Pastur and ShcherbinaPS11]:
$(u_{n,N}(\mathbf {t}),v_{n,N}(\mathbf {t}))_{n \geq 1}$
of Equation (2.1). The partition function itself can be computed as [Reference MehtaMeh04, Reference Pastur and ShcherbinaPS11]:
 $$ \begin{align*}Z_{N}^{V;\mathbb R } = N!\,\prod_{j = 0}^{N - 1} h_{j,N}. \end{align*} $$
$$ \begin{align*}Z_{N}^{V;\mathbb R } = N!\,\prod_{j = 0}^{N - 1} h_{j,N}. \end{align*} $$
We insist on the dependence on N and V by writing
![]() $h_{j,N} = h_{j}(NV)$
. Therefore, the norms can be retrieved as
$h_{j,N} = h_{j}(NV)$
. Therefore, the norms can be retrieved as
 $$ \begin{align} h_{n}(NV) = \frac{\prod_{j = 1}^{n} h_{j}(NV)}{\prod_{j = 1}^{n - 1} h_{j}(NV)} = \frac{1}{n + 1}\,\frac{Z_{n + 1}^{NV/(n + 1);\mathbb R}}{Z_{n}^{NV/n; \mathbb R}} = \frac{1}{n + 1}\,\frac{Z_{n + 1}^{\frac{V}{s(1 + 1/n)};\mathbb{R}}}{Z_{n}^{V/s;\mathbb{R}}},\qquad s = \frac{n}{N}. \end{align} $$
$$ \begin{align} h_{n}(NV) = \frac{\prod_{j = 1}^{n} h_{j}(NV)}{\prod_{j = 1}^{n - 1} h_{j}(NV)} = \frac{1}{n + 1}\,\frac{Z_{n + 1}^{NV/(n + 1);\mathbb R}}{Z_{n}^{NV/n; \mathbb R}} = \frac{1}{n + 1}\,\frac{Z_{n + 1}^{\frac{V}{s(1 + 1/n)};\mathbb{R}}}{Z_{n}^{V/s;\mathbb{R}}},\qquad s = \frac{n}{N}. \end{align} $$
The regime where
![]() $n,N \rightarrow \infty $
but
$n,N \rightarrow \infty $
but
![]() $s = \frac {n}{N}$
remains fixed and positive corresponds to the small dispersion regime in the Toda chain, where
$s = \frac {n}{N}$
remains fixed and positive corresponds to the small dispersion regime in the Toda chain, where
![]() $\frac {1}{n}$
plays the role of the dispersion parameter.
$\frac {1}{n}$
plays the role of the dispersion parameter.
2.2. Small dispersion asymptotics of
 $h_{n,N}$
$h_{n,N}$
When
![]() $V_{\mathbf {t}_0}/s_0$
satisfies Hypotheses 1.1 and 1.2 for a given set of times
$V_{\mathbf {t}_0}/s_0$
satisfies Hypotheses 1.1 and 1.2 for a given set of times
![]() $(s_0,\mathbf {t}_0)$
,
$(s_0,\mathbf {t}_0)$
,
![]() $V_{\mathbf {t}}/s$
satisfies the same assumptions at least for
$V_{\mathbf {t}}/s$
satisfies the same assumptions at least for
![]() $(s,\mathbf {t})$
in some neighbourhood
$(s,\mathbf {t})$
in some neighbourhood
![]() $\mathcal {U}$
of
$\mathcal {U}$
of
![]() $(s_0,\mathbf {t}_0)$
, and Theorem 1.5 determines the asymptotic expansion of
$(s_0,\mathbf {t}_0)$
, and Theorem 1.5 determines the asymptotic expansion of
![]() $\mathcal {T}_{N}(\mathbf {t})=Z_N^{V_{\mathbf {t}};\mathbb R}$
up to
$\mathcal {T}_{N}(\mathbf {t})=Z_N^{V_{\mathbf {t}};\mathbb R}$
up to
![]() $O(N^{-\infty })$
. Besides, we can apply Theorem 1.5 to study the ratio in the right-hand side of Equation (2.3) when
$O(N^{-\infty })$
. Besides, we can apply Theorem 1.5 to study the ratio in the right-hand side of Equation (2.3) when
![]() $n \rightarrow \infty $
up to
$n \rightarrow \infty $
up to
![]() $o(n^{-\infty })$
. For instance, we record below the expansion up to order
$o(n^{-\infty })$
. For instance, we record below the expansion up to order
![]() $O(n^{-2})$
.
$O(n^{-2})$
.
Theorem 2.1. In the regime
![]() $n,N \rightarrow \infty $
,
$n,N \rightarrow \infty $
,
![]() $s = \frac {n}{N}> 0$
fixed, and Hypotheses 1.1 and 1.2 are satisfied with soft edges, we have the following asymptotic expansion:
$s = \frac {n}{N}> 0$
fixed, and Hypotheses 1.1 and 1.2 are satisfied with soft edges, we have the following asymptotic expansion:
 $$ \begin{align} \nonumber u_{n,N}& = n\big(2\mathcal{F}^{[0]}_{\star} - \mathcal{L}_{\frac{V_{\mathbf{t}}}{s}}[\mathcal{W}_{1;\star}^{[0]}]\big) + 1 + \mathcal{F}^{[0]}_{\star} - \mathcal{L}_{\frac{V_{\mathbf{t}}}{s}}\big[\mathcal{W}_{1;\star}^{[0]}\big] + \frac{1}{2}\mathcal{L}^{\otimes 2}_{\frac{V_{\mathbf{t}}}{s}}\big[\mathcal{W}_{2;\star}^{[0]}\big] + \ln\Big(\frac{\tilde{\Theta}_{n}}{\Theta_{n}}\Big) \\ \nonumber & \quad + \frac{1}{n}\Bigg\{\varkappa - \frac{1}{2} + \mathcal{L}_{\frac{\boldsymbol{\mathcal{B}}}{2\mathrm{i}\pi}}\big[\mathcal{W}_{1;\star}^{[1]}\big] \cdot \nabla\ln\Big(\frac{\tilde{\Theta}_n}{\Theta_n}\Big) - \mathcal{L}_{\frac{V_{\mathbf{t}}}{s}}\big[\mathcal{W}_{1;\star}^{[1]}\big] \\ \nonumber & \quad \qquad + \frac{1}{6}\,\mathcal{L}_{\frac{\boldsymbol{\mathcal{B}}}{2\mathrm{i}\pi}}^{\otimes 3}\big[\mathcal{W}_{3;\star}^{[0]}\big] \cdot \Big(\frac{\nabla^{\otimes 3}\tilde{\Theta}_{n}}{\tilde{\Theta}_{n}} - \frac{\nabla^{\otimes 3} \Theta_{n}}{\Theta_n}\Big) - \frac{1}{2}\,\mathcal{L}_{\frac{\boldsymbol{\mathcal{B}}}{2\mathrm{i}\pi}}^{\otimes 2} \otimes \mathcal{L}_{\frac{V_{\mathbf{t}}}{s}}\big[W_{3;\star}^{[0]}\big] \cdot \frac{\nabla^{\otimes 2} \tilde{\Theta}_{n}}{\tilde{\Theta}_{n}} \\ & \quad \qquad + \frac{1}{2} \mathcal{L}_{\frac{\boldsymbol{\mathcal{B}}}{2\mathrm{i}\pi}} \otimes \mathcal{L}_{\frac{V_{\mathbf{t}}}{s}}^{\otimes 2}\big[\mathcal{W}_{3;\star}^{[0]}\big] \cdot \nabla \ln \tilde{\Theta}_n - \frac{1}{6} \mathcal{L}_{\frac{V_{\mathbf{t}}}{s}}^{\otimes 3}\big[\mathcal{W}_{3;\star}^{[0]}\big]\bigg\} + O(n^{-2}). \end{align} $$
$$ \begin{align} \nonumber u_{n,N}& = n\big(2\mathcal{F}^{[0]}_{\star} - \mathcal{L}_{\frac{V_{\mathbf{t}}}{s}}[\mathcal{W}_{1;\star}^{[0]}]\big) + 1 + \mathcal{F}^{[0]}_{\star} - \mathcal{L}_{\frac{V_{\mathbf{t}}}{s}}\big[\mathcal{W}_{1;\star}^{[0]}\big] + \frac{1}{2}\mathcal{L}^{\otimes 2}_{\frac{V_{\mathbf{t}}}{s}}\big[\mathcal{W}_{2;\star}^{[0]}\big] + \ln\Big(\frac{\tilde{\Theta}_{n}}{\Theta_{n}}\Big) \\ \nonumber & \quad + \frac{1}{n}\Bigg\{\varkappa - \frac{1}{2} + \mathcal{L}_{\frac{\boldsymbol{\mathcal{B}}}{2\mathrm{i}\pi}}\big[\mathcal{W}_{1;\star}^{[1]}\big] \cdot \nabla\ln\Big(\frac{\tilde{\Theta}_n}{\Theta_n}\Big) - \mathcal{L}_{\frac{V_{\mathbf{t}}}{s}}\big[\mathcal{W}_{1;\star}^{[1]}\big] \\ \nonumber & \quad \qquad + \frac{1}{6}\,\mathcal{L}_{\frac{\boldsymbol{\mathcal{B}}}{2\mathrm{i}\pi}}^{\otimes 3}\big[\mathcal{W}_{3;\star}^{[0]}\big] \cdot \Big(\frac{\nabla^{\otimes 3}\tilde{\Theta}_{n}}{\tilde{\Theta}_{n}} - \frac{\nabla^{\otimes 3} \Theta_{n}}{\Theta_n}\Big) - \frac{1}{2}\,\mathcal{L}_{\frac{\boldsymbol{\mathcal{B}}}{2\mathrm{i}\pi}}^{\otimes 2} \otimes \mathcal{L}_{\frac{V_{\mathbf{t}}}{s}}\big[W_{3;\star}^{[0]}\big] \cdot \frac{\nabla^{\otimes 2} \tilde{\Theta}_{n}}{\tilde{\Theta}_{n}} \\ & \quad \qquad + \frac{1}{2} \mathcal{L}_{\frac{\boldsymbol{\mathcal{B}}}{2\mathrm{i}\pi}} \otimes \mathcal{L}_{\frac{V_{\mathbf{t}}}{s}}^{\otimes 2}\big[\mathcal{W}_{3;\star}^{[0]}\big] \cdot \nabla \ln \tilde{\Theta}_n - \frac{1}{6} \mathcal{L}_{\frac{V_{\mathbf{t}}}{s}}^{\otimes 3}\big[\mathcal{W}_{3;\star}^{[0]}\big]\bigg\} + O(n^{-2}). \end{align} $$
We used the shortcut notations
 $$ \begin{align*}\tilde{\Theta}_{n} = \vartheta\!\left[\begin{array}{@{\hspace{-0.03cm}}c@{\hspace{-0.03cm}}} -(n + 1)\,\boldsymbol{\epsilon}_{\star}\, \\ \boldsymbol{0} \end{array}\right]\!\big(\boldsymbol{v} -\mathcal{L}_{V_{\mathbf{t}}/s}[\boldsymbol{\varpi}]\big|\boldsymbol{\tau}_{\star}\big),\qquad \Theta_{n} = \vartheta\!\left[\begin{array}{@{\hspace{-0.03cm}}c@{\hspace{-0.03cm}}} -n\,\boldsymbol{\epsilon}_{\star}\, \\ \boldsymbol{0} \end{array}\right]\!\big(\boldsymbol{v}\big|\boldsymbol{\tau}_{\star}\big), \end{align*} $$
$$ \begin{align*}\tilde{\Theta}_{n} = \vartheta\!\left[\begin{array}{@{\hspace{-0.03cm}}c@{\hspace{-0.03cm}}} -(n + 1)\,\boldsymbol{\epsilon}_{\star}\, \\ \boldsymbol{0} \end{array}\right]\!\big(\boldsymbol{v} -\mathcal{L}_{V_{\mathbf{t}}/s}[\boldsymbol{\varpi}]\big|\boldsymbol{\tau}_{\star}\big),\qquad \Theta_{n} = \vartheta\!\left[\begin{array}{@{\hspace{-0.03cm}}c@{\hspace{-0.03cm}}} -n\,\boldsymbol{\epsilon}_{\star}\, \\ \boldsymbol{0} \end{array}\right]\!\big(\boldsymbol{v}\big|\boldsymbol{\tau}_{\star}\big), \end{align*} $$
and in Equation (2.4), it is understood that the argument
![]() $\boldsymbol {v}$
is specialised to
$\boldsymbol {v}$
is specialised to
![]() $\boldsymbol {0}$
after application of the
$\boldsymbol {0}$
after application of the
![]() $\nabla = \nabla _{\boldsymbol {v}}$
. Besides,
$\nabla = \nabla _{\boldsymbol {v}}$
. Besides,
When
![]() $V_{\mathbf {t}}/s$
leads to a multi-cut regime, this asymptotic expansion features oscillations. Numerical evidence for such oscillations first appeared in [Reference JurkiewiczJur91], where plots of
$V_{\mathbf {t}}/s$
leads to a multi-cut regime, this asymptotic expansion features oscillations. Numerical evidence for such oscillations first appeared in [Reference JurkiewiczJur91], where plots of
![]() $h_{n - 1,N}/h_{n,N}$
displaying the phase transitions from a one-cut to a multi-cut regime can be found for a sextic potential.
$h_{n - 1,N}/h_{n,N}$
displaying the phase transitions from a one-cut to a multi-cut regime can be found for a sextic potential.
We recall that all the quantities
![]() $\mathcal {W}_{m;\star }^{[G]}$
can be computed from the equilibrium measure associated to the potential
$\mathcal {W}_{m;\star }^{[G]}$
can be computed from the equilibrium measure associated to the potential
![]() $V_{\mathbf {t}}$
, so making those asymptotic explicit just requires to solve the scalar Riemann–Hilbert problem for
$V_{\mathbf {t}}$
, so making those asymptotic explicit just requires to solve the scalar Riemann–Hilbert problem for
![]() $\mu _\mathrm{{eq}}^{sV_{\mathbf {t}}}$
. Notice that the number
$\mu _\mathrm{{eq}}^{sV_{\mathbf {t}}}$
. Notice that the number
![]() $(g + 1)$
of cuts a priori depends on
$(g + 1)$
of cuts a priori depends on
![]() $(s_0,\mathbf {t}_0)$
, and we do not address the issue of transitions between regimes with different number of cuts (because we cannot relax at present our off-criticality assumption), which are expected to be universal [Reference DubrovinDub08].
$(s_0,\mathbf {t}_0)$
, and we do not address the issue of transitions between regimes with different number of cuts (because we cannot relax at present our off-criticality assumption), which are expected to be universal [Reference DubrovinDub08].
2.3. Asymptotic expansion of orthogonal polynomials away from the bulk
The orthogonal polynomials can be computed thanks to Heine formula [Reference SzegöSze39]:
 $$ \begin{align*}P_n(x) = \mu_{n}^{V_{\mathbf{t}}/s;\mathbb{R}}\bigg[\prod_{i = 1}^n (x - \lambda_i)\bigg] = \mathsf{K}_{1,1}(x). \end{align*} $$
$$ \begin{align*}P_n(x) = \mu_{n}^{V_{\mathbf{t}}/s;\mathbb{R}}\bigg[\prod_{i = 1}^n (x - \lambda_i)\bigg] = \mathsf{K}_{1,1}(x). \end{align*} $$
Hence, as a consequence of Corollary 1.10, we obtain their asymptotic expansion away from the bulk. We first collect some notations that appeared throughout the introduction, specialised to the case
![]() $\beta = 2$
relevant here:
$\beta = 2$
relevant here:
 $$ \begin{align*}\mathcal{W}_{0;\star}^{[G]} = \mathcal{F}_{\star}^{[G]} = F_{\beta = 2;\boldsymbol{\epsilon}_{\star}}^{\{2G - 2\}},\qquad \mathcal{W}_{n;\star}^{[G]} = W_{n;\boldsymbol{\epsilon}_{\star}}^{\{2G - 2 + n\}},\qquad \boldsymbol{\tau}_{\star} = \frac{(\mathcal{F}^{[0]}_{\beta=2;\star})"}{2\mathrm{i}\pi}, \end{align*} $$
$$ \begin{align*}\mathcal{W}_{0;\star}^{[G]} = \mathcal{F}_{\star}^{[G]} = F_{\beta = 2;\boldsymbol{\epsilon}_{\star}}^{\{2G - 2\}},\qquad \mathcal{W}_{n;\star}^{[G]} = W_{n;\boldsymbol{\epsilon}_{\star}}^{\{2G - 2 + n\}},\qquad \boldsymbol{\tau}_{\star} = \frac{(\mathcal{F}^{[0]}_{\beta=2;\star})"}{2\mathrm{i}\pi}, \end{align*} $$
and
 $$ \begin{align*} T_{\star}^{\{k\}}[\boldsymbol{X}] & = \sum_{r = 1}^{k} \frac{1}{r!} \sum_{\substack{j_1,\ldots,j_r \geq 1 \\ G_1,\ldots,G_r \geq 0 \\ 2G_i - 2 + j_i> 0 \\ \sum_{i = 1}^{r} (2G_i - 2 + j_i) = k}} \Big(\bigotimes_{i = 1}^{r} \frac{(\mathcal{F}_{\star}^{[G_i]})^{(j_i)}}{j_i!}\Big)\cdot\boldsymbol{X}^{\otimes(\sum_{i = 1}^r j_i)}, \\ \tilde{T}_{\star}^{\{k\}}[\mathcal{L};\boldsymbol{X}] & = \sum_{r = 1}^{k} \frac{1}{r!} \sum_{\substack{j_1,\ldots,j_r \geq 1 \\ G_1,\ldots,G_r \geq 0 \\ n_1,\ldots,n_r \geq 0 \\ 2G_i - 2 + n_i + j_i > 0 \\ \sum_{i = 1}^{r} (2G_i - 2 + n_i + j_i) = k}} \Big(\bigotimes_{i = 1}^{r} \frac{\mathcal{L}^{\otimes n_i}[(\mathcal{W}_{n_i;\star}^{[G_i]})^{(j_i)}]}{n_i!\,j_i!}\Big)\cdot\boldsymbol{X}^{\otimes(\sum_{i = 1}^r j_i)}, \end{align*} $$
$$ \begin{align*} T_{\star}^{\{k\}}[\boldsymbol{X}] & = \sum_{r = 1}^{k} \frac{1}{r!} \sum_{\substack{j_1,\ldots,j_r \geq 1 \\ G_1,\ldots,G_r \geq 0 \\ 2G_i - 2 + j_i> 0 \\ \sum_{i = 1}^{r} (2G_i - 2 + j_i) = k}} \Big(\bigotimes_{i = 1}^{r} \frac{(\mathcal{F}_{\star}^{[G_i]})^{(j_i)}}{j_i!}\Big)\cdot\boldsymbol{X}^{\otimes(\sum_{i = 1}^r j_i)}, \\ \tilde{T}_{\star}^{\{k\}}[\mathcal{L};\boldsymbol{X}] & = \sum_{r = 1}^{k} \frac{1}{r!} \sum_{\substack{j_1,\ldots,j_r \geq 1 \\ G_1,\ldots,G_r \geq 0 \\ n_1,\ldots,n_r \geq 0 \\ 2G_i - 2 + n_i + j_i > 0 \\ \sum_{i = 1}^{r} (2G_i - 2 + n_i + j_i) = k}} \Big(\bigotimes_{i = 1}^{r} \frac{\mathcal{L}^{\otimes n_i}[(\mathcal{W}_{n_i;\star}^{[G_i]})^{(j_i)}]}{n_i!\,j_i!}\Big)\cdot\boldsymbol{X}^{\otimes(\sum_{i = 1}^r j_i)}, \end{align*} $$
where
Theorem 2.2. In the regime
![]() $n,N \rightarrow \infty $
,
$n,N \rightarrow \infty $
,
![]() $s = \frac {n}{N}> 0$
fixed, and Hypotheses 1.1 and 1.2 are satisfied, for
$s = \frac {n}{N}> 0$
fixed, and Hypotheses 1.1 and 1.2 are satisfied, for
![]() $x \in \mathbb {C}\setminus \mathsf {S}$
, we have the asymptotic expansion, for any
$x \in \mathbb {C}\setminus \mathsf {S}$
, we have the asymptotic expansion, for any
![]() $K \geq 0$
,
$K \geq 0$
,
 $$ \begin{align*} P_n(x) & = \exp\Big(\sum_{\substack{m \geq 1,\,\ G \geq 0 \\ 2G - 2 + m \leq K}} n^{2 - 2G - m} \frac{\mathcal{L}_{x}^{\otimes m}[\mathcal{W}_{m;\star}^{[G]}]}{m!}\Big)\big(1 + O(n^{-(K + 1)})\big) \\ & \quad \times \frac{\Big(\sum_{k = 0}^K n^{-k}\,\tilde{T}^{\{k\}}\big[\mathcal{L}_{x}\,;\,\frac{\nabla_{\boldsymbol{v}}}{2\mathrm{i}\pi}\big]\Big) \vartheta\!\left[\begin{array}{@{\hspace{-0.03cm}}c@{\hspace{-0.03cm}}} -n\,\boldsymbol{\epsilon}_{\star}\, \\ \boldsymbol{0} \end{array}\right]\!\big(\mathcal{L}_x[\boldsymbol{\varpi}]\big|\boldsymbol{\tau}_{\star}\big)}{\Big(\sum_{k = 0}^K n^{-k}\,T^{\{k\}}\big[\frac{\nabla_{\boldsymbol{v}}}{2\mathrm{i}\pi}\big]\Big) \vartheta\!\left[\begin{array}{@{\hspace{-0.03cm}}c@{\hspace{-0.03cm}}} -n\,\boldsymbol{\epsilon}_{\star}\, \\ \boldsymbol{0} \end{array}\right]\!\big(\boldsymbol{0}\big|\boldsymbol{\tau}_{\star}\big)}, \end{align*} $$
$$ \begin{align*} P_n(x) & = \exp\Big(\sum_{\substack{m \geq 1,\,\ G \geq 0 \\ 2G - 2 + m \leq K}} n^{2 - 2G - m} \frac{\mathcal{L}_{x}^{\otimes m}[\mathcal{W}_{m;\star}^{[G]}]}{m!}\Big)\big(1 + O(n^{-(K + 1)})\big) \\ & \quad \times \frac{\Big(\sum_{k = 0}^K n^{-k}\,\tilde{T}^{\{k\}}\big[\mathcal{L}_{x}\,;\,\frac{\nabla_{\boldsymbol{v}}}{2\mathrm{i}\pi}\big]\Big) \vartheta\!\left[\begin{array}{@{\hspace{-0.03cm}}c@{\hspace{-0.03cm}}} -n\,\boldsymbol{\epsilon}_{\star}\, \\ \boldsymbol{0} \end{array}\right]\!\big(\mathcal{L}_x[\boldsymbol{\varpi}]\big|\boldsymbol{\tau}_{\star}\big)}{\Big(\sum_{k = 0}^K n^{-k}\,T^{\{k\}}\big[\frac{\nabla_{\boldsymbol{v}}}{2\mathrm{i}\pi}\big]\Big) \vartheta\!\left[\begin{array}{@{\hspace{-0.03cm}}c@{\hspace{-0.03cm}}} -n\,\boldsymbol{\epsilon}_{\star}\, \\ \boldsymbol{0} \end{array}\right]\!\big(\boldsymbol{0}\big|\boldsymbol{\tau}_{\star}\big)}, \end{align*} $$
where
![]() $\mathcal {L}_{x} = \int _{\infty }^{x}$
. For a given K, this expansion is uniform for x in any compact of
$\mathcal {L}_{x} = \int _{\infty }^{x}$
. For a given K, this expansion is uniform for x in any compact of
![]() $\mathbb {C}\setminus \mathsf {S}$
.
$\mathbb {C}\setminus \mathsf {S}$
.
We remark that
![]() $\mathcal {L}_{x}[\boldsymbol {\varpi }] = \int _{\infty }^{x} \boldsymbol {\varpi }$
is the Abel map evaluated between the points x and
$\mathcal {L}_{x}[\boldsymbol {\varpi }] = \int _{\infty }^{x} \boldsymbol {\varpi }$
is the Abel map evaluated between the points x and
![]() $\infty $
. The variable
$\infty $
. The variable
![]() $s = \frac {n}{N}$
rescales the potential, and therefore, the equilibrium measure and all the coefficient of expansions depend on s.
$s = \frac {n}{N}$
rescales the potential, and therefore, the equilibrium measure and all the coefficient of expansions depend on s.
As such, the results presented in this article do not allow the study of the asymptotic expansion of orthogonal polynomials in the bulk (i.e., for
![]() $x \in \mathsf {S}$
). Indeed, this requires perturbing the potential
$x \in \mathsf {S}$
). Indeed, this requires perturbing the potential
![]() $V(\lambda )$
by a term
$V(\lambda )$
by a term
![]() $-\frac {1}{n}\,\ln (\lambda - x)$
having a singularity at
$-\frac {1}{n}\,\ln (\lambda - x)$
having a singularity at
![]() $x \in \mathsf {S}$
, a case going beyond our Hypothesis 1.3. Similarly, we cannot address at present the regime of transitions between a g-cut regime and a
$x \in \mathsf {S}$
, a case going beyond our Hypothesis 1.3. Similarly, we cannot address at present the regime of transitions between a g-cut regime and a
![]() $g'$
-cut regime with
$g'$
-cut regime with
![]() $g \neq g'$
because off-criticality was a key assumption in our derivation. Although it is the most interesting in regard of universality, the question of deriving uniform asymptotics, even at the leading order, valid for the crossover around a critical point is still open from the point of view of our methods.
$g \neq g'$
because off-criticality was a key assumption in our derivation. Although it is the most interesting in regard of universality, the question of deriving uniform asymptotics, even at the leading order, valid for the crossover around a critical point is still open from the point of view of our methods.
2.4. Asymptotic expansion of skew-orthogonal polynomials
The expectation values of
![]() $\prod _{i = 1}^N (x - \lambda _i)$
in the
$\prod _{i = 1}^N (x - \lambda _i)$
in the
![]() $\beta $
-ensembles for
$\beta $
-ensembles for
![]() $\beta = 1$
and
$\beta = 1$
and
![]() $4$
are skew-orthogonal polynomials. Let us review this point and just mention that the application of Corollary 1.10 implies all-order asymptotic for skew-orthogonal polynomials away from the bulk. Here, the relevant skew-symmetric bilinear products are
$4$
are skew-orthogonal polynomials. Let us review this point and just mention that the application of Corollary 1.10 implies all-order asymptotic for skew-orthogonal polynomials away from the bulk. Here, the relevant skew-symmetric bilinear products are
 $$ \begin{align} \nonumber \langle f,g \rangle_{n,\beta = 1} & = \int_{\mathbb{R}^2} \mathrm{d} x\mathrm{d} y\,e^{-n(V(x) + V(y))}\,\mathrm{sgn}(y - x)\,f(x)g(y), \\ \langle f,g \rangle_{n,\beta = 4} & = \int_{\mathbb{R}} \mathrm{d} x\,e^{-n\,V(x)}\big(f(x)g'(x) - f'(x)g(x)\big). \end{align} $$
$$ \begin{align} \nonumber \langle f,g \rangle_{n,\beta = 1} & = \int_{\mathbb{R}^2} \mathrm{d} x\mathrm{d} y\,e^{-n(V(x) + V(y))}\,\mathrm{sgn}(y - x)\,f(x)g(y), \\ \langle f,g \rangle_{n,\beta = 4} & = \int_{\mathbb{R}} \mathrm{d} x\,e^{-n\,V(x)}\big(f(x)g'(x) - f'(x)g(x)\big). \end{align} $$
A family of polynomials
![]() $(P_{N}(x))_{N \geq 0}$
is skew-orthogonal if
$(P_{N}(x))_{N \geq 0}$
is skew-orthogonal if
For a given skew-symmetric product, the family of skew-orthogonal polynomials is not unique since one can add to
![]() $P_{2N + 1}$
any multiple of
$P_{2N + 1}$
any multiple of
![]() $P_{2N}$
, and this does not change the skew-norms
$P_{2N}$
, and this does not change the skew-norms
![]() $h_N$
. If we add the requirement that the degree
$h_N$
. If we add the requirement that the degree
![]() $2N$
term in
$2N$
term in
![]() $P_{2N + 1}$
vanishes, the skew-orthogonal polynomials are then unique. The generalisation of Heine formula was proved in [Reference EynardEyn01]:
$P_{2N + 1}$
vanishes, the skew-orthogonal polynomials are then unique. The generalisation of Heine formula was proved in [Reference EynardEyn01]:
Theorem 2.3. Let
![]() $P_{N;n,\beta }$
be a set of monic skew-orthogonal polynomials associated to (2.5). We can take
$P_{N;n,\beta }$
be a set of monic skew-orthogonal polynomials associated to (2.5). We can take
 $$ \begin{align*} P_{2N;n,\beta = 1}(x) & = \mu_{2N,\beta = 1}^{nV/N;\mathbb{R}}\Big[\prod_{i = 1}^{2N} (x - \lambda_i)\Big], \\ P_{2N + 1;n,\beta = 1}(x) & = \mu_{2N,\beta=1}^{nV/N;\mathbb{R}}\Bigg[\Big(x + \sum_{i = 1}^{2N} \lambda_i\Big)\prod_{i = 1}^{2N}(x - \lambda_i)\Bigg], \\ P_{2N;n,\beta = 4}(x) & = \mu_{N,\beta = 4}^{nV/2N;\mathbb{R}}\Big[\prod_{i = 1}^{N} (x - \lambda_i)^2\Big], \\ P_{2N;n,\beta = 4}(x) & = \mu_{N,\beta = 4}^{nV/2N;\mathbb{R}}\Bigg[\Big(x + \sum_{i = 1}^{N} 2\lambda_i\Big)\prod_{i = 1}^{N} (x - \lambda_i)^2\Bigg]. \end{align*} $$
$$ \begin{align*} P_{2N;n,\beta = 1}(x) & = \mu_{2N,\beta = 1}^{nV/N;\mathbb{R}}\Big[\prod_{i = 1}^{2N} (x - \lambda_i)\Big], \\ P_{2N + 1;n,\beta = 1}(x) & = \mu_{2N,\beta=1}^{nV/N;\mathbb{R}}\Bigg[\Big(x + \sum_{i = 1}^{2N} \lambda_i\Big)\prod_{i = 1}^{2N}(x - \lambda_i)\Bigg], \\ P_{2N;n,\beta = 4}(x) & = \mu_{N,\beta = 4}^{nV/2N;\mathbb{R}}\Big[\prod_{i = 1}^{N} (x - \lambda_i)^2\Big], \\ P_{2N;n,\beta = 4}(x) & = \mu_{N,\beta = 4}^{nV/2N;\mathbb{R}}\Bigg[\Big(x + \sum_{i = 1}^{N} 2\lambda_i\Big)\prod_{i = 1}^{N} (x - \lambda_i)^2\Bigg]. \end{align*} $$
Corollary 1.10 then determines the asymptotics of the right-hand side. The partition function itself can be deduced from the skew-norms [Reference MehtaMeh04]
 $$ \begin{align*} Z_{2N,\beta = 1}^{nV/2N;\mathbb{R}} & = (2N)! \prod_{j = 0}^{N - 1} h_{j;n,\beta =1} \\ Z_{2N + 1,\beta = 1}^{nV/(2N + 1);\mathbb{R}} & = (2N + 1)!\prod_{j = 0}^{N - 1} h_{j;n,\beta = 1} \cdot \int_{\mathbb{R}} e^{-nV(x)} P_{N-1;n,\beta}(x)\mathrm{d} x \\ \qquad Z_{N,\beta = 4}^{nV/2N;\mathbb{R}} & = N! \prod_{j = 0}^{N - 1} h_{j;n,\ \beta = 4}, \end{align*} $$
$$ \begin{align*} Z_{2N,\beta = 1}^{nV/2N;\mathbb{R}} & = (2N)! \prod_{j = 0}^{N - 1} h_{j;n,\beta =1} \\ Z_{2N + 1,\beta = 1}^{nV/(2N + 1);\mathbb{R}} & = (2N + 1)!\prod_{j = 0}^{N - 1} h_{j;n,\beta = 1} \cdot \int_{\mathbb{R}} e^{-nV(x)} P_{N-1;n,\beta}(x)\mathrm{d} x \\ \qquad Z_{N,\beta = 4}^{nV/2N;\mathbb{R}} & = N! \prod_{j = 0}^{N - 1} h_{j;n,\ \beta = 4}, \end{align*} $$
and conversely,
 $$ \begin{align*}h_{N;n,\beta = 1} = \frac{1}{(2N + 2)(2N + 1)}\,\frac{Z_{2N + 2,\beta = 1}^{nV/(2N + 2);\mathbb{R}}}{Z_{2N,\beta}^{nV/2N;\mathbb{R}}},\qquad h_{N;n,\beta = 4} = \frac{1}{N + 1} \frac{Z_{N + 1,\beta = 4}^{nV/(2N + 2);\mathbb{R}}}{Z_{N,\beta = 4}^{nV/2N;\mathbb{R}}}. \end{align*} $$
$$ \begin{align*}h_{N;n,\beta = 1} = \frac{1}{(2N + 2)(2N + 1)}\,\frac{Z_{2N + 2,\beta = 1}^{nV/(2N + 2);\mathbb{R}}}{Z_{2N,\beta}^{nV/2N;\mathbb{R}}},\qquad h_{N;n,\beta = 4} = \frac{1}{N + 1} \frac{Z_{N + 1,\beta = 4}^{nV/(2N + 2);\mathbb{R}}}{Z_{N,\beta = 4}^{nV/2N;\mathbb{R}}}. \end{align*} $$
It has been shown that this partition function for
![]() $\beta = 1$
is a tau-function of the Pfaff lattice [Reference Adler, Horozov and van MoerbekeAHvM02, Reference Adler and van MoerbekeAvM02]. Here, we obtain its asymptotic expansion from Theorem 1.5.
$\beta = 1$
is a tau-function of the Pfaff lattice [Reference Adler, Horozov and van MoerbekeAHvM02, Reference Adler and van MoerbekeAvM02]. Here, we obtain its asymptotic expansion from Theorem 1.5.
3. Large deviations and concentration of measure
3.1. Restriction to a vicinity of the support
Our first step is to show that the interval of integration in Equation (1.1) can be restricted to a vicinity of the support of the equilibrium measure up to exponentially small corrections when N is large. The proofs are very similar to the one-cut case [Reference Borot and GuionnetBG11], and we recall briefly their idea in § 3.2. Let V be a regular and confining potential, and
![]() $\mu _\mathrm{{eq}}^{V;\mathsf {B}}$
the equilibrium measure determined by Theorem 1.1. We denote by
$\mu _\mathrm{{eq}}^{V;\mathsf {B}}$
the equilibrium measure determined by Theorem 1.1. We denote by
![]() $\mathsf {S}$
its (compact) support. We define the effective potential by
$\mathsf {S}$
its (compact) support. We define the effective potential by
when
![]() $x \in \mathsf {B}$
, and
$x \in \mathsf {B}$
, and
![]() $+\infty $
otherwise.
$+\infty $
otherwise.
Lemma 3.1. If V is regular, is confining, and converges uniformly to
![]() $V^{\{0\}}$
on
$V^{\{0\}}$
on
![]() $\mathsf {B}$
, then we have large deviation estimates: for any
$\mathsf {B}$
, then we have large deviation estimates: for any
![]() $\mathsf {F} \subseteq \overline {\mathsf {B}\backslash \mathsf {S}}$
closed in
$\mathsf {F} \subseteq \overline {\mathsf {B}\backslash \mathsf {S}}$
closed in
![]() $\mathsf {B}$
and
$\mathsf {B}$
and
![]() $\mathsf {O} \subseteq \mathsf {B}\backslash \mathsf {S}$
open in
$\mathsf {O} \subseteq \mathsf {B}\backslash \mathsf {S}$
open in
![]() $\mathsf {B}$
,
$\mathsf {B}$
,

Definition 3.1. We say that V satisfies a control of large deviations on
![]() $\mathsf {B}$
if
$\mathsf {B}$
if
![]() $\tilde {U}_{\mathrm{eq}}^{V;\mathsf {B}}$
is positive on
$\tilde {U}_{\mathrm{eq}}^{V;\mathsf {B}}$
is positive on
![]() $\mathsf {B}\setminus \mathsf {S}$
.
$\mathsf {B}\setminus \mathsf {S}$
.
Note that
![]() $\tilde {U}_{\mathrm{eq}}^{V;\mathsf {B}}$
vanishes at the boundary of
$\tilde {U}_{\mathrm{eq}}^{V;\mathsf {B}}$
vanishes at the boundary of
![]() $ \mathsf {S}$
. According to Lemma 3.1, such a property implies that large deviations outside
$ \mathsf {S}$
. According to Lemma 3.1, such a property implies that large deviations outside
![]() $\mathsf {S}$
are exponentially small when N is large.
$\mathsf {S}$
are exponentially small when N is large.
Corollary 3.2. Let V be regular, confining and satisfying a control of large deviations on
![]() $\mathsf {B}$
. Let
$\mathsf {B}$
. Let
![]() $ \mathsf {A} \subseteq \mathsf {B}$
be a finite union of segments which contains
$ \mathsf {A} \subseteq \mathsf {B}$
be a finite union of segments which contains
![]() $\{x\in \mathsf {B}: d(x,\mathsf {S}) \le \delta \}$
for some positive
$\{x\in \mathsf {B}: d(x,\mathsf {S}) \le \delta \}$
for some positive
![]() $\delta $
. There exists
$\delta $
. There exists
![]() $\eta (\mathsf {A})> 0$
so that
$\eta (\mathsf {A})> 0$
so that
and for any
![]() $n \geq 1$
, there exists a universal constant
$n \geq 1$
, there exists a universal constant
![]() $\gamma _n> 0$
so that, for any
$\gamma _n> 0$
so that, for any
![]() $x_1,\ldots ,x_n \in (\mathbb {C}\setminus \mathsf {B})^{n}$
,
$x_1,\ldots ,x_n \in (\mathbb {C}\setminus \mathsf {B})^{n}$
,
 $$ \begin{align} \big|W_n^{V;\mathsf{B}}(x_1,\ldots,x_n) - W_n^{V;\mathsf{A}}(x_1,\ldots,x_n)\big| \leq \frac{\gamma_{n}\,e^{-N\eta(\mathsf{A})}}{\prod_{i = 1}^{n} d(x_i,\mathsf{B})}. \end{align} $$
$$ \begin{align} \big|W_n^{V;\mathsf{B}}(x_1,\ldots,x_n) - W_n^{V;\mathsf{A}}(x_1,\ldots,x_n)\big| \leq \frac{\gamma_{n}\,e^{-N\eta(\mathsf{A})}}{\prod_{i = 1}^{n} d(x_i,\mathsf{B})}. \end{align} $$
Note that if all edges are hard, we have
![]() $\mathsf {B} = \mathsf {S}$
, and Lemma 3.1 and Corollary 3.2 are useless.
$\mathsf {B} = \mathsf {S}$
, and Lemma 3.1 and Corollary 3.2 are useless.
It is useful to have a local version of this result, saying that we can vary endpoints of the segments which are not hard edges for the equilibrium measure, up to exponentially small corrections.
Corollary 3.3. Let V be regular, confining and satisfying a control of large deviations on
![]() $\mathsf {B}$
. Let
$\mathsf {B}$
. Let
![]() $\mathsf {A} \subseteq \mathsf {B}$
be a finite union of segments which contains
$\mathsf {A} \subseteq \mathsf {B}$
be a finite union of segments which contains
![]() $\{x\in \mathsf {B}: d(x,\mathsf {S}) \le \delta \}$
for some positive
$\{x\in \mathsf {B}: d(x,\mathsf {S}) \le \delta \}$
for some positive
![]() $\delta $
. If
$\delta $
. If
![]() $a_0$
is the left edge of a connected component of
$a_0$
is the left edge of a connected component of
![]() $\mathsf {A}$
and
$\mathsf {A}$
and
![]() $a < a_0$
and is not in
$a < a_0$
and is not in
![]() $\mathsf {S}$
, let us define
$\mathsf {S}$
, let us define
![]() $\mathsf {A}_{a} = \mathsf {A} \cup [a,a_0]$
. For any
$\mathsf {A}_{a} = \mathsf {A} \cup [a,a_0]$
. For any
![]() $\varepsilon> 0$
small enough, there exists
$\varepsilon> 0$
small enough, there exists
![]() $\eta _{\varepsilon }> 0$
so that, for N large enough and any
$\eta _{\varepsilon }> 0$
so that, for N large enough and any
![]() $a \in (a_0 - \varepsilon ,a_0) \subseteq \mathsf {B}$
, we have
$a \in (a_0 - \varepsilon ,a_0) \subseteq \mathsf {B}$
, we have
and for N large enough and any
![]() $n \geq 1$
and
$n \geq 1$
and
![]() $x_1,\ldots ,x_n \in (\mathbb {C}\setminus \mathsf {A}_{a})$
,
$x_1,\ldots ,x_n \in (\mathbb {C}\setminus \mathsf {A}_{a})$
,
 $$ \begin{align} \left| \partial_{a} W_{n}^{V;\mathsf{A}_a}(x_1,\ldots,x_n)\right| \leq \frac{\gamma_{n}\,e^{-N\eta_{\varepsilon}}}{\prod_{i = 1}^{n} d(x_i,\mathsf{A}_{a})}. \end{align} $$
$$ \begin{align} \left| \partial_{a} W_{n}^{V;\mathsf{A}_a}(x_1,\ldots,x_n)\right| \leq \frac{\gamma_{n}\,e^{-N\eta_{\varepsilon}}}{\prod_{i = 1}^{n} d(x_i,\mathsf{A}_{a})}. \end{align} $$
A similar result holds at the right endpoint of a connected component of
![]() $\mathsf {A}$
.
$\mathsf {A}$
.
From now on, even though we initially want to study the model on
![]() $\mathsf {B}^N$
, we are first going to study the model on
$\mathsf {B}^N$
, we are first going to study the model on
![]() $\mathsf {A}^N\kern-1.3pt$
, where
$\mathsf {A}^N\kern-1.3pt$
, where
![]() $\mathsf {A}$
is a small (but fixed) enlargement of
$\mathsf {A}$
is a small (but fixed) enlargement of
![]() $\mathsf {S}$
within
$\mathsf {S}$
within
![]() $\mathsf {B}$
, as allowed above. In particular, when
$\mathsf {B}$
, as allowed above. In particular, when
![]() $\mathsf {S}$
is a disjoint union of finite segments
$\mathsf {S}$
is a disjoint union of finite segments
![]() $(\mathsf {S}_{h})_{h = 0}^g$
, we can take
$(\mathsf {S}_{h})_{h = 0}^g$
, we can take
![]() $\mathsf {A}$
to be a disjoint union of finite segments
$\mathsf {A}$
to be a disjoint union of finite segments
![]() $(\mathsf {A}_{h})_{h = 0}^g$
such that
$(\mathsf {A}_{h})_{h = 0}^g$
such that
![]() $\mathsf {A}_h$
is a neighbourhood of
$\mathsf {A}_h$
is a neighbourhood of
![]() $\mathsf {S}_h$
in
$\mathsf {S}_h$
in
![]() $\mathsf {B}$
. More precisely, we can take as endpoints of
$\mathsf {B}$
. More precisely, we can take as endpoints of
![]() $\mathsf {A}$
points close enough to the soft edges of the equilibrium measure but outside of its support, while the hard edges must remain endpoints common to
$\mathsf {A}$
points close enough to the soft edges of the equilibrium measure but outside of its support, while the hard edges must remain endpoints common to
![]() $\mathsf {S},\mathsf {A}$
and
$\mathsf {S},\mathsf {A}$
and
![]() $\mathsf {B}$
. We next state similar results for the fixed filling fractions model of Section 1.4. Recall that part of the data defining this model is a sequence (indexed by N) of g-uple of positive integers
$\mathsf {B}$
. We next state similar results for the fixed filling fractions model of Section 1.4. Recall that part of the data defining this model is a sequence (indexed by N) of g-uple of positive integers
![]() $\boldsymbol {N} = (N_1,\ldots ,N_g)$
such that
$\boldsymbol {N} = (N_1,\ldots ,N_g)$
such that
![]() $N_0 = N - \sum _{h = 1}^{g} N_h \geq 0$
and such that
$N_0 = N - \sum _{h = 1}^{g} N_h \geq 0$
and such that
![]() $\boldsymbol {\epsilon } = \boldsymbol {N}/N$
converges to a point in
$\boldsymbol {\epsilon } = \boldsymbol {N}/N$
converges to a point in
 $$ \begin{align*}\mathcal{E}_{g} = \Big\{\boldsymbol{\epsilon} \in (0,1)^{g}\,\,\Big|\,\,\,\sum_{h = 1}^{g} \epsilon_h < 1\Big\}. \end{align*} $$
$$ \begin{align*}\mathcal{E}_{g} = \Big\{\boldsymbol{\epsilon} \in (0,1)^{g}\,\,\Big|\,\,\,\sum_{h = 1}^{g} \epsilon_h < 1\Big\}. \end{align*} $$
In this context, the effective potential is defined for
![]() $x \in \mathsf {A}_{h}$
by the formula
$x \in \mathsf {A}_{h}$
by the formula
and for
![]() $x \notin \mathsf {A}$
, we declare
$x \notin \mathsf {A}$
, we declare
![]() $U^{V;\mathsf {A}}_{\mathrm{eq};\boldsymbol {\epsilon }} = \tilde {U}^{V;\mathsf {A}}_{\mathrm{eq};\boldsymbol {\epsilon }} = +\infty $
.
$U^{V;\mathsf {A}}_{\mathrm{eq};\boldsymbol {\epsilon }} = \tilde {U}^{V;\mathsf {A}}_{\mathrm{eq};\boldsymbol {\epsilon }} = +\infty $
.
Proposition 3.4. If V is regular, confining and uniformly to
![]() $V^{\{0\}}$
on
$V^{\{0\}}$
on
![]() $\mathsf {A}$
, then for any closed set
$\mathsf {A}$
, then for any closed set
![]() $\mathsf {F}$
and open set
$\mathsf {F}$
and open set
![]() $\mathsf {O}$
of
$\mathsf {O}$
of
![]() $\mathbb R$
,
$\mathbb R$
,

Moreover, Corollaries 3.2 and 3.3 also extend to this setting.
We may omit the superscript
![]() $\mathsf {A}$
in the equilibrium measure, the effective potential, etc. when it is clear that we work with the compact set
$\mathsf {A}$
in the equilibrium measure, the effective potential, etc. when it is clear that we work with the compact set
![]() $\mathsf {A}$
.
$\mathsf {A}$
.
3.2. Sketch of the proof of Lemma 3.1
We only sketch the proof since it is similar to [Reference Borot and GuionnetBG11] as well as [Reference Anderson, Guionnet and ZeitouniAGZ10, section 2.6.2]. The only technical difference is that the lower bound is achieved here by introducing the functions
![]() $H_{x,\varepsilon }$
and
$H_{x,\varepsilon }$
and
![]() $\phi _{x,K}$
below rather than localising
$\phi _{x,K}$
below rather than localising
![]() $L_{N-1}$
to probability measures on some smaller sets than
$L_{N-1}$
to probability measures on some smaller sets than
![]() $\mathsf {B}$
in [Reference Borot and GuionnetBG11]. We first give the proof for the initial model and at the end of the proof precise the necessary changes to deal with the model with fixed filling fractions.
$\mathsf {B}$
in [Reference Borot and GuionnetBG11]. We first give the proof for the initial model and at the end of the proof precise the necessary changes to deal with the model with fixed filling fractions.
Recall that
![]() $L_N = N^{-1}\sum _{i = 1}^N\delta _{ \lambda _i}$
denotes the normalised empirical measure. We observe that
$L_N = N^{-1}\sum _{i = 1}^N\delta _{ \lambda _i}$
denotes the normalised empirical measure. We observe that

where, for any measurable set
![]() $\mathsf {X}$
,
$\mathsf {X}$
,
 $$ \begin{align*}\Upsilon_{N,\beta}^{V;\mathsf{B}}(\mathsf{X}) = \mu_{N - 1,\beta}^{\frac{NV}{N - 1};\mathsf{B}}\left[\int_{\mathsf{X}} \mathrm{d}\xi\,\exp\Big\{-\frac{N\beta}{2}\,V(\xi) + (N - 1)\beta\int_{\mathsf{B}}\mathrm{d} L_{N - 1}(\lambda)\ln|\xi - \lambda| \Big\}\right]. \end{align*} $$
$$ \begin{align*}\Upsilon_{N,\beta}^{V;\mathsf{B}}(\mathsf{X}) = \mu_{N - 1,\beta}^{\frac{NV}{N - 1};\mathsf{B}}\left[\int_{\mathsf{X}} \mathrm{d}\xi\,\exp\Big\{-\frac{N\beta}{2}\,V(\xi) + (N - 1)\beta\int_{\mathsf{B}}\mathrm{d} L_{N - 1}(\lambda)\ln|\xi - \lambda| \Big\}\right]. \end{align*} $$
We shall hereafter estimate
![]() $\frac {1}{N}\ln \Upsilon _{N,\beta }^{V;\mathsf {B}}(\mathsf {X})$
.
$\frac {1}{N}\ln \Upsilon _{N,\beta }^{V;\mathsf {B}}(\mathsf {X})$
.
We first prove a lower bound for
![]() $\Upsilon _{N,\beta }^{V;\mathsf {B}}(\mathsf {X})$
with
$\Upsilon _{N,\beta }^{V;\mathsf {B}}(\mathsf {X})$
with
![]() $\mathsf {X}$
open in
$\mathsf {X}$
open in
![]() $\mathsf {B}$
. For any
$\mathsf {B}$
. For any
![]() $x\in \mathsf {X}$
, we can find
$x\in \mathsf {X}$
, we can find
![]() $\varepsilon>0$
such that
$\varepsilon>0$
such that
![]() $(x-\varepsilon ,x+\varepsilon ) \cap \mathsf {B} \subset \mathsf {X}$
. Let
$(x-\varepsilon ,x+\varepsilon ) \cap \mathsf {B} \subset \mathsf {X}$
. Let
 $$ \begin{align*}\delta_{\varepsilon}^{V} =\max_{\substack{|x - y| \leq \varepsilon \\ x,y \in \mathsf{B}}} |V(x)-V(y)|. \end{align*} $$
$$ \begin{align*}\delta_{\varepsilon}^{V} =\max_{\substack{|x - y| \leq \varepsilon \\ x,y \in \mathsf{B}}} |V(x)-V(y)|. \end{align*} $$
Using twice Jensen inequality and the convention
![]() $V(\xi ) = +\infty $
for
$V(\xi ) = +\infty $
for
![]() $\xi \notin \mathsf {B}$
, we get
$\xi \notin \mathsf {B}$
, we get
 $$ \begin{align*} \Upsilon_{N,\beta}^{V;\mathsf{B}}(\mathsf{X}) & \geq \mu_{N - 1,\beta}^{\frac{NV}{N - 1};\mathsf{B}}\left[\int_{x - \varepsilon}^{x + \varepsilon} \mathrm{d}\xi \exp\Big\{-\frac{N\beta}{2}\,V(\xi) + (N - 1)\beta\int_{\mathsf{B}} \mathrm{d} L_{N - 1}(\lambda)\ln|\xi - \lambda|\Big)\Big\}\right] \\ & \geq e^{-\frac{N\beta}{2}(V(x) + \delta_\varepsilon^V)}\,\mu_{N - 1,\beta}^{\frac{NV}{N - 1};\mathsf{B}}\left[\int_{x - \varepsilon}^{x + \varepsilon} \mathrm{d}\xi \exp\Big\{(N - 1)\beta\,\int_{\mathsf{B}} \mathrm{d} L_{N - 1}(\lambda)\ln|\xi - \lambda|\Big\}\right] \\ & \geq {2\varepsilon}\ e^{-\frac{N\beta}{2}(V(x) + \delta_\varepsilon^V)}\,\exp\Big\{(N - 1)\beta\,\mu_{N - 1,\beta}^{\frac{NV}{N - 1};\mathsf{B}}\Big[\int_{\mathsf{B}} \mathrm{d} L_{N - 1}(\lambda)\,H_{x,\varepsilon}(\lambda)\Big]\Big\} \\ & \geq 2\varepsilon\,e^{-\frac{N\beta}{2}(V(x) + \delta_{\varepsilon}^V)}\,\exp\Big\{(N - 1)\beta\,\mu_{N - 1,\beta}^{\frac{NV}{N - 1};\mathsf{B}}\Big[\int_{\mathsf{B}} \mathrm{d} L_{N - 1}(\lambda)\,\phi_{x,K}(\lambda) H_{x,\varepsilon}(\lambda)\Big]\Big\}, \end{align*} $$
$$ \begin{align*} \Upsilon_{N,\beta}^{V;\mathsf{B}}(\mathsf{X}) & \geq \mu_{N - 1,\beta}^{\frac{NV}{N - 1};\mathsf{B}}\left[\int_{x - \varepsilon}^{x + \varepsilon} \mathrm{d}\xi \exp\Big\{-\frac{N\beta}{2}\,V(\xi) + (N - 1)\beta\int_{\mathsf{B}} \mathrm{d} L_{N - 1}(\lambda)\ln|\xi - \lambda|\Big)\Big\}\right] \\ & \geq e^{-\frac{N\beta}{2}(V(x) + \delta_\varepsilon^V)}\,\mu_{N - 1,\beta}^{\frac{NV}{N - 1};\mathsf{B}}\left[\int_{x - \varepsilon}^{x + \varepsilon} \mathrm{d}\xi \exp\Big\{(N - 1)\beta\,\int_{\mathsf{B}} \mathrm{d} L_{N - 1}(\lambda)\ln|\xi - \lambda|\Big\}\right] \\ & \geq {2\varepsilon}\ e^{-\frac{N\beta}{2}(V(x) + \delta_\varepsilon^V)}\,\exp\Big\{(N - 1)\beta\,\mu_{N - 1,\beta}^{\frac{NV}{N - 1};\mathsf{B}}\Big[\int_{\mathsf{B}} \mathrm{d} L_{N - 1}(\lambda)\,H_{x,\varepsilon}(\lambda)\Big]\Big\} \\ & \geq 2\varepsilon\,e^{-\frac{N\beta}{2}(V(x) + \delta_{\varepsilon}^V)}\,\exp\Big\{(N - 1)\beta\,\mu_{N - 1,\beta}^{\frac{NV}{N - 1};\mathsf{B}}\Big[\int_{\mathsf{B}} \mathrm{d} L_{N - 1}(\lambda)\,\phi_{x,K}(\lambda) H_{x,\varepsilon}(\lambda)\Big]\Big\}, \end{align*} $$
where we have set
 $$ \begin{align*}H_{x,\varepsilon}(\lambda) = \int_{x - \varepsilon}^{x + \varepsilon} \frac{\mathrm{d}\xi}{2\varepsilon}\,\ln|\xi - \lambda|, \end{align*} $$
$$ \begin{align*}H_{x,\varepsilon}(\lambda) = \int_{x - \varepsilon}^{x + \varepsilon} \frac{\mathrm{d}\xi}{2\varepsilon}\,\ln|\xi - \lambda|, \end{align*} $$
and
![]() $\phi _{x,K}$
is a continuous function vanishing outside of a large compact K that includes the support of
$\phi _{x,K}$
is a continuous function vanishing outside of a large compact K that includes the support of
![]() $\mu _\mathrm{{eq}}^{V}$
, is equal to
$\mu _\mathrm{{eq}}^{V}$
, is equal to
![]() $1$
on a ball around x with radius
$1$
on a ball around x with radius
![]() $1+\varepsilon $
and on the support of
$1+\varepsilon $
and on the support of
![]() $\mu _\mathrm{{eq}}^{V}$
, and takes values in
$\mu _\mathrm{{eq}}^{V}$
, and takes values in
![]() $[0,1]$
. For any fixed
$[0,1]$
. For any fixed
![]() $\varepsilon> 0$
,
$\varepsilon> 0$
,
![]() $\phi _{x,K} \cdot H_{x,\varepsilon }$
is bounded continuous, so we have by Theorem 1.1
$\phi _{x,K} \cdot H_{x,\varepsilon }$
is bounded continuous, so we have by Theorem 1.1
with
![]() $\lim _{N \rightarrow \infty } R(\varepsilon ,N) = 0$
for all
$\lim _{N \rightarrow \infty } R(\varepsilon ,N) = 0$
for all
![]() $\varepsilon>0$
. Letting
$\varepsilon>0$
. Letting
![]() $N \rightarrow \infty $
, we deduce since
$N \rightarrow \infty $
, we deduce since
and since V converges uniformly towards
![]() $V^{\{0\}}$
, that
$V^{\{0\}}$
, that
Exchanging the integration over
![]() $\xi $
and
$\xi $
and
![]() $\lambda $
, observing that
$\lambda $
, observing that
![]() $\xi \rightarrow \int _{\mathsf {B}} \mathrm {d}\mu _\mathrm{{eq}}^{V}(\lambda )\,\ln |\xi -\lambda |$
is continuous and then letting
$\xi \rightarrow \int _{\mathsf {B}} \mathrm {d}\mu _\mathrm{{eq}}^{V}(\lambda )\,\ln |\xi -\lambda |$
is continuous and then letting
![]() $\varepsilon \rightarrow 0$
, we conclude that for all
$\varepsilon \rightarrow 0$
, we conclude that for all
![]() $x\in \mathsf {X}$
,
$x\in \mathsf {X}$
,
where we have recognised the effective potential of Equation (3.1). We finally optimise over
![]() $x\in \mathsf {X}$
to get the desired lower bound. To prove the upper bound, we note that for any
$x\in \mathsf {X}$
to get the desired lower bound. To prove the upper bound, we note that for any
![]() $M>0$
,
$M>0$
,
 $$ \begin{align*}\Upsilon_{N,\beta}^{V;\mathsf{B}}(\mathsf{X}) \le \mu_{N - 1,\beta}^{\frac{NV}{N - 1};\mathsf{B}}\left[\int_{\mathsf{X}} \mathrm{d}\xi\,\exp\Big\{-\frac{N\beta}{2}\,V(\xi) + (N - 1)\beta\int_{\mathsf{B}} \mathrm{d} L_{N - 1}(\lambda)\ln \mathrm{max}\big(|\xi - \lambda|,M^{-1}\big)\Big\}\right] \,. \end{align*} $$
$$ \begin{align*}\Upsilon_{N,\beta}^{V;\mathsf{B}}(\mathsf{X}) \le \mu_{N - 1,\beta}^{\frac{NV}{N - 1};\mathsf{B}}\left[\int_{\mathsf{X}} \mathrm{d}\xi\,\exp\Big\{-\frac{N\beta}{2}\,V(\xi) + (N - 1)\beta\int_{\mathsf{B}} \mathrm{d} L_{N - 1}(\lambda)\ln \mathrm{max}\big(|\xi - \lambda|,M^{-1}\big)\Big\}\right] \,. \end{align*} $$
Observe that there exists
![]() $C_0$
and
$C_0$
and
![]() $c>0$
and d finite such that for
$c>0$
and d finite such that for
![]() $|\xi | \geq C_0$
and all probability measures
$|\xi | \geq C_0$
and all probability measures
![]() $\mu $
on
$\mu $
on
![]() $\mathsf {B}$
,
$\mathsf {B}$
,
by the confinement Hypothesis 1.1. As a consequence, if
![]() $\mathsf {X}\subset \mathsf {B} \setminus [-C,C]$
for some C large enough, we deduce that
$\mathsf {X}\subset \mathsf {B} \setminus [-C,C]$
for some C large enough, we deduce that
where the last bound holds for N large enough. Combining Equations (3.7), (3.8) and (3.6) shows that
Hence, we may restrict ourselves to
![]() $\mathsf {X}$
bounded. Moreover, the same bound extends to
$\mathsf {X}$
bounded. Moreover, the same bound extends to
![]() $ \mu _{N - 1,\beta }^{\frac {NV}{N - 1};\mathsf {B}}$
so that we can restrict the expectation over
$ \mu _{N - 1,\beta }^{\frac {NV}{N - 1};\mathsf {B}}$
so that we can restrict the expectation over
![]() $L_{N-1}$
to probability measures supported on
$L_{N-1}$
to probability measures supported on
![]() $[-C,C]$
up to an arbitrary small error
$[-C,C]$
up to an arbitrary small error
![]() $e^{-N e(C)}$
, provided C is large enough and where
$e^{-N e(C)}$
, provided C is large enough and where
![]() $\lim _{C \rightarrow +\infty } e(C) = +\infty $
. The confinement hypothesis also guarantees that
$\lim _{C \rightarrow +\infty } e(C) = +\infty $
. The confinement hypothesis also guarantees that
![]() $V(\xi )-2\int _{\mathsf {B}} \mathrm {d} L_{N - 1}(\lambda )\ln \mathrm {max}\big (|\xi - \lambda |,M^{-1}\big )$
is uniformly bounded from below by a constant D. As
$V(\xi )-2\int _{\mathsf {B}} \mathrm {d} L_{N - 1}(\lambda )\ln \mathrm {max}\big (|\xi - \lambda |,M^{-1}\big )$
is uniformly bounded from below by a constant D. As
![]() $\lambda \mapsto \ln \mathrm {max}\big (|\xi - \lambda |,M^{-1}\big )$
is bounded continuous on compacts and M-Lipschitz on
$\lambda \mapsto \ln \mathrm {max}\big (|\xi - \lambda |,M^{-1}\big )$
is bounded continuous on compacts and M-Lipschitz on
![]() $\mathbb {R}$
, we can then use the large deviation principles of Theorem 1.1 to deduce that for any
$\mathbb {R}$
, we can then use the large deviation principles of Theorem 1.1 to deduce that for any
![]() $\varepsilon>0$
, any
$\varepsilon>0$
, any
![]() $C\ge C_0$
,
$C\ge C_0$
,
 $$ \begin{align*} \Upsilon_{N,\beta}^{V;\mathsf{B}}(\mathsf{X}) &\leq e^{ N^2 \tilde{R}(\varepsilon,N,C)} +e^{-N(e(C)-\frac{\beta}{2}D)} \\ & \quad +\int_{\mathsf{X}} \mathrm{d}\xi \,\exp\bigg(-\frac{N\beta}{2}\,V(\xi) + (N - 1)\beta\int_{\mathsf{B}} \mathrm{d}\mu_{\mathrm{eq}}^{V}(\lambda) \ln \mathrm{max}\big(|\xi - \lambda|,M^{-1}\big) +N M \varepsilon \bigg) \end{align*} $$
$$ \begin{align*} \Upsilon_{N,\beta}^{V;\mathsf{B}}(\mathsf{X}) &\leq e^{ N^2 \tilde{R}(\varepsilon,N,C)} +e^{-N(e(C)-\frac{\beta}{2}D)} \\ & \quad +\int_{\mathsf{X}} \mathrm{d}\xi \,\exp\bigg(-\frac{N\beta}{2}\,V(\xi) + (N - 1)\beta\int_{\mathsf{B}} \mathrm{d}\mu_{\mathrm{eq}}^{V}(\lambda) \ln \mathrm{max}\big(|\xi - \lambda|,M^{-1}\big) +N M \varepsilon \bigg) \end{align*} $$
with
In terms of the Vaserstein distance between two probability measures,
 $$ \begin{align*}\mathfrak{d}(\mu,\nu) = \sup\bigg\{\Big|\int_{\mathbb{R}} f(\xi)\mathrm{d}[\mu - \nu](\xi)\Big| \quad : \quad f: \mathbb{R} \rightarrow \mathbb{R} \,\,1\text{-Lipschitz}\bigg\}. \end{align*} $$
$$ \begin{align*}\mathfrak{d}(\mu,\nu) = \sup\bigg\{\Big|\int_{\mathbb{R}} f(\xi)\mathrm{d}[\mu - \nu](\xi)\Big| \quad : \quad f: \mathbb{R} \rightarrow \mathbb{R} \,\,1\text{-Lipschitz}\bigg\}. \end{align*} $$
Moreover,
![]() $\xi \mapsto V(\xi ) - 2\int _{\mathsf {B}} \mathrm {d}\mu _\mathrm{{eq}}^{V}(\lambda ) \ln \mathrm {max}\big (|\xi - \lambda |,M^{-1}\big )$
is bounded continuous so that a standard Laplace method yields, as V goes to
$\xi \mapsto V(\xi ) - 2\int _{\mathsf {B}} \mathrm {d}\mu _\mathrm{{eq}}^{V}(\lambda ) \ln \mathrm {max}\big (|\xi - \lambda |,M^{-1}\big )$
is bounded continuous so that a standard Laplace method yields, as V goes to
![]() $V^{\{0\}}$
,
$V^{\{0\}}$
,
 $$ \begin{align*}\limsup_{N \rightarrow \infty} \frac{1}{N}\kern1pt\ln\Upsilon_{N,\beta}^{V;\mathsf{B}}(\mathsf{X}) {\kern-1pt}\le{\kern-1pt} \max\!\bigg\{ {-}\,\inf_{\xi\in \mathsf{X}} \Big[\frac{\beta}{2}\Big(V^{\{0\}}(\xi) - 2\int_{\mathsf{B}} \mathrm{d}\mu_{\mathrm{eq}}^{V}(\lambda) \ln \max\big(|\xi - \lambda|,M^{-1}\big)\Big) {\kern-1pt}\Big], \frac{\beta D}{2} -e(C){\kern-1pt}\bigg\} . \end{align*} $$
$$ \begin{align*}\limsup_{N \rightarrow \infty} \frac{1}{N}\kern1pt\ln\Upsilon_{N,\beta}^{V;\mathsf{B}}(\mathsf{X}) {\kern-1pt}\le{\kern-1pt} \max\!\bigg\{ {-}\,\inf_{\xi\in \mathsf{X}} \Big[\frac{\beta}{2}\Big(V^{\{0\}}(\xi) - 2\int_{\mathsf{B}} \mathrm{d}\mu_{\mathrm{eq}}^{V}(\lambda) \ln \max\big(|\xi - \lambda|,M^{-1}\big)\Big) {\kern-1pt}\Big], \frac{\beta D}{2} -e(C){\kern-1pt}\bigg\} . \end{align*} $$
We finally choose C large enough so that the first term is larger than the second. Then, by the monotone convergence theorem, we deduce that
![]() $\int _{\mathsf {B}} \mathrm {d}\mu _\mathrm{{eq}}^{V}(\lambda ) \ln \mathrm {max}\big (|\xi - \lambda |,M^{-1}\big )$
increases as M goes to infinity towards
$\int _{\mathsf {B}} \mathrm {d}\mu _\mathrm{{eq}}^{V}(\lambda ) \ln \mathrm {max}\big (|\xi - \lambda |,M^{-1}\big )$
increases as M goes to infinity towards
![]() $\int _{\mathsf {B}} \mathrm {d}\mu _\mathrm{{eq}}^{V}(\lambda ) \ln |\xi - \lambda |$
. This completes the proof of the large deviation in the initial model.
$\int _{\mathsf {B}} \mathrm {d}\mu _\mathrm{{eq}}^{V}(\lambda ) \ln |\xi - \lambda |$
. This completes the proof of the large deviation in the initial model.
For the fixed filling fractions model, we make the decomposition

with

and
 $$ \begin{align*}\Upsilon_{N,\beta,h}^{V;\mathsf{B}}(\mathsf{X}\cap\mathsf{A}_h)=\mu_{N ,\beta;\boldsymbol{\epsilon}- 1_h/N}^{\frac{NV}{N - 1};\mathsf{A}}\left(\int_{\mathsf{X}\cap\mathsf{A}_h} \mathrm{d}\xi\,\exp\Big\{-\frac{N\beta}{2}\,V(\xi) + (N - 1)\beta\int_{\mathsf{B}}\mathrm{d} L_{N - 1}(\lambda)\ln|\xi - \lambda|\Big)\Big\}\right), \end{align*} $$
$$ \begin{align*}\Upsilon_{N,\beta,h}^{V;\mathsf{B}}(\mathsf{X}\cap\mathsf{A}_h)=\mu_{N ,\beta;\boldsymbol{\epsilon}- 1_h/N}^{\frac{NV}{N - 1};\mathsf{A}}\left(\int_{\mathsf{X}\cap\mathsf{A}_h} \mathrm{d}\xi\,\exp\Big\{-\frac{N\beta}{2}\,V(\xi) + (N - 1)\beta\int_{\mathsf{B}}\mathrm{d} L_{N - 1}(\lambda)\ln|\xi - \lambda|\Big)\Big\}\right), \end{align*} $$
where
![]() $\boldsymbol {\epsilon }-1_h/N$
corresponds to the filling fraction where one eigenvalue has been suppressed from
$\boldsymbol {\epsilon }-1_h/N$
corresponds to the filling fraction where one eigenvalue has been suppressed from
![]() $\mathsf {A}_h$
. The estimates for
$\mathsf {A}_h$
. The estimates for
![]() $\Upsilon _{N,\beta ,h}^{V;\mathsf {B}}(\mathsf {X}\cap \mathsf {A}_h)$
are done exactly as above and the result follows since the logarithm of a finite sum of exponentially small terms is asymptotically equivalent to the logarithm of the maximal term.
$\Upsilon _{N,\beta ,h}^{V;\mathsf {B}}(\mathsf {X}\cap \mathsf {A}_h)$
are done exactly as above and the result follows since the logarithm of a finite sum of exponentially small terms is asymptotically equivalent to the logarithm of the maximal term.
3.3. Concentration of measure and consequences
We will need rough a priori bounds on the correlators, which can be derived by purely probabilistic methods. This type of result first appeared in the work of [Reference Boutet de Monvel, Pastur and ShcherbinadMPS95, Reference JohanssonJoh98] and more recently [Reference Kriecherbauer and ShcherbinaKS10, Reference Maïda and Maurel-SegalaMMS12]. Given their importance, we find useful to prove independently the bound we need by elementary means.
Hereafter, we will say that a function
![]() $f\,:\,\mathbb R\rightarrow \mathbb {C}$
is b-Hölder if
$f\,:\,\mathbb R\rightarrow \mathbb {C}$
is b-Hölder if
 $$ \begin{align*}\kappa_b[f]= \sup_{x\neq y}\frac{|f(x)-f(y)|}{|x-y|^b}<\infty. \end{align*} $$
$$ \begin{align*}\kappa_b[f]= \sup_{x\neq y}\frac{|f(x)-f(y)|}{|x-y|^b}<\infty. \end{align*} $$
Our final goal is to control
![]() $\int _{\mathsf {A}} \varphi (x)\mathrm {d}[L_N - \mu _\mathrm{{eq}}^{V}](x)$
for a class of functions
$\int _{\mathsf {A}} \varphi (x)\mathrm {d}[L_N - \mu _\mathrm{{eq}}^{V}](x)$
for a class of functions
![]() $\varphi $
which is large enough and, in particular, contains analytic functions on a neighbourhood of the interval of integration
$\varphi $
which is large enough and, in particular, contains analytic functions on a neighbourhood of the interval of integration
![]() $\mathsf {A}$
. This problem can be settled by controlling the ‘distance’ between
$\mathsf {A}$
. This problem can be settled by controlling the ‘distance’ between
![]() $L_N$
and
$L_N$
and
![]() $\mu _\mathrm{{eq}}^{V}$
for an appropriate notion of ‘distance’. We introduce the pseudo-distance
$\mu _\mathrm{{eq}}^{V}$
for an appropriate notion of ‘distance’. We introduce the pseudo-distance
![]() $\mathfrak {D}$
between probability measures
$\mathfrak {D}$
between probability measures
![]() $\mu ,\nu $
given by
$\mu ,\nu $
given by
 $$ \begin{align} \mathfrak{D}[\mu,\nu] = \left(-\iint_{\mathbb{R}^2} \mathrm{d}[\mu - \nu](x)\mathrm{d}[\mu - \nu](y)\,\ln|x - y|\right)^{\frac{1}{2}}. \end{align} $$
$$ \begin{align} \mathfrak{D}[\mu,\nu] = \left(-\iint_{\mathbb{R}^2} \mathrm{d}[\mu - \nu](x)\mathrm{d}[\mu - \nu](y)\,\ln|x - y|\right)^{\frac{1}{2}}. \end{align} $$
It can be represented in terms of Fourier transform of the measures:
 $$ \begin{align} \mathfrak{D}[\mu,\nu] = \left(\int_{0}^{\infty} \frac{\mathrm{d} p}{|p|}\,\big|(\widehat{\mu} - \widehat{\nu})(p)\big|^2\right)^{\frac{1}{2}}. \end{align} $$
$$ \begin{align} \mathfrak{D}[\mu,\nu] = \left(\int_{0}^{\infty} \frac{\mathrm{d} p}{|p|}\,\big|(\widehat{\mu} - \widehat{\nu})(p)\big|^2\right)^{\frac{1}{2}}. \end{align} $$
Since
![]() $L_N$
has atoms, its pseudo-distance to another measure is, in general, infinite. There are several methods to circumvent this issue, and one of them, that we borrow from [Reference Maïda and Maurel-SegalaMMS12], is to define a regularised measure
$L_N$
has atoms, its pseudo-distance to another measure is, in general, infinite. There are several methods to circumvent this issue, and one of them, that we borrow from [Reference Maïda and Maurel-SegalaMMS12], is to define a regularised measure
![]() $\widetilde {L}_N^\mathrm{{u}}$
(see the beginning of § 3.4.1 below) from
$\widetilde {L}_N^\mathrm{{u}}$
(see the beginning of § 3.4.1 below) from
![]() $L_N$
. Then, the result of concentration takes the following form:
$L_N$
. Then, the result of concentration takes the following form:
Lemma 3.5. Let V be regular,
![]() $\mathcal {C}^3$
, confining, satisfying a control of large deviations on
$\mathcal {C}^3$
, confining, satisfying a control of large deviations on
![]() $\mathsf {A}$
and satisfying (1.8) for
$\mathsf {A}$
and satisfying (1.8) for
![]() $K=0$
(namely,
$K=0$
(namely,
![]() $N(V-V^{\{0\}})$
is uniformly bounded by a constant
$N(V-V^{\{0\}})$
is uniformly bounded by a constant
![]() $v^{\{1\}}$
on
$v^{\{1\}}$
on
![]() $\mathsf {A}$
). There exists
$\mathsf {A}$
). There exists
![]() $C> 0$
so that, for t small enough and N large enough,
$C> 0$
so that, for t small enough and N large enough,
Moreover, for any
![]() $\boldsymbol {N}=(N_1,\ldots ,N_g)$
so that
$\boldsymbol {N}=(N_1,\ldots ,N_g)$
so that
![]() $\boldsymbol {\epsilon }=\boldsymbol {N}/N\in \mathcal {E}$
,
$\boldsymbol {\epsilon }=\boldsymbol {N}/N\in \mathcal {E}$
,
We prove it in § 3.4.1 below. The assumption V of class
![]() $\mathcal {C}^3$
ensures that the effective potential (3.1) defined from the equilibrium measure is a
$\mathcal {C}^3$
ensures that the effective potential (3.1) defined from the equilibrium measure is a
![]() $\frac {1}{2}$
-Hölder function (and even Lipschitz if all edges are soft) on the compact set
$\frac {1}{2}$
-Hölder function (and even Lipschitz if all edges are soft) on the compact set
![]() $\mathsf {A}$
, as one can observe on Equation (A.9) given in Appendix A. This lemma allows an a priori control of expectation values of test functions.
$\mathsf {A}$
, as one can observe on Equation (A.9) given in Appendix A. This lemma allows an a priori control of expectation values of test functions.
Corollary 3.6. Let V be regular,
![]() $\mathcal {C}^3$
, confining, satisfying a control of large deviations on
$\mathcal {C}^3$
, confining, satisfying a control of large deviations on
![]() $\mathsf {A}$
and satisfying (1.8) for
$\mathsf {A}$
and satisfying (1.8) for
![]() $K=0$
(namely,
$K=0$
(namely,
![]() $N(V-V^{\{0\}})$
is uniformly bounded by a constant
$N(V-V^{\{0\}})$
is uniformly bounded by a constant
![]() $v^{\{1\}}$
on
$v^{\{1\}}$
on
![]() $\mathsf {A}$
). Let
$\mathsf {A}$
). Let
![]() $b> 0$
and assume
$b> 0$
and assume
![]() $\varphi \,:\,\mathbb {R} \rightarrow \mathbb {C}$
is a b-Hölder function with constant
$\varphi \,:\,\mathbb {R} \rightarrow \mathbb {C}$
is a b-Hölder function with constant
![]() $\kappa _{b}[\varphi ]$
such that
$\kappa _{b}[\varphi ]$
such that
 $$ \begin{align*}| \varphi |_{1/2} : = \Big(\int_{\mathbb{R}} \mathrm{d} p\,|p|\,|\widehat{\varphi}(p)|^2\Big)^{\frac{1}{2}} < \infty. \end{align*} $$
$$ \begin{align*}| \varphi |_{1/2} : = \Big(\int_{\mathbb{R}} \mathrm{d} p\,|p|\,|\widehat{\varphi}(p)|^2\Big)^{\frac{1}{2}} < \infty. \end{align*} $$
Then, there exists
![]() $C_3> 0$
such that, for t small enough and N large enough,
$C_3> 0$
such that, for t small enough and N large enough,
and for any
![]() $\boldsymbol {N}=(N_1,\ldots ,N_g)$
so that
$\boldsymbol {N}=(N_1,\ldots ,N_g)$
so that
![]() $\boldsymbol {\epsilon }=\boldsymbol {N}/N\in \mathcal {E}$
,
$\boldsymbol {\epsilon }=\boldsymbol {N}/N\in \mathcal {E}$
,
As a special case, we can obtain a rough a priori control on the correlators. Recall the notation, for
![]() $\boldsymbol {\epsilon }\in \mathcal {E}$
,
$\boldsymbol {\epsilon }\in \mathcal {E}$
,
 $$ \begin{align*}W_{1;\boldsymbol{\epsilon}}^{\{-1\}}(x) = \int_{\mathsf{A}} \frac{\mathrm{d}\mu^{V;\mathsf{A}}_{\mathrm{eq};\boldsymbol{\epsilon}}(\xi)}{x - \xi}. \end{align*} $$
$$ \begin{align*}W_{1;\boldsymbol{\epsilon}}^{\{-1\}}(x) = \int_{\mathsf{A}} \frac{\mathrm{d}\mu^{V;\mathsf{A}}_{\mathrm{eq};\boldsymbol{\epsilon}}(\xi)}{x - \xi}. \end{align*} $$
Corollary 3.7. Let V be regular,
![]() $\mathcal {C}^3$
, confining and satisfying a control of large deviations on
$\mathcal {C}^3$
, confining and satisfying a control of large deviations on
![]() $\mathsf {A}$
. Let
$\mathsf {A}$
. Let
![]() $D'> 0$
and
$D'> 0$
and
 $$ \begin{align*}w_N = \sqrt{N\ln N},\qquad f(\delta) = \frac{\sqrt{|\ln \delta|}}{\delta}, \qquad d(x,\mathsf{A}) = \inf_{\xi \in \mathsf{A}} |x - \xi| \geq \frac{D'}{\sqrt{N^2\ln N}}. \end{align*} $$
$$ \begin{align*}w_N = \sqrt{N\ln N},\qquad f(\delta) = \frac{\sqrt{|\ln \delta|}}{\delta}, \qquad d(x,\mathsf{A}) = \inf_{\xi \in \mathsf{A}} |x - \xi| \geq \frac{D'}{\sqrt{N^2\ln N}}. \end{align*} $$
There exists a constant
![]() $\gamma _1(\mathsf {A},D')> 0$
so that, for N large enough, for any
$\gamma _1(\mathsf {A},D')> 0$
so that, for N large enough, for any
![]() $\boldsymbol {N}=(N_1,\ldots ,N_g)$
so that
$\boldsymbol {N}=(N_1,\ldots ,N_g)$
so that
![]() $\boldsymbol {\epsilon }=\boldsymbol {N}/N\in \mathcal {E}$
$\boldsymbol {\epsilon }=\boldsymbol {N}/N\in \mathcal {E}$
Similarly, for any
![]() $n \geq 2$
, there exist constants
$n \geq 2$
, there exist constants
![]() $\gamma _n(\mathsf {A},D')> 0$
so that, for N large enough,
$\gamma _n(\mathsf {A},D')> 0$
so that, for N large enough,
 $$ \begin{align} \big|W_{n;\boldsymbol{\epsilon}}(x_1,\ldots,x_n)\big| \leq \gamma_n(\mathsf{A},D')\,w_N^{n} \prod_{i = 1}^n f\big(d(x_i,\mathsf{A})\big). \end{align} $$
$$ \begin{align} \big|W_{n;\boldsymbol{\epsilon}}(x_1,\ldots,x_n)\big| \leq \gamma_n(\mathsf{A},D')\,w_N^{n} \prod_{i = 1}^n f\big(d(x_i,\mathsf{A})\big). \end{align} $$
In the
![]() $(g + 1)$
-cut regime with
$(g + 1)$
-cut regime with
![]() $g \geq 1$
, we denote
$g \geq 1$
, we denote
![]() $(\mathsf {S}_h)_{0 \leq h \leq g}$
the connected components of the support of
$(\mathsf {S}_h)_{0 \leq h \leq g}$
the connected components of the support of
![]() $\mu _\mathrm{{eq}}^{V}$
, and we take
$\mu _\mathrm{{eq}}^{V}$
, and we take
![]() $\mathsf {A} = \bigcup _{h = 0}^{g} \mathsf {A}_h$
, where
$\mathsf {A} = \bigcup _{h = 0}^{g} \mathsf {A}_h$
, where
![]() $\mathsf {A}_h = [a_h^-,a_h^+] \subseteq \mathsf {B}$
are pairwise disjoint bounded segments such that
$\mathsf {A}_h = [a_h^-,a_h^+] \subseteq \mathsf {B}$
are pairwise disjoint bounded segments such that
![]() $\mathsf {S}_h \subset \mathring {\mathsf {A}}_h$
. For any configuration
$\mathsf {S}_h \subset \mathring {\mathsf {A}}_h$
. For any configuration
![]() $\lambda \in \mathsf {A}^N$
, we denote
$\lambda \in \mathsf {A}^N$
, we denote
![]() $N_h$
the number of
$N_h$
the number of
![]() $\lambda _i$
s in
$\lambda _i$
s in
![]() $\mathsf {A}_h$
, and
$\mathsf {A}_h$
, and
![]() $\boldsymbol {N} = (N_h)_{1 \leq h \leq g}$
. The following result gives an estimate for large deviations of
$\boldsymbol {N} = (N_h)_{1 \leq h \leq g}$
. The following result gives an estimate for large deviations of
![]() $\boldsymbol {N}$
away from
$\boldsymbol {N}$
away from
![]() $N\boldsymbol {\epsilon }_{\star }$
in the large N limit.
$N\boldsymbol {\epsilon }_{\star }$
in the large N limit.
Corollary 3.8. Let
![]() $\mathsf {A}$
be as above, and V be
$\mathsf {A}$
be as above, and V be
![]() $\mathcal {C}^3$
, confining, satisfying a control of large deviations on
$\mathcal {C}^3$
, confining, satisfying a control of large deviations on
![]() $\mathsf {A}$
and leading to a
$\mathsf {A}$
and leading to a
![]() $(g + 1)$
-cut regime. There exists positive constants
$(g + 1)$
-cut regime. There exists positive constants
![]() $C,C'$
such that, for N large enough and uniformly in t,
$C,C'$
such that, for N large enough and uniformly in t,
As an outcome of this article, we will obtain in Section 8.2 a stronger large deviation statement for filling fractions when the potential satisfies the stronger Hypotheses 1.1–1.3.
3.4. Concentration of
 $L_N$
: proof of Lemma 3.5
$L_N$
: proof of Lemma 3.5
Throughout this section, proofs will be given for the initial model. They are exactly the same for the fixed filling fractions model.
3.4.1. Regularisation of
 $L_N$
$L_N$
We start by following an idea introduced by Maïda and Maurel-Segala [Reference Maïda and Maurel-SegalaMMS12, Proposition 3.2]. Let
![]() $\sigma _N,\eta _N \rightarrow 0$
be two sequences of positive numbers. To any configuration of points
$\sigma _N,\eta _N \rightarrow 0$
be two sequences of positive numbers. To any configuration of points
![]() $\lambda _1 \leq \ldots \leq \lambda _N$
in
$\lambda _1 \leq \ldots \leq \lambda _N$
in
![]() $\mathsf {A}$
, we associate another configuration
$\mathsf {A}$
, we associate another configuration
![]() $\widetilde {\lambda }_1,\ldots ,\widetilde {\lambda }_N$
by the formula
$\widetilde {\lambda }_1,\ldots ,\widetilde {\lambda }_N$
by the formula
It has the properties
Let us denote by
![]() $\widetilde {L}_N = \frac{1}{N} \sum _{i = 1}^N \delta _{\widetilde {\lambda }_i}$
the new counting measure. Then, we define
$\widetilde {L}_N = \frac{1}{N} \sum _{i = 1}^N \delta _{\widetilde {\lambda }_i}$
the new counting measure. Then, we define
![]() $\widetilde {L}_N^\mathrm{{u}}$
be the convolution of
$\widetilde {L}_N^\mathrm{{u}}$
be the convolution of
![]() $\widetilde {L}_N$
with the uniform measure on
$\widetilde {L}_N$
with the uniform measure on
![]() $[0,\eta _N\sigma _N]$
.
$[0,\eta _N\sigma _N]$
.
We are going to compare the (opposite of the) logarithmic energy of
![]() $L_N$
to that of
$L_N$
to that of
![]() $\widetilde {L}_N^\mathrm{{u}}$
, which has the advantage of having no atom. We first have
$\widetilde {L}_N^\mathrm{{u}}$
, which has the advantage of having no atom. We first have
because the logarithm is increasing and the spacings of
![]() $\tilde {\lambda }$
s are larger than the spacings of
$\tilde {\lambda }$
s are larger than the spacings of
![]() $\lambda $
s. Let
$\lambda $
s. Let
denote the (opposite of the) logarithmic energy of a probability measure
![]() $\mu $
. Then,
$\mu $
. Then,
 $$ \begin{align*}N^2 \Sigma[\widetilde{L}_{N}^{\mathrm{u}}] - \sum_{i \neq j} \ln|\widetilde{\lambda}_i - \widetilde{\lambda}_j| = \sum_{i\neq j} \iint_{[0,1]^2} \!\!\mathrm{d} u \,\mathrm{d} v \ln \Big| 1+\eta_N\sigma_N \frac{(u-v)}{\tilde \lambda_i-\tilde\lambda_j}\Big| + \sum_{i = 1}^{N} \iint_{[0,1]^2} \!\!\mathrm{d} u \,\mathrm{d} v \ln\big|\eta_N\sigma_N(u - v)\big|. \end{align*} $$
$$ \begin{align*}N^2 \Sigma[\widetilde{L}_{N}^{\mathrm{u}}] - \sum_{i \neq j} \ln|\widetilde{\lambda}_i - \widetilde{\lambda}_j| = \sum_{i\neq j} \iint_{[0,1]^2} \!\!\mathrm{d} u \,\mathrm{d} v \ln \Big| 1+\eta_N\sigma_N \frac{(u-v)}{\tilde \lambda_i-\tilde\lambda_j}\Big| + \sum_{i = 1}^{N} \iint_{[0,1]^2} \!\!\mathrm{d} u \,\mathrm{d} v \ln\big|\eta_N\sigma_N(u - v)\big|. \end{align*} $$
Thanks to the minimal distance
![]() $\sigma _N$
enforced between the
$\sigma _N$
enforced between the
![]() $\widetilde {\lambda }_i$
s in Equation (3.16),
$\widetilde {\lambda }_i$
s in Equation (3.16),
![]() $\sigma _N\,\big |(u - v)/(\tilde \lambda _i-\tilde \lambda _j)\big |$
is bounded by
$\sigma _N\,\big |(u - v)/(\tilde \lambda _i-\tilde \lambda _j)\big |$
is bounded by
![]() $1$
, so that for
$1$
, so that for
![]() $\eta _N\le \frac {1}{2}$
(thus for N large enough),
$\eta _N\le \frac {1}{2}$
(thus for N large enough),
 $$ \begin{align*}\bigg| \sum_{i\neq j} \iint_{[0,1]^2} \mathrm{d} u\, \mathrm{d} v \ln \Big| 1+\eta_N\sigma_N \frac{(u-v)}{\widetilde \lambda_i-\widetilde\lambda_j}\Big|\bigg|\le 2 N(N-1)\eta_N\,. \end{align*} $$
$$ \begin{align*}\bigg| \sum_{i\neq j} \iint_{[0,1]^2} \mathrm{d} u\, \mathrm{d} v \ln \Big| 1+\eta_N\sigma_N \frac{(u-v)}{\widetilde \lambda_i-\widetilde\lambda_j}\Big|\bigg|\le 2 N(N-1)\eta_N\,. \end{align*} $$
Since
![]() $(u,v) \mapsto \ln |u - v|$
is integrable in
$(u,v) \mapsto \ln |u - v|$
is integrable in
![]() $[0,1]^2$
, we find for some constants
$[0,1]^2$
, we find for some constants
![]() $c_1,c_2> 0$
,
$c_1,c_2> 0$
,
 $$ \begin{align*}\Big|\sum_{i \neq j} \ln|\widetilde{\lambda}_i - \widetilde{\lambda}_j| - N^2\Sigma[\widetilde{L}_{N}^{u}] \Big| \leq c_1N\big|\ln(\eta_N\sigma_N)\big| + c_2N^2\eta_N, \end{align*} $$
$$ \begin{align*}\Big|\sum_{i \neq j} \ln|\widetilde{\lambda}_i - \widetilde{\lambda}_j| - N^2\Sigma[\widetilde{L}_{N}^{u}] \Big| \leq c_1N\big|\ln(\eta_N\sigma_N)\big| + c_2N^2\eta_N, \end{align*} $$
so that finally, with Equation (3.17), we have proved that for any
![]() $(\lambda _i)_{1\le i\le N}\in \mathbb R^N$
,
$(\lambda _i)_{1\le i\le N}\in \mathbb R^N$
,
Besides, if
![]() $b> 0$
and
$b> 0$
and
![]() $\varphi \,:\,\mathsf {A} \rightarrow \mathbb {C}$
is a b-Hölder function with constant
$\varphi \,:\,\mathsf {A} \rightarrow \mathbb {C}$
is a b-Hölder function with constant
![]() $\kappa _b[\varphi ]$
, we have by Equation(3.16),
$\kappa _b[\varphi ]$
, we have by Equation(3.16),
 $$ \begin{align} \kern-14pt\nonumber \Big|\int_{\mathsf{A}} \mathrm{d}[L_N - \widetilde{L}_N^{\mathrm{u}}](x)\,\varphi(x)\Big| & \leq \frac{\kappa_{b}[\varphi]}{N} \sum_{i = 1}^N \big((i - 1)\sigma_N + \eta_N\sigma_N\big)^b \\& \leq \frac{\kappa_b[\varphi]}{N}\Big(\sigma_N^b\eta_N^b + \sum_{i = 2}^{N} (i - 1)^b \sigma_N^b(1 + \eta_N)^b\Big) \leq \frac{2\kappa_b[\varphi]}{(1 + b)}\,(N\sigma_N)^b\,. \end{align} $$
$$ \begin{align} \kern-14pt\nonumber \Big|\int_{\mathsf{A}} \mathrm{d}[L_N - \widetilde{L}_N^{\mathrm{u}}](x)\,\varphi(x)\Big| & \leq \frac{\kappa_{b}[\varphi]}{N} \sum_{i = 1}^N \big((i - 1)\sigma_N + \eta_N\sigma_N\big)^b \\& \leq \frac{\kappa_b[\varphi]}{N}\Big(\sigma_N^b\eta_N^b + \sum_{i = 2}^{N} (i - 1)^b \sigma_N^b(1 + \eta_N)^b\Big) \leq \frac{2\kappa_b[\varphi]}{(1 + b)}\,(N\sigma_N)^b\,. \end{align} $$
3.4.2. Deviations of
 $\widetilde {L}_N^\mathrm{{u}}$
$\widetilde {L}_N^\mathrm{{u}}$
We would like to estimate the probability of deviations of
![]() $\widetilde {L}_N^\mathrm{{u}}$
from the equilibrium measure
$\widetilde {L}_N^\mathrm{{u}}$
from the equilibrium measure
![]() $\mu _\mathrm{{eq}}^V$
. We need first a lower bound on
$\mu _\mathrm{{eq}}^V$
. We need first a lower bound on
![]() $Z^{V;\mathsf {A}}_{N,\beta }$
similar to that of [Reference Ben Arous and GuionnetBAG97] obtained by localising the ordered eigenvalues at a distance
$Z^{V;\mathsf {A}}_{N,\beta }$
similar to that of [Reference Ben Arous and GuionnetBAG97] obtained by localising the ordered eigenvalues at a distance
![]() $N^{-3}$
of the quantiles
$N^{-3}$
of the quantiles
![]() $\lambda _i^\mathrm{{cl}}$
of the equilibrium measure
$\lambda _i^\mathrm{{cl}}$
of the equilibrium measure
![]() $\mu _\mathrm{{eq}}^{V}$
, which are defined as
$\mu _\mathrm{{eq}}^{V}$
, which are defined as
Since V is
![]() $\mathcal {C}^2$
,
$\mathcal {C}^2$
,
![]() $\mathrm {d}\mu _\mathrm{{eq}}^{V}$
has a continuous density on the interior of its support, which diverges only at hard edges, where it blows at most like the inverse of a squareroot and vanishes only at soft edges. Therefore, there exists a constant
$\mathrm {d}\mu _\mathrm{{eq}}^{V}$
has a continuous density on the interior of its support, which diverges only at hard edges, where it blows at most like the inverse of a squareroot and vanishes only at soft edges. Therefore, there exists a constant
![]() $C> 0$
such that, for N large enough,
$C> 0$
such that, for N large enough,
Then, since V is a fortiori
![]() $\mathcal {C}^1$
on
$\mathcal {C}^1$
on
![]() $\mathsf {A}$
compact,
$\mathsf {A}$
compact,
 $$ \begin{align*} Z^{V;\mathsf{A}}_{N,\beta}&\geq N!\int_{|\delta_i|\leq N^{-3}}\prod_{1 \leq i< j \leq N}|\lambda_i^{\mathrm{cl}}-\lambda_j^{\mathrm{cl}} + \delta_i - \delta_j|^\beta\,\prod_{i = 1}^N e^{-\frac{\beta N}{2} V(\lambda_i^{\mathrm{cl}}+\delta_i)} \mathrm{d}\delta_i \\ &\geq N!\,N^{-3N}e^{-C_1\,N} \prod_{1 \leq i< j \leq N}|\lambda_i^{\mathrm{cl}} -\lambda_j^{\mathrm{cl}}|^\beta\,\prod_{i = 1}^N e^{-\frac{N\beta}{2}\sum_{i = 1}^N V(\lambda_i^{\mathrm{cl}})}, \end{align*} $$
$$ \begin{align*} Z^{V;\mathsf{A}}_{N,\beta}&\geq N!\int_{|\delta_i|\leq N^{-3}}\prod_{1 \leq i< j \leq N}|\lambda_i^{\mathrm{cl}}-\lambda_j^{\mathrm{cl}} + \delta_i - \delta_j|^\beta\,\prod_{i = 1}^N e^{-\frac{\beta N}{2} V(\lambda_i^{\mathrm{cl}}+\delta_i)} \mathrm{d}\delta_i \\ &\geq N!\,N^{-3N}e^{-C_1\,N} \prod_{1 \leq i< j \leq N}|\lambda_i^{\mathrm{cl}} -\lambda_j^{\mathrm{cl}}|^\beta\,\prod_{i = 1}^N e^{-\frac{N\beta}{2}\sum_{i = 1}^N V(\lambda_i^{\mathrm{cl}})}, \end{align*} $$
for some constant
![]() $C_1> 0$
. Then,
$C_1> 0$
. Then,
 $$ \begin{align} \nonumber \sum_{1 \leq i < j \leq N} \ln |\lambda_i^{\mathrm{cl}} - \lambda_j^{\mathrm{cl}}| & = \sum_{\substack{1 \leq i,j \leq N \\ i + 1 < j}} \ln|\lambda_{i}^{\mathrm{cl}} - \lambda_j^{\mathrm{cl}}| + \sum_{i = 1}^{N - 1} \ln|\lambda_i^{\mathrm{cl}} - \lambda_{i + 1}^{\mathrm{cl}}| \\\nonumber & \geq \sum_{1 \leq i < j \leq N - 1} \ln|\lambda_{i}^{\mathrm{cl}} - \lambda_{j + 1}^{\mathrm{cl}}| + (N - 1)\ln\big(\tfrac{C}{N^2}\big) \\\nonumber & \geq N^2 \iint_{\lambda_1^{\mathrm{cl}} \leq x < y \leq \lambda_N^{\mathrm{cl}}} \ln|x - y| \mathrm{d} \mu_{\mathrm{eq}}^{V}(x)\mathrm{d} \mu_{\mathrm{eq}}^{V}(y) + (N - 1)\ln\big(\tfrac{c}{N^2}\big) \\\nonumber & \geq \frac{N^2}{2} \iint_{[\lambda_1^{\mathrm{cl}},\lambda_N^{\mathrm{cl}}]^2} \ln|x - y| \mathrm{d} \mu^{V}_{\mathrm{eq}}(x) \mathrm{d} \mu_{\mathrm{eq}}^{V}(y) + (N - 1)\ln\big(\tfrac{c}{N^2}\big) \\\nonumber & \geq \frac{N^2}{2} \iint_{\mathsf{A}^2} \ln|x - y| \mathrm{d}\mu_{\mathrm{eq}}^{V}(x)\mathrm{d}\mu_{\mathrm{eq}}^{V}(y) - \frac{N^2}{2} \iint_{\substack{x \in \mathsf{A} \\ y < \lambda_1^{\mathrm{cl}}}} \ln|x - y|\mathrm{d} \mu_{\mathrm{eq}}^{V}(x)\mathrm{d}\mu_{\mathrm{eq}}^{V}(y) \\\nonumber & \quad - \frac{N^2}{2} \iint_{\substack{x> \lambda_1^{\mathrm{cl}} \\y < \lambda_1^{\mathrm{cl}}}} \ln|x - y|\mathrm{d}\mu_{\mathrm{eq}}^{V}(x)\mathrm{d}\mu_{\mathrm{eq}}^V(y) + (N - 1)\ln\big(\tfrac{c}{N^2}\big) \\\nonumber & \geq \frac{N^2}{2} \iint_{\mathsf{A}^2} \ln|x - y| \mathrm{d}\mu_{\mathrm{eq}}^{V}(x)\mathrm{d}\mu_{\mathrm{eq}}^{V}(y) - \frac{N^2}{4} \int_{y < \lambda_1^{\mathrm{cl}}} \big(C + V^{\{0\}}(y)\big)\mathrm{d}\mu_{\mathrm{eq}}^V(y) \\& \quad - \frac{N^2}{2} \iint_{\substack{x> \lambda_1^{\mathrm{cl}} \\ y < \lambda_1^{\mathrm{cl}}}} \ln|x - y|\mathrm{d}\mu_{\mathrm{eq}}^V(x)\mathrm{d}\mu_{\mathrm{eq}}^V(y) + (N - 1)\ln\big(\tfrac{c}{N^2}\big). \end{align} $$
$$ \begin{align} \nonumber \sum_{1 \leq i < j \leq N} \ln |\lambda_i^{\mathrm{cl}} - \lambda_j^{\mathrm{cl}}| & = \sum_{\substack{1 \leq i,j \leq N \\ i + 1 < j}} \ln|\lambda_{i}^{\mathrm{cl}} - \lambda_j^{\mathrm{cl}}| + \sum_{i = 1}^{N - 1} \ln|\lambda_i^{\mathrm{cl}} - \lambda_{i + 1}^{\mathrm{cl}}| \\\nonumber & \geq \sum_{1 \leq i < j \leq N - 1} \ln|\lambda_{i}^{\mathrm{cl}} - \lambda_{j + 1}^{\mathrm{cl}}| + (N - 1)\ln\big(\tfrac{C}{N^2}\big) \\\nonumber & \geq N^2 \iint_{\lambda_1^{\mathrm{cl}} \leq x < y \leq \lambda_N^{\mathrm{cl}}} \ln|x - y| \mathrm{d} \mu_{\mathrm{eq}}^{V}(x)\mathrm{d} \mu_{\mathrm{eq}}^{V}(y) + (N - 1)\ln\big(\tfrac{c}{N^2}\big) \\\nonumber & \geq \frac{N^2}{2} \iint_{[\lambda_1^{\mathrm{cl}},\lambda_N^{\mathrm{cl}}]^2} \ln|x - y| \mathrm{d} \mu^{V}_{\mathrm{eq}}(x) \mathrm{d} \mu_{\mathrm{eq}}^{V}(y) + (N - 1)\ln\big(\tfrac{c}{N^2}\big) \\\nonumber & \geq \frac{N^2}{2} \iint_{\mathsf{A}^2} \ln|x - y| \mathrm{d}\mu_{\mathrm{eq}}^{V}(x)\mathrm{d}\mu_{\mathrm{eq}}^{V}(y) - \frac{N^2}{2} \iint_{\substack{x \in \mathsf{A} \\ y < \lambda_1^{\mathrm{cl}}}} \ln|x - y|\mathrm{d} \mu_{\mathrm{eq}}^{V}(x)\mathrm{d}\mu_{\mathrm{eq}}^{V}(y) \\\nonumber & \quad - \frac{N^2}{2} \iint_{\substack{x> \lambda_1^{\mathrm{cl}} \\y < \lambda_1^{\mathrm{cl}}}} \ln|x - y|\mathrm{d}\mu_{\mathrm{eq}}^{V}(x)\mathrm{d}\mu_{\mathrm{eq}}^V(y) + (N - 1)\ln\big(\tfrac{c}{N^2}\big) \\\nonumber & \geq \frac{N^2}{2} \iint_{\mathsf{A}^2} \ln|x - y| \mathrm{d}\mu_{\mathrm{eq}}^{V}(x)\mathrm{d}\mu_{\mathrm{eq}}^{V}(y) - \frac{N^2}{4} \int_{y < \lambda_1^{\mathrm{cl}}} \big(C + V^{\{0\}}(y)\big)\mathrm{d}\mu_{\mathrm{eq}}^V(y) \\& \quad - \frac{N^2}{2} \iint_{\substack{x> \lambda_1^{\mathrm{cl}} \\ y < \lambda_1^{\mathrm{cl}}}} \ln|x - y|\mathrm{d}\mu_{\mathrm{eq}}^V(x)\mathrm{d}\mu_{\mathrm{eq}}^V(y) + (N - 1)\ln\big(\tfrac{c}{N^2}\big). \end{align} $$
Between the first two lines, we used Equation (3.20) to get a lower bound for the second term. In the third line, we have used the fact that the logarithm is an increasing function. In the fourth line, we have symmetrised the integral. In the fifth line, we observed that the definition of
![]() $\lambda _N^{\mathrm{cl}}$
implies that
$\lambda _N^{\mathrm{cl}}$
implies that
![]() $\mu _{\mathrm{eq}}^V$
has support included in
$\mu _{\mathrm{eq}}^V$
has support included in
![]() $\mathsf {A}_- := \mathsf {A} \cap (-\infty ,\lambda _N^{\mathrm{cl}}]$
and completed the square domain
$\mathsf {A}_- := \mathsf {A} \cap (-\infty ,\lambda _N^{\mathrm{cl}}]$
and completed the square domain
![]() $[\lambda _1^{\mathrm{cl}},\lambda _N^{\mathrm{cl}}]$
to
$[\lambda _1^{\mathrm{cl}},\lambda _N^{\mathrm{cl}}]$
to
![]() $\mathsf {A}^2$
while subtracting the extra contributions coming from this procedure. In the last line, we used the equality case of the characterisation of the equilibrium measure. Since
$\mathsf {A}^2$
while subtracting the extra contributions coming from this procedure. In the last line, we used the equality case of the characterisation of the equilibrium measure. Since
![]() $\mathrm {d} \mu _{\mathrm{eq}}^V$
has a continuous density possibly blowing up like
$\mathrm {d} \mu _{\mathrm{eq}}^V$
has a continuous density possibly blowing up like
![]() $\alpha $
an inverse squareroot at the endpoints of its support,
$\alpha $
an inverse squareroot at the endpoints of its support,
![]() $y \mapsto \int _{x> \lambda _1^{\mathrm{cl}}} \ln |x - y| \mathrm {d} \mu _{\mathrm{eq}}^V(x)$
is uniformly
$y \mapsto \int _{x> \lambda _1^{\mathrm{cl}}} \ln |x - y| \mathrm {d} \mu _{\mathrm{eq}}^V(x)$
is uniformly
![]() $O(\ln N)$
for
$O(\ln N)$
for
![]() $y \in \mathsf {A}_-$
(recall that
$y \in \mathsf {A}_-$
(recall that
![]() $\mathsf {A}_-$
is compact since
$\mathsf {A}_-$
is compact since
![]() $\mathsf {A}$
is). Since
$\mathsf {A}$
is). Since
![]() $\mu _{\mathrm{eq}}^V\big ((-\infty ,\lambda _1^{\mathrm{cl}}]\big ) \leq \frac {1}{N}$
by definition of
$\mu _{\mathrm{eq}}^V\big ((-\infty ,\lambda _1^{\mathrm{cl}}]\big ) \leq \frac {1}{N}$
by definition of
![]() $\lambda _1^{\mathrm{cl}}$
, we deduce that the first term in the last line of Equation (3.21) is
$\lambda _1^{\mathrm{cl}}$
, we deduce that the first term in the last line of Equation (3.21) is
![]() $O(N\ln N)$
. Besides,
$O(N\ln N)$
. Besides,
![]() $V^{\{0\}} + C$
is continuous and hence bounded on
$V^{\{0\}} + C$
is continuous and hence bounded on
![]() $\mathsf {A}$
compact, showing for a similar reason that the last term in the penultimate line of Equation (3.21) is
$\mathsf {A}$
compact, showing for a similar reason that the last term in the penultimate line of Equation (3.21) is
![]() $O(N)$
. All in all, this shows the existence of a constant
$O(N)$
. All in all, this shows the existence of a constant
![]() $C_2$
such that for N large enough,
$C_2$
such that for N large enough,
 $$ \begin{align*}\sum_{1 \leq i < j \leq N} \ln |\lambda_i^{\mathrm{cl}} - \lambda_j^{\mathrm{cl}}| \geq \sum_{1 \leq i < j \leq N} \ln |\lambda_i^{\mathrm{cl}} - \lambda_j^{\mathrm{cl}}| - C_2 N \ln N. \end{align*} $$
$$ \begin{align*}\sum_{1 \leq i < j \leq N} \ln |\lambda_i^{\mathrm{cl}} - \lambda_j^{\mathrm{cl}}| \geq \sum_{1 \leq i < j \leq N} \ln |\lambda_i^{\mathrm{cl}} - \lambda_j^{\mathrm{cl}}| - C_2 N \ln N. \end{align*} $$
Next, we have
 $$ \begin{align*} & \left|\frac{1}{N}\sum_{i=1}^N V(\lambda_i^{\mathrm{cl}})-\int_{\mathsf{A}} V(x)\mathrm{d}\mu_{\mathrm{eq}}^{V}(x)\right| \\ & \quad = \frac{V(\lambda_N^{\mathrm{cl}})}{N} - \int_{x < \lambda_1^{\mathrm{cl}}} V(x) \mathrm{d}\mu_{\mathrm{eq}}^V(x) + \sum_{i = 1}^{N - 1} \int_{\lambda_i^{\mathrm{cl}}}^{\lambda_{i + 1}^{\mathrm{cl}}} \big(V(\lambda_i^{\mathrm{cl}}) - V(x)\big)\mathrm{d}\mu_{\mathrm{eq}}^V(x) \\ & \quad \leq \frac{2{\parallel} V {\parallel}_{\infty}^{\mathsf{A}}}{N} + {\parallel} V' {\parallel}_{\infty}^{\mathsf{A}} \bigg(\sum_{i = 1}^{N - 1} \int_{\lambda_i^{\mathrm{cl}}}^{\lambda_{i +1}^{\mathrm{cl}}} |x - \lambda_i^{\mathrm{cl}}| \mathrm{d} \mu_{\mathrm{eq}}^V(x)\bigg) \\ & \quad \leq \frac{2{\parallel} V {\parallel}_{\infty}^{\mathsf{A}}}{N} + \frac{{\parallel} V' {\parallel}_{\infty}^{\mathsf{A}}}{N} \sum_{i = 1}^{N - 1} (\lambda_{i + 1}^{\mathrm{cl}} - \lambda_i^{\mathrm{cl}}) \leq \frac{2 {\parallel} V {\parallel}_{\infty}^{\mathsf{A}} + C_3 {\parallel} V' {\parallel}_{\infty}^{\mathsf{A}}}{N} \end{align*} $$
$$ \begin{align*} & \left|\frac{1}{N}\sum_{i=1}^N V(\lambda_i^{\mathrm{cl}})-\int_{\mathsf{A}} V(x)\mathrm{d}\mu_{\mathrm{eq}}^{V}(x)\right| \\ & \quad = \frac{V(\lambda_N^{\mathrm{cl}})}{N} - \int_{x < \lambda_1^{\mathrm{cl}}} V(x) \mathrm{d}\mu_{\mathrm{eq}}^V(x) + \sum_{i = 1}^{N - 1} \int_{\lambda_i^{\mathrm{cl}}}^{\lambda_{i + 1}^{\mathrm{cl}}} \big(V(\lambda_i^{\mathrm{cl}}) - V(x)\big)\mathrm{d}\mu_{\mathrm{eq}}^V(x) \\ & \quad \leq \frac{2{\parallel} V {\parallel}_{\infty}^{\mathsf{A}}}{N} + {\parallel} V' {\parallel}_{\infty}^{\mathsf{A}} \bigg(\sum_{i = 1}^{N - 1} \int_{\lambda_i^{\mathrm{cl}}}^{\lambda_{i +1}^{\mathrm{cl}}} |x - \lambda_i^{\mathrm{cl}}| \mathrm{d} \mu_{\mathrm{eq}}^V(x)\bigg) \\ & \quad \leq \frac{2{\parallel} V {\parallel}_{\infty}^{\mathsf{A}}}{N} + \frac{{\parallel} V' {\parallel}_{\infty}^{\mathsf{A}}}{N} \sum_{i = 1}^{N - 1} (\lambda_{i + 1}^{\mathrm{cl}} - \lambda_i^{\mathrm{cl}}) \leq \frac{2 {\parallel} V {\parallel}_{\infty}^{\mathsf{A}} + C_3 {\parallel} V' {\parallel}_{\infty}^{\mathsf{A}}}{N} \end{align*} $$
for some constant
![]() $C_3> 0$
. Then, as
$C_3> 0$
. Then, as
![]() $N^{-1} \sum _{i = 1}^N \delta _{\lambda _i^{\mathrm{cl}}}$
is a sequence of measures converging to the minimiser
$N^{-1} \sum _{i = 1}^N \delta _{\lambda _i^{\mathrm{cl}}}$
is a sequence of measures converging to the minimiser
![]() $\mu _{\mathrm{eq}}^V$
of the energy functional E introduced in Equation (1.5), we find
$\mu _{\mathrm{eq}}^V$
of the energy functional E introduced in Equation (1.5), we find
for some positive constant
![]() $C_4$
.
$C_4$
.
Now, consider the event
![]() $\mathcal {S}_{N}(t) = \big \{\mathfrak {D}[\widetilde {L}_N^\mathrm{{u}},\mu _\mathrm{{eq}}^{V}] \geq t\big \}$
. Observing that
$\mathcal {S}_{N}(t) = \big \{\mathfrak {D}[\widetilde {L}_N^\mathrm{{u}},\mu _\mathrm{{eq}}^{V}] \geq t\big \}$
. Observing that
 $$ \begin{align*}\mu_{N,\beta}^{V;\mathsf{A}}\big(\mathcal{S}_N(t)\big) = \frac{1}{Z_{N,\beta}^{V;\mathsf{A}}} \int_{\mathcal{S}_N(t)} e^{\frac{\beta }{2}( \sum_{i\neq j} \ln |\lambda_i-\lambda_j| - N^2\int_{\mathsf{A}} \mathrm{d} L_N(x)\,V(x))}\prod_{i = 1}^N \mathrm{d}\lambda_i \end{align*} $$
$$ \begin{align*}\mu_{N,\beta}^{V;\mathsf{A}}\big(\mathcal{S}_N(t)\big) = \frac{1}{Z_{N,\beta}^{V;\mathsf{A}}} \int_{\mathcal{S}_N(t)} e^{\frac{\beta }{2}( \sum_{i\neq j} \ln |\lambda_i-\lambda_j| - N^2\int_{\mathsf{A}} \mathrm{d} L_N(x)\,V(x))}\prod_{i = 1}^N \mathrm{d}\lambda_i \end{align*} $$
and using the comparison (3.18) of § 3.4.1, we find, with the notations of Theorem 1.2,
 $$ \begin{align*}\mu_{N,\beta}^{V;\mathsf{A}}\big(\mathcal{S}_N(t)\big) \leq \frac{e^{\frac{\beta}{2}\,R_N}}{Z_{N,\beta}^{V;\mathsf{A}}} \int_{\mathcal{S}_N(t)} e^{\frac{\beta N^2}{2}(\Sigma[\widetilde{L}_N^{\mathrm{u}}] - \int_{\mathsf{A}} \mathrm{d}\widetilde{L}_N^{\mathrm{u}}(x)\,V^{\{0\}}(x))} \prod_{i = 1}^N\mathrm{d}\lambda_i, \end{align*} $$
$$ \begin{align*}\mu_{N,\beta}^{V;\mathsf{A}}\big(\mathcal{S}_N(t)\big) \leq \frac{e^{\frac{\beta}{2}\,R_N}}{Z_{N,\beta}^{V;\mathsf{A}}} \int_{\mathcal{S}_N(t)} e^{\frac{\beta N^2}{2}(\Sigma[\widetilde{L}_N^{\mathrm{u}}] - \int_{\mathsf{A}} \mathrm{d}\widetilde{L}_N^{\mathrm{u}}(x)\,V^{\{0\}}(x))} \prod_{i = 1}^N\mathrm{d}\lambda_i, \end{align*} $$
with
We then decompose
 $$ \begin{align*} E[\widetilde{L}_N^{\mathrm{u}}] & = \frac{\beta}{2}\Big(-\Sigma[\widetilde{L}_N^{\mathrm{u}}] + \int_{\mathsf{A}} \mathrm{d}\widetilde{L}_N^{\mathrm{u}}(x)\,V^{\{0\}}(x)\Big) \\ & = E[\mu_{\mathrm{eq}}^{V}] + \frac{\beta}{2}\Big(\int_{\mathsf{A}} U_{\mathrm{eq}}^{V}(x)\mathrm{d}[\widetilde{L}_{N}^{\mathrm{u}} - \mathrm{d}\mu_{\mathrm{eq}}^{V}](x) + \mathfrak{D}^2[\widetilde{L}_{N}^{\mathrm{u}},\mu_{\mathrm{eq}}^{V}]\Big). \end{align*} $$
$$ \begin{align*} E[\widetilde{L}_N^{\mathrm{u}}] & = \frac{\beta}{2}\Big(-\Sigma[\widetilde{L}_N^{\mathrm{u}}] + \int_{\mathsf{A}} \mathrm{d}\widetilde{L}_N^{\mathrm{u}}(x)\,V^{\{0\}}(x)\Big) \\ & = E[\mu_{\mathrm{eq}}^{V}] + \frac{\beta}{2}\Big(\int_{\mathsf{A}} U_{\mathrm{eq}}^{V}(x)\mathrm{d}[\widetilde{L}_{N}^{\mathrm{u}} - \mathrm{d}\mu_{\mathrm{eq}}^{V}](x) + \mathfrak{D}^2[\widetilde{L}_{N}^{\mathrm{u}},\mu_{\mathrm{eq}}^{V}]\Big). \end{align*} $$
The effective potential
![]() $U_{\mathrm{eq}}^{V}$
is defined in Equation (3.1), and since it is integrated against a signed measure of zero mass, we can add to it a constant and thus replace it with
$U_{\mathrm{eq}}^{V}$
is defined in Equation (3.1), and since it is integrated against a signed measure of zero mass, we can add to it a constant and thus replace it with
![]() $\tilde {U}_{\mathrm{eq}}^{V}$
. According to the characterisation of the equilibrium measure,
$\tilde {U}_{\mathrm{eq}}^{V}$
. According to the characterisation of the equilibrium measure,
![]() $\widetilde {U}_{\mathrm{eq}}^{V}$
vanishes
$\widetilde {U}_{\mathrm{eq}}^{V}$
vanishes
![]() $\mu _{\mathrm{eq}}^{V}$
-everywhere. Hence,
$\mu _{\mathrm{eq}}^{V}$
-everywhere. Hence,
and we obtain
 $$ \begin{align*}\mu_{N,\beta}^{V;\mathsf{A}}\big(\mathcal{S}_N(t)\big) \leq \frac{e^{\frac{\beta}{2}R_N - N^2\,E[\mu_{\mathrm{eq}}^{V}]}}{Z_{N,\beta}^{V;\mathsf{A}}}\int_{\mathcal{S}_N(t)} e^{-\frac{\beta N^2}{2}\big(\mathfrak{D}^2[\widetilde{L}_N^{\mathrm{u}},\mu_{\mathrm{eq}}^{V}] + \int_{\mathsf{A}} \mathrm{d}\widetilde{L}_N^{\mathrm{u}}(x)\,\widetilde{U}^{V}_{\mathrm{eq}}(x)\big)} \prod_{i = 1}^N \mathrm{d}\lambda_i\,. \end{align*} $$
$$ \begin{align*}\mu_{N,\beta}^{V;\mathsf{A}}\big(\mathcal{S}_N(t)\big) \leq \frac{e^{\frac{\beta}{2}R_N - N^2\,E[\mu_{\mathrm{eq}}^{V}]}}{Z_{N,\beta}^{V;\mathsf{A}}}\int_{\mathcal{S}_N(t)} e^{-\frac{\beta N^2}{2}\big(\mathfrak{D}^2[\widetilde{L}_N^{\mathrm{u}},\mu_{\mathrm{eq}}^{V}] + \int_{\mathsf{A}} \mathrm{d}\widetilde{L}_N^{\mathrm{u}}(x)\,\widetilde{U}^{V}_{\mathrm{eq}}(x)\big)} \prod_{i = 1}^N \mathrm{d}\lambda_i\,. \end{align*} $$
Since
![]() $\widetilde {U}^{V;\mathsf {A}}$
is at least
$\widetilde {U}^{V;\mathsf {A}}$
is at least
![]() $\frac {1}{2}$
-Hölder on
$\frac {1}{2}$
-Hölder on
![]() $\mathsf {A}$
(and even Lipschitz if all edges are soft), we find by Equation (3.19),
$\mathsf {A}$
(and even Lipschitz if all edges are soft), we find by Equation (3.19),
 $$ \begin{align*}\mu_{N,\beta}^{V;\mathsf{A}}\big(\mathcal{S}_N(t)\big) \leq \frac{e^{\frac{\beta}{2}(R_N + \kappa_{1/2}[\widetilde{U}_{\mathrm{eq}}^{V}]\,N^{\frac{5}{2}}\sigma_N^{\frac{1}{2}}) - N^2\,E[\mu_{\mathrm{eq}}^{V}]}}{Z_{N,\beta}^{V;\mathsf{A}}}\int_{\mathcal{S}_N(t)} e^{-\frac{\beta N^2}{2}\,\mathfrak{D}^2[\widetilde{L}_N^{\mathrm{u}},\mu_{\mathrm{eq}}^V]}\,\prod_{i = 1}^N e^{-\frac{\beta N}{2}\,\widetilde{U}_{\mathrm{eq}}^{V}(\lambda_i)}\,\mathrm{d}\lambda_i. \end{align*} $$
$$ \begin{align*}\mu_{N,\beta}^{V;\mathsf{A}}\big(\mathcal{S}_N(t)\big) \leq \frac{e^{\frac{\beta}{2}(R_N + \kappa_{1/2}[\widetilde{U}_{\mathrm{eq}}^{V}]\,N^{\frac{5}{2}}\sigma_N^{\frac{1}{2}}) - N^2\,E[\mu_{\mathrm{eq}}^{V}]}}{Z_{N,\beta}^{V;\mathsf{A}}}\int_{\mathcal{S}_N(t)} e^{-\frac{\beta N^2}{2}\,\mathfrak{D}^2[\widetilde{L}_N^{\mathrm{u}},\mu_{\mathrm{eq}}^V]}\,\prod_{i = 1}^N e^{-\frac{\beta N}{2}\,\widetilde{U}_{\mathrm{eq}}^{V}(\lambda_i)}\,\mathrm{d}\lambda_i. \end{align*} $$
We now use the lower bound (3.22) for the partition function and the definition of the event
![]() $\mathcal {S}_N(t)$
in order to obtain
$\mathcal {S}_N(t)$
in order to obtain
 $$ \begin{align*} \mu_{N,\beta}^{V;\mathsf{A}}\big(\mathcal{S}_N(t)\big) & \leq e^{\frac{\beta}{2}(R_N + \kappa_{1/2}[\widetilde{U}_{\mathrm{eq}}^{V}]\,N^{\frac{5}{2}}\sigma_N^{\frac{1}{2}} + C_2\,N\ln N - N^2t^2)}\Big(\int_{\mathsf{A}} \mathrm{d}\lambda\,e^{-\frac{\beta N}{2}\,\widetilde{U}_{\mathrm{eq}}^{V}(\lambda)}\Big)^N \\ & \leq e^{\frac{\beta}{2}(\tilde{R}_N + C_2\,N\ln N - N^2t^2)}, \end{align*} $$
$$ \begin{align*} \mu_{N,\beta}^{V;\mathsf{A}}\big(\mathcal{S}_N(t)\big) & \leq e^{\frac{\beta}{2}(R_N + \kappa_{1/2}[\widetilde{U}_{\mathrm{eq}}^{V}]\,N^{\frac{5}{2}}\sigma_N^{\frac{1}{2}} + C_2\,N\ln N - N^2t^2)}\Big(\int_{\mathsf{A}} \mathrm{d}\lambda\,e^{-\frac{\beta N}{2}\,\widetilde{U}_{\mathrm{eq}}^{V}(\lambda)}\Big)^N \\ & \leq e^{\frac{\beta}{2}(\tilde{R}_N + C_2\,N\ln N - N^2t^2)}, \end{align*} $$
with
Indeed, since
![]() $\widetilde {U}^{V;\mathsf {A}}$
is nonnegative on
$\widetilde {U}^{V;\mathsf {A}}$
is nonnegative on
![]() $\mathsf {A}$
, we observed that the integral in bracket is bounded by the total length
$\mathsf {A}$
, we observed that the integral in bracket is bounded by the total length
![]() $\ell (\mathsf {A})$
of the range of integration, which is here finite. We now choose
$\ell (\mathsf {A})$
of the range of integration, which is here finite. We now choose
which guarantees that
![]() $\tilde {R}_N = O(N\ln N)$
. Thus, there exists a positive constant
$\tilde {R}_N = O(N\ln N)$
. Thus, there exists a positive constant
![]() $C_3$
such that, for N large enough,
$C_3$
such that, for N large enough,
which concludes the proof of Proposition 3.5. We may rephrase this result by saying that the probability of
![]() $\mathcal {S}_N(t)$
becomes small for t larger than
$\mathcal {S}_N(t)$
becomes small for t larger than
![]() $\sqrt {\frac {2C_3\ln N}{N}}$
.
$\sqrt {\frac {2C_3\ln N}{N}}$
.
The proof of (3.11) for fixed filling faction is similar since the same algebra holds, cf. Equation (A.4) (with measures with same mass on the
![]() $\mathsf {A}_h$
).
$\mathsf {A}_h$
).
3.5. Large deviations for test functions
3.5.1. Proof of Corollary 3.6
Since
![]() $\varphi $
is b-Hölder, we can use the comparison (3.19) with
$\varphi $
is b-Hölder, we can use the comparison (3.19) with
![]() $\sigma _N = N^{-3}$
chosen in Equation (3.24):
$\sigma _N = N^{-3}$
chosen in Equation (3.24):
Then, we compute in Fourier space and using Cauchy–Schwarz inequality
 $$ \begin{align*}\Big|\int_{\mathsf{A}} \mathrm{d}[\widetilde{L_N^{\mathrm{u}}} - \mu_{\mathrm{eq}}^V](x)\,\varphi(x)\Big| = \Big|\int_{\mathbb{R}} \mathrm{d} p\big(\widehat{\widetilde{L}}_N^{\mathrm{u}} - \widehat{\mu_{\mathrm{eq}}^V}\big)(p)\,\overline{\widehat{\varphi}(p)} \Big| \leq |\varphi|_{1/2}\Big(\int_{\mathbb{R}} \frac{\mathrm{d} p}{|p|}\,\big|(\widehat{\widetilde{L}}_N^{\mathrm{u}} - \widehat{\mu_{\mathrm{eq}}^V})(p)|^2\Big)^{\frac{1}{2}}, \end{align*} $$
$$ \begin{align*}\Big|\int_{\mathsf{A}} \mathrm{d}[\widetilde{L_N^{\mathrm{u}}} - \mu_{\mathrm{eq}}^V](x)\,\varphi(x)\Big| = \Big|\int_{\mathbb{R}} \mathrm{d} p\big(\widehat{\widetilde{L}}_N^{\mathrm{u}} - \widehat{\mu_{\mathrm{eq}}^V}\big)(p)\,\overline{\widehat{\varphi}(p)} \Big| \leq |\varphi|_{1/2}\Big(\int_{\mathbb{R}} \frac{\mathrm{d} p}{|p|}\,\big|(\widehat{\widetilde{L}}_N^{\mathrm{u}} - \widehat{\mu_{\mathrm{eq}}^V})(p)|^2\Big)^{\frac{1}{2}}, \end{align*} $$
we recognise in the last factor the definition (3.10) of the pseudo-distance:
Corollary 3.6 then follows from this inequality combined with Lemma 3.5.
3.5.2. Bounds on correlators and filling fractions (Proof of Corollary 3.7 and 3.8)
Let
![]() $\mathsf {A}_{\eta } = \{x \in \mathbb {R},\,\,\,:\,\,\, d(x,\mathsf {A}) \leq \eta \}$
. As we have chosen
$\mathsf {A}_{\eta } = \{x \in \mathbb {R},\,\,\,:\,\,\, d(x,\mathsf {A}) \leq \eta \}$
. As we have chosen
![]() $\sigma _N = N^{-3}$
and
$\sigma _N = N^{-3}$
and
![]() $\eta _N = N^{-1}$
, the support of
$\eta _N = N^{-1}$
, the support of
![]() $\widetilde {L}_N^\mathrm{{u}}$
is included in
$\widetilde {L}_N^\mathrm{{u}}$
is included in
![]() $\mathsf {A}_{2/N^3}$
. If
$\mathsf {A}_{2/N^3}$
. If
![]() $\mu $
is a probability measure, let
$\mu $
is a probability measure, let
![]() $\mathcal {W}_{\mu }$
denote its Stieltjes transform. We have
$\mathcal {W}_{\mu }$
denote its Stieltjes transform. We have
Since
![]() $\psi _{x}$
is Lipschitz on
$\psi _{x}$
is Lipschitz on
![]() $\mathsf {A}_{2/N^3}$
with constant
$\mathsf {A}_{2/N^3}$
with constant
![]() $\kappa _{1}[\psi _{x}] = d^{-2}(x,\mathsf {A}_{2/N^3})$
, we have for
$\kappa _{1}[\psi _{x}] = d^{-2}(x,\mathsf {A}_{2/N^3})$
, we have for
![]() $d(x,\mathsf {A}) \geq \frac {3}{N^3}$
,
$d(x,\mathsf {A}) \geq \frac {3}{N^3}$
,
We focus on estimating
![]() $\mathcal {W}_{\widetilde {L}_N^\mathrm{{u}}} - \mathcal {W}_{\mu _\mathrm{{eq}}^V}$
. We have the freedom to replace
$\mathcal {W}_{\widetilde {L}_N^\mathrm{{u}}} - \mathcal {W}_{\mu _\mathrm{{eq}}^V}$
. We have the freedom to replace
![]() $\psi _{x}^{\bullet }$
by any function
$\psi _{x}^{\bullet }$
by any function
![]() $\phi _{x}^{\bullet }$
which coincides with
$\phi _{x}^{\bullet }$
which coincides with
![]() $\psi _{x}^{\bullet }$
on
$\psi _{x}^{\bullet }$
on
![]() $\mathsf {A}_{2/N^3}$
since the support of
$\mathsf {A}_{2/N^3}$
since the support of
![]() $\widetilde {L}_N^\mathrm{{u}}$
and
$\widetilde {L}_N^\mathrm{{u}}$
and
![]() $\mu _\mathrm{{eq}}^V$
are included in
$\mu _\mathrm{{eq}}^V$
are included in
![]() $\mathsf {A}_{2/N^3}$
. Then,
$\mathsf {A}_{2/N^3}$
. Then,
We wish to choose
![]() $\phi _x^\bullet $
so that our estimates depend on the distance to
$\phi _x^\bullet $
so that our estimates depend on the distance to
![]() $\mathsf {A}_{2/N^3}$
(whereas the choice of the function
$\mathsf {A}_{2/N^3}$
(whereas the choice of the function
![]() $\psi _x^\bullet $
would only gives bounds in terms of the distance to the real line and therefore would not allow bounds for
$\psi _x^\bullet $
would only gives bounds in terms of the distance to the real line and therefore would not allow bounds for
![]() $x\in \mathbb R\backslash \mathsf {A}_{2/N^3}$
). We now explain a suitable choice of
$x\in \mathbb R\backslash \mathsf {A}_{2/N^3}$
). We now explain a suitable choice of
![]() $\phi _{x}^{\bullet }$
. Let
$\phi _{x}^{\bullet }$
. Let
![]() $a_{x,h,2/N^3} \in \mathsf {A}_{h,2/N^3}$
the point such that
$a_{x,h,2/N^3} \in \mathsf {A}_{h,2/N^3}$
the point such that
![]() $d(x,\mathsf {A}_{h,2/N^3}) = |x - a_{x,h,2/N^3}|$
. Then, for
$d(x,\mathsf {A}_{h,2/N^3}) = |x - a_{x,h,2/N^3}|$
. Then, for
![]() $\xi \in \mathsf {A}_{h,2/N^3}$
, we have
$\xi \in \mathsf {A}_{h,2/N^3}$
, we have
 $$ \begin{align*}\big|(\psi^{\bullet}_{x})'(\xi)\big| \leq \frac{1}{d(x,\mathsf{A}_{h,2/N^3})^2 + (\xi - a_{x,h,2/N^3})^2}, \end{align*} $$
$$ \begin{align*}\big|(\psi^{\bullet}_{x})'(\xi)\big| \leq \frac{1}{d(x,\mathsf{A}_{h,2/N^3})^2 + (\xi - a_{x,h,2/N^3})^2}, \end{align*} $$
and therefore,
 $$ \begin{align} \forall \xi \in \mathsf{A}_{2/N^3},\qquad \big|(\psi^{\bullet}_{x})'(\xi)\big| \leq \sum_{h = 0}^{g} \frac{1}{d(x,\mathsf{A}_{h,1/N^2})^2 + (\xi - a_{x,h,2/N^3})^2}\,. \end{align} $$
$$ \begin{align} \forall \xi \in \mathsf{A}_{2/N^3},\qquad \big|(\psi^{\bullet}_{x})'(\xi)\big| \leq \sum_{h = 0}^{g} \frac{1}{d(x,\mathsf{A}_{h,1/N^2})^2 + (\xi - a_{x,h,2/N^3})^2}\,. \end{align} $$
Then, we take a function
![]() $(\phi ^{\bullet }_{x})'$
which coincides with
$(\phi ^{\bullet }_{x})'$
which coincides with
![]() $(\psi ^{\bullet }_{x})'$
on
$(\psi ^{\bullet }_{x})'$
on
![]() $\mathsf {A}_{1/N^2}$
and extends it continuously on
$\mathsf {A}_{1/N^2}$
and extends it continuously on
![]() $\mathbb {R}$
, with compact support included in
$\mathbb {R}$
, with compact support included in
![]() $\big [-\frac {M}{2},\frac {M}{2}\big ]$
for some M large enough, independent of N, and such that
$\big [-\frac {M}{2},\frac {M}{2}\big ]$
for some M large enough, independent of N, and such that
 $$ \begin{align} \forall \xi \in \mathbb{R},\qquad \big|(\phi^{\bullet}_{x})'(\xi)\big| \leq \sum_{h = 0}^{g} \frac{1}{d(x,\mathsf{A}_{h,1/N^2})^2 + (\xi - a_{x,h,1/N^2})^2}\,. \end{align} $$
$$ \begin{align} \forall \xi \in \mathbb{R},\qquad \big|(\phi^{\bullet}_{x})'(\xi)\big| \leq \sum_{h = 0}^{g} \frac{1}{d(x,\mathsf{A}_{h,1/N^2})^2 + (\xi - a_{x,h,1/N^2})^2}\,. \end{align} $$
We denote
![]() $\phi ^{\bullet }_{x}$
an antiderivative of this function and use it in Equation (3.29). We compute
$\phi ^{\bullet }_{x}$
an antiderivative of this function and use it in Equation (3.29). We compute
 $$ \begin{align} \nonumber |\phi_{x}^{\bullet}|_{1/2}^2 & = \int_{\mathbb{R}} |p|\,|\widehat{\phi_{x}^{\bullet}}(p)|^2 \mathrm{d} p = \int_{\mathbb{R}} \frac{1}{|p|}\,|\widehat{(\phi_{x}^{\bullet})'}(p)|^2 \mathrm{d} p \\ \nonumber & = -2\int_{\mathbb{R}^2} \ln|\xi_1 - \xi_2|\,(\phi_x^{\bullet})'(\xi_1)(\phi_x^{\bullet})'(\xi_2) \mathrm{d}\xi_1\mathrm{d}\xi_2 \\ & \leq 2 \int_{\mathbb{R}^2} \big|\ln|\xi_1 - \xi_2|\big|\,|(\phi^{\bullet}_x)'(\xi_1)|\,|(\phi_x^{\bullet})'(\xi_2)|\mathrm{d}\xi_1\mathrm{d}\xi_2. \end{align} $$
$$ \begin{align} \nonumber |\phi_{x}^{\bullet}|_{1/2}^2 & = \int_{\mathbb{R}} |p|\,|\widehat{\phi_{x}^{\bullet}}(p)|^2 \mathrm{d} p = \int_{\mathbb{R}} \frac{1}{|p|}\,|\widehat{(\phi_{x}^{\bullet})'}(p)|^2 \mathrm{d} p \\ \nonumber & = -2\int_{\mathbb{R}^2} \ln|\xi_1 - \xi_2|\,(\phi_x^{\bullet})'(\xi_1)(\phi_x^{\bullet})'(\xi_2) \mathrm{d}\xi_1\mathrm{d}\xi_2 \\ & \leq 2 \int_{\mathbb{R}^2} \big|\ln|\xi_1 - \xi_2|\big|\,|(\phi^{\bullet}_x)'(\xi_1)|\,|(\phi_x^{\bullet})'(\xi_2)|\mathrm{d}\xi_1\mathrm{d}\xi_2. \end{align} $$
We note that, for any
![]() $a_1,a_2\in [-M,M]$
,
$a_1,a_2\in [-M,M]$
,
![]() $b_1,b_2\in \mathbb R$
, we can find a finite constant C (depending only on M) such that
$b_1,b_2\in \mathbb R$
, we can find a finite constant C (depending only on M) such that
 $$ \begin{align*}\int_{\mathbb{R}^2} \big|\ln|\xi_1-\xi_2|\big|\frac{\mathrm{d}\xi_1}{(\xi_1-a_1)^2+b_1^2}\frac{\mathrm{d}\xi_2}{(\xi_2-a_2)^2+b_2^2}\le \frac{C}{b_1 b_2} (1+|\ln|b_1||+|\ln|b_2||)\,.\end{align*} $$
$$ \begin{align*}\int_{\mathbb{R}^2} \big|\ln|\xi_1-\xi_2|\big|\frac{\mathrm{d}\xi_1}{(\xi_1-a_1)^2+b_1^2}\frac{\mathrm{d}\xi_2}{(\xi_2-a_2)^2+b_2^2}\le \frac{C}{b_1 b_2} (1+|\ln|b_1||+|\ln|b_2||)\,.\end{align*} $$
So after we insert the bounds of (3.31) in (3.32), we obtain
 $$ \begin{align*}\big|\phi_{x}^{\bullet}\big|_{1/2}^{2} \leq \frac{D\,\ln d(x,\mathsf{A}_{2/N^3})}{d^2(x,\mathsf{A}_{2/N^3})} \end{align*} $$
$$ \begin{align*}\big|\phi_{x}^{\bullet}\big|_{1/2}^{2} \leq \frac{D\,\ln d(x,\mathsf{A}_{2/N^3})}{d^2(x,\mathsf{A}_{2/N^3})} \end{align*} $$
for some constant
![]() $D> 0$
depending only on
$D> 0$
depending only on
![]() $\mathsf {A}_{2/N^3}$
. If
$\mathsf {A}_{2/N^3}$
. If
![]() $d(x,\mathsf {A}) \geq \frac {3}{N^3}$
and for N large enough, we can also write with a larger constant D,
$d(x,\mathsf {A}) \geq \frac {3}{N^3}$
and for N large enough, we can also write with a larger constant D,
Then, with Equations (3.25), (3.27) and (3.26),
 $$ \begin{align*} \Big|\frac{1}{N}W_1(x) - \mathcal{W}_{\mu_{\mathrm{eq}}^V}(x)\Big| & = \Big|\mu_{N,\beta}^{V;\mathsf{A}}\big(\mathcal{W}_{L_N}(x) - \mathcal{W}_{\mu_{\mathrm{eq}}^V}(x)\big)\Big| \\ & \leq \frac{3}{N^2 d^2(x,\mathsf{A})} + 2D\,\sqrt{\frac{\ln N}{N}}\,\frac{\sqrt{|\ln d(x,\mathsf{A})}|}{d(x,\mathsf{A})}. \end{align*} $$
$$ \begin{align*} \Big|\frac{1}{N}W_1(x) - \mathcal{W}_{\mu_{\mathrm{eq}}^V}(x)\Big| & = \Big|\mu_{N,\beta}^{V;\mathsf{A}}\big(\mathcal{W}_{L_N}(x) - \mathcal{W}_{\mu_{\mathrm{eq}}^V}(x)\big)\Big| \\ & \leq \frac{3}{N^2 d^2(x,\mathsf{A})} + 2D\,\sqrt{\frac{\ln N}{N}}\,\frac{\sqrt{|\ln d(x,\mathsf{A})}|}{d(x,\mathsf{A})}. \end{align*} $$
If we restrict ourselves to
![]() $x \in \mathbb {C}\setminus \mathsf {A}$
such that
$x \in \mathbb {C}\setminus \mathsf {A}$
such that
 $$ \begin{align*}d(x,\mathsf{A}) \geq \frac{D'}{\sqrt{N^{2} \ln N}} \end{align*} $$
$$ \begin{align*}d(x,\mathsf{A}) \geq \frac{D'}{\sqrt{N^{2} \ln N}} \end{align*} $$
for some constant
![]() $D'> 0$
, then
$D'> 0$
, then
 $$ \begin{align*}\Big|\frac{1}{N}\, W_1(x) - \mathcal{W}_{\mu_{\mathrm{eq}}^V}(x)\Big| \leq (2D + D")\,\sqrt{\frac{\ln N}{N}}\,\frac{\sqrt{|\ln d(x,\mathsf{A})}|}{d(x,\mathsf{A})} \end{align*} $$
$$ \begin{align*}\Big|\frac{1}{N}\, W_1(x) - \mathcal{W}_{\mu_{\mathrm{eq}}^V}(x)\Big| \leq (2D + D")\,\sqrt{\frac{\ln N}{N}}\,\frac{\sqrt{|\ln d(x,\mathsf{A})}|}{d(x,\mathsf{A})} \end{align*} $$
for some constant
![]() $D"> 0$
.
$D"> 0$
.
Now let us consider the higher correlators. For any
![]() $n \geq 2$
, the same arguments show that there exists a finite constant
$n \geq 2$
, the same arguments show that there exists a finite constant
![]() $c_n$
so that for any
$c_n$
so that for any
![]() $x_i$
such that
$x_i$
such that
![]() $d(x_i,\mathsf {A}) \geq \frac {D'}{\sqrt {N^{2} \ln N}} $
,
$d(x_i,\mathsf {A}) \geq \frac {D'}{\sqrt {N^{2} \ln N}} $
,
 $$ \begin{align*}m_n(x_1,\ldots,x_n)=\mu_{N,\beta}^{V;\mathsf{A}}\Big[\prod_{i=1}^n (\mathcal{W}_{L_N} - \mathcal{W}_{\mu_{\mathrm{eq}}^V})(x_i)\Big] \end{align*} $$
$$ \begin{align*}m_n(x_1,\ldots,x_n)=\mu_{N,\beta}^{V;\mathsf{A}}\Big[\prod_{i=1}^n (\mathcal{W}_{L_N} - \mathcal{W}_{\mu_{\mathrm{eq}}^V})(x_i)\Big] \end{align*} $$
satisfies
 $$ \begin{align*}|m_n(x_1,\ldots,x_n)|\le c_n (N\ln N)^{\frac{n}{2}}\,\prod_{i = 1}^n \frac{\sqrt{|\ln d(x_i,\mathsf{A})|}}{d(x_i,\mathsf{A})}. \end{align*} $$
$$ \begin{align*}|m_n(x_1,\ldots,x_n)|\le c_n (N\ln N)^{\frac{n}{2}}\,\prod_{i = 1}^n \frac{\sqrt{|\ln d(x_i,\mathsf{A})|}}{d(x_i,\mathsf{A})}. \end{align*} $$
As
![]() $W_n^{V;\mathsf {A}}$
is a homogeneous polynomial of degree n in the moments
$W_n^{V;\mathsf {A}}$
is a homogeneous polynomial of degree n in the moments
![]() $(m_k)_{1 \leq k \leq n}$
, we conclude that
$(m_k)_{1 \leq k \leq n}$
, we conclude that
 $$ \begin{align*}|W_n(x_1,\ldots,x_n)| \leq \gamma_n\,(N\ln N)^{\frac{n}{2}}\,\prod_{i = 1}^n \frac{\sqrt{|\ln d(x_i,\mathsf{A})|}}{d(x_i,\mathsf{A})}. \end{align*} $$
$$ \begin{align*}|W_n(x_1,\ldots,x_n)| \leq \gamma_n\,(N\ln N)^{\frac{n}{2}}\,\prod_{i = 1}^n \frac{\sqrt{|\ln d(x_i,\mathsf{A})|}}{d(x_i,\mathsf{A})}. \end{align*} $$
for some constant
![]() $\gamma _n> 0$
, which depends only on
$\gamma _n> 0$
, which depends only on
![]() $\mathsf {A}$
. This concludes the proof of Corollary 3.7.
$\mathsf {A}$
. This concludes the proof of Corollary 3.7.
Similarly, to have a control on filling fractions, we write
Following the same steps to extend the function
![]() $x \mapsto \mathbf {1}_{\mathsf {A}_h}(x)$
initially defined on
$x \mapsto \mathbf {1}_{\mathsf {A}_h}(x)$
initially defined on
![]() $\mathsf {A}$
by a function defined on
$\mathsf {A}$
by a function defined on
![]() $\mathbb {R}$
and with finite
$\mathbb {R}$
and with finite
![]() $|\cdot |_{1/2}$
norm, we can apply Corollary 3.6 to deduce Corollary 3.8.
$|\cdot |_{1/2}$
norm, we can apply Corollary 3.6 to deduce Corollary 3.8.
4. Dyson–Schwinger equations for
 $\beta $
ensembles
$\beta $
ensembles
Let
![]() $\mathsf {A} = \bigcup _{h = 0}^{g} \mathsf {A}_h$
be a finite union of pairwise disjoint bounded segments, and let V be a
$\mathsf {A} = \bigcup _{h = 0}^{g} \mathsf {A}_h$
be a finite union of pairwise disjoint bounded segments, and let V be a
![]() $\mathcal {C}^1$
function of
$\mathcal {C}^1$
function of
![]() $\mathsf {A}$
. Dyson–Schwinger equations for the initial model
$\mathsf {A}$
. Dyson–Schwinger equations for the initial model
![]() $\mu _{N,\beta }^{V;\mathsf {A}}$
can be derived by integration by parts. Since the derivation does not use any information on the location of the
$\mu _{N,\beta }^{V;\mathsf {A}}$
can be derived by integration by parts. Since the derivation does not use any information on the location of the
![]() $\lambda $
s, it is equally valid for the model with fixed filling fractions
$\lambda $
s, it is equally valid for the model with fixed filling fractions
![]() $\mu _{N,\beta ;\boldsymbol {\epsilon }}^{V;\mathsf {A}}$
, in which
$\mu _{N,\beta ;\boldsymbol {\epsilon }}^{V;\mathsf {A}}$
, in which
![]() $N\epsilon _h = N_h$
are integers.
$N\epsilon _h = N_h$
are integers.
Since these equations are well known (and have been reproved in [Reference Borot and GuionnetBG11]), we state them without proof. They can be written in several equivalent forms, and here we recast them in a way which is convenient for our analysis. We assume that V extends to a holomorphic function in a neighbourhood of
![]() $\mathsf {A}$
, so that they can be written in terms of contour integrals of correlators – an extension to V harmonic will be mentioned in § 6.1. We introduce (arbitrarily for the moment) a partition
$\mathsf {A}$
, so that they can be written in terms of contour integrals of correlators – an extension to V harmonic will be mentioned in § 6.1. We introduce (arbitrarily for the moment) a partition
![]() $\partial \mathsf {A} = (\partial \mathsf {A})_+ \cup (\partial \mathsf {A})_-$
of the set of edges of the range of integration, and let
$\partial \mathsf {A} = (\partial \mathsf {A})_+ \cup (\partial \mathsf {A})_-$
of the set of edges of the range of integration, and let
 $$ \begin{align} L(x) = \prod_{a \in (\partial \mathsf{A})_-} (x - a),\qquad L_1(x,\xi) = \frac{L(x) - L(\xi)}{x - \xi},\qquad L_2(x;\xi_1,\xi_2) = \frac{L_1(x,\xi_1) - L_1(x,\xi_2)}{\xi_1 - \xi_2}. \end{align} $$
$$ \begin{align} L(x) = \prod_{a \in (\partial \mathsf{A})_-} (x - a),\qquad L_1(x,\xi) = \frac{L(x) - L(\xi)}{x - \xi},\qquad L_2(x;\xi_1,\xi_2) = \frac{L_1(x,\xi_1) - L_1(x,\xi_2)}{\xi_1 - \xi_2}. \end{align} $$
Theorem 4.1. Dyson–Schwinger equation in one variable. For any
![]() $x \in \mathbb {C}\setminus \mathsf {A}$
, we have
$x \in \mathbb {C}\setminus \mathsf {A}$
, we have

And similarly, for higher correlators, we have the following:
Theorem 4.2. Dyson–Schwinger equation in
![]() $n \geq 2$
variables. For any
$n \geq 2$
variables. For any
![]() $x,x_2,\ldots ,x_n \in \mathbb {C}\setminus \mathsf {A}$
, if we denote
$x,x_2,\ldots ,x_n \in \mathbb {C}\setminus \mathsf {A}$
, if we denote ![]() , we have
, we have

The last line in Equation (4.2) or (4.3) is a rational fraction in x, with poles at
![]() $a \in \partial \mathsf {A}$
, whose coefficients are linear combination of moments of
$a \in \partial \mathsf {A}$
, whose coefficients are linear combination of moments of
![]() $\lambda _i$
.
$\lambda _i$
.
We stress that the Dyson–Schwinger equations are exact for any finite N and hold for any choice of splitting
![]() $\partial \mathsf {A} = (\partial \mathsf {A})_+ \cup (\partial \mathsf {A})_-$
. Note here that
$\partial \mathsf {A} = (\partial \mathsf {A})_+ \cup (\partial \mathsf {A})_-$
. Note here that
![]() $L,L_{1},L_{2}$
depend on
$L,L_{1},L_{2}$
depend on
![]() $A_{-}$
so that, in fact, all the terms except those in the first line of Dyson–Schwinger equations depend a priori on this splitting. Later, when we perform a large
$A_{-}$
so that, in fact, all the terms except those in the first line of Dyson–Schwinger equations depend a priori on this splitting. Later, when we perform a large
![]() $N \rightarrow \infty $
asymptotic analysis, we are led to distinguish soft edges and hard edges (this is a property of the equilibrium measure). It will then be convenient to declare
$N \rightarrow \infty $
asymptotic analysis, we are led to distinguish soft edges and hard edges (this is a property of the equilibrium measure). It will then be convenient to declare
![]() $\partial \mathsf {A}_-$
to be the set of hard edges and
$\partial \mathsf {A}_-$
to be the set of hard edges and
![]() $\partial \mathsf {A}_+$
the set of soft edges. This will have for consequence that the simple poles in (4.2)–(4.3) at
$\partial \mathsf {A}_+$
the set of soft edges. This will have for consequence that the simple poles in (4.2)–(4.3) at
![]() $x = a \in \partial \mathsf {A}_+$
have exponentially small residues and therefore can be neglected to any order
$x = a \in \partial \mathsf {A}_+$
have exponentially small residues and therefore can be neglected to any order
![]() $O(N^{-K})$
in the asymptotic analysis.
$O(N^{-K})$
in the asymptotic analysis.
5. Fixed filling fractions: expansion of correlators
5.1. Notations, assumptions and operator norms
The model with fixed filling fractions corresponds to the case where we condition the number of eigenvalues in each segment
![]() $\mathsf {A}_h$
to be a given integer
$\mathsf {A}_h$
to be a given integer
![]() $N_{h}$
. We set
$N_{h}$
. We set
![]() $\epsilon _h = N_h/N$
for
$\epsilon _h = N_h/N$
for ![]() and
and
![]() $\boldsymbol {\epsilon } = (\epsilon _1,\ldots ,\epsilon _{g})$
. Throughout this section, the equilibrium measure, the correlators
$\boldsymbol {\epsilon } = (\epsilon _1,\ldots ,\epsilon _{g})$
. Throughout this section, the equilibrium measure, the correlators
![]() $W_{n} = W_{n;\boldsymbol {\epsilon }}$
, etc. all depend on
$W_{n} = W_{n;\boldsymbol {\epsilon }}$
, etc. all depend on
![]() $\boldsymbol {\epsilon }$
. The vector
$\boldsymbol {\epsilon }$
. The vector
![]() $\boldsymbol {\epsilon }$
itself could also depend on N, but this dependence will remain implicit. Accordingly, all coefficients we will find in the asymptotic expansion of the correlators will implicitly be functions of
$\boldsymbol {\epsilon }$
itself could also depend on N, but this dependence will remain implicit. Accordingly, all coefficients we will find in the asymptotic expansion of the correlators will implicitly be functions of
![]() $\boldsymbol {\epsilon }$
.
$\boldsymbol {\epsilon }$
.
As explained in Section 4, the correlators in the fixed filling fractions model satisfy the same Dyson–Schwinger equation as in the initial model. We analyse them under the following assumptions:
Hypothesis 5.1.
-
○
 $\mathsf {A}$
is a disjoint finite union of bounded segments
$\mathsf {A}$
is a disjoint finite union of bounded segments
 $\mathsf {A}_h = [a_h^-,a_h^+]$
.
$\mathsf {A}_h = [a_h^-,a_h^+]$
. -
○ (Real-analyticity)
 $V\,:\,\mathsf {A} \rightarrow \mathbb {R}$
extends to a holomorphic function in a neighbourhood
$V\,:\,\mathsf {A} \rightarrow \mathbb {R}$
extends to a holomorphic function in a neighbourhood
 $\mathsf {U} \subseteq \mathbb {C}$
of
$\mathsf {U} \subseteq \mathbb {C}$
of
 $\mathsf {A}$
.
$\mathsf {A}$
. -
○ (Expansion for the potential) There exists a sequence
 $(V^{\{k\}})_{k \geq 0}$
of holomorphic functions in
$(V^{\{k\}})_{k \geq 0}$
of holomorphic functions in
 $\mathsf {U}$
and constants
$\mathsf {U}$
and constants
 $(v^{\{k\}})_{k \geq 1}$
, so that, for any
$(v^{\{k\}})_{k \geq 1}$
, so that, for any
 $K \geq 0$
,
$K \geq 0$
,  $$ \begin{align*}\sup_{\xi \in \mathsf{U}} \Big| V(\xi) - \sum_{k = 0}^{K} N^{-k}\,V^{\{k\}}(\xi)\Big| \leq v^{\{K + 1\}}\,N^{-(K + 1)}. \end{align*} $$
$$ \begin{align*}\sup_{\xi \in \mathsf{U}} \Big| V(\xi) - \sum_{k = 0}^{K} N^{-k}\,V^{\{k\}}(\xi)\Big| \leq v^{\{K + 1\}}\,N^{-(K + 1)}. \end{align*} $$
-
○ (
 $(g + 1)$
-cut regime) The probability measure
$(g + 1)$
-cut regime) The probability measure
 $\mu _\mathrm{{eq};\boldsymbol {\epsilon }}^V$
is supported on
$\mu _\mathrm{{eq};\boldsymbol {\epsilon }}^V$
is supported on
 $\mathsf {S}$
which is a disjoint union of
$\mathsf {S}$
which is a disjoint union of
 $(g + 1)$
segments
$(g + 1)$
segments
 $\mathsf {S}_h = [\alpha _h^-,\alpha _h^+] \subseteq \mathsf {A}_h$
. We set
$\mathsf {S}_h = [\alpha _h^-,\alpha _h^+] \subseteq \mathsf {A}_h$
. We set
 $W_{1}^{\{-1\}}$
to be its Stieltjes transform and recall that uniformly for x in any compact of
$W_{1}^{\{-1\}}$
to be its Stieltjes transform and recall that uniformly for x in any compact of $$ \begin{align*}\lim_{N \rightarrow \infty} (N^{-1}\,W_{1}(x)-W_1^{\{-1\}}(x))=0, \end{align*} $$
$$ \begin{align*}\lim_{N \rightarrow \infty} (N^{-1}\,W_{1}(x)-W_1^{\{-1\}}(x))=0, \end{align*} $$
 $\mathbb {C}\setminus \mathsf {A}$
.
$\mathbb {C}\setminus \mathsf {A}$
.
-
○ (Off-criticality)
 $y(x) = \frac {(V^{\{0\}})'(x)}{2} - W_1^{\{-1\}}(x)$
takes the form (5.1)where S does not vanish on
$y(x) = \frac {(V^{\{0\}})'(x)}{2} - W_1^{\{-1\}}(x)$
takes the form (5.1)where S does not vanish on $$ \begin{align} y(x) = S(x)\,\prod_{h = 0}^{g} \sqrt{(x - \alpha_{h}^+)^{\rho_{h}^+}(x - \alpha_{h}^-)^{\rho_{h}^-}}, \end{align} $$
$$ \begin{align} y(x) = S(x)\,\prod_{h = 0}^{g} \sqrt{(x - \alpha_{h}^+)^{\rho_{h}^+}(x - \alpha_{h}^-)^{\rho_{h}^-}}, \end{align} $$
 $\mathsf {A}$
,
$\mathsf {A}$
,
 $\alpha _{h}^{\bullet }$
are all pairwise distinct, and
$\alpha _{h}^{\bullet }$
are all pairwise distinct, and
 $\rho _{h}^{\bullet } = -1$
if
$\rho _{h}^{\bullet } = -1$
if
 $\alpha _{h}^{\bullet } \in \partial \mathsf {A}$
, and
$\alpha _{h}^{\bullet } \in \partial \mathsf {A}$
, and
 $\rho _{h}^{\bullet } = 1$
otherwise.
$\rho _{h}^{\bullet } = 1$
otherwise.
Later in Section 8, we will come back to the analysis of the initial model, which has
![]() $\mu _{\mathrm{eq}}^V = \mu _{\mathrm{eq};\boldsymbol {\epsilon }_{\star }}^V$
as equilibrium measure. We will show in Lemma A.2 that the initial Hypotheses 1.1–1.3 imply the present Hypotheses 5.1 for
$\mu _{\mathrm{eq}}^V = \mu _{\mathrm{eq};\boldsymbol {\epsilon }_{\star }}^V$
as equilibrium measure. We will show in Lemma A.2 that the initial Hypotheses 1.1–1.3 imply the present Hypotheses 5.1 for
![]() $\boldsymbol {\epsilon }$
in some neighbourhood of
$\boldsymbol {\epsilon }$
in some neighbourhood of
![]() $\boldsymbol {\epsilon }_{\star }$
; in particular, the off-criticality assumption (5.1) is verified, making the results of the present section applicable.
$\boldsymbol {\epsilon }_{\star }$
; in particular, the off-criticality assumption (5.1) is verified, making the results of the present section applicable.
Definition 5.2. If
![]() $\delta> 0$
, we introduce the norm
$\delta> 0$
, we introduce the norm
![]() ${\parallel } \cdot {\parallel }_{\delta }$
on the space
${\parallel } \cdot {\parallel }_{\delta }$
on the space
![]() $\mathcal {H}_{m_1,\ldots ,m_n}^{(n)}(\mathsf {A})$
of holomorphic functions on
$\mathcal {H}_{m_1,\ldots ,m_n}^{(n)}(\mathsf {A})$
of holomorphic functions on
![]() $(\mathbb {C}\setminus \mathsf {A})^n$
which behave like
$(\mathbb {C}\setminus \mathsf {A})^n$
which behave like
![]() $O(\frac {1}{x_i^{m_i}})$
when
$O(\frac {1}{x_i^{m_i}})$
when
![]() $x_i \rightarrow \infty $
:
$x_i \rightarrow \infty $
:
the last equality following from the maximum principle. If
![]() $n \geq 2$
, we denote
$n \geq 2$
, we denote
![]() $\mathcal {H}_m^{(n)} = \mathcal {H}_{m,\ldots ,m}^{(n)}$
.
$\mathcal {H}_m^{(n)} = \mathcal {H}_{m,\ldots ,m}^{(n)}$
.
From Cauchy residue formula, we have a naive bound on the derivatives of a function
![]() $f \in \mathcal {H}_{1}^{(1)}$
in terms of f itself:
$f \in \mathcal {H}_{1}^{(1)}$
in terms of f itself:
In practice, we will take
![]() $\delta $
independent of N, and therefore, the constants depending on
$\delta $
independent of N, and therefore, the constants depending on
![]() $\delta $
will not matter.
$\delta $
will not matter.
Our goal in the next section is to establish under Hypothesis 5.1 below an asymptotic expansion for the correlators when
![]() $N \rightarrow \infty $
, exploiting the Dyson–Schwinger equations. We already notice that it is convenient to choose
$N \rightarrow \infty $
, exploiting the Dyson–Schwinger equations. We already notice that it is convenient to choose
as bipartition of
![]() $\partial \mathsf {A}$
to write down the Dyson–Schwinger equation, since the terms involving
$\partial \mathsf {A}$
to write down the Dyson–Schwinger equation, since the terms involving
![]() $\partial _a \ln Z$
and
$\partial _a \ln Z$
and
![]() $\partial _a W_{n - 1}$
for
$\partial _a W_{n - 1}$
for
![]() $a \in (\partial \mathsf {A})_+$
will be exponentially small according to Corollary 3.3. If
$a \in (\partial \mathsf {A})_+$
will be exponentially small according to Corollary 3.3. If
![]() $a = a_{h}^{\bullet }$
, we denote
$a = a_{h}^{\bullet }$
, we denote
![]() $\alpha (a) = \alpha _{h}^{\bullet }$
.
$\alpha (a) = \alpha _{h}^{\bullet }$
.
To perform the asymptotic analysis to all order, we need a rough a priori estimate on the correlators. We have established in § 3.3 (actually under weaker assumptions than Hypothesis 5.1) that for any
![]() $\delta>0$
,
$\delta>0$
,
and for any
![]() $n \geq 2$
,
$n \geq 2$
,
5.2. Some relevant linear operators
In this subsection, we give the list of linear operators that are used in § 5.3.1 to recast the Dyson–Schwinger equations in a form suitable for the asymptotic analysis. The precise expression of these operators is not essential, but we establish bounds on suitable operator norms that are needed later in the analysis.
5.2.1. Periods
We fix once for all a neighbourhood
![]() $\mathsf {U}$
of
$\mathsf {U}$
of
![]() $\mathsf {A}$
so that S has no zeroes in
$\mathsf {A}$
so that S has no zeroes in
![]() $\mathsf {U}$
, and pairwise nonintersecting contours
$\mathsf {U}$
, and pairwise nonintersecting contours
![]() $\boldsymbol {\mathcal {A}} = (\mathcal {A}_h)_{1 \leq h \leq g}$
surrounding
$\boldsymbol {\mathcal {A}} = (\mathcal {A}_h)_{1 \leq h \leq g}$
surrounding
![]() $\mathsf {A}_h$
in
$\mathsf {A}_h$
in
![]() $\mathsf {U}$
. It is not necessary to introduce a contour surrounding
$\mathsf {U}$
. It is not necessary to introduce a contour surrounding
![]() $\mathsf {A}_0$
since it is homologically equivalent to
$\mathsf {A}_0$
since it is homologically equivalent to
![]() $-\sum _{h = 1}^g \mathcal {A}_{h}$
in
$-\sum _{h = 1}^g \mathcal {A}_{h}$
in
![]() $\widehat {\mathbb {C}}\setminus \mathsf {A}$
. We define the period operator
$\widehat {\mathbb {C}}\setminus \mathsf {A}$
. We define the period operator
![]() $\mathcal {L}_{\boldsymbol {\mathcal {A}}}\,:\,\mathcal {H}^{(1)}_{1} \rightarrow \mathbb {C}^{g}$
by the formula
$\mathcal {L}_{\boldsymbol {\mathcal {A}}}\,:\,\mathcal {H}^{(1)}_{1} \rightarrow \mathbb {C}^{g}$
by the formula
 $$ \begin{align} \mathcal{L}_{\boldsymbol{\mathcal{A}}}[f] = \Big(\oint_{\mathcal{A}_{1}} \frac{\mathrm{d}\xi}{2\mathrm{i}\pi}\,f(\xi)\,,\,\ldots\,,\,\oint_{\mathcal{A}_{g}} \frac{\mathrm{d}\xi}{2\mathrm{i}\pi}\,f(\xi)\Big). \end{align} $$
$$ \begin{align} \mathcal{L}_{\boldsymbol{\mathcal{A}}}[f] = \Big(\oint_{\mathcal{A}_{1}} \frac{\mathrm{d}\xi}{2\mathrm{i}\pi}\,f(\xi)\,,\,\ldots\,,\,\oint_{\mathcal{A}_{g}} \frac{\mathrm{d}\xi}{2\mathrm{i}\pi}\,f(\xi)\Big). \end{align} $$
By Cauchy residue formula, the periods of the Stieltjes transform of the empirical measure are the filling fractions:
Since the
![]() $(W_n)_{n \geq 1}$
are cumulants and the
$(W_n)_{n \geq 1}$
are cumulants and the
![]() $\boldsymbol {\epsilon }$
are fixed (see the remark in Section 1.4), we have
$\boldsymbol {\epsilon }$
are fixed (see the remark in Section 1.4), we have
In other words, we know that in the model with fixed filling fractions, the correlators (as functions of one of their variables) have to satisfy the g constraints (5.5).
Definition 5.3. If
![]() $\boldsymbol {X}$
is an element of
$\boldsymbol {X}$
is an element of
![]() $(\mathbb {C}^{g})^{\otimes n}$
, we define its
$(\mathbb {C}^{g})^{\otimes n}$
, we define its
![]() $L^1$
-norm:
$L^1$
-norm:
 $$ \begin{align*}|\boldsymbol{X}|_{1} = \sum_{1 \leq h_1,\ldots,h_n \leq g} |X_{h_1,\ldots,h_n}|. \end{align*} $$
$$ \begin{align*}|\boldsymbol{X}|_{1} = \sum_{1 \leq h_1,\ldots,h_n \leq g} |X_{h_1,\ldots,h_n}|. \end{align*} $$
5.2.2. The operator
 $\mathcal {K}$
$\mathcal {K}$
We introduce an operator
![]() $\mathcal {K}$
which is the linearisation around the equilibrium measure of the generator of Dyson–Schwinger equations. It is defined on functions
$\mathcal {K}$
which is the linearisation around the equilibrium measure of the generator of Dyson–Schwinger equations. It is defined on functions
![]() $f \in \mathcal {H}^{(1)}_{2}(\mathsf {A})$
by the formula
$f \in \mathcal {H}^{(1)}_{2}(\mathsf {A})$
by the formula
 $$ \begin{align} \mathcal{K}[f](x) = 2W_1^{\{-1\}}(x)f(x) - \frac{1}{L(x)}\oint_{\mathsf{A}}\frac{\mathrm{d}\xi}{2\mathrm{i}\pi}\Big[\frac{L(\xi)\,(V^{\{0\}})'(\xi)}{x - \xi} + P^{\{-1\}}(x;\xi)\Big]f(\xi), \end{align} $$
$$ \begin{align} \mathcal{K}[f](x) = 2W_1^{\{-1\}}(x)f(x) - \frac{1}{L(x)}\oint_{\mathsf{A}}\frac{\mathrm{d}\xi}{2\mathrm{i}\pi}\Big[\frac{L(\xi)\,(V^{\{0\}})'(\xi)}{x - \xi} + P^{\{-1\}}(x;\xi)\Big]f(\xi), \end{align} $$
where x is outside the contour of integration and
We remind that
![]() $L(x) = \prod _{a \in (\partial \mathsf {A})_-} (x - \alpha (a))$
and
$L(x) = \prod _{a \in (\partial \mathsf {A})_-} (x - \alpha (a))$
and
![]() $L_2$
was defined in Equation (4.1). Notice that
$L_2$
was defined in Equation (4.1). Notice that
![]() $W_1^{\{-1\}}(x) \sim \frac {1}{x}$
when
$W_1^{\{-1\}}(x) \sim \frac {1}{x}$
when
![]() $x \rightarrow \infty $
, and
$x \rightarrow \infty $
, and
![]() $P^{\{-1\}}(x,\xi )$
is a polynomial in two variables, of maximal total degree
$P^{\{-1\}}(x,\xi )$
is a polynomial in two variables, of maximal total degree
![]() $|\# \partial \mathsf {A}_{-}| - 2$
(and it is zero if
$|\# \partial \mathsf {A}_{-}| - 2$
(and it is zero if
![]() $|\# \partial \mathsf {A}_-| < 2$
). Hence, we have at least
$|\# \partial \mathsf {A}_-| < 2$
). Hence, we have at least
![]() $\mathcal {K}[f](x) = O(\frac {1}{x})$
when
$\mathcal {K}[f](x) = O(\frac {1}{x})$
when
![]() $x \rightarrow \infty $
. This gives us a linear operator:
$x \rightarrow \infty $
. This gives us a linear operator:
Notice also that
 $$ \begin{align} y(x) = \frac{\big(V^{\{0\}}\big)'(x)}{2} - W_1^{\{-1\}}(x) = S(x)\,\sqrt{\frac{\tilde{L}(x)}{L(x)}}, \end{align} $$
$$ \begin{align} y(x) = \frac{\big(V^{\{0\}}\big)'(x)}{2} - W_1^{\{-1\}}(x) = S(x)\,\sqrt{\frac{\tilde{L}(x)}{L(x)}}, \end{align} $$
where
![]() $\tilde {L}(x) = \prod _{a \in (\partial \mathsf {A})_+} (x - \alpha (a))$
, and by the off-criticality assumption the zeroes of S are away from
$\tilde {L}(x) = \prod _{a \in (\partial \mathsf {A})_+} (x - \alpha (a))$
, and by the off-criticality assumption the zeroes of S are away from
![]() $\mathsf {A}$
. If we define
$\mathsf {A}$
. If we define
 $$ \begin{align*}\sigma(x) = \sqrt{\prod_{a \in (\partial \mathsf{A})} (x - \alpha(a))} = \sqrt{\tilde{L}(x)L(x)}, \end{align*} $$
$$ \begin{align*}\sigma(x) = \sqrt{\prod_{a \in (\partial \mathsf{A})} (x - \alpha(a))} = \sqrt{\tilde{L}(x)L(x)}, \end{align*} $$
we can rewrite
Then,
where
 $$ \begin{align*}\mathcal{Q}[f](x) = - \oint_{\mathsf{A}} \frac{\mathrm{d}\xi}{2\mathrm{i}\pi}\,\Big[\frac{L(\xi)\,(V^{\{0\}})'(\xi) - L(x)\,(V^{\{0\}})'(x)}{x - \xi} + P^{\{-1\}}(x;\xi)\Big]\,f(\xi). \end{align*} $$
$$ \begin{align*}\mathcal{Q}[f](x) = - \oint_{\mathsf{A}} \frac{\mathrm{d}\xi}{2\mathrm{i}\pi}\,\Big[\frac{L(\xi)\,(V^{\{0\}})'(\xi) - L(x)\,(V^{\{0\}})'(x)}{x - \xi} + P^{\{-1\}}(x;\xi)\Big]\,f(\xi). \end{align*} $$
For any
![]() $f \in \mathcal {H}_{2}^{(1)}(\mathsf {A})$
,
$f \in \mathcal {H}_{2}^{(1)}(\mathsf {A})$
,
![]() $x \mapsto \mathcal {Q}[f](x)$
is holomorphic in a neighbourhood of
$x \mapsto \mathcal {Q}[f](x)$
is holomorphic in a neighbourhood of
![]() $\mathsf {A}$
. It is clear from Equation (5.6) that
$\mathsf {A}$
. It is clear from Equation (5.6) that
![]() $\mathrm {Im}\,\mathcal {K} \subseteq \mathcal {H}_{1}^{(1)}(\mathsf {A})$
. Let
$\mathrm {Im}\,\mathcal {K} \subseteq \mathcal {H}_{1}^{(1)}(\mathsf {A})$
. Let
![]() $\varphi \in \mathrm {Im}\,\mathcal {K}$
and
$\varphi \in \mathrm {Im}\,\mathcal {K}$
and
![]() $f \in \mathcal {H}_{2}^{(1)}(\mathsf {A})$
such that
$f \in \mathcal {H}_{2}^{(1)}(\mathsf {A})$
such that
![]() $\varphi = \mathcal {K}[f]$
. We can write
$\varphi = \mathcal {K}[f]$
. We can write
where
Since
![]() $f(x) = O(\frac {1}{x^2})$
,
$f(x) = O(\frac {1}{x^2})$
,
![]() $\psi (x)$
is a polynomial in x of degree at most
$\psi (x)$
is a polynomial in x of degree at most
![]() $g - 1$
. Recall that
$g - 1$
. Recall that
![]() $\mathcal {K}[f]=\varphi $
. We then compute
$\mathcal {K}[f]=\varphi $
. We then compute
 $$ \begin{align} \nonumber \sigma(x)f(x) & = \psi(x) - \oint_{\mathsf{A}} \frac{\mathrm{d}\xi}{2\mathrm{i}\pi}\,\frac{1}{\xi - x}\,\frac{\sigma(\xi)}{2y(\xi)}\Big(- \varphi(\xi) + \frac{\mathcal{Q}[f](\xi)}{L(\xi)}\Big) \\ \nonumber & = \psi(x) + \oint_{\mathsf{A}} \frac{\mathrm{d}\xi}{2\mathrm{i}\pi}\,\frac{1}{\xi - x}\,\frac{1}{2S(\xi)}\,\Big[L(\xi)\,\varphi(\xi) - \mathcal{Q}[f](\xi)\Big]\\ & = \psi(x) + \oint_{\mathsf{A}} \frac{\mathrm{d}\xi}{2\mathrm{i}\pi}\,\frac{1}{\xi - x}\,\frac{L(\xi)}{2S(\xi)}\,\varphi(\xi), \end{align} $$
$$ \begin{align} \nonumber \sigma(x)f(x) & = \psi(x) - \oint_{\mathsf{A}} \frac{\mathrm{d}\xi}{2\mathrm{i}\pi}\,\frac{1}{\xi - x}\,\frac{\sigma(\xi)}{2y(\xi)}\Big(- \varphi(\xi) + \frac{\mathcal{Q}[f](\xi)}{L(\xi)}\Big) \\ \nonumber & = \psi(x) + \oint_{\mathsf{A}} \frac{\mathrm{d}\xi}{2\mathrm{i}\pi}\,\frac{1}{\xi - x}\,\frac{1}{2S(\xi)}\,\Big[L(\xi)\,\varphi(\xi) - \mathcal{Q}[f](\xi)\Big]\\ & = \psi(x) + \oint_{\mathsf{A}} \frac{\mathrm{d}\xi}{2\mathrm{i}\pi}\,\frac{1}{\xi - x}\,\frac{L(\xi)}{2S(\xi)}\,\varphi(\xi), \end{align} $$
using the fact that S has no zeroes on
![]() $\mathsf {A}$
and
$\mathsf {A}$
and
![]() $\mathcal {Q}[f]$
is analytic in a neighbourhood of
$\mathcal {Q}[f]$
is analytic in a neighbourhood of
![]() $\mathsf {A}$
. Let us denote
$\mathsf {A}$
. Let us denote
![]() $\mathcal {G}\,:\,\mathrm {Im}\,\mathcal {K} \rightarrow \mathcal {H}_{2}^{(1)}(\mathsf {A})$
, the linear operator defined by
$\mathcal {G}\,:\,\mathrm {Im}\,\mathcal {K} \rightarrow \mathcal {H}_{2}^{(1)}(\mathsf {A})$
, the linear operator defined by
One deduces
5.2.3. The extended operator
 $\widehat {\mathcal {K}}$
and its inverse
$\widehat {\mathcal {K}}$
and its inverse
It was observed in [Reference AkemannAke96] that
![]() $\psi (x)\mathrm {d} x/\sigma (x)$
defines a holomorphic one-form on the compactification
$\psi (x)\mathrm {d} x/\sigma (x)$
defines a holomorphic one-form on the compactification
![]() $\Sigma $
of the Riemann surface of equation
$\Sigma $
of the Riemann surface of equation
![]() $\sigma ^2 = \prod _{a \in (\partial \mathsf {A})} (x - \alpha (a))$
. The space
$\sigma ^2 = \prod _{a \in (\partial \mathsf {A})} (x - \alpha (a))$
. The space
![]() $H^1(\Sigma )$
of holomorphic one-forms on
$H^1(\Sigma )$
of holomorphic one-forms on
![]() $\Sigma $
has dimension g if all
$\Sigma $
has dimension g if all
![]() $\alpha (a)$
are pairwise distinct (which is the case by off-criticality) and the number of cuts is
$\alpha (a)$
are pairwise distinct (which is the case by off-criticality) and the number of cuts is
![]() $(g + 1)$
. So if
$(g + 1)$
. So if
![]() $g \geq 1$
,
$g \geq 1$
,
![]() $\mathcal {K}$
is not invertible. But we can define an extended operator:
$\mathcal {K}$
is not invertible. But we can define an extended operator:
 $$ \begin{align} \widehat{\mathcal{K}}\,:\,\mathcal{H}_{2}^{(1)}(\mathsf{A}) & \longrightarrow \mathrm{Im}\,\mathcal{K} \times \mathbb{C}^g \nonumber \\ f & \longmapsto \big(\mathcal{K}[f],\mathcal{L}_{\boldsymbol{\mathcal{A}}}[f]\big). \end{align} $$
$$ \begin{align} \widehat{\mathcal{K}}\,:\,\mathcal{H}_{2}^{(1)}(\mathsf{A}) & \longrightarrow \mathrm{Im}\,\mathcal{K} \times \mathbb{C}^g \nonumber \\ f & \longmapsto \big(\mathcal{K}[f],\mathcal{L}_{\boldsymbol{\mathcal{A}}}[f]\big). \end{align} $$
Since
![]() $\big (x^{j - 1}\mathrm {d} x/\mathcal{C} (x)\big )_{0 \leq j \leq g - 1}$
is linearly independent over
$\big (x^{j - 1}\mathrm {d} x/\mathcal{C} (x)\big )_{0 \leq j \leq g - 1}$
is linearly independent over
![]() $\mathbb {C}$
and holomorphic one-forms on
$\mathbb {C}$
and holomorphic one-forms on
![]() $\Sigma $
, it forms a basis of
$\Sigma $
, it forms a basis of
![]() $H^1(\Sigma )$
which can be thus identified with
$H^1(\Sigma )$
which can be thus identified with
![]() $\mathcal{C} (x)^{-1}\cdot \mathbb {C}_{g - 1}[x]$
, where
$\mathcal{C} (x)^{-1}\cdot \mathbb {C}_{g - 1}[x]$
, where
![]() $\mathbb {C}_{g - 1}[x]$
is the set of polynomials in x of degree
$\mathbb {C}_{g - 1}[x]$
is the set of polynomials in x of degree
![]() $\leq (g-1)$
. However, the family of linear forms
$\leq (g-1)$
. However, the family of linear forms
![]() $\mathcal {L}_{\boldsymbol {\mathcal {A}}}$
defined in Equation (5.4) is linearly independent (see, for example, [Reference Farkas and KraFK07]), so it determines a unique basis
$\mathcal {L}_{\boldsymbol {\mathcal {A}}}$
defined in Equation (5.4) is linearly independent (see, for example, [Reference Farkas and KraFK07]), so it determines a unique basis
such that
Therefore, we can define an operator
![]() $\mathcal {L}_{\boldsymbol {\mathcal {A}}}^{-1}\,:\,\mathbb {C}^{g} \rightarrow \sigma (x)^{-1}\cdot \mathbb {C}_{g - 1}[x] \subseteq \mathcal {H}_2^{(1)}$
by the formula
$\mathcal {L}_{\boldsymbol {\mathcal {A}}}^{-1}\,:\,\mathbb {C}^{g} \rightarrow \sigma (x)^{-1}\cdot \mathbb {C}_{g - 1}[x] \subseteq \mathcal {H}_2^{(1)}$
by the formula
 $$ \begin{align} \mathcal{L}_{\boldsymbol{\mathcal{A}}}^{-1}[\boldsymbol{w}] = \sum_{h = 1}^g w_h\,\varpi_{h}(x). \end{align} $$
$$ \begin{align} \mathcal{L}_{\boldsymbol{\mathcal{A}}}^{-1}[\boldsymbol{w}] = \sum_{h = 1}^g w_h\,\varpi_{h}(x). \end{align} $$
We deduce that
![]() $\widehat {\mathcal {K}}$
is an isomorphism. Indeed,
$\widehat {\mathcal {K}}$
is an isomorphism. Indeed,
![]() $\widehat {\mathcal {K}}[f]=(\varphi , \boldsymbol {w})$
if and only if we have, according to Equation (5.12),
$\widehat {\mathcal {K}}[f]=(\varphi , \boldsymbol {w})$
if and only if we have, according to Equation (5.12),
Plugging the first equality into the second, we deduce
which is equivalent to
Plugging this back into Equation (5.18), we deduce that
![]() $\widehat {\mathcal {K}}$
is invertible, with inverse given by
$\widehat {\mathcal {K}}$
is invertible, with inverse given by
where
![]() $ \mathcal {G}$
is defined in Equation (5.12). We will use the notation
$ \mathcal {G}$
is defined in Equation (5.12). We will use the notation
![]() $\widehat {\mathcal {K}}^{-1}_{\boldsymbol {w}}[\varphi ] = \widehat {\mathcal {K}}^{-1}[\varphi ,\boldsymbol {w}]$
. In other words,
$\widehat {\mathcal {K}}^{-1}_{\boldsymbol {w}}[\varphi ] = \widehat {\mathcal {K}}^{-1}[\varphi ,\boldsymbol {w}]$
. In other words,
![]() $\widehat {\mathcal {K}}_{\boldsymbol {w}}^{-1}[\varphi ] = f$
is the unique solution of
$\widehat {\mathcal {K}}_{\boldsymbol {w}}^{-1}[\varphi ] = f$
is the unique solution of
![]() $\mathcal {K}[f] = \varphi $
with
$\mathcal {K}[f] = \varphi $
with
![]() $\boldsymbol {\mathcal {A}}$
-periods equal to
$\boldsymbol {\mathcal {A}}$
-periods equal to
![]() $\boldsymbol {w}$
. It is equal to
$\boldsymbol {w}$
. It is equal to
![]() $\psi (x)\sigma (x)^{-1}+\mathcal {G}[\varphi ](x)$
for some polynomial
$\psi (x)\sigma (x)^{-1}+\mathcal {G}[\varphi ](x)$
for some polynomial
![]() $\psi (x)$
of degree smaller than
$\psi (x)$
of degree smaller than
![]() $g-1$
so that the
$g-1$
so that the
![]() $\boldsymbol {\mathcal {A}}$
-periods equal to
$\boldsymbol {\mathcal {A}}$
-periods equal to
![]() $\boldsymbol {w}$
. The continuity of this inverse operator is the key ingredient of our method.
$\boldsymbol {w}$
. The continuity of this inverse operator is the key ingredient of our method.
Lemma 5.1.
![]() $\mathrm {Im}\,\mathcal {K}$
is closed in
$\mathrm {Im}\,\mathcal {K}$
is closed in
![]() $\mathcal {H}_{2}^{(1)}(\mathsf {A})$
, and for
$\mathcal {H}_{2}^{(1)}(\mathsf {A})$
, and for
![]() $\delta> 0$
small enough, there exist constants
$\delta> 0$
small enough, there exist constants
![]() $C,C',C"> 0$
such that
$C,C',C"> 0$
such that
with exponent
![]() $\kappa = \frac {1}{2}$
and
$\kappa = \frac {1}{2}$
and
![]() $D_c(\delta )$
defined in Equation (5.22). When the potential is off-critical,
$D_c(\delta )$
defined in Equation (5.22). When the potential is off-critical,
![]() $D_c(\delta )$
remains bounded.
$D_c(\delta )$
remains bounded.
Remark 5.4. In the analysis of the model with fixed filling fractions, we will only make use of
![]() $\widehat {\mathcal {K}}_{\boldsymbol {0}}^{-1}$
.
$\widehat {\mathcal {K}}_{\boldsymbol {0}}^{-1}$
.
Proof. If one is interested in controlling the large N expansion of the correlators explicitly in terms of the distance of
![]() $x_i$
s to
$x_i$
s to
![]() $\mathsf {A}$
, it is useful to give an explicit bound on the norm of
$\mathsf {A}$
, it is useful to give an explicit bound on the norm of
![]() $\widehat {\mathcal {K}}^{-1}_{\boldsymbol {w}}$
. Let
$\widehat {\mathcal {K}}^{-1}_{\boldsymbol {w}}$
. Let
![]() $\delta _0> 0$
be small enough but fixed once for all, and let us move the contour in Equation (5.12) to a contour staying at distance larger than
$\delta _0> 0$
be small enough but fixed once for all, and let us move the contour in Equation (5.12) to a contour staying at distance larger than
![]() $\delta _0$
from
$\delta _0$
from
![]() $\mathsf {A}$
. If we choose now a point x so that
$\mathsf {A}$
. If we choose now a point x so that
![]() $d(x,\mathsf {A}) < \delta _0$
, we can write
$d(x,\mathsf {A}) < \delta _0$
, we can write
 $$ \begin{align*}\mathcal{G}[\varphi](x) = \frac{\varphi(x) L(x)}{2S(x)\sigma(x)} - \frac{\varphi(x)}{\sigma(x)}\oint_{d(\xi,\mathsf{A}) = \delta_0} \frac{\mathrm{d}\xi}{2\mathrm{i}\pi}\,\frac{L(\xi)}{2S(\xi)}\,\frac{1}{x - \xi} + \frac{1}{\sigma(x)}\oint_{d(\xi,\mathsf{A}) = \delta_0} \frac{\mathrm{d}\xi}{2\mathrm{i}\pi}\,\frac{L(\xi)}{2S(\xi)}\,\frac{\varphi(\xi)}{x - \xi}. \end{align*} $$
$$ \begin{align*}\mathcal{G}[\varphi](x) = \frac{\varphi(x) L(x)}{2S(x)\sigma(x)} - \frac{\varphi(x)}{\sigma(x)}\oint_{d(\xi,\mathsf{A}) = \delta_0} \frac{\mathrm{d}\xi}{2\mathrm{i}\pi}\,\frac{L(\xi)}{2S(\xi)}\,\frac{1}{x - \xi} + \frac{1}{\sigma(x)}\oint_{d(\xi,\mathsf{A}) = \delta_0} \frac{\mathrm{d}\xi}{2\mathrm{i}\pi}\,\frac{L(\xi)}{2S(\xi)}\,\frac{\varphi(\xi)}{x - \xi}. \end{align*} $$
Hence, there exist constants
![]() $\tilde {C},\tilde {C}'> 0$
depending only on the position of the pairwise disjoint segments
$\tilde {C},\tilde {C}'> 0$
depending only on the position of the pairwise disjoint segments
![]() $\mathsf {A}_h$
such that, for any
$\mathsf {A}_h$
such that, for any
![]() $\delta> 0$
smaller than
$\delta> 0$
smaller than
![]() $\frac {\delta _0}{2}$
,
$\frac {\delta _0}{2}$
,
where
 $$ \begin{align} D_c(\delta) = \sup_{d(\xi,\mathsf{A}) = \delta} \Big|\frac{L(\xi)}{S(\xi)}\Big|\,. \end{align} $$
$$ \begin{align} D_c(\delta) = \sup_{d(\xi,\mathsf{A}) = \delta} \Big|\frac{L(\xi)}{S(\xi)}\Big|\,. \end{align} $$
For
![]() $\delta $
small enough but fixed,
$\delta $
small enough but fixed,
![]() $D_c(\delta )$
blows up when the parameters of the model are tuned to achieve a critical point (i.e., it measures a distance to criticality). Besides, we have for the operator
$D_c(\delta )$
blows up when the parameters of the model are tuned to achieve a critical point (i.e., it measures a distance to criticality). Besides, we have for the operator
![]() $\mathcal {L}_{\boldsymbol {\mathcal {A}}}$
,
$\mathcal {L}_{\boldsymbol {\mathcal {A}}}$
,
and for
![]() $\mathcal {L}_{\boldsymbol {\mathcal {A}}}^{-1}$
written in Equation (5.17), we find
$\mathcal {L}_{\boldsymbol {\mathcal {A}}}^{-1}$
written in Equation (5.17), we find
 $$ \begin{align} {\parallel} \mathcal{L}_{\boldsymbol{\mathcal{A}}}^{-1}[\boldsymbol{w}] {\parallel}_{\delta} \leq \frac{\max_{1 \leq h \leq g} {\parallel} \psi_{h} {\parallel}_{\mathsf{U}}^{\infty}}{\mathrm{inf}_{d(\xi,\mathsf{A}) = \delta} |\sigma(x)|}\,|\boldsymbol{w}|_{1}, \end{align} $$
$$ \begin{align} {\parallel} \mathcal{L}_{\boldsymbol{\mathcal{A}}}^{-1}[\boldsymbol{w}] {\parallel}_{\delta} \leq \frac{\max_{1 \leq h \leq g} {\parallel} \psi_{h} {\parallel}_{\mathsf{U}}^{\infty}}{\mathrm{inf}_{d(\xi,\mathsf{A}) = \delta} |\sigma(x)|}\,|\boldsymbol{w}|_{1}, \end{align} $$
and the denominator behaves like
![]() $\delta ^{-\frac {1}{2}}$
when
$\delta ^{-\frac {1}{2}}$
when
![]() $\delta \rightarrow 0$
. We then deduce from Equation (5.19) the existence of constants
$\delta \rightarrow 0$
. We then deduce from Equation (5.19) the existence of constants
![]() $C,C',C"> 0$
so that
$C,C',C"> 0$
so that
 $$ \begin{align} \nonumber {\parallel} \widehat{\mathcal{K}}^{-1}_{\boldsymbol{w}}[\varphi] {\parallel}_{\delta} &\leq (\tilde{C}D_c(\delta) + \tilde{C}')\delta^{-\frac{1}{2}}{\parallel} \varphi {\parallel}_{\delta} + \delta^{-\frac{1}{2}}\,|\boldsymbol{w}- \mathcal{L}_{\boldsymbol{\mathcal{A}}}\big[\mathcal{G}[\varphi]\big]|_1 \\ &\le (CD_c(\delta) + C')\delta^{-\frac{1}{2}}{\parallel} \varphi {\parallel}_{\delta} + C"\delta^{-\frac{1}{2}}\,|\boldsymbol{w}|_1. \end{align} $$
$$ \begin{align} \nonumber {\parallel} \widehat{\mathcal{K}}^{-1}_{\boldsymbol{w}}[\varphi] {\parallel}_{\delta} &\leq (\tilde{C}D_c(\delta) + \tilde{C}')\delta^{-\frac{1}{2}}{\parallel} \varphi {\parallel}_{\delta} + \delta^{-\frac{1}{2}}\,|\boldsymbol{w}- \mathcal{L}_{\boldsymbol{\mathcal{A}}}\big[\mathcal{G}[\varphi]\big]|_1 \\ &\le (CD_c(\delta) + C')\delta^{-\frac{1}{2}}{\parallel} \varphi {\parallel}_{\delta} + C"\delta^{-\frac{1}{2}}\,|\boldsymbol{w}|_1. \end{align} $$
Remark. From the expression (5.19) for the inverse, we observe that, if
![]() $\varphi $
is holomorphic in
$\varphi $
is holomorphic in
![]() $\mathbb {C}\setminus \mathsf {S}$
, so is
$\mathbb {C}\setminus \mathsf {S}$
, so is
![]() $\widehat {\mathcal {K}}^{-1}_{\boldsymbol {w}}[\varphi ]$
for any
$\widehat {\mathcal {K}}^{-1}_{\boldsymbol {w}}[\varphi ]$
for any
![]() $\boldsymbol {w} \in \mathbb {C}^g$
. In other words,
$\boldsymbol {w} \in \mathbb {C}^g$
. In other words,
![]() $\widehat {\mathcal {K}}^{-1}_{\boldsymbol {w}}(\mathrm {Im}\,\mathcal {K}\cap \mathcal {H}_{1}^{(1)}(\mathsf {S})) \subseteq \mathcal {H}_{2}^{(1)}(\mathsf {S})$
.
$\widehat {\mathcal {K}}^{-1}_{\boldsymbol {w}}(\mathrm {Im}\,\mathcal {K}\cap \mathcal {H}_{1}^{(1)}(\mathsf {S})) \subseteq \mathcal {H}_{2}^{(1)}(\mathsf {S})$
.
5.2.4. Other linear operators
Some other linear operators appear naturally in the Dyson–Schwinger equation. We collect them below. Let us first define, with the notations of Equation (4.1),
 $$ \begin{align} \nonumber \Delta_{-1} W_1(x) & = N^{-1}\,W_1(x) - W_1^{\{-1\}}(x), \\ \nonumber \Delta_{-1}P(x;\xi) & = \oint_{\mathsf{A}} \frac{\mathrm{d}\eta}{2\mathrm{i}\pi}\,2L_2(x;\xi,\eta) \Delta_{-1} W_1 (\eta), \\ \Delta_0 V(x) & = V(x) - V^{\{0\}}(x). \end{align} $$
$$ \begin{align} \nonumber \Delta_{-1} W_1(x) & = N^{-1}\,W_1(x) - W_1^{\{-1\}}(x), \\ \nonumber \Delta_{-1}P(x;\xi) & = \oint_{\mathsf{A}} \frac{\mathrm{d}\eta}{2\mathrm{i}\pi}\,2L_2(x;\xi,\eta) \Delta_{-1} W_1 (\eta), \\ \Delta_0 V(x) & = V(x) - V^{\{0\}}(x). \end{align} $$
Let also
![]() $h_1,h_2$
be two holomorphic functions in
$h_1,h_2$
be two holomorphic functions in
![]() $\mathsf {U}$
. We define
$\mathsf {U}$
. We define
 $$ \begin{align} \nonumber \mathcal{L}_1\,:\,\mathcal{H}_1^{(1)}(\mathsf{A}) \rightarrow \mathcal{H}_2^{(1)}(\mathsf{A}) & \qquad \mathcal{L}_1[f](x) = \oint_{\mathsf{A}} \frac{\mathrm{d}\xi}{2\mathrm{i}\pi}\,\frac{L_2(x;\xi,\xi)}{L(x)}\,f(\xi)\,, \\\nonumber \mathcal{L}_{2}\,:\,\mathcal{H}_{1}^{(2)}(\mathsf{A}) \rightarrow \mathcal{H}_{1}^{(1)}(\mathsf{A}) & \qquad \mathcal{L}_2[f](x) = \oint_{\mathsf{A}} \frac{\mathrm{d}\xi_1\mathrm{d}\xi_2}{(2\mathrm{i}\pi)^2}\,\frac{L_2(x;\xi_1,\xi_2)}{L(x)}\,f(\xi_1,\xi_2)\,, \\\nonumber \mathcal{M}_{x'}\,:\,\mathcal{H}_{1}^{(1)}(\mathsf{A}) \rightarrow \mathcal{H}^{(2)}_{1}(\mathsf{A}) & \qquad \mathcal{M}_{x'}[f](x) = \oint_{\mathsf{A}} \frac{\mathrm{d}\xi}{2\mathrm{i}\pi}\,\frac{L(\xi)}{L(x)}\,\frac{f(\xi)}{(x - \xi)(x' - \xi)^2}\,, \\\nonumber \mathcal{N}_{h_1,h_2}\,:\,\mathcal{H}_1^{(1)}(\mathsf{A}) \rightarrow \mathcal{H}_1^{(1)}(\mathsf{A}) & \qquad \mathcal{N}_{h_1,h_2}[f](x) = \frac{1}{L(x)} \oint_{\mathsf{A}} \frac{\mathrm{d}\xi}{2\mathrm{i}\pi}\Big(\frac{L(\xi)h_1(\xi)}{x - \xi} + h_2(\xi)\Big)f(\xi)\,, \\\nonumber \Delta\mathcal{K}\,:\,\mathcal{H}_{1}^{(1)}(\mathsf{A}) \rightarrow \mathcal{H}_1^{(1)}(\mathsf{A}) & \qquad \Delta\mathcal{K}[f](x) = -\mathcal{N}_{(\Delta_0 V)',\Delta_{-1}P(x;\bullet)}[f](x) + 2\Delta_{-1}W_1(x)\,f(x) \\\nonumber & \qquad\phantom{\Delta\mathcal{K}[f](x) = } + \frac{1}{N}\Big(1 - \frac{2}{\beta}\Big)(\partial_x + \mathcal{L}_1)[f](x). \\\nonumber \Delta\mathcal{J}\,:\,\mathcal{H}_{1}^{(1)}(\mathsf{A}) \rightarrow \mathcal{H}_{1}^{(1)}(\mathsf{A}) & \qquad \Delta\mathcal{J}[f](x) = -\mathcal{N}_{(\Delta_0 V)',\Delta_{-1}P(x;\bullet)/2}[f](x) + \Delta_{-1}W_1(x)\,f(x) \\& \qquad\phantom{(\Delta\mathcal{J})f(x) = } + \frac{1}{N}\Big(1 - \frac{2}{\beta}\Big)(\partial_{x} + \mathcal{L}_{1})[f](x). \end{align} $$
$$ \begin{align} \nonumber \mathcal{L}_1\,:\,\mathcal{H}_1^{(1)}(\mathsf{A}) \rightarrow \mathcal{H}_2^{(1)}(\mathsf{A}) & \qquad \mathcal{L}_1[f](x) = \oint_{\mathsf{A}} \frac{\mathrm{d}\xi}{2\mathrm{i}\pi}\,\frac{L_2(x;\xi,\xi)}{L(x)}\,f(\xi)\,, \\\nonumber \mathcal{L}_{2}\,:\,\mathcal{H}_{1}^{(2)}(\mathsf{A}) \rightarrow \mathcal{H}_{1}^{(1)}(\mathsf{A}) & \qquad \mathcal{L}_2[f](x) = \oint_{\mathsf{A}} \frac{\mathrm{d}\xi_1\mathrm{d}\xi_2}{(2\mathrm{i}\pi)^2}\,\frac{L_2(x;\xi_1,\xi_2)}{L(x)}\,f(\xi_1,\xi_2)\,, \\\nonumber \mathcal{M}_{x'}\,:\,\mathcal{H}_{1}^{(1)}(\mathsf{A}) \rightarrow \mathcal{H}^{(2)}_{1}(\mathsf{A}) & \qquad \mathcal{M}_{x'}[f](x) = \oint_{\mathsf{A}} \frac{\mathrm{d}\xi}{2\mathrm{i}\pi}\,\frac{L(\xi)}{L(x)}\,\frac{f(\xi)}{(x - \xi)(x' - \xi)^2}\,, \\\nonumber \mathcal{N}_{h_1,h_2}\,:\,\mathcal{H}_1^{(1)}(\mathsf{A}) \rightarrow \mathcal{H}_1^{(1)}(\mathsf{A}) & \qquad \mathcal{N}_{h_1,h_2}[f](x) = \frac{1}{L(x)} \oint_{\mathsf{A}} \frac{\mathrm{d}\xi}{2\mathrm{i}\pi}\Big(\frac{L(\xi)h_1(\xi)}{x - \xi} + h_2(\xi)\Big)f(\xi)\,, \\\nonumber \Delta\mathcal{K}\,:\,\mathcal{H}_{1}^{(1)}(\mathsf{A}) \rightarrow \mathcal{H}_1^{(1)}(\mathsf{A}) & \qquad \Delta\mathcal{K}[f](x) = -\mathcal{N}_{(\Delta_0 V)',\Delta_{-1}P(x;\bullet)}[f](x) + 2\Delta_{-1}W_1(x)\,f(x) \\\nonumber & \qquad\phantom{\Delta\mathcal{K}[f](x) = } + \frac{1}{N}\Big(1 - \frac{2}{\beta}\Big)(\partial_x + \mathcal{L}_1)[f](x). \\\nonumber \Delta\mathcal{J}\,:\,\mathcal{H}_{1}^{(1)}(\mathsf{A}) \rightarrow \mathcal{H}_{1}^{(1)}(\mathsf{A}) & \qquad \Delta\mathcal{J}[f](x) = -\mathcal{N}_{(\Delta_0 V)',\Delta_{-1}P(x;\bullet)/2}[f](x) + \Delta_{-1}W_1(x)\,f(x) \\& \qquad\phantom{(\Delta\mathcal{J})f(x) = } + \frac{1}{N}\Big(1 - \frac{2}{\beta}\Big)(\partial_{x} + \mathcal{L}_{1})[f](x). \end{align} $$
We shall encounter
![]() $\Delta \mathcal {K}$
as a correction to the operator
$\Delta \mathcal {K}$
as a correction to the operator
![]() $\mathcal {K}$
of § 5.2.2, which appears in the Dyson–Schwinger equations with
$\mathcal {K}$
of § 5.2.2, which appears in the Dyson–Schwinger equations with
![]() $n \geq 2$
variables. For
$n \geq 2$
variables. For
![]() $n = 1$
variable equation, we shall need the modified version denoted
$n = 1$
variable equation, we shall need the modified version denoted
![]() $\Delta \mathcal {J}$
, which only differs from
$\Delta \mathcal {J}$
, which only differs from
![]() $\Delta \mathcal {K}$
by some symmetry factors
$\Delta \mathcal {K}$
by some symmetry factors
![]() $\frac {1}{2}$
.
$\frac {1}{2}$
.
All those operators are continuous for appropriate norms since we have the bounds, for
![]() $\delta _0$
small enough but fixed, and
$\delta _0$
small enough but fixed, and
![]() $\delta <\delta _0$
small enough,
$\delta <\delta _0$
small enough,
 $$ \begin{align} \nonumber {\parallel} \mathcal{L}_1[f] {\parallel}_{\delta} & \leq \frac{C\,{\parallel} L" {\parallel}^{\mathsf{U}}_{\infty}}{D_{L}(\delta)}\,{\parallel} f {\parallel}_{\delta_0}\,, \\ \nonumber {\parallel} \mathcal{L}_2[f] {\parallel}_{\delta} & \leq \frac{C^2\,{\parallel} L" {\parallel}^{\mathsf{U}}_{\infty}}{D_L(\delta)}\,{\parallel} f {\parallel}_{\delta_0}\,, \\ \nonumber \sup_{d(x',\mathsf{A})\ge\delta} {\parallel}\mathcal{M}_{x'} f {\parallel}_{\delta} & \leq \frac{C {\parallel} L {\parallel}^{\mathsf{U}}_{\infty}}{D_L(\delta)\,\delta^3}\,{\parallel} f {\parallel}_{\delta/2}\,, \\ \nonumber {\parallel} \mathcal{N}_{h_1,h_2}[f]{\parallel}_{\delta} & \leq {\parallel} h_1 {\parallel}^{\mathsf{U}}_{\infty}\,{\parallel} f {\parallel}_{\delta} + C\,\frac{{\parallel} Lh_1 {\parallel}^{\mathsf{U}}_{\infty} + \nonumber {\parallel} h_2 {\parallel}^{\mathsf{U}}_{\infty}}{\delta_0\,D_L(\delta)}\,{\parallel} f {\parallel}_{\delta_0}\,, \\ \nonumber \max\big\{{\parallel} \Delta\mathcal{K}[f] {\parallel}_{\delta},{\parallel} \Delta\mathcal{J}[f] {\parallel}_{\delta}\big\} & \leq \big({\parallel} (\Delta_0 V)' {\parallel}^{\mathsf{U}}_{\infty} + 2\,{\parallel} \Delta_{-1} W_1 {\parallel}_{\delta} \big) {\parallel} f {\parallel}_{\delta} + \Big|1 - \frac{2}{\beta}\Big|\,\frac{2C}{N\delta^2}\,{\parallel} f {\parallel}_{\delta/2} \\ & \quad + C\,\frac{{\parallel} L\,(\Delta_0 V)' {\parallel}^{\mathsf{U}}_{\infty} + {\parallel} \Delta_{-1} P {\parallel}^{\mathsf{U}^2}_{\infty}}{D_L(\delta)\,\delta_0}\,{\parallel} f {\parallel}_{\delta_0} \end{align} $$
$$ \begin{align} \nonumber {\parallel} \mathcal{L}_1[f] {\parallel}_{\delta} & \leq \frac{C\,{\parallel} L" {\parallel}^{\mathsf{U}}_{\infty}}{D_{L}(\delta)}\,{\parallel} f {\parallel}_{\delta_0}\,, \\ \nonumber {\parallel} \mathcal{L}_2[f] {\parallel}_{\delta} & \leq \frac{C^2\,{\parallel} L" {\parallel}^{\mathsf{U}}_{\infty}}{D_L(\delta)}\,{\parallel} f {\parallel}_{\delta_0}\,, \\ \nonumber \sup_{d(x',\mathsf{A})\ge\delta} {\parallel}\mathcal{M}_{x'} f {\parallel}_{\delta} & \leq \frac{C {\parallel} L {\parallel}^{\mathsf{U}}_{\infty}}{D_L(\delta)\,\delta^3}\,{\parallel} f {\parallel}_{\delta/2}\,, \\ \nonumber {\parallel} \mathcal{N}_{h_1,h_2}[f]{\parallel}_{\delta} & \leq {\parallel} h_1 {\parallel}^{\mathsf{U}}_{\infty}\,{\parallel} f {\parallel}_{\delta} + C\,\frac{{\parallel} Lh_1 {\parallel}^{\mathsf{U}}_{\infty} + \nonumber {\parallel} h_2 {\parallel}^{\mathsf{U}}_{\infty}}{\delta_0\,D_L(\delta)}\,{\parallel} f {\parallel}_{\delta_0}\,, \\ \nonumber \max\big\{{\parallel} \Delta\mathcal{K}[f] {\parallel}_{\delta},{\parallel} \Delta\mathcal{J}[f] {\parallel}_{\delta}\big\} & \leq \big({\parallel} (\Delta_0 V)' {\parallel}^{\mathsf{U}}_{\infty} + 2\,{\parallel} \Delta_{-1} W_1 {\parallel}_{\delta} \big) {\parallel} f {\parallel}_{\delta} + \Big|1 - \frac{2}{\beta}\Big|\,\frac{2C}{N\delta^2}\,{\parallel} f {\parallel}_{\delta/2} \\ & \quad + C\,\frac{{\parallel} L\,(\Delta_0 V)' {\parallel}^{\mathsf{U}}_{\infty} + {\parallel} \Delta_{-1} P {\parallel}^{\mathsf{U}^2}_{\infty}}{D_L(\delta)\,\delta_0}\,{\parallel} f {\parallel}_{\delta_0} \end{align} $$
for any f in the domain of definition of the corresponding operator, and
If all edges are soft,
![]() $D_L(\delta ) \equiv 1$
, whereas if there exists at least one hard edge,
$D_L(\delta ) \equiv 1$
, whereas if there exists at least one hard edge,
![]() $D_L(\delta )$
scales like
$D_L(\delta )$
scales like
![]() $\delta $
as
$\delta $
as
![]() $\delta \rightarrow 0$
.
$\delta \rightarrow 0$
.
5.3. Recursive expansion of the correlators
5.3.1. Rewriting Dyson–Schwinger equations
For
![]() $n \geq 2$
variables, we can organise the Dyson–Schwinger equation of Theorem 4.2 as follows:
$n \geq 2$
variables, we can organise the Dyson–Schwinger equation of Theorem 4.2 as follows:
where
 $$ \begin{align} \nonumber A_{n + 1}(x;x_I) & = N^{-1}(\mathcal{L}_2 - \mathrm{id})[W_{n + 1}(\bullet_1,\bullet_2,x_I)](x), \\\nonumber B_{n}(x;x_I) & = N^{-1}(\mathcal{L}_2 - \mathrm{id})\Big[\sum_{\substack{J \subseteq I \\ J \neq \emptyset,I}} W_{\# J + 1}(\bullet_1,x_J)W_{n - \# J}(\bullet_2,x_{I\setminus J})\Big](x), \\\nonumber C_{n - 1}(x;x_I) & = - \frac{2}{\beta N} \sum_{i \in I} \mathcal{M}_{x_i}[W_{n - 1}(\bullet,x_{I\setminus\{i\}})](x), \\D_{n - 1}(x;x_I) & = \frac{2}{\beta N}\,\sum_{a \in (\partial \mathsf{A})_+} \frac{L(a)}{x - a}\,\partial_{a} W_{n - 1}(x_I). \end{align} $$
$$ \begin{align} \nonumber A_{n + 1}(x;x_I) & = N^{-1}(\mathcal{L}_2 - \mathrm{id})[W_{n + 1}(\bullet_1,\bullet_2,x_I)](x), \\\nonumber B_{n}(x;x_I) & = N^{-1}(\mathcal{L}_2 - \mathrm{id})\Big[\sum_{\substack{J \subseteq I \\ J \neq \emptyset,I}} W_{\# J + 1}(\bullet_1,x_J)W_{n - \# J}(\bullet_2,x_{I\setminus J})\Big](x), \\\nonumber C_{n - 1}(x;x_I) & = - \frac{2}{\beta N} \sum_{i \in I} \mathcal{M}_{x_i}[W_{n - 1}(\bullet,x_{I\setminus\{i\}})](x), \\D_{n - 1}(x;x_I) & = \frac{2}{\beta N}\,\sum_{a \in (\partial \mathsf{A})_+} \frac{L(a)}{x - a}\,\partial_{a} W_{n - 1}(x_I). \end{align} $$
For
![]() $n = 1$
, the equation has the same structure, but some terms come with an extra symmetry factor. With the notation of (5.26), and in view of Equation (4.2), we can write
$n = 1$
, the equation has the same structure, but some terms come with an extra symmetry factor. With the notation of (5.26), and in view of Equation (4.2), we can write
where the operator
![]() $\Delta \mathcal {J}$
was introduced in § 5.2.4 and
$\Delta \mathcal {J}$
was introduced in § 5.2.4 and
![]() $D_0$
is given by formula (5.31) with the convention
$D_0$
is given by formula (5.31) with the convention
![]() $W_0=\ln Z^{V;\mathsf {A}}_{N,\beta ;\boldsymbol {\epsilon }}$
.
$W_0=\ln Z^{V;\mathsf {A}}_{N,\beta ;\boldsymbol {\epsilon }}$
.
Since we are in the model with fixed filling fractions, the
![]() $\boldsymbol {\mathcal {A}}$
-periods of
$\boldsymbol {\mathcal {A}}$
-periods of
![]() $W_n(\bullet ,x_I)$
for
$W_n(\bullet ,x_I)$
for
![]() $n \geq 2$
, and of
$n \geq 2$
, and of
![]() $\Delta _{-1}W_1$
, vanish – cf. (5.5). So we are left with equations of the form
$\Delta _{-1}W_1$
, vanish – cf. (5.5). So we are left with equations of the form
and the function
![]() $\varphi $
to determine satisfies
$\varphi $
to determine satisfies
![]() $\mathcal {L}_{\boldsymbol {\mathcal {A}}}[\varphi ] = 0$
by (5.5). We can then invert
$\mathcal {L}_{\boldsymbol {\mathcal {A}}}[\varphi ] = 0$
by (5.5). We can then invert
![]() $\mathcal {K}$
on the subspace of functions with zero periods and write
$\mathcal {K}$
on the subspace of functions with zero periods and write
We will need to check under which conditions the contribution of
![]() $\Delta \mathcal {X}$
is negligible compared to the contribution of
$\Delta \mathcal {X}$
is negligible compared to the contribution of
![]() $\mathcal {K}$
in Equation (5.30). This is achieved with the following lemma.
$\mathcal {K}$
in Equation (5.30). This is achieved with the following lemma.
Lemma 5.2. There exists a finite constant
![]() $C_3$
such that for any
$C_3$
such that for any
![]() $\delta> 0$
, for N large enough, if
$\delta> 0$
, for N large enough, if
![]() $\Delta \mathcal {X}$
is any of the operator
$\Delta \mathcal {X}$
is any of the operator
![]() $\Delta \mathcal {K}$
or
$\Delta \mathcal {K}$
or
![]() $\Delta \mathcal {J}$
, for any function
$\Delta \mathcal {J}$
, for any function
![]() $\varphi \in \mathcal {H}_1^{(1)}(\mathsf {A})$
, we have
$\varphi \in \mathcal {H}_1^{(1)}(\mathsf {A})$
, we have
 $$ \begin{align} \frac{{\parallel} \widehat{\mathcal{K}}_{\boldsymbol{0}}^{-1}\big[\Delta \mathcal{X}[\varphi]\big] {\parallel}_{2\delta}}{{\parallel} \varphi {\parallel}_{\delta}} \le C_3\Big(\sqrt{\frac{\ln N}{N}}\,\frac{\sqrt{\ln\delta}}{\delta^{\kappa + \theta}}\,\frac{D_{c}(2\delta)}{D_{L}(2\delta)} \Big),\, \end{align} $$
$$ \begin{align} \frac{{\parallel} \widehat{\mathcal{K}}_{\boldsymbol{0}}^{-1}\big[\Delta \mathcal{X}[\varphi]\big] {\parallel}_{2\delta}}{{\parallel} \varphi {\parallel}_{\delta}} \le C_3\Big(\sqrt{\frac{\ln N}{N}}\,\frac{\sqrt{\ln\delta}}{\delta^{\kappa + \theta}}\,\frac{D_{c}(2\delta)}{D_{L}(2\delta)} \Big),\, \end{align} $$
with
![]() $\kappa = \frac {1}{2}$
coming from the inversion of
$\kappa = \frac {1}{2}$
coming from the inversion of
![]() $\widehat {\mathcal {K}}$
and
$\widehat {\mathcal {K}}$
and
![]() $\theta = 1$
coming from the a priori bound (3.12).
$\theta = 1$
coming from the a priori bound (3.12).
Proof. We have from Equation (5.20),
Since we have the same bound (5.28) for the operator norm of
![]() $\Delta \mathcal {X} = \Delta \mathcal {K}$
or
$\Delta \mathcal {X} = \Delta \mathcal {K}$
or
![]() $\Delta \mathcal {J}$
, we can keep the generic letter
$\Delta \mathcal {J}$
, we can keep the generic letter
![]() $\mathcal {X}$
in the proof. We have the a priori bound from Corollary 3.7:
$\mathcal {X}$
in the proof. We have the a priori bound from Corollary 3.7:
 $$ \begin{align*}{\parallel} \Delta_{-1} W_1 {\parallel}_{\delta} \leq C_1\,\sqrt{\frac{\ln N}{N}}\,\frac{\sqrt{\ln \delta}}{\delta^{\theta}},\qquad \theta = 1\,, \end{align*} $$
$$ \begin{align*}{\parallel} \Delta_{-1} W_1 {\parallel}_{\delta} \leq C_1\,\sqrt{\frac{\ln N}{N}}\,\frac{\sqrt{\ln \delta}}{\delta^{\theta}},\qquad \theta = 1\,, \end{align*} $$
which also implies
 $$ \begin{align*}{\parallel} \Delta_{-1} P {\parallel}^{\mathsf{U}^2}_{\infty} \leq C_1'\,\sqrt{\frac{\ln N}{N}} \end{align*} $$
$$ \begin{align*}{\parallel} \Delta_{-1} P {\parallel}^{\mathsf{U}^2}_{\infty} \leq C_1'\,\sqrt{\frac{\ln N}{N}} \end{align*} $$
with the notations of § 5.2.4. We also remind that by Hypothesis 5.1,
![]() ${\parallel } \Delta _0 V {\parallel }_{\mathsf {U}}^{\infty } = O(\frac {1}{N})$
. We insert these bounds in Equation (5.28) and use
${\parallel } \Delta _0 V {\parallel }_{\mathsf {U}}^{\infty } = O(\frac {1}{N})$
. We insert these bounds in Equation (5.28) and use
![]() ${\parallel } \varphi {\parallel }_{2\delta } \leq {\parallel } \varphi {\parallel }_{\delta }$
to find
${\parallel } \varphi {\parallel }_{2\delta } \leq {\parallel } \varphi {\parallel }_{\delta }$
to find
 $$ \begin{align*}{\parallel} \Delta\mathcal{X}[\varphi] {\parallel}_{2\delta} \leq C_2\Big(\sqrt{\frac{\ln N}{N}}\,\frac{\sqrt{\ln \delta}}{\delta^{\theta}\,D_L(2\delta)} + \Big|1 - \frac{2}{\beta}\Big|\frac{1}{N\delta^{\theta + 1}}\Big) {\parallel} \varphi {\parallel}_{\delta}. \end{align*} $$
$$ \begin{align*}{\parallel} \Delta\mathcal{X}[\varphi] {\parallel}_{2\delta} \leq C_2\Big(\sqrt{\frac{\ln N}{N}}\,\frac{\sqrt{\ln \delta}}{\delta^{\theta}\,D_L(2\delta)} + \Big|1 - \frac{2}{\beta}\Big|\frac{1}{N\delta^{\theta + 1}}\Big) {\parallel} \varphi {\parallel}_{\delta}. \end{align*} $$
Together with Equation (5.34), this yields
 $$ \begin{align} \frac{{\parallel} \widehat{\mathcal{K}}_{\boldsymbol{0}}^{-1}\big[\Delta\mathcal{X}[\varphi]\big] {\parallel}_{2\delta}}{{\parallel} \varphi {\parallel}_{\delta}} \leq C_2'\Big(\sqrt{\frac{\ln N}{N}}\,\frac{\sqrt{\ln\delta}}{\delta^{\kappa + \theta}}\,\frac{CD_{c}(2\delta)+C'}{D_{L}(2\delta)} + \Big|1 - \frac{2}{\beta}\Big|\,\frac{CD_c(2\delta)+C'}{N\delta^{\kappa + \theta + 1}}\Big). \end{align} $$
$$ \begin{align} \frac{{\parallel} \widehat{\mathcal{K}}_{\boldsymbol{0}}^{-1}\big[\Delta\mathcal{X}[\varphi]\big] {\parallel}_{2\delta}}{{\parallel} \varphi {\parallel}_{\delta}} \leq C_2'\Big(\sqrt{\frac{\ln N}{N}}\,\frac{\sqrt{\ln\delta}}{\delta^{\kappa + \theta}}\,\frac{CD_{c}(2\delta)+C'}{D_{L}(2\delta)} + \Big|1 - \frac{2}{\beta}\Big|\,\frac{CD_c(2\delta)+C'}{N\delta^{\kappa + \theta + 1}}\Big). \end{align} $$
As we pointed out at the end of § 5.2.4, the fact that the potential is off-critical ensures that
![]() $D_{c}(\delta )$
remains bounded when
$D_{c}(\delta )$
remains bounded when
![]() $\delta \rightarrow 0$
, while we have in the worst case,
$\delta \rightarrow 0$
, while we have in the worst case,
![]() $\frac {1}{D_L(\delta )} = o(\frac {1}{\delta })$
; see Equation (5.29). In any case, the second term in the above right-hand side is negligible with respect to the first one, and we can replace
$\frac {1}{D_L(\delta )} = o(\frac {1}{\delta })$
; see Equation (5.29). In any case, the second term in the above right-hand side is negligible with respect to the first one, and we can replace
![]() $CD_{c}(2\delta )+C'$
by
$CD_{c}(2\delta )+C'$
by
![]() $D_c(\delta )$
up to a change in the constant.
$D_c(\delta )$
up to a change in the constant.
Hereafter, we shall not use the precise dependency of the constants on
![]() $\delta $
; we simply use the fact that they are finite when
$\delta $
; we simply use the fact that they are finite when
![]() $\delta $
is positive independent of N. We will denote
$\delta $
is positive independent of N. We will denote
![]() $c(\delta )$
for a generic finite constant depending only on
$c(\delta )$
for a generic finite constant depending only on
![]() $\delta $
, which may change from line to line.
$\delta $
, which may change from line to line.
5.3.2. Initialisation and order of magnitude of
 $W_n$
$W_n$
The goal of this section is to prove the following bounds for
![]() $\delta $
independent of N and N large enough. We know from Corollary 3.3 that the D-terms in Equations (5.30)–(5.32) are exponentially small and remain so after application of
$\delta $
independent of N and N large enough. We know from Corollary 3.3 that the D-terms in Equations (5.30)–(5.32) are exponentially small and remain so after application of
![]() $\mathcal {K}_{\boldsymbol {0}}^{-1}$
, so they will never contribute to the order we are looking at, and we will not bother mentioning them again.
$\mathcal {K}_{\boldsymbol {0}}^{-1}$
, so they will never contribute to the order we are looking at, and we will not bother mentioning them again.
Proposition 5.3. There exists a function
![]() $W_1^{\{0\}} \in \mathcal {H}_{2}^{(1)}(\mathsf {S})$
depending only on
$W_1^{\{0\}} \in \mathcal {H}_{2}^{(1)}(\mathsf {S})$
depending only on
![]() $W_1^{\{-1\}}, V^{\{0\}},V^{\{1\}}$
so that
$W_1^{\{-1\}}, V^{\{0\}},V^{\{1\}}$
so that
so that for all
![]() $\delta>0$
, there exists a finite constant
$\delta>0$
, there exists a finite constant
![]() $C(\delta )$
such that for N large enough,
$C(\delta )$
such that for N large enough,
 $$ \begin{align*}\|\Delta_{0}W_1\|_\delta\le C(\delta) \frac{(\ln N)^{\frac{3}{2}}}{N^{\frac{1}{2}}}\,. \end{align*} $$
$$ \begin{align*}\|\Delta_{0}W_1\|_\delta\le C(\delta) \frac{(\ln N)^{\frac{3}{2}}}{N^{\frac{1}{2}}}\,. \end{align*} $$
It is given by
Proposition 5.4. For any
![]() $n \geq 1$
, we have
$n \geq 1$
, we have
where for
![]() $n\ge 2$
, we have defined
$n\ge 2$
, we have defined
 $$ \begin{align} \nonumber W_{n}^{\{n - 2\}}(x,x_I) & = \widehat{\mathcal{K}}^{-1}_{\boldsymbol{0}}\Big[- \frac{2}{\beta}\sum_{i \in I} \mathcal{M}_{x_i}[W_{n - 1}^{\{n - 3\}}(\bullet,x_I)](x) \\& \quad + (\mathcal{L}_2 - \mathrm{id})\Big[\sum_{\substack{J \subseteq I \\ J\neq \emptyset,I}} W_{\# J + 1}^{\{\# J - 1\}}(\bullet_1,x_J)W_{n - \# J}^{\{n - \# J - 2\}}(\bullet_2,x_{I\setminus J})\Big](x), \end{align} $$
$$ \begin{align} \nonumber W_{n}^{\{n - 2\}}(x,x_I) & = \widehat{\mathcal{K}}^{-1}_{\boldsymbol{0}}\Big[- \frac{2}{\beta}\sum_{i \in I} \mathcal{M}_{x_i}[W_{n - 1}^{\{n - 3\}}(\bullet,x_I)](x) \\& \quad + (\mathcal{L}_2 - \mathrm{id})\Big[\sum_{\substack{J \subseteq I \\ J\neq \emptyset,I}} W_{\# J + 1}^{\{\# J - 1\}}(\bullet_1,x_J)W_{n - \# J}^{\{n - \# J - 2\}}(\bullet_2,x_{I\setminus J})\Big](x), \end{align} $$
and for any
![]() $\delta>0$
, there exists a finite constant
$\delta>0$
, there exists a finite constant
![]() $C_n(\delta )$
such that for N large enough,
$C_n(\delta )$
such that for N large enough,
 $$ \begin{align*}\|\Delta_{n - 2}W_n \|_{\delta}\le C_n(\delta) \frac{(\ln N)^{2n -\frac{1}{2}}}{{N}^{\frac{1}{2}}}\,. \end{align*} $$
$$ \begin{align*}\|\Delta_{n - 2}W_n \|_{\delta}\le C_n(\delta) \frac{(\ln N)^{2n -\frac{1}{2}}}{{N}^{\frac{1}{2}}}\,. \end{align*} $$
In this result, the main information about the error is its order of magnitude. Prior to those results, we are going to prove the following.
Lemma 5.5. Denote
![]() $r^*_n = 3n - 4$
. For any integers
$r^*_n = 3n - 4$
. For any integers
![]() $n \geq 2$
and
$n \geq 2$
and
![]() $\delta>0$
, there exists a finite constant
$\delta>0$
, there exists a finite constant
![]() $C_n(\delta )$
such that for N large enough,
$C_n(\delta )$
such that for N large enough,
Proof. We shall prove by induction that for any integers
![]() $n \geq 2$
and
$n \geq 2$
and
![]() $r \geq 0$
such that
$r \geq 0$
such that
![]() $r \leq r^*_n$
, for any
$r \leq r^*_n$
, for any
![]() $\delta>0$
, there exists a finite constant
$\delta>0$
, there exists a finite constant
![]() $C_{n,r}(\delta )$
such that for N large enough,
$C_{n,r}(\delta )$
such that for N large enough,
The a priori control of correlators (3.13) provides the result for
![]() $r = 0$
. Let s be an integer and assume the result is true for any
$r = 0$
. Let s be an integer and assume the result is true for any ![]() . Let n be such that
. Let n be such that
![]() $s + 1 \leq r^*_n = 3n - 4$
. We consider Equation (5.30) which gives after application of
$s + 1 \leq r^*_n = 3n - 4$
. We consider Equation (5.30) which gives after application of
![]() $\widehat {\mathcal {K}}^{-1}_{\boldsymbol {0}}$
that if
$\widehat {\mathcal {K}}^{-1}_{\boldsymbol {0}}$
that if
![]() $x_I=(x_2,\ldots ,x_n)$
,
$x_I=(x_2,\ldots ,x_n)$
,
It is understood that all linear operators appearing here (and defined in § 5.2) act on the variables which at the end are assigned the value x. This formula gives the correlator
![]() $W_{n}$
in terms of
$W_{n}$
in terms of
![]() $W_{n + 1}$
and
$W_{n + 1}$
and
![]() $W_{n'}$
for
$W_{n'}$
for
![]() $n' < n$
. We systematically use the control (5.25) on the operator norm of
$n' < n$
. We systematically use the control (5.25) on the operator norm of
![]() $\widehat {\mathcal {K}}^{-1}_{\boldsymbol {0}}$
and the fact that
$\widehat {\mathcal {K}}^{-1}_{\boldsymbol {0}}$
and the fact that
![]() $\Delta \mathcal {K}$
only gives negligible contributions compared to the latter (Lemma 5.2). At each step of application of Lemma 5.2, we have to use the operator norm with smaller
$\Delta \mathcal {K}$
only gives negligible contributions compared to the latter (Lemma 5.2). At each step of application of Lemma 5.2, we have to use the operator norm with smaller
![]() $\delta $
– namely,
$\delta $
– namely,
![]() $\delta \rightarrow \frac {\delta }{2}$
. This is fine since our induction hypothesis holds for all
$\delta \rightarrow \frac {\delta }{2}$
. This is fine since our induction hypothesis holds for all
![]() $\delta>0$
and we use these bounds only a finite number of times (in fact, at most r times to get the bound at step r). Note here that this reduction a priori holds only on the variable x as
$\delta>0$
and we use these bounds only a finite number of times (in fact, at most r times to get the bound at step r). Note here that this reduction a priori holds only on the variable x as
![]() $x_I$
is kept fixed, but this is bounded above by the norm where all are greater or equal to
$x_I$
is kept fixed, but this is bounded above by the norm where all are greater or equal to
![]() $\frac {\delta }{2}$
.
$\frac {\delta }{2}$
.
We obtain the following bound on the A-term by using the induction at
![]() $(n+1,s)$
and Equation (5.28),
$(n+1,s)$
and Equation (5.28),
 $$ \begin{align*} \|\widehat{\mathcal{K}}_{\boldsymbol{0}}^{-1}[A_{n + 1}] \|_\delta & \le c(\delta) \|A_{n+1}\|_{\delta/2}\\& \le \frac{c(\delta)}{N}\|W_{n+1}\|_{\delta/2}\le \frac{c(\delta)}{N} C_{n + 1,s}(\delta/2) N^{\frac{n+1 - s}{2}}(\ln N)^{\frac{n+1 + s}{2}},\, \end{align*} $$
$$ \begin{align*} \|\widehat{\mathcal{K}}_{\boldsymbol{0}}^{-1}[A_{n + 1}] \|_\delta & \le c(\delta) \|A_{n+1}\|_{\delta/2}\\& \le \frac{c(\delta)}{N}\|W_{n+1}\|_{\delta/2}\le \frac{c(\delta)}{N} C_{n + 1,s}(\delta/2) N^{\frac{n+1 - s}{2}}(\ln N)^{\frac{n+1 + s}{2}},\, \end{align*} $$
so that rearranging terms yields a finite constant
![]() $c^A_{n,s + 1}(\delta )$
such that
$c^A_{n,s + 1}(\delta )$
such that
Let us consider the B term. It involves linear combinations of
![]() $W_{j + 1}W_{n - j}$
. Notice that
$W_{j + 1}W_{n - j}$
. Notice that
Thus, it is always possible to decompose (arbitrarily)
![]() $s = s' + s"$
such that
$s = s' + s"$
such that
![]() $s' \leq r_{j + 1}^*$
and
$s' \leq r_{j + 1}^*$
and
![]() $s" \leq r_{n - j}^*$
, and we can use the induction hypothesis with
$s" \leq r_{n - j}^*$
, and we can use the induction hypothesis with
![]() $r = s'$
for
$r = s'$
for
![]() $W_{j + 1}$
and with
$W_{j + 1}$
and with
![]() $r = s"$
for
$r = s"$
for
![]() $W_{n - j}$
. Multiplying the bounds and using the control (5.25) on
$W_{n - j}$
. Multiplying the bounds and using the control (5.25) on
![]() $\widehat {\mathcal {K}}^{-1}_{\boldsymbol {0}}$
and Equation (5.28), we obtain
$\widehat {\mathcal {K}}^{-1}_{\boldsymbol {0}}$
and Equation (5.28), we obtain
 $$ \begin{align*}\|\widehat{\mathcal{K}}_{\boldsymbol{0}}^{-1}[B_{n}]\|_\delta \le \frac{c(\delta)}{N} \sum_{J}\|W_{\# J+1}\|_{\delta/2} \|W_{n-\# J}\|_{\delta/2} \le c^B_{n,s+1}(\delta) N^{\frac{n - (s + 1)}{2}}(\ln N)^{\frac{n + s + 1}{2}}\,. \end{align*} $$
$$ \begin{align*}\|\widehat{\mathcal{K}}_{\boldsymbol{0}}^{-1}[B_{n}]\|_\delta \le \frac{c(\delta)}{N} \sum_{J}\|W_{\# J+1}\|_{\delta/2} \|W_{n-\# J}\|_{\delta/2} \le c^B_{n,s+1}(\delta) N^{\frac{n - (s + 1)}{2}}(\ln N)^{\frac{n + s + 1}{2}}\,. \end{align*} $$
The C-term involves
![]() $W_{n - 1}$
. If
$W_{n - 1}$
. If
![]() $s \leq r^*_{n - 1}$
, we can use the induction hypothesis with
$s \leq r^*_{n - 1}$
, we can use the induction hypothesis with
![]() $r = s$
to find by Equation (5.28) that
$r = s$
to find by Equation (5.28) that
 $$ \begin{align*}\|\widehat{\mathcal{K}}_{\boldsymbol{0}}^{-1}[C_{n - 1}]\|_\delta\le \frac{c(\delta)}{N}\sup_{d(x,\mathsf{A})\geq \delta} \|\mathcal M_{x}[W_{n-1}]\|_{\delta/2} \le \frac{c(\delta)}{N}\|W_{n-1}\|_{\delta/4} \le \frac{c^C_{n,s+1}(\delta)}{N\ln N} N^{\frac{n - (s + 1)}{2}}(\ln N)^{\frac{n + s + 1}{2}}\,. \end{align*} $$
$$ \begin{align*}\|\widehat{\mathcal{K}}_{\boldsymbol{0}}^{-1}[C_{n - 1}]\|_\delta\le \frac{c(\delta)}{N}\sup_{d(x,\mathsf{A})\geq \delta} \|\mathcal M_{x}[W_{n-1}]\|_{\delta/2} \le \frac{c(\delta)}{N}\|W_{n-1}\|_{\delta/4} \le \frac{c^C_{n,s+1}(\delta)}{N\ln N} N^{\frac{n - (s + 1)}{2}}(\ln N)^{\frac{n + s + 1}{2}}\,. \end{align*} $$
If
![]() $s> r^*_{n - 1}$
, we can only use the induction hypothesis for
$s> r^*_{n - 1}$
, we can only use the induction hypothesis for
![]() $r = r^*_{n - 1}$
and find the bound
$r = r^*_{n - 1}$
and find the bound
Using that
![]() $r_n^*=r_{n-1}^*+3$
and
$r_n^*=r_{n-1}^*+3$
and ![]() , we see that the above right-hand side is of the same order than the A-term. Finally, by Equation (5.33) and the induction hypothesis at s, we find the bound
, we see that the above right-hand side is of the same order than the A-term. Finally, by Equation (5.33) and the induction hypothesis at s, we find the bound
 $$ \begin{align*}\| \widehat{\mathcal{K}}_{\boldsymbol{0}}^{-1}\big[\Delta\mathcal{K}[W_n]\big] \|_\delta\le c(\delta)\sqrt{\frac{\ln N}{N}}\,\|W_n\|_{\delta/2}\le c^{\Delta\mathcal K}_{n,s+1}(\delta)\sqrt{\frac{\ln N}{N}} N^{\frac{n-s}{2}}(\ln N)^{\frac{n+s}{2}}, \end{align*} $$
$$ \begin{align*}\| \widehat{\mathcal{K}}_{\boldsymbol{0}}^{-1}\big[\Delta\mathcal{K}[W_n]\big] \|_\delta\le c(\delta)\sqrt{\frac{\ln N}{N}}\,\|W_n\|_{\delta/2}\le c^{\Delta\mathcal K}_{n,s+1}(\delta)\sqrt{\frac{\ln N}{N}} N^{\frac{n-s}{2}}(\ln N)^{\frac{n+s}{2}}, \end{align*} $$
which is of the same order as the bound on the A-term. Using Equation (5.42) and summing all our bounds on the error terms proves the bound (5.41) for
![]() $r=s+1$
and, we can conclude by induction.
$r=s+1$
and, we can conclude by induction.
Proof of Proposition 5.3
It appears in Equation (5.32) that
![]() $N\Delta _{-1}W_1=W_1-NW_1^{\{-1\}}$
is given by
$N\Delta _{-1}W_1=W_1-NW_1^{\{-1\}}$
is given by
where
 $$ \begin{align} \nonumber W_1^{\{0\}}(x) &= \widehat{\mathcal{K}}_{\boldsymbol{0}}^{-1}\Big[-\Big(1 - \frac{2}{\beta}\Big)(\partial_{x} + \mathcal{L}_{1})[W_1^{\{-1\}}] + \mathcal{N}_{(V^{\{1\}})',0}[W_1^{\{-1\}}]\Big](x), \\ \Delta_0 W_1(x) &= \widehat{\mathcal{K}}^{-1}_{\boldsymbol{0}}\Big[\mathcal{N}_{(N(\Delta_0 V)'-(V^{\{1\}})'),0}[W_1^{\{-1\}}] +A_2+D_0- \Delta\mathcal{J}[N\Delta_{-1}W_{1}]\Big](x). \end{align} $$
$$ \begin{align} \nonumber W_1^{\{0\}}(x) &= \widehat{\mathcal{K}}_{\boldsymbol{0}}^{-1}\Big[-\Big(1 - \frac{2}{\beta}\Big)(\partial_{x} + \mathcal{L}_{1})[W_1^{\{-1\}}] + \mathcal{N}_{(V^{\{1\}})',0}[W_1^{\{-1\}}]\Big](x), \\ \Delta_0 W_1(x) &= \widehat{\mathcal{K}}^{-1}_{\boldsymbol{0}}\Big[\mathcal{N}_{(N(\Delta_0 V)'-(V^{\{1\}})'),0}[W_1^{\{-1\}}] +A_2+D_0- \Delta\mathcal{J}[N\Delta_{-1}W_{1}]\Big](x). \end{align} $$
Recalling Remark page 44,
![]() $W_1^{\{0\}}$
belongs to
$W_1^{\{0\}}$
belongs to
![]() $\mathcal {H}_{2}^{(1)}(\mathsf {S})$
. To bound the norm of the first term in
$\mathcal {H}_{2}^{(1)}(\mathsf {S})$
. To bound the norm of the first term in
![]() $\Delta _0 W_1$
, observe that by Hypothesis 5.1,
$\Delta _0 W_1$
, observe that by Hypothesis 5.1,
 $$ \begin{align*}N\Delta_{0}V = V^{\{1\}} + \Delta_{1}V,\qquad {\parallel} \Delta_{1} V {\parallel}_{\infty}^{\mathsf{U}} = O\bigg(\frac{1}{N}\bigg)\,, \end{align*} $$
$$ \begin{align*}N\Delta_{0}V = V^{\{1\}} + \Delta_{1}V,\qquad {\parallel} \Delta_{1} V {\parallel}_{\infty}^{\mathsf{U}} = O\bigg(\frac{1}{N}\bigg)\,, \end{align*} $$
so that Equation (5.28) yields
For the second term, note that Lemma 5.5 for
![]() $n=2$
gives the bound
$n=2$
gives the bound
Equations (5.20) and (5.28) imply
Moreover,
![]() $D_0$
is exponentially small by Proposition 3.4. By Lemma 5.2 and the a priori bound (3.12) on
$D_0$
is exponentially small by Proposition 3.4. By Lemma 5.2 and the a priori bound (3.12) on
![]() $\Delta _{-1}W_1$
,
$\Delta _{-1}W_1$
,
This already shows that
![]() $\|\Delta _0 W_1\|_\delta $
is at most of order
$\|\Delta _0 W_1\|_\delta $
is at most of order
![]() $\ln N$
. To improve this bound, observe that
$\ln N$
. To improve this bound, observe that
From Lemma 5.2 we deduce that
 $$ \begin{align} \|\widehat{\mathcal{K}}_{\boldsymbol{0}}^{-1}\big[\Delta\mathcal{J}[W_1^{\{0\}}]\big] \|_\delta\le c(\delta) \sqrt{\frac{\ln N}{N}}\,,\qquad \|\widehat{\mathcal{K}}^{-1}_{\boldsymbol{0}}\big[\Delta\mathcal{J}[\Delta_{0}W_{1}]\big]\|_\delta \le c(\delta)\frac{(\ln N)^{\frac{3}{2}}}{N^{\frac{1}{2}}}\,. \end{align} $$
$$ \begin{align} \|\widehat{\mathcal{K}}_{\boldsymbol{0}}^{-1}\big[\Delta\mathcal{J}[W_1^{\{0\}}]\big] \|_\delta\le c(\delta) \sqrt{\frac{\ln N}{N}}\,,\qquad \|\widehat{\mathcal{K}}^{-1}_{\boldsymbol{0}}\big[\Delta\mathcal{J}[\Delta_{0}W_{1}]\big]\|_\delta \le c(\delta)\frac{(\ln N)^{\frac{3}{2}}}{N^{\frac{1}{2}}}\,. \end{align} $$
We finally deduce, from Equation (5.46) and the fact that the other error terms are smaller, the error bound
 $$ \begin{align*}\| \Delta_{0}W_1\|_\delta \le c(\delta) \frac{(\ln N)^{\frac{3}{2}}}{N^{\frac{1}{2}}}\,.\\[-42pt] \end{align*} $$
$$ \begin{align*}\| \Delta_{0}W_1\|_\delta \le c(\delta) \frac{(\ln N)^{\frac{3}{2}}}{N^{\frac{1}{2}}}\,.\\[-42pt] \end{align*} $$
Proof of Proposition 5.4
We already know the result for
![]() $n = 1$
by Proposition 5.3. Let
$n = 1$
by Proposition 5.3. Let
![]() $n \geq 2$
and assume the result holds for all
$n \geq 2$
and assume the result holds for all ![]() . We want to use Equation (5.30) once more to compute
. We want to use Equation (5.30) once more to compute
![]() $W_{n}$
. We have
$W_{n}$
. We have
![]() $W_{n} = N^{2 - n}(W_{n}^{\{n - 2\}} + \Delta _{n - 2}W_{n})$
with
$W_{n} = N^{2 - n}(W_{n}^{\{n - 2\}} + \Delta _{n - 2}W_{n})$
with
![]() $W_n^{\{n-2\}}$
as in Equation (5.39). The error term
$W_n^{\{n-2\}}$
as in Equation (5.39). The error term
![]() $\Delta _{n - 2}W_{n}$
receives contributions from
$\Delta _{n - 2}W_{n}$
receives contributions from
-
○ The term in
 $\Delta \mathcal K$
. It can be estimated by applying Lemma 5.5 which yields the bound
$\Delta \mathcal K$
. It can be estimated by applying Lemma 5.5 which yields the bound
 $W_n = O\big (N^{2 - n}(\ln N)^{2n - 2}\big )$
and Lemma 5.2 to show that
$W_n = O\big (N^{2 - n}(\ln N)^{2n - 2}\big )$
and Lemma 5.2 to show that  $$ \begin{align*}\|\widehat{\mathcal{K}}^{-1}_{\boldsymbol{0}}\big[\Delta\mathcal K[W_n]\big]\|_\delta \le c(\delta)\sqrt{\frac{\ln N}{N}} \|W_n\|_{\delta/2}\le c(\delta) N^{\frac{3}{2} -n}\,(\ln N)^{2n - \frac{3}{2}}\,.\end{align*} $$
$$ \begin{align*}\|\widehat{\mathcal{K}}^{-1}_{\boldsymbol{0}}\big[\Delta\mathcal K[W_n]\big]\|_\delta \le c(\delta)\sqrt{\frac{\ln N}{N}} \|W_n\|_{\delta/2}\le c(\delta) N^{\frac{3}{2} -n}\,(\ln N)^{2n - \frac{3}{2}}\,.\end{align*} $$
-
○ The A-term. Applying Lemma 5.5 for
 $W_{n+1}$
and Equation (5.28), we find (5.47)
$W_{n+1}$
and Equation (5.28), we find (5.47) $$ \begin{align} \| \widehat{\mathcal{K}}^{-1}_{\boldsymbol{0}}[A_{n + 1}]\|_\delta \le \frac{c(\delta)}{N}\|W_{n+1}\|_{\delta}\le N^{ - n}\,(\ln N)^{2n }. \end{align} $$
$$ \begin{align} \| \widehat{\mathcal{K}}^{-1}_{\boldsymbol{0}}[A_{n + 1}]\|_\delta \le \frac{c(\delta)}{N}\|W_{n+1}\|_{\delta}\le N^{ - n}\,(\ln N)^{2n }. \end{align} $$
-
○ The B-term contributes to the second term in the definition of
 $W_n^{\{n-2\}}$
and also from errors
$W_n^{\{n-2\}}$
and also from errors
 $\Delta _{n' - 2}W_{n'}$
with
$\Delta _{n' - 2}W_{n'}$
with
 $n'\le n-1$
to this limiting term. They are, by the induction hypothesis, of order
$n'\le n-1$
to this limiting term. They are, by the induction hypothesis, of order
 $ N^{2-n - \frac {1}{2}} (\ln N)^{2n-\frac {1}{2}}$
.
$ N^{2-n - \frac {1}{2}} (\ln N)^{2n-\frac {1}{2}}$
. -
○ The C-term yields the first contribution in
 $W_n^{\{n-2\}}$
, and the remaining term from
$W_n^{\{n-2\}}$
, and the remaining term from
 $C_{n - 1}$
is of the same order than the error coming from the B-term, divided by
$C_{n - 1}$
is of the same order than the error coming from the B-term, divided by
 $(\ln N)^2$
.
$(\ln N)^2$
.Hence, we deduce by subtracting
 $W_{n}^{\{n - 2\}}$
and applying
$W_{n}^{\{n - 2\}}$
and applying
 $\widehat {\mathcal {K}}_{\boldsymbol {0}}^{-1}$
that which is the desired result for the n-point correlator. We conclude by induction.
$\widehat {\mathcal {K}}_{\boldsymbol {0}}^{-1}$
that which is the desired result for the n-point correlator. We conclude by induction. $$ \begin{align*}\|\Delta_{n - 2}W_{n} \|_\delta \le c(\delta) \frac{(\ln N)^{2n -\frac{1}{2}}}{{N^{\frac{1}{2}}}}, \end{align*} $$
$$ \begin{align*}\|\Delta_{n - 2}W_{n} \|_\delta \le c(\delta) \frac{(\ln N)^{2n -\frac{1}{2}}}{{N^{\frac{1}{2}}}}, \end{align*} $$
5.4. Recursive expansion of the correlators
Proposition 5.6. For any
![]() $n \geq 1$
and
$n \geq 1$
and
![]() $k_0 \geq n-2$
, we have an expansion of the form
$k_0 \geq n-2$
, we have an expansion of the form
 $$ \begin{align*}W_{n}(x_1,\ldots,x_n) = \sum_{k = n - 2}^{ k_0} N^{-k}\,W_{n}^{\{k\}}(x_1,\ldots,x_n) + N^{-k_0}(\Delta_{k_0} W_{n})(x_1,\ldots,x_n), \end{align*} $$
$$ \begin{align*}W_{n}(x_1,\ldots,x_n) = \sum_{k = n - 2}^{ k_0} N^{-k}\,W_{n}^{\{k\}}(x_1,\ldots,x_n) + N^{-k_0}(\Delta_{k_0} W_{n})(x_1,\ldots,x_n), \end{align*} $$
where
-
(i) for any
 $n \geq 1$
and any
$n \geq 1$
and any  ,
,
 $W_{n}^{\{k\}}$
in
$W_{n}^{\{k\}}$
in
 $\mathcal {H}_{2}^{(n)}(\mathsf {S})$
are specified by the data of
$\mathcal {H}_{2}^{(n)}(\mathsf {S})$
are specified by the data of
 $W_1^{\{-1\}}$
and
$W_1^{\{-1\}}$
and
 $V^{\{j\}}$
for
$V^{\{j\}}$
for
 $0 \leq j \leq k + 3 - n$
. More precisely, they are defined inductively by Equation (5.39) and the equation (5.48)with for
$0 \leq j \leq k + 3 - n$
. More precisely, they are defined inductively by Equation (5.39) and the equation (5.48)with for $$ \begin{align} W_{n}^{\{k + 1\}}(x,x_I) = \widehat{\mathcal{K}}^{-1}_{\boldsymbol{0}}\big[E_{n}^{\{k\}}(\bullet,x_I)\big](x), \end{align} $$
$$ \begin{align} W_{n}^{\{k + 1\}}(x,x_I) = \widehat{\mathcal{K}}^{-1}_{\boldsymbol{0}}\big[E_{n}^{\{k\}}(\bullet,x_I)\big](x), \end{align} $$
 $n=1$
, (5.49)whereas for
$n=1$
, (5.49)whereas for $$ \begin{align} \nonumber E_{1}^{\{k\}}(x) & = (\mathcal{L}_2 - \mathrm{id})\big[W_{2}^{\{k\}}(\bullet_1,\bullet_2)\big](x) \\ \nonumber & \quad + (\mathcal{L}_{2} - \mathrm{id})\Big[\sum_{l=0}^{k} W_1^{\{k-l \}}(\bullet_1) W_1^{\{l\}}(\bullet_2)\Big](x) \\ & \quad - \Big(1 - \frac{2}{\beta}\Big)(\partial_x + \mathcal{L}_1)[W_{1}^{\{k\}}](x) +\sum_{\ell=1}^{k+2} \mathcal{N}_{(V^{\{\ell \}})',0}[W_{1}^{\{k+1-\ell\}}](x) \,, \end{align} $$
$$ \begin{align} \nonumber E_{1}^{\{k\}}(x) & = (\mathcal{L}_2 - \mathrm{id})\big[W_{2}^{\{k\}}(\bullet_1,\bullet_2)\big](x) \\ \nonumber & \quad + (\mathcal{L}_{2} - \mathrm{id})\Big[\sum_{l=0}^{k} W_1^{\{k-l \}}(\bullet_1) W_1^{\{l\}}(\bullet_2)\Big](x) \\ & \quad - \Big(1 - \frac{2}{\beta}\Big)(\partial_x + \mathcal{L}_1)[W_{1}^{\{k\}}](x) +\sum_{\ell=1}^{k+2} \mathcal{N}_{(V^{\{\ell \}})',0}[W_{1}^{\{k+1-\ell\}}](x) \,, \end{align} $$
 $n\ge 2$
, (5.50)In the above formula,
$n\ge 2$
, (5.50)In the above formula, $$ \begin{align} \nonumber E_{n}^{\{k\}}(x;x_I) & = (\mathcal{L}_2 - \mathrm{id})\big[W_{n + 1}^{\{k\}}(\bullet_1,\bullet_2,x_I)\big](x) \\ \nonumber & \quad + \sum_{\substack{0 \leq \ell \leq k \\ J \subseteq I}} (\mathcal{L}_{2} - \mathrm{id})\big[W_{|J| + 1}^{\{\ell\}}(\bullet_1,x_J)W_{n - |J|}^{\{k - \ell\}}(\bullet_2,x_{I\setminus J})\big](x) \\ \nonumber & \quad - \Big(1 - \frac{2}{\beta}\Big)(\partial_x + \mathcal{L}_1)\big[W_{n}^{\{k\}}(\bullet,x_I)\big](x) + \sum_{\ell = n - 2}^{k} \mathcal{N}_{(V^{\{k + 1 - \ell\}})',0}\big[W_{n}^{\{\ell\}}(\bullet,x_I)\big](x) \\ & \quad - \frac{2}{\beta}\sum_{i \in I} \mathcal{M}_{x_i}\big[W_{n - 1}^{\{k\}}(\bullet,x_{I\setminus\{i\}})\big](x). \end{align} $$
$$ \begin{align} \nonumber E_{n}^{\{k\}}(x;x_I) & = (\mathcal{L}_2 - \mathrm{id})\big[W_{n + 1}^{\{k\}}(\bullet_1,\bullet_2,x_I)\big](x) \\ \nonumber & \quad + \sum_{\substack{0 \leq \ell \leq k \\ J \subseteq I}} (\mathcal{L}_{2} - \mathrm{id})\big[W_{|J| + 1}^{\{\ell\}}(\bullet_1,x_J)W_{n - |J|}^{\{k - \ell\}}(\bullet_2,x_{I\setminus J})\big](x) \\ \nonumber & \quad - \Big(1 - \frac{2}{\beta}\Big)(\partial_x + \mathcal{L}_1)\big[W_{n}^{\{k\}}(\bullet,x_I)\big](x) + \sum_{\ell = n - 2}^{k} \mathcal{N}_{(V^{\{k + 1 - \ell\}})',0}\big[W_{n}^{\{\ell\}}(\bullet,x_I)\big](x) \\ & \quad - \frac{2}{\beta}\sum_{i \in I} \mathcal{M}_{x_i}\big[W_{n - 1}^{\{k\}}(\bullet,x_{I\setminus\{i\}})\big](x). \end{align} $$
 $W_p^{\{\ell \}}$
vanishes if
$W_p^{\{\ell \}}$
vanishes if
 $\ell \le p-1$
.
$\ell \le p-1$
.
-
(ii) for any
 $n \geq 1$
,
$n \geq 1$
,
 $\Delta _{k_0}W_{n} \in \mathcal {H}_{2}^{(n)}(\mathsf {A})$
, and there exists a finite constant
$\Delta _{k_0}W_{n} \in \mathcal {H}_{2}^{(n)}(\mathsf {A})$
, and there exists a finite constant
 $c_{n,k_0}(\delta )$
so that for any
$c_{n,k_0}(\delta )$
so that for any
 $\delta>0$
, for N large enough, (5.51)
$\delta>0$
, for N large enough, (5.51) $$ \begin{align} \|\Delta_{k_0} W_{n}\|_\delta \le c_{n, k_0}(\delta) \frac{(\ln N)^{2n-\frac{1}{2}+2(k_0-n+2)}}{{N^{\frac{1}{2}}}}\,. \end{align} $$
$$ \begin{align} \|\Delta_{k_0} W_{n}\|_\delta \le c_{n, k_0}(\delta) \frac{(\ln N)^{2n-\frac{1}{2}+2(k_0-n+2)}}{{N^{\frac{1}{2}}}}\,. \end{align} $$
Proof. The case
![]() $k_0 = n-2$
follows from § 5.3.2, and we prove the general case by induction on
$k_0 = n-2$
follows from § 5.3.2, and we prove the general case by induction on
![]() $k_0$
, which can be seen as the continuation of the proof of Proposition 5.4. Assume the result holds for all
$k_0$
, which can be seen as the continuation of the proof of Proposition 5.4. Assume the result holds for all
![]() $n\ge 1$
and all
$n\ge 1$
and all
![]() $k \le n-2+j=:k_n-1 $
for some
$k \le n-2+j=:k_n-1 $
for some
![]() $j\ge 0$
. We prove it by induction for all n and
$j\ge 0$
. We prove it by induction for all n and
![]() $k_n$
. Let us decompose
$k_n$
. Let us decompose
 $$ \begin{align*}V = \sum_{k = 0}^{j + 2} N^{-k}\,V^{\{k\}} + N^{-(j + 2)}\Delta_{j + 2}V. \end{align*} $$
$$ \begin{align*}V = \sum_{k = 0}^{j + 2} N^{-k}\,V^{\{k\}} + N^{-(j + 2)}\Delta_{j + 2}V. \end{align*} $$
We already know that the Dyson–Schwinger equation for
![]() $W_n$
is satisfied up to order
$W_n$
is satisfied up to order
![]() $N^{1 - k_n}$
for all n. We first show that it holds at
$N^{1 - k_n}$
for all n. We first show that it holds at
![]() $k_1$
for
$k_1$
for
![]() $n=1$
. Returning to Equation (4.2), we see that
$n=1$
. Returning to Equation (4.2), we see that
 $$ \begin{align*} N\Delta_{k_1-1}W_1 (x) &= W_{1}^{\{k_1\}}(x)+ \widehat{\mathcal{K}}^{-1}_{\boldsymbol{0}}[R_1^{\{k_1\}}](x) \\ R_1^{\{k_1\}}(x)&= (\mathcal{L}_2 - \mathrm{id})\big[\Delta_{k_1-1}W_{2}(\bullet_1,\bullet_2)\big](x) -\Big(1 - \frac{2}{\beta}\Big)(\partial_{x} + \mathcal{L}_{1})[\Delta_{k_1-1} W_1] \\ & \quad +2(\mathcal{L}_{2} - \mathrm{id})\big[\Delta_{k_1-1} W_1(\bullet_1) (\Delta_{-1} W_1)(\bullet_2)](x) \\ & \quad - \Big(1 - \frac{2}{\beta}\Big)(\partial_x + \mathcal{L}_1)[\Delta_{k_1-1} W_{1}](x) + \mathcal{N}_{(\Delta_{0} V)',0}[\Delta_{k_1-1} W_{1}](x). \end{align*} $$
$$ \begin{align*} N\Delta_{k_1-1}W_1 (x) &= W_{1}^{\{k_1\}}(x)+ \widehat{\mathcal{K}}^{-1}_{\boldsymbol{0}}[R_1^{\{k_1\}}](x) \\ R_1^{\{k_1\}}(x)&= (\mathcal{L}_2 - \mathrm{id})\big[\Delta_{k_1-1}W_{2}(\bullet_1,\bullet_2)\big](x) -\Big(1 - \frac{2}{\beta}\Big)(\partial_{x} + \mathcal{L}_{1})[\Delta_{k_1-1} W_1] \\ & \quad +2(\mathcal{L}_{2} - \mathrm{id})\big[\Delta_{k_1-1} W_1(\bullet_1) (\Delta_{-1} W_1)(\bullet_2)](x) \\ & \quad - \Big(1 - \frac{2}{\beta}\Big)(\partial_x + \mathcal{L}_1)[\Delta_{k_1-1} W_{1}](x) + \mathcal{N}_{(\Delta_{0} V)',0}[\Delta_{k_1-1} W_{1}](x). \end{align*} $$
Strictly speaking, we should also add the D-terms, but since they are always exponentially small, we will systematically omit them. But we have bounded by induction the
![]() $\delta $
-norms of
$\delta $
-norms of
-
○
 $\Delta _{k_1-1} W_1$
by
$\Delta _{k_1-1} W_1$
by
 $ c_{1,k_1-1}(\delta )(\ln N)^{2-\frac {1}{2}+2 k_1}N^{-\frac {1}{2}}$
,
$ c_{1,k_1-1}(\delta )(\ln N)^{2-\frac {1}{2}+2 k_1}N^{-\frac {1}{2}}$
, -
○
 $\Delta _{k_1-1} W_2$
(notice that
$\Delta _{k_1-1} W_2$
(notice that
 $k_2\ge k_1$
) by
$k_2\ge k_1$
) by
 $c_{2, k_1-1}(\delta ) (\ln N)^{4-\frac {1}{2}+2(k_1-1)} N^{-\frac {1}{2}}$
,
$c_{2, k_1-1}(\delta ) (\ln N)^{4-\frac {1}{2}+2(k_1-1)} N^{-\frac {1}{2}}$
, -
○
 $\Delta _{-1} W_1$
has norm of order
$\Delta _{-1} W_1$
has norm of order
 $\frac {1}{N}$
by Proposition 5.3 and
$\frac {1}{N}$
by Proposition 5.3 and
 $(\Delta _0 V)'$
has also norm of order
$(\Delta _0 V)'$
has also norm of order
 $\frac {1}{N}$
by hypothesis.
$\frac {1}{N}$
by hypothesis.
Hence, the continuity of
![]() $ \widehat {\mathcal {K}}^{-1}_{\boldsymbol {0}}$
implies that
$ \widehat {\mathcal {K}}^{-1}_{\boldsymbol {0}}$
implies that
 $$ \begin{align*}\| \widehat{\mathcal{K}}^{-1}_{\boldsymbol{0}}[R^{\{k_1\}}]\|_\delta\le c_{1,k_1}(\delta) \frac{(\ln N)^{2-\frac{1}{2}+2 k_1}}{N^{\frac{1}{2}}}, \end{align*} $$
$$ \begin{align*}\| \widehat{\mathcal{K}}^{-1}_{\boldsymbol{0}}[R^{\{k_1\}}]\|_\delta\le c_{1,k_1}(\delta) \frac{(\ln N)^{2-\frac{1}{2}+2 k_1}}{N^{\frac{1}{2}}}, \end{align*} $$
which is our inductive bound.
This proves the induction hypothesis for
![]() $n=1$
and
$n=1$
and
![]() $k_1$
. Let us assume that it was proved for all n and
$k_1$
. Let us assume that it was proved for all n and
![]() $k_n-1$
, and for
$k_n-1$
, and for
![]() $n\le n_0$
at
$n\le n_0$
at
![]() $k_n$
. Let us prove it at
$k_n$
. Let us prove it at
![]() $n=n_0+1$
and
$n=n_0+1$
and
![]() $k_0$
with
$k_0$
with
![]() $k_0=k_{n_0}$
. We can decompose the remainder for
$k_0=k_{n_0}$
. We can decompose the remainder for
![]() $n\ge 2$
as
$n\ge 2$
as
Where
![]() $E_n^{\{k\}}$
was defined in Proposition 5.6, we have set
$E_n^{\{k\}}$
was defined in Proposition 5.6, we have set
 $$ \begin{align*} R_{n}^{\{k_0\}}(x;x_I) & = (\mathcal{L}_2 - \mathrm{id})\big[\Delta_{k_0-1}W_{n + 1}(\bullet_1,\bullet_2,x_I)\big](x) \\& \quad + \sum_{J \subseteq I} (\mathcal{L}_2 - \mathrm{id})\big[\Delta_{k_{\# J+1}}W_{\# J + 1}(\bullet_1,x_J)W_{n - \# J}^{\{k_0-k_{\# J+1}\}}(\bullet_2,x_{I\setminus J})\big](x) \\& \quad + \sum_{J \subseteq I} (\mathcal{L}_2 - \mathrm{id})\big[W_{\# J + 1}^{\{ k_0- k_{n-\# J}-1\} }(\bullet_1,x_J)\Delta_{ k_{n-\# J}} W_{n - \# J}(\bullet_2,x_{I\setminus J})\big](x) \\& \quad + \mathcal{N}_{N[( V'-V^{\{0\}})'],0}\big[\Delta_{k_0-1} W_{n}(\bullet,x_I)\big](x) - \frac{2}{\beta}\sum_{i \in I} \mathcal{M}_{x_i}\big[\Delta_{k_0-1}W_{n - 1}(\bullet,x_{I\setminus\{i\}})\big](x). \end{align*} $$
$$ \begin{align*} R_{n}^{\{k_0\}}(x;x_I) & = (\mathcal{L}_2 - \mathrm{id})\big[\Delta_{k_0-1}W_{n + 1}(\bullet_1,\bullet_2,x_I)\big](x) \\& \quad + \sum_{J \subseteq I} (\mathcal{L}_2 - \mathrm{id})\big[\Delta_{k_{\# J+1}}W_{\# J + 1}(\bullet_1,x_J)W_{n - \# J}^{\{k_0-k_{\# J+1}\}}(\bullet_2,x_{I\setminus J})\big](x) \\& \quad + \sum_{J \subseteq I} (\mathcal{L}_2 - \mathrm{id})\big[W_{\# J + 1}^{\{ k_0- k_{n-\# J}-1\} }(\bullet_1,x_J)\Delta_{ k_{n-\# J}} W_{n - \# J}(\bullet_2,x_{I\setminus J})\big](x) \\& \quad + \mathcal{N}_{N[( V'-V^{\{0\}})'],0}\big[\Delta_{k_0-1} W_{n}(\bullet,x_I)\big](x) - \frac{2}{\beta}\sum_{i \in I} \mathcal{M}_{x_i}\big[\Delta_{k_0-1}W_{n - 1}(\bullet,x_{I\setminus\{i\}})\big](x). \end{align*} $$
Again, by the continuity of the involved operators, and because
![]() $k_0-k_{\# J+1}-1\le k_{n-\# J}+1$
so that the induction hypothesis can be used, we get the announced bound. Again, the largest error comes from the first term and is by induction of order
$k_0-k_{\# J+1}-1\le k_{n-\# J}+1$
so that the induction hypothesis can be used, we get the announced bound. Again, the largest error comes from the first term and is by induction of order
![]() $(\ln N)^{2(n+1)-\frac {1}{2}+2(k_0-1-n+2)}N^{-\frac {1}{2}}$
which is of the announced order.
$(\ln N)^{2(n+1)-\frac {1}{2}+2(k_0-1-n+2)}N^{-\frac {1}{2}}$
which is of the announced order.
This proves the first part of Theorem 1.3 for real-analytic potentials (i.e., the stronger Hypothesis 1.2 instead of 1.3). For given n and k, the bound on the error
![]() $\Delta _{k}W_n$
depends only on a finite number of constants
$\Delta _{k}W_n$
depends only on a finite number of constants
![]() $v^{\{k'\}}$
appearing in Hypothesis 5.1.
$v^{\{k'\}}$
appearing in Hypothesis 5.1.
5.5. Central limit theorem
With Proposition 5.3 at our disposal, we can already establish a central limit theorem for linear statistics of analytic functions in the fixed filling fractions model.
Proposition 5.7. Let
![]() $\varphi \,:\,\mathsf {A} \rightarrow \mathbb {R}$
extending to a holomorphic function in a neighbourhood of
$\varphi \,:\,\mathsf {A} \rightarrow \mathbb {R}$
extending to a holomorphic function in a neighbourhood of
![]() $\mathsf {S}$
. Let
$\mathsf {S}$
. Let
![]() $\boldsymbol {N}=(N_1,\ldots , N_g)$
be a sequence (indexed by N) of g-tuples of integers such that
$\boldsymbol {N}=(N_1,\ldots , N_g)$
be a sequence (indexed by N) of g-tuples of integers such that
![]() $\sum _{h = 1}^g N_h \leq N$
, denote
$\sum _{h = 1}^g N_h \leq N$
, denote
![]() $\boldsymbol {\epsilon }=\boldsymbol {N}/N$
, and assume all limit points of
$\boldsymbol {\epsilon }=\boldsymbol {N}/N$
, and assume all limit points of
![]() $\boldsymbol {\epsilon }$
are in
$\boldsymbol {\epsilon }$
are in
![]() $\mathcal {E}$
. Assume Hypothesis 5.1. Then, when
$\mathcal {E}$
. Assume Hypothesis 5.1. Then, when
![]() $N \rightarrow \infty $
,
$N \rightarrow \infty $
,
 $$ \begin{align} \mu_{N,\beta;\boldsymbol{\epsilon}}^{V;\mathsf{A}}\Big[\exp\Big(\sum_{i = 1}^N \varphi(\lambda_i)\Big)\Big] = \exp\Big(N\int_{\mathsf{A}} \mathrm{d} \mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}(x) \varphi(x) + M_{\beta;\boldsymbol{\epsilon}}[\varphi] + \frac{1}{2}\,Q_{\beta;\boldsymbol{\epsilon}}[\varphi,\varphi]\Big) + o(1), \end{align} $$
$$ \begin{align} \mu_{N,\beta;\boldsymbol{\epsilon}}^{V;\mathsf{A}}\Big[\exp\Big(\sum_{i = 1}^N \varphi(\lambda_i)\Big)\Big] = \exp\Big(N\int_{\mathsf{A}} \mathrm{d} \mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}(x) \varphi(x) + M_{\beta;\boldsymbol{\epsilon}}[\varphi] + \frac{1}{2}\,Q_{\beta;\boldsymbol{\epsilon}}[\varphi,\varphi]\Big) + o(1), \end{align} $$
where

Here,
![]() $W_1^{\{0\}} = W_{1;\boldsymbol {\epsilon }}^{\{0\}}$
is the term of order
$W_1^{\{0\}} = W_{1;\boldsymbol {\epsilon }}^{\{0\}}$
is the term of order
![]() $1$
(subleading correction) in
$1$
(subleading correction) in
![]() $W_1$
– cf. Equation (5.36) – and
$W_1$
– cf. Equation (5.36) – and
![]() $W_2^{\{0\}} = W_{2;\boldsymbol {\epsilon }}^{\{0\}}$
is the leading order of
$W_2^{\{0\}} = W_{2;\boldsymbol {\epsilon }}^{\{0\}}$
is the leading order of
![]() $W_2$
– cf. Equation (5.39). Observe above that
$W_2$
– cf. Equation (5.39). Observe above that
![]() $\boldsymbol {\epsilon }$
may depend on N and therefore so does the right-hand side of Equation (5.52).
$\boldsymbol {\epsilon }$
may depend on N and therefore so does the right-hand side of Equation (5.52).
Proof. Let us define
![]() $V_{t} = V - \frac {2t}{\beta N}\,\varphi $
. Since the equilibrium measure is the same for
$V_{t} = V - \frac {2t}{\beta N}\,\varphi $
. Since the equilibrium measure is the same for
![]() $V_{t}$
and V, we still have the result of Proposition 5.3 for the model with potential
$V_{t}$
and V, we still have the result of Proposition 5.3 for the model with potential
![]() $V_{t}$
for any
$V_{t}$
for any
![]() $t \in [0,1]$
, with uniform errors. We can thus write
$t \in [0,1]$
, with uniform errors. We can thus write
 $$ \begin{align} \nonumber \ln \mu_{N,\beta;\boldsymbol{\epsilon}}^{V;\mathsf{A}}\Big[\exp\Big(\sum_{i = 1}^N \,\varphi(\lambda_i)\Big)\Big] & = \int_{0}^{1}\mathrm{d} t \oint_{\mathsf{A}} \frac{\mathrm{d}\xi}{2\mathrm{i}\pi}\,W_{1;\boldsymbol{\epsilon}}^{V_{t}}(\xi)\,\varphi(\xi) \\ & = \int_{0}^1 \mathrm{d} t\oint_{\mathsf{A}} \frac{\mathrm{d}\xi}{2\mathrm{i}\pi}\,\varphi(\xi)\big[N\,W_{1;\boldsymbol{\epsilon}}^{V_t;\{-1\}}(\xi) + W_{1;\boldsymbol{\epsilon}}^{V_t;\{0\}}(\xi)\big] + o(1). \end{align} $$
$$ \begin{align} \nonumber \ln \mu_{N,\beta;\boldsymbol{\epsilon}}^{V;\mathsf{A}}\Big[\exp\Big(\sum_{i = 1}^N \,\varphi(\lambda_i)\Big)\Big] & = \int_{0}^{1}\mathrm{d} t \oint_{\mathsf{A}} \frac{\mathrm{d}\xi}{2\mathrm{i}\pi}\,W_{1;\boldsymbol{\epsilon}}^{V_{t}}(\xi)\,\varphi(\xi) \\ & = \int_{0}^1 \mathrm{d} t\oint_{\mathsf{A}} \frac{\mathrm{d}\xi}{2\mathrm{i}\pi}\,\varphi(\xi)\big[N\,W_{1;\boldsymbol{\epsilon}}^{V_t;\{-1\}}(\xi) + W_{1;\boldsymbol{\epsilon}}^{V_t;\{0\}}(\xi)\big] + o(1). \end{align} $$
As already pointed out,
![]() $W_{1;\boldsymbol {\epsilon }}^{V_t;\{-1\}} = W_{1;\boldsymbol {\epsilon }}^{V;\{-1\}}$
, and from Equation (5.37),
$W_{1;\boldsymbol {\epsilon }}^{V_t;\{-1\}} = W_{1;\boldsymbol {\epsilon }}^{V;\{-1\}}$
, and from Equation (5.37),
Hence, Equation (5.53) yields Equation (5.52) with
This expression can be transformed by comparing with (5.39) for
![]() $n = 2$
, but we can cut this short by observing that
$n = 2$
, but we can cut this short by observing that
![]() $Q_{\beta ;\boldsymbol {\epsilon }}[\varphi ,\varphi ]$
must also be the limiting covariance of
$Q_{\beta ;\boldsymbol {\epsilon }}[\varphi ,\varphi ]$
must also be the limiting covariance of
![]() $\sum _{i=1}^N \varphi (\lambda _i)$
. Hence,
$\sum _{i=1}^N \varphi (\lambda _i)$
. Hence,
where
![]() $W_{2;\boldsymbol {\epsilon }}^{V;\{0\}}$
has been introduced in Equation (5.38). From the proof of Proposition 5.3, we observe that the
$W_{2;\boldsymbol {\epsilon }}^{V;\{0\}}$
has been introduced in Equation (5.38). From the proof of Proposition 5.3, we observe that the
![]() $o(1)$
in (5.52) is uniform in
$o(1)$
in (5.52) is uniform in
![]() $\varphi $
such that
$\varphi $
such that
![]() $\sup _{d(\xi ,\mathsf {A}) \geq \delta } |\varphi (\xi )|$
is bounded by a fixed constant.
$\sup _{d(\xi ,\mathsf {A}) \geq \delta } |\varphi (\xi )|$
is bounded by a fixed constant.
In other words, if
![]() $\lim _{N \rightarrow \infty } \boldsymbol {\epsilon } = \boldsymbol {\epsilon }_{\infty }$
, the random variable
$\lim _{N \rightarrow \infty } \boldsymbol {\epsilon } = \boldsymbol {\epsilon }_{\infty }$
, the random variable
![]() $\Phi _N = \sum _{i = 1}^N \varphi (\lambda _i) - N \int _{\mathsf {A}}\varphi (\xi ) \mathrm {d}\mu _{\mathrm{eq};\boldsymbol {\epsilon }}^V(\xi )$
converges in law to a Gaussian variable with mean
$\Phi _N = \sum _{i = 1}^N \varphi (\lambda _i) - N \int _{\mathsf {A}}\varphi (\xi ) \mathrm {d}\mu _{\mathrm{eq};\boldsymbol {\epsilon }}^V(\xi )$
converges in law to a Gaussian variable with mean
![]() $M_{\boldsymbol {\epsilon }_{\infty }}[\varphi ]$
and variance
$M_{\boldsymbol {\epsilon }_{\infty }}[\varphi ]$
and variance
![]() $Q_{\boldsymbol {\epsilon }_{\infty }}[\varphi ,\varphi ]$
when
$Q_{\boldsymbol {\epsilon }_{\infty }}[\varphi ,\varphi ]$
when
![]() $N \rightarrow \infty $
. This is a generalisation of the central limit theorem already known in the one-cut regime [Reference JohanssonJoh98, Reference Borot and GuionnetBG11]. A similar result was recently obtained in [Reference ShcherbinaShc12]. In the next section, we are going to extend it to holomorphic
$N \rightarrow \infty $
. This is a generalisation of the central limit theorem already known in the one-cut regime [Reference JohanssonJoh98, Reference Borot and GuionnetBG11]. A similar result was recently obtained in [Reference ShcherbinaShc12]. In the next section, we are going to extend it to holomorphic
![]() $\varphi $
which could be complex-valued on
$\varphi $
which could be complex-valued on
![]() $\mathsf {A}$
(Proposition 6.1).
$\mathsf {A}$
(Proposition 6.1).
6. Fixed filling fractions: refined results
In this section, we show how to extend our results to the case of harmonic potentials and potentials containing a complex-valued term of order
![]() $O(\frac {1}{N})$
. The latter is performed by using fine properties of analytic functions (the two-constants theorem) as was recently proposed in [Reference ShcherbinaShc12].
$O(\frac {1}{N})$
. The latter is performed by using fine properties of analytic functions (the two-constants theorem) as was recently proposed in [Reference ShcherbinaShc12].
6.1. Extension to harmonic potentials
The main use of the assumption that V is analytic came from the representation (1.3) of n-linear statistics described by a holomorphic function, in terms of contour integrals of the n-point correlator. If
![]() $\varphi $
is holomorphic in a neighbourhood of
$\varphi $
is holomorphic in a neighbourhood of
![]() $\mathsf {A}$
, its complex conjugate
$\mathsf {A}$
, its complex conjugate
![]() $\overline {\varphi }$
is anti-holomorphic, and we can also represent
$\overline {\varphi }$
is anti-holomorphic, and we can also represent
 $$ \begin{align} \mu_{N,\beta;\boldsymbol{\epsilon}}^{V;\mathsf{A}}\Big[\sum_{i = 1}^N \overline{\varphi(\lambda_i)}\Big] = \overline{\oint_{\mathsf{A}} \frac{\mathrm{d} x}{2\mathrm{i}\pi}\,\varphi(x)\,W_{1;\boldsymbol{\epsilon}}(x)}. \end{align} $$
$$ \begin{align} \mu_{N,\beta;\boldsymbol{\epsilon}}^{V;\mathsf{A}}\Big[\sum_{i = 1}^N \overline{\varphi(\lambda_i)}\Big] = \overline{\oint_{\mathsf{A}} \frac{\mathrm{d} x}{2\mathrm{i}\pi}\,\varphi(x)\,W_{1;\boldsymbol{\epsilon}}(x)}. \end{align} $$
In this paragraph, we explain how to use a weaker set of assumptions than Hypothesis 1.2, where ‘analyticity’ and ‘
![]() $\frac {1}{N}$
expansion of the potential’ are weakened as follows.
$\frac {1}{N}$
expansion of the potential’ are weakened as follows.
Hypothesis 6.1.
-
○ (Harmonicity)
 $V\,:\,\mathsf {A} \rightarrow \mathbb {R}$
can be decomposed
$V\,:\,\mathsf {A} \rightarrow \mathbb {R}$
can be decomposed
 $V = \mathcal {V}_1 + \overline {\mathcal {V}_2}$
, where
$V = \mathcal {V}_1 + \overline {\mathcal {V}_2}$
, where
 $\mathcal {V}_1,\mathcal {V}_2$
extends to holomorphic functions in a neighbourhood
$\mathcal {V}_1,\mathcal {V}_2$
extends to holomorphic functions in a neighbourhood
 $\mathsf {U}$
of
$\mathsf {U}$
of
 $\mathsf {A}$
.
$\mathsf {A}$
. -
○ (
 $\frac {1}{N}$
expansion of the potential) For
$\frac {1}{N}$
expansion of the potential) For
 $j = 1,2$
, there exists a sequence of holomorphic functions
$j = 1,2$
, there exists a sequence of holomorphic functions
 $(\mathcal {V}_j^{\{k\}})_{k \geq 0}$
and constants
$(\mathcal {V}_j^{\{k\}})_{k \geq 0}$
and constants
 $(v_{j}^{\{k\}})_{k}$
so that for any
$(v_{j}^{\{k\}})_{k}$
so that for any
 $K \geq 0$
, (6.2)
$K \geq 0$
, (6.2) $$ \begin{align} \sup_{\xi \in \mathsf{U}} \Big|\mathcal{V}_j(\xi) - \sum_{k = 0}^{K} N^{-k}\,\mathcal{V}_j^{\{k\}}(\xi)\Big| \leq v_{j}^{\{K\}}\,N^{-(K + 1)}. \end{align} $$
$$ \begin{align} \sup_{\xi \in \mathsf{U}} \Big|\mathcal{V}_j(\xi) - \sum_{k = 0}^{K} N^{-k}\,\mathcal{V}_j^{\{k\}}(\xi)\Big| \leq v_{j}^{\{K\}}\,N^{-(K + 1)}. \end{align} $$
In other words, we only assume
![]() $\mathcal {V}$
to be harmonic. ‘Analyticity’ corresponds to the special case
$\mathcal {V}$
to be harmonic. ‘Analyticity’ corresponds to the special case
![]() $\mathcal {V}_2 \equiv 0$
. The main difference lies in the representation (6.1) of expectation values of antiholomorphic statistics, which come into play at various stages but do not affect the reasoning. Let us enumerate the small changes to take into account in the order they appear in Section 5.
$\mathcal {V}_2 \equiv 0$
. The main difference lies in the representation (6.1) of expectation values of antiholomorphic statistics, which come into play at various stages but do not affect the reasoning. Let us enumerate the small changes to take into account in the order they appear in Section 5.
In § 4, in the Dyson–Schwinger equations (Theorem 4.2 and 4.2), we encounter a term
 $$ \begin{align} \mu_{N,\beta;\boldsymbol{\epsilon}}^{V;\mathsf{A}}\Big[\sum_{i = 1}^N \frac{L(\lambda_i)}{L(x)}\,\frac{V'(\lambda_i)}{x - \lambda_i} \prod_{j = 2}^{n}\Big(\sum_{i_j = 1}^{N} \frac{1}{x_j - \lambda_{i_j}}\Big)\Big]_{c}. \end{align} $$
$$ \begin{align} \mu_{N,\beta;\boldsymbol{\epsilon}}^{V;\mathsf{A}}\Big[\sum_{i = 1}^N \frac{L(\lambda_i)}{L(x)}\,\frac{V'(\lambda_i)}{x - \lambda_i} \prod_{j = 2}^{n}\Big(\sum_{i_j = 1}^{N} \frac{1}{x_j - \lambda_{i_j}}\Big)\Big]_{c}. \end{align} $$
It is now equal to
 $$ \begin{align} \frac{1}{L(x)}\oint_{\mathsf{A}} \frac{\mathrm{d}\xi}{2\mathrm{i}\pi}\,L(\xi)\,\frac{\mathcal{V}^{\prime}_1(\xi)}{x - \xi}\,W_{n;\boldsymbol{\epsilon}}(\xi,x_I) - \frac{1}{L(x)}\overline{\oint_{\mathsf{A}}\frac{\mathrm{d}\xi}{2\mathrm{i}\pi}\,L(\xi)\,\frac{\mathcal{V}^{\prime}_2(\xi)}{\overline{x} - \xi}\,W_{n;\boldsymbol{\epsilon}}(\xi,x_I)}. \end{align} $$
$$ \begin{align} \frac{1}{L(x)}\oint_{\mathsf{A}} \frac{\mathrm{d}\xi}{2\mathrm{i}\pi}\,L(\xi)\,\frac{\mathcal{V}^{\prime}_1(\xi)}{x - \xi}\,W_{n;\boldsymbol{\epsilon}}(\xi,x_I) - \frac{1}{L(x)}\overline{\oint_{\mathsf{A}}\frac{\mathrm{d}\xi}{2\mathrm{i}\pi}\,L(\xi)\,\frac{\mathcal{V}^{\prime}_2(\xi)}{\overline{x} - \xi}\,W_{n;\boldsymbol{\epsilon}}(\xi,x_I)}. \end{align} $$
Remark that Equation (6.3) or (6.4) still defines a holomorphic function of x in
![]() $\mathbb {C}\setminus \mathsf {A}$
. In § 5.2, we can define the operator
$\mathbb {C}\setminus \mathsf {A}$
. In § 5.2, we can define the operator
![]() $\mathcal {K}$
by Equation (5.9) with
$\mathcal {K}$
by Equation (5.9) with
![]() $\mathcal {Q}(x)$
now given by
$\mathcal {Q}(x)$
now given by
 $$ \begin{align*} \mathcal{Q}[f](x) & = - \oint_{\mathsf{A}} \frac{\mathrm{d}\xi}{2\mathrm{i}\pi} P^{\{-1\}}_{\boldsymbol{\epsilon}}(\xi)(x;\xi)\,f(\xi) \\ & \quad + \oint_{\mathsf{A}} \frac{\mathrm{d}\xi}{2\mathrm{i}\pi}\,\frac{L(\xi)(\mathcal{V}_1^{\{0\}})'(\xi) - L(x)(\mathcal{V}_1^{\{0\}})'(x)}{\xi - x}\,f(\xi) \\ & \quad + \overline{\oint_{\mathsf{A}} \frac{\mathrm{d}\xi}{2\mathrm{i}\pi}\,\frac{L(\xi)(\mathcal{V}_2^{\{0\}})'(\xi) - L(x)(\mathcal{V}_2^{\{0\}})'(x)}{\xi - \overline{x}}\,f(\xi)}. \end{align*} $$
$$ \begin{align*} \mathcal{Q}[f](x) & = - \oint_{\mathsf{A}} \frac{\mathrm{d}\xi}{2\mathrm{i}\pi} P^{\{-1\}}_{\boldsymbol{\epsilon}}(\xi)(x;\xi)\,f(\xi) \\ & \quad + \oint_{\mathsf{A}} \frac{\mathrm{d}\xi}{2\mathrm{i}\pi}\,\frac{L(\xi)(\mathcal{V}_1^{\{0\}})'(\xi) - L(x)(\mathcal{V}_1^{\{0\}})'(x)}{\xi - x}\,f(\xi) \\ & \quad + \overline{\oint_{\mathsf{A}} \frac{\mathrm{d}\xi}{2\mathrm{i}\pi}\,\frac{L(\xi)(\mathcal{V}_2^{\{0\}})'(\xi) - L(x)(\mathcal{V}_2^{\{0\}})'(x)}{\xi - \overline{x}}\,f(\xi)}. \end{align*} $$
It is still a holomorphic function of x in a neighbourhood of
![]() $\mathsf {A}$
; thus, it disappears in the computation leading to Equation (5.13) for the inverse of
$\mathsf {A}$
; thus, it disappears in the computation leading to Equation (5.13) for the inverse of
![]() $\mathcal {K}$
, which still holds. In § 5.2.4, the expression (5.27) for the operator
$\mathcal {K}$
, which still holds. In § 5.2.4, the expression (5.27) for the operator
![]() $\Delta \mathcal {K}$
used in Equation (5.30) should be replaced by
$\Delta \mathcal {K}$
used in Equation (5.30) should be replaced by
 $$ \begin{align*} \Delta\mathcal{K}[f](x) & = 2\Delta_{-1}W_{1;\boldsymbol{\epsilon}}(x)\,f(x) + \frac{1}{N}\Big(1 - \frac{2}{\beta}\Big)\mathcal{L}_1[f](x) \\ & \quad - \mathcal{N}_{(\Delta_0 \mathcal{V}_1)',\Delta_{-1} P_{\boldsymbol{\epsilon}}(x;\bullet)}[f](x) - \overline{\mathcal{N}_{(\Delta_0 \mathcal{V}_2)',0}[f](\overline{x})}, \end{align*} $$
$$ \begin{align*} \Delta\mathcal{K}[f](x) & = 2\Delta_{-1}W_{1;\boldsymbol{\epsilon}}(x)\,f(x) + \frac{1}{N}\Big(1 - \frac{2}{\beta}\Big)\mathcal{L}_1[f](x) \\ & \quad - \mathcal{N}_{(\Delta_0 \mathcal{V}_1)',\Delta_{-1} P_{\boldsymbol{\epsilon}}(x;\bullet)}[f](x) - \overline{\mathcal{N}_{(\Delta_0 \mathcal{V}_2)',0}[f](\overline{x})}, \end{align*} $$
and the bound of the form (5.28) still holds and involves the constants
![]() $v_{1}^{{\{1}\}}$
and
$v_{1}^{{\{1}\}}$
and
![]() $v_{2}^{\{1\}}$
introduced in Equation (6.2).
$v_{2}^{\{1\}}$
introduced in Equation (6.2).
![]() $\Delta \mathcal {J}$
is defined and bounded similarly. In § 5.3.1–5.4, all occurrences of
$\Delta \mathcal {J}$
is defined and bounded similarly. In § 5.3.1–5.4, all occurrences of
![]() $\mathcal {N}_{V',0}[f](x)$
should be replaced by
$\mathcal {N}_{V',0}[f](x)$
should be replaced by
![]() $\mathcal {N}_{(\mathcal {V}_1)',0}[f](x) + \overline {\mathcal {N}_{(\mathcal {V}_2)',0}[f](\overline {x})}$
(and similarly for
$\mathcal {N}_{(\mathcal {V}_1)',0}[f](x) + \overline {\mathcal {N}_{(\mathcal {V}_2)',0}[f](\overline {x})}$
(and similarly for
![]() $\mathcal {N}_{(\Delta _{k} V)',0}$
or
$\mathcal {N}_{(\Delta _{k} V)',0}$
or
![]() $\mathcal {N}_{(V^{\{k\}})',0}$
). The key remark is that the terms where
$\mathcal {N}_{(V^{\{k\}})',0}$
). The key remark is that the terms where
![]() $\overline {\mathcal {V}_2}$
appear involve complex conjugates of contour integrals of the type
$\overline {\mathcal {V}_2}$
appear involve complex conjugates of contour integrals of the type
![]() $f(\xi )\,W_{n;\boldsymbol {\epsilon }}^{\{k\}}(\xi ,x_I)$
or
$f(\xi )\,W_{n;\boldsymbol {\epsilon }}^{\{k\}}(\xi ,x_I)$
or
![]() $f(\xi )\,\Delta _k W_{n;\boldsymbol {\epsilon }}(\xi ,x_I)$
where f is some holomorphic function in a neighbourhood of
$f(\xi )\,\Delta _k W_{n;\boldsymbol {\epsilon }}(\xi ,x_I)$
where f is some holomorphic function in a neighbourhood of
![]() $\mathsf {A}$
. Their norm can be controlled in terms of the norms of
$\mathsf {A}$
. Their norm can be controlled in terms of the norms of
![]() $W_{n;\boldsymbol {\epsilon }}^{\{k\}}$
or
$W_{n;\boldsymbol {\epsilon }}^{\{k\}}$
or
![]() $\Delta _k W_{n;\boldsymbol {\epsilon }}$
on contours, as were the terms involving
$\Delta _k W_{n;\boldsymbol {\epsilon }}$
on contours, as were the terms involving
![]() $\mathcal {V}_1$
, so the inductive control of errors in the large N expansion of correlators for the fixed filling fractions model is still valid, leading to the first part of Theorem 1.3 and to the central limit theorem (Proposition 5.7) for harmonic potentials in a neighbourhood of
$\mathcal {V}_1$
, so the inductive control of errors in the large N expansion of correlators for the fixed filling fractions model is still valid, leading to the first part of Theorem 1.3 and to the central limit theorem (Proposition 5.7) for harmonic potentials in a neighbourhood of
![]() $\mathsf {A}$
, which are still real-valued on
$\mathsf {A}$
, which are still real-valued on
![]() $\mathsf {A}$
.
$\mathsf {A}$
.
6.2. Complex perturbations of the potential
Proposition 6.1. The central limit theorem (5.52) holds for
![]() $\varphi \,:\,\mathsf {A} \rightarrow \mathbb {C}$
, which can be decomposed as
$\varphi \,:\,\mathsf {A} \rightarrow \mathbb {C}$
, which can be decomposed as
![]() $\varphi = \varphi _1 + \overline {\varphi _2}$
, where
$\varphi = \varphi _1 + \overline {\varphi _2}$
, where
![]() $\varphi _1,\varphi _2$
are holomorphic functions in a neighbourhood of
$\varphi _1,\varphi _2$
are holomorphic functions in a neighbourhood of
![]() $\mathsf {A}$
.
$\mathsf {A}$
.
Proof. We present the proof for
![]() $\varphi = t\,f$
, where
$\varphi = t\,f$
, where
![]() $t \in \mathbb {C}$
and
$t \in \mathbb {C}$
and
![]() $f\,:\,\mathsf {A} \rightarrow \mathbb {R}$
extends to a holomorphic function in a neighbourhood of
$f\,:\,\mathsf {A} \rightarrow \mathbb {R}$
extends to a holomorphic function in a neighbourhood of
![]() $\mathsf {A}$
. Indeed, the case of
$\mathsf {A}$
. Indeed, the case of
![]() $f\,:\,\mathsf {A} \rightarrow \mathbb {R}$
, which can be decomposed as
$f\,:\,\mathsf {A} \rightarrow \mathbb {R}$
, which can be decomposed as
![]() $f = f_1 + \overline {f_2}$
with
$f = f_1 + \overline {f_2}$
with
![]() $f_1,f_2$
extending to holomorphic functions in a neighbourhood of
$f_1,f_2$
extending to holomorphic functions in a neighbourhood of
![]() $\mathsf {A}$
, can be treated similarly with the modifications pointed out in § 6.1. Then, if
$\mathsf {A}$
, can be treated similarly with the modifications pointed out in § 6.1. Then, if
![]() $\varphi \,:\,\mathsf {A} \rightarrow \mathbb {C}$
can be decomposed as
$\varphi \,:\,\mathsf {A} \rightarrow \mathbb {C}$
can be decomposed as
![]() $\varphi = \varphi _1 + \overline {\varphi _2}$
with
$\varphi = \varphi _1 + \overline {\varphi _2}$
with
![]() $\varphi _1,\varphi _2$
holomorphic, we may decompose further
$\varphi _1,\varphi _2$
holomorphic, we may decompose further
![]() $\varphi _j = \varphi _j^{R} + \mathrm{i}\varphi _j^{I}$
and then write
$\varphi _j = \varphi _j^{R} + \mathrm{i}\varphi _j^{I}$
and then write
![]() $\tilde {V} = V - \frac {2}{\beta N}(\varphi _1^{R} + \varphi _2^{R})$
and
$\tilde {V} = V - \frac {2}{\beta N}(\varphi _1^{R} + \varphi _2^{R})$
and
![]() $f = (\varphi _1^{I} - \varphi _2^{I})$
, and
$f = (\varphi _1^{I} - \varphi _2^{I})$
, and
 $$ \begin{align*}\mu_{N,\beta;\boldsymbol{\epsilon}}^{V;\mathsf{A}}\Big[\exp\Big(\sum_{i = 1}^N \varphi(\lambda_i)\Big)\Big] = \mu_{N,\beta;\boldsymbol{\epsilon}}^{V;\mathsf{A}}\Big[\exp\Big(\sum_{i = 1}^N (\varphi_1^{R} + \varphi_2^{R})(\lambda_i)\Big)\Big]\,\mu_{N,\beta;\boldsymbol{\epsilon}}^{\tilde{V};\mathsf{A}}\Big[\exp\Big(\sum_{i = 1}^N \mathrm{i}f(\lambda_i)\Big)\Big]. \end{align*} $$
$$ \begin{align*}\mu_{N,\beta;\boldsymbol{\epsilon}}^{V;\mathsf{A}}\Big[\exp\Big(\sum_{i = 1}^N \varphi(\lambda_i)\Big)\Big] = \mu_{N,\beta;\boldsymbol{\epsilon}}^{V;\mathsf{A}}\Big[\exp\Big(\sum_{i = 1}^N (\varphi_1^{R} + \varphi_2^{R})(\lambda_i)\Big)\Big]\,\mu_{N,\beta;\boldsymbol{\epsilon}}^{\tilde{V};\mathsf{A}}\Big[\exp\Big(\sum_{i = 1}^N \mathrm{i}f(\lambda_i)\Big)\Big]. \end{align*} $$
The first factor can be treated with the initial central limit theorem (Proposition 5.7), while an equivalent of the second factor for large N will be deduced from the following proof applied to the potential
![]() $\tilde {V}$
.
$\tilde {V}$
.
This proof is inspired from the one of [Reference ShcherbinaShc12, Lemma 1]. From Theorem 1.3 applied to V up to
![]() $o(1)$
, we introduce
$o(1)$
, we introduce
![]() $W_{n;\boldsymbol {\epsilon }}^{\{k\}}$
for
$W_{n;\boldsymbol {\epsilon }}^{\{k\}}$
for
![]() $(n,k) = (1,-1),(2,0),(1,0)$
(see (5.38)–(5.36)). If
$(n,k) = (1,-1),(2,0),(1,0)$
(see (5.38)–(5.36)). If
![]() $t \in \mathbb {R}$
, the central limit theorem (Proposition 5.7) applied to
$t \in \mathbb {R}$
, the central limit theorem (Proposition 5.7) applied to
![]() $\varphi = t\,f$
implies
$\varphi = t\,f$
implies
 $$ \begin{align} \mu_{N,\beta;\boldsymbol{\epsilon}}^{V;\mathsf{A}}\Big[\Big(\sum_{i = 1}^N t\,f(\lambda_i)\Big)\Big] = G_N(t)(1 + R_N(t)),\qquad G_N(t) = \exp\Big(Nt\,\Lambda_{\beta;\boldsymbol{\epsilon}}[f] + t\,M_{\beta;\boldsymbol{\epsilon}}[f] + \frac{t^2}{2}\,Q_{\beta;\boldsymbol{\epsilon}}[f,f]\Big), \end{align} $$
$$ \begin{align} \mu_{N,\beta;\boldsymbol{\epsilon}}^{V;\mathsf{A}}\Big[\Big(\sum_{i = 1}^N t\,f(\lambda_i)\Big)\Big] = G_N(t)(1 + R_N(t)),\qquad G_N(t) = \exp\Big(Nt\,\Lambda_{\beta;\boldsymbol{\epsilon}}[f] + t\,M_{\beta;\boldsymbol{\epsilon}}[f] + \frac{t^2}{2}\,Q_{\beta;\boldsymbol{\epsilon}}[f,f]\Big), \end{align} $$
where
![]() $\sup _{t \in [-T_0,T_0]} |R_N(t)| \leq C(T_0)\,\eta _N$
and
$\sup _{t \in [-T_0,T_0]} |R_N(t)| \leq C(T_0)\,\eta _N$
and
![]() $\lim _{N \rightarrow \infty } \eta _N = 0$
. Let
$\lim _{N \rightarrow \infty } \eta _N = 0$
. Let
![]() $T_0> 0$
, and introduce the function
$T_0> 0$
, and introduce the function
For any fixed N, it is an entire function of t, and by construction,
Besides, for any
![]() $t \in \mathbb {C}$
, we have
$t \in \mathbb {C}$
, we have
 $$ \begin{align*}\Big|\mu_{N,\beta;\boldsymbol{\epsilon}}^{V;\mathsf{A}}\Big[\exp\Big(\sum_{i = 1}^N t\,f(\lambda_i)\Big)\Big]\Big| \leq \mu_{N,\beta;\boldsymbol{\epsilon}}^{V;\mathsf{A}}\Big[\exp\Big(\sum_{i = 1}^N (\mathrm{Re}\,t)\,f(\lambda_i)\Big)\Big]. \end{align*} $$
$$ \begin{align*}\Big|\mu_{N,\beta;\boldsymbol{\epsilon}}^{V;\mathsf{A}}\Big[\exp\Big(\sum_{i = 1}^N t\,f(\lambda_i)\Big)\Big]\Big| \leq \mu_{N,\beta;\boldsymbol{\epsilon}}^{V;\mathsf{A}}\Big[\exp\Big(\sum_{i = 1}^N (\mathrm{Re}\,t)\,f(\lambda_i)\Big)\Big]. \end{align*} $$
Using that f is real-valued on
![]() $\mathsf {A}$
, we deduce that
$\mathsf {A}$
, we deduce that
 $$ \begin{align} \nonumber \sup_{|t| \leq T_0}\,|\tilde{R}_N(t)| & \leq \frac{1}{C(T_0)\eta_N}\Big(1 + \sup_{|t|\le T_0}\frac{G_N(\mathrm{Re}\,t)}{|G_N(t)|}\Big) \\ \nonumber & \leq \frac{1}{C(T_0)\eta_N}\sup_{|t|\le T_0} \exp\Big(\frac{(\mathrm{Im}\,t)^2}{2}\,Q_{\beta;\boldsymbol{\epsilon}}[f,f]\Big) \\ & \leq \frac{1}{C'(T_0)\eta_N} \end{align} $$
$$ \begin{align} \nonumber \sup_{|t| \leq T_0}\,|\tilde{R}_N(t)| & \leq \frac{1}{C(T_0)\eta_N}\Big(1 + \sup_{|t|\le T_0}\frac{G_N(\mathrm{Re}\,t)}{|G_N(t)|}\Big) \\ \nonumber & \leq \frac{1}{C(T_0)\eta_N}\sup_{|t|\le T_0} \exp\Big(\frac{(\mathrm{Im}\,t)^2}{2}\,Q_{\beta;\boldsymbol{\epsilon}}[f,f]\Big) \\ & \leq \frac{1}{C'(T_0)\eta_N} \end{align} $$
for some constant
![]() $C'(T_0)$
. By the two-constants lemma [Reference Nevanlinna and NevanlinnaNN22] (see [Reference NevanlinnaN70, p41] for a more recent reference), Equations (6.6)–(6.7) imply
$C'(T_0)$
. By the two-constants lemma [Reference Nevanlinna and NevanlinnaNN22] (see [Reference NevanlinnaN70, p41] for a more recent reference), Equations (6.6)–(6.7) imply
 $$ \begin{align*}\forall T \in (0,T_0),\qquad \sup_{|t| \leq T} |\tilde{R}_N(t)| \leq (C'(T_0)\eta_N)^{-2\phi(T,T_0)/\pi},\qquad \phi(T,T_0) = \mathrm{arctan}\Big(\frac{2T/T_0}{1 - (T/T_0)^2}\Big). \end{align*} $$
$$ \begin{align*}\forall T \in (0,T_0),\qquad \sup_{|t| \leq T} |\tilde{R}_N(t)| \leq (C'(T_0)\eta_N)^{-2\phi(T,T_0)/\pi},\qquad \phi(T,T_0) = \mathrm{arctan}\Big(\frac{2T/T_0}{1 - (T/T_0)^2}\Big). \end{align*} $$
In particular, for any compact
![]() $\mathsf {K} \subset \mathbb {C}$
, we can find an open disk of radius
$\mathsf {K} \subset \mathbb {C}$
, we can find an open disk of radius
![]() $T_0$
containing
$T_0$
containing
![]() $\mathsf {K}$
and thus show (6.5) with
$\mathsf {K}$
and thus show (6.5) with
![]() $R_N(t) = o(1)$
uniformly in
$R_N(t) = o(1)$
uniformly in
![]() $\mathsf {K}$
.
$\mathsf {K}$
.
We observe from the proof that Proposition 6.1 cannot be easily extended to
![]() $|t|$
going to
$|t|$
going to
![]() $\infty $
with N. Indeed, the ratio
$\infty $
with N. Indeed, the ratio
![]() $G_N(T_N(\mathrm {Re}\,t))/|G_N(T_N t)|$
in Equation (6.7) will not be bounded when
$G_N(T_N(\mathrm {Re}\,t))/|G_N(T_N t)|$
in Equation (6.7) will not be bounded when
![]() $N \rightarrow \infty $
; hence, applying the two-constants lemma as above does not show
$N \rightarrow \infty $
; hence, applying the two-constants lemma as above does not show
![]() $R_N(t) \rightarrow 0$
.
$R_N(t) \rightarrow 0$
.
Corollary 6.2. In the model with fixed filling fractions
![]() $\boldsymbol {\epsilon }$
, assume the potential
$\boldsymbol {\epsilon }$
, assume the potential
![]() $V_0$
satisfies Hypotheses 5.1. If
$V_0$
satisfies Hypotheses 5.1. If
![]() $\varphi \,:\,\mathsf {A} \rightarrow \mathbb {C}$
can be decomposed as
$\varphi \,:\,\mathsf {A} \rightarrow \mathbb {C}$
can be decomposed as
![]() $\varphi = \varphi _1 + \overline {\varphi _2}$
with
$\varphi = \varphi _1 + \overline {\varphi _2}$
with
![]() $\varphi _1,\varphi _2$
extending to holomorphic functions in a neighbourhood of
$\varphi _1,\varphi _2$
extending to holomorphic functions in a neighbourhood of
![]() $\mathsf {A}$
, then the model with fixed filling fractions
$\mathsf {A}$
, then the model with fixed filling fractions
![]() $\boldsymbol {\epsilon }$
and potential
$\boldsymbol {\epsilon }$
and potential
![]() $V = V_0 + \varphi /N$
satisfies Hypotheses 5.1. Therefore, the result of Proposition 5.6 also holds. More generally, if there exists a sequence of holomorphic functions
$V = V_0 + \varphi /N$
satisfies Hypotheses 5.1. Therefore, the result of Proposition 5.6 also holds. More generally, if there exists a sequence of holomorphic functions
![]() $\mathcal {V}_i^{\{k\}}, k\ge 0, i=1,2$
on a neighbourhood
$\mathcal {V}_i^{\{k\}}, k\ge 0, i=1,2$
on a neighbourhood
![]() $\mathsf {U}$
of
$\mathsf {U}$
of
![]() $\mathsf {A}$
so that
$\mathsf {A}$
so that
 $$ \begin{align*}\limsup_{N\ge 1} N^{K+1} \sup_{\xi\in \mathsf{U}} \Big| \varphi(\xi)-\sum_{k=0}^K N^{-k} [\mathcal{V}_1^{\{k\}}+\overline{\mathcal{V}_1^{\{k\}}}](\xi)\Big|<\infty, \end{align*} $$
$$ \begin{align*}\limsup_{N\ge 1} N^{K+1} \sup_{\xi\in \mathsf{U}} \Big| \varphi(\xi)-\sum_{k=0}^K N^{-k} [\mathcal{V}_1^{\{k\}}+\overline{\mathcal{V}_1^{\{k\}}}](\xi)\Big|<\infty, \end{align*} $$
the result of Proposition 5.6 also holds with
![]() $V=V_0+\varphi /N$
.
$V=V_0+\varphi /N$
.
Proof. Hypothesis 5.1 constrains only the leading order of the potential (i.e., it holds for
![]() $(V_0,\boldsymbol {\epsilon })$
if and only if it holds for
$(V_0,\boldsymbol {\epsilon })$
if and only if it holds for
![]() $(V = V_0 + \varphi /N,\boldsymbol {\epsilon })$
). Proposition 6.1 implies a fortiori the existence of constants
$(V = V_0 + \varphi /N,\boldsymbol {\epsilon })$
). Proposition 6.1 implies a fortiori the existence of constants
![]() $C_+,C_-> 0$
and
$C_+,C_-> 0$
and
![]() $C=\exp \big (-\mathrm{{Re}}\:( \int _{\mathsf {A}} \varphi (x) \mathrm {d}\mu _\mathrm{{eq};\boldsymbol {\epsilon }}^{V}(x))\big )$
, such that
$C=\exp \big (-\mathrm{{Re}}\:( \int _{\mathsf {A}} \varphi (x) \mathrm {d}\mu _\mathrm{{eq};\boldsymbol {\epsilon }}^{V}(x))\big )$
, such that
 $$ \begin{align*}C_-\,C^{N} \leq \frac{ |Z_{N,\beta;\boldsymbol{\epsilon}}^{V;\mathsf{A}}|}{ |Z_{N,\beta;\boldsymbol{\epsilon}}^{V_0;\mathsf{A}}|} \leq C_+\,C^N. \end{align*} $$
$$ \begin{align*}C_-\,C^{N} \leq \frac{ |Z_{N,\beta;\boldsymbol{\epsilon}}^{V;\mathsf{A}}|}{ |Z_{N,\beta;\boldsymbol{\epsilon}}^{V_0;\mathsf{A}}|} \leq C_+\,C^N. \end{align*} $$
Using this inequality as an input, we can repeat the proof of the large deviation principles given in Section 3 to check Lemma 3.1 (i.e., the restriction to the vicinity of the support) and Corollary 3.7 (i.e., the a priori control reminded in (5.2)–(5.3)) for the potential V. Then, in the recursive analysis of the Dyson–Schwinger equation of Section 5 for the model with fixed filling fractions, the fact that the potential is complex-valued does not matter; we have established the expansion of the correlators.
This proves Theorem 1.3 in full generality.
6.3.
 $\frac {1}{N}$
expansion of n-point kernels
$\frac {1}{N}$
expansion of n-point kernels
We can apply Corollary 6.2 to study potentials of the form
 $$ \begin{align*}V_{\boldsymbol{x},{\mathbf c}}(\xi) = V - \frac{2}{\beta N}\sum_{j = 1}^n c_j \ln(x_j - \xi), \end{align*} $$
$$ \begin{align*}V_{\boldsymbol{x},{\mathbf c}}(\xi) = V - \frac{2}{\beta N}\sum_{j = 1}^n c_j \ln(x_j - \xi), \end{align*} $$
where
![]() $x_j \in \mathbb {C}\setminus \mathsf {A}$
, and thus derive the asymptotic expansion of the kernels in the complex plane (i.e., Corollaries 1.9 and 1.10).
$x_j \in \mathbb {C}\setminus \mathsf {A}$
, and thus derive the asymptotic expansion of the kernels in the complex plane (i.e., Corollaries 1.9 and 1.10).
First, let us choose a simply connected domain
![]() $\mathsf {D} \subset \mathbb {C}^*$
in which the complex logarithm is an analytic function. Choose
$\mathsf {D} \subset \mathbb {C}^*$
in which the complex logarithm is an analytic function. Choose
![]() $x_1,\ldots ,x_r$
and an extra reference point p such that all
$x_1,\ldots ,x_r$
and an extra reference point p such that all
![]() $x_j - \xi $
for
$x_j - \xi $
for
![]() $\xi $
in a complex neighbourhood
$\xi $
in a complex neighbourhood
![]() $\mathsf {A}_{\mathbb {C}}$
of
$\mathsf {A}_{\mathbb {C}}$
of
![]() $\mathsf {A}$
and
$\mathsf {A}$
and
![]() $x_j - p$
belong to
$x_j - p$
belong to
![]() $\mathsf {D}$
. Then, we can write for
$\mathsf {D}$
. Then, we can write for
![]() $\xi \in \mathsf {A}_{\mathbb {C}}$
,
$\xi \in \mathsf {A}_{\mathbb {C}}$
,
 $$ \begin{align*}\ln(x_j - \xi) - \ln(p - \xi) = \int_{p}^{x_j} \frac{\mathrm{d} z}{z - \xi}. \end{align*} $$
$$ \begin{align*}\ln(x_j - \xi) - \ln(p - \xi) = \int_{p}^{x_j} \frac{\mathrm{d} z}{z - \xi}. \end{align*} $$
Recalling the notation
![]() $\mathbb {L} = \mathrm{diag}(\lambda _1,\ldots ,\lambda _N)$
for the random matrix, we have for
$\mathbb {L} = \mathrm{diag}(\lambda _1,\ldots ,\lambda _N)$
for the random matrix, we have for
![]() $r \geq 1$
,
$r \geq 1$
,
 $$ \begin{align} \partial_{c_{j_{1}}}\cdots\partial_{c_{j_{r}}}\ln Z^{V_{\boldsymbol{x},{\mathbf c}};\mathsf{A}}_{N,\beta} &= \mu_{N,\beta}^{V_{\boldsymbol{x},{\mathbf c}};\mathsf{A}}\Big[\mathrm{Tr}\big(\ln(x_{j_1} - \mathbb{L}) - \ln(p - \mathbb{L})\big),\ldots,\mathrm{Tr}\big(\ln(x_{j_r} - \mathbb{L}) - \ln(p - \mathbb{L})\big)\Big]_c \nonumber\\&= \int_{p}^{x_{j_1}} \cdots \int_{p}^{x_{j_r}} W_{r;\boldsymbol{\epsilon}}(\xi_1,\ldots,\xi_r) \prod_{i = 1}^r \mathrm{d} \xi_i, \end{align} $$
$$ \begin{align} \partial_{c_{j_{1}}}\cdots\partial_{c_{j_{r}}}\ln Z^{V_{\boldsymbol{x},{\mathbf c}};\mathsf{A}}_{N,\beta} &= \mu_{N,\beta}^{V_{\boldsymbol{x},{\mathbf c}};\mathsf{A}}\Big[\mathrm{Tr}\big(\ln(x_{j_1} - \mathbb{L}) - \ln(p - \mathbb{L})\big),\ldots,\mathrm{Tr}\big(\ln(x_{j_r} - \mathbb{L}) - \ln(p - \mathbb{L})\big)\Big]_c \nonumber\\&= \int_{p}^{x_{j_1}} \cdots \int_{p}^{x_{j_r}} W_{r;\boldsymbol{\epsilon}}(\xi_1,\ldots,\xi_r) \prod_{i = 1}^r \mathrm{d} \xi_i, \end{align} $$
where we pick the unique relative homology class of path between p and
![]() $x_{j_r}$
in
$x_{j_r}$
in
![]() $\mathsf {D}' := \bigcap _{\xi \in \mathsf {A}_{\mathbb {C}}} (\xi + \mathsf {D})$
to perform the integration. Here, the subscript c refers to the cumulant expectation value as in (1.2). Since
$\mathsf {D}' := \bigcap _{\xi \in \mathsf {A}_{\mathbb {C}}} (\xi + \mathsf {D})$
to perform the integration. Here, the subscript c refers to the cumulant expectation value as in (1.2). Since
![]() $\ln (p - \mathbb {L})$
is deterministic up a
$\ln (p - \mathbb {L})$
is deterministic up a
![]() $o(1)$
when
$o(1)$
when
![]() $p \rightarrow \infty $
, we can take the limit
$p \rightarrow \infty $
, we can take the limit
![]() $p \rightarrow \infty $
in (6.8) for
$p \rightarrow \infty $
in (6.8) for
![]() $r \geq 2$
and find
$r \geq 2$
and find
 $$ \begin{align} \mathbb{E}_c\big[\mathrm{Tr}\,\ln(x_{j_1} - \mathbb{L}),\ldots,\mathrm{Tr}\,\ln(x_{j_r} - \mathbb{L})\big] = \int_{\infty}^{x_{j_1}} \cdots \int_{\infty}^{x_{j_r}} W_{r;\boldsymbol{\epsilon}}(\xi_1,\ldots,\xi_r) \prod_{i = 1}^r \mathrm{d} \xi_i. \end{align} $$
$$ \begin{align} \mathbb{E}_c\big[\mathrm{Tr}\,\ln(x_{j_1} - \mathbb{L}),\ldots,\mathrm{Tr}\,\ln(x_{j_r} - \mathbb{L})\big] = \int_{\infty}^{x_{j_1}} \cdots \int_{\infty}^{x_{j_r}} W_{r;\boldsymbol{\epsilon}}(\xi_1,\ldots,\xi_r) \prod_{i = 1}^r \mathrm{d} \xi_i. \end{align} $$
Since
![]() $W_{r;\boldsymbol {\epsilon }}(\xi _1,\ldots ,\xi _r)$
for
$W_{r;\boldsymbol {\epsilon }}(\xi _1,\ldots ,\xi _r)$
for
![]() $r \geq 2$
behaves as
$r \geq 2$
behaves as
![]() $O(1/\xi _i^2)$
when
$O(1/\xi _i^2)$
when
![]() $\xi _i \rightarrow \infty $
and has vanishing periods around
$\xi _i \rightarrow \infty $
and has vanishing periods around
![]() $\mathsf {A}_h$
for any h, the left-hand side of (6.9) is a well-defined single-valued analytic function of
$\mathsf {A}_h$
for any h, the left-hand side of (6.9) is a well-defined single-valued analytic function of
![]() $x_1,\ldots ,x_r \in \mathbb {C} \setminus \mathsf {A}$
which does not depend on the choice of path from
$x_1,\ldots ,x_r \in \mathbb {C} \setminus \mathsf {A}$
which does not depend on the choice of path from
![]() $\infty $
to
$\infty $
to
![]() $x_{j_i}$
in this domain. For
$x_{j_i}$
in this domain. For
![]() $r = 1$
, the situation is different. We have indeed
$r = 1$
, the situation is different. We have indeed
By taking
![]() $|p|$
large enough, we may assume that
$|p|$
large enough, we may assume that
![]() $p \in \mathsf {D}$
, and we can always choose
$p \in \mathsf {D}$
, and we can always choose
![]() $\mathsf {D}$
in conjunction with
$\mathsf {D}$
in conjunction with
![]() $x_1,\ldots ,x_r$
such that
$x_1,\ldots ,x_r$
such that
![]() $x_1,\ldots ,x_r \in \mathsf {D}$
. Then we can write
$x_1,\ldots ,x_r \in \mathsf {D}$
. Then we can write
 $$ \begin{align*}\mathbb{E}\big[\mathrm{Tr}\,\ln(x_j - \mathbb{L})\big] = \mathbb{E}\big[\mathrm{Tr}\,\ln(p - \mathbb{L})\big] + N\big(\ln x_{j} - \ln p\big) + \int_{p}^{x_j} \Big(W_{1;\boldsymbol{\epsilon}}(\xi) - \frac{N}{\xi}\Big)\mathrm{d} \xi, \end{align*} $$
$$ \begin{align*}\mathbb{E}\big[\mathrm{Tr}\,\ln(x_j - \mathbb{L})\big] = \mathbb{E}\big[\mathrm{Tr}\,\ln(p - \mathbb{L})\big] + N\big(\ln x_{j} - \ln p\big) + \int_{p}^{x_j} \Big(W_{1;\boldsymbol{\epsilon}}(\xi) - \frac{N}{\xi}\Big)\mathrm{d} \xi, \end{align*} $$
where the path from p to
![]() $x_j$
remains in
$x_j$
remains in
![]() $\mathsf {D}'$
. Choosing a continuous path
$\mathsf {D}'$
. Choosing a continuous path
![]() $\tilde {\ell } \subseteq \mathsf {D}$
going to
$\tilde {\ell } \subseteq \mathsf {D}$
going to
![]() $\infty $
, the limit
$\infty $
, the limit
exists and is independent of
![]() $\xi \in \mathsf {A}_{\mathbb {C}}$
but depends on the choice of path
$\xi \in \mathsf {A}_{\mathbb {C}}$
but depends on the choice of path
![]() $\tilde {\ell }$
and domain
$\tilde {\ell }$
and domain
![]() $\mathsf {D}$
. Therefore,
$\mathsf {D}$
. Therefore,
We stress that the ambiguity
![]() $\chi _j$
only appears for
$\chi _j$
only appears for
![]() $r = 1$
and with a prefactor N. It depends on various choices pertaining to the determination of the logarithm, also restricting the allowed domain of
$r = 1$
and with a prefactor N. It depends on various choices pertaining to the determination of the logarithm, also restricting the allowed domain of
![]() $x_j$
, but in such a way that
$x_j$
, but in such a way that
![]() $(\mathbb {C} \setminus \mathsf {A})^r$
can be covered by finitely many opens in which various domains
$(\mathbb {C} \setminus \mathsf {A})^r$
can be covered by finitely many opens in which various domains
![]() $\mathsf {D}$
and determinations of the logarithm can be chosen to fulfil our needs.
$\mathsf {D}$
and determinations of the logarithm can be chosen to fulfil our needs.
Let us now introduce the random variable
![]() $H_{\boldsymbol {x},\mathbf {c}} = \sum _{j = 1}^r c_j \mathrm{Tr}\,\ln (x_j - \mathbb {L})$
. We know from Proposition 6.1 that
$H_{\boldsymbol {x},\mathbf {c}} = \sum _{j = 1}^r c_j \mathrm{Tr}\,\ln (x_j - \mathbb {L})$
. We know from Proposition 6.1 that
![]() $\ln \mu _{N,\beta ;\boldsymbol {\epsilon }}^{V;\mathsf {A}}\big (e^{tH_{\boldsymbol {x},\mathbf {c}}}\big )$
is an entire function. Therefore, its Taylor series is convergent for any
$\ln \mu _{N,\beta ;\boldsymbol {\epsilon }}^{V;\mathsf {A}}\big (e^{tH_{\boldsymbol {x},\mathbf {c}}}\big )$
is an entire function. Therefore, its Taylor series is convergent for any
![]() $t \in \mathbb {C}$
, and we have at
$t \in \mathbb {C}$
, and we have at
![]() $t = 1$
,
$t = 1$
,
 $$ \begin{align*}\mathsf{K}_{r,{\mathbf c};\boldsymbol{\epsilon}}(\boldsymbol{x}) = \bigg[\prod_{j = 1}^{r} (x_j - p)^{Nc_j}\bigg]\exp\Big(\ln \mu_{N,\beta;\boldsymbol{\epsilon}}^{V;\mathsf{A}}\big(e^{H_{\boldsymbol{x},\mathbf{c}}}\big)\Big). \end{align*} $$
$$ \begin{align*}\mathsf{K}_{r,{\mathbf c};\boldsymbol{\epsilon}}(\boldsymbol{x}) = \bigg[\prod_{j = 1}^{r} (x_j - p)^{Nc_j}\bigg]\exp\Big(\ln \mu_{N,\beta;\boldsymbol{\epsilon}}^{V;\mathsf{A}}\big(e^{H_{\boldsymbol{x},\mathbf{c}}}\big)\Big). \end{align*} $$
The right-hand side can be computed via the cumulants and thus (6.9)–(6.10). We arrive to
 $$ \begin{align} \mathsf{K}_{r,{\mathbf c};\boldsymbol{\epsilon}}(\boldsymbol{x}) = \exp\bigg(\sum_{j = 1}^{r} Nc_j\big(\ln x_j + 2\mathrm{i}\pi \chi_j\big) + \sum_{n \geq 1} \frac{1}{n!} \mathcal{L}_{\boldsymbol{x},\mathbf{c}}^{\otimes n}[W_{n;\boldsymbol{\epsilon}}]\bigg), \end{align} $$
$$ \begin{align} \mathsf{K}_{r,{\mathbf c};\boldsymbol{\epsilon}}(\boldsymbol{x}) = \exp\bigg(\sum_{j = 1}^{r} Nc_j\big(\ln x_j + 2\mathrm{i}\pi \chi_j\big) + \sum_{n \geq 1} \frac{1}{n!} \mathcal{L}_{\boldsymbol{x},\mathbf{c}}^{\otimes n}[W_{n;\boldsymbol{\epsilon}}]\bigg), \end{align} $$
where
 $$ \begin{align} \mathcal{L}_{\boldsymbol{x},\mathbf{c}}[f](x) = \sum_{j = 1}^r c_j \int_{\infty}^{x_j} \check{f}(\xi)\mathrm{d} \xi,\qquad \check{f}(x) = f(x) + \frac{1}{x} \mathop{\,\mathrm Res\,}_{x = \infty} f(\xi)\mathrm{d} \xi. \end{align} $$
$$ \begin{align} \mathcal{L}_{\boldsymbol{x},\mathbf{c}}[f](x) = \sum_{j = 1}^r c_j \int_{\infty}^{x_j} \check{f}(\xi)\mathrm{d} \xi,\qquad \check{f}(x) = f(x) + \frac{1}{x} \mathop{\,\mathrm Res\,}_{x = \infty} f(\xi)\mathrm{d} \xi. \end{align} $$
The difference between
![]() $\check {f}$
and f in (6.12) is only relevant for the
$\check {f}$
and f in (6.12) is only relevant for the
![]() $r = 1$
term in (6.11), and
$r = 1$
term in (6.11), and
![]() $\check {f}(x) = O(1/x^2)$
as
$\check {f}(x) = O(1/x^2)$
as
![]() $x \rightarrow \infty $
, and so is integrable near
$x \rightarrow \infty $
, and so is integrable near
![]() $\infty $
. For this
$\infty $
. For this
![]() $r = 1$
term, the integral does depend on choices of paths from
$r = 1$
term, the integral does depend on choices of paths from
![]() $\infty $
to
$\infty $
to
![]() $x_j$
because the
$x_j$
because the
![]() $W_{1;\boldsymbol {\epsilon }}$
has nonvanishing
$W_{1;\boldsymbol {\epsilon }}$
has nonvanishing
![]() $\mathsf {A}_h$
-periods, but these ambiguities are the same as the ambiguities in the definition of the kernels before taking any asymptotics (see § 1.1.3); they only appear in the leading order term of the asymptotics. As we have explained above, they can be resolved if we work with a fixed
$\mathsf {A}_h$
-periods, but these ambiguities are the same as the ambiguities in the definition of the kernels before taking any asymptotics (see § 1.1.3); they only appear in the leading order term of the asymptotics. As we have explained above, they can be resolved if we work with a fixed
![]() $x_1,\ldots ,X_r$
and fixed domain
$x_1,\ldots ,X_r$
and fixed domain
![]() $\mathsf {D}$
of definition of the logarithm.
$\mathsf {D}$
of definition of the logarithm.
As a consequence of Proposition 5.6,
![]() $W_{n;\boldsymbol {\epsilon }} = O(N^{2 - n})$
and has a
$W_{n;\boldsymbol {\epsilon }} = O(N^{2 - n})$
and has a
![]() $\frac {1}{N}$
expansion. Therefore, only a finite number of terms contribute to each order in the n-point kernels, and we find
$\frac {1}{N}$
expansion. Therefore, only a finite number of terms contribute to each order in the n-point kernels, and we find
Proposition 6.3. Assume Hypothesis 1.2. Then, for any given
![]() $K \geq -1$
and
$K \geq -1$
and
![]() $\delta> 0$
, we have a uniform asymptotic expansion for
$\delta> 0$
, we have a uniform asymptotic expansion for
![]() $\min _{1 \leq j \leq r} d(x_j,\mathsf {A}) \geq \delta $
:
$\min _{1 \leq j \leq r} d(x_j,\mathsf {A}) \geq \delta $
:
 $$ \begin{align*}\mathsf{K}_{r,{\mathbf c};\boldsymbol{\epsilon}}(\boldsymbol{x}) = \exp\left\{\sum_{j = 1}^{r} Nc_j(\ln x_j + 2\mathrm{i}\pi \chi_j\big) + \sum_{k = -1}^{K} N^{-k} \Big(\sum_{n = 1}^{k + 2} \frac{1}{n!} \mathcal{L}_{{\boldsymbol x},{\boldsymbol c}}^{\otimes n}[W_{n;\boldsymbol{\epsilon}}^{\{k\}}]\Big) + O(N^{-(K + 1)})\Big)\right\}\,. \end{align*} $$
$$ \begin{align*}\mathsf{K}_{r,{\mathbf c};\boldsymbol{\epsilon}}(\boldsymbol{x}) = \exp\left\{\sum_{j = 1}^{r} Nc_j(\ln x_j + 2\mathrm{i}\pi \chi_j\big) + \sum_{k = -1}^{K} N^{-k} \Big(\sum_{n = 1}^{k + 2} \frac{1}{n!} \mathcal{L}_{{\boldsymbol x},{\boldsymbol c}}^{\otimes n}[W_{n;\boldsymbol{\epsilon}}^{\{k\}}]\Big) + O(N^{-(K + 1)})\Big)\right\}\,. \end{align*} $$
7. Fixed filling fractions:
 $\frac {1}{N}$
expansion of the partition function
$\frac {1}{N}$
expansion of the partition function
In this section, we continue to work within the fixed filling fractions model:
![]() $\boldsymbol {N} = (N_1,\ldots ,N_{g})$
is a sequence of integer vectors, we set
$\boldsymbol {N} = (N_1,\ldots ,N_{g})$
is a sequence of integer vectors, we set
![]() $\boldsymbol {\epsilon } = \boldsymbol {N}/N$
(which may depend implicitly on N), and we assume Hypothesis 5.1.
$\boldsymbol {\epsilon } = \boldsymbol {N}/N$
(which may depend implicitly on N), and we assume Hypothesis 5.1.
7.1. First step: one-cut interpolation
7.1.1. The result
We remind that in the one-cut case
![]() $g = 1$
, the main Theorem 1.5 was proved in [Reference Borot and GuionnetBG11] and ensures that the partition function has an asymptotic expansion of the form, for any
$g = 1$
, the main Theorem 1.5 was proved in [Reference Borot and GuionnetBG11] and ensures that the partition function has an asymptotic expansion of the form, for any
![]() $K \geq 0$
,
$K \geq 0$
,
 $$ \begin{align} Z_{N,\beta}^{V} = N^{\frac{\beta}{2} N + \varkappa} \exp\Big(\sum_{k = -2}^{K} N^{-k}\,F^{\{k\};V}_{\beta} + O(N^{-(K + 1)}) \Big). \end{align} $$
$$ \begin{align} Z_{N,\beta}^{V} = N^{\frac{\beta}{2} N + \varkappa} \exp\Big(\sum_{k = -2}^{K} N^{-k}\,F^{\{k\};V}_{\beta} + O(N^{-(K + 1)}) \Big). \end{align} $$
The leading term is of order
![]() $N^2$
and given by potential theory
$N^2$
and given by potential theory
 $$ \begin{align} F^{\{-2\};V}_{\beta} = \frac{\beta}{2}\bigg(\iint_{\mathsf{A}^2} \mathrm{d}\mu_{\mathrm{eq}}^{V}(x)\mathrm{d}\mu_{\mathrm{eq}}^{V}(y)\,\ln|x - y| - \int_{\mathsf{A}} V^{\{0\}}(x)\mathrm{d}\mu_{\mathrm{eq}}^{V}(x)\bigg). \end{align} $$
$$ \begin{align} F^{\{-2\};V}_{\beta} = \frac{\beta}{2}\bigg(\iint_{\mathsf{A}^2} \mathrm{d}\mu_{\mathrm{eq}}^{V}(x)\mathrm{d}\mu_{\mathrm{eq}}^{V}(y)\,\ln|x - y| - \int_{\mathsf{A}} V^{\{0\}}(x)\mathrm{d}\mu_{\mathrm{eq}}^{V}(x)\bigg). \end{align} $$
It is well known – and we reprove below with Lemma 7.3 and Equation (7.21) – that the terms of order N are related to the entropy of the equilibrium measure.
Proposition 7.1. We have
where
In [Reference Borot and GuionnetBG11], the potential was assumed independent of N, but it is straightforward to include a V having a
![]() $\frac {1}{N}$
expansion, and this results in
$\frac {1}{N}$
expansion, and this results in
![]() $F^{\{-1\};V}_{\beta }$
in the extra term involving
$F^{\{-1\};V}_{\beta }$
in the extra term involving
![]() $V^{\{1\}}$
. The exponent
$V^{\{1\}}$
. The exponent
![]() $\varkappa $
describing the
$\varkappa $
describing the
![]() $O(\ln N)$
correction is identified in [Reference Borot and GuionnetBG11] as
$O(\ln N)$
correction is identified in [Reference Borot and GuionnetBG11] as
 $$ \begin{align} \varkappa = \left\{\begin{array}{lll} \frac{3 + \beta/2 + 2/\beta}{12} & & \mathrm{if}\,\,\mathrm{both}\,\,\mathrm{edges}\,\,\mathrm{are}\,\,\mathrm{soft}, \\ \frac{\beta/2 + 2/\beta}{6} & & \mathrm{if}\,\,\mathrm{one}\,\,\mathrm{edge}\,\,\mathrm{is}\,\,\mathrm{soft}\,\,\mathrm{and}\,\,\mathrm{the}\,\,\mathrm{other}\,\,\mathrm{is}\,\,\mathrm{hard}, \\ \frac{-1 + \beta/2 + 2/\beta}{4} && \mathrm{if}\,\,\mathrm{both}\,\,\mathrm{edges}\,\,\mathrm{are}\,\,\mathrm{hard}. \end{array} \right. \end{align} $$
$$ \begin{align} \varkappa = \left\{\begin{array}{lll} \frac{3 + \beta/2 + 2/\beta}{12} & & \mathrm{if}\,\,\mathrm{both}\,\,\mathrm{edges}\,\,\mathrm{are}\,\,\mathrm{soft}, \\ \frac{\beta/2 + 2/\beta}{6} & & \mathrm{if}\,\,\mathrm{one}\,\,\mathrm{edge}\,\,\mathrm{is}\,\,\mathrm{soft}\,\,\mathrm{and}\,\,\mathrm{the}\,\,\mathrm{other}\,\,\mathrm{is}\,\,\mathrm{hard}, \\ \frac{-1 + \beta/2 + 2/\beta}{4} && \mathrm{if}\,\,\mathrm{both}\,\,\mathrm{edges}\,\,\mathrm{are}\,\,\mathrm{hard}. \end{array} \right. \end{align} $$
This exponent can be compactly rewritten:
7.1.2. Strategy to prove this result and computation of coefficients
As we now review, this theorem was proved by interpolating, for fixed location of the cut
![]() $\gamma = [\gamma _-,\gamma _+]$
and nature of the edges, the partition function
$\gamma = [\gamma _-,\gamma _+]$
and nature of the edges, the partition function
![]() $Z^{V;\mathsf {A}}_{N,\beta }$
with a partition function
$Z^{V;\mathsf {A}}_{N,\beta }$
with a partition function
![]() $Z_{N,\beta }^{\mathrm{ref}}$
, which is exactly computable by Selberg integrals. We denote
$Z_{N,\beta }^{\mathrm{ref}}$
, which is exactly computable by Selberg integrals. We denote
![]() $V_{\mathrm{ref}}$
the potential of these reference models. The choice of reference models will be made explicit in Section 7.2 and depends only on the position of edges
$V_{\mathrm{ref}}$
the potential of these reference models. The choice of reference models will be made explicit in Section 7.2 and depends only on the position of edges
![]() $\gamma _{\pm }$
and of their nature (soft or hard). For the moment, it is enough to mention that its associated equilibrium measure
$\gamma _{\pm }$
and of their nature (soft or hard). For the moment, it is enough to mention that its associated equilibrium measure
![]() $\mu _{\mathrm{eq}}^{\mathrm{ref}}$
has same support
$\mu _{\mathrm{eq}}^{\mathrm{ref}}$
has same support
![]() $[\gamma _-,\gamma _+]$
as
$[\gamma _-,\gamma _+]$
as
![]() $\mu _{\mathrm{eq}}^{V}$
, and
$\mu _{\mathrm{eq}}^{V}$
, and
![]() $\gamma _{+}$
(resp.
$\gamma _{+}$
(resp.
![]() $\gamma _{-}$
) have same nature – hard or soft – in
$\gamma _{-}$
) have same nature – hard or soft – in
![]() $\mu _{\mathrm{eq}}^{\mathrm{ref}}$
and
$\mu _{\mathrm{eq}}^{\mathrm{ref}}$
and
![]() $\mu _{\mathrm{eq}}^{V}$
. Moreover,
$\mu _{\mathrm{eq}}^{V}$
. Moreover,
![]() $V_{\mathrm{ref}}$
will satisfy Hypothesis 5.1. Then, we observe that the measure
$V_{\mathrm{ref}}$
will satisfy Hypothesis 5.1. Then, we observe that the measure
satisfies the characterisation of the equilibrium measure for the potential
Thus, by uniqueness,
![]() $\mu _{\mathrm{eq}}^{t}$
must be the equilibrium measure for
$\mu _{\mathrm{eq}}^{t}$
must be the equilibrium measure for
![]() $V_{t}$
. It is then clear that if V satisfies Hypothesis 5.1, so does
$V_{t}$
. It is then clear that if V satisfies Hypothesis 5.1, so does
![]() $V_{t}$
uniformly for
$V_{t}$
uniformly for
![]() $t \in [0,1]$
. Proposition 5.6 guarantees that the one-point correlator
$t \in [0,1]$
. Proposition 5.6 guarantees that the one-point correlator
![]() $W_{1}^{t}$
for the model with potential
$W_{1}^{t}$
for the model with potential
![]() $V_{t}$
on
$V_{t}$
on
![]() $\mathsf {A}$
has an asymptotic expansion, for all
$\mathsf {A}$
has an asymptotic expansion, for all
![]() $K \geq 0$
,
$K \geq 0$
,
 $$ \begin{align} W_{1}^{t} = \sum_{k = -1}^{K}N^{-k}\,W_{1}^{\{k\};t} + O(N^{-(K + 1)}), \end{align} $$
$$ \begin{align} W_{1}^{t} = \sum_{k = -1}^{K}N^{-k}\,W_{1}^{\{k\};t} + O(N^{-(K + 1)}), \end{align} $$
and the error is uniform for
![]() $t \in [0,1]$
. Therefore, the exact formula
$t \in [0,1]$
. Therefore, the exact formula
 $$ \begin{align*}\ln\Big(\frac{Z_{N,\beta}^{V;\mathsf{A}}}{Z_{N,\beta}^{\mathrm{ref}}}\Big) = - \frac{N\beta}{2} \oint_{\mathsf{A}} \frac{\mathrm{d} x}{2\mathrm{i}\pi} (V(x) - V^{\mathrm{ref}}(x))\Big(\int_{0}^{1} W_{1}^{t}(x)\mathrm{d} t\Big) \end{align*} $$
$$ \begin{align*}\ln\Big(\frac{Z_{N,\beta}^{V;\mathsf{A}}}{Z_{N,\beta}^{\mathrm{ref}}}\Big) = - \frac{N\beta}{2} \oint_{\mathsf{A}} \frac{\mathrm{d} x}{2\mathrm{i}\pi} (V(x) - V^{\mathrm{ref}}(x))\Big(\int_{0}^{1} W_{1}^{t}(x)\mathrm{d} t\Big) \end{align*} $$
turns into an asymptotic expansion.
Lemma 7.2. For any
![]() $K \geq -2$
, we have
$K \geq -2$
, we have
 $$ \begin{align} \ln\Big(\frac{Z_{N,\beta}^{V;\mathsf{A}}}{Z_{N,\beta}^{\mathrm{ref}}}\Big) = \frac{\beta}{2} \sum_{k = - 2}^{K} N^{-k}\,F_{\beta}^{\{k\};V \rightarrow \mathrm{ref}} + O(N^{-(K + 1)}), \end{align} $$
$$ \begin{align} \ln\Big(\frac{Z_{N,\beta}^{V;\mathsf{A}}}{Z_{N,\beta}^{\mathrm{ref}}}\Big) = \frac{\beta}{2} \sum_{k = - 2}^{K} N^{-k}\,F_{\beta}^{\{k\};V \rightarrow \mathrm{ref}} + O(N^{-(K + 1)}), \end{align} $$
where
 $$ \begin{align} F_{\beta}^{\{k\};V \rightarrow \mathrm{ref}} = \frac{\beta}{2} \oint_{\mathsf{A}} \frac{\mathrm{d} x}{2\mathrm{i}\pi}\,(V^{\mathrm{ref}}(x) - V(x))\Big(\int_{0}^{1} W_{1}^{\{k + 1\};t}(x)\,\mathrm{d} t\Big). \end{align} $$
$$ \begin{align} F_{\beta}^{\{k\};V \rightarrow \mathrm{ref}} = \frac{\beta}{2} \oint_{\mathsf{A}} \frac{\mathrm{d} x}{2\mathrm{i}\pi}\,(V^{\mathrm{ref}}(x) - V(x))\Big(\int_{0}^{1} W_{1}^{\{k + 1\};t}(x)\,\mathrm{d} t\Big). \end{align} $$
Let us explain the principles giving more explicit computations of
![]() $F_{\beta }^{\{k\};V \rightarrow \mathrm{ref}}$
. As
$F_{\beta }^{\{k\};V \rightarrow \mathrm{ref}}$
. As
![]() $W_{1}^{\{-1\};t}$
is the Stieltjes transform of
$W_{1}^{\{-1\};t}$
is the Stieltjes transform of
![]() $\mu _{\mathrm{eq}}^{t}$
, we have
$\mu _{\mathrm{eq}}^{t}$
, we have
with obvious notations. In this one-cut case, we remind the notations
 $$ \begin{align*}\sigma(x) = \sqrt{(x - \gamma_+)(x - \gamma_-)},\qquad L(x) = \prod_{\gamma\ =\ \mathrm{hard}\,\,\mathrm{edge}} (x - \gamma), \end{align*} $$
$$ \begin{align*}\sigma(x) = \sqrt{(x - \gamma_+)(x - \gamma_-)},\qquad L(x) = \prod_{\gamma\ =\ \mathrm{hard}\,\,\mathrm{edge}} (x - \gamma), \end{align*} $$
and the decomposition (see Equation (5.7))
 $$ \begin{align} W_{1}^{\{-1\};t}(x) = \frac{V^{\prime}_t(x)}{2} - S_{t}(x)\,\frac{\sigma(x)}{L(x)}. \end{align} $$
$$ \begin{align} W_{1}^{\{-1\};t}(x) = \frac{V^{\prime}_t(x)}{2} - S_{t}(x)\,\frac{\sigma(x)}{L(x)}. \end{align} $$
By construction, we have
and it is a property of our choice of reference models that
![]() $S^{\mathrm{ref}}(x) = S^{\mathrm{ref}}$
is a constant only depending on
$S^{\mathrm{ref}}(x) = S^{\mathrm{ref}}$
is a constant only depending on
![]() $\gamma _{\pm }$
and the nature of the edges. The proof of the expansion (7.6) – either in [Reference Borot and GuionnetBG11] or here in Section 5 specialised to the one-cut case – also provides a recursive computation of the coefficients
$\gamma _{\pm }$
and the nature of the edges. The proof of the expansion (7.6) – either in [Reference Borot and GuionnetBG11] or here in Section 5 specialised to the one-cut case – also provides a recursive computation of the coefficients
![]() $W_{1}^{\{k\kern-0.5pt\};t}$
for
$W_{1}^{\{k\kern-0.5pt\};t}$
for
![]() $k \geq 0$
. The only place where t is involved is via the initial data
$k \geq 0$
. The only place where t is involved is via the initial data
![]() $W_{1}^{\{-1\};t}$
, as well as the inverse operator
$W_{1}^{\{-1\};t}$
, as well as the inverse operator
![]() $\mathcal {K}_{t}^{-1}$
, which reads in the present one-cut case (see Equation (5.11) with
$\mathcal {K}_{t}^{-1}$
, which reads in the present one-cut case (see Equation (5.11) with
![]() $g=0$
):
$g=0$
):
 $$ \begin{align} \mathcal{K}^{-1}_{t}[f](x) = \frac{1}{2\sigma(x)}\oint_{\gamma} \frac{\mathrm{d} \xi}{2\mathrm{i}\pi}\,\frac{L(\xi)\,f(\xi)}{S_{t}(\xi)(\xi - x)}. \end{align} $$
$$ \begin{align} \mathcal{K}^{-1}_{t}[f](x) = \frac{1}{2\sigma(x)}\oint_{\gamma} \frac{\mathrm{d} \xi}{2\mathrm{i}\pi}\,\frac{L(\xi)\,f(\xi)}{S_{t}(\xi)(\xi - x)}. \end{align} $$
Therefore, the integrand of the k-th term in Equation (7.7) is a priori a rational function of t and the integral over t can be in principle explicitly performed.
In the present one-cut case,
![]() $L_2(x;\xi _1,\xi _2)$
defined in Equation (4.1) is equal to
$L_2(x;\xi _1,\xi _2)$
defined in Equation (4.1) is equal to
![]() $1$
if the two edges are hard, and
$1$
if the two edges are hard, and
![]() $0$
otherwise. One can then check using that
$0$
otherwise. One can then check using that
![]() $(W_{1} - N W_{1}^{\{-1\!\}})(\xi ) = O(\frac {1}{\xi ^2})$
when
$(W_{1} - N W_{1}^{\{-1\!\}})(\xi ) = O(\frac {1}{\xi ^2})$
when
![]() $\xi \rightarrow \infty $
and for
$\xi \rightarrow \infty $
and for
![]() $n \geq 2$
using that
$n \geq 2$
using that
![]() $W_{n}(\xi _1,\ldots ,\xi _n) = O(\frac {1}{\xi _i^2})$
uniformly for
$W_{n}(\xi _1,\ldots ,\xi _n) = O(\frac {1}{\xi _i^2})$
uniformly for
![]() $(\xi _j)_{j \neq i}$
away from
$(\xi _j)_{j \neq i}$
away from
![]() $\mathsf {A}$
, that the terms involving the operators
$\mathsf {A}$
, that the terms involving the operators
![]() $\mathcal {L}_{1}$
and
$\mathcal {L}_{1}$
and
![]() $\mathcal {L}_{2}$
in the Dyson–Schwinger equations vanish in the recursive computation of
$\mathcal {L}_{2}$
in the Dyson–Schwinger equations vanish in the recursive computation of
![]() $W_{n}^{\{k\}}$
s, independently of the nature of the edges.
$W_{n}^{\{k\}}$
s, independently of the nature of the edges.
We can easily check that
![]() $F_{\beta }^{\{-2\};V \rightarrow \mathrm{ref}}$
given by Equation (7.8) is indeed the difference of (7.2) for V and for
$F_{\beta }^{\{-2\};V \rightarrow \mathrm{ref}}$
given by Equation (7.8) is indeed the difference of (7.2) for V and for
![]() $V^\mathrm{{ref}}$
, since
$V^\mathrm{{ref}}$
, since
![]() $W_{1}^{\{-1\};t}$
being a convex combination with respect to t implies
$W_{1}^{\{-1\};t}$
being a convex combination with respect to t implies
 $$ \begin{align*}\int_{0}^1 W_{1}^{\{-1\};t}(x)\,\mathrm{d} t = \frac{W_{1}^{\{-1\};V}(x)+W_{1}^{\{-1\};\mathrm{ref}}(x)}{2}. \end{align*} $$
$$ \begin{align*}\int_{0}^1 W_{1}^{\{-1\};t}(x)\,\mathrm{d} t = \frac{W_{1}^{\{-1\};V}(x)+W_{1}^{\{-1\};\mathrm{ref}}(x)}{2}. \end{align*} $$
To obtain the order N, we need to compute
![]() $W_{1}^{\{0\};t}$
given by Equation (5.37), taking into account the disappearance of
$W_{1}^{\{0\};t}$
given by Equation (5.37), taking into account the disappearance of
![]() $\mathcal {L}$
s:
$\mathcal {L}$
s:
Using Equation (5.7) and the analyticity of V, we find
 $$ \begin{align*}W_1^{\{0\};t}(x)= \Big(\frac{2}{\beta} - 1\Big)\oint_{\gamma} \frac{\mathrm{d} \xi}{2\mathrm{i}\pi}\,\frac{1}{\xi-x}\frac{\sigma(\xi)}{2\sigma(x)}\partial_\xi \ln \left(S_t(\xi)\frac{\sigma(\xi)}{L(\xi)}\right). \end{align*} $$
$$ \begin{align*}W_1^{\{0\};t}(x)= \Big(\frac{2}{\beta} - 1\Big)\oint_{\gamma} \frac{\mathrm{d} \xi}{2\mathrm{i}\pi}\,\frac{1}{\xi-x}\frac{\sigma(\xi)}{2\sigma(x)}\partial_\xi \ln \left(S_t(\xi)\frac{\sigma(\xi)}{L(\xi)}\right). \end{align*} $$
Some algebra reveals the following:
Lemma 7.3.
Proof. We first make some preliminary remarks. If we denote
![]() $G_t(x) = S_t(x)\sigma (x)/L(x)$
, the density of the equilibrium measure is given by
$G_t(x) = S_t(x)\sigma (x)/L(x)$
, the density of the equilibrium measure is given by
In particular, the total mass is
 $$ \begin{align*}1 = -\oint_{\gamma} G_t(x)\,\frac{\mathrm{d} x}{2\mathrm{i}\pi}. \end{align*} $$
$$ \begin{align*}1 = -\oint_{\gamma} G_t(x)\,\frac{\mathrm{d} x}{2\mathrm{i}\pi}. \end{align*} $$
Therefore,
![]() $x \mapsto \partial _{t} G(x)$
has zero period around
$x \mapsto \partial _{t} G(x)$
has zero period around
![]() $\gamma $
. This implies that, for an arbitrary choice of
$\gamma $
. This implies that, for an arbitrary choice of
![]() $o \in \mathbb {C}\setminus \gamma $
, the function
$o \in \mathbb {C}\setminus \gamma $
, the function
is analytic for x in a neighbourhood of
![]() $\gamma $
in
$\gamma $
in
![]() $\mathbb {C}\setminus \gamma $
. As
$\mathbb {C}\setminus \gamma $
. As
![]() $G_t(x)$
has at most inverse squareroot singularities, we conclude that
$G_t(x)$
has at most inverse squareroot singularities, we conclude that
![]() $H_{t}(x)$
remains bounded when x approaches
$H_{t}(x)$
remains bounded when x approaches
![]() $\gamma $
. Besides, applying
$\gamma $
. Besides, applying
![]() $\int ^{x}\partial _{t}$
to
$\int ^{x}\partial _{t}$
to
![]() $G_t(x + \mathrm{i}0) + G_t(x - \mathrm{i}0) = 0$
and taking into account that
$G_t(x + \mathrm{i}0) + G_t(x - \mathrm{i}0) = 0$
and taking into account that
![]() $\oint _{\gamma } \partial _t G_t(x)\,\mathrm {d} x = 0$
, we deduce that
$\oint _{\gamma } \partial _t G_t(x)\,\mathrm {d} x = 0$
, we deduce that
![]() $H_{t}(x + \mathrm{i}0) + H_{t}(x - \mathrm{i}0) = 0$
as well.
$H_{t}(x + \mathrm{i}0) + H_{t}(x - \mathrm{i}0) = 0$
as well.
We can now start the computation of
 $$ \begin{align*}F_{\beta}^{\{-1\};V \rightarrow \mathrm{ref}} = - \frac{\beta}{2}\int_0^1 \mathrm{d} t \oint_{\gamma} \frac{\mathrm{d} x}{2\mathrm{i}\pi} \,\partial_t V_t(x)\,W_1^{\{0\};t}(x). \end{align*} $$
$$ \begin{align*}F_{\beta}^{\{-1\};V \rightarrow \mathrm{ref}} = - \frac{\beta}{2}\int_0^1 \mathrm{d} t \oint_{\gamma} \frac{\mathrm{d} x}{2\mathrm{i}\pi} \,\partial_t V_t(x)\,W_1^{\{0\};t}(x). \end{align*} $$
We substitute and find by Equation (7.9),
where
![]() $C_t$
is independent of x. Since
$C_t$
is independent of x. Since
![]() $W_1^{t}(x) = \frac {N}{x} + O(\frac {1}{x^2})$
, we have
$W_1^{t}(x) = \frac {N}{x} + O(\frac {1}{x^2})$
, we have
![]() $W_1^{\{-1\};t}(x) = \frac {1}{x} + O(\frac {1}{x^2})$
and
$W_1^{\{-1\};t}(x) = \frac {1}{x} + O(\frac {1}{x^2})$
and
![]() $W_1^{\{0\};t}(x) = O(\frac {1}{x^2})$
when
$W_1^{\{0\};t}(x) = O(\frac {1}{x^2})$
when
![]() $x \rightarrow \infty $
. This implies as well
$x \rightarrow \infty $
. This implies as well
![]() $\partial _t W_1^{\{-1\}}(x) = O(\frac {1}{x^2})$
and
$\partial _t W_1^{\{-1\}}(x) = O(\frac {1}{x^2})$
and
![]() $\int ^{x}_o \partial _t W_{1}^{\{-1\};t}(\xi )\mathrm {d} \xi $
. Then, as we can transform the contour integral into a residue at infinity, only
$\int ^{x}_o \partial _t W_{1}^{\{-1\};t}(\xi )\mathrm {d} \xi $
. Then, as we can transform the contour integral into a residue at infinity, only
![]() $H_{t}(x)$
contributes to the contour integral. We then substitute
$H_{t}(x)$
contributes to the contour integral. We then substitute
![]() $W_{1}^{\{0\};t}(x)$
for its expression to deduce
$W_{1}^{\{0\};t}(x)$
for its expression to deduce
 $$ \begin{align*}F_{\beta}^{\{-1\};V \rightarrow \mathrm{ref}} = \Big(1 - \frac{\beta}{2}\Big)\int_{0}^{1} \mathrm{d} t\oint_{\gamma} \frac{\mathrm{d} x}{2\mathrm{i}\pi}\,\frac{H_{t}(x)}{\sigma(x)}\,\oint_{\gamma} \frac{\mathrm{d}\xi}{2\mathrm{i}\pi}\,\frac{\sigma(\xi)}{\xi - x}\,\partial_{\xi}\ln G_t(\xi), \end{align*} $$
$$ \begin{align*}F_{\beta}^{\{-1\};V \rightarrow \mathrm{ref}} = \Big(1 - \frac{\beta}{2}\Big)\int_{0}^{1} \mathrm{d} t\oint_{\gamma} \frac{\mathrm{d} x}{2\mathrm{i}\pi}\,\frac{H_{t}(x)}{\sigma(x)}\,\oint_{\gamma} \frac{\mathrm{d}\xi}{2\mathrm{i}\pi}\,\frac{\sigma(\xi)}{\xi - x}\,\partial_{\xi}\ln G_t(\xi), \end{align*} $$
where the contour for x surrounds the contour for
![]() $\xi $
. If we exchange the two contours, we receive an extra term picking up the residue at
$\xi $
. If we exchange the two contours, we receive an extra term picking up the residue at
![]() $x = \xi $
and contour integrating
$x = \xi $
and contour integrating
![]() $\xi $
,
$\xi $
,
 $$ \begin{align} \nonumber F_{\beta}^{\{-1\};V \rightarrow \mathrm{ref}} & = \Big(1 - \frac{\beta}{2}\Big) \int_{0}^{1}\,\mathrm{d} t \bigg\{- \oint_{\gamma} \frac{\mathrm{d} \xi}{2\mathrm{i}\pi}\,H_{t}(\xi)\,\partial_{\xi} \ln G_t(\xi) \\&\qquad\qquad\qquad\qquad + \oint_{\gamma} \frac{\mathrm{d}\xi}{2\mathrm{i}\pi}\,\sigma(\xi)\,\partial_{\xi}\ln G_t(\xi) \oint_{\gamma} \frac{\mathrm{d} x}{2\mathrm{i}\pi}\,\frac{H_{t}(x)}{\sigma(x)(\xi - x)}\bigg\} , \end{align} $$
$$ \begin{align} \nonumber F_{\beta}^{\{-1\};V \rightarrow \mathrm{ref}} & = \Big(1 - \frac{\beta}{2}\Big) \int_{0}^{1}\,\mathrm{d} t \bigg\{- \oint_{\gamma} \frac{\mathrm{d} \xi}{2\mathrm{i}\pi}\,H_{t}(\xi)\,\partial_{\xi} \ln G_t(\xi) \\&\qquad\qquad\qquad\qquad + \oint_{\gamma} \frac{\mathrm{d}\xi}{2\mathrm{i}\pi}\,\sigma(\xi)\,\partial_{\xi}\ln G_t(\xi) \oint_{\gamma} \frac{\mathrm{d} x}{2\mathrm{i}\pi}\,\frac{H_{t}(x)}{\sigma(x)(\xi - x)}\bigg\} , \end{align} $$
where in the second term,
![]() $\xi $
is now outside the contour of integration for x. The properties of
$\xi $
is now outside the contour of integration for x. The properties of
![]() $H_{t}$
imply that
$H_{t}$
imply that
![]() $\frac {H_{t}(x)}{\sigma (x)(\xi - x)}$
is integrable on
$\frac {H_{t}(x)}{\sigma (x)(\xi - x)}$
is integrable on
![]() $(\gamma \pm \mathrm{i}0)$
. We can then squeeze the contour of integration to the union of
$(\gamma \pm \mathrm{i}0)$
. We can then squeeze the contour of integration to the union of
![]() $(\gamma - \mathrm{i}0)$
from left to right and
$(\gamma - \mathrm{i}0)$
from left to right and
![]() $(\gamma + \mathrm{i}0)$
from right to left, and as
$(\gamma + \mathrm{i}0)$
from right to left, and as
![]() $H_t(x)$
and
$H_t(x)$
and
![]() $\sigma (x)$
both take a minus sign when x crosses
$\sigma (x)$
both take a minus sign when x crosses
![]() $\gamma $
, the contribution of the upper and lower parts of the contour cancel each other. So only the first term in Equation (7.13) remains, which can be written after integration by parts
$\gamma $
, the contribution of the upper and lower parts of the contour cancel each other. So only the first term in Equation (7.13) remains, which can be written after integration by parts
 $$ \begin{align*}F_{\beta}^{\{-1\};V \rightarrow \mathrm{ref}} = \Big(1 - \frac{\beta}{2}\Big) \int_{0}^{1}\mathrm{d} t \oint_{\gamma} \frac{\mathrm{d}\xi}{2\mathrm{i}\pi} \partial_{t} G_t(\xi)\,\ln G_t(\xi). \end{align*} $$
$$ \begin{align*}F_{\beta}^{\{-1\};V \rightarrow \mathrm{ref}} = \Big(1 - \frac{\beta}{2}\Big) \int_{0}^{1}\mathrm{d} t \oint_{\gamma} \frac{\mathrm{d}\xi}{2\mathrm{i}\pi} \partial_{t} G_t(\xi)\,\ln G_t(\xi). \end{align*} $$
Squeezing the contour to
![]() $\gamma = [\gamma _-,\gamma _+]$
and using Equation (7.12), we find
$\gamma = [\gamma _-,\gamma _+]$
and using Equation (7.12), we find
 $$ \begin{align*}F_{\beta}^{\{-1\};V \rightarrow \mathrm{ref}} = -\Big(1 - \frac{\beta}{2}\Big) \int_{0}^{1} \mathrm{d} t \bigg\{\int_{\gamma_-}^{\gamma_+} \mathrm{d} \xi\,\partial_{t} \rho_t(\xi)\,\ln(\rho_t(\xi))\bigg\}. \end{align*} $$
$$ \begin{align*}F_{\beta}^{\{-1\};V \rightarrow \mathrm{ref}} = -\Big(1 - \frac{\beta}{2}\Big) \int_{0}^{1} \mathrm{d} t \bigg\{\int_{\gamma_-}^{\gamma_+} \mathrm{d} \xi\,\partial_{t} \rho_t(\xi)\,\ln(\rho_t(\xi))\bigg\}. \end{align*} $$
Here, we recognise
 $$ \begin{align*}\partial_{t} \mathrm{Ent}[\mu_{\mathrm{eq}}^{t}] = \partial_{t}\bigg(-\int_{\gamma_-}^{\gamma_+} \rho_t(x) \ln(\rho_t(x))\mathrm{d} x\bigg) = -\int_{\gamma_-}^{\gamma_+} \partial_{t}\rho_t(x)\,\ln(\rho_t(x))\,\mathrm{d} x, \end{align*} $$
$$ \begin{align*}\partial_{t} \mathrm{Ent}[\mu_{\mathrm{eq}}^{t}] = \partial_{t}\bigg(-\int_{\gamma_-}^{\gamma_+} \rho_t(x) \ln(\rho_t(x))\mathrm{d} x\bigg) = -\int_{\gamma_-}^{\gamma_+} \partial_{t}\rho_t(x)\,\ln(\rho_t(x))\,\mathrm{d} x, \end{align*} $$
given that
![]() $\int _{\gamma _-}^{\gamma _+} \rho _t(x)\mathrm {d} x = 1$
is independent of t. Performing the integration over
$\int _{\gamma _-}^{\gamma _+} \rho _t(x)\mathrm {d} x = 1$
is independent of t. Performing the integration over
![]() $t \in [0,1]$
entails the claim.
$t \in [0,1]$
entails the claim.
To obtain the order
![]() $1$
, we need to compute the leading covariance
$1$
, we need to compute the leading covariance
![]() $W_{2}^{\{0\};t}$
and use the formula (5.48), taking into account the disappearance of
$W_{2}^{\{0\};t}$
and use the formula (5.48), taking into account the disappearance of
![]() $\mathcal {L}$
s:
$\mathcal {L}$
s:
where
![]() $\iota [f](x) = f(x,x)$
. The leading covariance is itself obtained from the formula (5.39) for
$\iota [f](x) = f(x,x)$
. The leading covariance is itself obtained from the formula (5.39) for
![]() $n = 2$
:
$n = 2$
:
It can be computed explicitly and only depends on
![]() $\beta ,\gamma _{\pm }$
and is independent of t and of the nature of the edges.
$\beta ,\gamma _{\pm }$
and is independent of t and of the nature of the edges.
Lemma 7.4. We have
and
 $$ \begin{align*}\iota[W_{2}^{\{0\};t}](x) = \frac{2}{\beta}\,\frac{(\gamma_+ - \gamma_-)^2}{16 \sigma^4(x)}. \end{align*} $$
$$ \begin{align*}\iota[W_{2}^{\{0\};t}](x) = \frac{2}{\beta}\,\frac{(\gamma_+ - \gamma_-)^2}{16 \sigma^4(x)}. \end{align*} $$
Proof. This is the well-known universal expression for the leading covariance in the
![]() $1$
-cut situation. The derivation of (7.14) from (5.39) is classical, but we include it for the reader convenience (the formula for
$1$
-cut situation. The derivation of (7.14) from (5.39) is classical, but we include it for the reader convenience (the formula for
![]() $\iota [W_2^{\{0\};t}]$
is then a direct consequence). We use the formula (7.11) for
$\iota [W_2^{\{0\};t}]$
is then a direct consequence). We use the formula (7.11) for
![]() $\mathcal {K}_t^{-1}$
and the definition (5.27) of
$\mathcal {K}_t^{-1}$
and the definition (5.27) of
![]() $\mathcal {M}_{x_2}$
to rewrite (5.39) as
$\mathcal {M}_{x_2}$
to rewrite (5.39) as
 $$ \begin{align} W_2^{\{0\};t}(x_1,x_2) = -\frac{2}{\beta}\,\frac{1}{2\sigma(x_1)} \oint_{\gamma} \frac{\mathrm{d} \xi}{2\mathrm{i}\pi}\,\frac{1}{S_t(\xi_1)(\xi_1 - x_1)} \oint_{\gamma} \frac{\mathrm{d}\xi_2}{2\mathrm{i}\pi}\,\frac{L(\xi_2)W_1^{\{-1\};t}(\xi_2)}{(x_2 - \xi_2)^2(\xi_1 - \xi_2)}. \end{align} $$
$$ \begin{align} W_2^{\{0\};t}(x_1,x_2) = -\frac{2}{\beta}\,\frac{1}{2\sigma(x_1)} \oint_{\gamma} \frac{\mathrm{d} \xi}{2\mathrm{i}\pi}\,\frac{1}{S_t(\xi_1)(\xi_1 - x_1)} \oint_{\gamma} \frac{\mathrm{d}\xi_2}{2\mathrm{i}\pi}\,\frac{L(\xi_2)W_1^{\{-1\};t}(\xi_2)}{(x_2 - \xi_2)^2(\xi_1 - \xi_2)}. \end{align} $$
Here, it is understood that the
![]() $\xi _2$
-integration contour is closer to the cut
$\xi _2$
-integration contour is closer to the cut
![]() $\gamma $
and the
$\gamma $
and the
![]() $\xi _1$
-integration contour, and that both
$\xi _1$
-integration contour, and that both
![]() $x_1,x_2$
are kept outside those contours. We are going to prove the desired formula (7.14) for
$x_1,x_2$
are kept outside those contours. We are going to prove the desired formula (7.14) for
![]() $x_2$
in the domain
$x_2$
in the domain
![]() $\mathsf {U}$
of analyticity of V (which is a complex neighbourhood of the cut). By uniqueness of analytic continuation, this implies the formula without this restriction on
$\mathsf {U}$
of analyticity of V (which is a complex neighbourhood of the cut). By uniqueness of analytic continuation, this implies the formula without this restriction on
![]() $x_2$
. We can always assume that the contours in (7.15) remain inside
$x_2$
. We can always assume that the contours in (7.15) remain inside
![]() $\mathsf {U}$
.
$\mathsf {U}$
.
From the decomposition (5.7)–(5.8) with our specific potential (7.5), we have
 $$ \begin{align*}W_1^{\{-1\};t}(\xi_2) = \frac{(V_t^{\{0\}}(\xi_2))'}{2} - \frac{S_t(\xi_2)}{L(\xi_2)}\sigma(\xi_2). \end{align*} $$
$$ \begin{align*}W_1^{\{-1\};t}(\xi_2) = \frac{(V_t^{\{0\}}(\xi_2))'}{2} - \frac{S_t(\xi_2)}{L(\xi_2)}\sigma(\xi_2). \end{align*} $$
Since
![]() $V_t^{\{0\}}$
is analytic in
$V_t^{\{0\}}$
is analytic in
![]() $\mathsf {U}$
, its contribution to the
$\mathsf {U}$
, its contribution to the
![]() $\xi _2$
-integration in (7.15) vanishes. We can then rewrite
$\xi _2$
-integration in (7.15) vanishes. We can then rewrite
 $$ \begin{align*}W_2^{\{0\};t}(x_1,x_2) = \frac{2}{\beta}\,\frac{1}{2\sigma(x_1)} \partial_{x_2}\bigg( \oint_{\gamma} \frac{\mathrm{d} \xi_1}{2\mathrm{i}\pi}\,\frac{1}{S_t(\xi_1)(\xi_1 - x_1)} \oint_{\gamma} \frac{\mathrm{d} \xi_2}{2\mathrm{i}\pi}\,\frac{S_t(\xi_2)\sigma(\xi_2)}{(\xi_2 - x_2)(\xi_1 - \xi_2)}\bigg). \end{align*} $$
$$ \begin{align*}W_2^{\{0\};t}(x_1,x_2) = \frac{2}{\beta}\,\frac{1}{2\sigma(x_1)} \partial_{x_2}\bigg( \oint_{\gamma} \frac{\mathrm{d} \xi_1}{2\mathrm{i}\pi}\,\frac{1}{S_t(\xi_1)(\xi_1 - x_1)} \oint_{\gamma} \frac{\mathrm{d} \xi_2}{2\mathrm{i}\pi}\,\frac{S_t(\xi_2)\sigma(\xi_2)}{(\xi_2 - x_2)(\xi_1 - \xi_2)}\bigg). \end{align*} $$
We push the
![]() $\xi _2$
-integration contours towards the exterior while staying in the neighbourhood
$\xi _2$
-integration contours towards the exterior while staying in the neighbourhood
![]() $\mathsf {U}$
. This picks up residues (with a minus sign) at
$\mathsf {U}$
. This picks up residues (with a minus sign) at
![]() $\xi _2 = x_2$
and
$\xi _2 = x_2$
and
![]() $\xi _1$
, while the new
$\xi _1$
, while the new
![]() $\xi _2$
-integration contour is now larger than the
$\xi _2$
-integration contour is now larger than the
![]() $\xi _1$
-integration contour. The latter gives a vanishing contribution, as the integrand is an analytic function with respect to
$\xi _1$
-integration contour. The latter gives a vanishing contribution, as the integrand is an analytic function with respect to
![]() $\xi _1$
inside the
$\xi _1$
inside the
![]() $\xi _1$
-integration contour. It remains only to evaluate the two residues, which gives
$\xi _1$
-integration contour. It remains only to evaluate the two residues, which gives
 $$ \begin{align*}W_2^{\{0\};t}(x_1,x_2) = \frac{2}{\beta}\,\frac{1}{2\sigma(x_1)} \partial_{x_2} \bigg(\oint_{\gamma} \frac{\mathrm{d} \xi_1}{2\mathrm{i}\pi}\,\frac{1}{S_t(\xi_1)(\xi_1 - x_1)} \frac{S_t(\xi_1)\sigma(\xi_1) - S_t(x_2)\sigma(x_2)}{\xi_1 - x_2}\bigg). \end{align*} $$
$$ \begin{align*}W_2^{\{0\};t}(x_1,x_2) = \frac{2}{\beta}\,\frac{1}{2\sigma(x_1)} \partial_{x_2} \bigg(\oint_{\gamma} \frac{\mathrm{d} \xi_1}{2\mathrm{i}\pi}\,\frac{1}{S_t(\xi_1)(\xi_1 - x_1)} \frac{S_t(\xi_1)\sigma(\xi_1) - S_t(x_2)\sigma(x_2)}{\xi_1 - x_2}\bigg). \end{align*} $$
We split the numerator of the ratio in two. The second term is holomorphic inside the integration contour, thus gives zero, and remains the first term:
 $$ \begin{align*}W_2^{\{0\};t}(x_1,x_2) = \frac{2}{\beta}\,\frac{1}{2\sigma(x_1)}\partial_{x_2} \bigg(\oint_{\gamma} \frac{\mathrm{d} \xi_1}{2\mathrm{i}\pi}\,\frac{\sigma(\xi_1)}{(\xi_1 - x_1)(\xi_1 - x_2)}\bigg). \end{align*} $$
$$ \begin{align*}W_2^{\{0\};t}(x_1,x_2) = \frac{2}{\beta}\,\frac{1}{2\sigma(x_1)}\partial_{x_2} \bigg(\oint_{\gamma} \frac{\mathrm{d} \xi_1}{2\mathrm{i}\pi}\,\frac{\sigma(\xi_1)}{(\xi_1 - x_1)(\xi_1 - x_2)}\bigg). \end{align*} $$
We now see that all the peculiarities of the model have disappeared and the answer only involves
Moving the integration contour towards
![]() $\infty $
, we pick (with a minus sign) the residues at
$\infty $
, we pick (with a minus sign) the residues at
![]() $\xi _1 = x_1, x_2,\infty $
, but the residue at
$\xi _1 = x_1, x_2,\infty $
, but the residue at
![]() $\infty $
gives a contribution independent of
$\infty $
gives a contribution independent of
![]() $x_2$
and so disappears when we apply the derivative. This yields
$x_2$
and so disappears when we apply the derivative. This yields
 $$ \begin{align*}W_2^{\{0\};t}(x_1,x_2) = -\frac{2}{\beta}\,\frac{1}{2\sigma(x_1)} \partial_{x_2} \bigg(\frac{\sigma(x_1) - \sigma(x_2)}{x_1 - x_2}\bigg). \end{align*} $$
$$ \begin{align*}W_2^{\{0\};t}(x_1,x_2) = -\frac{2}{\beta}\,\frac{1}{2\sigma(x_1)} \partial_{x_2} \bigg(\frac{\sigma(x_1) - \sigma(x_2)}{x_1 - x_2}\bigg). \end{align*} $$
With
![]() $\sigma '(x) = (2x - \gamma _- - \gamma _+)/\sigma (x)$
, we get
$\sigma '(x) = (2x - \gamma _- - \gamma _+)/\sigma (x)$
, we get
 $$ \begin{align*}W_2^{\{0\};t}(x_1,x_2) = \frac{2}{\beta}\,\frac{1}{2(x_1 - x_2)^2} \bigg(-1 + \frac{\sigma^2(x_2) + (x_1 - x_2)(x_2 - \frac{\gamma- + \gamma_+}{2})}{\sigma(x_1)\sigma(x_2)}\bigg), \end{align*} $$
$$ \begin{align*}W_2^{\{0\};t}(x_1,x_2) = \frac{2}{\beta}\,\frac{1}{2(x_1 - x_2)^2} \bigg(-1 + \frac{\sigma^2(x_2) + (x_1 - x_2)(x_2 - \frac{\gamma- + \gamma_+}{2})}{\sigma(x_1)\sigma(x_2)}\bigg), \end{align*} $$
and this evaluates to (7.14).
These are all ingredients necessary to compute
![]() $W_{1}^{\{1\};t}$
and thus the term of order
$W_{1}^{\{1\};t}$
and thus the term of order
![]() $1$
in Equation (7.7). We do not push the computation further.
$1$
in Equation (7.7). We do not push the computation further.
7.2. The reference partition functions
To complete the description of the asymptotic expansion of
![]() $Z_{N,\beta }^{V;\mathsf {A}}$
in the one-cut regime, we describe, as promised, the reference potentials and the asymptotic expansion of
$Z_{N,\beta }^{V;\mathsf {A}}$
in the one-cut regime, we describe, as promised, the reference potentials and the asymptotic expansion of
![]() $Z_{N,\beta }^{\mathrm{ref}}$
.
$Z_{N,\beta }^{\mathrm{ref}}$
.
7.2.1. Preliminaries
The result builds on the properties of the double Gamma function
![]() $\Gamma _2$
which we now review following [Reference SpreaficoSpr09]. The Barnes double Zeta function is defined for
$\Gamma _2$
which we now review following [Reference SpreaficoSpr09]. The Barnes double Zeta function is defined for
![]() $b_1,b_2> 0$
by
$b_1,b_2> 0$
by
 $$ \begin{align*}\zeta_2(s;x;b_1,b_2) = \frac{1}{\Gamma(s)}\int_{0}^{\infty} \frac{e^{-tx}t^{s - 1}\mathrm{d} t}{(1 - e^{-b_1t})(1 - e^{-b_2t})}, \end{align*} $$
$$ \begin{align*}\zeta_2(s;x;b_1,b_2) = \frac{1}{\Gamma(s)}\int_{0}^{\infty} \frac{e^{-tx}t^{s - 1}\mathrm{d} t}{(1 - e^{-b_1t})(1 - e^{-b_2t})}, \end{align*} $$
for
![]() $\mathrm{Re}\,s> 2$
, and admits a meromorphic analytic continuation to
$\mathrm{Re}\,s> 2$
, and admits a meromorphic analytic continuation to
![]() $s \in \mathbb {C}$
. Barnes double Gamma function is then defined by
$s \in \mathbb {C}$
. Barnes double Gamma function is then defined by
In particular, it satisfies the functional equation
 $$ \begin{align} \Gamma_2(x + b_2;b_1,b_2) = \frac{\Gamma_2(x;b_1,b_2)}{\Gamma\big(\frac{x}{b_1}\big)}\,\sqrt{2\pi}\,b_1^{\frac{1}{2} - \frac{x}{b_1}},\qquad \Gamma_2(1;b_1,b_2) = 1. \end{align} $$
$$ \begin{align} \Gamma_2(x + b_2;b_1,b_2) = \frac{\Gamma_2(x;b_1,b_2)}{\Gamma\big(\frac{x}{b_1}\big)}\,\sqrt{2\pi}\,b_1^{\frac{1}{2} - \frac{x}{b_1}},\qquad \Gamma_2(1;b_1,b_2) = 1. \end{align} $$
We will only need the specialisation to
![]() $b_1 = \frac {2}{\beta }$
and
$b_1 = \frac {2}{\beta }$
and
![]() $b_2 = 1$
. It admits the asymptotic expansion, for any
$b_2 = 1$
. It admits the asymptotic expansion, for any
![]() $K \geq 1$
,
$K \geq 1$
,
 $$ \begin{align} \nonumber \ln\Gamma_{2}\big(x;\tfrac{2}{\beta},1\big) & = -\frac{\beta x^2 \ln x}{4} + \frac{3\beta x^2}{8} + \frac{1}{2}\Big(1 + \frac{\beta}{2}\Big)(x\ln x - x) - \frac{3 + \beta/2 + 2/\beta}{12}\ln x \\ & \quad - \chi'\big(0;\tfrac{2}{\beta},1\big) + \sum_{k = 1}^{K} (k - 1)!\,E_{k}\big(\tfrac{2}{\beta},1\big)\,x^{-k} + O(x^{-(K + 1)}), \end{align} $$
$$ \begin{align} \nonumber \ln\Gamma_{2}\big(x;\tfrac{2}{\beta},1\big) & = -\frac{\beta x^2 \ln x}{4} + \frac{3\beta x^2}{8} + \frac{1}{2}\Big(1 + \frac{\beta}{2}\Big)(x\ln x - x) - \frac{3 + \beta/2 + 2/\beta}{12}\ln x \\ & \quad - \chi'\big(0;\tfrac{2}{\beta},1\big) + \sum_{k = 1}^{K} (k - 1)!\,E_{k}\big(\tfrac{2}{\beta},1\big)\,x^{-k} + O(x^{-(K + 1)}), \end{align} $$
where
![]() $E_{k}(b_1,b_2)$
are the polynomials in two variables defined by the series expansion, for any
$E_{k}(b_1,b_2)$
are the polynomials in two variables defined by the series expansion, for any
![]() $K \geq 0$
,
$K \geq 0$
,
 $$ \begin{align*}\frac{1}{(1 - e^{-b_1t})(1 - e^{-b_2t})} \mathop{=}_{t \rightarrow 0} \sum_{k = -2}^K E_k(b_1,b_2)\,t^{k} + O(t^{K + 1}), \end{align*} $$
$$ \begin{align*}\frac{1}{(1 - e^{-b_1t})(1 - e^{-b_2t})} \mathop{=}_{t \rightarrow 0} \sum_{k = -2}^K E_k(b_1,b_2)\,t^{k} + O(t^{K + 1}), \end{align*} $$
and
![]() $\chi (s;b_1,b_2)$
is the analytic continuation to the complex plane of the series defined for
$\chi (s;b_1,b_2)$
is the analytic continuation to the complex plane of the series defined for
![]() $\mathrm{Re}\,s> 2$
:
$\mathrm{Re}\,s> 2$
:
 $$ \begin{align*}\chi(s;b_1,b_2) = \sum_{\substack{m_1,m_2 \geq 0 \\ (m_1,m_2) \neq (0,0)}} \frac{1}{(m_1b_1 + m_2b_2)^{s}}. \end{align*} $$
$$ \begin{align*}\chi(s;b_1,b_2) = \sum_{\substack{m_1,m_2 \geq 0 \\ (m_1,m_2) \neq (0,0)}} \frac{1}{(m_1b_1 + m_2b_2)^{s}}. \end{align*} $$
For instance,
in terms of the Riemann zeta function. We also remind Stirling formula for the asymptotic expansion of the Gamma function, for any
![]() $K \geq 0$
,
$K \geq 0$
,
 $$ \begin{align} \ln \Gamma(x) \mathop{=}_{x \rightarrow \infty} x\ln x - x - \frac{\ln x}{2} + \frac{\ln(2\pi)}{2} + \sum_{k = 1}^{K} \frac{B_{k + 1}}{k(k + 1)x^{k}} + O(x^{-(K + 1)}), \end{align} $$
$$ \begin{align} \ln \Gamma(x) \mathop{=}_{x \rightarrow \infty} x\ln x - x - \frac{\ln x}{2} + \frac{\ln(2\pi)}{2} + \sum_{k = 1}^{K} \frac{B_{k + 1}}{k(k + 1)x^{k}} + O(x^{-(K + 1)}), \end{align} $$
where
![]() $B_{k}$
are the Bernoulli numbers:
$B_{k}$
are the Bernoulli numbers:
![]() $B_{2} = \frac {1}{6}$
,
$B_{2} = \frac {1}{6}$
,
![]() $B_{4} = -\frac {1}{30}$
,
$B_{4} = -\frac {1}{30}$
,
![]() $B_6 = \frac {1}{42}$
, etc. and
$B_6 = \frac {1}{42}$
, etc. and
![]() $B_{2j + 1} = 0$
for
$B_{2j + 1} = 0$
for
![]() $j \geq 1$
.
$j \geq 1$
.
7.2.2. Two soft edges
We have
![]() $L(x) = 1$
. We take as reference the Gaussian potential
$L(x) = 1$
. We take as reference the Gaussian potential
Its equilibrium measure is the semi-circle law, and its Stieltjes transform is
 $$ \begin{align*}W_{1}^{\{-1\};\mathrm{ref}}(x) = \frac{(V^{\mathrm{ref}})'(x)}{2} - S^{\mathrm{ref}}\frac{\sigma(x)}{L(x)},\qquad S^{\mathrm{ref}} = \frac{8}{(\gamma_+ - \gamma_-)^2}. \end{align*} $$
$$ \begin{align*}W_{1}^{\{-1\};\mathrm{ref}}(x) = \frac{(V^{\mathrm{ref}})'(x)}{2} - S^{\mathrm{ref}}\frac{\sigma(x)}{L(x)},\qquad S^{\mathrm{ref}} = \frac{8}{(\gamma_+ - \gamma_-)^2}. \end{align*} $$
The partition function with potential
![]() $V^\mathrm{{ref}}$
over
$V^\mathrm{{ref}}$
over
![]() $\mathbb {R}^N$
is equal to [Reference MehtaMeh04]:
$\mathbb {R}^N$
is equal to [Reference MehtaMeh04]:
 $$ \begin{align} Z_{N,\beta}^{\mathrm{ref}} = \Big[\prod_{j = 1}^N \frac{\Gamma\big(1 + j\frac{\beta}{2}\big)}{\Gamma\big(1 + \frac{\beta}{2}\big)}\Big]\,(2\pi)^{\frac{N}{2}}\,\Big(\frac{(\gamma_+ - \gamma_-)^2}{16}\,\frac{2/\beta}{N}\Big)^{\frac{\beta}{4}N^2 + (1 - \frac{\beta}{2})\frac{N}{2}}, \end{align} $$
$$ \begin{align} Z_{N,\beta}^{\mathrm{ref}} = \Big[\prod_{j = 1}^N \frac{\Gamma\big(1 + j\frac{\beta}{2}\big)}{\Gamma\big(1 + \frac{\beta}{2}\big)}\Big]\,(2\pi)^{\frac{N}{2}}\,\Big(\frac{(\gamma_+ - \gamma_-)^2}{16}\,\frac{2/\beta}{N}\Big)^{\frac{\beta}{4}N^2 + (1 - \frac{\beta}{2})\frac{N}{2}}, \end{align} $$
and it differs from the partition function on
![]() $\mathsf {A}$
by exponentially small corrections (see Corollary 3.2). Equation (7.19) can be rewritten in terms of Barnes double Gamma function: if we express the Gamma function using Equation (7.16) with
$\mathsf {A}$
by exponentially small corrections (see Corollary 3.2). Equation (7.19) can be rewritten in terms of Barnes double Gamma function: if we express the Gamma function using Equation (7.16) with
![]() $b_1 = \frac {2}{\beta }$
and
$b_1 = \frac {2}{\beta }$
and
![]() $b_2 = 1$
, the product becomes telescopic. The result is
$b_2 = 1$
, the product becomes telescopic. The result is
 $$ \begin{align*} Z_{N,\beta}^{\mathrm{ref}} & = \frac{N!\,(2\pi)^N\,\big(\frac{\beta}{2}\big)^{(\frac{\beta}{2} - 1)N}}{\Gamma^N\big(\frac{\beta}{2}\big)\,\Gamma_2\big(N + 1;\frac{2}{\beta},1\big)} \Big(\frac{(\gamma_+ - \gamma_-)^2}{16N}\Big)^{\frac{\beta}{4} N^2 + (1 - \frac{\beta}{2})\frac{N}{2}}, \end{align*} $$
$$ \begin{align*} Z_{N,\beta}^{\mathrm{ref}} & = \frac{N!\,(2\pi)^N\,\big(\frac{\beta}{2}\big)^{(\frac{\beta}{2} - 1)N}}{\Gamma^N\big(\frac{\beta}{2}\big)\,\Gamma_2\big(N + 1;\frac{2}{\beta},1\big)} \Big(\frac{(\gamma_+ - \gamma_-)^2}{16N}\Big)^{\frac{\beta}{4} N^2 + (1 - \frac{\beta}{2})\frac{N}{2}}, \end{align*} $$
and its asymptotic expansion can be computed with help of Equations (7.17)–(7.18). It yields an expansion of the form (7.1) with
 $$ \begin{align*} F_{\beta}^{\{-2\};\mathrm{ref}} & = \frac{\beta}{2}\Big[-\frac{3}{4} + \ln\Big(\frac{\gamma_+ - \gamma_-}{4}\Big)\Big], \\ F_{\beta}^{\{-1\};\mathrm{ref}}& = \Big(1 - \frac{\beta}{2}\Big)\ln\Big(\frac{\gamma_+ - \gamma_-}{4}\Big) -\frac{1}{2} - \frac{\beta}{4} + \ln(2\pi) - \ln\Gamma\big(\tfrac{\beta}{2}\big) + \big(\tfrac{\beta}{2} - 1\big)\ln\big(\tfrac{\beta}{2}\big), \\ F_{\beta}^{\{0\};\mathrm{ref}} & = \chi'\big(0;\tfrac{2}{\beta},1\big) + \frac{\ln(2\pi)}{2}, \\ \varkappa^\mathrm{ref} & = \frac{3 + \beta/2 + 2/\beta}{12}, \end{align*} $$
$$ \begin{align*} F_{\beta}^{\{-2\};\mathrm{ref}} & = \frac{\beta}{2}\Big[-\frac{3}{4} + \ln\Big(\frac{\gamma_+ - \gamma_-}{4}\Big)\Big], \\ F_{\beta}^{\{-1\};\mathrm{ref}}& = \Big(1 - \frac{\beta}{2}\Big)\ln\Big(\frac{\gamma_+ - \gamma_-}{4}\Big) -\frac{1}{2} - \frac{\beta}{4} + \ln(2\pi) - \ln\Gamma\big(\tfrac{\beta}{2}\big) + \big(\tfrac{\beta}{2} - 1\big)\ln\big(\tfrac{\beta}{2}\big), \\ F_{\beta}^{\{0\};\mathrm{ref}} & = \chi'\big(0;\tfrac{2}{\beta},1\big) + \frac{\ln(2\pi)}{2}, \\ \varkappa^\mathrm{ref} & = \frac{3 + \beta/2 + 2/\beta}{12}, \end{align*} $$
and explicitly computable higher
![]() $F^{\{k\};\mathrm{ref}}_{\beta }$
.
$F^{\{k\};\mathrm{ref}}_{\beta }$
.
7.2.3. One soft edge, one hard edge
Up to exchanging the role of
![]() $\gamma _{\pm }$
, we can assume that
$\gamma _{\pm }$
, we can assume that
![]() $\gamma _+$
is hard and
$\gamma _+$
is hard and
![]() $\gamma _-$
is soft. Then,
$\gamma _-$
is soft. Then,
![]() $L(x) = (x - \gamma _+)$
. We take as reference the linear potential
$L(x) = (x - \gamma _+)$
. We take as reference the linear potential
Its equilibrium measure is the Marčenko–Pastur law, whose Stieltjes transform is
 $$ \begin{align*}W_{1}^{\{-1\};\mathrm{ref}}(x) = \frac{(V^{\mathrm{ref}})'(x)}{2} - S^{\mathrm{ref}}\frac{\sigma(x)}{L(x)},\qquad S^{\mathrm{ref}} = \frac{2}{\gamma_+ - \gamma_-}. \end{align*} $$
$$ \begin{align*}W_{1}^{\{-1\};\mathrm{ref}}(x) = \frac{(V^{\mathrm{ref}})'(x)}{2} - S^{\mathrm{ref}}\frac{\sigma(x)}{L(x)},\qquad S^{\mathrm{ref}} = \frac{2}{\gamma_+ - \gamma_-}. \end{align*} $$
The partition function for
![]() $V^\mathrm{{ref}}$
over
$V^\mathrm{{ref}}$
over
![]() $(-\infty ,\gamma _+]$
is the Laguerre Selberg integral
$(-\infty ,\gamma _+]$
is the Laguerre Selberg integral
 $$ \begin{align*}Z_{N,\beta}^{\mathrm{ref}} = \prod_{j = 1}^{N} \frac{\Gamma\big(1 + (j - 1)\frac{\beta}{2}\big)\Gamma\big(1 + j\frac{\beta}{2}\big)}{\Gamma\big(1 + \frac{\beta}{2}\big)}\,\Big(\frac{2/\beta}{N}\,\frac{\gamma_+ - \gamma_-}{4}\Big)^{\frac{\beta}{2}N^2 + (1 - \frac{\beta}{2})N}, \end{align*} $$
$$ \begin{align*}Z_{N,\beta}^{\mathrm{ref}} = \prod_{j = 1}^{N} \frac{\Gamma\big(1 + (j - 1)\frac{\beta}{2}\big)\Gamma\big(1 + j\frac{\beta}{2}\big)}{\Gamma\big(1 + \frac{\beta}{2}\big)}\,\Big(\frac{2/\beta}{N}\,\frac{\gamma_+ - \gamma_-}{4}\Big)^{\frac{\beta}{2}N^2 + (1 - \frac{\beta}{2})N}, \end{align*} $$
and it differs from the partition function over
![]() $\mathsf {A}$
by exponentially small corrections. We transform it using Barnes double Gamma function:
$\mathsf {A}$
by exponentially small corrections. We transform it using Barnes double Gamma function:
 $$ \begin{align*} Z_{N,\beta}^{\mathrm{ref}} & = \frac{N!^2\,(2\pi)^N\, \big(\frac{\beta}{2}\big)^{(\beta - 1)N}}{\Gamma\big(1 + N\frac{\beta}{2}\big)\,\Gamma^N\big(\frac{\beta}{2}\big)\, \Gamma_2^2\big(N + 1;\frac{2}{\beta},1\big)}\Big(\frac{\gamma_+ - \gamma_-}{4N}\Big)^{\frac{\beta}{2}N^2 + (1 - \frac{\beta}{2})N}. \end{align*} $$
$$ \begin{align*} Z_{N,\beta}^{\mathrm{ref}} & = \frac{N!^2\,(2\pi)^N\, \big(\frac{\beta}{2}\big)^{(\beta - 1)N}}{\Gamma\big(1 + N\frac{\beta}{2}\big)\,\Gamma^N\big(\frac{\beta}{2}\big)\, \Gamma_2^2\big(N + 1;\frac{2}{\beta},1\big)}\Big(\frac{\gamma_+ - \gamma_-}{4N}\Big)^{\frac{\beta}{2}N^2 + (1 - \frac{\beta}{2})N}. \end{align*} $$
We then deduce the asymptotic expansion with coefficients
 $$ \begin{align*} F_{\beta}^{\{-2\};\mathrm{ref}} & = \frac{\beta}{2}\Big[-\frac{3}{2} + \ln\Big(\frac{\gamma_+ - \gamma_-}{4}\Big)\Big], \\ F_{\beta}^{\{-1\};\mathrm{ref}} & = \Big(1 - \frac{\beta}{2}\Big)\ln\Big(\frac{\gamma_+ - \gamma_-}{4}\Big) -1 + \ln(2\pi) - \ln \Gamma\big(\tfrac{\beta}{2}\big) + (\tfrac{\beta}{2} - 1)\ln\big(\tfrac{\beta}{2}\big), \\ F_{\beta}^{\{0\};\mathrm{ref}} &= 2\chi'\big(0;\tfrac{2}{\beta},1\big) - \frac{\ln(\beta/2)}{2} + \frac{\ln(2\pi)}{2}, \\ \varkappa^\mathrm{ref} & = \frac{\beta/2 + 2/\beta}{6}, \end{align*} $$
$$ \begin{align*} F_{\beta}^{\{-2\};\mathrm{ref}} & = \frac{\beta}{2}\Big[-\frac{3}{2} + \ln\Big(\frac{\gamma_+ - \gamma_-}{4}\Big)\Big], \\ F_{\beta}^{\{-1\};\mathrm{ref}} & = \Big(1 - \frac{\beta}{2}\Big)\ln\Big(\frac{\gamma_+ - \gamma_-}{4}\Big) -1 + \ln(2\pi) - \ln \Gamma\big(\tfrac{\beta}{2}\big) + (\tfrac{\beta}{2} - 1)\ln\big(\tfrac{\beta}{2}\big), \\ F_{\beta}^{\{0\};\mathrm{ref}} &= 2\chi'\big(0;\tfrac{2}{\beta},1\big) - \frac{\ln(\beta/2)}{2} + \frac{\ln(2\pi)}{2}, \\ \varkappa^\mathrm{ref} & = \frac{\beta/2 + 2/\beta}{6}, \end{align*} $$
and explicitly computable higher
![]() $F^{\{k\};\mathrm{ref}}_{\beta }$
.
$F^{\{k\};\mathrm{ref}}_{\beta }$
.
7.2.4. Two hard edges
We have
![]() $L(x) = (x - \gamma _+)(x - \gamma _-)$
. We take as reference potential
$L(x) = (x - \gamma _+)(x - \gamma _-)$
. We take as reference potential
![]() $V^\mathrm{{ref}} = 0$
on
$V^\mathrm{{ref}} = 0$
on
![]() $[\gamma _-,\gamma _+]$
. The equilibrium measure is the arcsine law, and its Stieltjes transform is
$[\gamma _-,\gamma _+]$
. The equilibrium measure is the arcsine law, and its Stieltjes transform is
 $$ \begin{align*}W^{\{-1\};\mathrm{ref}}_{1} = \frac{1}{\sigma(x)} = \frac{(V^{\mathrm{ref}})'(x)}{2} - S^{\mathrm{ref}}\,\frac{\sigma(x)}{L(x)},\qquad S_{\mathrm{ref}} = -1. \end{align*} $$
$$ \begin{align*}W^{\{-1\};\mathrm{ref}}_{1} = \frac{1}{\sigma(x)} = \frac{(V^{\mathrm{ref}})'(x)}{2} - S^{\mathrm{ref}}\,\frac{\sigma(x)}{L(x)},\qquad S_{\mathrm{ref}} = -1. \end{align*} $$
The partition function for the zero potential on
![]() $[\gamma _-,\gamma _+]$
is the Jacobi Selberg integral:
$[\gamma _-,\gamma _+]$
is the Jacobi Selberg integral:
 $$ \begin{align*}Z_{N,\beta}^{\mathrm{ref}} = \frac{1}{\Gamma^2\big(1 + N\frac{\beta}{2}\big)} \prod_{j = 1}^N \frac{\Gamma^3\big(1 + j\frac{\beta}{2}\big)}{\Gamma\big(2 + (N + j - 2)\frac{\beta}{2}\big)\Gamma\big(1+ \frac{\beta}{2}\big)}\,(\gamma_+ - \gamma_-)^{\frac{\beta}{2}N^2 + (1 - \frac{\beta}{2})N}. \end{align*} $$
$$ \begin{align*}Z_{N,\beta}^{\mathrm{ref}} = \frac{1}{\Gamma^2\big(1 + N\frac{\beta}{2}\big)} \prod_{j = 1}^N \frac{\Gamma^3\big(1 + j\frac{\beta}{2}\big)}{\Gamma\big(2 + (N + j - 2)\frac{\beta}{2}\big)\Gamma\big(1+ \frac{\beta}{2}\big)}\,(\gamma_+ - \gamma_-)^{\frac{\beta}{2}N^2 + (1 - \frac{\beta}{2})N}. \end{align*} $$
We rewrite it in terms of the Barnes double Gamma function
 $$ \begin{align*} Z_{N,\beta}^{\mathrm{ref}} & = \frac{(2\pi)^N\,N!^3\, (N - 2)!\,\Gamma\big(\frac{2}{\beta} + N - 1\big)\,\big(\frac{\beta}{2}\big)^{(\frac{3\beta}{2} - 1)N}}{(2N - 2)!\,\Gamma\big(\frac{2}{\beta} + 2N - 1)\,\Gamma^N\big(\frac{\beta}{2}\big)\, \Gamma^2\big(1 + N\frac{\beta}{2}\big)}\,\frac{\Gamma_2\big(2N - 1;\frac{2}{\beta},1\big)}{\Gamma_{2}\big(N - 1;\frac{2}{\beta},1\big)\Gamma_2^3\big(N + 1;\frac{2}{\beta},1\big)} \\ & \quad \times (\gamma_+ - \gamma_-)^{\frac{\beta}{2}N^2 + (1 - \frac{\beta}{2})N}, \end{align*} $$
$$ \begin{align*} Z_{N,\beta}^{\mathrm{ref}} & = \frac{(2\pi)^N\,N!^3\, (N - 2)!\,\Gamma\big(\frac{2}{\beta} + N - 1\big)\,\big(\frac{\beta}{2}\big)^{(\frac{3\beta}{2} - 1)N}}{(2N - 2)!\,\Gamma\big(\frac{2}{\beta} + 2N - 1)\,\Gamma^N\big(\frac{\beta}{2}\big)\, \Gamma^2\big(1 + N\frac{\beta}{2}\big)}\,\frac{\Gamma_2\big(2N - 1;\frac{2}{\beta},1\big)}{\Gamma_{2}\big(N - 1;\frac{2}{\beta},1\big)\Gamma_2^3\big(N + 1;\frac{2}{\beta},1\big)} \\ & \quad \times (\gamma_+ - \gamma_-)^{\frac{\beta}{2}N^2 + (1 - \frac{\beta}{2})N}, \end{align*} $$
and we find the asymptotic expansion with coefficients
 $$ \begin{align*} F_{\beta}^{\{-2\};\mathrm{ref}} & = \frac{\beta}{2}\ln\Big(\frac{\gamma_+ - \gamma_-}{4}\Big), \\F_{\beta}^{\{-1\};\mathrm{ref}}& = \Big(1 - \frac{\beta}{2}\Big)\ln\Big(\frac{\gamma_+ - \gamma_-}{8}\Big) - \tfrac{\beta}{2} + \ln(2\pi) - \ln \Gamma\big(\tfrac{\beta}{2}\big) + \big(\tfrac{\beta}{2} - 1\big)\ln\big(\tfrac{\beta}{2}\big), \\F_{\beta}^{\{0\};\mathrm{ref}}& = 3\chi'\big(0;\tfrac{2}{\beta},1\big) + \frac{27 - 13(\beta/2 + 2/\beta)}{12}\ln(2) - \ln\big(\tfrac{\beta}{2}\big) + \frac{\ln(2\pi)}{2}, \\\varkappa^\mathrm{ref} & = \frac{-1 + \beta/2 + 2/\beta}{4}, \end{align*} $$
$$ \begin{align*} F_{\beta}^{\{-2\};\mathrm{ref}} & = \frac{\beta}{2}\ln\Big(\frac{\gamma_+ - \gamma_-}{4}\Big), \\F_{\beta}^{\{-1\};\mathrm{ref}}& = \Big(1 - \frac{\beta}{2}\Big)\ln\Big(\frac{\gamma_+ - \gamma_-}{8}\Big) - \tfrac{\beta}{2} + \ln(2\pi) - \ln \Gamma\big(\tfrac{\beta}{2}\big) + \big(\tfrac{\beta}{2} - 1\big)\ln\big(\tfrac{\beta}{2}\big), \\F_{\beta}^{\{0\};\mathrm{ref}}& = 3\chi'\big(0;\tfrac{2}{\beta},1\big) + \frac{27 - 13(\beta/2 + 2/\beta)}{12}\ln(2) - \ln\big(\tfrac{\beta}{2}\big) + \frac{\ln(2\pi)}{2}, \\\varkappa^\mathrm{ref} & = \frac{-1 + \beta/2 + 2/\beta}{4}, \end{align*} $$
with explicitly computable higher
![]() $F^{\{k\};\mathrm{ref}}_{\beta }$
.
$F^{\{k\};\mathrm{ref}}_{\beta }$
.
7.2.5. Nondecaying terms
The asymptotic expansion of the reference partition takes the form, for any
![]() $K \geq 0$
,
$K \geq 0$
,
 $$ \begin{align*}\ln Z_{N,\beta}^{\mathrm{ref}} = \sum_{k = - 2}^{K} N^{-k}\,F_{\beta}^{\{k\};\mathrm{ref}} + \frac{\beta}{2}\ln N + \varkappa^{\mathrm{ref}} \ln N + O(N^{-(K + 1)}). \end{align*} $$
$$ \begin{align*}\ln Z_{N,\beta}^{\mathrm{ref}} = \sum_{k = - 2}^{K} N^{-k}\,F_{\beta}^{\{k\};\mathrm{ref}} + \frac{\beta}{2}\ln N + \varkappa^{\mathrm{ref}} \ln N + O(N^{-(K + 1)}). \end{align*} $$
As the reference equilibrium measures are explicit, we can check by explicit computation that the potential-theoretic formula (7.2) holds. Using the change of variables
![]() $x = \frac {\gamma _+ + \gamma _-}{2}$
, we can also compute the entropy of the reference equilibrium measures. The result is
$x = \frac {\gamma _+ + \gamma _-}{2}$
, we can also compute the entropy of the reference equilibrium measures. The result is
 $$ \begin{align} {\mathrm{Ent}}[\mu_{\mathrm{eq}}^{\mathrm{ref}}] = \left\{\begin{array}{lll} -\frac{1}{2} + \ln(2\pi) + \ln\Big(\frac{\gamma_+ - \gamma_-}{4}\Big) && \mathrm{if}\,\,\gamma_{+}\,\,\mathrm{and}\,\,\gamma_{-}\,\,\mathrm{are}\,\,\mathrm{soft}, \\ -1 + \ln(2\pi) + \ln\Big(\frac{\gamma_+ - \gamma_-}{4}\Big) & & \mathrm{if}\,\,\gamma_{\pm}\,\,\mathrm{is}\,\,\mathrm{soft}\,\,\mathrm{and}\,\,\gamma_{\mp}\,\,\mathrm{is}\,\,\mathrm{hard}, \\ -\ln(2) + \ln(2\pi) + \ln\Big(\frac{\gamma_+ - \gamma_-}{4}\Big) & & \mathrm{if}\,\,\gamma_{+}\,\,\mathrm{and}\,\,\gamma_{-}\,\,\mathrm{are}\,\,\mathrm{hard}. \end{array} \right. \end{align} $$
$$ \begin{align} {\mathrm{Ent}}[\mu_{\mathrm{eq}}^{\mathrm{ref}}] = \left\{\begin{array}{lll} -\frac{1}{2} + \ln(2\pi) + \ln\Big(\frac{\gamma_+ - \gamma_-}{4}\Big) && \mathrm{if}\,\,\gamma_{+}\,\,\mathrm{and}\,\,\gamma_{-}\,\,\mathrm{are}\,\,\mathrm{soft}, \\ -1 + \ln(2\pi) + \ln\Big(\frac{\gamma_+ - \gamma_-}{4}\Big) & & \mathrm{if}\,\,\gamma_{\pm}\,\,\mathrm{is}\,\,\mathrm{soft}\,\,\mathrm{and}\,\,\gamma_{\mp}\,\,\mathrm{is}\,\,\mathrm{hard}, \\ -\ln(2) + \ln(2\pi) + \ln\Big(\frac{\gamma_+ - \gamma_-}{4}\Big) & & \mathrm{if}\,\,\gamma_{+}\,\,\mathrm{and}\,\,\gamma_{-}\,\,\mathrm{are}\,\,\mathrm{hard}. \end{array} \right. \end{align} $$
Collecting the previous expressions, we find that independently of the nature of the edges,
Adding this contribution to the formula of Lemma 7.3 gives a proof of Proposition 7.1 relating
![]() $F_{\beta }^{\{-1\};V}$
to the entropy of the equilibrium measure for general potential V. We also remark from the previous expressions that
$F_{\beta }^{\{-1\};V}$
to the entropy of the equilibrium measure for general potential V. We also remark from the previous expressions that
 $$ \begin{align*} \varkappa^{\mathrm{ref}} & = \frac{1}{2} + (\# \mathrm{soft} + 3\#\mathrm{hard}) \frac{-3 + \beta/2 + 2/\beta}{24}, \\ F_{\beta}^{\{0\};\mathrm{ref}} & = \frac{\# \mathrm{soft} + 3 \# \mathrm{hard}}{2}\,\chi'\big(0;\tfrac{2}{\beta},1\big) + \frac{\ln(2\pi)}{2} - \frac{\#\mathrm{hard}}{2}\,\ln\big(\tfrac{\beta}{2}\big) \\ & \quad + \delta_{\# \mathrm{hard},2} \frac{27 - 13(\beta/2 + 2/\beta)}{12}\,\ln(2). \end{align*} $$
$$ \begin{align*} \varkappa^{\mathrm{ref}} & = \frac{1}{2} + (\# \mathrm{soft} + 3\#\mathrm{hard}) \frac{-3 + \beta/2 + 2/\beta}{24}, \\ F_{\beta}^{\{0\};\mathrm{ref}} & = \frac{\# \mathrm{soft} + 3 \# \mathrm{hard}}{2}\,\chi'\big(0;\tfrac{2}{\beta},1\big) + \frac{\ln(2\pi)}{2} - \frac{\#\mathrm{hard}}{2}\,\ln\big(\tfrac{\beta}{2}\big) \\ & \quad + \delta_{\# \mathrm{hard},2} \frac{27 - 13(\beta/2 + 2/\beta)}{12}\,\ln(2). \end{align*} $$
7.3. Second step: decoupling the cuts
7.3.1. General strategy
This step is new compared to the one-cut situation treated in [Reference Borot and GuionnetBG11]. We are going to interpolate between the partition function of a
![]() $(g + 1)$
-cut model with fixed filling fractions to a product of
$(g + 1)$
-cut model with fixed filling fractions to a product of
![]() $(g + 1)$
partition functions of one-cut models. For this purpose, we introduce a slightly more general model
$(g + 1)$
partition functions of one-cut models. For this purpose, we introduce a slightly more general model
 $$ \begin{align*} & Z_{N,\beta;\boldsymbol{\epsilon}}^{V;\mathsf{A}}(s) \quad \\ & = \! \int_{\mathsf{A}_h^{N_h}} \Big[\prod_{h = 0}^{g} \prod_{i = 1}^{N_h} \mathrm{d}\lambda_{h,i}\,e^{-N\frac{\beta}{2}V(\lambda_{h,i})}\Big] \Big[\prod_{0 \leq h < h' \leq g} \prod_{\substack{1 \leq i \leq N_h \\ 1 \leq i' \leq N_{h'}}}\!\! |\lambda_{h,i} - \lambda_{h',i'}|^{s\beta}\Big] \Big[\prod_{h = 0}^{g} \prod_{1 \leq i < j \leq N_{h}} \!\! |\lambda_{h,i} - \lambda_{h,j}|^{\beta}\Big], \end{align*} $$
$$ \begin{align*} & Z_{N,\beta;\boldsymbol{\epsilon}}^{V;\mathsf{A}}(s) \quad \\ & = \! \int_{\mathsf{A}_h^{N_h}} \Big[\prod_{h = 0}^{g} \prod_{i = 1}^{N_h} \mathrm{d}\lambda_{h,i}\,e^{-N\frac{\beta}{2}V(\lambda_{h,i})}\Big] \Big[\prod_{0 \leq h < h' \leq g} \prod_{\substack{1 \leq i \leq N_h \\ 1 \leq i' \leq N_{h'}}}\!\! |\lambda_{h,i} - \lambda_{h',i'}|^{s\beta}\Big] \Big[\prod_{h = 0}^{g} \prod_{1 \leq i < j \leq N_{h}} \!\! |\lambda_{h,i} - \lambda_{h,j}|^{\beta}\Big], \end{align*} $$
which realises our interpolation for
![]() $s \in [0,1]$
. Although this s-dependent model is not of the form of the
$s \in [0,1]$
. Although this s-dependent model is not of the form of the
![]() $\beta $
-ensemble announced in introduction, we justify the following in § 7.4 below:
$\beta $
-ensemble announced in introduction, we justify the following in § 7.4 below:
Lemma 7.5. Assume Hypothesis 1.1–1.3 for V and consider the s-dependent model with s-dependent potential
 $$ \begin{align} T_s(x) = V(x) - 2(1 - s)\sum_{h' \neq h} \int_{\mathsf{A}_{h'}} \mathrm{d}\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}(\xi)\,\ln|x - \xi|,\qquad x \in \mathsf{A}_{h}. \end{align} $$
$$ \begin{align} T_s(x) = V(x) - 2(1 - s)\sum_{h' \neq h} \int_{\mathsf{A}_{h'}} \mathrm{d}\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}(\xi)\,\ln|x - \xi|,\qquad x \in \mathsf{A}_{h}. \end{align} $$
The correlators
![]() $W_{n;\boldsymbol {\epsilon }}^{s}$
of the model
$W_{n;\boldsymbol {\epsilon }}^{s}$
of the model
![]() $ Z_{N,\beta ;\boldsymbol {\epsilon }}^{T_{s};\mathsf {A}}(s)$
have a
$ Z_{N,\beta ;\boldsymbol {\epsilon }}^{T_{s};\mathsf {A}}(s)$
have a
![]() $\frac {1}{N}$
asymptotic expansion of the form
$\frac {1}{N}$
asymptotic expansion of the form
 $$ \begin{align*}W_{n;\boldsymbol{\epsilon}}^{s} = \sum_{k = n - 2}^{K} N^{-k}\,W_{n;\boldsymbol{\epsilon}}^{\{k\};s} + O(N^{-(K + 1)}) \end{align*} $$
$$ \begin{align*}W_{n;\boldsymbol{\epsilon}}^{s} = \sum_{k = n - 2}^{K} N^{-k}\,W_{n;\boldsymbol{\epsilon}}^{\{k\};s} + O(N^{-(K + 1)}) \end{align*} $$
for any
![]() $K \geq -2$
, for some N-independent functions
$K \geq -2$
, for some N-independent functions
![]() $W_{n;\boldsymbol {\epsilon }}^{\{k\};s}$
. This expansion is uniform for
$W_{n;\boldsymbol {\epsilon }}^{\{k\};s}$
. This expansion is uniform for
![]() $s \in [0,1]$
. Besides,
$s \in [0,1]$
. Besides,
![]() $W_{1;\boldsymbol {\epsilon }}^{\{-1\};s}$
is independent of s and therefore equals the Stieltjes transform of the equilibrium measure
$W_{1;\boldsymbol {\epsilon }}^{\{-1\};s}$
is independent of s and therefore equals the Stieltjes transform of the equilibrium measure
![]() $\mu _{\mathrm{eq};\boldsymbol {\epsilon }}^{V}$
. It is simply denoted by
$\mu _{\mathrm{eq};\boldsymbol {\epsilon }}^{V}$
. It is simply denoted by
![]() $W_{1;\boldsymbol {\epsilon }}^{\{-1\}}$
. Moreover, for any
$W_{1;\boldsymbol {\epsilon }}^{\{-1\}}$
. Moreover, for any
![]() $K\ge 0$
, we have
$K\ge 0$
, we have
 $$ \begin{align} \ln\bigg(\frac{Z_{N,\beta;\boldsymbol{\epsilon}}^{V;\mathsf{A}}}{Z_{N,\beta;\boldsymbol{\epsilon}}^{T_0;\mathsf{A}}(s = 0)}\bigg)= N^{2}F^{\{-2\};T}_{\beta;\boldsymbol{\epsilon}} +\sum_{k=0}^{K} N^{-k}F^{\{k\};T}_{\beta;\boldsymbol{\epsilon}}+O(N^{-K-1}) \end{align} $$
$$ \begin{align} \ln\bigg(\frac{Z_{N,\beta;\boldsymbol{\epsilon}}^{V;\mathsf{A}}}{Z_{N,\beta;\boldsymbol{\epsilon}}^{T_0;\mathsf{A}}(s = 0)}\bigg)= N^{2}F^{\{-2\};T}_{\beta;\boldsymbol{\epsilon}} +\sum_{k=0}^{K} N^{-k}F^{\{k\};T}_{\beta;\boldsymbol{\epsilon}}+O(N^{-K-1}) \end{align} $$
with
 $$ \begin{align*}F^{\{-2\};T}_{\beta;\boldsymbol{\epsilon}}=\frac{\beta}{2} \sum_{0 \leq h \neq h' \leq g} \int_{\mathsf{A}_{h}} \int_{\mathsf{A}_{h'}} \ln|x - y|\,\mathrm{d}\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}(x)\mathrm{d}\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}(y)\end{align*} $$
$$ \begin{align*}F^{\{-2\};T}_{\beta;\boldsymbol{\epsilon}}=\frac{\beta}{2} \sum_{0 \leq h \neq h' \leq g} \int_{\mathsf{A}_{h}} \int_{\mathsf{A}_{h'}} \ln|x - y|\,\mathrm{d}\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}(x)\mathrm{d}\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}(y)\end{align*} $$
and some constants
![]() $F^{\{k\};T}_{\beta ;\boldsymbol {\epsilon }}$
depending on
$F^{\{k\};T}_{\beta ;\boldsymbol {\epsilon }}$
depending on
![]() $W_{n;\boldsymbol {\epsilon }}^{s}$
with
$W_{n;\boldsymbol {\epsilon }}^{s}$
with
![]() $n = 1,2$
and
$n = 1,2$
and
![]() $s\in [0,1]$
.
$s\in [0,1]$
.
The choice of our interpolation has two advantages. First, at
![]() $s=1$
, we get our initial model, whereas at
$s=1$
, we get our initial model, whereas at
![]() $s=0$
, we get a product of one cut models which have already been analysed; see Section 7.3.2. However, our choice is such that the equilibrium measure for the model
$s=0$
, we get a product of one cut models which have already been analysed; see Section 7.3.2. However, our choice is such that the equilibrium measure for the model
![]() $\mu _{N,\beta ;\boldsymbol {\epsilon }}^{T_{s};\mathsf {A}}(s)$
is independent of s and equals
$\mu _{N,\beta ;\boldsymbol {\epsilon }}^{T_{s};\mathsf {A}}(s)$
is independent of s and equals
![]() $\mu _{\mathrm{eq};\boldsymbol {\epsilon }}^{V}$
; see Section 7.4.5. This implies clearly that
$\mu _{\mathrm{eq};\boldsymbol {\epsilon }}^{V}$
; see Section 7.4.5. This implies clearly that
![]() $W_{1;\boldsymbol {\epsilon }}^{\{-1\};s}$
is independent of s. Integrating the log-derivative of
$W_{1;\boldsymbol {\epsilon }}^{\{-1\};s}$
is independent of s. Integrating the log-derivative of
![]() $Z_{N,\beta ;\boldsymbol {\epsilon }}^{T_s;\mathsf {A}}(s)$
along the family of potentials
$Z_{N,\beta ;\boldsymbol {\epsilon }}^{T_s;\mathsf {A}}(s)$
along the family of potentials
![]() $(T_s)_{s \in [0,1]}$
given in Equation (7.22), we have the exact formula
$(T_s)_{s \in [0,1]}$
given in Equation (7.22), we have the exact formula
 $$ \begin{align*} & \ln\bigg(\frac{Z_{N,\beta;\boldsymbol{\epsilon}}^{V;\mathsf{A}}}{Z_{N,\beta;\boldsymbol{\epsilon}}^{T_0;\mathsf{A}}(s = 0)}\bigg) \\& \quad = \beta\! \int_{0}^{1} \!\mathrm{d} s\, \mu_{N,\beta;\boldsymbol{\epsilon}}^{T_{s};\mathsf{A}} \Bigg[\sum_{0 \leq h< h' \leq g}\sum_{{\substack{1 \leq i \leq N_h \\1 \leq i' \leq N_{h'}}}\!\! }\ln|\lambda_{h,i} - \lambda_{h',i'}| -N\sum_{0 \leq h' \neq h \leq g}\sum_{{\substack{1 \leq i \leq N_h }}} \int_{\mathsf S_{h'}} \!\ln |\lambda_{h,i}-x| \mathrm{d}\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}(x)\Bigg] \\& \quad = -N\beta \sum_{0 \leq h \neq h' \leq g} \oint_{\mathsf{A}_{h}}\oint_{\mathsf{A}_{h'}} \frac{\mathrm{d} x\,\mathrm{d} x'}{(2\mathrm{i}\pi)^2}\,\ln[(x - x')\mathrm{sgn}(h - h')]\,W_{1;\boldsymbol{\epsilon}}^{\{-1\}}(x)\,\bigg(\int_{0}^{1} \mathrm{d} s\, W_{1;\boldsymbol{\epsilon}}^{s}(x')\bigg) \\&\qquad + \sum_{0 \leq h' \neq h \leq g} \frac{\beta}{2} \oint_{\mathsf{A}_{h}}\oint_{\mathsf{A}_{h'}} \frac{\mathrm{d} x\,\mathrm{d} x'}{(2\mathrm{i}\pi)^2} \ln[(x - x')\mathrm{sgn}(h - h')]\bigg(\int_{0}^{1} \mathrm{d} s \big[W_{2;\boldsymbol{\epsilon}}^{s}(x,x') + W_{1;\boldsymbol{\epsilon}}^{s}(x)W_{1;\boldsymbol{\epsilon}}^{s}(x')\big]\bigg), \end{align*} $$
$$ \begin{align*} & \ln\bigg(\frac{Z_{N,\beta;\boldsymbol{\epsilon}}^{V;\mathsf{A}}}{Z_{N,\beta;\boldsymbol{\epsilon}}^{T_0;\mathsf{A}}(s = 0)}\bigg) \\& \quad = \beta\! \int_{0}^{1} \!\mathrm{d} s\, \mu_{N,\beta;\boldsymbol{\epsilon}}^{T_{s};\mathsf{A}} \Bigg[\sum_{0 \leq h< h' \leq g}\sum_{{\substack{1 \leq i \leq N_h \\1 \leq i' \leq N_{h'}}}\!\! }\ln|\lambda_{h,i} - \lambda_{h',i'}| -N\sum_{0 \leq h' \neq h \leq g}\sum_{{\substack{1 \leq i \leq N_h }}} \int_{\mathsf S_{h'}} \!\ln |\lambda_{h,i}-x| \mathrm{d}\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}(x)\Bigg] \\& \quad = -N\beta \sum_{0 \leq h \neq h' \leq g} \oint_{\mathsf{A}_{h}}\oint_{\mathsf{A}_{h'}} \frac{\mathrm{d} x\,\mathrm{d} x'}{(2\mathrm{i}\pi)^2}\,\ln[(x - x')\mathrm{sgn}(h - h')]\,W_{1;\boldsymbol{\epsilon}}^{\{-1\}}(x)\,\bigg(\int_{0}^{1} \mathrm{d} s\, W_{1;\boldsymbol{\epsilon}}^{s}(x')\bigg) \\&\qquad + \sum_{0 \leq h' \neq h \leq g} \frac{\beta}{2} \oint_{\mathsf{A}_{h}}\oint_{\mathsf{A}_{h'}} \frac{\mathrm{d} x\,\mathrm{d} x'}{(2\mathrm{i}\pi)^2} \ln[(x - x')\mathrm{sgn}(h - h')]\bigg(\int_{0}^{1} \mathrm{d} s \big[W_{2;\boldsymbol{\epsilon}}^{s}(x,x') + W_{1;\boldsymbol{\epsilon}}^{s}(x)W_{1;\boldsymbol{\epsilon}}^{s}(x')\big]\bigg), \end{align*} $$
and in the right-hand side, the uniformity of the asymptotic expansion when
![]() $N \rightarrow \infty $
of
$N \rightarrow \infty $
of
![]() $W_{1;\boldsymbol {\epsilon }}^{s}$
and
$W_{1;\boldsymbol {\epsilon }}^{s}$
and
![]() $W_{2;\boldsymbol {\epsilon }}^{s}$
with respect to s allows integrating over
$W_{2;\boldsymbol {\epsilon }}^{s}$
with respect to s allows integrating over
![]() $s \in [0,1]$
term by term. We obtain, for any
$s \in [0,1]$
term by term. We obtain, for any
![]() $K \geq 0$
,
$K \geq 0$
,
 $$ \begin{align*} & \ln\bigg(\frac{Z_{N,\beta;\boldsymbol{\epsilon}}^{V;\mathsf{A}}}{Z_{N,\beta;\boldsymbol{\epsilon}}^{T_0;\mathsf{A}}(s = 0)}\bigg) \\& \quad = - \frac{\beta N^2}{2} \sum_{0 \leq h \neq h' \leq g} \int_{\mathsf{A}_{h}} \int_{\mathsf{A}_{h'}} \ln|x - y|\,\mathrm{d}\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}(x)\mathrm{d}\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}(y) \\& \qquad + \sum_{k = 0}^{K} N^{-k} \sum_{0 \leq h' \neq h \leq g} \frac{\beta}{2}\oint_{\mathsf{A}_{h}}\oint_{\mathsf{A}_{h'}} \frac{\mathrm{d} x\,\mathrm{d} x'}{(2\mathrm{i}\pi)^2} \ln[(x - x')\mathrm{sgn}(h - h')] \\& \qquad\times\bigg\{\int_{0}^1\Big(W_{2;\boldsymbol{\epsilon}}^{\{k\};s}(x,x') + \sum_{\substack{k',k" \geq 0 \\ k' + k" = k}} W_{1;\boldsymbol{\epsilon}}^{\{k'\};s}(x)W_{1;\boldsymbol{\epsilon}}^{\{k"\};s}(x')\Big)\mathrm{d} s\bigg\} + O(N^{-(K + 1)}), \end{align*} $$
$$ \begin{align*} & \ln\bigg(\frac{Z_{N,\beta;\boldsymbol{\epsilon}}^{V;\mathsf{A}}}{Z_{N,\beta;\boldsymbol{\epsilon}}^{T_0;\mathsf{A}}(s = 0)}\bigg) \\& \quad = - \frac{\beta N^2}{2} \sum_{0 \leq h \neq h' \leq g} \int_{\mathsf{A}_{h}} \int_{\mathsf{A}_{h'}} \ln|x - y|\,\mathrm{d}\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}(x)\mathrm{d}\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}(y) \\& \qquad + \sum_{k = 0}^{K} N^{-k} \sum_{0 \leq h' \neq h \leq g} \frac{\beta}{2}\oint_{\mathsf{A}_{h}}\oint_{\mathsf{A}_{h'}} \frac{\mathrm{d} x\,\mathrm{d} x'}{(2\mathrm{i}\pi)^2} \ln[(x - x')\mathrm{sgn}(h - h')] \\& \qquad\times\bigg\{\int_{0}^1\Big(W_{2;\boldsymbol{\epsilon}}^{\{k\};s}(x,x') + \sum_{\substack{k',k" \geq 0 \\ k' + k" = k}} W_{1;\boldsymbol{\epsilon}}^{\{k'\};s}(x)W_{1;\boldsymbol{\epsilon}}^{\{k"\};s}(x')\Big)\mathrm{d} s\bigg\} + O(N^{-(K + 1)}), \end{align*} $$
where we noticed that the term depending linearly on N vanishes since the two first terms of the expansion reads
![]() $W_{1;\boldsymbol {\epsilon }}^{s}=NW_{1;\boldsymbol {\epsilon }}^{\{-1\}}(x)+W_{1,\boldsymbol {\epsilon }}^{\{0\};s}(x)+....$
This proves (7.23) if the first part of the Lemma is granted.
$W_{1;\boldsymbol {\epsilon }}^{s}=NW_{1;\boldsymbol {\epsilon }}^{\{-1\}}(x)+W_{1,\boldsymbol {\epsilon }}^{\{0\};s}(x)+....$
This proves (7.23) if the first part of the Lemma is granted.
7.3.2. The decoupled partition function
For
![]() $s = 0$
, we have
$s = 0$
, we have
 $$ \begin{align} Z_{N,\beta;\boldsymbol{\epsilon}}^{T_0;\mathsf{A}}(s = 0) = \prod_{h = 0}^{g} Z_{N\epsilon_h,\beta}^{T_0/\epsilon_h;\mathsf{A}_h}, \end{align} $$
$$ \begin{align} Z_{N,\beta;\boldsymbol{\epsilon}}^{T_0;\mathsf{A}}(s = 0) = \prod_{h = 0}^{g} Z_{N\epsilon_h,\beta}^{T_0/\epsilon_h;\mathsf{A}_h}, \end{align} $$
and its asymptotic expansion follows from (7.1). We remind that, in the partition function of the usual model (1.1) where filling fractions are not fixed, the eigenvalues are not ordered, while in (7.24) the groups of eigenvalues are ordered. We shall therefore study the asymptotic expansion of
![]() $\frac {N!}{\prod _{h = 0}^{g} N_h!}\,Z_{N,\beta ;\boldsymbol {\epsilon }}^{T_0;\mathsf {A}}(s = 0)$
. Taking into account
$\frac {N!}{\prod _{h = 0}^{g} N_h!}\,Z_{N,\beta ;\boldsymbol {\epsilon }}^{T_0;\mathsf {A}}(s = 0)$
. Taking into account
![]() $\sum _{h = 0}^g \epsilon _h = 1$
, Stirling expansion (7.18) yields
$\sum _{h = 0}^g \epsilon _h = 1$
, Stirling expansion (7.18) yields
 $$ \begin{align*} \frac{N!}{\prod_{h = 0}^{g} N_h!} & = \Big[\prod_{h = 0}^{g} \epsilon_h^{-\frac{1}{2}}\Big]\,\exp\Big\{-N\Big(\sum_{h = 0}^g \epsilon_h\ln \epsilon_h\Big) - \frac{g\ln N}{2} - \frac{g\ln(2\pi)}{2} \\ &\quad + \sum_{k = 1}^K \frac{N^{-k}\,B_{k + 1}}{k(k + 1)}\Big(1 - \sum_{h = 0}^{g} \epsilon_h^{-k}\Big)\Big\} + O(N^{-(K + 1)}). \end{align*} $$
$$ \begin{align*} \frac{N!}{\prod_{h = 0}^{g} N_h!} & = \Big[\prod_{h = 0}^{g} \epsilon_h^{-\frac{1}{2}}\Big]\,\exp\Big\{-N\Big(\sum_{h = 0}^g \epsilon_h\ln \epsilon_h\Big) - \frac{g\ln N}{2} - \frac{g\ln(2\pi)}{2} \\ &\quad + \sum_{k = 1}^K \frac{N^{-k}\,B_{k + 1}}{k(k + 1)}\Big(1 - \sum_{h = 0}^{g} \epsilon_h^{-k}\Big)\Big\} + O(N^{-(K + 1)}). \end{align*} $$
As the equilibrium measure of the s-dependent model with potential
![]() $T_{s}$
is independent of s, the equilibrium measure corresponding to the h-th model in (7.24) is the restriction to
$T_{s}$
is independent of s, the equilibrium measure corresponding to the h-th model in (7.24) is the restriction to
![]() $\mathsf {A}_{h}$
of
$\mathsf {A}_{h}$
of
![]() $\epsilon _h^{-1}\mu _{\mathrm{eq};\boldsymbol {\epsilon }}^{T_0/\epsilon _h}$
, and it has only one cut
$\epsilon _h^{-1}\mu _{\mathrm{eq};\boldsymbol {\epsilon }}^{T_0/\epsilon _h}$
, and it has only one cut
![]() $\mathsf {S}_h$
. Noticing that the entropy is additive for measures with disjoint support, we find the asymptotic expansion
$\mathsf {S}_h$
. Noticing that the entropy is additive for measures with disjoint support, we find the asymptotic expansion
 $$ \begin{align} \nonumber & \ln\bigg(\frac{N!\,Z_{N,\beta;\boldsymbol{\epsilon}}^{T_0;\mathsf{A}}(s = 0)}{\prod_{h = 0}^{g} N_h!}\bigg) \\\nonumber & \quad = N^2\bigg\{-E[\mu^{V}_{\mathrm{eq};\boldsymbol{\epsilon}}] + \frac{\beta}{2}\sum_{0 \leq h \neq h' \leq g} \iint_{\mathsf{A}_h \times \mathsf{A}_{h'}} \ln|x - y|\mathrm{d}\mu_{\mathrm{eq};\boldsymbol{\epsilon},h}^{V}(x)\mathrm{d}\mu_{\mathrm{eq};\boldsymbol{\epsilon},h}^{V}(y)\bigg\} \\\nonumber &\qquad + \frac{\beta}{2}N\ln N + N \Bigg\{- \frac{\beta}{2} \int_{\mathsf{A}} V^{\{1\}}(x)\mathrm{d}\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}(x) \\\nonumber & \qquad + \Big(1 - \frac{\beta}{2}\Big)\Big(\mathrm{Ent}[\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}] - \ln\big(\tfrac{\beta}{2}\big)\Big) + \frac{\beta}{2}\ln\Big(\frac{2\pi}{e}\Big) - \ln\Gamma\big(\tfrac{\beta}{2}\big)\bigg\} \\\nonumber & \qquad + \Big(\frac{1}{2} + (\#\mathrm{soft} + 3\#\mathrm{hard})\frac{-3 + \beta/2 + 2/\beta}{24}\Big)\ln N + \sum_{h = 0}^{g} \Big(F^{\{0\};T_0/\epsilon_h,\mathsf{A}_h}_{\beta} +\big(-\tfrac{\epsilon_h}{2} + \varkappa_{h}\big)\ln \epsilon_h\Big) \\& \qquad + \sum_{k = 1}^K N^{-k}\bigg\{\frac{B_{k + 1}}{k(k + 1)} + \sum_{h = 0}^{g} \frac{1}{\epsilon_h^{k}}\Big(F_{\beta}^{\{k\};T_0/\epsilon_h,\mathsf{A}_h} - \frac{B_{k + 1}}{k(k + 1)}\Big)\bigg\} + O(N^{-(K + 1)}), \end{align} $$
$$ \begin{align} \nonumber & \ln\bigg(\frac{N!\,Z_{N,\beta;\boldsymbol{\epsilon}}^{T_0;\mathsf{A}}(s = 0)}{\prod_{h = 0}^{g} N_h!}\bigg) \\\nonumber & \quad = N^2\bigg\{-E[\mu^{V}_{\mathrm{eq};\boldsymbol{\epsilon}}] + \frac{\beta}{2}\sum_{0 \leq h \neq h' \leq g} \iint_{\mathsf{A}_h \times \mathsf{A}_{h'}} \ln|x - y|\mathrm{d}\mu_{\mathrm{eq};\boldsymbol{\epsilon},h}^{V}(x)\mathrm{d}\mu_{\mathrm{eq};\boldsymbol{\epsilon},h}^{V}(y)\bigg\} \\\nonumber &\qquad + \frac{\beta}{2}N\ln N + N \Bigg\{- \frac{\beta}{2} \int_{\mathsf{A}} V^{\{1\}}(x)\mathrm{d}\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}(x) \\\nonumber & \qquad + \Big(1 - \frac{\beta}{2}\Big)\Big(\mathrm{Ent}[\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}] - \ln\big(\tfrac{\beta}{2}\big)\Big) + \frac{\beta}{2}\ln\Big(\frac{2\pi}{e}\Big) - \ln\Gamma\big(\tfrac{\beta}{2}\big)\bigg\} \\\nonumber & \qquad + \Big(\frac{1}{2} + (\#\mathrm{soft} + 3\#\mathrm{hard})\frac{-3 + \beta/2 + 2/\beta}{24}\Big)\ln N + \sum_{h = 0}^{g} \Big(F^{\{0\};T_0/\epsilon_h,\mathsf{A}_h}_{\beta} +\big(-\tfrac{\epsilon_h}{2} + \varkappa_{h}\big)\ln \epsilon_h\Big) \\& \qquad + \sum_{k = 1}^K N^{-k}\bigg\{\frac{B_{k + 1}}{k(k + 1)} + \sum_{h = 0}^{g} \frac{1}{\epsilon_h^{k}}\Big(F_{\beta}^{\{k\};T_0/\epsilon_h,\mathsf{A}_h} - \frac{B_{k + 1}}{k(k + 1)}\Big)\bigg\} + O(N^{-(K + 1)}), \end{align} $$
where
 $$ \begin{align*}\varkappa_h = \left\{\begin{array}{lll} \frac{3 + \beta/2 + 2/\beta}{12} && \mathrm{if} \,\,\mathrm{two}\,\,\mathrm{soft}\,\,\mathrm{edges}\,\,\mathrm{in}\,\,\mathsf{S}_h \\ \frac{\beta/2 + 2/\beta}{6} && \mathrm{if}\,\,\mathrm{one}\,\,\mathrm{soft}\,\,\mathrm{and}\,\,\mathrm{one}\,\,\mathrm{hard}\,\,\mathrm{edge}\,\,\mathrm{in}\,\,\mathsf{S}_h \\ \frac{-3 + \beta/2 + 2/\beta}{4} && \mathrm{if}\,\,\mathrm{two}\,\,\mathrm{hard}\,\,\mathrm{edges}\,\,\mathrm{in}\,\,\mathsf{S}_h.\end{array} \right. \end{align*} $$
$$ \begin{align*}\varkappa_h = \left\{\begin{array}{lll} \frac{3 + \beta/2 + 2/\beta}{12} && \mathrm{if} \,\,\mathrm{two}\,\,\mathrm{soft}\,\,\mathrm{edges}\,\,\mathrm{in}\,\,\mathsf{S}_h \\ \frac{\beta/2 + 2/\beta}{6} && \mathrm{if}\,\,\mathrm{one}\,\,\mathrm{soft}\,\,\mathrm{and}\,\,\mathrm{one}\,\,\mathrm{hard}\,\,\mathrm{edge}\,\,\mathrm{in}\,\,\mathsf{S}_h \\ \frac{-3 + \beta/2 + 2/\beta}{4} && \mathrm{if}\,\,\mathrm{two}\,\,\mathrm{hard}\,\,\mathrm{edges}\,\,\mathrm{in}\,\,\mathsf{S}_h.\end{array} \right. \end{align*} $$
We are going to use the notation
![]() $\mathrm{ref}(h)$
for the reference model that we associate to the one-cut model
$\mathrm{ref}(h)$
for the reference model that we associate to the one-cut model
![]() $Z_{N\epsilon _h,\beta }^{T_0/\epsilon _h;\mathsf {A}_h}$
. When we write the coefficients of the large N asymptotic expansion of
$Z_{N\epsilon _h,\beta }^{T_0/\epsilon _h;\mathsf {A}_h}$
. When we write the coefficients of the large N asymptotic expansion of
![]() $\ln \big (Z_{N\epsilon _h,\beta }^{T_0/\epsilon _h;\mathsf {A}_h}/Z_{N\epsilon _h,\beta }^{\mathrm{ref}(h)}\big )$
as in Equation (7.7), we find two possible sourcesFootnote 1 of explicit dependence in
$\ln \big (Z_{N\epsilon _h,\beta }^{T_0/\epsilon _h;\mathsf {A}_h}/Z_{N\epsilon _h,\beta }^{\mathrm{ref}(h)}\big )$
as in Equation (7.7), we find two possible sourcesFootnote 1 of explicit dependence in
![]() $\epsilon _h$
:
$\epsilon _h$
:
![]() $(N\epsilon _h)^{-k}$
, which is the natural variable of expansion for the h-th model, and a factor of
$(N\epsilon _h)^{-k}$
, which is the natural variable of expansion for the h-th model, and a factor of
![]() $\frac {1}{\epsilon _h}$
from each occurrence of
$\frac {1}{\epsilon _h}$
from each occurrence of
![]() $S_{s}$
(i.e., each application of
$S_{s}$
(i.e., each application of
![]() $\mathcal {K}^{-1}_{s}$
) due to the normalisation of the equilibrium measure of the h-th model. We then obtain
$\mathcal {K}^{-1}_{s}$
) due to the normalisation of the equilibrium measure of the h-th model. We then obtain
 $$ \begin{align*}\ln Z_{N\epsilon_h,\beta}^{T_0/\epsilon_h;\mathsf{A}_h} = \sum_{k = -2}^{K} N^{-k}\,F_{\beta}^{\{k\};T_0/\epsilon_h,\mathsf{A}_h} + O(N^{-(K + 1)}), \end{align*} $$
$$ \begin{align*}\ln Z_{N\epsilon_h,\beta}^{T_0/\epsilon_h;\mathsf{A}_h} = \sum_{k = -2}^{K} N^{-k}\,F_{\beta}^{\{k\};T_0/\epsilon_h,\mathsf{A}_h} + O(N^{-(K + 1)}), \end{align*} $$
with
 $$ \begin{align} F_{\beta}^{\{k\};T_0/\epsilon_h,\mathsf{A}_{h}} = F_{\beta}^{\{k\};\mathrm{ref}(h)} + \frac{\beta}{2} \oint_{\mathsf{S}_{h}} \frac{\mathrm{d} x}{2\mathrm{i}\pi}\,\big(V^{\mathrm{ref}(h)}(x)- T_0(x)/\epsilon_h\big)\Big(\int_{0}^{1} W_{1;(h)}^{\{k + 1\};s}(x)\,\mathrm{d} s\Big), \end{align} $$
$$ \begin{align} F_{\beta}^{\{k\};T_0/\epsilon_h,\mathsf{A}_{h}} = F_{\beta}^{\{k\};\mathrm{ref}(h)} + \frac{\beta}{2} \oint_{\mathsf{S}_{h}} \frac{\mathrm{d} x}{2\mathrm{i}\pi}\,\big(V^{\mathrm{ref}(h)}(x)- T_0(x)/\epsilon_h\big)\Big(\int_{0}^{1} W_{1;(h)}^{\{k + 1\};s}(x)\,\mathrm{d} s\Big), \end{align} $$
where by convention,
![]() $V^{\mathrm{ref}(h)}$
denotes the reference potential associated with the equilibrium measure of the h-th model – it only depends on the edges of the support
$V^{\mathrm{ref}(h)}$
denotes the reference potential associated with the equilibrium measure of the h-th model – it only depends on the edges of the support
![]() $\mathsf {S}_{h}$
and their nature and not on the filling fractions
$\mathsf {S}_{h}$
and their nature and not on the filling fractions
![]() $\boldsymbol {\epsilon }$
. Besides,
$\boldsymbol {\epsilon }$
. Besides,
![]() $W_{1;(h)}^{\{k + 1\};s}$
(here denoting the
$W_{1;(h)}^{\{k + 1\};s}$
(here denoting the
![]() $1$
-point correlator of the h-th model) is obtained by
$1$
-point correlator of the h-th model) is obtained by
![]() $k + 2$
successive applications of
$k + 2$
successive applications of
![]() $\mathcal {K}_{s}^{-1}$
to a quantity involving
$\mathcal {K}_{s}^{-1}$
to a quantity involving
![]() $W_{1;(h)}^{\{-1\};s}$
, the latter being proportional to
$W_{1;(h)}^{\{-1\};s}$
, the latter being proportional to
![]() $\epsilon _h^{-1}$
. Therefore,
$\epsilon _h^{-1}$
. Therefore,
![]() $W_{1;(h)}^{\{k + 1\};s}$
is proportional to
$W_{1;(h)}^{\{k + 1\};s}$
is proportional to
![]() $\epsilon _h^{-1 + (k + 2)}$
. As a result, the contributions from (7.26) result in Equation (7.25) in affine functions of
$\epsilon _h^{-1 + (k + 2)}$
. As a result, the contributions from (7.26) result in Equation (7.25) in affine functions of
![]() $\epsilon _h$
, and the terms of degree
$\epsilon _h$
, and the terms of degree
![]() $1$
in
$1$
in
![]() $\epsilon _h$
are the ones involving
$\epsilon _h$
are the ones involving
![]() $V^\mathrm{{ref}(h)}(x)$
.
$V^\mathrm{{ref}(h)}(x)$
.
7.3.3. Comparison with decoupled partition function
Note that there is no contribution of order N in the right-hand side and that the contribution of order
![]() $N^2$
reconstructs with that in
$N^2$
reconstructs with that in
![]() $\ln Z_{N,\beta ;\boldsymbol {\epsilon }}^{T_0;\mathsf {A}}\big (s = 0)$
the energy functional for
$\ln Z_{N,\beta ;\boldsymbol {\epsilon }}^{T_0;\mathsf {A}}\big (s = 0)$
the energy functional for
![]() $\mu _{\mathrm{eq}, {\boldsymbol \epsilon}}^{V}$
. Putting all results together (mainly Lemma 7.5 and (7.25)), we find the following:
$\mu _{\mathrm{eq}, {\boldsymbol \epsilon}}^{V}$
. Putting all results together (mainly Lemma 7.5 and (7.25)), we find the following:
Proposition 7.6. Assume Hypothesis 5.1. The partition function with fixed filling fractions admits an asymptotic expansion of the form, for any
![]() $K \geq 0$
,
$K \geq 0$
,
 $$ \begin{align*} \ln\bigg(\frac{N!\,Z_{N,\beta;\boldsymbol{\epsilon}}^{V;\mathsf{A}}}{\prod_{h = 0}^{g} N_h!}\bigg) & = -N^2 E[\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}] + \frac{\beta}{2}N\ln N \\& \quad + N\bigg\{-\frac{\beta}{2} \int_{\mathsf{A}} V^{\{1\}}(x)\mathrm{d}\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}(x) + \Big(1 - \frac{\beta}{2}\Big)\Big(\mathrm{Ent}[\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}] - \ln\big(\tfrac{\beta}{2}\big)\Big) + \frac{\beta}{2}\ln\Big(\frac{2\pi}{e}\Big) - \ln\Gamma\big(\tfrac{\beta}{2}\big)\bigg\} \\& \quad + \varkappa \ln N + \sum_{k = 0}^{K} N^{-k}\,F_{\beta;\boldsymbol{\epsilon}}^{\{k\};V} + O(N^{-(K + 1)}). \end{align*} $$
$$ \begin{align*} \ln\bigg(\frac{N!\,Z_{N,\beta;\boldsymbol{\epsilon}}^{V;\mathsf{A}}}{\prod_{h = 0}^{g} N_h!}\bigg) & = -N^2 E[\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}] + \frac{\beta}{2}N\ln N \\& \quad + N\bigg\{-\frac{\beta}{2} \int_{\mathsf{A}} V^{\{1\}}(x)\mathrm{d}\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}(x) + \Big(1 - \frac{\beta}{2}\Big)\Big(\mathrm{Ent}[\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}] - \ln\big(\tfrac{\beta}{2}\big)\Big) + \frac{\beta}{2}\ln\Big(\frac{2\pi}{e}\Big) - \ln\Gamma\big(\tfrac{\beta}{2}\big)\bigg\} \\& \quad + \varkappa \ln N + \sum_{k = 0}^{K} N^{-k}\,F_{\beta;\boldsymbol{\epsilon}}^{\{k\};V} + O(N^{-(K + 1)}). \end{align*} $$
The coefficient of
![]() $\ln N$
is
$\ln N$
is
The constant term is

The corrections for
![]() $k \geq 1$
are
$k \geq 1$
are

To compute the last term in Equation (7.28), at least in principle, we need formulas for
![]() $W_{1;\boldsymbol {\epsilon }}^{\{0\};V}$
and
$W_{1;\boldsymbol {\epsilon }}^{\{0\};V}$
and
![]() $W_{2;\boldsymbol {\epsilon }}^{\{0\};V}$
in the multi-cut fixed filling fractions case.
$W_{2;\boldsymbol {\epsilon }}^{\{0\};V}$
in the multi-cut fixed filling fractions case.
![]() $W_{1;\boldsymbol {\epsilon }}^{\{0\};V}$
is computed by Equation (5.45). Although we can use Equation (5.48) to compute
$W_{1;\boldsymbol {\epsilon }}^{\{0\};V}$
is computed by Equation (5.45). Although we can use Equation (5.48) to compute
![]() $W_{2}^{\{0\};V}$
, it is better expressed via its relation to the fundamental bidifferential of the second kind; see Equations (1.26)–(1.27).
$W_{2}^{\{0\};V}$
, it is better expressed via its relation to the fundamental bidifferential of the second kind; see Equations (1.26)–(1.27).
7.4. Proof of Lemma 7.5: expansion of correlators in the s-dependent model
We indicate how the arguments used so far in the article can be carried to the s-dependent model with fixed filling fractions without any difficulty. The interested reader can find all the details – in the greater generality of arbitrary pairwise interactions – in [Reference Borot, Guionnet and KozlowskiBGK15]. Let us take Hypotheses 1.1 and 1.3, as the weakening of the latter to Hypothesis 1.2 can be done as in Section 6.
7.4.1. Preliminary: the s-dependent energy functional and associated pseudo-distance
Hereafter, we study the energy functional associated with
![]() $Z_{N,\beta ;\boldsymbol {\epsilon }}^{V;\mathsf {A}}(s)$
. We introduce the matrix
$Z_{N,\beta ;\boldsymbol {\epsilon }}^{V;\mathsf {A}}(s)$
. We introduce the matrix
It is positive semi-definite, has an eigenvector
![]() $(1)_{h = 0}^{g}$
with positive eigenvalue
$(1)_{h = 0}^{g}$
with positive eigenvalue
![]() $(g + 1)$
and has a g-dimensional nullspace orthogonal to it. We define the s-dependent energy functional
$(g + 1)$
and has a g-dimensional nullspace orthogonal to it. We define the s-dependent energy functional
 $$ \begin{align*}E_s^V[\mu] = \frac{\beta}{2}\bigg(-\sum_{0 \leq h,h' \leq g} \iint_{\mathsf{A}_h \times \mathsf{A}_{h'}} \varsigma^s_{h,h'} \ln|x - y| \mathrm{d}\mu_{h}(x) \mathrm{d}\mu_{h'}(y) + \sum_{h = 0}^{g} \int_{\mathsf{A}_h} V^{\{0\}}(x) \mathrm{d} \mu_h(x)\bigg) \end{align*} $$
$$ \begin{align*}E_s^V[\mu] = \frac{\beta}{2}\bigg(-\sum_{0 \leq h,h' \leq g} \iint_{\mathsf{A}_h \times \mathsf{A}_{h'}} \varsigma^s_{h,h'} \ln|x - y| \mathrm{d}\mu_{h}(x) \mathrm{d}\mu_{h'}(y) + \sum_{h = 0}^{g} \int_{\mathsf{A}_h} V^{\{0\}}(x) \mathrm{d} \mu_h(x)\bigg) \end{align*} $$
depending on a probability measure
![]() $\mu $
supported
$\mu $
supported
![]() $\mathsf {A}$
, which we decompose as
$\mathsf {A}$
, which we decompose as
![]() $\mu = \sum _{h = 0}^{g} \mu _h$
, where
$\mu = \sum _{h = 0}^{g} \mu _h$
, where
![]() $\mu _h$
is supported on
$\mu _h$
is supported on
![]() $\mathsf {A}_h$
. We see that, with
$\mathsf {A}_h$
. We see that, with
![]() $E=E^{V}$
as defined in (1.5),
$E=E^{V}$
as defined in (1.5),
 $$ \begin{align} E_s^{V}[\mu] = \sum_{h = 0}^{g} E^{V}[\mu_h] + s \iint_{\mathsf{A}^2}\Lambda(x,y)\mathrm{d} \mu(x)\mathrm{d} \mu(y)\,, \end{align} $$
$$ \begin{align} E_s^{V}[\mu] = \sum_{h = 0}^{g} E^{V}[\mu_h] + s \iint_{\mathsf{A}^2}\Lambda(x,y)\mathrm{d} \mu(x)\mathrm{d} \mu(y)\,, \end{align} $$
where
 $$ \begin{align} \Lambda(\xi,\xi') = \left\{\begin{array}{lll} \ln|\xi - \xi'| & & \mathrm{if}\,\,(\xi,\xi') \in \mathsf{A}_{h}\times \mathsf{A}_{h'}\,\,\mathrm{and}\,\,h \neq h' \\ 0 & & \mathrm{otherwise} \end{array} \right. \end{align} $$
$$ \begin{align} \Lambda(\xi,\xi') = \left\{\begin{array}{lll} \ln|\xi - \xi'| & & \mathrm{if}\,\,(\xi,\xi') \in \mathsf{A}_{h}\times \mathsf{A}_{h'}\,\,\mathrm{and}\,\,h \neq h' \\ 0 & & \mathrm{otherwise} \end{array} \right. \end{align} $$
is a smooth bounded function on
![]() $\mathsf {A}^2$
. Since
$\mathsf {A}^2$
. Since
![]() $E[\mu _h]$
is well defined in
$E[\mu _h]$
is well defined in
![]() $\mathbb {R} \cup \{+\infty \}$
, this shows that
$\mathbb {R} \cup \{+\infty \}$
, this shows that
![]() $E_s^{V}[\mu ]$
is also well defined in
$E_s^{V}[\mu ]$
is also well defined in
![]() $\mathbb {R} \cup \{+\infty \}$
.
$\mathbb {R} \cup \{+\infty \}$
.
In intermediate steps, we will need the s-dependent analog of the pseudo-distance
![]() $\mathfrak {D}$
– namely,
$\mathfrak {D}$
– namely,
 $$ \begin{align} \nonumber \mathfrak{D}_{s}[\mu,\nu] & = \bigg(- s\sum_{0 \leq h \neq h' \leq g} \iint_{\mathsf{A}_{h} \times \mathsf{A}_{h'}} \ln|x - y|\mathrm{d}[\mu - \nu](x)\mathrm{d}[\mu - \nu](y) \\ \nonumber & \qquad - \sum_{h = 0}^{g} \iint_{\mathsf{A}_{h}^2} \ln|x - y| \mathrm{d}[\mu - \nu](x)\mathrm{d}[\mu - \nu](y)\bigg)^{\frac{1}{2}} \\ & = \bigg(\int_{0}^{\infty} \frac{\mathrm{d} p}{p}\Big\{ \sum_{0 \leq h,h' \leq g} \varsigma_{h,h'}^s (\widehat{\mu_{h}} - \widehat{\nu_{h}})(p)\overline{(\widehat{\mu_{h'}} - \widehat{\nu_{h'}})(p)}\Big\}\bigg)^{\frac{1}{2}}. \end{align} $$
$$ \begin{align} \nonumber \mathfrak{D}_{s}[\mu,\nu] & = \bigg(- s\sum_{0 \leq h \neq h' \leq g} \iint_{\mathsf{A}_{h} \times \mathsf{A}_{h'}} \ln|x - y|\mathrm{d}[\mu - \nu](x)\mathrm{d}[\mu - \nu](y) \\ \nonumber & \qquad - \sum_{h = 0}^{g} \iint_{\mathsf{A}_{h}^2} \ln|x - y| \mathrm{d}[\mu - \nu](x)\mathrm{d}[\mu - \nu](y)\bigg)^{\frac{1}{2}} \\ & = \bigg(\int_{0}^{\infty} \frac{\mathrm{d} p}{p}\Big\{ \sum_{0 \leq h,h' \leq g} \varsigma_{h,h'}^s (\widehat{\mu_{h}} - \widehat{\nu_{h}})(p)\overline{(\widehat{\mu_{h'}} - \widehat{\nu_{h'}})(p)}\Big\}\bigg)^{\frac{1}{2}}. \end{align} $$
We claim that it is well defined in
![]() $[0,+\infty ]$
for any two positive measures
$[0,+\infty ]$
for any two positive measures
![]() $\mu ,\nu $
of finite mass on
$\mu ,\nu $
of finite mass on
![]() $\mathsf {A}$
such that
$\mathsf {A}$
such that
![]() $\mu (\mathsf {A}_h) = \nu (\mathsf {A}_h)$
for any
$\mu (\mathsf {A}_h) = \nu (\mathsf {A}_h)$
for any ![]() . This is also the setting in which we need it since we work with the s-dependent model for fixed filling fractions. To see this, we first remark that
. This is also the setting in which we need it since we work with the s-dependent model for fixed filling fractions. To see this, we first remark that
 $$ \begin{align*}-\sum_{h = 0}^{g} \iint_{\mathsf{A}_h^2} \ln|x - y|\mathrm{d}[\mu - \nu](x)\mathrm{d}[\mu - \nu](y) = \sum_{h = 0}^{g} \mathfrak{D}^2[\mu_h,\nu_h] \end{align*} $$
$$ \begin{align*}-\sum_{h = 0}^{g} \iint_{\mathsf{A}_h^2} \ln|x - y|\mathrm{d}[\mu - \nu](x)\mathrm{d}[\mu - \nu](y) = \sum_{h = 0}^{g} \mathfrak{D}^2[\mu_h,\nu_h] \end{align*} $$
is well defined in
![]() $[0,+\infty ]$
. Again, as
$[0,+\infty ]$
. Again, as
![]() $(x,y) \mapsto \Lambda (x,y)$
is continuous bounded for
$(x,y) \mapsto \Lambda (x,y)$
is continuous bounded for
![]() $(x,y) \in \bigcup _{h \neq h'} \mathsf {A}_h \times \mathsf {A}_{h'}$
, we see that
$(x,y) \in \bigcup _{h \neq h'} \mathsf {A}_h \times \mathsf {A}_{h'}$
, we see that
 $$ \begin{align*}- \sum_{0 \leq h \neq h' \leq g}\iint_{\mathsf{A}_h \times \mathsf{A}_{h'}} \ln|x - y|\mathrm{d}[\mu - \nu](x)\mathrm{d}[\mu - \nu](y) \end{align*} $$
$$ \begin{align*}- \sum_{0 \leq h \neq h' \leq g}\iint_{\mathsf{A}_h \times \mathsf{A}_{h'}} \ln|x - y|\mathrm{d}[\mu - \nu](x)\mathrm{d}[\mu - \nu](y) \end{align*} $$
is well defined in
![]() $\mathbb {R}$
. So the quantity under the squareroot in Equation (7.32) is well defined a priori in
$\mathbb {R}$
. So the quantity under the squareroot in Equation (7.32) is well defined a priori in
![]() $\mathbb {R} \cup \{+\infty \}$
. Since
$\mathbb {R} \cup \{+\infty \}$
. Since
![]() $\boldsymbol {\varsigma }^{s}$
is positive semi-definite, we deduce that
$\boldsymbol {\varsigma }^{s}$
is positive semi-definite, we deduce that
![]() $\mathfrak {D}_s[\mu ,\nu ] \in [0,+\infty ]$
is well defined. If
$\mathfrak {D}_s[\mu ,\nu ] \in [0,+\infty ]$
is well defined. If
![]() $\mathfrak {D}_s[\mu ,\nu ] = 0$
, we must have
$\mathfrak {D}_s[\mu ,\nu ] = 0$
, we must have
![]() $\sum _{h = 0}^{g} \big (\widehat {\mu _h}(p) - \widehat {\nu _h}(p)\big ) = 0$
for p almost everywhere (corresponding to projection on the eigenvector with positive eigenvalue); hence,
$\sum _{h = 0}^{g} \big (\widehat {\mu _h}(p) - \widehat {\nu _h}(p)\big ) = 0$
for p almost everywhere (corresponding to projection on the eigenvector with positive eigenvalue); hence,
![]() $\sum _{h = 0}^{g} (\mu _h - \nu _h) = 0$
. Since the summands have pairwise disjoint supports, this implies
$\sum _{h = 0}^{g} (\mu _h - \nu _h) = 0$
. Since the summands have pairwise disjoint supports, this implies
![]() $\mu _h = \nu _h$
for all
$\mu _h = \nu _h$
for all ![]() – that is,
– that is,
![]() $\mu = \nu $
. So,
$\mu = \nu $
. So,
![]() $\mathfrak {D}_s$
is a pseudo-distance.
$\mathfrak {D}_s$
is a pseudo-distance.
We now explain how to control linear statistics in terms of
![]() $\mathfrak {D}_s$
, uniformly in s. Let
$\mathfrak {D}_s$
, uniformly in s. Let
![]() $\mu ,\nu $
be two positive measures on
$\mu ,\nu $
be two positive measures on
![]() $\mathsf {A}$
such that
$\mathsf {A}$
such that
![]() $\mu (\mathsf {A}_h) = \nu (\mathsf {A}_h)$
for any
$\mu (\mathsf {A}_h) = \nu (\mathsf {A}_h)$
for any ![]() . We decompose
. We decompose
![]() $\rho = \mu - \nu = \sum _{h = 0}^g \rho _{h}$
, where
$\rho = \mu - \nu = \sum _{h = 0}^g \rho _{h}$
, where
![]() $\rho _h$
is a signed measure of zero mass supported on
$\rho _h$
is a signed measure of zero mass supported on
![]() $\mathsf {A}_h$
. Let f be a smooth test function on
$\mathsf {A}_h$
. Let f be a smooth test function on
![]() $\mathsf {A}$
. Let
$\mathsf {A}$
. Let
![]() $\chi _{h}[f]$
be a smooth function on
$\chi _{h}[f]$
be a smooth function on
![]() $\mathbb {R}$
which is equal to f in
$\mathbb {R}$
which is equal to f in
![]() $\mathsf {A}_{h}$
,
$\mathsf {A}_{h}$
,
![]() $0$
outside a compact neighbourhood of
$0$
outside a compact neighbourhood of
![]() $\mathsf {A}_{h}$
and, in particular,
$\mathsf {A}_{h}$
and, in particular,
![]() $0$
on
$0$
on
![]() $\bigcup _{h' \neq h} \mathsf {A}_{h'}$
. One can choose the extension procedure so that
$\bigcup _{h' \neq h} \mathsf {A}_{h'}$
. One can choose the extension procedure so that
for a constant
![]() $C> 0$
independent of f and
$C> 0$
independent of f and ![]() (it is controlled by the minimum distance between the segments
(it is controlled by the minimum distance between the segments
![]() $\mathsf {A}_h$
). We observe that for
$\mathsf {A}_h$
). We observe that for
![]() $s \in [0,1]$
, the matrix
$s \in [0,1]$
, the matrix
![]() $\tilde {\boldsymbol {\varsigma }}^s = (u^s + v^s \delta _{h,h'})_{0 \leq h,h' \leq g}$
squares to
$\tilde {\boldsymbol {\varsigma }}^s = (u^s + v^s \delta _{h,h'})_{0 \leq h,h' \leq g}$
squares to
![]() $\boldsymbol {\varsigma }^s$
when we choose
$\boldsymbol {\varsigma }^s$
when we choose
 $$ \begin{align*}u^s = \frac{\sqrt{1 + gs} - \sqrt{1 - s}}{g + 1},\qquad v^s = \sqrt{1 - s}. \end{align*} $$
$$ \begin{align*}u^s = \frac{\sqrt{1 + gs} - \sqrt{1 - s}}{g + 1},\qquad v^s = \sqrt{1 - s}. \end{align*} $$
On the diagonal, this matrix has diagonal entries
 $$ \begin{align} u^s + v^s = \frac{g\sqrt{1 - s} + \sqrt{1 + gs}}{g + 1} \geq \frac{1}{g + 1}. \end{align} $$
$$ \begin{align} u^s + v^s = \frac{g\sqrt{1 - s} + \sqrt{1 + gs}}{g + 1} \geq \frac{1}{g + 1}. \end{align} $$
Let us write
 $$ \begin{align*} \bigg|\int_{\mathsf{A}} f(x)\mathrm{d}[\mu - \nu](x)\bigg| & = \bigg| \sum_{h = 0}^{g} \int_{\mathbb{R}} \chi_h[f](x) \mathrm{d}\rho_{h}(x) \Big| = \frac{1}{u^s + v^s} \bigg|\int_{\mathbb{R}} \sum_{h = 0}^{g} \chi_h[f](x) \Big(\sum_{h' = 0}^{g} \tilde{\varsigma}^s_{h,h'} \mathrm{d} \rho_{h'}(x)\Big) \bigg| \\ & \leq (g + 1)\bigg| \int_{\mathbb{R}} \sum_{h = 0}^{g} \overline{\widehat{\chi_h[f]}(p)}\Big(\sum_{h' = 0}^{g} \tilde{\varsigma}^s_{h,h'} \widehat{\nu_{h'}}(p)\Big) \mathrm{d} p\bigg|, \end{align*} $$
$$ \begin{align*} \bigg|\int_{\mathsf{A}} f(x)\mathrm{d}[\mu - \nu](x)\bigg| & = \bigg| \sum_{h = 0}^{g} \int_{\mathbb{R}} \chi_h[f](x) \mathrm{d}\rho_{h}(x) \Big| = \frac{1}{u^s + v^s} \bigg|\int_{\mathbb{R}} \sum_{h = 0}^{g} \chi_h[f](x) \Big(\sum_{h' = 0}^{g} \tilde{\varsigma}^s_{h,h'} \mathrm{d} \rho_{h'}(x)\Big) \bigg| \\ & \leq (g + 1)\bigg| \int_{\mathbb{R}} \sum_{h = 0}^{g} \overline{\widehat{\chi_h[f]}(p)}\Big(\sum_{h' = 0}^{g} \tilde{\varsigma}^s_{h,h'} \widehat{\nu_{h'}}(p)\Big) \mathrm{d} p\bigg|, \end{align*} $$
where we have used the bound (7.33) in the last line. We then use the Cauchy–Schwarz inequality:
 $$ \begin{align} \nonumber & \bigg|\int_{\mathsf{A}} f(x)\mathrm{d}[\mu - \nu](x)\bigg| \\\nonumber & \quad \leq (g + 1) \bigg(\int_{\mathbb{R}} \sum_{h = 0}^{g} \big|\widehat{\chi_h[f]}(p) \big|^2 |p|\,\mathrm{d} p \bigg)^{\frac{1}{2}} \bigg(\int_{\mathbb{R}} \sum_{0 \leq h,h',h" \leq g} \tilde{\varsigma}^{s}_{h,h'} \tilde{\varsigma}^s_{h,h"} \widehat{\nu_{h'}}(p)\,\overline{\widehat{\nu_{h"}}(p)} \frac{\mathrm{d} p}{|p|}\bigg)^{\frac{1}{2}} \\\nonumber & \quad \leq \sqrt{2}(g + 1)\Big(\sum_{h = 0}^{g} |\chi_h[f]|_{1/2}\Big)\Bigg(\int_{0}^{\infty} \sum_{0 \leq h',h" \leq g} \varsigma^{s}_{h',h"} \widehat{\nu_{h'}}(p) \overline{\widehat{\nu_{h"}}(p)} \frac{\mathrm{d} p}{|p|}\bigg)^{\frac{1}{2}} \\& \quad \leq \sqrt{2}C(g + 1)^{2}|f|_{1/2} \mathfrak{D}_s[\mu,\nu], \end{align} $$
$$ \begin{align} \nonumber & \bigg|\int_{\mathsf{A}} f(x)\mathrm{d}[\mu - \nu](x)\bigg| \\\nonumber & \quad \leq (g + 1) \bigg(\int_{\mathbb{R}} \sum_{h = 0}^{g} \big|\widehat{\chi_h[f]}(p) \big|^2 |p|\,\mathrm{d} p \bigg)^{\frac{1}{2}} \bigg(\int_{\mathbb{R}} \sum_{0 \leq h,h',h" \leq g} \tilde{\varsigma}^{s}_{h,h'} \tilde{\varsigma}^s_{h,h"} \widehat{\nu_{h'}}(p)\,\overline{\widehat{\nu_{h"}}(p)} \frac{\mathrm{d} p}{|p|}\bigg)^{\frac{1}{2}} \\\nonumber & \quad \leq \sqrt{2}(g + 1)\Big(\sum_{h = 0}^{g} |\chi_h[f]|_{1/2}\Big)\Bigg(\int_{0}^{\infty} \sum_{0 \leq h',h" \leq g} \varsigma^{s}_{h',h"} \widehat{\nu_{h'}}(p) \overline{\widehat{\nu_{h"}}(p)} \frac{\mathrm{d} p}{|p|}\bigg)^{\frac{1}{2}} \\& \quad \leq \sqrt{2}C(g + 1)^{2}|f|_{1/2} \mathfrak{D}_s[\mu,\nu], \end{align} $$
where we have used
![]() $\sqrt {X_0 + \cdots + X_g} \leq \sqrt {X_0} + \cdots + \sqrt {X_g}$
for nonnegative
$\sqrt {X_0 + \cdots + X_g} \leq \sqrt {X_0} + \cdots + \sqrt {X_g}$
for nonnegative
![]() $X_i$
in the first squareroot factor to get the second line.
$X_i$
in the first squareroot factor to get the second line.
7.4.2. Equilibrium measure
The properties of
![]() $E_s^{V}$
and its quadratic part established in the previous paragraph allow to apply the standard potential theoretic arguments. This leads to an analog of Theorem 1.2 for the s-dependent model with fixed filling fractions
$E_s^{V}$
and its quadratic part established in the previous paragraph allow to apply the standard potential theoretic arguments. This leads to an analog of Theorem 1.2 for the s-dependent model with fixed filling fractions
![]() $\boldsymbol {\epsilon }$
and potential V. It states the existence and uniqueness of the minimiser
$\boldsymbol {\epsilon }$
and potential V. It states the existence and uniqueness of the minimiser
![]() $\mu _{\mathrm{eq};\boldsymbol {\epsilon }}^{V;s}$
of
$\mu _{\mathrm{eq};\boldsymbol {\epsilon }}^{V;s}$
of
![]() $E_s^V$
among probability measures supported in
$E_s^V$
among probability measures supported in
![]() $\mathsf {A}$
and having fixed filling fractions
$\mathsf {A}$
and having fixed filling fractions
![]() $\boldsymbol {\epsilon }$
. The analog of (1.12) (i.e., the characterisation of the s-dependent equilibrium measure) is as follows: for each
$\boldsymbol {\epsilon }$
. The analog of (1.12) (i.e., the characterisation of the s-dependent equilibrium measure) is as follows: for each ![]() , there exists a constant
, there exists a constant
![]() $C_{\boldsymbol {\epsilon },h}^{V;s}$
such that
$C_{\boldsymbol {\epsilon },h}^{V;s}$
such that
 $$ \begin{align} 2\int_{\mathsf{A}_{h}} \mathrm{d}\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V;s}(\xi)\ln|x - \xi| + \sum_{h' \neq h} 2s\int_{\mathsf{A}_{h'}} \mathrm{d}\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V;s}(\xi)\ln|x - \xi| -V(x) \leq C^{V;s}_{\boldsymbol{\epsilon},h}, \end{align} $$
$$ \begin{align} 2\int_{\mathsf{A}_{h}} \mathrm{d}\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V;s}(\xi)\ln|x - \xi| + \sum_{h' \neq h} 2s\int_{\mathsf{A}_{h'}} \mathrm{d}\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V;s}(\xi)\ln|x - \xi| -V(x) \leq C^{V;s}_{\boldsymbol{\epsilon},h}, \end{align} $$
with equality
![]() $\mu _{\mathrm{eq};\boldsymbol {\epsilon }}^{V;s}$
almost surely.
$\mu _{\mathrm{eq};\boldsymbol {\epsilon }}^{V;s}$
almost surely.
7.4.3. Concentration estimates
The s-dependent model differs from the
![]() $\beta $
-ensemble (i.e.,
$\beta $
-ensemble (i.e.,
![]() $s = 1$
) by multiplication of the weight by
$s = 1$
) by multiplication of the weight by
 $$ \begin{align*}\exp\Big((1 - s)\beta \sum_{0 \leq h < h' \leq g} \sum_{\substack{1 \leq i \leq N_{h} \\ 1 \leq i' \leq N_{h'}}} \ln|\lambda_{h,i} - \lambda_{h',i'}|\Big) = \exp\Big( \frac{(1 - s)\beta}{2} \iint_{\mathbb{R}^2} \mathrm{d} L_N(\xi_1)\mathrm{d} L_N(\xi_2) \Lambda(\xi_1,\xi_2)\Big), \end{align*} $$
$$ \begin{align*}\exp\Big((1 - s)\beta \sum_{0 \leq h < h' \leq g} \sum_{\substack{1 \leq i \leq N_{h} \\ 1 \leq i' \leq N_{h'}}} \ln|\lambda_{h,i} - \lambda_{h',i'}|\Big) = \exp\Big( \frac{(1 - s)\beta}{2} \iint_{\mathbb{R}^2} \mathrm{d} L_N(\xi_1)\mathrm{d} L_N(\xi_2) \Lambda(\xi_1,\xi_2)\Big), \end{align*} $$
where
![]() $\Lambda $
was introduced in Equation (7.31) and is smooth bounded on
$\Lambda $
was introduced in Equation (7.31) and is smooth bounded on
![]() $\mathsf {A}^2$
. This is a perturbation of the
$\mathsf {A}^2$
. This is a perturbation of the
![]() $\beta $
-ensemble by a smooth functional of the empirical measure
$\beta $
-ensemble by a smooth functional of the empirical measure
![]() $L_{N}$
. Therefore, using
$L_{N}$
. Therefore, using
![]() $E_s$
and
$E_s$
and
![]() $\mathfrak {D}_s$
instead of E and
$\mathfrak {D}_s$
instead of E and
![]() $\mathfrak {D}$
, we can estimate the error made by replacing
$\mathfrak {D}$
, we can estimate the error made by replacing
![]() $L_N$
with the regularised empirical measure
$L_N$
with the regularised empirical measure
![]() $\widetilde {L}_N^{\mathrm{u}}$
as done in Section 3.4.1 and estimate the large deviations of
$\widetilde {L}_N^{\mathrm{u}}$
as done in Section 3.4.1 and estimate the large deviations of
![]() $\mathfrak {D}_s[\widetilde {L}_N^{\mathrm{u}},\mu _{\mathrm{eq};\boldsymbol {\epsilon }}^{T;s}]$
as in Section 3.4.2, leading to an analog of Lemma 3.5 with s-independent constants. We can then proceed to estimate the large deviations of fluctuations of linear statistics like in Section 3.5.1 – using the new Equation (7.34) instead of (3.26) – and obtain an analog of Corollary 3.6, where the constants are chosen independent of s and the only difference is that
$\mathfrak {D}_s[\widetilde {L}_N^{\mathrm{u}},\mu _{\mathrm{eq};\boldsymbol {\epsilon }}^{T;s}]$
as in Section 3.4.2, leading to an analog of Lemma 3.5 with s-independent constants. We can then proceed to estimate the large deviations of fluctuations of linear statistics like in Section 3.5.1 – using the new Equation (7.34) instead of (3.26) – and obtain an analog of Corollary 3.6, where the constants are chosen independent of s and the only difference is that
![]() $|\varphi |_{1/2}$
should be replaced by
$|\varphi |_{1/2}$
should be replaced by
![]() $C^{-1}|\varphi |_{1/2}$
for some
$C^{-1}|\varphi |_{1/2}$
for some
![]() $C> 0$
independent of s. We also get the a priori bound of the n-point correlators of the s-dependent model with filling fractions
$C> 0$
independent of s. We also get the a priori bound of the n-point correlators of the s-dependent model with filling fractions
![]() $\boldsymbol {\epsilon }$
(analog of Corollary 3.7) and an estimate of the large deviations of the filling fractions (analog of Corollary 3.8 with t replaced by
$\boldsymbol {\epsilon }$
(analog of Corollary 3.7) and an estimate of the large deviations of the filling fractions (analog of Corollary 3.8 with t replaced by
![]() $C t$
in the right-hand side) by a similar adaptation of Section 3.5.2. We conclude that all results of Section 3 extend to the s-dependent model with constants that can be chosen independent of
$C t$
in the right-hand side) by a similar adaptation of Section 3.5.2. We conclude that all results of Section 3 extend to the s-dependent model with constants that can be chosen independent of
![]() $s \in [0,1]$
.
$s \in [0,1]$
.
7.4.4. Dyson–Schwinger equations
If f is a holomorphic function in
![]() $\mathbb {C}\setminus \mathsf {A}$
and is decaying like
$\mathbb {C}\setminus \mathsf {A}$
and is decaying like
![]() $O(\frac {1}{x})$
at infinity, we may write
$O(\frac {1}{x})$
at infinity, we may write
 $$ \begin{align*}f(x) = \sum_{h = 0}^{g} \mathcal{P}_{h}[f](x),\qquad \mathcal{P}_{h}[f](x) = \oint_{\mathsf{A}_{h}} \frac{\mathrm{d}\xi}{2\mathrm{i}\pi}\,\frac{f(\xi)}{x - \xi}. \end{align*} $$
$$ \begin{align*}f(x) = \sum_{h = 0}^{g} \mathcal{P}_{h}[f](x),\qquad \mathcal{P}_{h}[f](x) = \oint_{\mathsf{A}_{h}} \frac{\mathrm{d}\xi}{2\mathrm{i}\pi}\,\frac{f(\xi)}{x - \xi}. \end{align*} $$
The operator
![]() $\mathcal {P}_{h}$
is a projector, and by construction,
$\mathcal {P}_{h}$
is a projector, and by construction,
![]() $\mathcal {P}_{h}[f]$
is holomorphic in
$\mathcal {P}_{h}[f]$
is holomorphic in
![]() $\mathbb {C}\setminus \mathsf {A}_{h}$
, is continuous across
$\mathbb {C}\setminus \mathsf {A}_{h}$
, is continuous across
![]() $\mathsf {A}_{h'}$
for
$\mathsf {A}_{h'}$
for
![]() $h' \neq h$
, and behaves like
$h' \neq h$
, and behaves like
![]() $O(\frac {1}{x})$
at infinity.
$O(\frac {1}{x})$
at infinity.
As in Section 4, we can derive the one-variable Dyson–Schwinger equation for the s-dependent model with potential V by integration by parts. The result is a small modification of Equation (4.2):

For
![]() $n \geq 2$
, a similar modification of Equation (4.3) for the n-variables Dyson–Schwinger equations can be written down.
$n \geq 2$
, a similar modification of Equation (4.3) for the n-variables Dyson–Schwinger equations can be written down.
7.4.5. Analysis of the Dyson–Schwinger equations
Let
![]() $\mu _{\mathrm{eq};\boldsymbol {\epsilon }}^{V}$
be the equilibrium measure of the
$\mu _{\mathrm{eq};\boldsymbol {\epsilon }}^{V}$
be the equilibrium measure of the
![]() $\beta $
-ensemble (i.e.,
$\beta $
-ensemble (i.e.,
![]() $s = 1$
) and fix
$s = 1$
) and fix
![]() $\mathsf {U}_{h}$
pairwise disjoint neighbourhoods of
$\mathsf {U}_{h}$
pairwise disjoint neighbourhoods of
![]() $\mathsf {A}_{h}$
. We remark that the equilibrium measure
$\mathsf {A}_{h}$
. We remark that the equilibrium measure
![]() $\mu _{\mathrm{eq};\boldsymbol {\epsilon }}^{T_{s};s}$
in the s-dependent model with the choice of a s-dependent potential on the h-th segment (h fixed),
$\mu _{\mathrm{eq};\boldsymbol {\epsilon }}^{T_{s};s}$
in the s-dependent model with the choice of a s-dependent potential on the h-th segment (h fixed),
 $$ \begin{align*}T_s(x) := V(x) - 2(1 - s)\sum_{0 \leq h' \neq h \leq g} \int_{\mathsf{A}_{h'}} \mathrm{d}\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}(\xi)\ln[(x - \xi)\mathrm{sgn}(h - h')], \end{align*} $$
$$ \begin{align*}T_s(x) := V(x) - 2(1 - s)\sum_{0 \leq h' \neq h \leq g} \int_{\mathsf{A}_{h'}} \mathrm{d}\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}(\xi)\ln[(x - \xi)\mathrm{sgn}(h - h')], \end{align*} $$
satisfies from (7.35) with
![]() $T_{s}$
in place of V the same characterisation as
$T_{s}$
in place of V the same characterisation as
![]() $\mu _{\mathrm{eq};\boldsymbol {\epsilon }}^{V}$
and hence, by uniqueness, is equal to
$\mu _{\mathrm{eq};\boldsymbol {\epsilon }}^{V}$
and hence, by uniqueness, is equal to
![]() $\mu _{\mathrm{eq};\boldsymbol {\epsilon }}^{V}$
for any
$\mu _{\mathrm{eq};\boldsymbol {\epsilon }}^{V}$
for any
![]() $s \in [0,1]$
. This justifies the choice of
$s \in [0,1]$
. This justifies the choice of
![]() $T_{s}$
in Lemma 7.5.
$T_{s}$
in Lemma 7.5.
Let us study the s-dependent model with this choice of s-dependent potential. The correlators are still denoted
![]() $W_{k}^{s}$
. The previous remark means that
$W_{k}^{s}$
. The previous remark means that
where
![]() $W_{1}^{\{-1\}}$
is the (s-independent) Stieltjes transform of
$W_{1}^{\{-1\}}$
is the (s-independent) Stieltjes transform of
![]() $\mu _{\mathrm{eq};\boldsymbol {\epsilon }}^{V}$
, and the error is uniform in
$\mu _{\mathrm{eq};\boldsymbol {\epsilon }}^{V}$
, and the error is uniform in
![]() $s \in [0,1]$
. We now decompose the modified Dyson–Schwinger equations (7.36) with
$s \in [0,1]$
. We now decompose the modified Dyson–Schwinger equations (7.36) with
![]() $V_h=T_{s}$
and the many variables analogue as in Equation (5.30), Section 5.3.1. Note that for x near
$V_h=T_{s}$
and the many variables analogue as in Equation (5.30), Section 5.3.1. Note that for x near
![]() $\mathsf {A}_h$
for a fixed h, we have
$\mathsf {A}_h$
for a fixed h, we have
 $$ \begin{align} T_s'(x) = V'(x) - 2(1-s)\sum_{0 \leq h' \neq h \leq g} \mathcal{P}_{h'}[W_1^{\{-1\}}](x)\,. \end{align} $$
$$ \begin{align} T_s'(x) = V'(x) - 2(1-s)\sum_{0 \leq h' \neq h \leq g} \mathcal{P}_{h'}[W_1^{\{-1\}}](x)\,. \end{align} $$
The relevant operators
![]() $\mathcal {K}^{s}$
and
$\mathcal {K}^{s}$
and
![]() $\Delta \mathcal {K}^{s}$
are now
$\Delta \mathcal {K}^{s}$
are now
 $$ \begin{align*} \mathcal{K}^{s} & = \mathcal{K} + \mathcal{D}^s, \\ \Delta\mathcal{K}^{s} & = \Delta\mathcal{K} + \Delta\mathcal{D}^s, \\ \Delta\mathcal{J}^s & = \Delta\mathcal{J} + \tfrac{1}{2}\Delta\mathcal{D}^s, \end{align*} $$
$$ \begin{align*} \mathcal{K}^{s} & = \mathcal{K} + \mathcal{D}^s, \\ \Delta\mathcal{K}^{s} & = \Delta\mathcal{K} + \Delta\mathcal{D}^s, \\ \Delta\mathcal{J}^s & = \Delta\mathcal{J} + \tfrac{1}{2}\Delta\mathcal{D}^s, \end{align*} $$
where
 $$ \begin{align*} \mathcal{D}^s[f](x) & = 2(s - 1) \sum_{0 \leq h \neq h' \leq g} \Big(\mathcal{P}_{h}[W_{1}^{\{-1\}}](x)\cdot \mathcal{P}_{h'}[f](x) - \mathcal{P}_{h'}\big[\mathcal{P}_{h}[W_1^{\{-1\}}] \cdot f\big](x)\Big), \\ \Delta\mathcal{D}^s[f](x) & = 2(s - 1) \sum_{0 \leq h \neq h' \leq g} \Big(\mathcal{P}_{h}[\Delta W_{1}^{\{-1\};s}](x)\cdot \mathcal{P}_{h'}[f](x) - \mathcal{P}_{h'}\big[\mathcal{P}_{h}[W_1^{\{-1\}}] \cdot f\big](x)\Big). \end{align*} $$
$$ \begin{align*} \mathcal{D}^s[f](x) & = 2(s - 1) \sum_{0 \leq h \neq h' \leq g} \Big(\mathcal{P}_{h}[W_{1}^{\{-1\}}](x)\cdot \mathcal{P}_{h'}[f](x) - \mathcal{P}_{h'}\big[\mathcal{P}_{h}[W_1^{\{-1\}}] \cdot f\big](x)\Big), \\ \Delta\mathcal{D}^s[f](x) & = 2(s - 1) \sum_{0 \leq h \neq h' \leq g} \Big(\mathcal{P}_{h}[\Delta W_{1}^{\{-1\};s}](x)\cdot \mathcal{P}_{h'}[f](x) - \mathcal{P}_{h'}\big[\mathcal{P}_{h}[W_1^{\{-1\}}] \cdot f\big](x)\Big). \end{align*} $$
The second term in
![]() $\mathcal {D}^s$
is the contribution of the extra term in the s-dependent potential (7.37) to the linearisation of the fourth line of the s-dependent Dyson–Schwinger equation (7.36), while the first term is what remains from the linearisation of the two first lines of (7.36) after we isolate the contribution of the usual
$\mathcal {D}^s$
is the contribution of the extra term in the s-dependent potential (7.37) to the linearisation of the fourth line of the s-dependent Dyson–Schwinger equation (7.36), while the first term is what remains from the linearisation of the two first lines of (7.36) after we isolate the contribution of the usual
![]() $s = 1$
operator
$s = 1$
operator
![]() $\mathcal {K}$
.
$\mathcal {K}$
.
In general,
![]() $\mathcal {D}^s$
and
$\mathcal {D}^s$
and
![]() $\Delta \mathcal {D}^s$
are nonzero operators. Indeed, if
$\Delta \mathcal {D}^s$
are nonzero operators. Indeed, if
![]() $g_h \in \mathcal {H}_1^{(1)}(\mathsf {A}_h)$
and
$g_h \in \mathcal {H}_1^{(1)}(\mathsf {A}_h)$
and
![]() $f \in \mathcal {H}_2^{(1)}(\mathsf {A})$
, we have for
$f \in \mathcal {H}_2^{(1)}(\mathsf {A})$
, we have for
![]() $h \neq h'$
,
$h \neq h'$
,
 $$ \begin{align*} g_h(x) \cdot \mathcal{P}_{h'}[f](x) - \mathcal{P}_{h'}[g_h \cdot f](x) & = g_h(x) \oint_{\mathsf{A}_{h'}} \frac{\mathrm{d} \xi}{2\mathrm{i}\pi}\,\frac{f(\xi)}{x - \xi} - \oint_{\mathsf{A}_{h'}} \frac{\mathrm{d} \xi}{2\mathrm{i}\pi}\,\frac{g_h(\xi) f(\xi)}{x - \xi} \\ & = \oint_{\mathsf{A}_{h'}} f(\xi)\,\frac{g_h(x) - g_h(\xi)}{x - \xi} \frac{\mathrm{d} \xi}{2\mathrm{i}\pi}= - \oint_{\mathsf{A}_h} f(\xi)\,\frac{g_h(x) - g_h(\xi)}{x - \xi} \frac{\mathrm{d} \xi}{2\mathrm{i}\pi}, \end{align*} $$
$$ \begin{align*} g_h(x) \cdot \mathcal{P}_{h'}[f](x) - \mathcal{P}_{h'}[g_h \cdot f](x) & = g_h(x) \oint_{\mathsf{A}_{h'}} \frac{\mathrm{d} \xi}{2\mathrm{i}\pi}\,\frac{f(\xi)}{x - \xi} - \oint_{\mathsf{A}_{h'}} \frac{\mathrm{d} \xi}{2\mathrm{i}\pi}\,\frac{g_h(\xi) f(\xi)}{x - \xi} \\ & = \oint_{\mathsf{A}_{h'}} f(\xi)\,\frac{g_h(x) - g_h(\xi)}{x - \xi} \frac{\mathrm{d} \xi}{2\mathrm{i}\pi}= - \oint_{\mathsf{A}_h} f(\xi)\,\frac{g_h(x) - g_h(\xi)}{x - \xi} \frac{\mathrm{d} \xi}{2\mathrm{i}\pi}, \end{align*} $$
where the last expression comes from moving the contour away from
![]() $\mathsf {A}_h$
, noticing that
$\mathsf {A}_h$
, noticing that
![]() $\xi \mapsto \frac {g_h(x) - g_h(\xi )}{x - \xi }$
is holomorphic in
$\xi \mapsto \frac {g_h(x) - g_h(\xi )}{x - \xi }$
is holomorphic in
![]() $\mathbb {C} \setminus \mathsf {A}_h$
and that there is no contribution from
$\mathbb {C} \setminus \mathsf {A}_h$
and that there is no contribution from
![]() $\infty $
since the integrands are
$\infty $
since the integrands are
![]() $O(\frac {1}{\xi ^2})$
as
$O(\frac {1}{\xi ^2})$
as
![]() $\xi \rightarrow \infty $
(by definition of the spaces
$\xi \rightarrow \infty $
(by definition of the spaces
![]() $\mathcal {H}^{(1)}_m$
). The nature of (7.4.5) is better seen if we further assume that f and
$\mathcal {H}^{(1)}_m$
). The nature of (7.4.5) is better seen if we further assume that f and
![]() $g_h$
have upper/lower boundaries values on
$g_h$
have upper/lower boundaries values on
![]() $\mathsf {A}$
(resp.
$\mathsf {A}$
(resp.
![]() $\mathsf {A}_{h'}$
). Indeed, by computing the difference of upper and lower boundary values of (7.4.5) for
$\mathsf {A}_{h'}$
). Indeed, by computing the difference of upper and lower boundary values of (7.4.5) for
![]() $x \in \mathsf {A}_h$
, we find
$x \in \mathsf {A}_h$
, we find
while for
![]() $x \in \mathsf {A}_{k}$
for
$x \in \mathsf {A}_{k}$
for
![]() $k \neq h$
(including
$k \neq h$
(including
![]() $k = h'$
), we find
$k = h'$
), we find
![]() $0$
. Therefore, (7.4.5) reconstructs the unique function in
$0$
. Therefore, (7.4.5) reconstructs the unique function in
![]() $\mathcal {H}_2^{(1)}(\mathsf {A}_{h})$
, whose jump (from upper to lower boundary value) is (7.38). The
$\mathcal {H}_2^{(1)}(\mathsf {A}_{h})$
, whose jump (from upper to lower boundary value) is (7.38). The
![]() $(h,h')$
-term in
$(h,h')$
-term in
![]() $\mathcal {D}^s[f]$
is
$\mathcal {D}^s[f]$
is
![]() $2(s-1)$
times (7.4.5) with
$2(s-1)$
times (7.4.5) with
![]() $g_h = \mathcal {P}_{h}[W_1^{\{-1\}}](x)$
.
$g_h = \mathcal {P}_{h}[W_1^{\{-1\}}](x)$
.
Unlike
![]() $\mathcal {K}$
, the operator
$\mathcal {K}$
, the operator
![]() $\mathcal {K}^s$
cannot be explicitly inverted, but we can nevertheless prove the analogue of Lemma 5.1 and 5.2 by functional analysis arguments.
$\mathcal {K}^s$
cannot be explicitly inverted, but we can nevertheless prove the analogue of Lemma 5.1 and 5.2 by functional analysis arguments.
Proposition 7.7. Assume Hypothesis 1.1.
![]() $\mathrm{Im}\,\mathcal {K}^s$
is closed in
$\mathrm{Im}\,\mathcal {K}^s$
is closed in
![]() $\mathcal {H}_{2}^{(1)}(\mathsf {A})$
, and there exists an operator
$\mathcal {H}_{2}^{(1)}(\mathsf {A})$
, and there exists an operator
![]() $(\widehat {\mathcal {K}}^s_{\boldsymbol {0}})^{-1}$
, with domain
$(\widehat {\mathcal {K}}^s_{\boldsymbol {0}})^{-1}$
, with domain
![]() $\mathrm{Im}\,\mathcal {K}^s$
and target the subspace of functions
$\mathrm{Im}\,\mathcal {K}^s$
and target the subspace of functions
![]() $\mathcal {H}_{2}^{(1)}(\mathsf {A})$
with zero
$\mathcal {H}_{2}^{(1)}(\mathsf {A})$
with zero
![]() $\boldsymbol {\mathcal {A}}$
-periods, providing the unique such solution
$\boldsymbol {\mathcal {A}}$
-periods, providing the unique such solution
![]() $f(x) = (\widehat {\mathcal {K}}^s_{\boldsymbol {0}})^{-1}[\varphi ](x)$
to the equation
$f(x) = (\widehat {\mathcal {K}}^s_{\boldsymbol {0}})^{-1}[\varphi ](x)$
to the equation
![]() $\mathcal {K}^s[f](x) = \varphi (x)$
. For any
$\mathcal {K}^s[f](x) = \varphi (x)$
. For any
![]() $\delta> 0$
independent of N, there exists s-independent constant
$\delta> 0$
independent of N, there exists s-independent constant
![]() $C(\delta )> 0$
such that
$C(\delta )> 0$
such that
Besides,
 $$ \begin{align} {\parallel} (\widehat{\mathcal{K}}^{s}_{\boldsymbol{0}})^{-1}[\Delta\mathcal{X}^{s}] {\parallel}_{2\delta} \leq C'(\delta)\,\sqrt{\frac{\ln N}{N}} {\parallel} \varphi {\parallel}_{\delta},\qquad \mathcal{X} = \mathcal{K}\,\,\mathrm{or}\,\,\mathcal{J}. \end{align} $$
$$ \begin{align} {\parallel} (\widehat{\mathcal{K}}^{s}_{\boldsymbol{0}})^{-1}[\Delta\mathcal{X}^{s}] {\parallel}_{2\delta} \leq C'(\delta)\,\sqrt{\frac{\ln N}{N}} {\parallel} \varphi {\parallel}_{\delta},\qquad \mathcal{X} = \mathcal{K}\,\,\mathrm{or}\,\,\mathcal{J}. \end{align} $$
Proof. Given
![]() $\varphi $
, let us try to solve the equation
$\varphi $
, let us try to solve the equation
![]() $\mathcal {K}^s[f](x) = \varphi (x)$
for a function f such that
$\mathcal {K}^s[f](x) = \varphi (x)$
for a function f such that
![]() $\oint _{\mathsf {A}_{h}} \frac {f(x)\mathrm {d} x}{2\mathrm{i}\pi } = 0$
for any
$\oint _{\mathsf {A}_{h}} \frac {f(x)\mathrm {d} x}{2\mathrm{i}\pi } = 0$
for any ![]() . Following the computations of Section 5.2.2, we have
. Following the computations of Section 5.2.2, we have
where
We now prove that the operator
![]() $(\mathrm{id} + \mathcal {G}\circ \mathcal {D}^s + \Pi )$
, with domain the subspace of functions in
$(\mathrm{id} + \mathcal {G}\circ \mathcal {D}^s + \Pi )$
, with domain the subspace of functions in
![]() $\mathcal {H}^{(1)}_{2}$
with zero
$\mathcal {H}^{(1)}_{2}$
with zero
![]() $\boldsymbol {\mathcal {A}}$
-periods, is injective. Assume we have an element q in the kernel of this operator. The expression,
$\boldsymbol {\mathcal {A}}$
-periods, is injective. Assume we have an element q in the kernel of this operator. The expression,
and the fact that
![]() $\mathcal {P}_{h'}[q](x)$
is holomorphic in a neighbourhood of
$\mathcal {P}_{h'}[q](x)$
is holomorphic in a neighbourhood of
![]() $\mathsf {A}_{h}$
for
$\mathsf {A}_{h}$
for
![]() $h \neq h'$
, shows that
$h \neq h'$
, shows that
![]() $\sigma (x)q(x)$
admits continuous upper and lower boundary values on
$\sigma (x)q(x)$
admits continuous upper and lower boundary values on
![]() $\mathsf {S}_{h}$
and is continuous across
$\mathsf {S}_{h}$
and is continuous across
![]() $\mathsf {A}_{h}\setminus \mathsf {S}_{h}$
. Hence, there exists an integrable measure
$\mathsf {A}_{h}\setminus \mathsf {S}_{h}$
. Hence, there exists an integrable measure
![]() $\nu ^{q}$
supported on
$\nu ^{q}$
supported on
![]() $\bigcup _{h = 0}^g \mathsf {S}_{h}$
such that
$\bigcup _{h = 0}^g \mathsf {S}_{h}$
such that
As
![]() $q(x)$
has zero
$q(x)$
has zero
![]() $\boldsymbol {\mathcal {A}}$
-periods, we have
$\boldsymbol {\mathcal {A}}$
-periods, we have
![]() $\nu ^{q}(\mathsf {A}_{h}) = 0$
for every h. Besides, computation with Equation (7.41) shows that
$\nu ^{q}(\mathsf {A}_{h}) = 0$
for every h. Besides, computation with Equation (7.41) shows that

which means in terms of the measure
![]() $\nu ^q$
,
$\nu ^q$
,

Integrating this equation from the left edge of
![]() $\mathsf {S}_{h}$
to x in the segment
$\mathsf {S}_{h}$
to x in the segment
![]() $\mathsf {S}_{h}$
yields
$\mathsf {S}_{h}$
yields

for some constant
![]() $c_h$
, where we remind that
$c_h$
, where we remind that
![]() $\varsigma _{h,h'}^{s} = 1$
if
$\varsigma _{h,h'}^{s} = 1$
if
![]() $h = h'$
, and s if
$h = h'$
, and s if
![]() $h \neq h'$
. Integrating this equation against the measure
$h \neq h'$
. Integrating this equation against the measure
![]() $\mathrm {d}\nu ^q$
over
$\mathrm {d}\nu ^q$
over
![]() $\mathsf {S}_{h}$
, the constant in the right-hand side disappears as
$\mathsf {S}_{h}$
, the constant in the right-hand side disappears as
![]() $\nu ^{q}(\mathsf {A}_{h}) = 0$
. Then summing over h, we find
$\nu ^{q}(\mathsf {A}_{h}) = 0$
. Then summing over h, we find
 $$ \begin{align*}\sum_{0 \leq h,h' \leq g} \iint_{\mathsf{S}_h \times \mathsf{S}_{h'}} \varsigma_{h,h'}^{s} \ln|x - \xi|\mathrm{d}\nu^q_{h}(x)\mathrm{d}\nu^q_{h'}(\xi) = 0, \end{align*} $$
$$ \begin{align*}\sum_{0 \leq h,h' \leq g} \iint_{\mathsf{S}_h \times \mathsf{S}_{h'}} \varsigma_{h,h'}^{s} \ln|x - \xi|\mathrm{d}\nu^q_{h}(x)\mathrm{d}\nu^q_{h'}(\xi) = 0, \end{align*} $$
but we have shown that in § 7.4.3 that this equality implies
![]() $\nu ^{q} = 0$
; hence,
$\nu ^{q} = 0$
; hence,
![]() $q = 0$
. This concludes the proof of injectivity.
$q = 0$
. This concludes the proof of injectivity.
Therefore,
![]() $(\mathrm{id} + \mathcal {G}\circ \mathcal {D}^s + \Pi )$
is invertible on its image. We proceed to show the continuity of this inverse. For this purpose, we fix once for all contours
$(\mathrm{id} + \mathcal {G}\circ \mathcal {D}^s + \Pi )$
is invertible on its image. We proceed to show the continuity of this inverse. For this purpose, we fix once for all contours
![]() $\gamma _h$
surrounding
$\gamma _h$
surrounding
![]() $\mathsf {A}_{h}$
and not
$\mathsf {A}_{h}$
and not
![]() $(\mathsf {A}_{h'})_{h' \neq h}$
, and set
$(\mathsf {A}_{h'})_{h' \neq h}$
, and set
![]() $\gamma = \bigcup _{h = 1}^{g} \gamma _{h}$
and
$\gamma = \bigcup _{h = 1}^{g} \gamma _{h}$
and
![]() $\boldsymbol {\gamma } = (\gamma _h)_{h = 1}^{g}$
. We equip
$\boldsymbol {\gamma } = (\gamma _h)_{h = 1}^{g}$
. We equip
![]() $\gamma $
with a curvilinear measure. From the expression of these operators – by moving the contour of integration to
$\gamma $
with a curvilinear measure. From the expression of these operators – by moving the contour of integration to
![]() $\gamma $
– one readily sees that
$\gamma $
– one readily sees that
![]() $(\mathcal {G}\circ \mathcal {D}^s + \Pi )$
can be considered as endomorphisms of
$(\mathcal {G}\circ \mathcal {D}^s + \Pi )$
can be considered as endomorphisms of
![]() $L^2(\gamma )$
, denote
$L^2(\gamma )$
, denote
![]() $\mathfrak {N}^s$
, which is compact. Let
$\mathfrak {N}^s$
, which is compact. Let
![]() $\tilde {\gamma }$
be the disjoint union of the set
$\tilde {\gamma }$
be the disjoint union of the set ![]() (equipped with the uniform measure) and
(equipped with the uniform measure) and
![]() $\gamma $
(equipped with the curvilinear measure), so
$\gamma $
(equipped with the curvilinear measure), so
![]() $L^2(\tilde {\gamma }) = \mathbb {C}^{g} \oplus L^2(\gamma )$
. We consider further the operator
$L^2(\tilde {\gamma }) = \mathbb {C}^{g} \oplus L^2(\gamma )$
. We consider further the operator
 $$ \begin{align*}\widehat{\mathfrak{N}}^s\,:\,\begin{array}{rcl} L^2(\tilde{\gamma}) & \longrightarrow & L^2(\tilde{\gamma}) \\ \big(\boldsymbol{w}, \phi\big) & \longmapsto & \big(-\boldsymbol{w} + \oint_{\boldsymbol{\gamma}} \frac{\phi(\xi)\,\mathrm{d} \xi}{2\mathrm{i}\pi}\,,\, \mathfrak{N}^s[\phi]\big) \end{array}, \end{align*} $$
$$ \begin{align*}\widehat{\mathfrak{N}}^s\,:\,\begin{array}{rcl} L^2(\tilde{\gamma}) & \longrightarrow & L^2(\tilde{\gamma}) \\ \big(\boldsymbol{w}, \phi\big) & \longmapsto & \big(-\boldsymbol{w} + \oint_{\boldsymbol{\gamma}} \frac{\phi(\xi)\,\mathrm{d} \xi}{2\mathrm{i}\pi}\,,\, \mathfrak{N}^s[\phi]\big) \end{array}, \end{align*} $$
and one can check as before that
![]() $\mathrm{id} + \widehat {\mathfrak {N}}^s$
is injective. As
$\mathrm{id} + \widehat {\mathfrak {N}}^s$
is injective. As
![]() $\widehat {\mathfrak {N}}^s$
is compact, Fredholm alternative ensures that
$\widehat {\mathfrak {N}}^s$
is compact, Fredholm alternative ensures that
![]() $\mathrm{id} + \widehat {\mathfrak {N}}^s$
is continuously invertible. Its inverse is
$\mathrm{id} + \widehat {\mathfrak {N}}^s$
is continuously invertible. Its inverse is
![]() $\mathrm{id} - \mathfrak {R}^s$
, where
$\mathrm{id} - \mathfrak {R}^s$
, where
![]() $\mathfrak {R}^s$
is the resolvent operator of
$\mathfrak {R}^s$
is the resolvent operator of
![]() $\widehat {\mathfrak {N}}^s$
, and it has a smooth integral kernel. This is enough to prove continuous invertibility of
$\widehat {\mathfrak {N}}^s$
, and it has a smooth integral kernel. This is enough to prove continuous invertibility of
![]() $\widehat {\mathcal {K}}^s$
and a bound for the norm of its inverse. The sought-for inverse for
$\widehat {\mathcal {K}}^s$
and a bound for the norm of its inverse. The sought-for inverse for
![]() $\widehat {\mathcal {K}}^s$
is
$\widehat {\mathcal {K}}^s$
is
where
![]() $\mathrm{pr}_{2}$
is the projection on the second factor
$\mathrm{pr}_{2}$
is the projection on the second factor
![]() $L^2(\tilde {\gamma })$
. The fact that this solution is actually in
$L^2(\tilde {\gamma })$
. The fact that this solution is actually in
![]() $\mathcal {H}_{2}^{(1)}(\mathsf {A})$
can be read from the equivalent versions of Equation (7.40) that we have encountered earlier – namely, (5.13), where one takes into account that
$\mathcal {H}_{2}^{(1)}(\mathsf {A})$
can be read from the equivalent versions of Equation (7.40) that we have encountered earlier – namely, (5.13), where one takes into account that
![]() $\mathrm{Im}\,\mathcal {G} \subseteq \mathcal {H}_2^{(1)}(\mathsf {A})$
(manifest on (5.12)) and the fact that
$\mathrm{Im}\,\mathcal {G} \subseteq \mathcal {H}_2^{(1)}(\mathsf {A})$
(manifest on (5.12)) and the fact that
![]() $\psi (x)$
is a polynomial of degree
$\psi (x)$
is a polynomial of degree
![]() $g - 1$
, while
$g - 1$
, while
![]() $\sigma (x)$
is the squareroot of a polynomial of degree
$\sigma (x)$
is the squareroot of a polynomial of degree
![]() $2g + 2$
.
$2g + 2$
.
The very construction of
![]() $\widehat {\mathfrak {N}}^s$
guarantees that
$\widehat {\mathfrak {N}}^s$
guarantees that
![]() $\oint _{\boldsymbol {\gamma }} \frac {f\!(x)\mathrm {d} x}{2\mathrm{i}\pi } = 0$
as desired, and the estimate on the norm of
$\oint _{\boldsymbol {\gamma }} \frac {f\!(x)\mathrm {d} x}{2\mathrm{i}\pi } = 0$
as desired, and the estimate on the norm of
![]() $(\widehat {\mathcal {K}}^{s}_{\boldsymbol {0}})^{-1}$
comes from the properties of the resolvent kernel. The proof of the estimate (7.39) follows the steps of Lemma 5.2 and is omitted.
$(\widehat {\mathcal {K}}^{s}_{\boldsymbol {0}})^{-1}$
comes from the properties of the resolvent kernel. The proof of the estimate (7.39) follows the steps of Lemma 5.2 and is omitted.
For
![]() $n \geq 2$
variables, the Dyson–Schwinger equations of the s-deformed model can be recast as
$n \geq 2$
variables, the Dyson–Schwinger equations of the s-deformed model can be recast as
with modified expression for A and B. For
![]() $n \geq 2$
, we have
$n \geq 2$
, we have
 $$ \begin{align*} A_{n + 1}^{s}(x;x_I) & = N^{-1}(\mathcal{L}_{2} - \mathrm{id})\bigg\{ s\Big(\sum_{0 \leq h \neq h' \leq g} \mathcal{P}_{h}\otimes \mathcal{P}_{h'}[W_{n + 1}^s(\bullet_1,\bullet_2,x_I)](x,x)\Big) \\& \quad \qquad \qquad \qquad + \sum_{h = 0}^g \mathcal{P}_{h}\otimes \mathcal{P}_{h}[W_{n + 1}^{s}(\bullet_1,\bullet_2,x_I)](x,x)\Big)\bigg\}, \\ B_{n + 1}^{t}(x;x_I) & = N^{-1}(\mathcal{L}_2 - \mathrm{id})\bigg\{\sum_{\substack{J \subseteq I \\J \neq (\emptyset,I)}} \sum_{0 \leq h \neq h' \leq g} s\mathcal{P}_{h}[W_{\# J + 1}^{s}(\bullet,x_J)](x)\cdot \mathcal{P}_{h'}[W_{n - \# J}^{s}(\bullet,x_{I\setminus J})](x) \\& \quad \qquad\qquad\qquad + \sum_{h = 0}^g \mathcal{P}_{h}[W_{\# J + 1}^{s}(\bullet,x_J)](x)\cdot\mathcal{P}_{h}[W_{n - \# J}^{s}(\bullet,x_{I\setminus J})](x)\bigg\}, \\C_{n - 1}^{s}(x;x_I) & = -\frac{2}{\beta N} \sum_{i \in I} \mathcal{M}_{x_i}[W_{n - 1}^{s}(\bullet,x_{I\setminus\{i\}})](x), \\D_{n - 1}^{s}(x;x_I) & = \frac{2}{\beta N} \sum_{a \in (\partial\mathsf{A})_+} \frac{L(a)}{x - a}\,\partial_{a} W_{n - 1}^{s}(x_I). \end{align*} $$
$$ \begin{align*} A_{n + 1}^{s}(x;x_I) & = N^{-1}(\mathcal{L}_{2} - \mathrm{id})\bigg\{ s\Big(\sum_{0 \leq h \neq h' \leq g} \mathcal{P}_{h}\otimes \mathcal{P}_{h'}[W_{n + 1}^s(\bullet_1,\bullet_2,x_I)](x,x)\Big) \\& \quad \qquad \qquad \qquad + \sum_{h = 0}^g \mathcal{P}_{h}\otimes \mathcal{P}_{h}[W_{n + 1}^{s}(\bullet_1,\bullet_2,x_I)](x,x)\Big)\bigg\}, \\ B_{n + 1}^{t}(x;x_I) & = N^{-1}(\mathcal{L}_2 - \mathrm{id})\bigg\{\sum_{\substack{J \subseteq I \\J \neq (\emptyset,I)}} \sum_{0 \leq h \neq h' \leq g} s\mathcal{P}_{h}[W_{\# J + 1}^{s}(\bullet,x_J)](x)\cdot \mathcal{P}_{h'}[W_{n - \# J}^{s}(\bullet,x_{I\setminus J})](x) \\& \quad \qquad\qquad\qquad + \sum_{h = 0}^g \mathcal{P}_{h}[W_{\# J + 1}^{s}(\bullet,x_J)](x)\cdot\mathcal{P}_{h}[W_{n - \# J}^{s}(\bullet,x_{I\setminus J})](x)\bigg\}, \\C_{n - 1}^{s}(x;x_I) & = -\frac{2}{\beta N} \sum_{i \in I} \mathcal{M}_{x_i}[W_{n - 1}^{s}(\bullet,x_{I\setminus\{i\}})](x), \\D_{n - 1}^{s}(x;x_I) & = \frac{2}{\beta N} \sum_{a \in (\partial\mathsf{A})_+} \frac{L(a)}{x - a}\,\partial_{a} W_{n - 1}^{s}(x_I). \end{align*} $$
And for
![]() $n = 1$
variable, we find the analogue of Equation (5.32),
$n = 1$
variable, we find the analogue of Equation (5.32),
with
 $$ \begin{align*} \Delta_{-1}P^{s}(x;\xi) & = \oint_{\mathsf{A}} \frac{\mathrm{d}\eta}{2\mathrm{i}\pi}\,2L_2(x;\xi,\eta)\,\Delta_{-1}W_1^{s}(\eta), \\ \Delta \mathcal{J}^{s}[f](x) & = - \mathcal{N}_{(\Delta_0 V)',\Delta_{-1}P^{s}(x;\bullet)/2}[f](x) + \sum_{0 \leq h \neq h' \leq g} s\mathcal{P}_{h}[\Delta_{-1}W_1^{s}](x)\,\mathcal{P}_{h'}f(x) \\ & \quad + \sum_{h} \mathcal{P}_{h}[\Delta_{-1}W_1^{s}](x)\,\mathcal{P}_{h}[f](x) + \frac{1}{N}\Big(1 - \frac{2}{\beta}\Big)(\partial_{x} + \mathcal{L}_{1})[f](x). \end{align*} $$
$$ \begin{align*} \Delta_{-1}P^{s}(x;\xi) & = \oint_{\mathsf{A}} \frac{\mathrm{d}\eta}{2\mathrm{i}\pi}\,2L_2(x;\xi,\eta)\,\Delta_{-1}W_1^{s}(\eta), \\ \Delta \mathcal{J}^{s}[f](x) & = - \mathcal{N}_{(\Delta_0 V)',\Delta_{-1}P^{s}(x;\bullet)/2}[f](x) + \sum_{0 \leq h \neq h' \leq g} s\mathcal{P}_{h}[\Delta_{-1}W_1^{s}](x)\,\mathcal{P}_{h'}f(x) \\ & \quad + \sum_{h} \mathcal{P}_{h}[\Delta_{-1}W_1^{s}](x)\,\mathcal{P}_{h}[f](x) + \frac{1}{N}\Big(1 - \frac{2}{\beta}\Big)(\partial_{x} + \mathcal{L}_{1})[f](x). \end{align*} $$
One can then repeat all the steps of Section 5.3, with the key point being that we use the inverse
![]() $(\widehat {\mathcal {K}}^{s}_{\boldsymbol {0}})^{-1}$
of
$(\widehat {\mathcal {K}}^{s}_{\boldsymbol {0}})^{-1}$
of
![]() $\mathcal {K}^s$
and its norm estimate constructed in Proposition 7.7. This results in the proof of an asymptotic expansion, for any
$\mathcal {K}^s$
and its norm estimate constructed in Proposition 7.7. This results in the proof of an asymptotic expansion, for any
![]() $K \geq 0$
,
$K \geq 0$
,
 $$ \begin{align*}W_{n}^{s}(x_1,\ldots,x_n) = \sum_{k = n - 2}^{K} N^{-k}\,W_n^{\{k\};s}(x_1,\ldots,x_n) + O(N^{-(K + 1)}), \end{align*} $$
$$ \begin{align*}W_{n}^{s}(x_1,\ldots,x_n) = \sum_{k = n - 2}^{K} N^{-k}\,W_n^{\{k\};s}(x_1,\ldots,x_n) + O(N^{-(K + 1)}), \end{align*} $$
where the coefficients
![]() $W_n^{\{k\};s}$
are N-independent, are given by a s-dependent recursion which is a s-dependent modification of the recursions provided in Section 5.4.
$W_n^{\{k\};s}$
are N-independent, are given by a s-dependent recursion which is a s-dependent modification of the recursions provided in Section 5.4.
7.5. Regularity with respect to the filling fractions
Let
![]() $\boldsymbol {\epsilon }_{\star }$
be the equilibrium filling fraction in the initial model
$\boldsymbol {\epsilon }_{\star }$
be the equilibrium filling fraction in the initial model
![]() $\mu _{N,\beta }^{V;\mathsf {A}}$
. In order to finish the proof of Theorem 1.3, it remains to show that the Hypotheses 1.1–1.2 for
$\mu _{N,\beta }^{V;\mathsf {A}}$
. In order to finish the proof of Theorem 1.3, it remains to show that the Hypotheses 1.1–1.2 for
![]() $\mu _{N,\beta }^{V;\mathsf {A}}$
imply Hypothesis 5.1 for the model
$\mu _{N,\beta }^{V;\mathsf {A}}$
imply Hypothesis 5.1 for the model
![]() $\mu _{N,\beta ;\boldsymbol {\epsilon }}^{V;\mathsf {A}}$
with fixed filling fractions
$\mu _{N,\beta ;\boldsymbol {\epsilon }}^{V;\mathsf {A}}$
with fixed filling fractions
![]() $\boldsymbol {\epsilon } \in \mathcal {E}$
close enough to
$\boldsymbol {\epsilon } \in \mathcal {E}$
close enough to
![]() $\boldsymbol {\epsilon }_{\star }$
, that all coefficients of the expansion extend as smooth functions of
$\boldsymbol {\epsilon }_{\star }$
, that all coefficients of the expansion extend as smooth functions of
![]() $\boldsymbol {\epsilon }$
, and that the Hessian of
$\boldsymbol {\epsilon }$
, and that the Hessian of
![]() $F^{\{-2\}}_{\boldsymbol {\epsilon }}$
with respect to filling fractions is negative definite. These properties are proved in the Appendix; see Propositions A.2–A.4.
$F^{\{-2\}}_{\boldsymbol {\epsilon }}$
with respect to filling fractions is negative definite. These properties are proved in the Appendix; see Propositions A.2–A.4.
Lemma 7.8. If V satisfies Hypotheses 1.1–1.3, then
![]() $(V,\boldsymbol {\epsilon })$
satisfies Hypotheses 5.1 for
$(V,\boldsymbol {\epsilon })$
satisfies Hypotheses 5.1 for
![]() $\boldsymbol {\epsilon } \in \mathcal {E}$
close enough to
$\boldsymbol {\epsilon } \in \mathcal {E}$
close enough to
![]() $\boldsymbol {\epsilon }_{\star }$
. Besides, the soft edges
$\boldsymbol {\epsilon }_{\star }$
. Besides, the soft edges
![]() $\alpha _h^{\bullet }$
and
$\alpha _h^{\bullet }$
and
![]() $W_{1;\boldsymbol {\epsilon }}^{\{-1\}}(x)$
(for x away from the edges) extend as
$W_{1;\boldsymbol {\epsilon }}^{\{-1\}}(x)$
(for x away from the edges) extend as
![]() $\mathcal {C}^{\infty }$
functions of
$\mathcal {C}^{\infty }$
functions of
![]() $\boldsymbol {\epsilon }$
, while the hard edges remain unchanged, at least for
$\boldsymbol {\epsilon }$
, while the hard edges remain unchanged, at least for
![]() $\boldsymbol {\epsilon }$
close enough to
$\boldsymbol {\epsilon }$
close enough to
![]() $\boldsymbol {\epsilon }_{\star }$
.
$\boldsymbol {\epsilon }_{\star }$
.
We observe that once
![]() $W^{\{-1\}}_{1;\boldsymbol {\epsilon }}$
and the edges of the support
$W^{\{-1\}}_{1;\boldsymbol {\epsilon }}$
and the edges of the support
![]() $\alpha _{\boldsymbol {\epsilon },h}^{\bullet }$
are known, the
$\alpha _{\boldsymbol {\epsilon },h}^{\bullet }$
are known, the
![]() $W_{n;\boldsymbol {\epsilon }}^{\{k\}}$
for any
$W_{n;\boldsymbol {\epsilon }}^{\{k\}}$
for any
![]() $n \geq 1$
and
$n \geq 1$
and
![]() $k \geq 0$
are determined recursively by Equations (5.38)–(5.36) and (5.50)–(5.48), where the linear operator
$k \geq 0$
are determined recursively by Equations (5.38)–(5.36) and (5.50)–(5.48), where the linear operator
![]() $\widehat {\mathcal {K}}^{-1}$
is given explicitly in Equations (5.12)–(5.19), and thus depends smoothly on
$\widehat {\mathcal {K}}^{-1}$
is given explicitly in Equations (5.12)–(5.19), and thus depends smoothly on
![]() $\boldsymbol {\epsilon }$
close enough to
$\boldsymbol {\epsilon }$
close enough to
![]() $\boldsymbol {\epsilon }_{\star }$
. Similarly,
$\boldsymbol {\epsilon }_{\star }$
. Similarly,
![]() $F^{\{k\}}_{\beta ;\boldsymbol {\epsilon }}$
for
$F^{\{k\}}_{\beta ;\boldsymbol {\epsilon }}$
for
![]() $k \geq 0$
are obtained from Equation (7.1) leading to Equations (7.28)–(7.29), which shows their smooth dependence for
$k \geq 0$
are obtained from Equation (7.1) leading to Equations (7.28)–(7.29), which shows their smooth dependence for
![]() $\boldsymbol {\epsilon }$
close enough to
$\boldsymbol {\epsilon }$
close enough to
![]() $\boldsymbol {\epsilon }_{\star }$
.
$\boldsymbol {\epsilon }_{\star }$
.
Corollary 7.9. If V satisfies Hypotheses 1.1–1.3, then
![]() $W_{n;\boldsymbol {\epsilon }}^{\{k\}}(x_1,\ldots ,x_k)$
(for
$W_{n;\boldsymbol {\epsilon }}^{\{k\}}(x_1,\ldots ,x_k)$
(for
![]() $x_1,\ldots ,x_k$
away from the support) and
$x_1,\ldots ,x_k$
away from the support) and
![]() $F^{\{k\}}_{\beta ;\boldsymbol {\epsilon }}$
extend as
$F^{\{k\}}_{\beta ;\boldsymbol {\epsilon }}$
extend as
![]() $\mathcal {C}^{\infty }$
functions of
$\mathcal {C}^{\infty }$
functions of
![]() $\boldsymbol {\epsilon } \in \mathcal {E}_{g}$
close enough to
$\boldsymbol {\epsilon } \in \mathcal {E}_{g}$
close enough to
![]() $\boldsymbol {\epsilon }_{\star }$
.
$\boldsymbol {\epsilon }_{\star }$
.
This concludes the proof of Theorem 1.4 announced in Section 1.4.
8. Asymptotic expansion in the initial model in the multi-cut regime
8.1. The partition function (Proof of Theorem 1.5)
We come back to the initial model
![]() $\mu _{N,\beta }^{V;\mathsf {A}}$
, and we assume Hypotheses 1.1–1.3 with number of cuts
$\mu _{N,\beta }^{V;\mathsf {A}}$
, and we assume Hypotheses 1.1–1.3 with number of cuts
![]() $(g + 1) \geq 2$
. We remind the notation
$(g + 1) \geq 2$
. We remind the notation
![]() $\boldsymbol {N} = (N_h)_{1 \leq h \leq g}$
for the number of eigenvalues in
$\boldsymbol {N} = (N_h)_{1 \leq h \leq g}$
for the number of eigenvalues in
![]() $\mathsf {A}_h$
, and the number of eigenvalues in
$\mathsf {A}_h$
, and the number of eigenvalues in
![]() $\mathsf {A}_0$
is
$\mathsf {A}_0$
is
![]() $N_0 = N - \sum _{h = 1}^{g} N_h$
. The
$N_0 = N - \sum _{h = 1}^{g} N_h$
. The
![]() $N_h$
are here random variables, which take the value
$N_h$
are here random variables, which take the value
![]() $N\boldsymbol {\epsilon }$
with probability
$N\boldsymbol {\epsilon }$
with probability
![]() $Z_{N,\beta ;\boldsymbol {\epsilon }}^{V;\mathsf {A}}/Z_{N,\beta }^{V;\mathsf {A}}$
. We denote
$Z_{N,\beta ;\boldsymbol {\epsilon }}^{V;\mathsf {A}}/Z_{N,\beta }^{V;\mathsf {A}}$
. We denote
![]() $\boldsymbol {\epsilon }_{\star }$
the vector of equilibrium filling fractions, and
$\boldsymbol {\epsilon }_{\star }$
the vector of equilibrium filling fractions, and
![]() $\boldsymbol {N}_\star = N\boldsymbol {\epsilon }_{\star }$
. Let us summarise five essential points:
$\boldsymbol {N}_\star = N\boldsymbol {\epsilon }_{\star }$
. Let us summarise five essential points:
-
○ By concentration of measures, Corollary 3.8 yields the existence of a constant
 $c,c'> 0$
such that, for N large enough, (8.1)
$c,c'> 0$
such that, for N large enough, (8.1) $$ \begin{align} \mu_{N,\beta}^{V;\mathsf{A}}\Big(|\boldsymbol{N} - \boldsymbol{N}_{\star}|_1> c\sqrt{N \ln N}\Big) \leq e^{-c'N\ln N}. \end{align} $$
$$ \begin{align} \mu_{N,\beta}^{V;\mathsf{A}}\Big(|\boldsymbol{N} - \boldsymbol{N}_{\star}|_1> c\sqrt{N \ln N}\Big) \leq e^{-c'N\ln N}. \end{align} $$
-
○ We have established in Theorem 1.4 an expansion for the partition function with fixed filling fractions.
-
○ Thanks to the strong off-criticality assumption and Lemma 7.8, we can apply Proposition 7.6: there exists
 $c">0$
small enough such that for
$c">0$
small enough such that for
 $|\boldsymbol {\epsilon } - \boldsymbol {\epsilon }_{\star}|_1 \leq c"$
, the model with fixed filling fractions
$|\boldsymbol {\epsilon } - \boldsymbol {\epsilon }_{\star}|_1 \leq c"$
, the model with fixed filling fractions
 $\boldsymbol {\epsilon }$
admits an asymptotic expansion of the form, for any
$\boldsymbol {\epsilon }$
admits an asymptotic expansion of the form, for any
 $K \geq 0$
, (8.2)with
$K \geq 0$
, (8.2)with $$ \begin{align} \frac{N!\,Z_{N,\beta;\boldsymbol{\epsilon}}^{V;\mathsf{A}}}{\prod_{h = 0}^g (N\epsilon_h)!} = N^{\frac{\beta}{2}N + \varkappa}\exp\Big(\sum_{k = -2}^{K} N^{-k}\,F_{\beta;\boldsymbol{\epsilon}}^{\{k\};V} + O(N^{-(K + 1)})\Big), \end{align} $$
$$ \begin{align} \frac{N!\,Z_{N,\beta;\boldsymbol{\epsilon}}^{V;\mathsf{A}}}{\prod_{h = 0}^g (N\epsilon_h)!} = N^{\frac{\beta}{2}N + \varkappa}\exp\Big(\sum_{k = -2}^{K} N^{-k}\,F_{\beta;\boldsymbol{\epsilon}}^{\{k\};V} + O(N^{-(K + 1)})\Big), \end{align} $$
 $\varkappa $
independent of
$\varkappa $
independent of
 $\boldsymbol {\epsilon }$
and given by Equation (7.27) and an error depending only on
$\boldsymbol {\epsilon }$
and given by Equation (7.27) and an error depending only on
 $c"$
.
$c"$
.
-
○ As established later in Proposition A.4, the Hessian
 $(F^{\{-2\}}_{\beta ;\star })"$
is negative definite.
$(F^{\{-2\}}_{\beta ;\star })"$
is negative definite. -
○ According to Lemma 7.8,
 $\boldsymbol {\epsilon } \mapsto F^{\{k\};V}_{\beta ;\boldsymbol {\epsilon }}$
is smooth in the domain
$\boldsymbol {\epsilon } \mapsto F^{\{k\};V}_{\beta ;\boldsymbol {\epsilon }}$
is smooth in the domain
 $|\boldsymbol {\epsilon } - \boldsymbol {\epsilon }_\star | < c"$
. From there, we deduce that, for any
$|\boldsymbol {\epsilon } - \boldsymbol {\epsilon }_\star | < c"$
. From there, we deduce that, for any
 $K,k \geq -2$
, there exist a constant
$K,k \geq -2$
, there exist a constant
 $C_{k,K}> 0$
and tensors
$C_{k,K}> 0$
and tensors
 $(F_{\beta ;\star }^{\{k\}})^{(j)} = \partial _{\boldsymbol {\epsilon }}^{\otimes j} F_{\beta ;\boldsymbol {\epsilon }}^{\{k\};V}|_{\boldsymbol {\epsilon } = \boldsymbol {\epsilon }_{\star }}$
, such that (8.3)
$(F_{\beta ;\star }^{\{k\}})^{(j)} = \partial _{\boldsymbol {\epsilon }}^{\otimes j} F_{\beta ;\boldsymbol {\epsilon }}^{\{k\};V}|_{\boldsymbol {\epsilon } = \boldsymbol {\epsilon }_{\star }}$
, such that (8.3) $$ \begin{align} \left| N^{-k}\,F^{\{k\};V}_{\beta;\boldsymbol{N}/N} - \sum_{j = 0}^{K - k} N^{-(k + j)}\frac{(F^{\{k\}}_{\beta;\star})^{(j)}}{j!}\cdot(\boldsymbol{N} - \boldsymbol{N}_{\star})^{\otimes j}\right| \leq C_{k,K}\,N^{-(K + 1)}|\boldsymbol{N}- \boldsymbol{N}_{\star}|^{K - k + 1}_1. \end{align} $$
$$ \begin{align} \left| N^{-k}\,F^{\{k\};V}_{\beta;\boldsymbol{N}/N} - \sum_{j = 0}^{K - k} N^{-(k + j)}\frac{(F^{\{k\}}_{\beta;\star})^{(j)}}{j!}\cdot(\boldsymbol{N} - \boldsymbol{N}_{\star})^{\otimes j}\right| \leq C_{k,K}\,N^{-(K + 1)}|\boldsymbol{N}- \boldsymbol{N}_{\star}|^{K - k + 1}_1. \end{align} $$
We now proceed with the proof of Theorem 1.5.
8.1.1. Taylor expansion around the equilibrium filling fraction
Due to the large deviation estimates for filling fractions (8.1), we can write for N large enough,
 $$ \begin{align*}(Z_{N,\beta}^{V;\mathsf{A}})^{-1} \bigg(\sum_{\substack{0 \leq N_1,\cdots,N_g \leq N \\ |\boldsymbol{N} - \boldsymbol{N}_{\star}|_1 \leq c\sqrt{N \ln N}}} \frac{N!\,Z_{N,\beta;\boldsymbol{N}/N}^{V;\mathsf{A}}}{\prod_{h = 0}^{g} N_h!} \bigg)= \mu_{N,\beta}^{V;\mathsf{A}}\Big(|\boldsymbol{N} - \boldsymbol{N}_{\star}|_1 \le c\sqrt{N \ln N}\Big)= 1 + O(e^{-c'N \ln N}). \end{align*} $$
$$ \begin{align*}(Z_{N,\beta}^{V;\mathsf{A}})^{-1} \bigg(\sum_{\substack{0 \leq N_1,\cdots,N_g \leq N \\ |\boldsymbol{N} - \boldsymbol{N}_{\star}|_1 \leq c\sqrt{N \ln N}}} \frac{N!\,Z_{N,\beta;\boldsymbol{N}/N}^{V;\mathsf{A}}}{\prod_{h = 0}^{g} N_h!} \bigg)= \mu_{N,\beta}^{V;\mathsf{A}}\Big(|\boldsymbol{N} - \boldsymbol{N}_{\star}|_1 \le c\sqrt{N \ln N}\Big)= 1 + O(e^{-c'N \ln N}). \end{align*} $$
In other words,
 $$ \begin{align*}Z_{N,\beta}^{V;\mathsf{A}}= \bigg(\sum_{\substack{0 \leq N_1,\cdots,N_g \leq N \\ |\boldsymbol{N} - \boldsymbol{N}_{\star}|_1 \leq c\sqrt{N \ln N}}} \frac{N!\,Z_{N,\beta;\boldsymbol{N}/N}^{V;\mathsf{A}}}{\prod_{h = 0}^{g} N_h!} \bigg)\big(1 + O(e^{-c'N \ln N})\big)\,.\end{align*} $$
$$ \begin{align*}Z_{N,\beta}^{V;\mathsf{A}}= \bigg(\sum_{\substack{0 \leq N_1,\cdots,N_g \leq N \\ |\boldsymbol{N} - \boldsymbol{N}_{\star}|_1 \leq c\sqrt{N \ln N}}} \frac{N!\,Z_{N,\beta;\boldsymbol{N}/N}^{V;\mathsf{A}}}{\prod_{h = 0}^{g} N_h!} \bigg)\big(1 + O(e^{-c'N \ln N})\big)\,.\end{align*} $$
For the range of filling fractions appearing in the sum in the right-hand side, we dispose of an asymptotic expansion of each term which are the partition functions of the model with fixed filling fractions by (8.2). Moreover, we can do the Taylor expansion of its coefficients with respect to
![]() $\boldsymbol {N}/N$
around
$\boldsymbol {N}/N$
around
![]() $\boldsymbol {\epsilon }_{\star }$
by (8.3) up to order
$\boldsymbol {\epsilon }_{\star }$
by (8.3) up to order
![]() $O(N^{-(2K + 1)})$
(and these errors are uniform for the range of filling fractions considered). This gives
$O(N^{-(2K + 1)})$
(and these errors are uniform for the range of filling fractions considered). This gives
 $$ \begin{align} \nonumber & \sum_{\substack{0 \leq N_1,\ldots,N_g \leq N \\ |\boldsymbol{N} - \boldsymbol{N}_{\star}|_1 \leq c\sqrt{N \ln N}}} \frac{N!\,Z_{N,\beta;\boldsymbol{N}/N}^{V;\mathsf{A}}}{\prod_{h = 0}^g N_h!}\, \\& \quad = \sum_{\substack{0 \leq N_1,\ldots,N_g \leq N \\ |\boldsymbol{N} - \boldsymbol{N}_{\star}|_1 \leq c\sqrt{N} \ln N}} \exp\bigg(\sum_{k = -2}^{2K} \sum_{j = 0}^{2K - k} N^{-(k + j)}\,\frac{(F^{\{k\}}_{\beta;\star})^{(j)}}{j!}\cdot(\boldsymbol{N} - \boldsymbol{N}_{\star})^{\otimes j} + N^{-(2K + 1)}R_{2K}(\boldsymbol{N})\bigg). \end{align} $$
$$ \begin{align} \nonumber & \sum_{\substack{0 \leq N_1,\ldots,N_g \leq N \\ |\boldsymbol{N} - \boldsymbol{N}_{\star}|_1 \leq c\sqrt{N \ln N}}} \frac{N!\,Z_{N,\beta;\boldsymbol{N}/N}^{V;\mathsf{A}}}{\prod_{h = 0}^g N_h!}\, \\& \quad = \sum_{\substack{0 \leq N_1,\ldots,N_g \leq N \\ |\boldsymbol{N} - \boldsymbol{N}_{\star}|_1 \leq c\sqrt{N} \ln N}} \exp\bigg(\sum_{k = -2}^{2K} \sum_{j = 0}^{2K - k} N^{-(k + j)}\,\frac{(F^{\{k\}}_{\beta;\star})^{(j)}}{j!}\cdot(\boldsymbol{N} - \boldsymbol{N}_{\star})^{\otimes j} + N^{-(2K + 1)}R_{2K}(\boldsymbol{N})\bigg). \end{align} $$
The error
![]() $N^{-(2K + 1)}R_{2K}(\boldsymbol {N})$
can be controlled according to Equation (8.3) using the constraint
$N^{-(2K + 1)}R_{2K}(\boldsymbol {N})$
can be controlled according to Equation (8.3) using the constraint
![]() ${|\boldsymbol {N} - \boldsymbol {N}_{\star }|_1 \leq c \sqrt {N \ln N}}$
, as follows:
${|\boldsymbol {N} - \boldsymbol {N}_{\star }|_1 \leq c \sqrt {N \ln N}}$
, as follows:
 $$ \begin{align} \nonumber |N^{-(2K + 1)}R_{2K}(\boldsymbol{N})| & \leq N^{-(2K+1)}\sum_{k=-2}^{2K} C_{k,2K}c^{2K - k}|\boldsymbol{N}-\boldsymbol{N}_{\star}|_1^{2K - k} \\ & \leq C_Kc^{2K} N^{-(2K+1)} N^{K}(\ln N)^{K}=C^{\prime}_K N^{-K-1} (\ln N)^K\,. \end{align} $$
$$ \begin{align} \nonumber |N^{-(2K + 1)}R_{2K}(\boldsymbol{N})| & \leq N^{-(2K+1)}\sum_{k=-2}^{2K} C_{k,2K}c^{2K - k}|\boldsymbol{N}-\boldsymbol{N}_{\star}|_1^{2K - k} \\ & \leq C_Kc^{2K} N^{-(2K+1)} N^{K}(\ln N)^{K}=C^{\prime}_K N^{-K-1} (\ln N)^K\,. \end{align} $$
Note here that all sums are finite since we stop them up to an error term which is uniformly bounded. Observing that
![]() $\exp (N^{-(K + 1)}R_K(\boldsymbol {N})) - 1 = O\big (N^{-K - 1}(\ln N)^{K}\big )$
when
$\exp (N^{-(K + 1)}R_K(\boldsymbol {N})) - 1 = O\big (N^{-K - 1}(\ln N)^{K}\big )$
when
![]() $N \rightarrow \infty $
uniformly over the range of filling fractions on which we sum in Equation (8.4), we get
$N \rightarrow \infty $
uniformly over the range of filling fractions on which we sum in Equation (8.4), we get
 $$ \begin{align} \frac{Z_{N,\beta}^{V;\mathsf{A}}}{1 + O(N^{-(K + 1)}(\ln N)^{K})} = \sum_{\substack{0 \leq N_1,\ldots,N_g \leq N \\ |\boldsymbol{N} - \boldsymbol{N}_{\star}|_1 \leq c \sqrt{N\ln N}}} \exp\bigg(\sum_{k = -2}^{2K} \sum_{j = 0}^{2K - k} N^{-(k + j)}\,\frac{(F^{\{k\}}_{\beta;\star})^{(j)}}{j!}\cdot(\boldsymbol{N} - \boldsymbol{N}_{\star})^{\otimes j}\bigg).\end{align} $$
$$ \begin{align} \frac{Z_{N,\beta}^{V;\mathsf{A}}}{1 + O(N^{-(K + 1)}(\ln N)^{K})} = \sum_{\substack{0 \leq N_1,\ldots,N_g \leq N \\ |\boldsymbol{N} - \boldsymbol{N}_{\star}|_1 \leq c \sqrt{N\ln N}}} \exp\bigg(\sum_{k = -2}^{2K} \sum_{j = 0}^{2K - k} N^{-(k + j)}\,\frac{(F^{\{k\}}_{\beta;\star})^{(j)}}{j!}\cdot(\boldsymbol{N} - \boldsymbol{N}_{\star})^{\otimes j}\bigg).\end{align} $$
Here, the previous error
![]() $O(e^{-c'N \ln N})$
has been absorbed in the larger error
$O(e^{-c'N \ln N})$
has been absorbed in the larger error
![]() $O(N^{-(K + 1)}(\ln N)^K)$
.
$O(N^{-(K + 1)}(\ln N)^K)$
.
Since
![]() $\boldsymbol {\epsilon }_{\star }$
is the equilibrium filling fraction, which is characterised as the filling fraction maximising
$\boldsymbol {\epsilon }_{\star }$
is the equilibrium filling fraction, which is characterised as the filling fraction maximising
![]() $F^{\{-2\}}_{\beta ;\boldsymbol {\epsilon }}$
, we have
$F^{\{-2\}}_{\beta ;\boldsymbol {\epsilon }}$
, we have
![]() $(F^{\{-2\}}_{\beta ;\star })' = 0$
. We can factor out the exponential containing the
$(F^{\{-2\}}_{\beta ;\star })' = 0$
. We can factor out the exponential containing the
![]() $F_{\beta ;\star }^{\{-k\}}$
without derivative. We then expand the exponential of terms containing
$F_{\beta ;\star }^{\{-k\}}$
without derivative. We then expand the exponential of terms containing
![]() $(F_{\beta ;\star }^{\{k\}})^{(j)}$
with
$(F_{\beta ;\star }^{\{k\}})^{(j)}$
with
![]() $k + j> 0$
, doing so up to an error of magnitude
$k + j> 0$
, doing so up to an error of magnitude
![]() $O(N^{-(K + 1)}(\ln N)^{K})$
. In this way only, remain in the exponential
$O(N^{-(K + 1)}(\ln N)^{K})$
. In this way only, remain in the exponential
![]() $(F_{\beta ;\star }^{\{-2\}})' = 0$
,
$(F_{\beta ;\star }^{\{-2\}})' = 0$
,
![]() $(F_{\beta ;\star }^{\{-2\}})"$
and
$(F_{\beta ;\star }^{\{-2\}})"$
and
![]() $(F_{\beta ;\star }^{\{-1\}})'$
. The result is the following expansion (note here that all sums are finite, including the one on r):
$(F_{\beta ;\star }^{\{-1\}})'$
. The result is the following expansion (note here that all sums are finite, including the one on r):
 $$ \begin{align} \nonumber & \frac{Z_{N,\beta}^{V;\mathsf{A}}}{1 + O(N^{-(K + 1)}(\ln N)^{K})} \\\nonumber & \quad = \exp\bigg(\sum_{k = -2}^{K} N^{-k} F_{\beta;\star}^{\{k\}}\bigg) \times \Bigg\{ \sum_{r \geq 0} \frac{1}{r!} \sum_{\substack{k_1,\ldots,k_r \geq -2 \\ j_1,\ldots,j_r \geq 1 \\ k_i + j_i> 0 \\ \sum_{i = 1}^{r} k_i + j_i \leq 2K}} \bigotimes_{i = 1}^{r} \frac{(F_{\beta;\star}^{\{k_i\}})^{(j_i)}}{j_i!} \\& \qquad \cdot \bigg(\sum_{\substack{0 \leq N_1,\ldots,N_g \leq N \\ |\boldsymbol{N} - \boldsymbol{N}_{\star} |_1 \leq c \sqrt{N \ln N}}} N^{-\sum_{i = 1}^r (k_i + j_i)} \,(\boldsymbol{N} - \boldsymbol{N}_{\star})^{\otimes (\sum_{i = 1}^r j_i)} e^{\frac{1}{2}(F_{\beta;\star}^{\{-2\}})" \cdot (\boldsymbol{N} - \boldsymbol{N}_{\star})^{\otimes 2} + (F_{\beta;\star}^{\{-1\}})' \cdot (\boldsymbol{N} - \boldsymbol{N}_{\star})}\bigg)\Bigg\}. \end{align} $$
$$ \begin{align} \nonumber & \frac{Z_{N,\beta}^{V;\mathsf{A}}}{1 + O(N^{-(K + 1)}(\ln N)^{K})} \\\nonumber & \quad = \exp\bigg(\sum_{k = -2}^{K} N^{-k} F_{\beta;\star}^{\{k\}}\bigg) \times \Bigg\{ \sum_{r \geq 0} \frac{1}{r!} \sum_{\substack{k_1,\ldots,k_r \geq -2 \\ j_1,\ldots,j_r \geq 1 \\ k_i + j_i> 0 \\ \sum_{i = 1}^{r} k_i + j_i \leq 2K}} \bigotimes_{i = 1}^{r} \frac{(F_{\beta;\star}^{\{k_i\}})^{(j_i)}}{j_i!} \\& \qquad \cdot \bigg(\sum_{\substack{0 \leq N_1,\ldots,N_g \leq N \\ |\boldsymbol{N} - \boldsymbol{N}_{\star} |_1 \leq c \sqrt{N \ln N}}} N^{-\sum_{i = 1}^r (k_i + j_i)} \,(\boldsymbol{N} - \boldsymbol{N}_{\star})^{\otimes (\sum_{i = 1}^r j_i)} e^{\frac{1}{2}(F_{\beta;\star}^{\{-2\}})" \cdot (\boldsymbol{N} - \boldsymbol{N}_{\star})^{\otimes 2} + (F_{\beta;\star}^{\{-1\}})' \cdot (\boldsymbol{N} - \boldsymbol{N}_{\star})}\bigg)\Bigg\}. \end{align} $$
8.1.2. Waiving the constraint on the sum
Our next task will be, for each of the finitely many tuples
![]() $(j_1,\ldots ,j_r)$
involved in the sum in the last line, to replace the constrained sum over
$(j_1,\ldots ,j_r)$
involved in the sum in the last line, to replace the constrained sum over
![]() $\boldsymbol {N}$
such that
$\boldsymbol {N}$
such that
![]() $|\boldsymbol {N} - \boldsymbol {N}_{\star }|_1 \leq c \sqrt {N \ln N}$
, with an unconstrained sum over
$|\boldsymbol {N} - \boldsymbol {N}_{\star }|_1 \leq c \sqrt {N \ln N}$
, with an unconstrained sum over
![]() $\boldsymbol {N} \in \mathbb {Z}^g$
. This will be possible because
$\boldsymbol {N} \in \mathbb {Z}^g$
. This will be possible because
![]() $(F^{\{-2\}}_{\beta ;\star })"$
is negative definite (Proposition A.4) – in other words, because the minimum eigenvalue q of the symmetric matrix
$(F^{\{-2\}}_{\beta ;\star })"$
is negative definite (Proposition A.4) – in other words, because the minimum eigenvalue q of the symmetric matrix
![]() $-(F^{\{-2\}}_{\beta ;\star })"$
is positive. More precisely, set
$-(F^{\{-2\}}_{\beta ;\star })"$
is positive. More precisely, set
![]() $J = \sum _{i = 1}^{r} j_i$
and notice Equation (8.7) only involves
$J = \sum _{i = 1}^{r} j_i$
and notice Equation (8.7) only involves
![]() $J \leq 2K$
. Let us equip
$J \leq 2K$
. Let us equip
![]() $\mathbb {R}^{g}$
with the euclidean norm
$\mathbb {R}^{g}$
with the euclidean norm
 $$ \begin{align*}\forall \boldsymbol{w} \in \mathbb{R}^g,\qquad |\boldsymbol{w}|_2 = \sqrt{\sum_{h = 1}^{g} w_h^2}. \end{align*} $$
$$ \begin{align*}\forall \boldsymbol{w} \in \mathbb{R}^g,\qquad |\boldsymbol{w}|_2 = \sqrt{\sum_{h = 1}^{g} w_h^2}. \end{align*} $$
In particular, we denote
![]() $r = \big |(F_{\beta ;\star }^{\{-1\}})'|_2$
. The tensor product
$r = \big |(F_{\beta ;\star }^{\{-1\}})'|_2$
. The tensor product
![]() $(\mathbb {R}^{g})^{\otimes J}$
is naturally equipped with a euclidean norm also denoted
$(\mathbb {R}^{g})^{\otimes J}$
is naturally equipped with a euclidean norm also denoted
![]() $|\cdot |_2$
, such that
$|\cdot |_2$
, such that
Let m be a positive integer. We shall estimate the contribution – with respect of the aforementioned euclidean norm in
![]() $(\mathbb {R}^{g})^{\otimes J}$
– that the
$(\mathbb {R}^{g})^{\otimes J}$
– that the
![]() $\boldsymbol {N} \in \mathbb {Z}^g$
in the shell between the euclidean balls of radius
$\boldsymbol {N} \in \mathbb {Z}^g$
in the shell between the euclidean balls of radius
![]() $m - 1$
and m would give to the sum
$m - 1$
and m would give to the sum
 $$ \begin{align*} & \sum_{\substack{\boldsymbol{N} \in \mathbb{Z}^g \\ |\boldsymbol{N} - \boldsymbol{N}_{\star}|_{2} \geq m}} \big|\boldsymbol{N} - \boldsymbol{N}_{\star}\big|_{2}^J e^{\frac{1}{2}(F_{\beta;\star}^{\{-2\}})" \cdot (\boldsymbol{N} - \boldsymbol{N}_{\star})^{\otimes 2} + (F_{\beta;\star}^{\{-1\}})' \cdot (\boldsymbol{N} - \boldsymbol{N}_{\star})} \\& \quad \leq \sum_{\substack{\boldsymbol{N} \in \mathbb{Z}^g \\ m - 1 \leq |\boldsymbol{N} - \boldsymbol{N}_{\star}|_{2} < m}} m^J e^{-\frac{q}{2}(m - 1)^2 + mr}, \\& \quad \leq C\,m^{J + g - 1} e^{-\frac{q}{2}m^2 + mr'} \end{align*} $$
$$ \begin{align*} & \sum_{\substack{\boldsymbol{N} \in \mathbb{Z}^g \\ |\boldsymbol{N} - \boldsymbol{N}_{\star}|_{2} \geq m}} \big|\boldsymbol{N} - \boldsymbol{N}_{\star}\big|_{2}^J e^{\frac{1}{2}(F_{\beta;\star}^{\{-2\}})" \cdot (\boldsymbol{N} - \boldsymbol{N}_{\star})^{\otimes 2} + (F_{\beta;\star}^{\{-1\}})' \cdot (\boldsymbol{N} - \boldsymbol{N}_{\star})} \\& \quad \leq \sum_{\substack{\boldsymbol{N} \in \mathbb{Z}^g \\ m - 1 \leq |\boldsymbol{N} - \boldsymbol{N}_{\star}|_{2} < m}} m^J e^{-\frac{q}{2}(m - 1)^2 + mr}, \\& \quad \leq C\,m^{J + g - 1} e^{-\frac{q}{2}m^2 + mr'} \end{align*} $$
for some constants
![]() $C> 0$
coming from the number of integer points in the spherical shell in g-dimensional space, and
$C> 0$
coming from the number of integer points in the spherical shell in g-dimensional space, and
![]() $r' = r + q$
. Then, there exists
$r' = r + q$
. Then, there exists
![]() $M_K> 0$
such that for
$M_K> 0$
such that for
![]() $m \geq M_K$
, we have
$m \geq M_K$
, we have
![]() $C\,m^{J + g - 1} e^{-qm^2 + mr'} \leq e^{-\frac {q}{4}m^2}$
. Up to choosing a larger
$C\,m^{J + g - 1} e^{-qm^2 + mr'} \leq e^{-\frac {q}{4}m^2}$
. Up to choosing a larger
![]() $M_K$
, we can assume as well for
$M_K$
, we can assume as well for
![]() $M> M_K$
,
$M> M_K$
,
 $$ \begin{align*}e^{-\frac{q}{2}M} < 1,\qquad \frac{e^{-\frac{q}{4}M^2}}{1 - e^{-\frac{q}{2}M}} \leq e^{-\frac{q}{8}M^2}. \end{align*} $$
$$ \begin{align*}e^{-\frac{q}{2}M} < 1,\qquad \frac{e^{-\frac{q}{4}M^2}}{1 - e^{-\frac{q}{2}M}} \leq e^{-\frac{q}{8}M^2}. \end{align*} $$
Then,
 $$ \begin{align*} & \sum_{\substack{\boldsymbol{N} \in \mathbb{Z}^g \\ |\boldsymbol{N} - \boldsymbol{N}_{\star}|_{2} \geq M}} \big|\boldsymbol{N} - \boldsymbol{N}_{\star}\big|_{2}^J \exp\Big(\frac{1}{2} (F_{\beta;\star}^{\{-2\}})" \cdot (\boldsymbol{N} - \boldsymbol{N}_{\star})^{\otimes 2} + (F_{\beta;\star}^{\{-1\}})' \cdot (\boldsymbol{N} - \boldsymbol{N}_{\star})\Big) \\ & \quad \leq \sum_{m \geq M} e^{-\frac{q}{4}m^2} \leq \sum_{m \geq 0} e^{-\frac{q}{4}M^2 - \frac{q}{2}mM} = \frac{e^{-\frac{q}{4}M^2}}{1 - e^{-\frac{q}{2}M}} \leq e^{-\frac{q}{8}M^2}. \end{align*} $$
$$ \begin{align*} & \sum_{\substack{\boldsymbol{N} \in \mathbb{Z}^g \\ |\boldsymbol{N} - \boldsymbol{N}_{\star}|_{2} \geq M}} \big|\boldsymbol{N} - \boldsymbol{N}_{\star}\big|_{2}^J \exp\Big(\frac{1}{2} (F_{\beta;\star}^{\{-2\}})" \cdot (\boldsymbol{N} - \boldsymbol{N}_{\star})^{\otimes 2} + (F_{\beta;\star}^{\{-1\}})' \cdot (\boldsymbol{N} - \boldsymbol{N}_{\star})\Big) \\ & \quad \leq \sum_{m \geq M} e^{-\frac{q}{4}m^2} \leq \sum_{m \geq 0} e^{-\frac{q}{4}M^2 - \frac{q}{2}mM} = \frac{e^{-\frac{q}{4}M^2}}{1 - e^{-\frac{q}{2}M}} \leq e^{-\frac{q}{8}M^2}. \end{align*} $$
By Cauchy–Schwarz inequality, we have
![]() $|\boldsymbol {N} - \boldsymbol {N}_{\star }|_1 \leq \sqrt {g}|\boldsymbol {N} - \boldsymbol {N}_{\star }|_2$
. Therefore, the terms
$|\boldsymbol {N} - \boldsymbol {N}_{\star }|_1 \leq \sqrt {g}|\boldsymbol {N} - \boldsymbol {N}_{\star }|_2$
. Therefore, the terms
![]() $\boldsymbol {N} \in \mathbb {Z}^{g}$
not included in Equation (8.7) can be bounded by Equation (8.1.2) with the choice
$\boldsymbol {N} \in \mathbb {Z}^{g}$
not included in Equation (8.7) can be bounded by Equation (8.1.2) with the choice
![]() $M = \big \lceil c\sqrt {\frac {N}{g} \ln N} \big \rceil $
:
$M = \big \lceil c\sqrt {\frac {N}{g} \ln N} \big \rceil $
:
 $$ \begin{align*} & \bigg| \sum_{\substack{\boldsymbol{N} \in \mathbb{Z}^g \\ |\boldsymbol{N} - \boldsymbol{N}_{\star}|_{1} \geq c \sqrt{N \ln N}}} (\boldsymbol{N} - \boldsymbol{N}_{\star})_{2}^{\otimes J} \exp\Big((F_{\beta;\star}^{\{-2\}})" \cdot (\boldsymbol{N} - \boldsymbol{N}_{\star})^{\otimes 2} + (F_{\beta;\star}^{\{-1\}})' \cdot (\boldsymbol{N} - \boldsymbol{N}_{\star})\Big)\bigg|_{2} \\ & \quad = O\big(e^{-\frac{q}{8}(\lceil c\sqrt{\frac{N}{g}\ln N} \rceil)^2}\big) = O(e^{-q'N \ln N}) \end{align*} $$
$$ \begin{align*} & \bigg| \sum_{\substack{\boldsymbol{N} \in \mathbb{Z}^g \\ |\boldsymbol{N} - \boldsymbol{N}_{\star}|_{1} \geq c \sqrt{N \ln N}}} (\boldsymbol{N} - \boldsymbol{N}_{\star})_{2}^{\otimes J} \exp\Big((F_{\beta;\star}^{\{-2\}})" \cdot (\boldsymbol{N} - \boldsymbol{N}_{\star})^{\otimes 2} + (F_{\beta;\star}^{\{-1\}})' \cdot (\boldsymbol{N} - \boldsymbol{N}_{\star})\Big)\bigg|_{2} \\ & \quad = O\big(e^{-\frac{q}{8}(\lceil c\sqrt{\frac{N}{g}\ln N} \rceil)^2}\big) = O(e^{-q'N \ln N}) \end{align*} $$
for some constant
![]() $q'> 0$
when
$q'> 0$
when
![]() $N \rightarrow \infty $
. As a result,
$N \rightarrow \infty $
. As a result,
 $$ \begin{align} \nonumber & \frac{Z_{N,\beta}^{V;\mathsf{A}}}{1 + O(N^{-(K + 1)}(\ln N)^{K})} \\& \quad = \exp\bigg(\sum_{k = -2}^{K} N^{-k} F_{\beta;\star}^{V}\bigg) \times \Bigg\{ \sum_{r \geq 0} \frac{1}{r!} \sum_{\substack{k_1,\ldots,k_r \geq -2 \\ j_1,\ldots,j_r \geq 0 \\ k_i + j_i> 0 \\ \sum_{i = 1}^{r} k_i + j_i \leq 2K}} N^{-\sum_{i = 1}^r (k_i + j_i)} \bigotimes_{i = 1}^{r} \frac{(F_{\beta;\star}^{\{k_i\}})^{(j_i)}}{j_i!} \nonumber \\& \qquad \cdot \bigg(\sum_{\boldsymbol{N} \in \mathbb{Z}^g} (\boldsymbol{N} - \boldsymbol{N}_{\star})^{\otimes (\sum_{i = 1}^r j_i)} \exp\Big((F_{\beta;\star}^{\{-2\}})" \cdot (\boldsymbol{N} - \boldsymbol{N}_{\star})^{\otimes 2} + (F_{\beta;\star}^{\{-1\}})' \cdot (\boldsymbol{N} - \boldsymbol{N}_{\star})\Big)\bigg)\Bigg\}. \end{align} $$
$$ \begin{align} \nonumber & \frac{Z_{N,\beta}^{V;\mathsf{A}}}{1 + O(N^{-(K + 1)}(\ln N)^{K})} \\& \quad = \exp\bigg(\sum_{k = -2}^{K} N^{-k} F_{\beta;\star}^{V}\bigg) \times \Bigg\{ \sum_{r \geq 0} \frac{1}{r!} \sum_{\substack{k_1,\ldots,k_r \geq -2 \\ j_1,\ldots,j_r \geq 0 \\ k_i + j_i> 0 \\ \sum_{i = 1}^{r} k_i + j_i \leq 2K}} N^{-\sum_{i = 1}^r (k_i + j_i)} \bigotimes_{i = 1}^{r} \frac{(F_{\beta;\star}^{\{k_i\}})^{(j_i)}}{j_i!} \nonumber \\& \qquad \cdot \bigg(\sum_{\boldsymbol{N} \in \mathbb{Z}^g} (\boldsymbol{N} - \boldsymbol{N}_{\star})^{\otimes (\sum_{i = 1}^r j_i)} \exp\Big((F_{\beta;\star}^{\{-2\}})" \cdot (\boldsymbol{N} - \boldsymbol{N}_{\star})^{\otimes 2} + (F_{\beta;\star}^{\{-1\}})' \cdot (\boldsymbol{N} - \boldsymbol{N}_{\star})\Big)\bigg)\Bigg\}. \end{align} $$
Note that the error may not be uniform when K increases due to the choice of
![]() $M_K$
in the intermediate steps.
$M_K$
in the intermediate steps.
Eventually, we recognise in the sum of the last line the J-th tensor of derivatives of the Theta function defined in Equation (1.20), with arguments:
 $$ \begin{align*}\tau_{\beta;\star} = \frac{(F^{\{-2\}}_{\beta;\star})"}{2\mathrm{i}\pi},\qquad \boldsymbol{v}_{\beta;\star} = \frac{(F_{\beta;\star}^{\{-1\}})'}{2\mathrm{i}\pi}. \end{align*} $$
$$ \begin{align*}\tau_{\beta;\star} = \frac{(F^{\{-2\}}_{\beta;\star})"}{2\mathrm{i}\pi},\qquad \boldsymbol{v}_{\beta;\star} = \frac{(F_{\beta;\star}^{\{-1\}})'}{2\mathrm{i}\pi}. \end{align*} $$
More precisely,
 $$ \begin{align*}\sum_{\boldsymbol{N} \in \mathbb{Z}^g} (\boldsymbol{N} - \boldsymbol{N}_{\star})^{\otimes J} e^{\frac{1}{2}(F_{\beta;\star}^{\{-2\}})" \cdot (\boldsymbol{N} - \boldsymbol{N}_{\star})^{\otimes 2} + (F_{\beta;\star}^{\{-1\}})' \cdot (\boldsymbol{N} - \boldsymbol{N}_{\star})} = \Big(\frac{\nabla_{\boldsymbol{v}}}{2\mathrm{i}\pi}\Big)^{\otimes J} \vartheta\!\left[\begin{array}{@{\hspace{-0.02cm}}l@{\hspace{-0.02cm}}} -\boldsymbol{N}_{\star} \\\,\,\,\, \boldsymbol{0} \end{array}\right]\!\!(\boldsymbol{v}|\boldsymbol{\tau}_{\beta;\star})\Big|_{\boldsymbol{v} = \boldsymbol{v}_{\beta;\star}}, \end{align*} $$
$$ \begin{align*}\sum_{\boldsymbol{N} \in \mathbb{Z}^g} (\boldsymbol{N} - \boldsymbol{N}_{\star})^{\otimes J} e^{\frac{1}{2}(F_{\beta;\star}^{\{-2\}})" \cdot (\boldsymbol{N} - \boldsymbol{N}_{\star})^{\otimes 2} + (F_{\beta;\star}^{\{-1\}})' \cdot (\boldsymbol{N} - \boldsymbol{N}_{\star})} = \Big(\frac{\nabla_{\boldsymbol{v}}}{2\mathrm{i}\pi}\Big)^{\otimes J} \vartheta\!\left[\begin{array}{@{\hspace{-0.02cm}}l@{\hspace{-0.02cm}}} -\boldsymbol{N}_{\star} \\\,\,\,\, \boldsymbol{0} \end{array}\right]\!\!(\boldsymbol{v}|\boldsymbol{\tau}_{\beta;\star})\Big|_{\boldsymbol{v} = \boldsymbol{v}_{\beta;\star}}, \end{align*} $$
and this contribution is of order
![]() $1$
, so that we only need to sum up to
$1$
, so that we only need to sum up to
![]() $\sum _{i = 1}^{r} k_i + j_i \leq K$
in Equation (8.8) to get the expansion up to
$\sum _{i = 1}^{r} k_i + j_i \leq K$
in Equation (8.8) to get the expansion up to
![]() $O(N^{-(K + 1)}(\ln N)^{K})$
. By looking at the expansion for
$O(N^{-(K + 1)}(\ln N)^{K})$
. By looking at the expansion for
![]() $K \mapsto K + 1$
, we know that this error done for the expansion with K is, in fact,
$K \mapsto K + 1$
, we know that this error done for the expansion with K is, in fact,
![]() $O(N^{-(K + 1)})$
. This concludes the proof of Theorem 1.5.
$O(N^{-(K + 1)})$
. This concludes the proof of Theorem 1.5.
8.2. Deviations of filling fractions from their mean value (proof of Theorem 1.6)
We now describe the fluctuations of the number of eigenvalues in each segment. Let
![]() $\boldsymbol {P} = (P_1,\ldots ,P_g)$
be a vector of integers, depending on N in such a way that
$\boldsymbol {P} = (P_1,\ldots ,P_g)$
be a vector of integers, depending on N in such a way that
![]() $\boldsymbol {P} - N\epsilon _{\star ,h} = o(N^{\frac {1}{3}})$
when
$\boldsymbol {P} - N\epsilon _{\star ,h} = o(N^{\frac {1}{3}})$
when
![]() $N \rightarrow \infty $
. We set
$N \rightarrow \infty $
. We set
![]() $P_0 = N - \sum _{h = 1}^{g} P_h$
. The joint probability for
$P_0 = N - \sum _{h = 1}^{g} P_h$
. The joint probability for ![]() to find
to find
![]() $P_h$
eigenvalues in the segment
$P_h$
eigenvalues in the segment
![]() $\mathsf {A}_h$
is
$\mathsf {A}_h$
is
 $$ \begin{align*}\mu_{N,\beta}^{V;\mathsf{A}}[\boldsymbol{N} = \boldsymbol{P}] = \frac{N!}{\prod_{h = 0}^g P_h!}\,\frac{Z_{N,\beta;\boldsymbol{P}/N}^{V;\mathsf{A}}}{Z_{N,\beta}^{V;\mathsf{A}}}. \end{align*} $$
$$ \begin{align*}\mu_{N,\beta}^{V;\mathsf{A}}[\boldsymbol{N} = \boldsymbol{P}] = \frac{N!}{\prod_{h = 0}^g P_h!}\,\frac{Z_{N,\beta;\boldsymbol{P}/N}^{V;\mathsf{A}}}{Z_{N,\beta}^{V;\mathsf{A}}}. \end{align*} $$
We recall that the coefficients of the large N expansion of the numerator are smooth functions of
![]() $\boldsymbol {P}/N$
. Therefore, we can perform a Taylor expansion in
$\boldsymbol {P}/N$
. Therefore, we can perform a Taylor expansion in
![]() $\boldsymbol {P}/N$
close to
$\boldsymbol {P}/N$
close to
![]() $\boldsymbol {\epsilon }_{\star }$
with the method used in Section 8. We leave out the details and only state the result: provided
$\boldsymbol {\epsilon }_{\star }$
with the method used in Section 8. We leave out the details and only state the result: provided
![]() $\boldsymbol {P} - N\boldsymbol {\epsilon }_{\star } = o(N^{\frac {1}{3}})$
, only the quadratic term of the Taylor expansion remains when
$\boldsymbol {P} - N\boldsymbol {\epsilon }_{\star } = o(N^{\frac {1}{3}})$
, only the quadratic term of the Taylor expansion remains when
![]() $N \rightarrow \infty $
:
$N \rightarrow \infty $
:
 $$ \begin{align*} \mu_{N,\beta}^{V;\mathsf{A}}[\boldsymbol{N} = \boldsymbol{P}] & \sim \frac{e^{\frac{1}{2}\,(F^{\{-2\}}_{\beta;\star})^{"}\cdot(\boldsymbol{P} - N\boldsymbol{\epsilon}_{\star})^{\otimes 2} + (F^{\{-1\}}_{\beta;\star})'\cdot(\boldsymbol{P} - N\boldsymbol{\epsilon}_{\star})}}{\vartheta\big[\begin{smallmatrix} -\boldsymbol{N}_{\star}\\ \boldsymbol{0} \end{smallmatrix}\big](\boldsymbol{v}_{\beta;\star}|\boldsymbol{\tau}_{\beta;\star})}. \end{align*} $$
$$ \begin{align*} \mu_{N,\beta}^{V;\mathsf{A}}[\boldsymbol{N} = \boldsymbol{P}] & \sim \frac{e^{\frac{1}{2}\,(F^{\{-2\}}_{\beta;\star})^{"}\cdot(\boldsymbol{P} - N\boldsymbol{\epsilon}_{\star})^{\otimes 2} + (F^{\{-1\}}_{\beta;\star})'\cdot(\boldsymbol{P} - N\boldsymbol{\epsilon}_{\star})}}{\vartheta\big[\begin{smallmatrix} -\boldsymbol{N}_{\star}\\ \boldsymbol{0} \end{smallmatrix}\big](\boldsymbol{v}_{\beta;\star}|\boldsymbol{\tau}_{\beta;\star})}. \end{align*} $$
In other words, the random vector
![]() $\Delta \boldsymbol {N} = (\Delta N_1,\ldots ,\Delta N_g)$
defined by
$\Delta \boldsymbol {N} = (\Delta N_1,\ldots ,\Delta N_g)$
defined by
 $$ \begin{align*}\Delta N_{h} = N_h - N\epsilon_{\star,h} + \sum_{h' = 1}^g [(F^{\{-2\}}_{\beta;\star})"]^{-1}_{h,h'}\,(F^{\{-1\}}_{\beta;\star})^{\prime}_{h'} \end{align*} $$
$$ \begin{align*}\Delta N_{h} = N_h - N\epsilon_{\star,h} + \sum_{h' = 1}^g [(F^{\{-2\}}_{\beta;\star})"]^{-1}_{h,h'}\,(F^{\{-1\}}_{\beta;\star})^{\prime}_{h'} \end{align*} $$
is approximated in law by a random Gaussian vector, with covariance
![]() $[(F^{\{-2\}}_{\beta ;\star })"]^{-1}$
and conditioned to live in the shifted lattice
$[(F^{\{-2\}}_{\beta ;\star })"]^{-1}$
and conditioned to live in the shifted lattice
 $$ \begin{align*}\Delta\boldsymbol{N} \in \Big(\mathbb{Z}^{g} - \lfloor N\boldsymbol{\epsilon}_{\star} \rfloor +\sum_{h' = 1}^g [(F^{\{-2\}}_{\beta;\star})"]^{-1}_{h,h'}\,(F^{\{-1\}}_{\beta;\star})^{\prime}_{h'}\Big), \end{align*} $$
$$ \begin{align*}\Delta\boldsymbol{N} \in \Big(\mathbb{Z}^{g} - \lfloor N\boldsymbol{\epsilon}_{\star} \rfloor +\sum_{h' = 1}^g [(F^{\{-2\}}_{\beta;\star})"]^{-1}_{h,h'}\,(F^{\{-1\}}_{\beta;\star})^{\prime}_{h'}\Big), \end{align*} $$
where for
![]() $\boldsymbol {w} \in \mathbb {R}^g$
, we denote
$\boldsymbol {w} \in \mathbb {R}^g$
, we denote
![]() $\lfloor \boldsymbol {w} \rfloor = \big (\lfloor w_1 \rfloor ,\cdots ,\lfloor w_g \rfloor \big )$
. Strictly speaking, we cannot say that we have a convergence in law to a discrete Gaussian because the shift of the lattice oscillates with N. We observe that, when
$\lfloor \boldsymbol {w} \rfloor = \big (\lfloor w_1 \rfloor ,\cdots ,\lfloor w_g \rfloor \big )$
. Strictly speaking, we cannot say that we have a convergence in law to a discrete Gaussian because the shift of the lattice oscillates with N. We observe that, when
![]() $\beta = 2$
and the potential V is independent of N, the vector
$\beta = 2$
and the potential V is independent of N, the vector
![]() $F^{\{-1\}}_{\beta ;\star }$
vanishes so that
$F^{\{-1\}}_{\beta ;\star }$
vanishes so that
![]() $\boldsymbol {N} - N\boldsymbol {\epsilon }_{\star }$
is approximated in law by a centered Gaussian vector conditioned to live in the shifted lattice
$\boldsymbol {N} - N\boldsymbol {\epsilon }_{\star }$
is approximated in law by a centered Gaussian vector conditioned to live in the shifted lattice
![]() $\big (\mathbb {Z}^g - \lfloor N \boldsymbol {\epsilon }_{\star }\rfloor \big )$
.
$\big (\mathbb {Z}^g - \lfloor N \boldsymbol {\epsilon }_{\star }\rfloor \big )$
.
8.3. Fluctuations of linear statistics
With a strategy similar to § 5.5, the result of Section 8.1 implies, for
![]() $\varphi $
a test function which is analytic in a neighbourhood of
$\varphi $
a test function which is analytic in a neighbourhood of
![]() $\mathsf {A}$
,
$\mathsf {A}$
,
 $$ \begin{align} \mu_{N,\beta}^{V;\mathsf{A}}\big(e^{\mathrm{i}s\big(\sum_{i = 1}^N \varphi(\lambda_i) - N\int_{\mathsf{S}} \varphi(\xi)\mathrm{d}\mu_{\mathrm{eq}}^V(\xi)\big)}\big) \sim e^{\mathrm{i}s\,M_{\beta;\star}[\varphi] - \frac{s^2}{2}\,Q_{\beta;\star}[\varphi,\varphi]}\,\frac{\vartheta\big[\begin{smallmatrix} -N\boldsymbol{\epsilon}_{\star} \\ \boldsymbol{0} \end{smallmatrix}\big]\big(\boldsymbol{v}_{\beta;\star} + \mathrm{i}s\,\boldsymbol{u}_{\beta;\star}[\varphi]|\boldsymbol{\tau}_{\beta;\star}\big)}{\vartheta\big[\begin{smallmatrix} -N\boldsymbol{\epsilon}_{\star} \\ \boldsymbol{0} \end{smallmatrix}\big]\big(\boldsymbol{v}_{\beta;\star}|\boldsymbol{\tau}_{\beta;\star}\big)}. \end{align} $$
$$ \begin{align} \mu_{N,\beta}^{V;\mathsf{A}}\big(e^{\mathrm{i}s\big(\sum_{i = 1}^N \varphi(\lambda_i) - N\int_{\mathsf{S}} \varphi(\xi)\mathrm{d}\mu_{\mathrm{eq}}^V(\xi)\big)}\big) \sim e^{\mathrm{i}s\,M_{\beta;\star}[\varphi] - \frac{s^2}{2}\,Q_{\beta;\star}[\varphi,\varphi]}\,\frac{\vartheta\big[\begin{smallmatrix} -N\boldsymbol{\epsilon}_{\star} \\ \boldsymbol{0} \end{smallmatrix}\big]\big(\boldsymbol{v}_{\beta;\star} + \mathrm{i}s\,\boldsymbol{u}_{\beta;\star}[\varphi]|\boldsymbol{\tau}_{\beta;\star}\big)}{\vartheta\big[\begin{smallmatrix} -N\boldsymbol{\epsilon}_{\star} \\ \boldsymbol{0} \end{smallmatrix}\big]\big(\boldsymbol{v}_{\beta;\star}|\boldsymbol{\tau}_{\beta;\star}\big)}. \end{align} $$
This formula gives an equivalent when
![]() $N \rightarrow \infty $
, which features an oscillatory behaviour. We have set
$N \rightarrow \infty $
, which features an oscillatory behaviour. We have set
where
![]() $\varpi _{h}(\xi )\mathrm {d}\xi $
are the holomorphic one-forms introduced in Equation (5.16). The linear (resp. bilinear) form
$\varpi _{h}(\xi )\mathrm {d}\xi $
are the holomorphic one-forms introduced in Equation (5.16). The linear (resp. bilinear) form
![]() $M_{\beta ;\boldsymbol {\epsilon }}[\varphi ]$
(resp.
$M_{\beta ;\boldsymbol {\epsilon }}[\varphi ]$
(resp.
![]() $Q_{\beta ;\boldsymbol {\epsilon }}[\varphi ,\varphi ]$
) is defined in § 5.5, and in Equation (8.9) it is evaluated at
$Q_{\beta ;\boldsymbol {\epsilon }}[\varphi ,\varphi ]$
) is defined in § 5.5, and in Equation (8.9) it is evaluated at
![]() $\boldsymbol {\epsilon } = \boldsymbol {\epsilon }_{\star }$
. We recognise that the right-hand side of Equation (8.9) is the Fourier transform of the sum of two independent random variables: one of them being Gaussian and the other being the scalar product with
$\boldsymbol {\epsilon } = \boldsymbol {\epsilon }_{\star }$
. We recognise that the right-hand side of Equation (8.9) is the Fourier transform of the sum of two independent random variables: one of them being Gaussian and the other being the scalar product with
![]() $2\mathrm{i}\pi \boldsymbol {u}_{\beta ;\star }[\varphi ]$
of the sampling of a g-dimensional Gaussian vector at points belonging to
$2\mathrm{i}\pi \boldsymbol {u}_{\beta ;\star }[\varphi ]$
of the sampling of a g-dimensional Gaussian vector at points belonging to
![]() $-\boldsymbol {N}_{\star } + \mathbb {Z}^{g}$
. Therefore, among a codimension g subspace of test functions determined by the equation
$-\boldsymbol {N}_{\star } + \mathbb {Z}^{g}$
. Therefore, among a codimension g subspace of test functions determined by the equation
![]() $\boldsymbol {u}_{\beta ;\star }[\varphi ] = \boldsymbol {0}$
, the ratio of Theta functions is
$\boldsymbol {u}_{\beta ;\star }[\varphi ] = \boldsymbol {0}$
, the ratio of Theta functions is
![]() $1$
, and we do find a central limit theorem for fluctuations of linear statistics, as in the one-cut regime. But when
$1$
, and we do find a central limit theorem for fluctuations of linear statistics, as in the one-cut regime. But when
![]() $\boldsymbol {u}_{\beta ;\star }[\varphi ] \neq \boldsymbol {0}$
, we only find subsequential convergence in law – along subsequences so that
$\boldsymbol {u}_{\beta ;\star }[\varphi ] \neq \boldsymbol {0}$
, we only find subsequential convergence in law – along subsequences so that
![]() $(-N\boldsymbol {\epsilon }_{\star }\,\mathrm {mod}\,\mathbb {Z}^{g})$
converges – to the sum of a random Gaussian vector and an independent random Gaussian vector conditioned to belong to a lattice with oscillating center. Accordingly, the probability distribution of those fluctuations displays interference patterns varying with N.
$(-N\boldsymbol {\epsilon }_{\star }\,\mathrm {mod}\,\mathbb {Z}^{g})$
converges – to the sum of a random Gaussian vector and an independent random Gaussian vector conditioned to belong to a lattice with oscillating center. Accordingly, the probability distribution of those fluctuations displays interference patterns varying with N.
A. Elementary properties of the equilibrium measure with fixed filling fractions
We now prove Theorem 7.8 stating that if V is analytic in a neighbourhood of
![]() $\mathsf {A}$
, if we denote
$\mathsf {A}$
, if we denote
![]() $(g + 1)$
the number of cuts of the equilibrium measure
$(g + 1)$
the number of cuts of the equilibrium measure
![]() $\mu _\mathrm{{eq}}^V$
in the initial model, and if we assume it is off-critical, then
$\mu _\mathrm{{eq}}^V$
in the initial model, and if we assume it is off-critical, then
![]() $\mu _\mathrm{{eq};\boldsymbol {\epsilon }}^V$
still has
$\mu _\mathrm{{eq};\boldsymbol {\epsilon }}^V$
still has
![]() $(g + 1)$
cuts and remains off-critical for
$(g + 1)$
cuts and remains off-critical for
![]() $\boldsymbol {\epsilon }$
close enough to
$\boldsymbol {\epsilon }$
close enough to
![]() $\boldsymbol {\epsilon }_{\star }$
and depends smoothly on such
$\boldsymbol {\epsilon }_{\star }$
and depends smoothly on such
![]() $\boldsymbol {\epsilon }$
.
$\boldsymbol {\epsilon }$
.
A.1. Lipschitz property
We may decompose
 $$ \begin{align} \mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V} = \sum_{h = 0}^{g} \epsilon_h\,\mu_{\mathrm{eq};\boldsymbol{\epsilon},h}^{V}, \end{align} $$
$$ \begin{align} \mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V} = \sum_{h = 0}^{g} \epsilon_h\,\mu_{\mathrm{eq};\boldsymbol{\epsilon},h}^{V}, \end{align} $$
where
![]() $\mu _{\mathrm{eq};\boldsymbol {\epsilon },h}^{V}$
are probability measures in
$\mu _{\mathrm{eq};\boldsymbol {\epsilon },h}^{V}$
are probability measures in
![]() $\mathsf {A}_h$
, and we know that
$\mathsf {A}_h$
, and we know that
![]() $\mu _\mathrm{{eq};\boldsymbol {\epsilon }}^{V}$
minimises the energy functional
$\mu _\mathrm{{eq};\boldsymbol {\epsilon }}^{V}$
minimises the energy functional
![]() $E[\mu ]$
– see Equation (1.5) – among such choices of probability measures. We first establish that linear statistics of the equilibrium measure in the fixed filling fraction model are Lipschitz in
$E[\mu ]$
– see Equation (1.5) – among such choices of probability measures. We first establish that linear statistics of the equilibrium measure in the fixed filling fraction model are Lipschitz in
![]() $\boldsymbol {\epsilon }$
. Let
$\boldsymbol {\epsilon }$
. Let
![]() $\delta \in (0,1]$
and set
$\delta \in (0,1]$
and set
 $$ \begin{align*}\mathcal{E}_{\delta} = \Big\{\boldsymbol{\epsilon} \in (\delta,1-\delta)^{g}\quad \Big|\quad \delta < 1 - \sum_{h = 1}^{g} \epsilon_h < 1 - \delta\Big\}. \end{align*} $$
$$ \begin{align*}\mathcal{E}_{\delta} = \Big\{\boldsymbol{\epsilon} \in (\delta,1-\delta)^{g}\quad \Big|\quad \delta < 1 - \sum_{h = 1}^{g} \epsilon_h < 1 - \delta\Big\}. \end{align*} $$
If
![]() $\boldsymbol {\epsilon } \in \mathcal {E}_{\delta }$
, we denote
$\boldsymbol {\epsilon } \in \mathcal {E}_{\delta }$
, we denote
![]() $\epsilon _0 = 1 - \sum _{h = 1}^{g} \epsilon _h$
. If
$\epsilon _0 = 1 - \sum _{h = 1}^{g} \epsilon _h$
. If
![]() $(\kappa _0,\ldots ,\kappa _g)$
is such that
$(\kappa _0,\ldots ,\kappa _g)$
is such that
![]() $\sum _{h = 0}^{g} \kappa _h = 1$
, we denote
$\sum _{h = 0}^{g} \kappa _h = 1$
, we denote
![]() $\boldsymbol {\kappa } = (\kappa _1,\ldots ,\kappa _g)$
.
$\boldsymbol {\kappa } = (\kappa _1,\ldots ,\kappa _g)$
.
Lemma A.1. For
![]() $\delta> 0$
small enough, there exists a finite constant
$\delta> 0$
small enough, there exists a finite constant
![]() $c(\delta )$
such that, for any
$c(\delta )$
such that, for any
![]() $\boldsymbol {\epsilon } \in \mathcal {E}_{\delta }$
, for any
$\boldsymbol {\epsilon } \in \mathcal {E}_{\delta }$
, for any
![]() $\kappa _h \in (0,2\epsilon _h]$
such that
$\kappa _h \in (0,2\epsilon _h]$
such that
![]() $\sum _{h = 0}^g \kappa _{h} = 1$
, we have for any test function
$\sum _{h = 0}^g \kappa _{h} = 1$
, we have for any test function
![]() $\varphi $
,
$\varphi $
,
Proof. As we have seen in Theorem 1.2,
![]() $\mu _\mathrm{{eq};\boldsymbol {\epsilon }}^{V}$
is also characterised by saying that for (A.1), there exist constants
$\mu _\mathrm{{eq};\boldsymbol {\epsilon }}^{V}$
is also characterised by saying that for (A.1), there exist constants
![]() $(C_{\boldsymbol {\epsilon },h}^{V})_{0 \leq h \leq g}$
so that for any
$(C_{\boldsymbol {\epsilon },h}^{V})_{0 \leq h \leq g}$
so that for any ![]() and
and
![]() $x \in \mathsf {A}_h$
,
$x \in \mathsf {A}_h$
,
with equality
![]() $\mu _{\mathrm{{eq};\boldsymbol {\epsilon }},h}^{V}$
almost everywhere. Recall the definition of the effective potential (here including the constants for convenience):
$\mu _{\mathrm{{eq};\boldsymbol {\epsilon }},h}^{V}$
almost everywhere. Recall the definition of the effective potential (here including the constants for convenience):
 $$ \begin{align*}\tilde{U}_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}(x) = V(x) - 2 \int_{\mathsf{A}} \ln|x - \xi|\mathrm{d}\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}(\xi) - \sum_{h = 0}^g C_{\boldsymbol{\epsilon},h}^{V}\mathbf{1}_{\mathsf{A}_h}(x), \end{align*} $$
$$ \begin{align*}\tilde{U}_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}(x) = V(x) - 2 \int_{\mathsf{A}} \ln|x - \xi|\mathrm{d}\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}(\xi) - \sum_{h = 0}^g C_{\boldsymbol{\epsilon},h}^{V}\mathbf{1}_{\mathsf{A}_h}(x), \end{align*} $$
and of the pseudo-distance between two probability measures
![]() $\mu $
and
$\mu $
and
![]() $\nu $
:
$\nu $
:
We have for all probability measures on
![]() $\mathsf {A} = \bigcup _{h = 0}^{g} \mathsf {A}_h$
,
$\mathsf {A} = \bigcup _{h = 0}^{g} \mathsf {A}_h$
,
 $$ \begin{align} E[\mu] = \frac{\beta}{2}\Big(\mathfrak{D}^2[\mu,\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}] + \int_{\mathsf{A}} \tilde{U}^{V}_{\mathrm{eq};\boldsymbol{\epsilon}}(x)\mathrm{d}\mu(x) + \sum_{h = 0}^{g} C_{\boldsymbol{\epsilon},h}^{V}\,\mu(\mathsf{A}_h) + I_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}\Big), \end{align} $$
$$ \begin{align} E[\mu] = \frac{\beta}{2}\Big(\mathfrak{D}^2[\mu,\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}] + \int_{\mathsf{A}} \tilde{U}^{V}_{\mathrm{eq};\boldsymbol{\epsilon}}(x)\mathrm{d}\mu(x) + \sum_{h = 0}^{g} C_{\boldsymbol{\epsilon},h}^{V}\,\mu(\mathsf{A}_h) + I_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}\Big), \end{align} $$
with
Indeed, a simple algebra shows that
 $$ \begin{align} \nonumber E[\mu]&= E[\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}]+ \frac{\beta}{2}\Big(\mathfrak{D}^2[\mu,\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}] +\int_{\mathsf{A}} \Bigg(V(x)-2\int_{\mathsf{A}}\ln|x-y|\mathrm{d}\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}(y)\Big)\mathrm{d}[\mu-\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}](x)\Big) \\ &= E[\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}]+\frac{\beta}{2}\Big(\mathfrak{D}^2[\mu,\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}] +\int_{\mathsf{A}} \tilde U_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}(x) \mathrm{d}[\mu-\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}](x) + \sum_{h=0}^g C_{\boldsymbol{\epsilon},h}^{V}(\mu-\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V})(\mathsf{A}_h)\Big). \end{align} $$
$$ \begin{align} \nonumber E[\mu]&= E[\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}]+ \frac{\beta}{2}\Big(\mathfrak{D}^2[\mu,\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}] +\int_{\mathsf{A}} \Bigg(V(x)-2\int_{\mathsf{A}}\ln|x-y|\mathrm{d}\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}(y)\Big)\mathrm{d}[\mu-\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}](x)\Big) \\ &= E[\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}]+\frac{\beta}{2}\Big(\mathfrak{D}^2[\mu,\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}] +\int_{\mathsf{A}} \tilde U_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}(x) \mathrm{d}[\mu-\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}](x) + \sum_{h=0}^g C_{\boldsymbol{\epsilon},h}^{V}(\mu-\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V})(\mathsf{A}_h)\Big). \end{align} $$
Using the characterisation of
![]() $\mu _\mathrm{{eq};\boldsymbol {\epsilon }}^{V}$
, one finds that
$\mu _\mathrm{{eq};\boldsymbol {\epsilon }}^{V}$
, one finds that
 $$ \begin{align*}E[\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}]- \frac{\beta}{2} \sum_{h=0}^g C_{\boldsymbol{\epsilon},h}^{V}\epsilon_h= \frac{\beta}{2}\,I_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}, \end{align*} $$
$$ \begin{align*}E[\mu_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}]- \frac{\beta}{2} \sum_{h=0}^g C_{\boldsymbol{\epsilon},h}^{V}\epsilon_h= \frac{\beta}{2}\,I_{\mathrm{eq};\boldsymbol{\epsilon}}^{V}, \end{align*} $$
which completes the proof of Equation (A.3). We next choose
![]() $\boldsymbol {\kappa } \neq \boldsymbol {\epsilon }$
and write that if
$\boldsymbol {\kappa } \neq \boldsymbol {\epsilon }$
and write that if
![]() $\mu _{\boldsymbol {\kappa }}$
is any probability measure such that
$\mu _{\boldsymbol {\kappa }}$
is any probability measure such that
![]() $\mu _{\boldsymbol {\kappa }}(\mathsf {A}_h)=\kappa _h$
, we must have
$\mu _{\boldsymbol {\kappa }}(\mathsf {A}_h)=\kappa _h$
, we must have
Since
![]() $\mu _\mathrm{{eq};\boldsymbol {\kappa }}^{V}$
and
$\mu _\mathrm{{eq};\boldsymbol {\kappa }}^{V}$
and
![]() $\mu _{\boldsymbol {\kappa }}$
put the same masses on the
$\mu _{\boldsymbol {\kappa }}$
put the same masses on the
![]() $\mathsf {A}_h$
, we deduce from Equation (A.3) that
$\mathsf {A}_h$
, we deduce from Equation (A.3) that
We next choose
![]() $\mu _{\boldsymbol {\kappa }}$
, whose support is included in the support of
$\mu _{\boldsymbol {\kappa }}$
, whose support is included in the support of
![]() $\mu _{\mathrm{eq};\boldsymbol {\epsilon }}^{V}$
, so that since
$\mu _{\mathrm{eq};\boldsymbol {\epsilon }}^{V}$
, so that since
![]() $\tilde {U}_{\mathrm{eq};\boldsymbol {\epsilon }}^{V}$
vanishes there and is nonnegative everywhere, we deduce
$\tilde {U}_{\mathrm{eq};\boldsymbol {\epsilon }}^{V}$
vanishes there and is nonnegative everywhere, we deduce
We put
![]() $\mu _{\boldsymbol {\kappa }} = t\,\mu _{\mathrm{eq};\boldsymbol {\epsilon }}^{V} +(1-t)\nu $
for
$\mu _{\boldsymbol {\kappa }} = t\,\mu _{\mathrm{eq};\boldsymbol {\epsilon }}^{V} +(1-t)\nu $
for
![]() $t \in [0,1]$
and a probability measure
$t \in [0,1]$
and a probability measure
![]() $\nu $
on
$\nu $
on
![]() $\mathsf {A}$
whose support is included in the support
$\mathsf {A}$
whose support is included in the support
![]() $\mu _{\mathrm{eq};\boldsymbol {\epsilon }}^{V}$
and such that for all h,
$\mu _{\mathrm{eq};\boldsymbol {\epsilon }}^{V}$
and such that for all h,
We have from Equation (A.5) that
We take
If
![]() $\kappa _h\in (0,2\epsilon _h]$
and is such that
$\kappa _h\in (0,2\epsilon _h]$
and is such that
![]() $\nu (\mathsf {A}_h)\ge 0$
for any h, as it should for
$\nu (\mathsf {A}_h)\ge 0$
for any h, as it should for
![]() $\nu $
to be a probability measure. We finally choose
$\nu $
to be a probability measure. We finally choose
![]() $\nu $
such that
$\nu $
such that
![]() $\mathfrak {D}^2[\nu ,\mu _{\mathrm{eq};\boldsymbol {\epsilon }}^{V}]$
is finite (for instance the renormalised Lebesgue measure on the support of
$\mathfrak {D}^2[\nu ,\mu _{\mathrm{eq};\boldsymbol {\epsilon }}^{V}]$
is finite (for instance the renormalised Lebesgue measure on the support of
![]() $\mu _\mathrm{{eq};\boldsymbol {\epsilon }}^{V}$
) to conclude that there exists a constant
$\mu _\mathrm{{eq};\boldsymbol {\epsilon }}^{V}$
) to conclude that there exists a constant
![]() $\tilde {c}(\delta )$
valid for all
$\tilde {c}(\delta )$
valid for all
![]() $\boldsymbol {\epsilon } \in \mathcal {E}_{\delta }$
such that
$\boldsymbol {\epsilon } \in \mathcal {E}_{\delta }$
such that
Recalling that
we deduce that for all
![]() $\varphi \in L^1(\mathsf {A})$
,
$\varphi \in L^1(\mathsf {A})$
,
This implies that for all
![]() $\varphi $
with
$\varphi $
with
![]() $|\varphi |_{1/2} < \infty $
, we have
$|\varphi |_{1/2} < \infty $
, we have
Lemma A.2. If
![]() $\mu _{\mathrm{eq};\boldsymbol {\epsilon }}^{V}$
is off-critical and its support has
$\mu _{\mathrm{eq};\boldsymbol {\epsilon }}^{V}$
is off-critical and its support has
![]() $g_{\boldsymbol {\epsilon }} + 1$
cuts denoted
$g_{\boldsymbol {\epsilon }} + 1$
cuts denoted
![]() $[\alpha _{\boldsymbol {\epsilon },h}^-,\alpha _{\boldsymbol {\epsilon },h}^+]$
, then for
$[\alpha _{\boldsymbol {\epsilon },h}^-,\alpha _{\boldsymbol {\epsilon },h}^+]$
, then for
![]() $\boldsymbol {\epsilon }'$
in a small enough neighbourhood of
$\boldsymbol {\epsilon }'$
in a small enough neighbourhood of
![]() $\boldsymbol {\epsilon }$
,
$\boldsymbol {\epsilon }$
,
![]() $\mu _{\mathrm{eq};\boldsymbol {\epsilon }'}^V$
is off-critical and has the same number of cuts, of the form
$\mu _{\mathrm{eq};\boldsymbol {\epsilon }'}^V$
is off-critical and has the same number of cuts, of the form
![]() $[\alpha _{\boldsymbol {\epsilon }',h}^{-},\alpha _{\boldsymbol {\epsilon }',h}^{+}]$
, and
$[\alpha _{\boldsymbol {\epsilon }',h}^{-},\alpha _{\boldsymbol {\epsilon }',h}^{+}]$
, and
![]() $\alpha _{\boldsymbol {\epsilon }',h}^{\bullet }$
are Lipschitz functions of
$\alpha _{\boldsymbol {\epsilon }',h}^{\bullet }$
are Lipschitz functions of
![]() $\boldsymbol {\epsilon }'$
. Moreover, for
$\boldsymbol {\epsilon }'$
. Moreover, for
![]() $\delta>0$
small enough, assume that
$\delta>0$
small enough, assume that
![]() $\mathsf {A}$
contains
$\mathsf {A}$
contains
 $$ \begin{align*}\bigcup_{\boldsymbol{\epsilon}'} \bigcup_{\alpha_{\boldsymbol{\epsilon}'}\,\,\mathrm{soft}\,\,\mathrm{edge}}\big\{x \quad :\quad d(x,\alpha_{\boldsymbol{\epsilon}'})\le \delta\big\} \end{align*} $$
$$ \begin{align*}\bigcup_{\boldsymbol{\epsilon}'} \bigcup_{\alpha_{\boldsymbol{\epsilon}'}\,\,\mathrm{soft}\,\,\mathrm{edge}}\big\{x \quad :\quad d(x,\alpha_{\boldsymbol{\epsilon}'})\le \delta\big\} \end{align*} $$
when the union ranges over a small enough neighbourhood of
![]() $\boldsymbol {\epsilon }$
. Then in the same neighbourhood of
$\boldsymbol {\epsilon }$
. Then in the same neighbourhood of
![]() $\boldsymbol {\epsilon }$
, the function
$\boldsymbol {\epsilon }$
, the function
![]() $\boldsymbol {\epsilon }' \mapsto W^{\{-1\}}_{1;\boldsymbol {\epsilon }'}(x)$
is Lipschitz uniformly for x in any compact of
$\boldsymbol {\epsilon }' \mapsto W^{\{-1\}}_{1;\boldsymbol {\epsilon }'}(x)$
is Lipschitz uniformly for x in any compact of
![]() $\mathbb {C} \setminus \mathsf {A}$
.
$\mathbb {C} \setminus \mathsf {A}$
.
Proof. Restricting to x in the domain
![]() $\mathsf {U}$
where V is analytic, let us rewrite the leading order of the one-variable Dyson–Schwinger equation
$\mathsf {U}$
where V is analytic, let us rewrite the leading order of the one-variable Dyson–Schwinger equation
where
and we have chosen
![]() $L_0(x) = \prod _{a \in \partial \mathsf {A}} (x - a)$
. Solving the quadratic equation (A.7), we find
$L_0(x) = \prod _{a \in \partial \mathsf {A}} (x - a)$
. Solving the quadratic equation (A.7), we find
 $$ \begin{align} W_{1;\boldsymbol{\epsilon}'}^{\{-1\}}(x) = \frac{V'(x)}{2} - \sqrt{\frac{L_0(x)\,V'(x)^2 - 4Q_{\boldsymbol{\epsilon}'}(x)}{4L_0(x)}}, \end{align} $$
$$ \begin{align} W_{1;\boldsymbol{\epsilon}'}^{\{-1\}}(x) = \frac{V'(x)}{2} - \sqrt{\frac{L_0(x)\,V'(x)^2 - 4Q_{\boldsymbol{\epsilon}'}(x)}{4L_0(x)}}, \end{align} $$
where the dependence in
![]() $\boldsymbol {\epsilon }'$
only appears through
$\boldsymbol {\epsilon }'$
only appears through
![]() $Q_{\boldsymbol {\epsilon }'}(x)$
. Owing to Lemma A.1, since
$Q_{\boldsymbol {\epsilon }'}(x)$
. Owing to Lemma A.1, since
![]() $V'$
is analytic in a neighbourhood of
$V'$
is analytic in a neighbourhood of
![]() $\mathsf {A}$
,
$\mathsf {A}$
,
![]() $Q_{\boldsymbol {\epsilon }'}(x)$
is analytic for x in this neighbourhood and is Lipschitz in
$Q_{\boldsymbol {\epsilon }'}(x)$
is analytic for x in this neighbourhood and is Lipschitz in
![]() $\boldsymbol {\epsilon }'$
, uniformly for x in any compact of this neighbourhood. The edges of the support of
$\boldsymbol {\epsilon }'$
, uniformly for x in any compact of this neighbourhood. The edges of the support of
![]() $\mu _\mathrm{{eq};\boldsymbol {\epsilon }'}^{V}$
are precisely the zeroes or poles of
$\mu _\mathrm{{eq};\boldsymbol {\epsilon }'}^{V}$
are precisely the zeroes or poles of
![]() $R_{\boldsymbol {\epsilon }'}(x) = (L_0(x)V'(x)^2 - 4Q_{\boldsymbol {\epsilon }'}(x))/L_0(x)$
on
$R_{\boldsymbol {\epsilon }'}(x) = (L_0(x)V'(x)^2 - 4Q_{\boldsymbol {\epsilon }'}(x))/L_0(x)$
on
![]() $\mathsf {A}$
. Since
$\mathsf {A}$
. Since
![]() $\mu _{\mathrm{eq};\boldsymbol {\epsilon }}^{V}$
is off-critical, for
$\mu _{\mathrm{eq};\boldsymbol {\epsilon }}^{V}$
is off-critical, for
![]() $\boldsymbol {\epsilon }' = \boldsymbol {\epsilon }$
, these zeroes and poles are all simple. By a classical theorem of complex analysis, it implies that the zeroes of
$\boldsymbol {\epsilon }' = \boldsymbol {\epsilon }$
, these zeroes and poles are all simple. By a classical theorem of complex analysis, it implies that the zeroes of
![]() $R_{\boldsymbol {\epsilon }'}$
in
$R_{\boldsymbol {\epsilon }'}$
in
![]() $\mathsf {A}$
occur as Lipschitz functions
$\mathsf {A}$
occur as Lipschitz functions
![]() $\boldsymbol {\epsilon }' \mapsto a_{\boldsymbol {\epsilon }',h}^{\bullet }$
; in particular,
$\boldsymbol {\epsilon }' \mapsto a_{\boldsymbol {\epsilon }',h}^{\bullet }$
; in particular,
![]() $\mu _{\mathrm{eq};\boldsymbol {\epsilon }}^{V}$
keeps the same number of cuts. Lemma A.1 also implies that
$\mu _{\mathrm{eq};\boldsymbol {\epsilon }}^{V}$
keeps the same number of cuts. Lemma A.1 also implies that
![]() $W_{1;\boldsymbol {\epsilon }'}^{\{-1\}}(x)$
is a Lipschitz function of
$W_{1;\boldsymbol {\epsilon }'}^{\{-1\}}(x)$
is a Lipschitz function of
![]() $\boldsymbol {\epsilon }'$
for any fixed
$\boldsymbol {\epsilon }'$
for any fixed
![]() $x \notin \mathsf {A}$
, and this is, in fact, uniform away from
$x \notin \mathsf {A}$
, and this is, in fact, uniform away from
![]() $\mathsf {A}$
.
$\mathsf {A}$
.
A.2. Smooth dependence in the filling fractions
The following result allows the conclusion that
![]() $\mathrm {d}\mu _{\mathrm{eq};\boldsymbol {\epsilon }}^{V}/\mathrm {d} x$
(or
$\mathrm {d}\mu _{\mathrm{eq};\boldsymbol {\epsilon }}^{V}/\mathrm {d} x$
(or
![]() $W_{1;\boldsymbol {\epsilon }}^{\{-1\}}$
) is smooth with respect to
$W_{1;\boldsymbol {\epsilon }}^{\{-1\}}$
) is smooth with respect to
![]() $\boldsymbol {\epsilon }$
for x away from the edges.
$\boldsymbol {\epsilon }$
for x away from the edges.
Proposition A.3. Lemma A.2 holds with
![]() $C^{\infty }$
regularity instead of Lipschitz.
$C^{\infty }$
regularity instead of Lipschitz.
Proof. We first prove that the Stieltjes transform
![]() $W_{1;\boldsymbol {\epsilon }}^{\{-1\}}(z)$
is a differentiable function of the filling fractions, for any
$W_{1;\boldsymbol {\epsilon }}^{\{-1\}}(z)$
is a differentiable function of the filling fractions, for any
![]() $z \in \mathbb {C}\setminus \mathsf {S}_{\boldsymbol {\epsilon }}$
. We take
$z \in \mathbb {C}\setminus \mathsf {S}_{\boldsymbol {\epsilon }}$
. We take
![]() $\boldsymbol {\epsilon },\boldsymbol {\kappa },\boldsymbol {\kappa '} \in \mathcal {E}_{\delta }$
. We choose
$\boldsymbol {\epsilon },\boldsymbol {\kappa },\boldsymbol {\kappa '} \in \mathcal {E}_{\delta }$
. We choose
![]() $z,z' \in \mathbb {C}$
at distance at least
$z,z' \in \mathbb {C}$
at distance at least
![]() $\delta '$
of
$\delta '$
of
![]() $\mathsf {A}$
for
$\mathsf {A}$
for
![]() $\delta '> 0$
fixed but small enough. Let
$\delta '> 0$
fixed but small enough. Let
![]() $\psi _{z}(x) = \frac {1}{z - x}$
and
$\psi _{z}(x) = \frac {1}{z - x}$
and
![]() $\psi _{z,z'}(x) = \psi _{z}(x) - \psi _{z'}(x)$
. As in § 3.5.2, we can build functions
$\psi _{z,z'}(x) = \psi _{z}(x) - \psi _{z'}(x)$
. As in § 3.5.2, we can build functions
![]() $\varphi _{z}(x)$
and
$\varphi _{z}(x)$
and
![]() $\varphi _{z,z'}(x)$
defined for
$\varphi _{z,z'}(x)$
defined for
![]() $x \in \mathbb {R}$
, which coincide with
$x \in \mathbb {R}$
, which coincide with
![]() $\psi _{z}$
and
$\psi _{z}$
and
![]() $\psi _{z,z'}$
for
$\psi _{z,z'}$
for
![]() $x \in \mathsf {A}$
, and for which
$x \in \mathsf {A}$
, and for which
After Lemma A.1, we have
 $$ \begin{align} \nonumber |W_{1;\boldsymbol{\kappa}}^{\{-1\}}(z) - W_{1;\boldsymbol{\kappa}'}^{\{-1\}}(z)\big| & \leq C\,|\boldsymbol{\kappa} - \boldsymbol{\kappa}'|_{1}, \\ \big|\big(W_{1;\boldsymbol{\kappa}}^{\{-1\}}(z) - W_{1;\boldsymbol{\kappa}'}^{\{-1\}}(z)\big) - \big(W_{1;\boldsymbol{\kappa}}^{\{-1\}}(z') - W_{1;\boldsymbol{\kappa}'}^{\{-1\}}(z')\big)\big| & \leq C'\,|z - z'|\,|\boldsymbol{\kappa} - \boldsymbol{\kappa}'|_{1}. \end{align} $$
$$ \begin{align} \nonumber |W_{1;\boldsymbol{\kappa}}^{\{-1\}}(z) - W_{1;\boldsymbol{\kappa}'}^{\{-1\}}(z)\big| & \leq C\,|\boldsymbol{\kappa} - \boldsymbol{\kappa}'|_{1}, \\ \big|\big(W_{1;\boldsymbol{\kappa}}^{\{-1\}}(z) - W_{1;\boldsymbol{\kappa}'}^{\{-1\}}(z)\big) - \big(W_{1;\boldsymbol{\kappa}}^{\{-1\}}(z') - W_{1;\boldsymbol{\kappa}'}^{\{-1\}}(z')\big)\big| & \leq C'\,|z - z'|\,|\boldsymbol{\kappa} - \boldsymbol{\kappa}'|_{1}. \end{align} $$
We fix
![]() $\boldsymbol {\eta } \in \mathbb {R}^{g + 1}$
such that
$\boldsymbol {\eta } \in \mathbb {R}^{g + 1}$
such that
![]() $\sum _{h = 0}^{g} \eta _h = 0$
, and for a given z and
$\sum _{h = 0}^{g} \eta _h = 0$
, and for a given z and
![]() $\boldsymbol {\kappa }$
, we consider the function
$\boldsymbol {\kappa }$
, we consider the function
![]() $t \mapsto W_{1;\boldsymbol {\kappa }+t\boldsymbol {\eta }}^{\{-1\}}(z)$
defined over
$t \mapsto W_{1;\boldsymbol {\kappa }+t\boldsymbol {\eta }}^{\{-1\}}(z)$
defined over
We deduce from Equation (A.10) and Rademacher theorem (stating that Lipschitz functions are almost surely differentiable) that
 $$ \begin{align*}\partial_{s}W_{1;\boldsymbol{\kappa}+s\boldsymbol{\eta}}^{\{-1\}}(z) = \lim_{t \rightarrow 0} \frac{W_{1;\boldsymbol{\kappa} + (s+t)\boldsymbol{\eta}}^{\{-1\}}(z) - W_{1;\boldsymbol{\kappa}+s\boldsymbol{\eta}}^{\{-1\}}(z)}{t} \end{align*} $$
$$ \begin{align*}\partial_{s}W_{1;\boldsymbol{\kappa}+s\boldsymbol{\eta}}^{\{-1\}}(z) = \lim_{t \rightarrow 0} \frac{W_{1;\boldsymbol{\kappa} + (s+t)\boldsymbol{\eta}}^{\{-1\}}(z) - W_{1;\boldsymbol{\kappa}+s\boldsymbol{\eta}}^{\{-1\}}(z)}{t} \end{align*} $$
exists for s in a subset
![]() $\mathcal {U}^{z}_{\boldsymbol {\kappa },\boldsymbol {\eta }}$
with probability
$\mathcal {U}^{z}_{\boldsymbol {\kappa },\boldsymbol {\eta }}$
with probability
![]() $1$
in
$1$
in
![]() $\mathcal {V}_{\boldsymbol {\kappa },\boldsymbol {\eta }}$
. Let
$\mathcal {V}_{\boldsymbol {\kappa },\boldsymbol {\eta }}$
. Let
![]() $\mathfrak {N}_{\delta '}^{[\zeta ]}$
be a countable
$\mathfrak {N}_{\delta '}^{[\zeta ]}$
be a countable
![]() $\zeta $
-net of
$\zeta $
-net of
By the previous point, we find a subset
![]() $\mathcal {U}_{\boldsymbol {\kappa },\boldsymbol {\eta }}^{\delta ',[\zeta ]}$
with probability
$\mathcal {U}_{\boldsymbol {\kappa },\boldsymbol {\eta }}^{\delta ',[\zeta ]}$
with probability
![]() $1$
in
$1$
in
![]() $\mathcal {V}_{\boldsymbol {\kappa },\boldsymbol {\eta }}$
, such that for any
$\mathcal {V}_{\boldsymbol {\kappa },\boldsymbol {\eta }}$
, such that for any
![]() $s\in \mathcal {U}_{\boldsymbol {\kappa },\boldsymbol {\eta }}^{\delta ',[\zeta ]}$
and
$s\in \mathcal {U}_{\boldsymbol {\kappa },\boldsymbol {\eta }}^{\delta ',[\zeta ]}$
and
![]() $z \in \mathfrak {N}_{\delta '}^{[\zeta ]}$
,
$z \in \mathfrak {N}_{\delta '}^{[\zeta ]}$
,
![]() $\partial _{s}W_{1;\boldsymbol {\kappa }+s\boldsymbol {\eta }}^{\{-1\}}$
exists. We then choose the
$\partial _{s}W_{1;\boldsymbol {\kappa }+s\boldsymbol {\eta }}^{\{-1\}}$
exists. We then choose the
![]() $\zeta $
-nets to be increasing when
$\zeta $
-nets to be increasing when
![]() $\zeta $
decreases and denote
$\zeta $
decreases and denote
![]() $\mathcal {U}_{\boldsymbol {\kappa },\boldsymbol {\eta }}^{\delta '}$
has still probability
$\mathcal {U}_{\boldsymbol {\kappa },\boldsymbol {\eta }}^{\delta '}$
has still probability
![]() $1$
in
$1$
in
![]() $\mathcal {V}_{\boldsymbol {\kappa },\boldsymbol {\eta }}$
, and for any
$\mathcal {V}_{\boldsymbol {\kappa },\boldsymbol {\eta }}$
, and for any
![]() $s \in \mathcal {U}_{\boldsymbol {\kappa },\boldsymbol {\eta }}^{\delta '}$
in this set,
$s \in \mathcal {U}_{\boldsymbol {\kappa },\boldsymbol {\eta }}^{\delta '}$
in this set,
![]() $\partial _{s}W_{1;\boldsymbol {\kappa }+s\boldsymbol {\eta }}^{\{-1\}}(z)$
exists for all
$\partial _{s}W_{1;\boldsymbol {\kappa }+s\boldsymbol {\eta }}^{\{-1\}}(z)$
exists for all
![]() $z \in \bigcup _{n \geq 1} \mathfrak {N}_{\delta '}^{[1/n]}$
. By Equation (A.10), this implies the existence of a Lipschitz (with respect to z) differential (with respect to s) for all
$z \in \bigcup _{n \geq 1} \mathfrak {N}_{\delta '}^{[1/n]}$
. By Equation (A.10), this implies the existence of a Lipschitz (with respect to z) differential (with respect to s) for all
![]() $z \in \tilde {\mathsf {A}}_{\delta '}$
and any
$z \in \tilde {\mathsf {A}}_{\delta '}$
and any
![]() $s \in \mathcal {U}_{\boldsymbol {\kappa },\boldsymbol {\eta }}^{\delta '}$
. By Montel theorem and Equation (A.10),
$s \in \mathcal {U}_{\boldsymbol {\kappa },\boldsymbol {\eta }}^{\delta '}$
. By Montel theorem and Equation (A.10),
![]() $z \mapsto \partial _{s}W_{1;\boldsymbol {\kappa } + s\boldsymbol {\eta }}^{\{-1\}}(z)$
is a holomorphic function in z for any s such that it exists.
$z \mapsto \partial _{s}W_{1;\boldsymbol {\kappa } + s\boldsymbol {\eta }}^{\{-1\}}(z)$
is a holomorphic function in z for any s such that it exists.
By Equation (A.8),
![]() $Q_{\boldsymbol {\kappa } + s\boldsymbol {\eta }}$
is the expectation value of an analytic function under
$Q_{\boldsymbol {\kappa } + s\boldsymbol {\eta }}$
is the expectation value of an analytic function under
![]() $\mu _{\mathrm{eq};\boldsymbol {\kappa } + s\boldsymbol {\eta }}^V$
; therefore,
$\mu _{\mathrm{eq};\boldsymbol {\kappa } + s\boldsymbol {\eta }}^V$
; therefore,
with a contour
![]() $\mathcal {C}$
included in
$\mathcal {C}$
included in
![]() $\tilde {\mathsf {A}}_{\delta '}$
. Besides,
$\tilde {\mathsf {A}}_{\delta '}$
. Besides,
![]() $Q_{\boldsymbol {\kappa } + s\boldsymbol {\eta }}(x)$
is a holomorphic function of x in a neighbourhood
$Q_{\boldsymbol {\kappa } + s\boldsymbol {\eta }}(x)$
is a holomorphic function of x in a neighbourhood
![]() $\mathsf {U}$
of
$\mathsf {U}$
of
![]() $\mathsf {A}$
in
$\mathsf {A}$
in
![]() $\mathbb {C}$
as V is. Hence,
$\mathbb {C}$
as V is. Hence,
![]() $s \mapsto Q_{\boldsymbol {\kappa } + s\boldsymbol {\eta }}(x)$
is differentiable for
$s \mapsto Q_{\boldsymbol {\kappa } + s\boldsymbol {\eta }}(x)$
is differentiable for
![]() $s \in \mathcal {U}_{\boldsymbol {\kappa },\boldsymbol {\eta }}^{\delta '}$
for each
$s \in \mathcal {U}_{\boldsymbol {\kappa },\boldsymbol {\eta }}^{\delta '}$
for each
![]() $x \in \mathsf {U}$
, and Lipschitz in z. By Montel theorem, its derivative – where it exists – is holomorphic in
$x \in \mathsf {U}$
, and Lipschitz in z. By Montel theorem, its derivative – where it exists – is holomorphic in
![]() $z \in \mathsf {U}$
. Then, Equation (A.9) implies that
$z \in \mathsf {U}$
. Then, Equation (A.9) implies that
![]() $s \mapsto W_{1;\boldsymbol {\kappa } + s\boldsymbol {\eta }}^{\{-1\}}(x)$
is differentiable for
$s \mapsto W_{1;\boldsymbol {\kappa } + s\boldsymbol {\eta }}^{\{-1\}}(x)$
is differentiable for
![]() $s \in \mathcal {U}_{\boldsymbol {\kappa },\boldsymbol {\eta }}^{\delta '}$
and any
$s \in \mathcal {U}_{\boldsymbol {\kappa },\boldsymbol {\eta }}^{\delta '}$
and any
![]() $x \in \mathbb {C}\setminus \partial \mathsf {S}_{\boldsymbol {\kappa } + s\boldsymbol {\eta }}$
.
$x \in \mathbb {C}\setminus \partial \mathsf {S}_{\boldsymbol {\kappa } + s\boldsymbol {\eta }}$
.
Now, let us fix a compact neighbourhood of
![]() $\boldsymbol {\epsilon } \in \mathcal {E}_{\delta }$
such that the regularity result of Lemma A.2 applies. When we intersect
$\boldsymbol {\epsilon } \in \mathcal {E}_{\delta }$
such that the regularity result of Lemma A.2 applies. When we intersect
![]() $\mathcal {V}_{\boldsymbol {\kappa },\boldsymbol {\eta }}$
with a small enough neighbourhood of an off-critical
$\mathcal {V}_{\boldsymbol {\kappa },\boldsymbol {\eta }}$
with a small enough neighbourhood of an off-critical
![]() $\boldsymbol {\epsilon } \in \mathcal {E}_{\delta }$
, Lemma A.2 guarantees that
$\boldsymbol {\epsilon } \in \mathcal {E}_{\delta }$
, Lemma A.2 guarantees that
![]() $\mu _{\mathrm{eq};\boldsymbol {\kappa }}^V$
remains uniformly off-critical. Arguments already used in Lemma A.2 for Lipschitz regularity implies that edges at which
$\mu _{\mathrm{eq};\boldsymbol {\kappa }}^V$
remains uniformly off-critical. Arguments already used in Lemma A.2 for Lipschitz regularity implies that edges at which
![]() $W_{1;\boldsymbol {\kappa }+s\boldsymbol {\eta }}^{\{-1\}}$
has a squareroot behaviour are functions
$W_{1;\boldsymbol {\kappa }+s\boldsymbol {\eta }}^{\{-1\}}$
has a squareroot behaviour are functions
![]() $s \mapsto \alpha _{\boldsymbol {\kappa } + s \boldsymbol {\eta },h}^{\bullet }$
which are differentiable for
$s \mapsto \alpha _{\boldsymbol {\kappa } + s \boldsymbol {\eta },h}^{\bullet }$
which are differentiable for
![]() $s \in \mathcal {U}_{\boldsymbol {\kappa },\boldsymbol {\eta }}^{\delta '}$
. And, by Equation (A.9), we can write at a hard edge
$s \in \mathcal {U}_{\boldsymbol {\kappa },\boldsymbol {\eta }}^{\delta '}$
. And, by Equation (A.9), we can write at a hard edge
![]() $\alpha $
– necessarily independent of s,
$\alpha $
– necessarily independent of s,
 $$ \begin{align*}W_{1;\boldsymbol{\kappa}+ s\boldsymbol{\eta}}^{\{-1\}}(x) = \frac{M_{\boldsymbol{\kappa} + s\boldsymbol{\eta}}^{[\alpha]}(x)}{(x - \alpha)^{\frac{1}{2}}}, \end{align*} $$
$$ \begin{align*}W_{1;\boldsymbol{\kappa}+ s\boldsymbol{\eta}}^{\{-1\}}(x) = \frac{M_{\boldsymbol{\kappa} + s\boldsymbol{\eta}}^{[\alpha]}(x)}{(x - \alpha)^{\frac{1}{2}}}, \end{align*} $$
and at a soft edge
![]() $\alpha _{\boldsymbol {\kappa } + s\boldsymbol {\eta }}$
,
$\alpha _{\boldsymbol {\kappa } + s\boldsymbol {\eta }}$
,
with functions
![]() $M_{\boldsymbol {\kappa } + s\boldsymbol {\eta }}^{[\alpha ]}(x)$
differentiable in
$M_{\boldsymbol {\kappa } + s\boldsymbol {\eta }}^{[\alpha ]}(x)$
differentiable in
![]() $s\in \mathcal {U}_{\boldsymbol {\kappa },\boldsymbol {\eta }}^{\delta '}$
and holomorphic in x a neighbourhood of the edge
$s\in \mathcal {U}_{\boldsymbol {\kappa },\boldsymbol {\eta }}^{\delta '}$
and holomorphic in x a neighbourhood of the edge
![]() $\alpha $
. Therefore, for s in this set, we have the behaviours
$\alpha $
. Therefore, for s in this set, we have the behaviours
at any edge. Given the properties of the Stieltjes transform, we also know that
-
○
 $\partial _s W_{1;\boldsymbol {\kappa }+s\boldsymbol {\eta }}^{\{-1\}}(x)$
behaves like
$\partial _s W_{1;\boldsymbol {\kappa }+s\boldsymbol {\eta }}^{\{-1\}}(x)$
behaves like
 $O(\frac {1}{x^2})$
when
$O(\frac {1}{x^2})$
when
 $x \rightarrow \infty $
– recall that the term in
$x \rightarrow \infty $
– recall that the term in
 $\frac {1}{x}$
in
$\frac {1}{x}$
in
 $W_{1;\boldsymbol {\kappa }+s\boldsymbol {\eta }}^{\{-1\}}$
has constant coefficient.
$W_{1;\boldsymbol {\kappa }+s\boldsymbol {\eta }}^{\{-1\}}$
has constant coefficient. -
○ for any
 $x \in \mathring {\mathsf {S}}_{\boldsymbol {\kappa }+s\boldsymbol {\eta }}$
, we have
$x \in \mathring {\mathsf {S}}_{\boldsymbol {\kappa }+s\boldsymbol {\eta }}$
, we have
 $\partial _s W_{1;\boldsymbol {\kappa }+s\boldsymbol {\eta }}^{\{-1\}} (x + \mathrm{i}0) + \partial _s W_{1;\boldsymbol {\kappa }+s\boldsymbol {\eta }}^{\{-1\}}(x - \mathrm{i}0) = 0$
.
$\partial _s W_{1;\boldsymbol {\kappa }+s\boldsymbol {\eta }}^{\{-1\}} (x + \mathrm{i}0) + \partial _s W_{1;\boldsymbol {\kappa }+s\boldsymbol {\eta }}^{\{-1\}}(x - \mathrm{i}0) = 0$
. -
○ for any
 ,
,
 $\oint _{\mathsf {A}_h} \partial _s W_{1;\boldsymbol {\kappa }+s\boldsymbol {\eta }}^{\{-1\}}(x)\,\frac {\mathrm{d} x}{2\mathrm{i}\pi } = \eta _h$
.
$\oint _{\mathsf {A}_h} \partial _s W_{1;\boldsymbol {\kappa }+s\boldsymbol {\eta }}^{\{-1\}}(x)\,\frac {\mathrm{d} x}{2\mathrm{i}\pi } = \eta _h$
.
These properties imply that
![]() $\partial _s W_{1;\boldsymbol {\kappa } + s\boldsymbol {\eta }}^{\{-1\}}(x)\mathrm {d} x$
can be analytically continued to a holomorphic one-formFootnote 2 on the Riemann surface of genus g specified by the equation
$\partial _s W_{1;\boldsymbol {\kappa } + s\boldsymbol {\eta }}^{\{-1\}}(x)\mathrm {d} x$
can be analytically continued to a holomorphic one-formFootnote 2 on the Riemann surface of genus g specified by the equation
![]() $\sigma ^2 = \prod _{\alpha \in \partial \mathsf {S}_{\boldsymbol {\kappa }+s\boldsymbol {\eta }}}(x - \alpha )$
with periods
$\sigma ^2 = \prod _{\alpha \in \partial \mathsf {S}_{\boldsymbol {\kappa }+s\boldsymbol {\eta }}}(x - \alpha )$
with periods
![]() $\eta _h$
around the h-th cut. As holomorphic one-forms are characterised by their periods, we deduce that
$\eta _h$
around the h-th cut. As holomorphic one-forms are characterised by their periods, we deduce that
 $$ \begin{align} \partial_s W_{1;\boldsymbol{\kappa}+s\boldsymbol{\eta}}^{\{-1\}}(x) = 2\mathrm{i}\pi\,\sum_{h = 1}^{g} \eta_h\,{\varpi_{h}(x)}, \end{align} $$
$$ \begin{align} \partial_s W_{1;\boldsymbol{\kappa}+s\boldsymbol{\eta}}^{\{-1\}}(x) = 2\mathrm{i}\pi\,\sum_{h = 1}^{g} \eta_h\,{\varpi_{h}(x)}, \end{align} $$
where
![]() $(\varpi _h(x)\mathrm {d} x)_{h = 1}^{g}$
is the basis of holomorphic one-forms on the Riemann surface introduced in Equation (5.16). These are completely determined by the endpoints and depend smoothly on them. Since the right-hand side of Equation (A.11) is a continuous function of s, we deduce that
$(\varpi _h(x)\mathrm {d} x)_{h = 1}^{g}$
is the basis of holomorphic one-forms on the Riemann surface introduced in Equation (5.16). These are completely determined by the endpoints and depend smoothly on them. Since the right-hand side of Equation (A.11) is a continuous function of s, we deduce that
![]() $s \mapsto W_{1;\boldsymbol {\kappa }+s{\boldsymbol \eta }}^{\{-1\}}(x)$
is actually
$s \mapsto W_{1;\boldsymbol {\kappa }+s{\boldsymbol \eta }}^{\{-1\}}(x)$
is actually
![]() $\mathcal {C}^1$
for s such that
$\mathcal {C}^1$
for s such that
![]() $\boldsymbol {\kappa }+s\boldsymbol {\eta }$
is in a vicinity of
$\boldsymbol {\kappa }+s\boldsymbol {\eta }$
is in a vicinity of
![]() $\boldsymbol {\epsilon }$
. These arguments holding for any
$\boldsymbol {\epsilon }$
. These arguments holding for any
![]() $\boldsymbol {\eta }, \boldsymbol {\kappa }$
, we deduce that
$\boldsymbol {\eta }, \boldsymbol {\kappa }$
, we deduce that
![]() $\boldsymbol {\kappa } \rightarrow W_{1;{\boldsymbol \kappa }}^{\{-1\}}$
is Gâteaux differentiable, and hence Fréchet differentiable, in a neighbourhood of
$\boldsymbol {\kappa } \rightarrow W_{1;{\boldsymbol \kappa }}^{\{-1\}}$
is Gâteaux differentiable, and hence Fréchet differentiable, in a neighbourhood of
![]() $\boldsymbol {\epsilon }$
. Therefore, all the reasoning of the proof of Lemma A.2 can be extended to show that the edges are
$\boldsymbol {\epsilon }$
. Therefore, all the reasoning of the proof of Lemma A.2 can be extended to show that the edges are
![]() $\mathcal {C}^1$
. The differential equation (A.11) (for any fixed x away from the edges) then implies
$\mathcal {C}^1$
. The differential equation (A.11) (for any fixed x away from the edges) then implies
![]() $\mathcal {C}^2$
, and inductively,
$\mathcal {C}^2$
, and inductively,
![]() $\mathcal {C}^{\infty }$
.
$\mathcal {C}^{\infty }$
.
A.3. Hessian of the energy with respect to filling fractions
We are now in position to prove the following:
Proposition A.4. If
![]() $\mu _{\mathrm{eq};\boldsymbol {\epsilon }}^{V}$
is off-critical, then
$\mu _{\mathrm{eq};\boldsymbol {\epsilon }}^{V}$
is off-critical, then
![]() $F^{\{-2\};V}_{\beta ;\boldsymbol {\epsilon }'}$
is
$F^{\{-2\};V}_{\beta ;\boldsymbol {\epsilon }'}$
is
![]() $\mathcal {C}^{2}$
with negative definite Hessian at least for
$\mathcal {C}^{2}$
with negative definite Hessian at least for
![]() $\boldsymbol {\epsilon }'$
in a vicinity of
$\boldsymbol {\epsilon }'$
in a vicinity of
![]() $\boldsymbol {\epsilon }$
.
$\boldsymbol {\epsilon }$
.
In other words, the
![]() $g \times g$
matrix
$g \times g$
matrix
![]() $\boldsymbol {\tau }_{\beta ;\boldsymbol {\epsilon }}$
with purely imaginary entries
$\boldsymbol {\tau }_{\beta ;\boldsymbol {\epsilon }}$
with purely imaginary entries

is such that
![]() $\mathrm {Im}\,\boldsymbol {\tau }_{\beta ;\boldsymbol {\epsilon }}> 0$
.
$\mathrm {Im}\,\boldsymbol {\tau }_{\beta ;\boldsymbol {\epsilon }}> 0$
.
Proof. Let
![]() $\boldsymbol {\eta },\boldsymbol {\eta }' \in \mathbb {R}^{g + 1}$
so that
$\boldsymbol {\eta },\boldsymbol {\eta }' \in \mathbb {R}^{g + 1}$
so that
![]() $\sum _{h = 0}^g \eta _h = \sum _{h = 0}^{g} \eta ^{\prime }_h = 0$
and
$\sum _{h = 0}^g \eta _h = \sum _{h = 0}^{g} \eta ^{\prime }_h = 0$
and
![]() $\boldsymbol {\epsilon }'$
be in a vicinity of
$\boldsymbol {\epsilon }'$
be in a vicinity of
![]() $\boldsymbol {\epsilon }$
. The last paragraph has shown the existence of an integrable, signed measure with
$\boldsymbol {\epsilon }$
. The last paragraph has shown the existence of an integrable, signed measure with
![]() $0$
total mass:
$0$
total mass:
 $$ \begin{align*}\nu_{\boldsymbol{\epsilon}';\boldsymbol{\eta}}^{V} = \lim_{t \rightarrow 0} \frac{\mu_{\mathrm{eq};\boldsymbol{\epsilon}' + t\boldsymbol{\eta}}^{V} - \mu_{\mathrm{eq};\boldsymbol{\epsilon}'}^{V}}{t}. \end{align*} $$
$$ \begin{align*}\nu_{\boldsymbol{\epsilon}';\boldsymbol{\eta}}^{V} = \lim_{t \rightarrow 0} \frac{\mu_{\mathrm{eq};\boldsymbol{\epsilon}' + t\boldsymbol{\eta}}^{V} - \mu_{\mathrm{eq};\boldsymbol{\epsilon}'}^{V}}{t}. \end{align*} $$
By Equation (A.4), we have
 $$ \begin{align*} F^{\{-2\};V}_{\beta;\boldsymbol{\kappa}}-F^{\{-2\};V}_{\beta;\boldsymbol{\epsilon}'}&= -\big(E[\mu_{\mathrm{eq};\boldsymbol{\kappa}}^{V}]-E[\mu_{\mathrm{eq};\boldsymbol{\epsilon}'}^{V}]\big)\\ &= \frac{\beta}{2}\Big(-\mathfrak{D}^2[\mu_{\mathrm{eq};\boldsymbol{\kappa}}^{V},\mu_{\mathrm{eq};\boldsymbol{\epsilon}'}^{V}] +\int_{\mathsf{A}} \tilde U_{\mathrm{eq};\boldsymbol{\epsilon}'}^{V}(x) \mathrm{d}[\mu_{\mathrm{eq};\boldsymbol{\kappa}}^{V}-\mu_{\mathrm{eq};\boldsymbol{\epsilon}'}^{V}](x) + \sum_{h=0}^g C_{h;\boldsymbol{\epsilon}'}^{V}(\kappa_h-\epsilon_h')\Big). \end{align*} $$
$$ \begin{align*} F^{\{-2\};V}_{\beta;\boldsymbol{\kappa}}-F^{\{-2\};V}_{\beta;\boldsymbol{\epsilon}'}&= -\big(E[\mu_{\mathrm{eq};\boldsymbol{\kappa}}^{V}]-E[\mu_{\mathrm{eq};\boldsymbol{\epsilon}'}^{V}]\big)\\ &= \frac{\beta}{2}\Big(-\mathfrak{D}^2[\mu_{\mathrm{eq};\boldsymbol{\kappa}}^{V},\mu_{\mathrm{eq};\boldsymbol{\epsilon}'}^{V}] +\int_{\mathsf{A}} \tilde U_{\mathrm{eq};\boldsymbol{\epsilon}'}^{V}(x) \mathrm{d}[\mu_{\mathrm{eq};\boldsymbol{\kappa}}^{V}-\mu_{\mathrm{eq};\boldsymbol{\epsilon}'}^{V}](x) + \sum_{h=0}^g C_{h;\boldsymbol{\epsilon}'}^{V}(\kappa_h-\epsilon_h')\Big). \end{align*} $$
Since
![]() $\tilde U_{\mathrm{eq};\boldsymbol {\epsilon }'}^{V;\mathsf {A}}$
vanishes on
$\tilde U_{\mathrm{eq};\boldsymbol {\epsilon }'}^{V;\mathsf {A}}$
vanishes on
![]() $\mathsf {S}_{\boldsymbol {\epsilon }'}$
and the derivatives of
$\mathsf {S}_{\boldsymbol {\epsilon }'}$
and the derivatives of
![]() $\boldsymbol {\epsilon }' \mapsto \mu _\mathrm{{eq};\boldsymbol {\epsilon }'}^{V}$
are smooth and supported in
$\boldsymbol {\epsilon }' \mapsto \mu _\mathrm{{eq};\boldsymbol {\epsilon }'}^{V}$
are smooth and supported in
![]() $\mathsf {S}_{\boldsymbol {\epsilon }'}$
, we deduce that
$\mathsf {S}_{\boldsymbol {\epsilon }'}$
, we deduce that
![]() $F^{\{-2\},V}_{\boldsymbol {\epsilon }'}$
is a
$F^{\{-2\},V}_{\boldsymbol {\epsilon }'}$
is a
![]() $\mathcal {C}^2$
function of
$\mathcal {C}^2$
function of
![]() $\boldsymbol {\epsilon }'$
and its Hessian is
$\boldsymbol {\epsilon }'$
and its Hessian is
 $$ \begin{align} \mathrm{Hessian}(F^{\{-2\};V}_{\beta;\boldsymbol{\epsilon}'})[\boldsymbol{\eta},\boldsymbol{\eta}'] = -\frac{\beta}{2} \sum_{h = 0}^{g} \mathfrak{D}^2[\nu_{\boldsymbol{\epsilon}';\boldsymbol{\eta}}^{V}\,\mathbf{1}_{\mathsf{A}_h},\nu_{\boldsymbol{\epsilon}';\boldsymbol{\eta}'}^{V}\,\mathbf{1}_{\mathsf{A}_h}], \end{align} $$
$$ \begin{align} \mathrm{Hessian}(F^{\{-2\};V}_{\beta;\boldsymbol{\epsilon}'})[\boldsymbol{\eta},\boldsymbol{\eta}'] = -\frac{\beta}{2} \sum_{h = 0}^{g} \mathfrak{D}^2[\nu_{\boldsymbol{\epsilon}';\boldsymbol{\eta}}^{V}\,\mathbf{1}_{\mathsf{A}_h},\nu_{\boldsymbol{\epsilon}';\boldsymbol{\eta}'}^{V}\,\mathbf{1}_{\mathsf{A}_h}], \end{align} $$
where we recall that
![]() $\mathfrak {D}$
is the pseudo-distance from Equation (A.2). Therefore, the Hessian is definite negative.
$\mathfrak {D}$
is the pseudo-distance from Equation (A.2). Therefore, the Hessian is definite negative.
Acknowledgements
We thank V. Gorin and the anonymous referees for useful comments. The work of G. B. has been supported by Fonds Européen S16905 (UE7 - CONFRA) and the Fonds National Suisse (200021-143434), and he would like to thank the ENS Lyon where part of this work was conducted. This research was supported by ANR GranMa ANR-08-BLAN-0311-01, Simons foundation and ERC Project LDRAM: ERC-2019-ADG Project 884584.
Competing interests
The authors have no competing interest to declare.