Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Mortenson, Eric T.
2014.
On the dual nature of partial theta functions and Appell–Lerch sums.
Advances in Mathematics,
Vol. 264,
Issue. ,
p.
236.
Bringmann, Kathrin
and
Mahlburg, Karl
2015.
False theta functions and companions to Capparelli's identities.
Advances in Mathematics,
Vol. 278,
Issue. ,
p.
121.
Bringmann, Kathrin
and
Milas, Antun
2015.
𝒲-Algebras, False Theta Functions and Quantum Modular Forms, I.
International Mathematics Research Notices,
Vol. 2015,
Issue. 21,
p.
11351.
Hikami, Kazuhiro
and
Lovejoy, Jeremy
2015.
Torus knots and quantum modular forms.
Research in the Mathematical Sciences,
Vol. 2,
Issue. 1,
Bringmann, Kathrin
and
Rolen, Larry
2015.
Radial limits of mock theta functions.
Research in the Mathematical Sciences,
Vol. 2,
Issue. 1,
Folsom, Amanda
2016.
Mock and mixed mock modular forms in the lower half-plane.
Archiv der Mathematik,
Vol. 107,
Issue. 5,
p.
487.
Bringmann, Kathrin
and
Rolen, Larry
2016.
Half-integral weight Eichler integrals and quantum modular forms.
Journal of Number Theory,
Vol. 161,
Issue. ,
p.
240.
Jang, Min-Joo
and
Löbrich, Steffen
2016.
Radial limits of the universal mock theta function 𝑔₃.
Proceedings of the American Mathematical Society,
Vol. 145,
Issue. 3,
p.
925.
Chen, Bin
and
Zhou, Haigang
2016.
Bilateral series in terms of mixed mock modular forms.
Journal of Inequalities and Applications,
Vol. 2016,
Issue. 1,
Mortenson, Eric
2016.
Ramanujan's Radial Limits and Mixed Mock Modular Bilateralq-Hypergeometric Series.
Proceedings of the Edinburgh Mathematical Society,
Vol. 59,
Issue. 3,
p.
787.
Kim, Byungchan
Lim, Subong
and
Lovejoy, Jeremy
2016.
Odd-balanced unimodal sequences and related functions: parity, mock modularity and quantum modularity.
Proceedings of the American Mathematical Society,
Vol. 144,
Issue. 9,
p.
3687.
Folsom, Amanda
Garthwaite, Sharon
Kang, Soon-Yi
Swisher, Holly
and
Treneer, Stephanie
2016.
Quantum mock modular forms arising from eta–theta functions.
Research in Number Theory,
Vol. 2,
Issue. 1,
Choi, Dohoon
and
Lim, Subong
2016.
Finite-dimensional period spaces for the spaces of cusp forms.
Israel Journal of Mathematics,
Vol. 216,
Issue. 2,
p.
507.
Bringmann, Kathrin
and
Folsom, Amanda
2016.
Quantum Jacobi forms and finite evaluations of unimodal rank generating functions.
Archiv der Mathematik,
Vol. 107,
Issue. 4,
p.
367.
Folsom, Amanda
Ki, Caleb
Truong Vu, Yen Nhi
and
Yang, Bowen
2017.
“Strange” combinatorial quantum modular forms.
Journal of Number Theory,
Vol. 170,
Issue. ,
p.
315.
Folsom, Amanda
2017.
Perspectives on mock modular forms.
Journal of Number Theory,
Vol. 176,
Issue. ,
p.
500.
Ngo, Hieu T.
and
Rhoades, Robert C.
2017.
Integer partitions, probabilities and quantum modular forms.
Research in the Mathematical Sciences,
Vol. 4,
Issue. 1,
Kimport, Susie
2017.
Analytic Number Theory, Modular Forms and q-Hypergeometric Series.
Vol. 221,
Issue. ,
p.
371.
2017.
An Invitation to the Rogers-Ramanujan Identities.
p.
213.
Bringmann, Kathrin
and
Mahlburg, Karl
2017.
Analytic Number Theory, Modular Forms and q-Hypergeometric Series.
Vol. 221,
Issue. ,
p.
139.
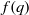 $f(q)$, Ramanujan claims that as
$f(q)$, Ramanujan claims that as 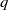 $q$ approaches an even-order
$q$ approaches an even-order 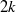 $2k$ root of unity, we have
$2k$ root of unity, we have 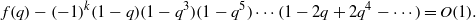 $$\begin{eqnarray*}f(q)- (- 1)^{k} (1- q)(1- {q}^{3} )(1- {q}^{5} )\cdots (1- 2q+ 2{q}^{4} - \cdots )= O(1).\end{eqnarray*}$$
$$\begin{eqnarray*}f(q)- (- 1)^{k} (1- q)(1- {q}^{3} )(1- {q}^{5} )\cdots (1- 2q+ 2{q}^{4} - \cdots )= O(1).\end{eqnarray*}$$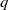 $q$-hypergeometric function which underlies a new relationship between Dyson’s rank mock theta function and the Andrews–Garvan crank modular form. Along these lines, we show that the Rogers–Fine false
$q$-hypergeometric function which underlies a new relationship between Dyson’s rank mock theta function and the Andrews–Garvan crank modular form. Along these lines, we show that the Rogers–Fine false 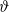 $\vartheta $-functions, functions which have not been well understood within the theory of modular forms, specialize to quantum modular forms.
$\vartheta $-functions, functions which have not been well understood within the theory of modular forms, specialize to quantum modular forms.



