1 Introduction
1.1 Background
The theory of newforms is fascinating and plays an important role in the theory of automorphic forms. It was first studied in the early 1970s by Atkin–Lehner [Reference Atkin and Lehner3] and Li [Reference Li23] in terms of classical modular forms, and by Casselman [Reference Casselman6] in terms of local newforms on
![]() $\mathrm {GL}_2$
. Their results become a bridge between classical modular forms and automorphic representations of
$\mathrm {GL}_2$
. Their results become a bridge between classical modular forms and automorphic representations of
![]() $\mathrm {GL}_2$
. Casselman’s result was generalised to
$\mathrm {GL}_2$
. Casselman’s result was generalised to
![]() $\mathrm {GL}_n$
by Jacquet–Piatetskii-Shapiro–Shalika [Reference Jacquet, Piatetski-Shapiro and Shalika14] (see also Jacquet’s erratum [Reference Jacquet13]) in the 1980s. Another proof was given by Matringe [Reference Matringe26] in 2013.
$\mathrm {GL}_n$
by Jacquet–Piatetskii-Shapiro–Shalika [Reference Jacquet, Piatetski-Shapiro and Shalika14] (see also Jacquet’s erratum [Reference Jacquet13]) in the 1980s. Another proof was given by Matringe [Reference Matringe26] in 2013.
After their works, the theory of local newforms was established
-
• for
 $\mathrm {PGSp}_4$
and for
$\mathrm {PGSp}_4$
and for
 $\widetilde {\mathrm {SL}}_2$
, which is the double cover of
$\widetilde {\mathrm {SL}}_2$
, which is the double cover of
 $\mathrm {SL}_2$
, by Roberts–Schmidt [Reference Roberts and Schmidt35, Reference Roberts and Schmidt36];
$\mathrm {SL}_2$
, by Roberts–Schmidt [Reference Roberts and Schmidt35, Reference Roberts and Schmidt36]; -
• for
 $\mathrm {GSp}_4$
by Okazaki [Reference Okazaki33];
$\mathrm {GSp}_4$
by Okazaki [Reference Okazaki33]; -
• for
 $\mathrm {U}(1,1)$
by Lansky–Raghuram [Reference Lansky and Raghuram19];
$\mathrm {U}(1,1)$
by Lansky–Raghuram [Reference Lansky and Raghuram19]; -
• for unramified
 $\mathrm {U}(2,1)$
by Miyauchi [Reference Miyauchi27, Reference Miyauchi28, Reference Miyauchi29, Reference Miyauchi30].
$\mathrm {U}(2,1)$
by Miyauchi [Reference Miyauchi27, Reference Miyauchi28, Reference Miyauchi29, Reference Miyauchi30].
In 2010, Gross gave a conjecture on the local newforms for
![]() $\mathrm {SO}_{2n+1}$
in a letter to Serre (see the expansion [Reference Gross9] of this letter). It is a natural extension of the
$\mathrm {SO}_{2n+1}$
in a letter to Serre (see the expansion [Reference Gross9] of this letter). It is a natural extension of the
![]() $\mathrm {GL}_2$
case [Reference Casselman6] and the
$\mathrm {GL}_2$
case [Reference Casselman6] and the
![]() $\mathrm {PGSp}_4$
case [Reference Roberts and Schmidt35]. This conjecture was proven for generic supercuspidal representations by Tsai [Reference Tsai41].
$\mathrm {PGSp}_4$
case [Reference Roberts and Schmidt35]. This conjecture was proven for generic supercuspidal representations by Tsai [Reference Tsai41].
One has to notice that in all previous works, representations are assumed to be generic. For
![]() $\mathrm {GL}_n$
, this assumption might be reasonable since all local components of an arbitrary irreducible cuspidal automorphic representation of
$\mathrm {GL}_n$
, this assumption might be reasonable since all local components of an arbitrary irreducible cuspidal automorphic representation of
![]() $\mathrm {GL}_n$
are generic. However, for other groups, this assumption is too strong because there are many irreducible cuspidal automorphic representations whose local components are not generic (and not tempered), such as the Saito–Kurokawa lifting of
$\mathrm {GL}_n$
are generic. However, for other groups, this assumption is too strong because there are many irreducible cuspidal automorphic representations whose local components are not generic (and not tempered), such as the Saito–Kurokawa lifting of
![]() $\mathrm {PGSp}_4$
.
$\mathrm {PGSp}_4$
.
In this paper, we generalise the results in [Reference Jacquet, Piatetski-Shapiro and Shalika14] to all the irreducible representations. Namely, we extend the theory of local newforms to not generic representations in the case of
![]() $\mathrm {GL}_n$
. By considering the endoscopic classification, our results would be useful for the study of local newforms for classical groups in the future.
$\mathrm {GL}_n$
. By considering the endoscopic classification, our results would be useful for the study of local newforms for classical groups in the future.
1.2 Main results
Let us describe our results. Let F be a nonarchimedean local field of characteristic zero with the ring of integers
![]() $\mathfrak {o}$
and the maximal ideal
$\mathfrak {o}$
and the maximal ideal
![]() $\mathfrak {p}$
. Fix a nontrivial additive character
$\mathfrak {p}$
. Fix a nontrivial additive character
![]() $\psi $
of F, which is trivial on
$\psi $
of F, which is trivial on
![]() $\mathfrak {o}$
but not on
$\mathfrak {o}$
but not on
![]() $\mathfrak {p}^{-1}$
. We denote by q the order of
$\mathfrak {p}^{-1}$
. We denote by q the order of
![]() $\mathfrak {o}/\mathfrak {p}$
.
$\mathfrak {o}/\mathfrak {p}$
.
For an integer
![]() $n \geq 1$
, set
$n \geq 1$
, set
![]() $\Lambda _n = \{(\lambda _1, \dots , \lambda _n) \in \mathbb {Z}^n \;|\; 0 \leq \lambda _1 \leq \dots \leq \lambda _n\}$
. We regard
$\Lambda _n = \{(\lambda _1, \dots , \lambda _n) \in \mathbb {Z}^n \;|\; 0 \leq \lambda _1 \leq \dots \leq \lambda _n\}$
. We regard
![]() $\Lambda _n$
as a totally ordered monoid with respect to the lexicographic order. For
$\Lambda _n$
as a totally ordered monoid with respect to the lexicographic order. For
![]() $\lambda = (\lambda _1, \dots , \lambda _n)$
, we set
$\lambda = (\lambda _1, \dots , \lambda _n)$
, we set
![]() $|\lambda | = \lambda _1+\dots +\lambda _n$
.
$|\lambda | = \lambda _1+\dots +\lambda _n$
.
We set
![]() $G_n = \mathrm {GL}_n(F)$
. For
$G_n = \mathrm {GL}_n(F)$
. For
![]() $\lambda = (\lambda _1,\dots ,\lambda _n) \in \Lambda _n$
, we define a subgroup
$\lambda = (\lambda _1,\dots ,\lambda _n) \in \Lambda _n$
, we define a subgroup
![]() $\mathbb {K}_{n,\lambda }$
of
$\mathbb {K}_{n,\lambda }$
of
![]() $\mathrm {GL}_n(\mathfrak {o})$
by
$\mathrm {GL}_n(\mathfrak {o})$
by
where
![]() $\delta _{i,j}$
is the Kronecker delta.
$\delta _{i,j}$
is the Kronecker delta.
Let
![]() $\pi $
be an irreducible smooth complex representation of
$\pi $
be an irreducible smooth complex representation of
![]() $G_n$
. Godement–Jacquet [Reference Godement and Jacquet8] associated two local factors
$G_n$
. Godement–Jacquet [Reference Godement and Jacquet8] associated two local factors
![]() $L(s,\pi )$
and
$L(s,\pi )$
and
![]() $\varepsilon (s,\pi ,\psi )$
with
$\varepsilon (s,\pi ,\psi )$
with
![]() $\pi $
. By [Reference Jacquet, Piatetski-Shapiro and Shalika14, (5.1) Théorème (i)] and [Reference Godement and Jacquet8, Corollary 3.6] (or by the local Langlands correspondence [Reference Harris, Taylor and Berkovich11], [Reference Henniart12]), we have
$\pi $
. By [Reference Jacquet, Piatetski-Shapiro and Shalika14, (5.1) Théorème (i)] and [Reference Godement and Jacquet8, Corollary 3.6] (or by the local Langlands correspondence [Reference Harris, Taylor and Berkovich11], [Reference Henniart12]), we have
![]() $\varepsilon (s,\pi ,\psi ) = \varepsilon (0,\pi ,\psi ) q^{-c_{\pi } s}$
for some nonnegative integer
$\varepsilon (s,\pi ,\psi ) = \varepsilon (0,\pi ,\psi ) q^{-c_{\pi } s}$
for some nonnegative integer
![]() $c_{\pi }$
. We call
$c_{\pi }$
. We call
![]() $c_{\pi }$
the conductor of
$c_{\pi }$
the conductor of
![]() $\pi $
.
$\pi $
.
Set
![]() $\pi ^{(0)} = \pi $
and
$\pi ^{(0)} = \pi $
and
![]() $\pi ^{(i)}$
to be the highest derivative of
$\pi ^{(i)}$
to be the highest derivative of
![]() $\pi ^{(i-1)}$
in the sense of Bernstein–Zelevinsky [Reference Bernstein and Zelevinsky4] for
$\pi ^{(i-1)}$
in the sense of Bernstein–Zelevinsky [Reference Bernstein and Zelevinsky4] for
![]() $i = 1,\dots , n$
. (Note that our notation is different from the original in [Reference Bernstein and Zelevinsky4].) It is known that
$i = 1,\dots , n$
. (Note that our notation is different from the original in [Reference Bernstein and Zelevinsky4].) It is known that
![]() $\pi ^{(i)}$
is irreducible so that one can consider its conductor
$\pi ^{(i)}$
is irreducible so that one can consider its conductor
![]() $c_{\pi ^{(i)}}$
. We then define
$c_{\pi ^{(i)}}$
. We then define
![]() $\lambda _{\pi } = (\lambda _1, \dots , \lambda _n)$
by
$\lambda _{\pi } = (\lambda _1, \dots , \lambda _n)$
by
for
![]() $1 \leq k \leq n$
. In Section 2.3 (especially in Proposition 2.4) below, we will see that
$1 \leq k \leq n$
. In Section 2.3 (especially in Proposition 2.4) below, we will see that
![]() $\lambda _{\pi } \in \Lambda _n$
. We note that
$\lambda _{\pi } \in \Lambda _n$
. We note that
![]() $|\lambda _{\pi }| = c_{\pi }$
.
$|\lambda _{\pi }| = c_{\pi }$
.
We denote by
![]() $\pi ^{\mathbb {K}_{n,\lambda }}$
the
$\pi ^{\mathbb {K}_{n,\lambda }}$
the
![]() $\mathbb {K}_{n,\lambda }$
-invariant subspace of
$\mathbb {K}_{n,\lambda }$
-invariant subspace of
![]() $\pi $
, which is finite-dimensional. Our main theorem is stated as follows:
$\pi $
, which is finite-dimensional. Our main theorem is stated as follows:
Theorem 1.1 (Theorems 2.1, 2.2)
Let
![]() $\pi $
be an irreducible representation of
$\pi $
be an irreducible representation of
![]() $G_n$
.
$G_n$
.
-
(1) For
 $\lambda \in \Lambda _n$
, we have
$\lambda \in \Lambda _n$
, we have  $$\begin{align*}\dim(\pi^{\mathbb{K}_{n,\lambda}}) = \left\{ \begin{aligned} &1 &\quad&\text{if } \lambda = \lambda_{\pi}, \\ &0 &\quad&\text{if } \lambda < \lambda_{\pi}. \end{aligned} \right. \end{align*}$$
$$\begin{align*}\dim(\pi^{\mathbb{K}_{n,\lambda}}) = \left\{ \begin{aligned} &1 &\quad&\text{if } \lambda = \lambda_{\pi}, \\ &0 &\quad&\text{if } \lambda < \lambda_{\pi}. \end{aligned} \right. \end{align*}$$
-
(2) If
 $\lambda \in \Lambda _n$
satisfies that
$\lambda \in \Lambda _n$
satisfies that
 $|\lambda | < |\lambda _{\pi }|$
, then
$|\lambda | < |\lambda _{\pi }|$
, then
 $\pi ^{\mathbb {K}_{n,\lambda }} = 0$
.
$\pi ^{\mathbb {K}_{n,\lambda }} = 0$
.
We call any nonzero element in
![]() $\pi ^{\mathbb {K}_{n,\lambda _{\pi }}}$
a local newform of
$\pi ^{\mathbb {K}_{n,\lambda _{\pi }}}$
a local newform of
![]() $\pi $
. Using Theorem 1.1, we can give a characterisation of the conductor in terms of the dimensions of fixed parts: that is,
$\pi $
. Using Theorem 1.1, we can give a characterisation of the conductor in terms of the dimensions of fixed parts: that is,
Note that when
![]() $\pi $
is generic, since
$\pi $
is generic, since
![]() $\pi ^{(i)}$
is the trivial representation
$\pi ^{(i)}$
is the trivial representation
![]() $\mathbf {1}_{G_0}$
for any
$\mathbf {1}_{G_0}$
for any
![]() $i \geq 1$
, we have
$i \geq 1$
, we have
![]() $\lambda _{\pi } = (0,\dots ,0,c_{\pi })$
. In this case,
$\lambda _{\pi } = (0,\dots ,0,c_{\pi })$
. In this case,
![]() $\mathbb {K}_{n,\lambda _{\pi }}$
is nothing but the compact group introduced by Jacquet–Piatetskii-Shapiro–Shalika [Reference Jacquet, Piatetski-Shapiro and Shalika14]. Hence Theorem 1.1 (1) is an extension of a result in [Reference Jacquet, Piatetski-Shapiro and Shalika14].
$\mathbb {K}_{n,\lambda _{\pi }}$
is nothing but the compact group introduced by Jacquet–Piatetskii-Shapiro–Shalika [Reference Jacquet, Piatetski-Shapiro and Shalika14]. Hence Theorem 1.1 (1) is an extension of a result in [Reference Jacquet, Piatetski-Shapiro and Shalika14].
According to the Zelevinsky classification, the set of isomorphism classes of irreducible representations of
![]() $G_n$
is classified by multisegments. We recall it in Section 2.1. When
$G_n$
is classified by multisegments. We recall it in Section 2.1. When
![]() $\pi = Z(\mathfrak {m})$
is the irreducible representation associated with a multisegment
$\pi = Z(\mathfrak {m})$
is the irreducible representation associated with a multisegment
![]() $\mathfrak {m}$
, we have another description of
$\mathfrak {m}$
, we have another description of
![]() $\lambda _{\pi }$
in terms of
$\lambda _{\pi }$
in terms of
![]() $\mathfrak {m}$
(Proposition 2.4), which allows us to compute
$\mathfrak {m}$
(Proposition 2.4), which allows us to compute
![]() $\lambda _{\pi }$
in many important cases (Example 2.5). Moreover, Corollary 2.8 tells us how to compute
$\lambda _{\pi }$
in many important cases (Example 2.5). Moreover, Corollary 2.8 tells us how to compute
![]() $\lambda _{\pi }$
inductively in general.
$\lambda _{\pi }$
inductively in general.
The proof of Theorem 1.1 takes the following three steps:
-
Step 1: Reduce to two cases: the case where
 $\pi $
is of type
$\pi $
is of type
 $\chi $
with an unramified character
$\chi $
with an unramified character
 $\chi $
of
$\chi $
of
 $F^{\times }$
and the case where
$F^{\times }$
and the case where
 $L(s,\pi ) = 1$
. Here, we say that an irreducible representation
$L(s,\pi ) = 1$
. Here, we say that an irreducible representation
 $\pi $
is of type
$\pi $
is of type
 $\chi $
if
$\chi $
if
 $\pi = Z(\Delta _1+\dots +\Delta _r)$
such that for
$\pi = Z(\Delta _1+\dots +\Delta _r)$
such that for
 $i=1,\ldots ,r$
, the segment
$i=1,\ldots ,r$
, the segment
 $\Delta _i$
is of the form
$\Delta _i$
is of the form
 $[a_i,b_i]_{\chi }$
for some integers
$[a_i,b_i]_{\chi }$
for some integers
 $a_i,b_i$
satisfying
$a_i,b_i$
satisfying
 $a_i \le b_i$
.
$a_i \le b_i$
. -
Step 2: Prove Theorem 1.1 for
 $\pi $
of type
$\pi $
of type
 $\chi $
with an unramified character
$\chi $
with an unramified character
 $\chi $
of
$\chi $
of
 $F^{\times }$
.
$F^{\times }$
. -
Step 3: Prove Theorem 1.1 for
 $\pi $
such that
$\pi $
such that
 $L(s,\pi ) = 1$
.
$L(s,\pi ) = 1$
.
Let us give the details of each step.
1.3 Reduction
Using the Mackey theory, we study the
![]() $\mathbb {K}_{n,\lambda }$
-invariant subspaces of parabolically induced representations in Section 5.1. To do this, in Section 4.1, we relate
$\mathbb {K}_{n,\lambda }$
-invariant subspaces of parabolically induced representations in Section 5.1. To do this, in Section 4.1, we relate
![]() $\Lambda _n$
with the set
$\Lambda _n$
with the set
![]() $|\mathcal {C}^n|$
of isomorphism classes
$|\mathcal {C}^n|$
of isomorphism classes
![]() $[M]$
of
$[M]$
of
![]() $\mathfrak {o}$
-modules such that M is generated by at most n elements. In Section 5.1, we associate a compact open subgroup
$\mathfrak {o}$
-modules such that M is generated by at most n elements. In Section 5.1, we associate a compact open subgroup
![]() $\mathbb {K}_{n,[M]}$
of
$\mathbb {K}_{n,[M]}$
of
![]() $G_n$
with
$G_n$
with
![]() $[M] \in |\mathcal {C}^n|$
. If
$[M] \in |\mathcal {C}^n|$
. If
![]() $\lambda = (\lambda _1,\dots ,\lambda _n) \in \Lambda _n$
and
$\lambda = (\lambda _1,\dots ,\lambda _n) \in \Lambda _n$
and
![]() $M = \oplus _{i=1}^n \mathfrak {o}/\mathfrak {p}^{\lambda _i}$
, then
$M = \oplus _{i=1}^n \mathfrak {o}/\mathfrak {p}^{\lambda _i}$
, then
![]() $\mathbb {K}_{n,[M]} = \mathbb {K}_{n,\lambda }$
. Proposition 5.2 says that the
$\mathbb {K}_{n,[M]} = \mathbb {K}_{n,\lambda }$
. Proposition 5.2 says that the
![]() $\mathbb {K}_{n,[M]}$
-invariant subspace of a parabolically induced representation decomposes into a direct sum indexed by certain filtrations on M by
$\mathbb {K}_{n,[M]}$
-invariant subspace of a parabolically induced representation decomposes into a direct sum indexed by certain filtrations on M by
![]() $\mathfrak {o}$
-modules. In particular, this proposition together with Corollary 4.7 reduces Theorem 1.1 to the following two types of irreducible representations:
$\mathfrak {o}$
-modules. In particular, this proposition together with Corollary 4.7 reduces Theorem 1.1 to the following two types of irreducible representations:
-
•
 $\pi \in \mathrm {Irr}(G_n)$
of type
$\pi \in \mathrm {Irr}(G_n)$
of type
 $\chi $
with a fixed unramified character
$\chi $
with a fixed unramified character
 $\chi $
of
$\chi $
of
 $F^{\times }$
$F^{\times }$
-
•
 $\pi \in \mathrm {Irr}(G_n)$
such that
$\pi \in \mathrm {Irr}(G_n)$
such that
 $L(s,\pi ) = 1$
$L(s,\pi ) = 1$
1.4 The case where
 $\pi $
is of type
$\pi $
is of type
 $\chi $
$\chi $
In Section 6, we prove Theorem 1.1 for irreducible representations
![]() $\pi \in \mathrm {Irr}(G_n)$
of type
$\pi \in \mathrm {Irr}(G_n)$
of type
![]() $\chi $
with a fixed unramified character
$\chi $
with a fixed unramified character
![]() $\chi $
of
$\chi $
of
![]() $F^{\times }$
.
$F^{\times }$
.
In the proof of Theorem 1.1 (1), we first consider the case where
![]() $\pi $
is a ladder representation. The main ingredient in this case is Tadić’s determinantal formula established by Lapid–Mínguez [Reference Lapid and Mínguez21]. This formula describes
$\pi $
is a ladder representation. The main ingredient in this case is Tadić’s determinantal formula established by Lapid–Mínguez [Reference Lapid and Mínguez21]. This formula describes
![]() $\pi $
explicitly as an alternating sum of standard modules. The key point is that the standard modules appearing here are parabolically induced representations from one-dimensional representations. In particular, for
$\pi $
explicitly as an alternating sum of standard modules. The key point is that the standard modules appearing here are parabolically induced representations from one-dimensional representations. In particular, for
![]() $[M] \in |\mathcal {C}^n|$
, the determinantal formula together with Proposition 5.2 expresses the dimension of
$[M] \in |\mathcal {C}^n|$
, the determinantal formula together with Proposition 5.2 expresses the dimension of
![]() $\pi ^{\mathbb {K}_{n,[M]}}$
explicitly as an alternating sum of the numbers of certain filtrations on M by
$\pi ^{\mathbb {K}_{n,[M]}}$
explicitly as an alternating sum of the numbers of certain filtrations on M by
![]() $\mathfrak {o}$
-modules (Proposition 6.1). Surprisingly, there are many cancellations in this alternating sum (Lemma 6.3). From this lemma, we can deduce Theorem 1.1 (1) for a ladder representation
$\mathfrak {o}$
-modules (Proposition 6.1). Surprisingly, there are many cancellations in this alternating sum (Lemma 6.3). From this lemma, we can deduce Theorem 1.1 (1) for a ladder representation
![]() $\pi $
of type
$\pi $
of type
![]() $\chi $
. For these miraculous cancellations, see Example 6.4.
$\chi $
. For these miraculous cancellations, see Example 6.4.
The proof of Theorem 1.1 (1) for general
![]() $\pi $
of type
$\pi $
of type
![]() $\chi $
is by induction on a certain totally ordered set. The key is Proposition 2.7, whose proof relies on a highly nontrivial result of Knight–Zelevinsky [Reference Knight and Zelevinsky16] that describes the Zelevinsky dual of
$\chi $
is by induction on a certain totally ordered set. The key is Proposition 2.7, whose proof relies on a highly nontrivial result of Knight–Zelevinsky [Reference Knight and Zelevinsky16] that describes the Zelevinsky dual of
![]() $\pi $
(see also Proposition 3.7).
$\pi $
(see also Proposition 3.7).
We reduce the proof of Theorem 1.1 (2) to the case where
![]() $\pi $
is a Steinberg representation. In this case, by Tadić’s determinantal formula (or by the definition of the Steinberg representations in Harish-Chandra [Reference Harish-Chandra10]), we can express
$\pi $
is a Steinberg representation. In this case, by Tadić’s determinantal formula (or by the definition of the Steinberg representations in Harish-Chandra [Reference Harish-Chandra10]), we can express
![]() $\pi ^{\mathbb {K}_{n,\lambda }}$
explicitly as an alternating sum of the numbers of certain filtrations on the
$\pi ^{\mathbb {K}_{n,\lambda }}$
explicitly as an alternating sum of the numbers of certain filtrations on the
![]() $\mathfrak {o}$
-module corresponding to
$\mathfrak {o}$
-module corresponding to
![]() $\lambda $
. We realise this alternating sum as a coefficient of certain formal power series in one variable whose coefficients are in a graded ring. By giving another description of this formal power series, we deduce that
$\lambda $
. We realise this alternating sum as a coefficient of certain formal power series in one variable whose coefficients are in a graded ring. By giving another description of this formal power series, we deduce that
![]() $\pi ^{\mathbb {K}_{n,\lambda }} = 0$
.
$\pi ^{\mathbb {K}_{n,\lambda }} = 0$
.
1.5 The case where
 $L(s,\pi ) = 1$
$L(s,\pi ) = 1$
In Section 7, we firstly prove Theorem 1.1 (2) for
![]() $\pi $
with
$\pi $
with
![]() $L(s,\pi ) = 1$
. We reduce the proof to the case where
$L(s,\pi ) = 1$
. We reduce the proof to the case where
![]() $\pi $
is cuspidal. In this case, Lemma 7.1 says that certain Hecke operators depending on
$\pi $
is cuspidal. In this case, Lemma 7.1 says that certain Hecke operators depending on
![]() $\lambda \in \Lambda _n$
act on
$\lambda \in \Lambda _n$
act on
![]() $\pi $
as nilpotent endomorphisms. We consider the Godement–Jacquet integral
$\pi $
as nilpotent endomorphisms. We consider the Godement–Jacquet integral
![]() $Z(\Phi ,s,f)$
defined in [Reference Godement and Jacquet8]. From this lemma, it follows that if
$Z(\Phi ,s,f)$
defined in [Reference Godement and Jacquet8]. From this lemma, it follows that if
![]() $\pi ^{\mathbb {K}_{n,\lambda }} \not = 0$
, then we can obtain data
$\pi ^{\mathbb {K}_{n,\lambda }} \not = 0$
, then we can obtain data
![]() $\Phi $
and f such that
$\Phi $
and f such that
![]() $Z(\Phi ,s,f)$
is a nonzero constant, whereas
$Z(\Phi ,s,f)$
is a nonzero constant, whereas
![]() $Z(\hat {\Phi },s,\check {f}) \in q^{|\lambda | s} \mathbb {C}[[q^{-s}]]$
. Since
$Z(\hat {\Phi },s,\check {f}) \in q^{|\lambda | s} \mathbb {C}[[q^{-s}]]$
. Since
![]() $\varepsilon (s,\pi ,\psi ) = \varepsilon (0,\pi ,\psi )q^{-|\lambda _{\pi }|s}$
, by the functional equation, we conclude that
$\varepsilon (s,\pi ,\psi ) = \varepsilon (0,\pi ,\psi )q^{-|\lambda _{\pi }|s}$
, by the functional equation, we conclude that
![]() $|\lambda | \geq |\lambda _{\pi }|$
.
$|\lambda | \geq |\lambda _{\pi }|$
.
By Proposition 5.2, we can reduce Theorem 1.1 (1) for
![]() $\pi $
with
$\pi $
with
![]() $L(s,\pi ) = 1$
to the case where
$L(s,\pi ) = 1$
to the case where
![]() $\pi = Z(\Delta )$
for a segment
$\pi = Z(\Delta )$
for a segment
![]() $\Delta $
(Lemma 7.2). The key point here is that the matrices defined by the multiplicities of irreducible representations appearing in standard modules are ‘triangular’ and unipotent ([Reference Zelevinsky42, 7.1 Theorem]).
$\Delta $
(Lemma 7.2). The key point here is that the matrices defined by the multiplicities of irreducible representations appearing in standard modules are ‘triangular’ and unipotent ([Reference Zelevinsky42, 7.1 Theorem]).
Finally, we prove Theorem 1.1 (1) for
![]() $\pi = Z(\Delta )$
with
$\pi = Z(\Delta )$
with
![]() $L(s,\pi ) = 1$
. Slightly generally, we do it in Section 9 for Speh representations
$L(s,\pi ) = 1$
. Slightly generally, we do it in Section 9 for Speh representations
![]() $\mathrm {Sp}(\pi _{\mathrm {temp}}, m)$
with an irreducible tempered representation
$\mathrm {Sp}(\pi _{\mathrm {temp}}, m)$
with an irreducible tempered representation
![]() $\pi _{\mathrm {temp}}$
of
$\pi _{\mathrm {temp}}$
of
![]() $G_n$
. For the notation of Speh representations, see Example 2.5 (4). The proof of this case is rather an analogue of the generic case in [Reference Jacquet, Piatetski-Shapiro and Shalika14]. Namely, it is an application of the theory of Rankin–Selberg integrals. To carry out the proof, we establish this theory for Speh representations in Section 8.
$G_n$
. For the notation of Speh representations, see Example 2.5 (4). The proof of this case is rather an analogue of the generic case in [Reference Jacquet, Piatetski-Shapiro and Shalika14]. Namely, it is an application of the theory of Rankin–Selberg integrals. To carry out the proof, we establish this theory for Speh representations in Section 8.
1.6 Rankin–Selberg integrals for Speh representations
The theory of Rankin–Selberg integrals was developed by Jacquet–Piatetskii-Shapiro–Shalika [Reference Jacquet, Piatetski-Shapiro and Shalika15]. These integrals are integrations of products of Whittaker functions of two irreducible representations of
![]() $G_n$
and
$G_n$
and
![]() $G_m$
, and they represent the Rankin–Selberg L-functions. Since representations are required to admit nontrivial Whittaker functions, they must be generic. As an application of Rankin–Selberg integrals for
$G_m$
, and they represent the Rankin–Selberg L-functions. Since representations are required to admit nontrivial Whittaker functions, they must be generic. As an application of Rankin–Selberg integrals for
![]() $G_n \times G_{n-1}$
, the theory of local newforms for generic representations of
$G_n \times G_{n-1}$
, the theory of local newforms for generic representations of
![]() $G_n$
was established in [Reference Jacquet, Piatetski-Shapiro and Shalika14].
$G_n$
was established in [Reference Jacquet, Piatetski-Shapiro and Shalika14].
To prove Theorem 1.1 (1) for Speh representations, we need to extend the theory of Rankin–Selberg integrals to the case of Speh representations. In the equal rank case, this extension was done by Lapid–Mao [Reference Lapid and Mao20]. In their paper, instead of Whittaker models, they used two models of a Speh representation that are called the Zelevinsky model and the Shalika model Footnote 1.
For our purpose, we need the Rankin–Selberg integrals in the ‘almost equal rank case’, which are easier than the equal rank case. The Zelevinsky model is a direct generalisation of the Whittaker model so that we can easily extend the theory of Rankin–Selberg integrals using this model (Theorem 8.5). On the other hand, the Shalika model has an important property of the Whittaker model (Theorem 8.2), which we need for the proof of Theorem 1.1 (1) for Speh representations. To transfer the Rankin–Selberg integrals in the Zelevinsky models to those in the Shalika models, we use the model transition established by Lapid–Mao (see Proposition 8.3).
After establishing the Rankin–Selberg integrals in the Shalika models, the proof of Theorem 1.1 (1) for Speh representations
![]() $\pi $
with
$\pi $
with
![]() $L(s,\pi ) = 1$
is exactly the same as in the generic case [Reference Jacquet, Piatetski-Shapiro and Shalika14]. We do not compute the greatest common divisors of the Rankin–Selberg integrals in general (see Proposition 8.7). This is a main reason this method cannot be applied to Speh representations
$L(s,\pi ) = 1$
is exactly the same as in the generic case [Reference Jacquet, Piatetski-Shapiro and Shalika14]. We do not compute the greatest common divisors of the Rankin–Selberg integrals in general (see Proposition 8.7). This is a main reason this method cannot be applied to Speh representations
![]() $\pi $
with
$\pi $
with
![]() $L(s,\pi ) \not = 1$
. However, as an application of Theorem 1.1 (1) for all cases, we can specify the greatest common divisor when the Speh representation of the group of smaller rank is unramified (see Theorem 9.1).
$L(s,\pi ) \not = 1$
. However, as an application of Theorem 1.1 (1) for all cases, we can specify the greatest common divisor when the Speh representation of the group of smaller rank is unramified (see Theorem 9.1).
1.7 Organisation
This paper is organised as follows. In Section 2, we state the main results (Theorems 2.1 and 2.2). We give two definitions of
![]() $\lambda _{\pi }$
(Proposition 2.4) and explain how to compute it (Corollary 2.8). Some important examples of
$\lambda _{\pi }$
(Proposition 2.4) and explain how to compute it (Corollary 2.8). Some important examples of
![]() $\lambda _{\pi }$
are given in Example 2.5. Propositions 2.4 and 2.7 are proven in Section 3. After preparing several facts on
$\lambda _{\pi }$
are given in Example 2.5. Propositions 2.4 and 2.7 are proven in Section 3. After preparing several facts on
![]() $\mathfrak {o}$
-modules in Section 4, we prove the Mackey decomposition of the
$\mathfrak {o}$
-modules in Section 4, we prove the Mackey decomposition of the
![]() $\mathbb {K}_{n,[M]}$
-invariant subspace of a parabolically induced representation (Proposition 5.2) in Section 5. It reduces the proofs of the main results to two cases:
$\mathbb {K}_{n,[M]}$
-invariant subspace of a parabolically induced representation (Proposition 5.2) in Section 5. It reduces the proofs of the main results to two cases:
![]() $\pi \in \mathrm {Irr}(G_n)$
of type
$\pi \in \mathrm {Irr}(G_n)$
of type
![]() $\chi $
with a fixed unramified character
$\chi $
with a fixed unramified character
![]() $\chi $
of
$\chi $
of
![]() $F^{\times }$
and
$F^{\times }$
and
![]() $\pi \in \mathrm {Irr}(G_n)$
such that
$\pi \in \mathrm {Irr}(G_n)$
such that
![]() $L(s,\pi ) = 1$
. For the former case, Theorems 2.1 and 2.2 are proven in Section 6. In Section 7, we treat the latter case. More precisely, for the latter case, we prove Theorem 2.2, but we reduce Theorem 2.1 to the case where
$L(s,\pi ) = 1$
. For the former case, Theorems 2.1 and 2.2 are proven in Section 6. In Section 7, we treat the latter case. More precisely, for the latter case, we prove Theorem 2.2, but we reduce Theorem 2.1 to the case where
![]() $\pi $
is a Speh representation. Theorem 2.1 for Speh representations
$\pi $
is a Speh representation. Theorem 2.1 for Speh representations
![]() $\pi $
with
$\pi $
with
![]() $L(s,\pi ) = 1$
is proven in Section 9 after establishing the theory of Rankin–Selberg integrals for Speh representations in Section 8.
$L(s,\pi ) = 1$
is proven in Section 9 after establishing the theory of Rankin–Selberg integrals for Speh representations in Section 8.
Notation
Let F be a nonarchimedean local field of characteristic zero. Denote the ring of integers and its maximal ideal by
![]() $\mathfrak {o}$
and
$\mathfrak {o}$
and
![]() $\mathfrak {p}$
, respectively. Fix a uniformiser
$\mathfrak {p}$
, respectively. Fix a uniformiser
![]() $\varpi $
of
$\varpi $
of
![]() $\mathfrak {o}$
, and normalise the absolute value
$\mathfrak {o}$
, and normalise the absolute value
![]() $|\cdot |$
on F so that
$|\cdot |$
on F so that
![]() $|\varpi | = q^{-1}$
, where
$|\varpi | = q^{-1}$
, where
![]() $q = \# (\mathfrak {o}/\mathfrak {p})$
. We fix a nontrivial additive character
$q = \# (\mathfrak {o}/\mathfrak {p})$
. We fix a nontrivial additive character
![]() $\psi $
of F such that
$\psi $
of F such that
![]() $\psi $
is trivial on
$\psi $
is trivial on
![]() $\mathfrak {o}$
but nontrivial on
$\mathfrak {o}$
but nontrivial on
![]() $\mathfrak {p}^{-1}$
.
$\mathfrak {p}^{-1}$
.
For an integer
![]() $n \ge 1$
and a commutative ring R, we let
$n \ge 1$
and a commutative ring R, we let
![]() $M_n(R)$
denote the R-module of n-by-n matrices with entries in R.
$M_n(R)$
denote the R-module of n-by-n matrices with entries in R.
In this paper, all representations are assumed to be smooth. For a representation
![]() $\pi $
of
$\pi $
of
![]() $\mathrm {GL}_n(F)$
, its contragredient representation is denoted by
$\mathrm {GL}_n(F)$
, its contragredient representation is denoted by
![]() $\widetilde {\pi }$
.
$\widetilde {\pi }$
.
2 Statements of the main results
In this section, we fix notations and state the main results.
2.1 The Zelevinsky classification
We recall the Zelevinsky classification [Reference Zelevinsky42] of irreducible representations of
![]() $G_n = \mathrm {GL}_n(F)$
. For a smooth representation
$G_n = \mathrm {GL}_n(F)$
. For a smooth representation
![]() $\pi $
of
$\pi $
of
![]() $G_n$
and a character
$G_n$
and a character
![]() $\chi $
of
$\chi $
of
![]() $F^{\times }$
, the twisted representation
$F^{\times }$
, the twisted representation
![]() $g \mapsto \pi (g)\chi (\det g)$
is denoted by
$g \mapsto \pi (g)\chi (\det g)$
is denoted by
![]() $\pi \chi $
. The set of equivalence classes of irreducible representations of
$\pi \chi $
. The set of equivalence classes of irreducible representations of
![]() $G_n$
is denoted by
$G_n$
is denoted by
![]() $\mathrm {Irr}(G_n)$
.
$\mathrm {Irr}(G_n)$
.
When
![]() $\pi _1, \dots , \pi _r$
are smooth representations of
$\pi _1, \dots , \pi _r$
are smooth representations of
![]() $G_{n_1}, \dots , G_{n_r}$
, respectively, with
$G_{n_1}, \dots , G_{n_r}$
, respectively, with
![]() $n_1+\dots +n_r = n$
, we write
$n_1+\dots +n_r = n$
, we write
![]() $\pi _1 \times \dots \times \pi _r$
for the parabolically induced representation of
$\pi _1 \times \dots \times \pi _r$
for the parabolically induced representation of
![]() $G_n$
from
$G_n$
from
![]() $\pi _1 \otimes \dots \otimes \pi _r$
via the standard parabolic subgroup whose Levi subgroup is
$\pi _1 \otimes \dots \otimes \pi _r$
via the standard parabolic subgroup whose Levi subgroup is
![]() $G_{n_1} \times \dots \times G_{n_r}$
.
$G_{n_1} \times \dots \times G_{n_r}$
.
A segment
![]() $\Delta $
is a finite set of representations of the form
$\Delta $
is a finite set of representations of the form
where
![]() $\rho $
is an irreducible cuspidal representation of
$\rho $
is an irreducible cuspidal representation of
![]() $G_d$
for some
$G_d$
for some
![]() $d \ge 1$
, and
$d \ge 1$
, and
![]() $x,y \in \mathbb {R}$
with
$x,y \in \mathbb {R}$
with
![]() $x \equiv y \bmod \mathbb {Z}$
and
$x \equiv y \bmod \mathbb {Z}$
and
![]() $x \leq y$
. We write
$x \leq y$
. We write
![]() $l(\Delta ) = y-x+1$
and call it the length of
$l(\Delta ) = y-x+1$
and call it the length of
![]() $\Delta $
.
$\Delta $
.
Let
![]() $\Delta = [x,y]_{\rho }$
be a segment. Then the parabolically induced representation
$\Delta = [x,y]_{\rho }$
be a segment. Then the parabolically induced representation
of
![]() $G_{dl(\Delta )}$
has a unique irreducible subrepresentation. We denote it by
$G_{dl(\Delta )}$
has a unique irreducible subrepresentation. We denote it by
![]() $Z(\Delta )$
. For example, if
$Z(\Delta )$
. For example, if
![]() $\rho = \chi $
is a character of
$\rho = \chi $
is a character of
![]() $F^{\times }$
, then
$F^{\times }$
, then
![]() $Z([x,y]_{\chi }) = |\det |^{\frac {x+y}{2}}\chi (\det )$
is a one-dimensional representation of
$Z([x,y]_{\chi }) = |\det |^{\frac {x+y}{2}}\chi (\det )$
is a one-dimensional representation of
![]() $G_{y-x+1}$
.
$G_{y-x+1}$
.
Let
![]() $r \geq 1$
. For
$r \geq 1$
. For
![]() $i=1,\ldots ,r$
, let
$i=1,\ldots ,r$
, let
![]() $\Delta _i = [x_i,y_i]_{\rho _i}$
be a segment and
$\Delta _i = [x_i,y_i]_{\rho _i}$
be a segment and
![]() $n_i \geq 1$
an integer such that
$n_i \geq 1$
an integer such that
![]() $\rho _i$
is a cuspidal representation of
$\rho _i$
is a cuspidal representation of
![]() $G_{n_i}$
. When
$G_{n_i}$
. When
![]() $\rho _i$
is unitary and the inequalities
$\rho _i$
is unitary and the inequalities
hold, the parabolically induced representation
has a unique irreducible subrepresentation. We denote it by
![]() $Z(\mathfrak {m})$
, where
$Z(\mathfrak {m})$
, where
![]() $\mathfrak {m}$
denotes the multisegment
$\mathfrak {m}$
denotes the multisegment
![]() $\mathfrak {m} = \Delta _1 + \dots + \Delta _r$
. The Zelevinsky classification says that for any irreducible representation
$\mathfrak {m} = \Delta _1 + \dots + \Delta _r$
. The Zelevinsky classification says that for any irreducible representation
![]() $\pi $
of
$\pi $
of
![]() $G_n$
, there exists a unique multisegment
$G_n$
, there exists a unique multisegment
![]() $\mathfrak {m} = \Delta _1 + \dots + \Delta _r$
such that
$\mathfrak {m} = \Delta _1 + \dots + \Delta _r$
such that
![]() $\pi \cong Z(\mathfrak {m})$
.
$\pi \cong Z(\mathfrak {m})$
.
When
![]() $x_1> \dots > x_t$
and
$x_1> \dots > x_t$
and
![]() $y_1> \dots > y_t$
, the irreducible representation
$y_1> \dots > y_t$
, the irreducible representation
is called a ladder representation. A ladder representation of the form
![]() $Z([x,y]_{\rho }, [x-1,y-1]_{\rho }, \dots , [x-t+1,y-t+1]_{\rho })$
for some positive integer t is called a Speh representation.
$Z([x,y]_{\rho }, [x-1,y-1]_{\rho }, \dots , [x-t+1,y-t+1]_{\rho })$
for some positive integer t is called a Speh representation.
2.2 Main results
Fix
![]() $n \geq 1$
. Let
$n \geq 1$
. Let
![]() $\Lambda _n$
be the subset of
$\Lambda _n$
be the subset of
![]() $\mathbb {Z}^n$
consisting of
$\mathbb {Z}^n$
consisting of
![]() $\lambda = (\lambda _1, \dots , \lambda _n) \in \mathbb {Z}^n$
such that
$\lambda = (\lambda _1, \dots , \lambda _n) \in \mathbb {Z}^n$
such that
![]() $0 \leq \lambda _1 \leq \dots \leq \lambda _n$
. Note that
$0 \leq \lambda _1 \leq \dots \leq \lambda _n$
. Note that
![]() $\Lambda _n$
is a submonoid of
$\Lambda _n$
is a submonoid of
![]() $\mathbb {Z}^n$
. We endow
$\mathbb {Z}^n$
. We endow
![]() $\Lambda _n$
with the total order induced by the lexicographic order: that is, for
$\Lambda _n$
with the total order induced by the lexicographic order: that is, for
![]() $\lambda = (\lambda _1, \dots , \lambda _n), \lambda ' = (\lambda ^{\prime }_1, \dots , \lambda ^{\prime }_n) \in \Lambda _n$
, we write
$\lambda = (\lambda _1, \dots , \lambda _n), \lambda ' = (\lambda ^{\prime }_1, \dots , \lambda ^{\prime }_n) \in \Lambda _n$
, we write
![]() $\lambda < \lambda '$
if and only if there exists
$\lambda < \lambda '$
if and only if there exists
![]() $1 \leq i \leq n$
such that
$1 \leq i \leq n$
such that
![]() $\lambda _j = \lambda ^{\prime }_j$
for
$\lambda _j = \lambda ^{\prime }_j$
for
![]() $j < i$
and
$j < i$
and
![]() $\lambda _i < \lambda ^{\prime }_i$
.
$\lambda _i < \lambda ^{\prime }_i$
.
For
![]() $\lambda = (\lambda _1, \dots , \lambda _n) \in \Lambda _n$
, define
$\lambda = (\lambda _1, \dots , \lambda _n) \in \Lambda _n$
, define
![]() $\mathbb {K}_{n,\lambda }$
to be the subgroup of
$\mathbb {K}_{n,\lambda }$
to be the subgroup of
![]() $G_n(\mathfrak {o}) = \mathrm {GL}_n(\mathfrak {o})$
consisting of matrices
$G_n(\mathfrak {o}) = \mathrm {GL}_n(\mathfrak {o})$
consisting of matrices
![]() $k = (k_{i,j})_{1 \le i,j \le n}$
such that
$k = (k_{i,j})_{1 \le i,j \le n}$
such that
for any
![]() $1\leq i,j \leq n$
. For example, if
$1\leq i,j \leq n$
. For example, if
![]() $n = 4$
and
$n = 4$
and
![]() $\lambda = (0,0,1,2)$
, then
$\lambda = (0,0,1,2)$
, then
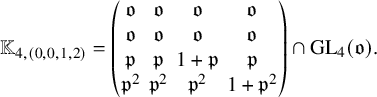 $$\begin{align*}\mathbb{K}_{4, (0,0,1,2)} = \begin{pmatrix} \mathfrak{o} & \mathfrak{o} & \mathfrak{o} & \mathfrak{o} \\ \mathfrak{o} & \mathfrak{o} & \mathfrak{o} & \mathfrak{o} \\ \mathfrak{p} & \mathfrak{p} & 1+\mathfrak{p} & \mathfrak{p} \\ \mathfrak{p}^2 & \mathfrak{p}^2 & \mathfrak{p}^2 & 1+\mathfrak{p}^2 \end{pmatrix} \cap \mathrm{GL}_4(\mathfrak{o}). \end{align*}$$
$$\begin{align*}\mathbb{K}_{4, (0,0,1,2)} = \begin{pmatrix} \mathfrak{o} & \mathfrak{o} & \mathfrak{o} & \mathfrak{o} \\ \mathfrak{o} & \mathfrak{o} & \mathfrak{o} & \mathfrak{o} \\ \mathfrak{p} & \mathfrak{p} & 1+\mathfrak{p} & \mathfrak{p} \\ \mathfrak{p}^2 & \mathfrak{p}^2 & \mathfrak{p}^2 & 1+\mathfrak{p}^2 \end{pmatrix} \cap \mathrm{GL}_4(\mathfrak{o}). \end{align*}$$
In Section 1.2, we defined
![]() $\lambda _{\pi } \in \Lambda _n$
for any
$\lambda _{\pi } \in \Lambda _n$
for any
![]() $\pi \in \mathrm {Irr}(G_n)$
. The main results are as follows.
$\pi \in \mathrm {Irr}(G_n)$
. The main results are as follows.
Theorem 2.1. Let
![]() $\pi \in \mathrm {Irr}(G_n)$
. Then the
$\pi \in \mathrm {Irr}(G_n)$
. Then the
![]() $\mathbb {K}_{n,\lambda _{\pi }}$
-invariant subspace
$\mathbb {K}_{n,\lambda _{\pi }}$
-invariant subspace
![]() $\pi ^{\mathbb {K}_{n,\lambda _{\pi }}}$
is one-dimensional. Moreover, if
$\pi ^{\mathbb {K}_{n,\lambda _{\pi }}}$
is one-dimensional. Moreover, if
![]() $\lambda \in \Lambda _n$
satisfies
$\lambda \in \Lambda _n$
satisfies
![]() $\lambda < \lambda _{\pi }$
, then
$\lambda < \lambda _{\pi }$
, then
![]() $\pi ^{\mathbb {K}_{n,\lambda }} = 0$
.
$\pi ^{\mathbb {K}_{n,\lambda }} = 0$
.
For
![]() $\lambda =(\lambda _1,\ldots ,\lambda _n) \in \Lambda _n$
, we write
$\lambda =(\lambda _1,\ldots ,\lambda _n) \in \Lambda _n$
, we write
![]() $|\lambda |$
for
$|\lambda |$
for
![]() $\lambda _1 + \cdots + \lambda _n$
.
$\lambda _1 + \cdots + \lambda _n$
.
Theorem 2.2. Let
![]() $\pi \in \mathrm {Irr}(G_n)$
. If
$\pi \in \mathrm {Irr}(G_n)$
. If
![]() $\lambda \in \Lambda _n$
satisfies
$\lambda \in \Lambda _n$
satisfies
![]() $|\lambda | < |\lambda _{\pi }|$
, then
$|\lambda | < |\lambda _{\pi }|$
, then
![]() $\pi ^{\mathbb {K}_{n,\lambda }} = 0$
.
$\pi ^{\mathbb {K}_{n,\lambda }} = 0$
.
2.3 Definition of
 $\lambda _{\mathfrak {m}}$
$\lambda _{\mathfrak {m}}$
For an irreducible representation
![]() $\pi $
of
$\pi $
of
![]() $G_n$
, we defined
$G_n$
, we defined
![]() $\lambda _{\pi } \in \mathbb {Z}^n$
in Section 1.2. Here we describe it in terms of multisegments, which then implies that
$\lambda _{\pi } \in \mathbb {Z}^n$
in Section 1.2. Here we describe it in terms of multisegments, which then implies that
![]() $\lambda _{\pi } \in \Lambda _n$
.
$\lambda _{\pi } \in \Lambda _n$
.
A segment
![]() $\Delta $
is written as
$\Delta $
is written as
![]() $\Delta =[a,b]_{\rho }$
, where
$\Delta =[a,b]_{\rho }$
, where
![]() $a,b \in \mathbb {Z}$
with
$a,b \in \mathbb {Z}$
with
![]() $a \leq b$
and
$a \leq b$
and
![]() $\rho $
is a cuspidal representation of
$\rho $
is a cuspidal representation of
![]() $G_d$
for some
$G_d$
for some
![]() $d \geq 0$
. We write a multisegment as a sum
$d \geq 0$
. We write a multisegment as a sum
![]() $\mathfrak {m} = \Delta _1+\dots +\Delta _r$
of segments, where r is a nonnegative integer. We call the integer r the cardinality of
$\mathfrak {m} = \Delta _1+\dots +\Delta _r$
of segments, where r is a nonnegative integer. We call the integer r the cardinality of
![]() $\mathfrak {m}$
and denote it by
$\mathfrak {m}$
and denote it by
![]() $\mathrm {Card}(\mathfrak {m})$
. Recall that we set
$\mathrm {Card}(\mathfrak {m})$
. Recall that we set
![]() $l(\Delta ) = b-a+1$
. We write
$l(\Delta ) = b-a+1$
. We write
![]() $l(\mathfrak {m})$
for the sum
$l(\mathfrak {m})$
for the sum
![]() $l(\Delta _1) + \cdots + l(\Delta _r)$
and call
$l(\Delta _1) + \cdots + l(\Delta _r)$
and call
![]() $l(\mathfrak {m})$
the length of
$l(\mathfrak {m})$
the length of
![]() $\mathfrak {m}$
.
$\mathfrak {m}$
.
If
![]() $a < b$
, we write
$a < b$
, we write
![]() $\Delta ^{-}$
for the segment
$\Delta ^{-}$
for the segment
![]() $[a,b-1]_{\rho }$
. When
$[a,b-1]_{\rho }$
. When
![]() $a=b$
, we understand
$a=b$
, we understand
![]() $\Delta ^{-}$
to be the empty multisegment. We set
$\Delta ^{-}$
to be the empty multisegment. We set
![]() $\mathfrak {m}^{-} = \Delta _1^{-} + \cdots + \Delta _r^{-}$
. By the fundamental result of Zelevinsky [Reference Zelevinsky42, 8.1 Theorem], the highest derivative of
$\mathfrak {m}^{-} = \Delta _1^{-} + \cdots + \Delta _r^{-}$
. By the fundamental result of Zelevinsky [Reference Zelevinsky42, 8.1 Theorem], the highest derivative of
![]() $Z(\mathfrak {m})$
is equivalent to
$Z(\mathfrak {m})$
is equivalent to
![]() $Z(\mathfrak {m}^{-})$
.
$Z(\mathfrak {m}^{-})$
.
We call
![]() $\Delta = [a,b]_{\rho }$
unipotent if
$\Delta = [a,b]_{\rho }$
unipotent if
![]() $\rho $
is an unramified character of
$\rho $
is an unramified character of
![]() $F^{\times }$
. Similarly, we say that
$F^{\times }$
. Similarly, we say that
![]() $\mathfrak {m} = \Delta _1 + \cdots + \Delta _r$
is unipotent if
$\mathfrak {m} = \Delta _1 + \cdots + \Delta _r$
is unipotent if
![]() $\Delta _i$
is unipotent for
$\Delta _i$
is unipotent for
![]() $i=1,\ldots ,r$
. Fix an unramified character
$i=1,\ldots ,r$
. Fix an unramified character
![]() $\chi $
of
$\chi $
of
![]() $F^{\times }$
. We say that a multisegment
$F^{\times }$
. We say that a multisegment
![]() $\mathfrak {m} = \Delta _1 + \cdots + \Delta _r$
is of type
$\mathfrak {m} = \Delta _1 + \cdots + \Delta _r$
is of type
![]() $\chi $
if for
$\chi $
if for
![]() $i=1,\ldots ,r$
, the segment
$i=1,\ldots ,r$
, the segment
![]() $\Delta _i$
is of the form
$\Delta _i$
is of the form
![]() $[a_i,b_i]_{\chi }$
for some integers
$[a_i,b_i]_{\chi }$
for some integers
![]() $a_i,b_i$
satisfying
$a_i,b_i$
satisfying
![]() $a_i \le b_i$
.
$a_i \le b_i$
.
We denote by
![]() $\mathfrak {m}^{\sharp }$
the unique multisegment such that
$\mathfrak {m}^{\sharp }$
the unique multisegment such that
![]() $Z(\mathfrak {m}^{\sharp })$
is equivalent to the Zelevinsky dual of
$Z(\mathfrak {m}^{\sharp })$
is equivalent to the Zelevinsky dual of
![]() $Z(\mathfrak {m})$
(see, e.g., [Reference Procter34, Section 7]). We denote by
$Z(\mathfrak {m})$
(see, e.g., [Reference Procter34, Section 7]). We denote by
![]() $\mathfrak {m}^{\mathrm {ram}}$
the multisegment
$\mathfrak {m}^{\mathrm {ram}}$
the multisegment
![]() $((\mathfrak {m}^{\sharp })^{-})^{\sharp }$
. When
$((\mathfrak {m}^{\sharp })^{-})^{\sharp }$
. When
![]() $\pi = Z(\mathfrak {m})$
, we set
$\pi = Z(\mathfrak {m})$
, we set
![]() $\pi ^{\mathrm {ram}} = Z(\mathfrak {m}^{\mathrm {ram}})$
. We use ‘ram’ only for unipotent multisegments. For an example of
$\pi ^{\mathrm {ram}} = Z(\mathfrak {m}^{\mathrm {ram}})$
. We use ‘ram’ only for unipotent multisegments. For an example of
![]() $\mathfrak {m}^{\mathrm {ram}}$
, see Section 2.5 below.
$\mathfrak {m}^{\mathrm {ram}}$
, see Section 2.5 below.
When
![]() $n' < n$
, we regard
$n' < n$
, we regard
![]() $\Lambda _{n'}$
as a submonoid of
$\Lambda _{n'}$
as a submonoid of
![]() $\Lambda _n$
via the inclusion
$\Lambda _n$
via the inclusion
![]() $\Lambda _{n'} \hookrightarrow \Lambda _n$
given by
$\Lambda _{n'} \hookrightarrow \Lambda _n$
given by
![]() $(\lambda _1, \dots , \lambda _{n'}) \mapsto (0,\dots ,0,\lambda _1,\dots ,\lambda _{n'})$
.
$(\lambda _1, \dots , \lambda _{n'}) \mapsto (0,\dots ,0,\lambda _1,\dots ,\lambda _{n'})$
.
Definition 2.3. Let
![]() $\mathfrak {m}$
be a multisegment.
$\mathfrak {m}$
be a multisegment.
-
(1) If
 $\mathfrak {m} = \Delta _1+\dots +\Delta _r$
with
$\mathfrak {m} = \Delta _1+\dots +\Delta _r$
with
 $\Delta _i = [a_i,b_i]_{\rho _i}$
being not unipotent for all
$\Delta _i = [a_i,b_i]_{\rho _i}$
being not unipotent for all
 $i = 1, \dots , r$
, then we set where
$i = 1, \dots , r$
, then we set where $$\begin{align*}\lambda_{\mathfrak{m}} = \sum_{i=1}^r (0,\dots,0,\underbrace{c_{\rho_i}, \dots, c_{\rho_i}}_{l(\Delta_i)}), \end{align*}$$
$$\begin{align*}\lambda_{\mathfrak{m}} = \sum_{i=1}^r (0,\dots,0,\underbrace{c_{\rho_i}, \dots, c_{\rho_i}}_{l(\Delta_i)}), \end{align*}$$
 $c_{\rho _i}$
is the conductor of
$c_{\rho _i}$
is the conductor of
 $\rho _i$
. Note that
$\rho _i$
. Note that
 $c_{\rho _i}> 0$
for
$c_{\rho _i}> 0$
for
 $1 \leq i \leq r$
by [Reference Jacquet, Piatetski-Shapiro and Shalika14, (5.1) Théorème].
$1 \leq i \leq r$
by [Reference Jacquet, Piatetski-Shapiro and Shalika14, (5.1) Théorème].
-
(2) If
 $\mathfrak {m}$
is unipotent, and if we write
$\mathfrak {m}$
is unipotent, and if we write
 $\mathfrak {m}^{\mathrm {ram}} = \Delta _1+\dots +\Delta _r$
, then we set
$\mathfrak {m}^{\mathrm {ram}} = \Delta _1+\dots +\Delta _r$
, then we set  $$\begin{align*}\lambda_{\mathfrak{m}} = \sum_{i=1}^r (0,\dots,0,\underbrace{1, \dots, 1}_{l(\Delta_i)}). \end{align*}$$
$$\begin{align*}\lambda_{\mathfrak{m}} = \sum_{i=1}^r (0,\dots,0,\underbrace{1, \dots, 1}_{l(\Delta_i)}). \end{align*}$$
-
(3) In general, we decompose
 $\mathfrak {m}$
as
$\mathfrak {m}$
as
 $\mathfrak {m} = \mathfrak {m}' + \mathfrak {m}_{\mathrm {unip}}$
, where
$\mathfrak {m} = \mathfrak {m}' + \mathfrak {m}_{\mathrm {unip}}$
, where
 $\mathfrak {m}_{\mathrm {unip}}$
is unipotent, and each segment in
$\mathfrak {m}_{\mathrm {unip}}$
is unipotent, and each segment in
 $\mathfrak {m}'$
is not unipotent. Then we set
$\mathfrak {m}'$
is not unipotent. Then we set  $$\begin{align*}\lambda_{\mathfrak{m}} = \lambda_{\mathfrak{m}'} + \lambda_{\mathfrak{m}_{\mathrm{unip}}}. \end{align*}$$
$$\begin{align*}\lambda_{\mathfrak{m}} = \lambda_{\mathfrak{m}'} + \lambda_{\mathfrak{m}_{\mathrm{unip}}}. \end{align*}$$
As seen in the next proposition, this is an alternative definition of
![]() $\lambda _{\pi }$
.
$\lambda _{\pi }$
.
Proposition 2.4. Let
![]() $n \geq 1$
, and let
$n \geq 1$
, and let
![]() $\pi = Z(\mathfrak {m})$
be the irreducible representation of
$\pi = Z(\mathfrak {m})$
be the irreducible representation of
![]() $G_n$
corresponding to a multisegment
$G_n$
corresponding to a multisegment
![]() $\mathfrak {m}$
. Then we have
$\mathfrak {m}$
. Then we have
![]() $\lambda _{\pi } = \lambda _{\mathfrak {m}}$
.
$\lambda _{\pi } = \lambda _{\mathfrak {m}}$
.
This proposition will be proven in Section 3.2 below. We now give some examples.
Example 2.5. Let
![]() $\pi $
be an irreducible representation of
$\pi $
be an irreducible representation of
![]() $G_n$
.
$G_n$
.
-
(1) When
 $L(s,\pi ) = 1$
, then
$L(s,\pi ) = 1$
, then
 $\pi = Z(\Delta _1 + \dots + \Delta _r)$
with
$\pi = Z(\Delta _1 + \dots + \Delta _r)$
with
 $\Delta _i$
not unipotent. If
$\Delta _i$
not unipotent. If
 $\pi = Z(\Delta )$
with a segment
$\pi = Z(\Delta )$
with a segment
 $\Delta = [x,y]_{\rho }$
, then we have Here, we note that
$\Delta = [x,y]_{\rho }$
, then we have Here, we note that $$\begin{align*}\lambda_{\pi} = \lambda_{\Delta} = (\underbrace{0, \dots, 0}_{n-l(\Delta)}, \underbrace{c_{\rho}, \dots, c_{\rho}}_{l(\Delta)}) \in \Lambda_n. \end{align*}$$
$$\begin{align*}\lambda_{\pi} = \lambda_{\Delta} = (\underbrace{0, \dots, 0}_{n-l(\Delta)}, \underbrace{c_{\rho}, \dots, c_{\rho}}_{l(\Delta)}) \in \Lambda_n. \end{align*}$$
 $c_{\rho }> 0$
. In general, if
$c_{\rho }> 0$
. In general, if
 $\pi = Z(\Delta _1 + \dots + \Delta _r)$
, we have
$\pi = Z(\Delta _1 + \dots + \Delta _r)$
, we have  $$\begin{align*}\lambda_{\pi} = \lambda_{\Delta_1} + \dots + \lambda_{\Delta_{r}} \in \Lambda_n. \end{align*}$$
$$\begin{align*}\lambda_{\pi} = \lambda_{\Delta_1} + \dots + \lambda_{\Delta_{r}} \in \Lambda_n. \end{align*}$$
-
(2) When
 $\pi = Z([x_1,y_1]_{\chi }, \dots , [x_t,y_t]_{\chi }) \in \mathrm {Irr}(G_n)$
is a ladder representation of type
$\pi = Z([x_1,y_1]_{\chi }, \dots , [x_t,y_t]_{\chi }) \in \mathrm {Irr}(G_n)$
is a ladder representation of type
 $\chi $
, where
$\chi $
, where
 $\chi $
is an unramified character of
$\chi $
is an unramified character of
 $F^{\times }$
, we have Indeed, by the description of the Zelevinsky duals of ladder representations in [Reference Lapid and Mínguez21, Section 3] (see also Section 2.5 below), we have
$F^{\times }$
, we have Indeed, by the description of the Zelevinsky duals of ladder representations in [Reference Lapid and Mínguez21, Section 3] (see also Section 2.5 below), we have $$\begin{align*}\lambda_{\pi} = \sum_{i=2}^t (0, \dots, 0, \underbrace{1, \dots, 1}_{\max\{y_i-x_{i-1}+2,0\}}) \in \Lambda_n. \end{align*}$$
Here, if
$$\begin{align*}\lambda_{\pi} = \sum_{i=2}^t (0, \dots, 0, \underbrace{1, \dots, 1}_{\max\{y_i-x_{i-1}+2,0\}}) \in \Lambda_n. \end{align*}$$
Here, if $$\begin{align*}\pi^{\mathrm{ram}} = Z([x_1-1,y_2]_{\chi}, [x_2-1,y_3]_{\chi}, \dots, [x_{t-1}-1,y_t]_{\chi}). \end{align*}$$
$$\begin{align*}\pi^{\mathrm{ram}} = Z([x_1-1,y_2]_{\chi}, [x_2-1,y_3]_{\chi}, \dots, [x_{t-1}-1,y_t]_{\chi}). \end{align*}$$
 $x_{i-1}-1> y_i$
, we ignore
$x_{i-1}-1> y_i$
, we ignore
 $[x_{i-1}-1,y_i]_{\chi }$
.
$[x_{i-1}-1,y_i]_{\chi }$
.
-
(3) Let
 $t \ge 1$
, and let
$t \ge 1$
, and let
 $\pi _i \in \mathrm {Irr}(G_{n_i})$
be as in either (1) or (2) above for
$\pi _i \in \mathrm {Irr}(G_{n_i})$
be as in either (1) or (2) above for
 $1 \le i \le t$
. Assume
$1 \le i \le t$
. Assume
 $\pi =\pi _1 \times \cdots \times \pi _t$
is irreducible. Then we have
$\pi =\pi _1 \times \cdots \times \pi _t$
is irreducible. Then we have
 $\lambda _{\pi }=\lambda _{\pi _1}+\cdots +\lambda _{\pi _t}$
.
$\lambda _{\pi }=\lambda _{\pi _1}+\cdots +\lambda _{\pi _t}$
. -
(4) Let
 $\pi $
be an irreducible tempered representation of
$\pi $
be an irreducible tempered representation of
 $G_n$
. Then the parabolically induced representation of
$G_n$
. Then the parabolically induced representation of $$\begin{align*}\pi|\cdot|^{-\frac{m-1}{2}} \times \pi|\cdot|^{-\frac{m-3}{2}} \times \dots \times \pi|\cdot|^{\frac{m-1}{2}} \end{align*}$$
$$\begin{align*}\pi|\cdot|^{-\frac{m-1}{2}} \times \pi|\cdot|^{-\frac{m-3}{2}} \times \dots \times \pi|\cdot|^{\frac{m-1}{2}} \end{align*}$$
 $G_{nm}$
has a unique irreducible subrepresentation
$G_{nm}$
has a unique irreducible subrepresentation
 $\sigma $
, which is denoted by
$\sigma $
, which is denoted by
 $\mathrm {Sp}(\pi , m)$
. Note that
$\mathrm {Sp}(\pi , m)$
. Note that
 $\sigma $
is a (unitary) Speh representation. Combining the cases above, we obtain
$\sigma $
is a (unitary) Speh representation. Combining the cases above, we obtain  $$\begin{align*}\lambda_{\sigma} = (\underbrace{0,\dots,0}_{(n-1)m}, \underbrace{c_{\pi}, \dots, c_{\pi}}_{m}) \in \Lambda_{nm}. \end{align*}$$
$$\begin{align*}\lambda_{\sigma} = (\underbrace{0,\dots,0}_{(n-1)m}, \underbrace{c_{\pi}, \dots, c_{\pi}}_{m}) \in \Lambda_{nm}. \end{align*}$$
Remark 2.6. In the appendix of the paper [Reference Kondo and Yasuda17] by the second and third authors, they introduce a notion of mirahoric representations (see Section A.1.6 of [Reference Kondo and Yasuda17]). Let us recall the definition. Two segments
![]() $\Delta $
and
$\Delta $
and
![]() $\Delta '$
are said to be tightly linked if they are linked and either
$\Delta '$
are said to be tightly linked if they are linked and either
![]() $\Delta $
is not unipotent or
$\Delta $
is not unipotent or
![]() $\Delta \cap \Delta '$
is nonempty. Let
$\Delta \cap \Delta '$
is nonempty. Let
![]() $\pi =L(\mathfrak {m})$
be an irreducible representation associated with a multisegment
$\pi =L(\mathfrak {m})$
be an irreducible representation associated with a multisegment
![]() $\mathfrak {m}$
in the Langlands classification: that is,
$\mathfrak {m}$
in the Langlands classification: that is,
![]() $\pi $
is the Zelevinsky dual of
$\pi $
is the Zelevinsky dual of
![]() $Z(\mathfrak {m})$
. They defined
$Z(\mathfrak {m})$
. They defined
![]() $\pi $
to be mirahoric if any two segments in
$\pi $
to be mirahoric if any two segments in
![]() $\mathfrak {m}$
are not tightly linked. In terms of the setup in this paper, the class of mirahoric representations is equal to the class of irreducible representations
$\mathfrak {m}$
are not tightly linked. In terms of the setup in this paper, the class of mirahoric representations is equal to the class of irreducible representations
![]() $\pi $
such that
$\pi $
such that
![]() $\lambda _{\pi }=(0,\ldots ,0,c)$
for some c. This can be seen from their proposition [Reference Kondo and Yasuda17, Proposition A.15], which says that a representation
$\lambda _{\pi }=(0,\ldots ,0,c)$
for some c. This can be seen from their proposition [Reference Kondo and Yasuda17, Proposition A.15], which says that a representation
![]() $\pi $
is mirahoric if and only if the conductor of the highest derivative of
$\pi $
is mirahoric if and only if the conductor of the highest derivative of
![]() $\pi $
is zero. Hence, a main result [Reference Kondo and Yasuda17, Proposition A.3] in the appendix can be interpreted as a special case of Theorem 2.1 restricted to the mirahoric representations.
$\pi $
is zero. Hence, a main result [Reference Kondo and Yasuda17, Proposition A.3] in the appendix can be interpreted as a special case of Theorem 2.1 restricted to the mirahoric representations.
An irreducible representation
![]() $\pi =L(\mathfrak {m})$
is generic if and only if any two segments of
$\pi =L(\mathfrak {m})$
is generic if and only if any two segments of
![]() $\mathfrak {m}$
are not linked. Therefore a generic representation is mirahoric. However, a simple multisegment such as
$\mathfrak {m}$
are not linked. Therefore a generic representation is mirahoric. However, a simple multisegment such as
![]() $\mathfrak {m}=[0,1]_{\rho } + [2,3]_{\rho }$
, where
$\mathfrak {m}=[0,1]_{\rho } + [2,3]_{\rho }$
, where
![]() $\rho $
is an unramified character, gives a mirahoric representation
$\rho $
is an unramified character, gives a mirahoric representation
![]() $L(\mathfrak {m})$
, which is not generic. (This is one of the reasons for treating the unipotent case and the case
$L(\mathfrak {m})$
, which is not generic. (This is one of the reasons for treating the unipotent case and the case
![]() $L(s, \pi )=1$
separately.)
$L(s, \pi )=1$
separately.)
2.4 Computation of
 $\lambda _{\mathfrak {m}}$
$\lambda _{\mathfrak {m}}$
When
![]() $\mathfrak {m}$
is a general unipotent multisegment, it is difficult to compute
$\mathfrak {m}$
is a general unipotent multisegment, it is difficult to compute
![]() $\lambda _{\mathfrak {m}}$
directly from the definition. In this subsection, we explain how to compute
$\lambda _{\mathfrak {m}}$
directly from the definition. In this subsection, we explain how to compute
![]() $\lambda _{\mathfrak {m}}$
efficiently.
$\lambda _{\mathfrak {m}}$
efficiently.
Let
![]() $\mathfrak {m}$
be a unipotent multisegment. We may assume that
$\mathfrak {m}$
be a unipotent multisegment. We may assume that
![]() $\mathfrak {m}$
is of type
$\mathfrak {m}$
is of type
![]() $\chi $
for some unramified character
$\chi $
for some unramified character
![]() $\chi $
of
$\chi $
of
![]() $F^{\times }$
. We denote by
$F^{\times }$
. We denote by
![]() $\mathfrak {m}_{\mathrm {max}}$
the set of segments
$\mathfrak {m}_{\mathrm {max}}$
the set of segments
![]() $\Delta $
in
$\Delta $
in
![]() $\mathfrak {m}$
such that
$\mathfrak {m}$
such that
![]() $\Delta $
is maximal with respect to the inclusion among the segments in
$\Delta $
is maximal with respect to the inclusion among the segments in
![]() $\mathfrak {m}$
. We regard
$\mathfrak {m}$
. We regard
![]() $\mathfrak {m}_{\mathrm {max}}$
as a multisegment in which each segment has multiplicity at most
$\mathfrak {m}_{\mathrm {max}}$
as a multisegment in which each segment has multiplicity at most
![]() $1$
. We set
$1$
. We set
![]() $\mathfrak {m}^{\mathrm {max}} = \mathfrak {m} - \mathfrak {m}_{\mathrm {max}}$
. For example, if
$\mathfrak {m}^{\mathrm {max}} = \mathfrak {m} - \mathfrak {m}_{\mathrm {max}}$
. For example, if
then we have
and
Proposition 2.7. We have
![]() $\mathfrak {m}^{\mathrm {ram}} = (\mathfrak {m}_{\mathrm {max}})^{\mathrm {ram}} + (\mathfrak {m}^{\mathrm {max}})^{\mathrm {ram}}$
.
$\mathfrak {m}^{\mathrm {ram}} = (\mathfrak {m}_{\mathrm {max}})^{\mathrm {ram}} + (\mathfrak {m}^{\mathrm {max}})^{\mathrm {ram}}$
.
We will prove this proposition in Section 3.3 below.
Corollary 2.8. We have
![]() $\lambda _{\mathfrak {m}} = \lambda _{\mathfrak {m}_{\mathrm {max}}} + \lambda _{\mathfrak {m}^{\mathrm {max}}}$
.
$\lambda _{\mathfrak {m}} = \lambda _{\mathfrak {m}_{\mathrm {max}}} + \lambda _{\mathfrak {m}^{\mathrm {max}}}$
.
Proof. Write
![]() $(\mathfrak {m}_{\mathrm {max}})^{\mathrm {ram}} = \Delta _1+\dots +\Delta _r$
and
$(\mathfrak {m}_{\mathrm {max}})^{\mathrm {ram}} = \Delta _1+\dots +\Delta _r$
and
![]() $(\mathfrak {m}^{\mathrm {max}})^{\mathrm {ram}} = \Delta _{r+1} + \dots + \Delta _t$
. Then
$(\mathfrak {m}^{\mathrm {max}})^{\mathrm {ram}} = \Delta _{r+1} + \dots + \Delta _t$
. Then
![]() $\mathfrak {m}^{\mathrm {ram}} = \Delta _1+\dots +\Delta _t$
by Proposition 2.7. Hence we have
$\mathfrak {m}^{\mathrm {ram}} = \Delta _1+\dots +\Delta _t$
by Proposition 2.7. Hence we have
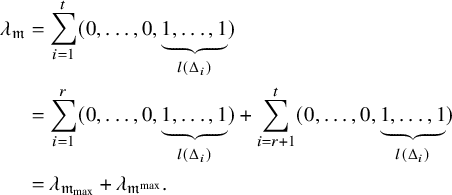 $$ \begin{align*} \lambda_{\mathfrak{m}} &= \sum_{i=1}^t (0,\dots,0,\underbrace{1, \dots, 1}_{l(\Delta_i)}) \\&= \sum_{i=1}^r (0,\dots,0,\underbrace{1, \dots, 1}_{l(\Delta_i)}) + \sum_{i=r+1}^t (0,\dots,0,\underbrace{1, \dots, 1}_{l(\Delta_i)}) \\&= \lambda_{\mathfrak{m}_{\mathrm{max}}} + \lambda_{\mathfrak{m}^{\mathrm{max}}}. \end{align*} $$
$$ \begin{align*} \lambda_{\mathfrak{m}} &= \sum_{i=1}^t (0,\dots,0,\underbrace{1, \dots, 1}_{l(\Delta_i)}) \\&= \sum_{i=1}^r (0,\dots,0,\underbrace{1, \dots, 1}_{l(\Delta_i)}) + \sum_{i=r+1}^t (0,\dots,0,\underbrace{1, \dots, 1}_{l(\Delta_i)}) \\&= \lambda_{\mathfrak{m}_{\mathrm{max}}} + \lambda_{\mathfrak{m}^{\mathrm{max}}}. \end{align*} $$
This completes the proof.
Since
![]() $\mathfrak {m}_{\mathrm {max}}$
is a ladder multisegment (i.e., the multisegment corresponding to a ladder representation), we can compute
$\mathfrak {m}_{\mathrm {max}}$
is a ladder multisegment (i.e., the multisegment corresponding to a ladder representation), we can compute
![]() $\lambda _{\mathfrak {m}_{\mathrm {max}}}$
as in Example 2.5 (2). Hence, using this corollary, we can compute
$\lambda _{\mathfrak {m}_{\mathrm {max}}}$
as in Example 2.5 (2). Hence, using this corollary, we can compute
![]() $\lambda _{\mathfrak {m}}$
inductively.
$\lambda _{\mathfrak {m}}$
inductively.
2.5 An example of computation of
 $\mathfrak {m}^{\mathrm {ram}}$
$\mathfrak {m}^{\mathrm {ram}}$
By using Proposition 2.7, one can compute
![]() $\mathfrak {m}^{\mathrm {ram}}$
for an arbitrary multisegment
$\mathfrak {m}^{\mathrm {ram}}$
for an arbitrary multisegment
![]() $\mathfrak {m}$
in a systematic way. Let us give an example.
$\mathfrak {m}$
in a systematic way. Let us give an example.
Let
![]() $\mathfrak {m}=\sum _{i=1}^7 \Delta _i$
be a multisegment where
$\mathfrak {m}=\sum _{i=1}^7 \Delta _i$
be a multisegment where
![]() $\Delta _1=[5,6]_{\chi }$
,
$\Delta _1=[5,6]_{\chi }$
,
![]() $\Delta _2=[3,7]_{\chi }$
,
$\Delta _2=[3,7]_{\chi }$
,
![]() $\Delta _3=[3,4]_{\chi }$
,
$\Delta _3=[3,4]_{\chi }$
,
![]() $\Delta _4=[2,5]_{\chi }$
,
$\Delta _4=[2,5]_{\chi }$
,
![]() $\Delta _5=[3,3]_{\chi }$
,
$\Delta _5=[3,3]_{\chi }$
,
![]() $\Delta _6=[1,2]_{\chi }$
,
$\Delta _6=[1,2]_{\chi }$
,
![]() $\Delta _7=[0,0]_{\chi }$
. Then
$\Delta _7=[0,0]_{\chi }$
. Then
![]() $\mathfrak {m}_{\mathrm {max}}=\Delta _2+\Delta _4+\Delta _6+\Delta _7$
and
$\mathfrak {m}_{\mathrm {max}}=\Delta _2+\Delta _4+\Delta _6+\Delta _7$
and
![]() $\mathfrak {m}^{\mathrm {max}}=\Delta _1+\Delta _3+\Delta _5$
. We also have
$\mathfrak {m}^{\mathrm {max}}=\Delta _1+\Delta _3+\Delta _5$
. We also have
![]() $(\mathfrak {m}^{\mathrm {max}})_{\mathrm {max}}=\Delta _1+\Delta _3$
and
$(\mathfrak {m}^{\mathrm {max}})_{\mathrm {max}}=\Delta _1+\Delta _3$
and
![]() $(\mathfrak {m}^{\mathrm {max}})^{\mathrm {max}}=\Delta _5$
. By Proposition 2.7, we are reduced to computing ‘
$(\mathfrak {m}^{\mathrm {max}})^{\mathrm {max}}=\Delta _5$
. By Proposition 2.7, we are reduced to computing ‘
![]() $\mathrm {ram}$
’ of the three ladder multisegments.
$\mathrm {ram}$
’ of the three ladder multisegments.
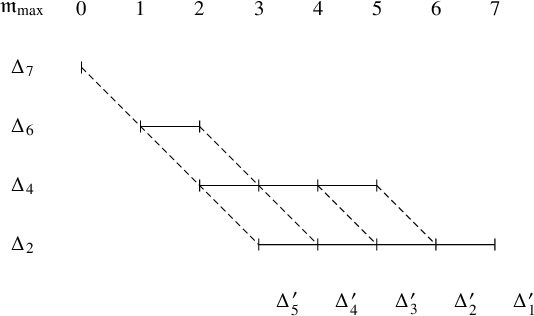
As explained in Section 3 of [Reference Lapid and Mínguez21], the Zelevinsky dual of a ladder multisegment can be calculated fairly easily. Let us compute the Zelevinsky of
![]() $\mathfrak {m}_{\mathrm {max}}$
by drawing pictures. In the
$\mathfrak {m}_{\mathrm {max}}$
by drawing pictures. In the
![]() $xy$
-plane, we draw each segment of
$xy$
-plane, we draw each segment of
![]() $\mathfrak {m}_{\mathrm {max}}$
so that each lies on the line
$\mathfrak {m}_{\mathrm {max}}$
so that each lies on the line
![]() $y=i$
for
$y=i$
for
![]() $i=1,\dots , 4$
. (See the following figure.) Whenever there exist points
$i=1,\dots , 4$
. (See the following figure.) Whenever there exist points
![]() $(e,f)$
and
$(e,f)$
and
![]() $(e+1, f-1)$
with
$(e+1, f-1)$
with
![]() $e,f \in \mathbb {Z}$
, we draw a dotted line connecting them. Then the dotted lines form the multisegment of the Zelevinsky dual
$e,f \in \mathbb {Z}$
, we draw a dotted line connecting them. Then the dotted lines form the multisegment of the Zelevinsky dual
![]() $(\mathfrak {m}_{\mathrm {max}})^{\sharp }$
. One can use the algorithm of Mœglin–Waldspurger [Reference Mœglin and Waldspurger32] to verify that the procedure above actually gives the Zelevinsky dual. We obtain
$(\mathfrak {m}_{\mathrm {max}})^{\sharp }$
. One can use the algorithm of Mœglin–Waldspurger [Reference Mœglin and Waldspurger32] to verify that the procedure above actually gives the Zelevinsky dual. We obtain
![]() $(\mathfrak {m}_{\mathrm {max}})^{\sharp } =\Delta ^{\prime }_1+\Delta ^{\prime }_2+\Delta ^{\prime }_3+\Delta ^{\prime }_4+\Delta ^{\prime }_5$
, where
$(\mathfrak {m}_{\mathrm {max}})^{\sharp } =\Delta ^{\prime }_1+\Delta ^{\prime }_2+\Delta ^{\prime }_3+\Delta ^{\prime }_4+\Delta ^{\prime }_5$
, where
![]() $\Delta ^{\prime }_1=[7,7]_{\chi }$
,
$\Delta ^{\prime }_1=[7,7]_{\chi }$
,
![]() $\Delta ^{\prime }_2=[5,6]_{\chi }$
,
$\Delta ^{\prime }_2=[5,6]_{\chi }$
,
![]() $\Delta ^{\prime }_3=[4,5]_{\chi }$
,
$\Delta ^{\prime }_3=[4,5]_{\chi }$
,
![]() $\Delta ^{\prime }_4=[2,4]_{\chi }$
,
$\Delta ^{\prime }_4=[2,4]_{\chi }$
,
![]() $\Delta ^{\prime }_5=[0,3]_{\chi }$
.
$\Delta ^{\prime }_5=[0,3]_{\chi }$
.
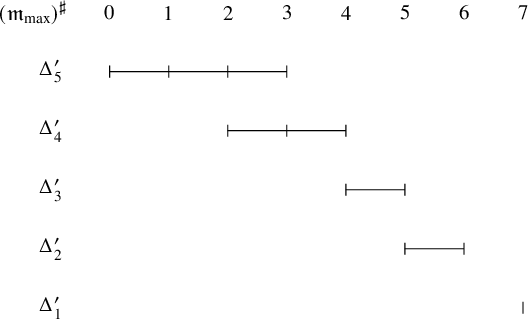
The multisegment of the highest derivative is obtained by shortening each segment by 1. Hence, we have
![]() $((\mathfrak {m}_{\mathrm {max}})^{\sharp })^-$
as in the following figure. We obtain
$((\mathfrak {m}_{\mathrm {max}})^{\sharp })^-$
as in the following figure. We obtain
![]() $((\mathfrak {m}_{\mathrm {max}})^{\sharp })^- =(\Delta ^{\prime }_1)^-+ (\Delta ^{\prime }_2)^-+ (\Delta ^{\prime }_3)^-+ (\Delta ^{\prime }_4)^-$
where
$((\mathfrak {m}_{\mathrm {max}})^{\sharp })^- =(\Delta ^{\prime }_1)^-+ (\Delta ^{\prime }_2)^-+ (\Delta ^{\prime }_3)^-+ (\Delta ^{\prime }_4)^-$
where
![]() $\Delta ^{\prime }_1=[5,5]_{\chi }$
,
$\Delta ^{\prime }_1=[5,5]_{\chi }$
,
![]() $\Delta ^{\prime }_2=[4,4]_{\chi }$
,
$\Delta ^{\prime }_2=[4,4]_{\chi }$
,
![]() $\Delta ^{\prime }_3=[2,3]_{\chi }$
,
$\Delta ^{\prime }_3=[2,3]_{\chi }$
,
![]() $\Delta ^{\prime }_4=[0,2]_{\chi }$
.
$\Delta ^{\prime }_4=[0,2]_{\chi }$
.
Taking the Zelevinsky dual again, we arrive at
![]() $(\mathfrak {m}_{\mathrm {max}})^{\mathrm {ram}}$
as in the following figure. We obtain
$(\mathfrak {m}_{\mathrm {max}})^{\mathrm {ram}}$
as in the following figure. We obtain
![]() $(\mathfrak {m}_{\mathrm {max}})^{\mathrm {ram}}=\Delta ^{\prime \prime }_1+\Delta ^{\prime \prime }_2+\Delta ^{\prime \prime }_3$
where
$(\mathfrak {m}_{\mathrm {max}})^{\mathrm {ram}}=\Delta ^{\prime \prime }_1+\Delta ^{\prime \prime }_2+\Delta ^{\prime \prime }_3$
where
![]() $\Delta ^{\prime \prime }_1=[2,5]_{\chi }, \Delta ^{\prime \prime }_2=[1,2]_{\chi }, \Delta ^{\prime \prime }_3=[0,0]_{\chi }$
.
$\Delta ^{\prime \prime }_1=[2,5]_{\chi }, \Delta ^{\prime \prime }_2=[1,2]_{\chi }, \Delta ^{\prime \prime }_3=[0,0]_{\chi }$
.
Similarly, we have
![]() $(\Delta _1+\Delta _3)^{\mathrm {ram}}=[4,4]_{\chi }$
and
$(\Delta _1+\Delta _3)^{\mathrm {ram}}=[4,4]_{\chi }$
and
![]() $(\Delta _5)^{\mathrm {ram}}=\emptyset $
. Thus
$(\Delta _5)^{\mathrm {ram}}=\emptyset $
. Thus
![]() $\mathfrak {m}^{\mathrm {ram}}=[4,4]_{\chi }+[2,5]_{\chi }+[1,2]_{\chi }+[0,0]_{\chi }$
.
$\mathfrak {m}^{\mathrm {ram}}=[4,4]_{\chi }+[2,5]_{\chi }+[1,2]_{\chi }+[0,0]_{\chi }$
.
2.6 The Weil–Deligne representations
In this subsection, we give some justification for the use of the term ‘ram’ in the notation
![]() $\pi ^{\mathrm {ram}}$
. This comes from the Galois side of the local Langlands correspondence ([Reference Harris, Taylor and Berkovich11], [Reference Henniart12]). For several materials in this subsection, see [Reference Tate40].
$\pi ^{\mathrm {ram}}$
. This comes from the Galois side of the local Langlands correspondence ([Reference Harris, Taylor and Berkovich11], [Reference Henniart12]). For several materials in this subsection, see [Reference Tate40].
Let us fix an algebraic closure
![]() $\overline {F}$
of F. Let
$\overline {F}$
of F. Let
![]() $W_F \subset \mathrm {Gal}(\overline {F}/F)$
denote the Weil group of F. By definition,
$W_F \subset \mathrm {Gal}(\overline {F}/F)$
denote the Weil group of F. By definition,
![]() $W_F$
is a locally profinite topological group. If we denote by
$W_F$
is a locally profinite topological group. If we denote by
![]() $W_F^{\mathrm {ab}}$
the quotient of
$W_F^{\mathrm {ab}}$
the quotient of
![]() $W_F$
by the closure of
$W_F$
by the closure of
![]() $[W_F,W_F]$
, then there exists an isomorphism
$[W_F,W_F]$
, then there exists an isomorphism
![]() $r_F \colon W_F^{\mathrm {ab}} \xrightarrow {\cong } F^{\times }$
that sends any lift of geometric Frobenius to a uniformiser of F.
$r_F \colon W_F^{\mathrm {ab}} \xrightarrow {\cong } F^{\times }$
that sends any lift of geometric Frobenius to a uniformiser of F.
A Weil–Deligne representation is a triple
![]() $(\tau ,V,N)$
, where
$(\tau ,V,N)$
, where
![]() $(\tau ,V)$
is a finite-dimensional complex representation of
$(\tau ,V)$
is a finite-dimensional complex representation of
![]() $W_F$
and N is a linear endomorphism of V such that the kernel of
$W_F$
and N is a linear endomorphism of V such that the kernel of
![]() $\tau $
is open in
$\tau $
is open in
![]() $W_F$
, and we have
$W_F$
, and we have
![]() $\tau(\sigma) N = |r_F(\sigma)| N \tau(\sigma)$
for any
$\tau(\sigma) N = |r_F(\sigma)| N \tau(\sigma)$
for any
![]() $\sigma \in W_F$
. Let
$\sigma \in W_F$
. Let
![]() $I_F \subset W_F$
denote the inertia subgroup. A Weil–Deligne representation
$I_F \subset W_F$
denote the inertia subgroup. A Weil–Deligne representation
![]() $(\tau ,V,N)$
is called unramified if
$(\tau ,V,N)$
is called unramified if
![]() $I_F$
acts trivially and N acts as
$I_F$
acts trivially and N acts as
![]() $0$
on V. Any Weil–Deligne representation
$0$
on V. Any Weil–Deligne representation
![]() $V=(\tau ,N,V)$
has a unique maximal unramified Weil–Deligne subrepresentation
$V=(\tau ,N,V)$
has a unique maximal unramified Weil–Deligne subrepresentation
![]() $V_{\mathrm {ur}}$
. Explicitly, we have
$V_{\mathrm {ur}}$
. Explicitly, we have
![]() $V_{\mathrm {ur}} = V^{I_F} \cap \mathrm {Ker}\, N$
. We denote by
$V_{\mathrm {ur}} = V^{I_F} \cap \mathrm {Ker}\, N$
. We denote by
![]() $V^{\mathrm {ram}}$
the quotient
$V^{\mathrm {ram}}$
the quotient
![]() $V/V_{\mathrm {ur}}$
, and we call it the ramified quotient of V.
$V/V_{\mathrm {ur}}$
, and we call it the ramified quotient of V.
The local Langlands correspondence gives a one-to-one correspondence between the isomorphism classes of irreducible complex representations of
![]() $G_n$
and the isomorphism classes of Frobenius semisimple n-dimensional Weil–Deligne representations over the complex numbers.
$G_n$
and the isomorphism classes of Frobenius semisimple n-dimensional Weil–Deligne representations over the complex numbers.
Lemma 2.9. Let
![]() $\pi $
be a unipotent irreducible admissible representation of
$\pi $
be a unipotent irreducible admissible representation of
![]() $G_n$
, and let V denote the Weil–Deligne representation corresponding to
$G_n$
, and let V denote the Weil–Deligne representation corresponding to
![]() $\pi $
via the local Langlands correspondence. Then
$\pi $
via the local Langlands correspondence. Then
![]() $V^{\mathrm {ram}}$
corresponds to
$V^{\mathrm {ram}}$
corresponds to
![]() $\pi ^{\mathrm {ram}}$
.
$\pi ^{\mathrm {ram}}$
.
Proof. For a segment
![]() $[a,b]_{\rho }$
, we denote by
$[a,b]_{\rho }$
, we denote by
![]() $\Delta [a,b]_{\rho }$
the generalised Steinberg representation: that is, the unique irreducible quotient of
$\Delta [a,b]_{\rho }$
the generalised Steinberg representation: that is, the unique irreducible quotient of
As in the Langlands classification, we write
![]() $\pi = L([a_1,b_1]_{\rho _1} + \dots + [a_r,b_r]_{\rho _r})$
if
$\pi = L([a_1,b_1]_{\rho _1} + \dots + [a_r,b_r]_{\rho _r})$
if
![]() $\pi $
is the unique irreducible subrepresentation of
$\pi $
is the unique irreducible subrepresentation of
with
![]() $\rho _i$
unitary and
$\rho _i$
unitary and
![]() $a_1+b_1 \leq \dots \leq a_r+b_r$
. Then the Zelevinsky dual
$a_1+b_1 \leq \dots \leq a_r+b_r$
. Then the Zelevinsky dual
![]() $\pi ^{\sharp }$
of
$\pi ^{\sharp }$
of
![]() $\pi $
is given by
$\pi $
is given by
By [Reference Zelevinsky42, 8.1 Theorem], the highest derivative
![]() $(\pi ^{\sharp })^-$
of
$(\pi ^{\sharp })^-$
of
![]() $\pi ^{\sharp }$
is
$\pi ^{\sharp }$
is
Here, if
![]() $a_i = b_i$
, we ignore
$a_i = b_i$
, we ignore
![]() $[a_i,b_i-1]_{\rho _i}$
. Hence
$[a_i,b_i-1]_{\rho _i}$
. Hence
Therefore, the map
![]() $\pi \mapsto \pi ^{\mathrm {ram}}$
corresponds to
$\pi \mapsto \pi ^{\mathrm {ram}}$
corresponds to
![]() $V \mapsto V/\mathrm {Ker}\, N$
(see, e.g., [Reference Rodier37]). Since
$V \mapsto V/\mathrm {Ker}\, N$
(see, e.g., [Reference Rodier37]). Since
![]() $\pi $
is unipotent, the corresponding V satisfies that
$\pi $
is unipotent, the corresponding V satisfies that
![]() $V = V^{I_F}$
so that
$V = V^{I_F}$
so that
![]() $V^{\mathrm {ram}} = V/\mathrm {Ker}\, N$
.
$V^{\mathrm {ram}} = V/\mathrm {Ker}\, N$
.
3 Proofs of Propositions 2.4 and 2.7
The purpose of this section is to prove Propositions 2.4 and 2.7. To do these, we introduce the notions of
![]() $VN$
-pairs and
$VN$
-pairs and
![]() $WL$
-pairs.
$WL$
-pairs.
3.1
 $VN$
-pairs and
$VN$
-pairs and
 $WL$
-pairs
$WL$
-pairs
A
![]() $VN$
-pair (over
$VN$
-pair (over
![]() $\mathbb {C}$
) is a pair
$\mathbb {C}$
) is a pair
![]() $(V,N)$
of a finite-dimensional
$(V,N)$
of a finite-dimensional
![]() $\mathbb {Z}$
-graded vector space V over
$\mathbb {Z}$
-graded vector space V over
![]() $\mathbb {C}$
and a
$\mathbb {C}$
and a
![]() $\mathbb {C}$
-linear endomorphism
$\mathbb {C}$
-linear endomorphism
![]() $N\colon V \to V$
of degree
$N\colon V \to V$
of degree
![]() $1$
. Similarly, a
$1$
. Similarly, a
![]() $WL$
-pair (over
$WL$
-pair (over
![]() $\mathbb {C}$
) is a pair
$\mathbb {C}$
) is a pair
![]() $(W,L)$
of a finite-dimensional
$(W,L)$
of a finite-dimensional
![]() $\mathbb {Z}$
-graded vector space W over
$\mathbb {Z}$
-graded vector space W over
![]() $\mathbb {C}$
and a
$\mathbb {C}$
and a
![]() $\mathbb {C}$
-linear endomorphism
$\mathbb {C}$
-linear endomorphism
![]() $L \colon W \to W$
of degree
$L \colon W \to W$
of degree
![]() $-1$
.
$-1$
.
Let
![]() $(V,N)$
and
$(V,N)$
and
![]() $(V',N')$
be two
$(V',N')$
be two
![]() $VN$
-pairs. A morphism
$VN$
-pairs. A morphism
![]() $f \colon (V,N) \rightarrow (V',N')$
is a
$f \colon (V,N) \rightarrow (V',N')$
is a
![]() $\mathbb {C}$
-linear map
$\mathbb {C}$
-linear map
![]() $V \rightarrow V'$
preserving the degrees such that
$V \rightarrow V'$
preserving the degrees such that
![]() $f \circ N = N' \circ f$
.
$f \circ N = N' \circ f$
.
Lemma 3.1. Let
![]() $(V,N)$
and
$(V,N)$
and
![]() $(V',N')$
be two
$(V',N')$
be two
![]() $VN$
-pairs. Then
$VN$
-pairs. Then
![]() $(V,N) \cong (V',N')$
if and only if
$(V,N) \cong (V',N')$
if and only if
![]() $V \cong V'$
as graded vector spaces and
$V \cong V'$
as graded vector spaces and
![]() $(\mathrm {Image}\, N, N|_{\mathrm {Image}\, N}) \cong (\mathrm {Image}\, N', N'|_{\mathrm {Image}\, N'})$
.
$(\mathrm {Image}\, N, N|_{\mathrm {Image}\, N}) \cong (\mathrm {Image}\, N', N'|_{\mathrm {Image}\, N'})$
.
Proof. The ‘only if’ part is trivial. We prove the ‘if’ part. Assume the two conditions. Let us choose an isomorphism
of
![]() $VN$
-pairs. Let us also choose homogeneous elements
$VN$
-pairs. Let us also choose homogeneous elements
![]() $v_1,\ldots ,v_r \in \mathrm {Image}\, N$
whose images in
$v_1,\ldots ,v_r \in \mathrm {Image}\, N$
whose images in
![]() $\mathrm {Image}\, N/\mathrm {Image}\, N^2$
form a basis of this space. For
$\mathrm {Image}\, N/\mathrm {Image}\, N^2$
form a basis of this space. For
![]() $i=1,\ldots ,r$
, let us choose homogeneous elements
$i=1,\ldots ,r$
, let us choose homogeneous elements
![]() $e_1,\ldots ,e_r \in V$
and
$e_1,\ldots ,e_r \in V$
and
![]() $e^{\prime }_1,\ldots ,e^{\prime }_r \in V'$
in such a way that we have
$e^{\prime }_1,\ldots ,e^{\prime }_r \in V'$
in such a way that we have
![]() $N(e_i) = v_i$
and
$N(e_i) = v_i$
and
![]() $N'(e^{\prime }_i) = f_1 (v_i)$
for
$N'(e^{\prime }_i) = f_1 (v_i)$
for
![]() $i=1,\ldots ,r$
. Let W (respectively,
$i=1,\ldots ,r$
. Let W (respectively,
![]() $W'$
) denote the graded vector subspace of V (respectively,
$W'$
) denote the graded vector subspace of V (respectively,
![]() $V'$
) generated by
$V'$
) generated by
![]() $\mathrm {Image}\, N$
and
$\mathrm {Image}\, N$
and
![]() $e_1,\ldots ,e_r$
(respectively,
$e_1,\ldots ,e_r$
(respectively,
![]() $\mathrm {Image}\, N'$
and
$\mathrm {Image}\, N'$
and
![]() $e^{\prime }_1,\ldots ,e^{\prime }_r$
).
$e^{\prime }_1,\ldots ,e^{\prime }_r$
).
Let
![]() $\overline {N}\colon V/\mathrm {Image}\, N \to \mathrm {Image}\, N/\mathrm {Image}\, N^2$
denote the homomorphism induced by N. It follows from the construction of W that the restriction of
$\overline {N}\colon V/\mathrm {Image}\, N \to \mathrm {Image}\, N/\mathrm {Image}\, N^2$
denote the homomorphism induced by N. It follows from the construction of W that the restriction of
![]() $\overline {N}$
to
$\overline {N}$
to
![]() $W/\mathrm {Image}\, N$
gives an isomorphism
$W/\mathrm {Image}\, N$
gives an isomorphism
![]() $W/\mathrm {Image}\, N \xrightarrow {\cong } \mathrm {Image}\, N/\mathrm {Image}\, N^2$
. Hence we have
$W/\mathrm {Image}\, N \xrightarrow {\cong } \mathrm {Image}\, N/\mathrm {Image}\, N^2$
. Hence we have
![]() $V/\mathrm {Image}\, N = \mathrm {Ker}\, \overline {N} \oplus (W/\mathrm {Image}\, N)$
. By applying the snake lemma to the commutative diagram
$V/\mathrm {Image}\, N = \mathrm {Ker}\, \overline {N} \oplus (W/\mathrm {Image}\, N)$
. By applying the snake lemma to the commutative diagram
we see that the homomorphism
![]() $\alpha \colon \mathrm {Ker}\, N \to \mathrm {Ker}\, \overline {N}$
induced by the quotient map
$\alpha \colon \mathrm {Ker}\, N \to \mathrm {Ker}\, \overline {N}$
induced by the quotient map
![]() $V \twoheadrightarrow V/\mathrm {Image}\, N$
is surjective. Let us choose a graded vector subspace
$V \twoheadrightarrow V/\mathrm {Image}\, N$
is surjective. Let us choose a graded vector subspace
![]() $U \subset \mathrm {Ker}\, N$
such that the restriction of
$U \subset \mathrm {Ker}\, N$
such that the restriction of
![]() $\alpha $
to U gives an isomorphism
$\alpha $
to U gives an isomorphism
![]() $U \xrightarrow {\cong } \mathrm {Ker}\, \overline {N}$
. Since
$U \xrightarrow {\cong } \mathrm {Ker}\, \overline {N}$
. Since
![]() $V/\mathrm {Image}\, N = \mathrm {Ker}\, \overline {N} \oplus (W/\mathrm {Image}\, N)$
, we have
$V/\mathrm {Image}\, N = \mathrm {Ker}\, \overline {N} \oplus (W/\mathrm {Image}\, N)$
, we have
![]() $V = U \oplus W$
.
$V = U \oplus W$
.
A similar argument shows that there exists a graded vector subspace
![]() $U' \subset \mathrm {Ker}\, N'$
such that
$U' \subset \mathrm {Ker}\, N'$
such that
![]() $V' = U' \oplus W'$
. Since V and
$V' = U' \oplus W'$
. Since V and
![]() $V'$
are isomorphic as graded vector spaces, U and
$V'$
are isomorphic as graded vector spaces, U and
![]() $U'$
are isomorphic as graded vector spaces. Let us choose an isomorphism
$U'$
are isomorphic as graded vector spaces. Let us choose an isomorphism
![]() $f_2 \colon U \to U'$
of graded vector spaces.
$f_2 \colon U \to U'$
of graded vector spaces.
Let
![]() $f \colon V \to V'$
denote the homomorphism defined as follows:
$f \colon V \to V'$
denote the homomorphism defined as follows:
![]() $f(v)=f_1(v)$
for
$f(v)=f_1(v)$
for
![]() $v \in \mathrm {Image}\, N$
,
$v \in \mathrm {Image}\, N$
,
![]() $f(e_i) = e^{\prime }_i$
for
$f(e_i) = e^{\prime }_i$
for
![]() $i=1,\ldots ,r$
and
$i=1,\ldots ,r$
and
![]() $f(u)=f_2(u)$
for
$f(u)=f_2(u)$
for
![]() $u \in U$
. Then f is an isomorphism of
$u \in U$
. Then f is an isomorphism of
![]() $VN$
-pairs from
$VN$
-pairs from
![]() $(V,N)$
to
$(V,N)$
to
![]() $(V',N')$
. This completes the proof.
$(V',N')$
. This completes the proof.
Let
![]() $(V,N)$
be a
$(V,N)$
be a
![]() $VN$
-pair. For an integer
$VN$
-pair. For an integer
![]() $c \in \mathbb {Z}$
, we let
$c \in \mathbb {Z}$
, we let
![]() $(V,N)(c)$
denote the cth degree-shift of
$(V,N)(c)$
denote the cth degree-shift of
![]() $(V,N)$
. By definition,
$(V,N)$
. By definition,
![]() $(V,N)(c)=(V(c),N(c))$
, where
$(V,N)(c)=(V(c),N(c))$
, where
![]() $V(c)$
is the
$V(c)$
is the
![]() $\mathbb {Z}$
-graded vector space over
$\mathbb {Z}$
-graded vector space over
![]() $\mathbb {C}$
whose degree-a-part is equal to the degree-
$\mathbb {C}$
whose degree-a-part is equal to the degree-
![]() $(a-c)$
-part of V for any
$(a-c)$
-part of V for any
![]() $a \in \mathbb {Z}$
, and
$a \in \mathbb {Z}$
, and
![]() $N(c)\colon V(c) \to V(c)$
is the endomorphism induced by N. (This notation of degree-shift corresponds to the Tate twist on the Galois side of the local Langlands correspondence.)
$N(c)\colon V(c) \to V(c)$
is the endomorphism induced by N. (This notation of degree-shift corresponds to the Tate twist on the Galois side of the local Langlands correspondence.)
For a segment
![]() $\Delta =[a,b]_{\chi }$
with
$\Delta =[a,b]_{\chi }$
with
![]() $a,b \in \mathbb {Z}$
, we let
$a,b \in \mathbb {Z}$
, we let
![]() $(V_{\Delta },N_{\Delta })$
denote the
$(V_{\Delta },N_{\Delta })$
denote the
![]() $VN$
-pair such that
$VN$
-pair such that
![]() $V_{\Delta }$
is the graded complex vector space with basis
$V_{\Delta }$
is the graded complex vector space with basis
![]() $e_a, e_{a+1},\ldots , e_b$
, where for
$e_a, e_{a+1},\ldots , e_b$
, where for
![]() $i=a,\ldots ,b$
, the vector
$i=a,\ldots ,b$
, the vector
![]() $e_i$
is homogeneous of degree i and
$e_i$
is homogeneous of degree i and
![]() $N_{\Delta } \colon V_{\Delta } \to V_{\Delta }$
is the endomorphism that sends
$N_{\Delta } \colon V_{\Delta } \to V_{\Delta }$
is the endomorphism that sends
![]() $e_i$
to
$e_i$
to
![]() $e_{i+1}$
for
$e_{i+1}$
for
![]() $i=a,\ldots ,b-1$
and sends
$i=a,\ldots ,b-1$
and sends
![]() $e_b$
to
$e_b$
to
![]() $0$
. Similarly, we denote by
$0$
. Similarly, we denote by
![]() $(W_{\Delta },L_{\Delta })$
the
$(W_{\Delta },L_{\Delta })$
the
![]() $WL$
-pair such that
$WL$
-pair such that
![]() $W_{\Delta } = V_{\Delta }$
and
$W_{\Delta } = V_{\Delta }$
and
![]() $L_{\Delta } \colon W_{\Delta } \to W_{\Delta }$
is the endomorphism that sends
$L_{\Delta } \colon W_{\Delta } \to W_{\Delta }$
is the endomorphism that sends
![]() $e_i$
to
$e_i$
to
![]() $e_{i-1}$
for
$e_{i-1}$
for
![]() $i=a+1,\ldots ,b$
and sends
$i=a+1,\ldots ,b$
and sends
![]() $e_a$
to
$e_a$
to
![]() $0$
.
$0$
.
Let
![]() $\chi $
be an unramified character of
$\chi $
be an unramified character of
![]() $F^{\times }$
. For a multisegment
$F^{\times }$
. For a multisegment
![]() $\mathfrak {m}=\Delta _1 + \cdots + \Delta _r$
of type
$\mathfrak {m}=\Delta _1 + \cdots + \Delta _r$
of type
![]() $\chi $
, we define the
$\chi $
, we define the
![]() $VN$
-pair
$VN$
-pair
![]() $(V_{\mathfrak {m}},N_{\mathfrak {m}})$
and the
$(V_{\mathfrak {m}},N_{\mathfrak {m}})$
and the
![]() $WL$
-pair
$WL$
-pair
![]() $(W_{\mathfrak {m}},L_{\mathfrak {m}})$
as the direct sums
$(W_{\mathfrak {m}},L_{\mathfrak {m}})$
as the direct sums
 $$\begin{align*}(V_{\mathfrak{m}},N_{\mathfrak{m}}) = \left( \bigoplus_{i=1}^r V_{\Delta_i}, \bigoplus_{i=1}^r N_{\Delta_i}\right) \end{align*}$$
$$\begin{align*}(V_{\mathfrak{m}},N_{\mathfrak{m}}) = \left( \bigoplus_{i=1}^r V_{\Delta_i}, \bigoplus_{i=1}^r N_{\Delta_i}\right) \end{align*}$$
and
 $$\begin{align*}(W_{\mathfrak{m}}, L_{\mathfrak{m}}) = \left( \bigoplus_{i=1}^r W_{\Delta_i}, \bigoplus_{i=1}^r L_{\Delta_i}\right). \end{align*}$$
$$\begin{align*}(W_{\mathfrak{m}}, L_{\mathfrak{m}}) = \left( \bigoplus_{i=1}^r W_{\Delta_i}, \bigoplus_{i=1}^r L_{\Delta_i}\right). \end{align*}$$
It follows from the Gabriel theory [Reference Gabriel7], or from the theory of Jordan normal forms and some elementary argument (compare to [Reference Knight and Zelevinsky16]), that these give one-to-one correspondence among the multisegments of type
![]() $\chi $
, the isomorphism classes of
$\chi $
, the isomorphism classes of
![]() $VN$
-pairs and the isomorphism classes of
$VN$
-pairs and the isomorphism classes of
![]() $WL$
-pairs.
$WL$
-pairs.
For a
![]() $VN$
-pair
$VN$
-pair
![]() $(V,N)$
(respectively, a
$(V,N)$
(respectively, a
![]() $WL$
-pair
$WL$
-pair
![]() $(W,L)$
), let us consider the set
$(W,L)$
), let us consider the set
![]() $S(V,N)$
(respectively,
$S(V,N)$
(respectively,
![]() $S(W,L)$
) of
$S(W,L)$
) of
![]() $\mathbb {C}$
-linear endomorphisms
$\mathbb {C}$
-linear endomorphisms
![]() $L\colon V \to V$
(respectively,
$L\colon V \to V$
(respectively,
![]() $N\colon V \to V$
) of degree
$N\colon V \to V$
) of degree
![]() $-1$
(respectively, degree
$-1$
(respectively, degree
![]() $1$
) satisfying
$1$
) satisfying
![]() $L\circ N=N \circ L$
. We sometimes regard
$L\circ N=N \circ L$
. We sometimes regard
![]() $S(V,N)$
and
$S(V,N)$
and
![]() $S(W,L)$
as algebraic varieties over
$S(W,L)$
as algebraic varieties over
![]() $\mathbb {C}$
. Since
$\mathbb {C}$
. Since
![]() $S(V,N)$
and
$S(V,N)$
and
![]() $S(W,L)$
are finite-dimensional complex vector spaces,
$S(W,L)$
are finite-dimensional complex vector spaces,
![]() $S(V,N)$
and
$S(V,N)$
and
![]() $S(W,L)$
are, as algebraic varieties over
$S(W,L)$
are, as algebraic varieties over
![]() $\mathbb {C}$
, isomorphic to affine spaces over
$\mathbb {C}$
, isomorphic to affine spaces over
![]() $\mathbb {C}$
.
$\mathbb {C}$
.
Lemma 3.2. Let
![]() $(V,N)$
be a
$(V,N)$
be a
![]() $VN$
-pair and
$VN$
-pair and
![]() $(W,L)$
be a
$(W,L)$
be a
![]() $WL$
-pair:
$WL$
-pair:
-
(1) The map
 $S(V,N) \to S(\mathrm {Image}\, N, N|_{\mathrm {Image}\, N})$
that sends L to
$S(V,N) \to S(\mathrm {Image}\, N, N|_{\mathrm {Image}\, N})$
that sends L to
 $L|_{\mathrm {Image}\, N}$
is surjective.
$L|_{\mathrm {Image}\, N}$
is surjective. -
(2) The map
 $S(W,L) \to S(\mathrm {Image}\, L, L|_{\mathrm {Image}\, L})$
that sends N to
$S(W,L) \to S(\mathrm {Image}\, L, L|_{\mathrm {Image}\, L})$
that sends N to
 $N|_{\mathrm {Image}\, L}$
is surjective.
$N|_{\mathrm {Image}\, L}$
is surjective.
Proof. We only give a proof of assertion (1). We can prove assertion (2) in a similar manner.
Let us choose homogeneous, linearly independent elements
![]() $v_1, \ldots , v_m \in V$
such that V is a direct sum of
$v_1, \ldots , v_m \in V$
such that V is a direct sum of
![]() $\mathrm {Image}\, N$
and the subspace of V generated by
$\mathrm {Image}\, N$
and the subspace of V generated by
![]() $v_1, \ldots , v_m$
. For
$v_1, \ldots , v_m$
. For
![]() $i=1,\ldots ,m$
, we let
$i=1,\ldots ,m$
, we let
![]() $d_i$
denote the degree of
$d_i$
denote the degree of
![]() $v_i$
. Given
$v_i$
. Given
![]() $L' \in S(\mathrm {Image}\, N, N|_{\mathrm {Image}\, N})$
, choose a homogeneous element
$L' \in S(\mathrm {Image}\, N, N|_{\mathrm {Image}\, N})$
, choose a homogeneous element
![]() $w_i \in V$
of degree
$w_i \in V$
of degree
![]() $d_i-1$
that satisfies
$d_i-1$
that satisfies
![]() $L'(N(v_i)) = N(w_i)$
for each
$L'(N(v_i)) = N(w_i)$
for each
![]() $i=1, \ldots , m$
. Let L denote the unique
$i=1, \ldots , m$
. Let L denote the unique
![]() $\mathbb {C}$
-linear map
$\mathbb {C}$
-linear map
![]() $V \to V$
such that
$V \to V$
such that
![]() $L(v) = L'(v)$
for
$L(v) = L'(v)$
for
![]() $v \in \mathrm {Image}\, N$
and that
$v \in \mathrm {Image}\, N$
and that
![]() $L(v_i) = w_i$
for
$L(v_i) = w_i$
for
![]() $i=1,\ldots ,m$
. It is then straightforward to check that
$i=1,\ldots ,m$
. It is then straightforward to check that
![]() $L \in S(V,N)$
. It follows from the construction of L that
$L \in S(V,N)$
. It follows from the construction of L that
![]() $L|_{\mathrm {Image}\, N} = L'$
. Hence the claim follows.
$L|_{\mathrm {Image}\, N} = L'$
. Hence the claim follows.
Let
![]() $(V,N)$
be a
$(V,N)$
be a
![]() $VN$
-pair, and let
$VN$
-pair, and let
![]() $\mathfrak {m}$
be the multisegment (of type
$\mathfrak {m}$
be the multisegment (of type
![]() $\chi $
) corresponding to
$\chi $
) corresponding to
![]() $(V,N)$
. It follows from [Reference Zelevinsky43] and [Reference Mœglin and Waldspurger31] that there exists a Zariski open dense subset
$(V,N)$
. It follows from [Reference Zelevinsky43] and [Reference Mœglin and Waldspurger31] that there exists a Zariski open dense subset
![]() $S^o(V,N) \subset S(V,N)$
such that, for
$S^o(V,N) \subset S(V,N)$
such that, for
![]() $L \in S(V,N)$
, the multisegment (of type
$L \in S(V,N)$
, the multisegment (of type
![]() $\chi $
) corresponding to
$\chi $
) corresponding to
![]() $(V,L)$
is equal to
$(V,L)$
is equal to
![]() $\mathfrak {m}^{\sharp }$
if and only if
$\mathfrak {m}^{\sharp }$
if and only if
![]() $L \in S^o(V,N)$
.
$L \in S^o(V,N)$
.
Let V be a finite-dimensional
![]() $\mathbb {Z}$
-graded vector space over
$\mathbb {Z}$
-graded vector space over
![]() $\mathbb {C}$
and
$\mathbb {C}$
and
![]() $N, L \colon V \to V$
be
$N, L \colon V \to V$
be
![]() $\mathbb {C}$
-linear endomorphisms of degree
$\mathbb {C}$
-linear endomorphisms of degree
![]() $1$
,
$1$
,
![]() $-1$
, respectively. We say that the triple
$-1$
, respectively. We say that the triple
![]() $(V,N,L)$
is admissible if
$(V,N,L)$
is admissible if
![]() $N \circ L = L\circ N$
and the multisegment corresponding to the
$N \circ L = L\circ N$
and the multisegment corresponding to the
![]() $WL$
-pair
$WL$
-pair
![]() $(V,L)$
is the Zelevinsky dual of the one corresponding to the
$(V,L)$
is the Zelevinsky dual of the one corresponding to the
![]() $VN$
-pair
$VN$
-pair
![]() $(V,N)$
.
$(V,N)$
.
Lemma 3.3. Let
![]() $(V,N)$
(respectively,
$(V,N)$
(respectively,
![]() $(W,L)$
) be a
$(W,L)$
) be a
![]() $VN$
-pair (respectively, a
$VN$
-pair (respectively, a
![]() $WL$
-pair), and let
$WL$
-pair), and let
![]() $\mathfrak {m}$
denote the multisegment corresponding to
$\mathfrak {m}$
denote the multisegment corresponding to
![]() $(V,N)$
(respectively,
$(V,N)$
(respectively,
![]() $(W,L)$
). Then the multisegment
$(W,L)$
). Then the multisegment
![]() $\mathfrak {m}^{-}$
corresponds to
$\mathfrak {m}^{-}$
corresponds to
![]() $(\mathrm {Image}\, N, N|_{\mathrm {Image}\, N})(-1)$
(respectively,
$(\mathrm {Image}\, N, N|_{\mathrm {Image}\, N})(-1)$
(respectively,
![]() $(\mathrm {Image}\, L, L|_{\mathrm {Image}\, L})$
).
$(\mathrm {Image}\, L, L|_{\mathrm {Image}\, L})$
).
Proof. Easy.
Let us give an example. Let
![]() $\mathfrak {m} = \Delta _1 + \Delta _2 + \Delta _3 + \Delta _4$
, where
$\mathfrak {m} = \Delta _1 + \Delta _2 + \Delta _3 + \Delta _4$
, where
![]() $\Delta _1=[3,7]_{\chi }$
,
$\Delta _1=[3,7]_{\chi }$
,
![]() $\Delta _2=[2,5]_{\chi }$
,
$\Delta _2=[2,5]_{\chi }$
,
![]() $\Delta _3= [1,2]_{\chi }$
and
$\Delta _3= [1,2]_{\chi }$
and
![]() $\Delta _4=[0,0]_{\chi }$
.
$\Delta _4=[0,0]_{\chi }$
.
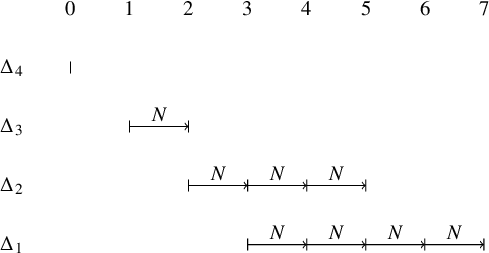
The picture of
![]() $(\mathrm {Image}\,\,N(-1), N|_{\mathrm {Image}\,\, N}(-1))$
is as follows:
$(\mathrm {Image}\,\,N(-1), N|_{\mathrm {Image}\,\, N}(-1))$
is as follows:
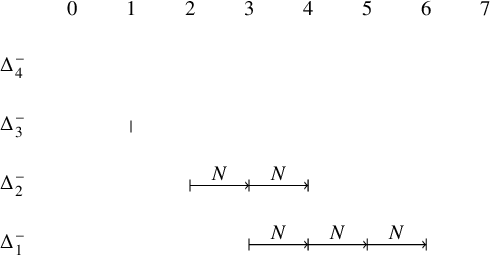
We see that this corresponds to
![]() $\mathfrak {m}^-$
.
$\mathfrak {m}^-$
.
Lemma 3.4. Let
![]() $(V,N)$
be a
$(V,N)$
be a
![]() $VN$
-pair, and let
$VN$
-pair, and let
![]() $\mathfrak {m}$
be the multisegment corresponding to
$\mathfrak {m}$
be the multisegment corresponding to
![]() $(V,N)$
. Then there exists a Zariski open dense subset
$(V,N)$
. Then there exists a Zariski open dense subset
![]() $S^{\theta }(V,N) \subset S(V,N)$
such that for
$S^{\theta }(V,N) \subset S(V,N)$
such that for
![]() $L \in S(V,N)$
, both
$L \in S(V,N)$
, both
![]() $(V,N,L)$
and
$(V,N,L)$
and
![]() $(\mathrm {Image}\, L, N|_{\mathrm {Image}\, L}, L|_{\mathrm {Image}\, L})$
are admissible triples if and only if
$(\mathrm {Image}\, L, N|_{\mathrm {Image}\, L}, L|_{\mathrm {Image}\, L})$
are admissible triples if and only if
![]() $L \in S^{\theta }(V,N)$
.
$L \in S^{\theta }(V,N)$
.
Proof. It is easy to see that there exists a Zariski open subset
![]() $S^{\theta }(V,N) \subset S(V,N)$
such that for
$S^{\theta }(V,N) \subset S(V,N)$
such that for
![]() $L \in S(V,N)$
, both
$L \in S(V,N)$
, both
![]() $(V,N,L)$
and
$(V,N,L)$
and
![]() $(\mathrm {Image}\, L, N|_{\mathrm {Image}\, L}, L|_{\mathrm {Image}\, L})$
are admissible triples if and only if
$(\mathrm {Image}\, L, N|_{\mathrm {Image}\, L}, L|_{\mathrm {Image}\, L})$
are admissible triples if and only if
![]() $L \in S^{\theta }(V,N)$
.
$L \in S^{\theta }(V,N)$
.
It remains to show that
![]() $S^{\theta }(V,N)$
is dense in
$S^{\theta }(V,N)$
is dense in
![]() $S(V,N)$
. Since
$S(V,N)$
. Since
![]() $S(V,N)$
is irreducible as an algebraic variety over
$S(V,N)$
is irreducible as an algebraic variety over
![]() $\mathbb {C}$
, it suffices to show that
$\mathbb {C}$
, it suffices to show that
![]() $S^{\theta }(V,N)$
is nonempty. Let us choose
$S^{\theta }(V,N)$
is nonempty. Let us choose
![]() $L \in S^o(V,N)$
. Since the morphism
$L \in S^o(V,N)$
. Since the morphism
![]() $S(V,L) \to S(\mathrm {Image}\, L, L|_{\mathrm {Image}\, L})$
is surjective by Lemma 3.2, there exists
$S(V,L) \to S(\mathrm {Image}\, L, L|_{\mathrm {Image}\, L})$
is surjective by Lemma 3.2, there exists
![]() $N' \in S(V,L)$
such that both
$N' \in S(V,L)$
such that both
![]() $(V,N',L)$
and
$(V,N',L)$
and
![]() $(\mathrm {Image}\, L, N'|_{\mathrm {Image}\, L}, L|_{\mathrm {Image}\, L})$
are admissible triples. Then
$(\mathrm {Image}\, L, N'|_{\mathrm {Image}\, L}, L|_{\mathrm {Image}\, L})$
are admissible triples. Then
![]() $(V,N)$
and
$(V,N)$
and
![]() $(V,N')$
are isomorphic since both correspond to the same multisegment. Hence
$(V,N')$
are isomorphic since both correspond to the same multisegment. Hence
![]() $(V,N',L)$
is isomorphic to
$(V,N',L)$
is isomorphic to
![]() $(V,N,L')$
for some
$(V,N,L')$
for some
![]() $L' \in S(V,N)$
. Since
$L' \in S(V,N)$
. Since
![]() $L'$
belongs to
$L'$
belongs to
![]() $S^{\theta }(V,N)$
, it follows that
$S^{\theta }(V,N)$
, it follows that
![]() $S^{\theta }(V,N)$
is nonempty, as desired.
$S^{\theta }(V,N)$
is nonempty, as desired.
3.2 Proof of Proposition 2.4
Now we prove Proposition 2.4.
Proof of Proposition 2.4
Let
![]() $\pi = Z(\mathfrak {m})$
be an irreducible representation of
$\pi = Z(\mathfrak {m})$
be an irreducible representation of
![]() $G_n$
. We decompose
$G_n$
. We decompose
![]() $\mathfrak {m}$
as
$\mathfrak {m}$
as
where
-
• each segment in
 $\mathfrak {m}'$
is not unipotent;
$\mathfrak {m}'$
is not unipotent; -
• each
 $\mathfrak {m}_i$
is of type
$\mathfrak {m}_i$
is of type
 $\chi _i$
for some unramified character
$\chi _i$
for some unramified character
 $\chi _i$
of
$\chi _i$
of
 $F^{\times }$
for
$F^{\times }$
for
 $1 \leq i \leq t$
;
$1 \leq i \leq t$
; -
• if
 $i \not = j$
, then
$i \not = j$
, then
 $\chi _i\chi _j^{-1}$
is not of the form
$\chi _i\chi _j^{-1}$
is not of the form
 $|\cdot |^a$
for any
$|\cdot |^a$
for any
 $a \in \mathbb {Z}$
.
$a \in \mathbb {Z}$
.
Set
![]() $\pi ' = Z(\mathfrak {m}')$
and
$\pi ' = Z(\mathfrak {m}')$
and
![]() $\pi _i = Z(\mathfrak {m}_i)$
. Then
$\pi _i = Z(\mathfrak {m}_i)$
. Then
![]() $\pi $
is isomorphic to the parabolic induction
$\pi $
is isomorphic to the parabolic induction
![]() $\pi ' \times \pi _1 \times \cdots \times \pi _{t}$
.
$\pi ' \times \pi _1 \times \cdots \times \pi _{t}$
.
For
![]() $\Pi = \pi , \pi ', \pi _1, \ldots , \pi _{t}$
, let
$\Pi = \pi , \pi ', \pi _1, \ldots , \pi _{t}$
, let
![]() $\Pi ^{(0)} = \Pi $
and
$\Pi ^{(0)} = \Pi $
and
![]() $\Pi ^{(i)}$
denote the highest derivative of
$\Pi ^{(i)}$
denote the highest derivative of
![]() $\Pi ^{(i-1)}$
for
$\Pi ^{(i-1)}$
for
![]() $i \geq 1$
. Then we have
$i \geq 1$
. Then we have
![]() $\pi ^{(i)} = \pi ^{\prime (i)} \times \pi _1^{(i)} \times \cdots \times \pi _{t}^{(i)}$
for any integer
$\pi ^{(i)} = \pi ^{\prime (i)} \times \pi _1^{(i)} \times \cdots \times \pi _{t}^{(i)}$
for any integer
![]() $i \ge 0$
. Thus, to prove the claim, we may assume that
$i \ge 0$
. Thus, to prove the claim, we may assume that
![]() $\mathfrak {m} = \mathfrak {m}'$
or
$\mathfrak {m} = \mathfrak {m}'$
or
![]() $\mathfrak {m} = \mathfrak {m}_1$
.
$\mathfrak {m} = \mathfrak {m}_1$
.
First, we consider the case where
![]() $\mathfrak {m} = \mathfrak {m}'$
. Let us write
$\mathfrak {m} = \mathfrak {m}'$
. Let us write
![]() $\pi = Z(\mathfrak {m})$
and
$\pi = Z(\mathfrak {m})$
and
![]() $\mathfrak {m} = [a_1,b_1]_{\rho _1} + \cdots +[a_r,b_r]_{\rho _r}$
. Then
$\mathfrak {m} = [a_1,b_1]_{\rho _1} + \cdots +[a_r,b_r]_{\rho _r}$
. Then
![]() $\rho _1, \ldots , \rho _r$
are ramified cuspidal representations. For
$\rho _1, \ldots , \rho _r$
are ramified cuspidal representations. For
![]() $i=1,\ldots ,r$
, let
$i=1,\ldots ,r$
, let
![]() $c_i = c_{\rho _i}$
denote the conductor of
$c_i = c_{\rho _i}$
denote the conductor of
![]() $\rho _i$
. Then for
$\rho _i$
. Then for
![]() $j \geq 0$
, we have
$j \geq 0$
, we have
![]() $\pi ^{(j)} = Z(\mathfrak {m}^{(j)})$
, where
$\pi ^{(j)} = Z(\mathfrak {m}^{(j)})$
, where
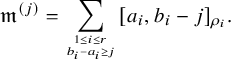 $$\begin{align*}\mathfrak{m}^{(j)} = \sum_{1 \le i \le r \atop b_i - a_i \ge j} [a_i, b_i -j]_{\rho_i}. \end{align*}$$
$$\begin{align*}\mathfrak{m}^{(j)} = \sum_{1 \le i \le r \atop b_i - a_i \ge j} [a_i, b_i -j]_{\rho_i}. \end{align*}$$
This shows that the conductor of
![]() $\pi ^{(j)}$
is equal to
$\pi ^{(j)}$
is equal to
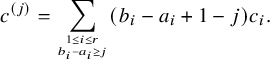 $$\begin{align*}c^{(j)} = \sum_{1 \le i \le r \atop b_i - a_i \ge j} (b_i -a_i + 1 -j) c_{i}. \end{align*}$$
$$\begin{align*}c^{(j)} = \sum_{1 \le i \le r \atop b_i - a_i \ge j} (b_i -a_i + 1 -j) c_{i}. \end{align*}$$
Hence we have
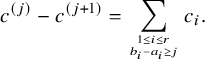 $$\begin{align*}c^{(j)} - c^{(j+1)} = \sum_{1 \le i \le r \atop b_i - a_i \ge j} c_{i}. \end{align*}$$
$$\begin{align*}c^{(j)} - c^{(j+1)} = \sum_{1 \le i \le r \atop b_i - a_i \ge j} c_{i}. \end{align*}$$
From this, one can easily see that
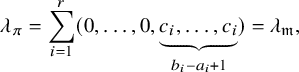 $$\begin{align*}\lambda_{\pi} = \sum_{i=1}^r (0,\ldots,0, \underbrace{c_i,\ldots,c_i}_{b_i-a_i+1}) = \lambda_{\mathfrak{m}}, \end{align*}$$
$$\begin{align*}\lambda_{\pi} = \sum_{i=1}^r (0,\ldots,0, \underbrace{c_i,\ldots,c_i}_{b_i-a_i+1}) = \lambda_{\mathfrak{m}}, \end{align*}$$
as desired.
Now we consider the case where
![]() $\pi = Z(\mathfrak {m})$
is of type
$\pi = Z(\mathfrak {m})$
is of type
![]() $\chi $
for an unramified character
$\chi $
for an unramified character
![]() $\chi $
of
$\chi $
of
![]() $F^{\times }$
. Let us consider the
$F^{\times }$
. Let us consider the
![]() $VN$
-pair
$VN$
-pair
![]() $(V,N)$
corresponding to
$(V,N)$
corresponding to
![]() $\mathfrak {m}$
. For
$\mathfrak {m}$
. For
![]() $i \ge 0$
, let us write
$i \ge 0$
, let us write
![]() $\pi ^{(i)} = Z(\mathfrak {m}^{(i)})$
. As we remarked at the beginning of Section 2.3, we have
$\pi ^{(i)} = Z(\mathfrak {m}^{(i)})$
. As we remarked at the beginning of Section 2.3, we have
![]() $\pi ^{(1)} = Z(\mathfrak {m}^{-})$
. Hence
$\pi ^{(1)} = Z(\mathfrak {m}^{-})$
. Hence
![]() $\mathfrak {m}^{(i)}$
is obtained from
$\mathfrak {m}^{(i)}$
is obtained from
![]() $\mathfrak {m}$
by the i-fold iteration of the operation
$\mathfrak {m}$
by the i-fold iteration of the operation
![]() $(\ )^{-}$
. Therefore, it follows from Lemma 3.3 that
$(\ )^{-}$
. Therefore, it follows from Lemma 3.3 that
![]() $\mathfrak {m}^{(i)}$
corresponds to the
$\mathfrak {m}^{(i)}$
corresponds to the
![]() $VN$
-pair
$VN$
-pair
![]() $(\mathrm {Image}\, N^i, N|_{\mathrm {Image}\, N^i})(-i)$
. Let us choose
$(\mathrm {Image}\, N^i, N|_{\mathrm {Image}\, N^i})(-i)$
. Let us choose
![]() $L \in S^{\theta }(V,N)$
such that
$L \in S^{\theta }(V,N)$
such that
![]() $L|_{\mathrm {Image}\, N^i}$
belongs to
$L|_{\mathrm {Image}\, N^i}$
belongs to
![]() $S^o(\mathrm {Image}\, N^i, N|_{\mathrm {Image}\, N^i})$
for any integer
$S^o(\mathrm {Image}\, N^i, N|_{\mathrm {Image}\, N^i})$
for any integer
![]() $i \ge 0$
. By Lemma 3.2, such an L exists. Then the conductor of
$i \ge 0$
. By Lemma 3.2, such an L exists. Then the conductor of
![]() $\pi ^{(i)}$
is equal to the dimension of
$\pi ^{(i)}$
is equal to the dimension of
![]() $\mathrm {Image}\, L \circ N^i$
. Hence if we write
$\mathrm {Image}\, L \circ N^i$
. Hence if we write
![]() $\lambda _{\pi } = (\lambda _1, \dots , \lambda _n)$
and
$\lambda _{\pi } = (\lambda _1, \dots , \lambda _n)$
and
![]() $d_i = \dim \mathrm {Image}\, L \circ N^i$
for
$d_i = \dim \mathrm {Image}\, L \circ N^i$
for
![]() $i \geq 0$
, then we have
$i \geq 0$
, then we have
for
![]() $k = 1, \dots , n$
. Let us write
$k = 1, \dots , n$
. Let us write
![]() $\pi ^{\mathrm {ram}} = Z(\mathfrak {m}^{\mathrm {ram}})$
with
$\pi ^{\mathrm {ram}} = Z(\mathfrak {m}^{\mathrm {ram}})$
with
![]() $\mathfrak {m}^{\mathrm {ram}} = \Delta _1+\dots +\Delta _r$
and
$\mathfrak {m}^{\mathrm {ram}} = \Delta _1+\dots +\Delta _r$
and
![]() $\Delta _i = [a_i,b_i]_{\chi }$
for
$\Delta _i = [a_i,b_i]_{\chi }$
for
![]() $1 \leq i \leq r$
. Then
$1 \leq i \leq r$
. Then
![]() $\lambda _{\mathfrak {m}} = (\lambda ^{\prime }_1,\dots ,\lambda ^{\prime }_n)$
, with
$\lambda _{\mathfrak {m}} = (\lambda ^{\prime }_1,\dots ,\lambda ^{\prime }_n)$
, with
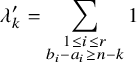 $$\begin{align*}\lambda^{\prime}_k = \sum_{\substack{1 \leq i \leq r \\ b_i-a_i \geq n-k}}1 \end{align*}$$
$$\begin{align*}\lambda^{\prime}_k = \sum_{\substack{1 \leq i \leq r \\ b_i-a_i \geq n-k}}1 \end{align*}$$
for
![]() $k = 1,\dots ,n$
. By Lemmas 3.3 and 3.4,
$k = 1,\dots ,n$
. By Lemmas 3.3 and 3.4,
![]() $\mathfrak {m}^{\mathrm {ram}}$
corresponds to the
$\mathfrak {m}^{\mathrm {ram}}$
corresponds to the
![]() $VN$
-pair
$VN$
-pair
![]() $(\mathrm {Image}\, L, N|_{\mathrm {Image}\, L})$
. Since L and N commute, we have
$(\mathrm {Image}\, L, N|_{\mathrm {Image}\, L})$
. Since L and N commute, we have
![]() $\dim \mathrm {Image}\, N^i \circ L = d_i$
for
$\dim \mathrm {Image}\, N^i \circ L = d_i$
for
![]() $i \geq 0$
. Hence we have
$i \geq 0$
. Hence we have
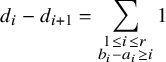 $$\begin{align*}d_i-d_{i+1} = \sum_{\substack{1 \leq i \leq r \\ b_i-a_i \geq i}}1 \end{align*}$$
$$\begin{align*}d_i-d_{i+1} = \sum_{\substack{1 \leq i \leq r \\ b_i-a_i \geq i}}1 \end{align*}$$
for
![]() $i = 0,\dots ,n-1$
. Therefore, we have
$i = 0,\dots ,n-1$
. Therefore, we have
for
![]() $k = 1,\dots ,n$
. This completes the proof.
$k = 1,\dots ,n$
. This completes the proof.
We do not use the following proposition, but it might be interesting.
Proposition 3.5. For any multisegment
![]() $\mathfrak {m}$
, we have
$\mathfrak {m}$
, we have
![]() $(\mathfrak {m}^{-})^{\mathrm {ram}} = (\mathfrak {m}^{\mathrm {ram}})^{-}$
.
$(\mathfrak {m}^{-})^{\mathrm {ram}} = (\mathfrak {m}^{\mathrm {ram}})^{-}$
.
Proof. Let
![]() $(V,N)$
be the
$(V,N)$
be the
![]() $VN$
-pair corresponding to the multisegment
$VN$
-pair corresponding to the multisegment
![]() $\mathfrak {m}$
. If we choose a sufficiently general
$\mathfrak {m}$
. If we choose a sufficiently general
![]() $L \in S(V,N)$
, then
$L \in S(V,N)$
, then
![]() $(\mathfrak {m}^{-})^{\mathrm {ram}}$
and
$(\mathfrak {m}^{-})^{\mathrm {ram}}$
and
![]() $(\mathfrak {m}^{\mathrm {ram}})^{-}$
correspond to the pairs
$(\mathfrak {m}^{\mathrm {ram}})^{-}$
correspond to the pairs
![]() $(\mathrm {Image}\, L\circ N, N|_{\mathrm {Image}\, L \circ N})(-1)$
and
$(\mathrm {Image}\, L\circ N, N|_{\mathrm {Image}\, L \circ N})(-1)$
and
![]() $(\mathrm {Image}\, N\circ L, N|_{\mathrm {Image}\, N \circ L})(-1)$
, respectively. Since
$(\mathrm {Image}\, N\circ L, N|_{\mathrm {Image}\, N \circ L})(-1)$
, respectively. Since
![]() $L\circ N=N \circ L$
, the claim follows.
$L\circ N=N \circ L$
, the claim follows.
3.3 Proof of Proposition 2.7
The following statement is easy to check. However, we record it as a lemma for later use. A proof is omitted.
Lemma 3.6. For any multisegment
![]() $\mathfrak {m}$
, we have
$\mathfrak {m}$
, we have
![]() $(\mathfrak {m}^{-})_{\mathrm {max}} = (\mathfrak {m}_{\mathrm {max}})^{-}$
and
$(\mathfrak {m}^{-})_{\mathrm {max}} = (\mathfrak {m}_{\mathrm {max}})^{-}$
and
![]() $(\mathfrak {m}^{-})^{\mathrm {max}} = (\mathfrak {m}^{\mathrm {max}})^{-}$
.
$(\mathfrak {m}^{-})^{\mathrm {max}} = (\mathfrak {m}^{\mathrm {max}})^{-}$
.
For a multisegment
![]() $\mathfrak {m}$
, a full-sub-multisegment of
$\mathfrak {m}$
, a full-sub-multisegment of
![]() $\mathfrak {m}$
is a multisegment
$\mathfrak {m}$
is a multisegment
![]() $\mathfrak {m}'$
such that for any segment
$\mathfrak {m}'$
such that for any segment
![]() $\Delta $
in
$\Delta $
in
![]() $\mathfrak {m}'$
, its multiplicity in
$\mathfrak {m}'$
, its multiplicity in
![]() $\mathfrak {m}'$
is equal to that in
$\mathfrak {m}'$
is equal to that in
![]() $\mathfrak {m}$
.
$\mathfrak {m}$
.
We say that a multisegment
![]() $\mathfrak {m}$
is totally ordered if for any two segments
$\mathfrak {m}$
is totally ordered if for any two segments
![]() $\Delta , \Delta '$
in
$\Delta , \Delta '$
in
![]() $\mathfrak {m}$
, we have either
$\mathfrak {m}$
, we have either
![]() $\Delta \subset \Delta '$
or
$\Delta \subset \Delta '$
or
![]() $\Delta ' \subset \Delta $
.
$\Delta ' \subset \Delta $
.
Proposition 3.7. Let
![]() $\mathfrak {m} = \Delta _1 + \cdots + \Delta _r$
be a multisegment of type
$\mathfrak {m} = \Delta _1 + \cdots + \Delta _r$
be a multisegment of type
![]() $\chi $
and
$\chi $
and
![]() $a \in \mathbb {Z}$
an integer. Let us write
$a \in \mathbb {Z}$
an integer. Let us write
![]() $\delta _a =[a,a+1]_{\chi }$
. Let
$\delta _a =[a,a+1]_{\chi }$
. Let
![]() $\mathfrak {m}_a$
denote the full-sub-multisegment of
$\mathfrak {m}_a$
denote the full-sub-multisegment of
![]() $\mathfrak {m}$
that consists of segments that intersect
$\mathfrak {m}$
that consists of segments that intersect
![]() $\delta _a$
, and let
$\delta _a$
, and let
![]() $\mathfrak {m}^{\sharp }_{(a)}$
denote the full-sub-multisegment of
$\mathfrak {m}^{\sharp }_{(a)}$
denote the full-sub-multisegment of
![]() $\mathfrak {m}^{\sharp } = \Delta ^{\prime }_1 + \cdots + \Delta ^{\prime }_s$
that consists of segments that contain
$\mathfrak {m}^{\sharp } = \Delta ^{\prime }_1 + \cdots + \Delta ^{\prime }_s$
that consists of segments that contain
![]() $\delta _a$
. Namely,
$\delta _a$
. Namely,
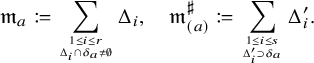
Then we have the equality
where
![]() $\mathfrak {m}'$
runs over the set of totally ordered full-sub-multisegments of
$\mathfrak {m}'$
runs over the set of totally ordered full-sub-multisegments of
![]() $\mathfrak {m}_a$
.
$\mathfrak {m}_a$
.
Proof. By replacing
![]() $\chi $
with
$\chi $
with
![]() $\chi |\cdot |^c$
for some integer c, we may and will assume that there exists an integer r such that any segment in
$\chi |\cdot |^c$
for some integer c, we may and will assume that there exists an integer r such that any segment in
![]() $\mathfrak {m}$
is contained in
$\mathfrak {m}$
is contained in
![]() $[1,r]_{\chi }$
.
$[1,r]_{\chi }$
.
For two integers
![]() $a,b$
with
$a,b$
with
![]() $1 \leq a \leq b \leq r$
, let
$1 \leq a \leq b \leq r$
, let
![]() $d_{a,b}=d_{a,b}(\mathfrak {m})$
denote the multiplicity of the segment
$d_{a,b}=d_{a,b}(\mathfrak {m})$
denote the multiplicity of the segment
![]() $[a,b]_{\chi }$
in
$[a,b]_{\chi }$
in
![]() $\mathfrak {m}$
. When
$\mathfrak {m}$
. When
![]() $a>b$
, we set
$a>b$
, we set
![]() $d_{a,b}=0$
. Then it follows from the result of Knight–Zelevinsky [Reference Knight and Zelevinsky16, Theorem 1.2] that
$d_{a,b}=0$
. Then it follows from the result of Knight–Zelevinsky [Reference Knight and Zelevinsky16, Theorem 1.2] that
![]() $\mathrm {Card}(\mathfrak {m}^{\sharp }_{(a)})$
is equal to the right-hand side of the equality (1.6) in [Reference Knight and Zelevinsky16] for
$\mathrm {Card}(\mathfrak {m}^{\sharp }_{(a)})$
is equal to the right-hand side of the equality (1.6) in [Reference Knight and Zelevinsky16] for
![]() $(i,j)=(a,a+1)$
.
$(i,j)=(a,a+1)$
.
For two integers
![]() $x,y$
with
$x,y$
with
![]() $x \leq y$
, let
$x \leq y$
, let
![]() $[x,y]$
denote the set of integers c satisfying
$[x,y]$
denote the set of integers c satisfying
![]() $x \le c \le y$
. Let
$x \le c \le y$
. Let
![]() $a \in [1,r-1]$
. We rewrite the right-hand side of (1.6) in [Reference Knight and Zelevinsky16] for
$a \in [1,r-1]$
. We rewrite the right-hand side of (1.6) in [Reference Knight and Zelevinsky16] for
![]() $(i,j)=(a,a+1)$
. Let us first recall some notation in [Reference Knight and Zelevinsky16]. They fix a positive integer r and consider the set S of pairs of integers
$(i,j)=(a,a+1)$
. Let us first recall some notation in [Reference Knight and Zelevinsky16]. They fix a positive integer r and consider the set S of pairs of integers
![]() $(i,j)$
such that
$(i,j)$
such that
![]() $1\leq i \leq j \leq r$
. For
$1\leq i \leq j \leq r$
. For
![]() $ 1 \leq i \leq j \leq r$
, they consider the set
$ 1 \leq i \leq j \leq r$
, they consider the set
![]() $T_{i,j}$
of functions
$T_{i,j}$
of functions
![]() $\nu \colon [1,i] \times [j,r] \to [i,j]$
such that
$\nu \colon [1,i] \times [j,r] \to [i,j]$
such that
![]() $\nu (k,l) \leq \nu (k', l')$
whenever
$\nu (k,l) \leq \nu (k', l')$
whenever
![]() $k\leq k', l \leq l'$
.
$k\leq k', l \leq l'$
.
Let
![]() $1 \leq a \leq r$
. We only use the case
$1 \leq a \leq r$
. We only use the case
![]() $i=a, j=a+1$
and consider
$i=a, j=a+1$
and consider
![]() $T_{a, a+1}$
. In this case, any function
$T_{a, a+1}$
. In this case, any function
![]() $\nu \in T_{a, a+1}$
takes one of two values
$\nu \in T_{a, a+1}$
takes one of two values
![]() $a, a+1$
. We express this using Figure 1. The rectangle depicts the set
$a, a+1$
. We express this using Figure 1. The rectangle depicts the set
![]() $[1,a] \times [a+1, r]$
. The upper-left corner is
$[1,a] \times [a+1, r]$
. The upper-left corner is
![]() $(1,a+1)$
, the lower-left corner is
$(1,a+1)$
, the lower-left corner is
![]() $(a,a+1)$
, the upper-right corner is
$(a,a+1)$
, the upper-right corner is
![]() $(1,r)$
and the lower-right corner is
$(1,r)$
and the lower-right corner is
![]() $(a, r)$
. Because of the condition on
$(a, r)$
. Because of the condition on
![]() $\nu $
, there exists a bold line as in the picture such that
$\nu $
, there exists a bold line as in the picture such that
![]() $\nu $
takes the value a on the left (call the region L) and the value
$\nu $
takes the value a on the left (call the region L) and the value
![]() $a+1$
on the right (call the region R).
$a+1$
on the right (call the region R).
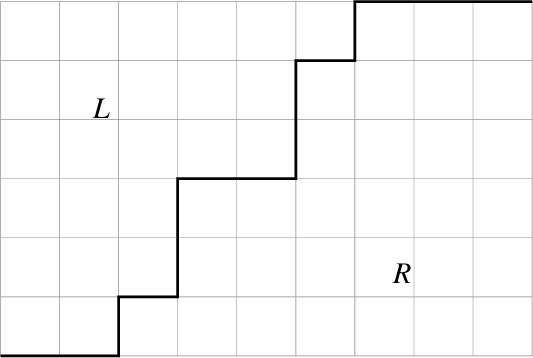
Figure 1
We look at the sum from
![]() $(1.6)$
[Reference Knight and Zelevinsky16]:
$(1.6)$
[Reference Knight and Zelevinsky16]:
This equals
Now consider Figure 2. The rectangle depicts the set
![]() $U=[1,a+1] \times [a, r]$
. Let
$U=[1,a+1] \times [a, r]$
. Let
![]() $L'$
be the region L moved to the left by 1 and
$L'$
be the region L moved to the left by 1 and
![]() $R'$
be the region R moved down by 1. These are subsets of U, and the complement
$R'$
be the region R moved down by 1. These are subsets of U, and the complement
![]() $V_{\nu }=U\setminus (L' \cup R')$
is shown in blue in the picture.
$V_{\nu }=U\setminus (L' \cup R')$
is shown in blue in the picture.
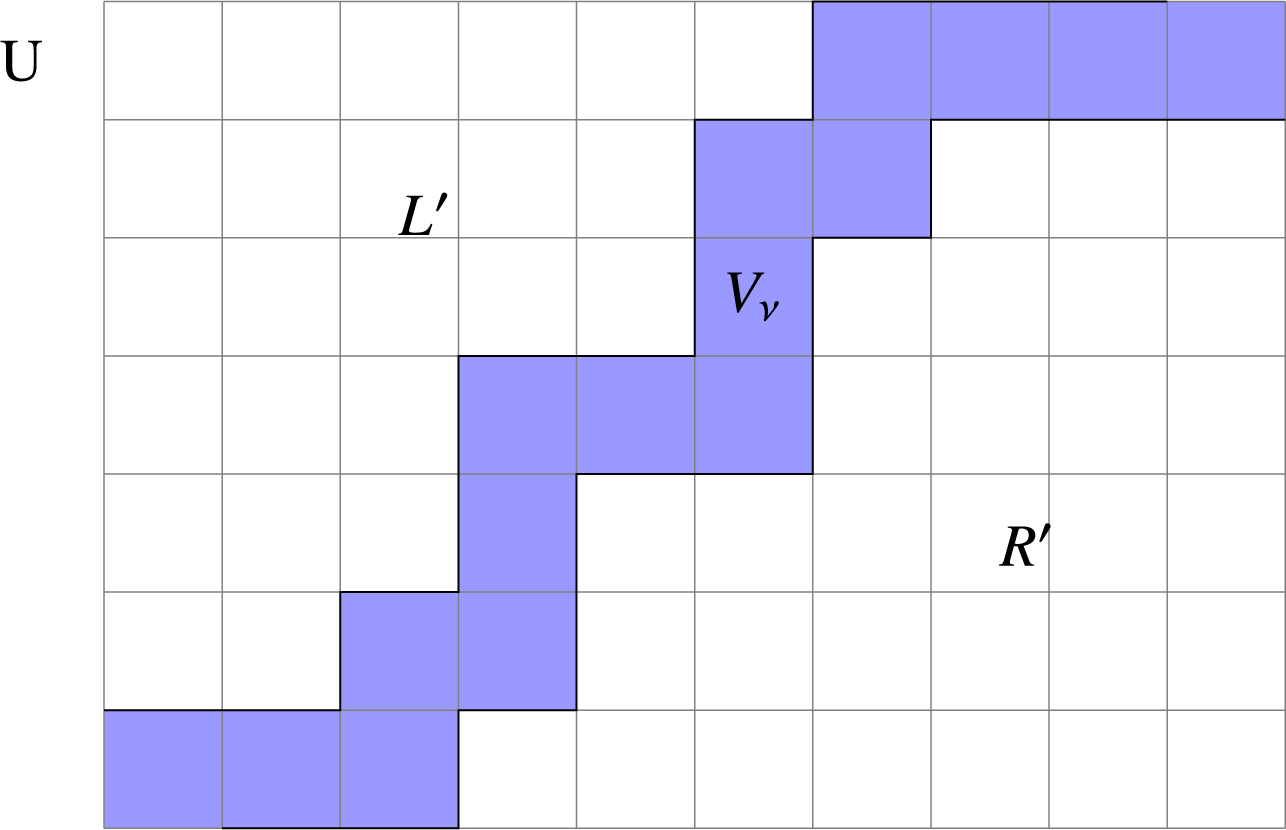
Figure 2
A path from
![]() $(a+1,a)$
to
$(a+1,a)$
to
![]() $(1,r)$
is a map
$(1,r)$
is a map
![]() $p\colon [0,r] \to \mathbb {Z} \times \mathbb {Z}$
satisfying the following conditions:
$p\colon [0,r] \to \mathbb {Z} \times \mathbb {Z}$
satisfying the following conditions:
-
(1)
 $p(0)=(a+1,a)$
.
$p(0)=(a+1,a)$
. -
(2) For
 $i=1, \ldots , r$
, the element
$i=1, \ldots , r$
, the element
 $p(i) \in \mathbb {Z} \times \mathbb {Z}$
is equal to
$p(i) \in \mathbb {Z} \times \mathbb {Z}$
is equal to
 $p(i-1)-(1,0)$
or
$p(i-1)-(1,0)$
or
 $p(i-1)+(0,1)$
.
$p(i-1)+(0,1)$
. -
(3)
 $p(r)=(1,r)$
.
$p(r)=(1,r)$
.
Then
![]() $V_{\nu }$
is equal to the image of a path from
$V_{\nu }$
is equal to the image of a path from
![]() $[a+1, a]$
to
$[a+1, a]$
to
![]() $[1,r]$
. By sending
$[1,r]$
. By sending
![]() $\nu $
to this path, we obtain a bijection from
$\nu $
to this path, we obtain a bijection from
![]() $T_{a, a+1}$
to the set
$T_{a, a+1}$
to the set
![]() $A_a$
of paths from
$A_a$
of paths from
![]() $(a+1,a)$
to
$(a+1,a)$
to
![]() $(1,r)$
.
$(1,r)$
.
Notice now that the sum above is equal to
Conversely, given a path from
![]() $[a+1, a]$
to
$[a+1, a]$
to
![]() $[a,1]$
, we obtain a function
$[a,1]$
, we obtain a function
![]() $\nu \in T_{a, a+1}$
such that
$\nu \in T_{a, a+1}$
such that
![]() $V_{\nu }$
is the image of the given path. Thus, the right-hand side of (1.6) of [Reference Knight and Zelevinsky16] is equal to
$V_{\nu }$
is the image of the given path. Thus, the right-hand side of (1.6) of [Reference Knight and Zelevinsky16] is equal to
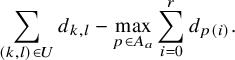 $$\begin{align*}\sum_{(k,l) \in U} d_{k,l} -\max_{p \in A_a} \sum_{i=0}^{r} d_{p(i)}. \end{align*}$$
$$\begin{align*}\sum_{(k,l) \in U} d_{k,l} -\max_{p \in A_a} \sum_{i=0}^{r} d_{p(i)}. \end{align*}$$
Notice that
![]() $\mathrm {Card}(\mathfrak {m}_a) = \sum _{(k,l) \in U}d_{k,l}$
. From this, we see that
$\mathrm {Card}(\mathfrak {m}_a) = \sum _{(k,l) \in U}d_{k,l}$
. From this, we see that
![]() $\mathrm {Card}(\mathfrak {m}^{\sharp }_{(a)})$
is equal to
$\mathrm {Card}(\mathfrak {m}^{\sharp }_{(a)})$
is equal to
where
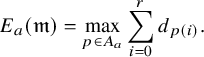 $$\begin{align*}E_a(\mathfrak{m}) = \max_{p \in A_a} \sum_{i=0}^{r} d_{p(i)}. \end{align*}$$
$$\begin{align*}E_a(\mathfrak{m}) = \max_{p \in A_a} \sum_{i=0}^{r} d_{p(i)}. \end{align*}$$
For
![]() $p \in A_a$
, let
$p \in A_a$
, let
![]() $\mathfrak {m}_{a,p}$
denote the full-sub-multisegment of
$\mathfrak {m}_{a,p}$
denote the full-sub-multisegment of
![]() $\mathfrak {m}_a$
that consists of the segments
$\mathfrak {m}_a$
that consists of the segments
![]() $[a',b']_{\chi }$
in
$[a',b']_{\chi }$
in
![]() $\mathfrak {m}_a$
of the form
$\mathfrak {m}_a$
of the form
![]() $(a',b') = p(i)$
for some integer
$(a',b') = p(i)$
for some integer
![]() $i \in [0,r]$
. Then
$i \in [0,r]$
. Then
![]() $\mathfrak {m}_{a,p}$
is totally ordered, and we have
$\mathfrak {m}_{a,p}$
is totally ordered, and we have
![]() $\sum _{i=0}^{r} d_{p(i)} = \mathrm {Card}(\mathfrak {m}_{a,p})$
. By sending p to
$\sum _{i=0}^{r} d_{p(i)} = \mathrm {Card}(\mathfrak {m}_{a,p})$
. By sending p to
![]() $\mathfrak {m}_{a,p}$
, we obtain a map from
$\mathfrak {m}_{a,p}$
, we obtain a map from
![]() $A_a$
to the set
$A_a$
to the set
![]() $T_a$
of totally ordered full-sub-multisegments of
$T_a$
of totally ordered full-sub-multisegments of
![]() $\mathfrak {m}_a$
. In general, this map is neither injective nor surjective. However, for any totally ordered full-sub-multisegment
$\mathfrak {m}_a$
. In general, this map is neither injective nor surjective. However, for any totally ordered full-sub-multisegment
![]() $\mathfrak {m}'$
of
$\mathfrak {m}'$
of
![]() $\mathfrak {m}_a$
, there exists a path
$\mathfrak {m}_a$
, there exists a path
![]() $p \in A_a$
such that
$p \in A_a$
such that
![]() $\mathfrak {m}'$
is a full-sub-multisegment of
$\mathfrak {m}'$
is a full-sub-multisegment of
![]() $\mathfrak {m}_{a,p}$
. In particular
$\mathfrak {m}_{a,p}$
. In particular
![]() $\mathrm {Card}(\mathfrak {m}') \le \mathrm {Card}(\mathfrak {m}_{a,p})$
for this p.
$\mathrm {Card}(\mathfrak {m}') \le \mathrm {Card}(\mathfrak {m}_{a,p})$
for this p.
Thus, we obtain an equality
which completes the proof.
Now we can prove Proposition 2.7.
Proof of Proposition 2.7
We prove the claim by induction on
![]() $l(\mathfrak {m})$
.
$l(\mathfrak {m})$
.
Let
![]() $(V,N)$
,
$(V,N)$
,
![]() $(V_1,N_1)$
and
$(V_1,N_1)$
and
![]() $(V_2,N_2)$
be the
$(V_2,N_2)$
be the
![]() $VN$
-pairs corresponding to the multisegments
$VN$
-pairs corresponding to the multisegments
![]() $\mathfrak {m}$
,
$\mathfrak {m}$
,
![]() $\mathfrak {m}_{\mathrm {max}}$
and
$\mathfrak {m}_{\mathrm {max}}$
and
![]() $\mathfrak {m}^{\mathrm {max}}$
, respectively. Let us consider the sets
$\mathfrak {m}^{\mathrm {max}}$
, respectively. Let us consider the sets
![]() $S(V,N)$
,
$S(V,N)$
,
![]() $S(V_1,N_1)$
and
$S(V_1,N_1)$
and
![]() $S(V_2,N_2)$
introduced in Section 3.1. Let us choose sufficiently general
$S(V_2,N_2)$
introduced in Section 3.1. Let us choose sufficiently general
![]() $L \in S(V,N)$
,
$L \in S(V,N)$
,
![]() $L_1 \in S(V_1,N_1)$
and
$L_1 \in S(V_1,N_1)$
and
![]() $L_2 \in S(V_2,N_2)$
. Then the six multisegments
$L_2 \in S(V_2,N_2)$
. Then the six multisegments
![]() $\mathfrak {m}^{\mathrm {ram}}$
,
$\mathfrak {m}^{\mathrm {ram}}$
,
![]() $(\mathfrak {m}^{-})^{\mathrm {ram}}$
,
$(\mathfrak {m}^{-})^{\mathrm {ram}}$
,
![]() $(\mathfrak {m}_{\mathrm {max}})^{\mathrm {ram}}$
,
$(\mathfrak {m}_{\mathrm {max}})^{\mathrm {ram}}$
,
![]() $((\mathfrak {m}_{\mathrm {max}})^{-})^{\mathrm {ram}}$
,
$((\mathfrak {m}_{\mathrm {max}})^{-})^{\mathrm {ram}}$
,
![]() $(\mathfrak {m}^{\mathrm {max}})^{\mathrm {ram}}$
and
$(\mathfrak {m}^{\mathrm {max}})^{\mathrm {ram}}$
and
![]() $((\mathfrak {m}^{\mathrm {max}})^{-})^{\mathrm {ram}}$
correspond to the pairs
$((\mathfrak {m}^{\mathrm {max}})^{-})^{\mathrm {ram}}$
correspond to the pairs
![]() $(\mathrm {Image}\, L, N|_{\mathrm {Image}\, L})$
,
$(\mathrm {Image}\, L, N|_{\mathrm {Image}\, L})$
,
![]() $(\mathrm {Image}\, L\circ N, N|_{\mathrm {Image}\, L \circ N})(-1)$
,
$(\mathrm {Image}\, L\circ N, N|_{\mathrm {Image}\, L \circ N})(-1)$
,
![]() $(\mathrm {Image}\, L_1, N_1|_{\mathrm {Image}\, L_1})$
,
$(\mathrm {Image}\, L_1, N_1|_{\mathrm {Image}\, L_1})$
,
![]() $(\mathrm {Image}\, L_1\circ N_1, N_1|_{\mathrm {Image}\, L_1 \circ N_1})(-1)$
,
$(\mathrm {Image}\, L_1\circ N_1, N_1|_{\mathrm {Image}\, L_1 \circ N_1})(-1)$
,
![]() $(\mathrm {Image}\, L_2, N_2|_{\mathrm {Image}\, L_2})$
and
$(\mathrm {Image}\, L_2, N_2|_{\mathrm {Image}\, L_2})$
and
![]() $(\mathrm {Image}\, L_2\circ N_2, N_2|_{\mathrm {Image}\, L_2 \circ N_2})(-1)$
, respectively.
$(\mathrm {Image}\, L_2\circ N_2, N_2|_{\mathrm {Image}\, L_2 \circ N_2})(-1)$
, respectively.
To prove the claim, it suffices to show that the pair
![]() $(\mathrm {Image}\, L, N|_{\mathrm {Image}\, L})$
is isomorphic to the pair
$(\mathrm {Image}\, L, N|_{\mathrm {Image}\, L})$
is isomorphic to the pair
![]() $(\mathrm {Image}\, L_1 \oplus \mathrm {Image}\, L_2, N_1|_{\mathrm {Image}\, L_1} \oplus N_2|_{\mathrm {Image}\, L_2})$
. By the inductive hypothesis, the claim is true for the multisegment
$(\mathrm {Image}\, L_1 \oplus \mathrm {Image}\, L_2, N_1|_{\mathrm {Image}\, L_1} \oplus N_2|_{\mathrm {Image}\, L_2})$
. By the inductive hypothesis, the claim is true for the multisegment
![]() $\mathfrak {m}^{-}$
. Hence it follows from Lemma 3.6 that
$\mathfrak {m}^{-}$
. Hence it follows from Lemma 3.6 that
Hence by Lemma 3.1, it suffices to show that the graded vector space
![]() $\mathrm {Image}\, L$
is isomorphic to the graded vector space
$\mathrm {Image}\, L$
is isomorphic to the graded vector space
![]() $\mathrm {Image}\, L_1 \oplus \mathrm {Image}\, L_2$
.
$\mathrm {Image}\, L_1 \oplus \mathrm {Image}\, L_2$
.
Let
![]() $\mathfrak {m}_a$
and
$\mathfrak {m}_a$
and
![]() $\mathfrak {m}^{\sharp }_{(a)}$
be as in Proposition 3.7. Note that the dimension of the degree-a-part of
$\mathfrak {m}^{\sharp }_{(a)}$
be as in Proposition 3.7. Note that the dimension of the degree-a-part of
![]() $\mathrm {Image}\, L$
is equal to
$\mathrm {Image}\, L$
is equal to
![]() $\mathrm {Card}(\mathfrak {m}^{\sharp }_{(a)})$
. Let
$\mathrm {Card}(\mathfrak {m}^{\sharp }_{(a)})$
. Let
![]() $\mathfrak {m}'$
be a totally ordered full-sub-multisegment of
$\mathfrak {m}'$
be a totally ordered full-sub-multisegment of
![]() $\mathfrak {m}_a$
with the maximum cardinality. When
$\mathfrak {m}_a$
with the maximum cardinality. When
![]() $\mathfrak {m}_a$
is nonempty, the maximal segment
$\mathfrak {m}_a$
is nonempty, the maximal segment
![]() $\Delta _1$
of
$\Delta _1$
of
![]() $\mathfrak {m}'$
must belong to
$\mathfrak {m}'$
must belong to
![]() $\mathfrak {m}_{\mathrm {max}}$
, since otherwise one can find a totally ordered full-sub-multisegment of
$\mathfrak {m}_{\mathrm {max}}$
, since otherwise one can find a totally ordered full-sub-multisegment of
![]() $\mathfrak {m}_a$
that strictly contains
$\mathfrak {m}_a$
that strictly contains
![]() $\mathfrak {m}'$
by adding to
$\mathfrak {m}'$
by adding to
![]() $\mathfrak {m}'$
a segment of
$\mathfrak {m}'$
a segment of
![]() $\mathfrak {m}_{\mathrm {max}}$
that contains
$\mathfrak {m}_{\mathrm {max}}$
that contains
![]() $\Delta _1$
, which is a contradiction. It is then easy to see that
$\Delta _1$
, which is a contradiction. It is then easy to see that
-
• when
 $\mathfrak {m}_a$
is nonempty,
$\mathfrak {m}_a$
is nonempty,
 $\mathfrak {m}' - \Delta _1$
is a totally ordered full-sub-multisegment of
$\mathfrak {m}' - \Delta _1$
is a totally ordered full-sub-multisegment of
 $(\mathfrak {m}^{\mathrm {max}})_a$
with the maximum cardinality; and
$(\mathfrak {m}^{\mathrm {max}})_a$
with the maximum cardinality; and -
•
 $\Delta _1$
, which is regarded as a multisegment with
$\Delta _1$
, which is regarded as a multisegment with
 $\mathrm {Card}(\Delta _1) = 1$
, is a totally ordered full-sub-multisegment of
$\mathrm {Card}(\Delta _1) = 1$
, is a totally ordered full-sub-multisegment of
 $(\mathfrak {m}_{\mathrm {max}})_a$
with the maximum cardinality.
$(\mathfrak {m}_{\mathrm {max}})_a$
with the maximum cardinality.
Thus, it follows from Proposition 3.7 that the dimension of the degree-a-part of
![]() $\mathrm {Image}\, L$
is equal to the sum of those of
$\mathrm {Image}\, L$
is equal to the sum of those of
![]() $\mathrm {Image}\, L_1$
and
$\mathrm {Image}\, L_1$
and
![]() $\mathrm {Image}\, L_2$
, as desired.
$\mathrm {Image}\, L_2$
, as desired.
4 Preliminaries on
 $\mathfrak {o}$
-modules
$\mathfrak {o}$
-modules
To prove our main theorems, we prepare some results on
![]() $\mathfrak {o}$
-modules in this section.
$\mathfrak {o}$
-modules in this section.
4.1 On
 $\mathfrak {o}$
-modules of finite length
$\mathfrak {o}$
-modules of finite length
In this subsection, we introduce some terminologies on
![]() $\mathfrak {o}$
-modules and give two basic results (Propositions 4.4, 4.6), which we call convexity and uniqueness, respectively. The authors suspect that these two results are well-known to some experts. In fact, one can deduce them from the description of Hall polynomials given in [Reference Macdonald25, II, (4.3)] in terms of sequences of partitions related with the Littlewood–Richardson rule. However, for the sake of completeness, we do not omit the proof of these results, which the authors believe to be helpful for most readers.
$\mathfrak {o}$
-modules and give two basic results (Propositions 4.4, 4.6), which we call convexity and uniqueness, respectively. The authors suspect that these two results are well-known to some experts. In fact, one can deduce them from the description of Hall polynomials given in [Reference Macdonald25, II, (4.3)] in terms of sequences of partitions related with the Littlewood–Richardson rule. However, for the sake of completeness, we do not omit the proof of these results, which the authors believe to be helpful for most readers.
Let
![]() $|\mathcal {C}|$
denote the set of isomorphism classes of
$|\mathcal {C}|$
denote the set of isomorphism classes of
![]() $\mathfrak {o}$
-modules of finite length. For an
$\mathfrak {o}$
-modules of finite length. For an
![]() $\mathfrak {o}$
-module M of finite length, we denote by
$\mathfrak {o}$
-module M of finite length, we denote by
![]() $[M] \in |\mathcal {C}|$
its isomorphism class.
$[M] \in |\mathcal {C}|$
its isomorphism class.
For an integer
![]() $n \geq 1$
, let
$n \geq 1$
, let
![]() $|\mathcal {C}^n| \subset |\mathcal {C}|$
denote the subset of isomorphism classes
$|\mathcal {C}^n| \subset |\mathcal {C}|$
denote the subset of isomorphism classes
![]() $[M]$
such that M is generated by at most n elements. We denote by
$[M]$
such that M is generated by at most n elements. We denote by
![]() $\iota _n \colon |\mathcal {C}^n| \hookrightarrow |\mathcal {C}^{n+1}|$
the inclusion map.
$\iota _n \colon |\mathcal {C}^n| \hookrightarrow |\mathcal {C}^{n+1}|$
the inclusion map.
Recall that
![]() $\Lambda _n$
is the set of n-tuples
$\Lambda _n$
is the set of n-tuples
![]() $(\lambda _1,\ldots ,\lambda _n)$
of integers satisfying
$(\lambda _1,\ldots ,\lambda _n)$
of integers satisfying
![]() $0 \leq \lambda _1 \leq \cdots \leq \lambda _n$
. For
$0 \leq \lambda _1 \leq \cdots \leq \lambda _n$
. For
![]() $[M] \in |\mathcal {C}^n|$
, there exists a unique element
$[M] \in |\mathcal {C}^n|$
, there exists a unique element
![]() $(\lambda _1,\ldots ,\lambda _n)$
of
$(\lambda _1,\ldots ,\lambda _n)$
of
![]() $\Lambda _n$
such that the
$\Lambda _n$
such that the
![]() $\mathfrak {o}$
-module M is isomorphic to
$\mathfrak {o}$
-module M is isomorphic to
By sending
![]() $[M]$
to the n-tuple
$[M]$
to the n-tuple
![]() $(\lambda _1,\ldots ,\lambda _n)$
, we obtain a bijective map
$(\lambda _1,\ldots ,\lambda _n)$
, we obtain a bijective map
![]() $\mathrm {seq}_n \colon |\mathcal {C}^n| \to \Lambda _n$
. We denote by
$\mathrm {seq}_n \colon |\mathcal {C}^n| \to \Lambda _n$
. We denote by
![]() $\jmath _n \colon \Lambda _n \to \Lambda _{n+1}$
the injective map that sends
$\jmath _n \colon \Lambda _n \to \Lambda _{n+1}$
the injective map that sends
![]() $(\lambda _1,\ldots , \lambda _n)$
to
$(\lambda _1,\ldots , \lambda _n)$
to
![]() $(0,\lambda _1,\ldots ,\lambda _n)$
. Then the diagram
$(0,\lambda _1,\ldots ,\lambda _n)$
. Then the diagram
is commutative.
For two elements
![]() $[M], [M'] \in |\mathcal {C}^n|$
, we write
$[M], [M'] \in |\mathcal {C}^n|$
, we write
![]() $[M] \leq [M']$
if
$[M] \leq [M']$
if
![]() $\mathrm {seq}_n([M]) \leq \mathrm {seq}_n([M'])$
with respect to the lexicographic order on
$\mathrm {seq}_n([M]) \leq \mathrm {seq}_n([M'])$
with respect to the lexicographic order on
![]() $\Lambda _n$
. This gives a total order on the set
$\Lambda _n$
. This gives a total order on the set
![]() $|\mathcal {C}^n|$
. The map
$|\mathcal {C}^n|$
. The map
![]() $\iota _n$
is compatible with the total orders on
$\iota _n$
is compatible with the total orders on
![]() $|\mathcal {C}^n|$
and on
$|\mathcal {C}^n|$
and on
![]() $|\mathcal {C}^{n+1}|$
since the map
$|\mathcal {C}^{n+1}|$
since the map
![]() $\jmath _n$
is compatible with the lexicographic orders on
$\jmath _n$
is compatible with the lexicographic orders on
![]() $\Lambda _n$
and on
$\Lambda _n$
and on
![]() $\Lambda _{n+1}$
. Hence the total orders on
$\Lambda _{n+1}$
. Hence the total orders on
![]() $|\mathcal {C}^n|$
for all n induce a total order
$|\mathcal {C}^n|$
for all n induce a total order
![]() $\leq $
on the set
$\leq $
on the set
![]() $|\mathcal {C}|$
.
$|\mathcal {C}|$
.
We regard
![]() $\Lambda _n$
as a subset of
$\Lambda _n$
as a subset of
![]() $\mathbb {Z}^n$
. Then
$\mathbb {Z}^n$
. Then
![]() $\Lambda _n$
is closed under the addition
$\Lambda _n$
is closed under the addition
![]() $+$
on
$+$
on
![]() $\mathbb {Z}^{n}$
and becomes a commutative submonoid of
$\mathbb {Z}^{n}$
and becomes a commutative submonoid of
![]() $\mathbb {Z}^n$
with the addition
$\mathbb {Z}^n$
with the addition
![]() $+$
. For two elements
$+$
. For two elements
![]() $[M], [M'] \in |\mathcal {C}^n|$
, we denote by
$[M], [M'] \in |\mathcal {C}^n|$
, we denote by
![]() $[M] \vee [M']$
the unique element of
$[M] \vee [M']$
the unique element of
![]() $|\mathcal {C}^n|$
whose image under
$|\mathcal {C}^n|$
whose image under
![]() $\mathrm {seq}_n$
is equal to
$\mathrm {seq}_n$
is equal to
![]() $\mathrm {seq}_n([M]) + \mathrm {seq}_n([M'])$
. Then the set
$\mathrm {seq}_n([M]) + \mathrm {seq}_n([M'])$
. Then the set
![]() $|\mathcal {C}^n|$
becomes a commutative monoid with the operation
$|\mathcal {C}^n|$
becomes a commutative monoid with the operation
![]() $\vee $
and the diagram
$\vee $
and the diagram
is commutative. The map
![]() $\iota _n$
is compatible with the monoid structures on
$\iota _n$
is compatible with the monoid structures on
![]() $|\mathcal {C}^n|$
and
$|\mathcal {C}^n|$
and
![]() $|\mathcal {C}^{n+1}|$
since the map
$|\mathcal {C}^{n+1}|$
since the map
![]() $\jmath _n$
is compatible with the addition
$\jmath _n$
is compatible with the addition
![]() $+$
. Hence the binary operations
$+$
. Hence the binary operations
![]() $\vee $
on
$\vee $
on
![]() $|\mathcal {C}^n|$
for all n induce a binary operation on the set
$|\mathcal {C}^n|$
for all n induce a binary operation on the set
![]() $|\mathcal {C}|$
, also denoted by
$|\mathcal {C}|$
, also denoted by
![]() $\vee $
. This gives a structure of a commutative monoid on the set
$\vee $
. This gives a structure of a commutative monoid on the set
![]() $|\mathcal {C}|$
.
$|\mathcal {C}|$
.
The following lemma says that the total order
![]() $\leq $
on
$\leq $
on
![]() $|\mathcal {C}|$
is compatible with the monoid structure on
$|\mathcal {C}|$
is compatible with the monoid structure on
![]() $|\mathcal {C}|$
.
$|\mathcal {C}|$
.
Lemma 4.1. Let
![]() $[M], [M'], [N], [N'] \in |\mathcal {C}|$
and suppose that
$[M], [M'], [N], [N'] \in |\mathcal {C}|$
and suppose that
![]() $[M] \leq [N]$
and
$[M] \leq [N]$
and
![]() $[M'] \leq [N']$
. Then we have
$[M'] \leq [N']$
. Then we have
![]() $[M] \vee [M'] \leq [N] \vee [N']$
.
$[M] \vee [M'] \leq [N] \vee [N']$
.
Proof. We can easily see that the lexicographic order on
![]() $\Lambda _n$
is compatible with the monoid structure on
$\Lambda _n$
is compatible with the monoid structure on
![]() $\Lambda _n$
given by
$\Lambda _n$
given by
![]() $+$
. Hence the claim follows.
$+$
. Hence the claim follows.
Recall that F is the field of fractions of
![]() $\mathfrak {o}$
. For an
$\mathfrak {o}$
. For an
![]() $\mathfrak {o}$
-module M of finite length, we let
$\mathfrak {o}$
-module M of finite length, we let
![]() $M^{\vee }$
denote the
$M^{\vee }$
denote the
![]() $\mathfrak {o}$
-module
$\mathfrak {o}$
-module
![]() $\mathrm {Hom}_{\mathfrak {o}}(M,F/\mathfrak {o})$
.
$\mathrm {Hom}_{\mathfrak {o}}(M,F/\mathfrak {o})$
.
Lemma 4.2. For any
![]() $\mathfrak {o}$
-module M of finite length, we have
$\mathfrak {o}$
-module M of finite length, we have
![]() $[M] = [M^{\vee }]$
.
$[M] = [M^{\vee }]$
.
Proof. We may assume
![]() $M= \mathfrak {o}/\mathfrak {p}^{\lambda _1} \oplus \cdots \oplus \mathfrak {o}/\mathfrak {p}^{\lambda _n}$
. Since
$M= \mathfrak {o}/\mathfrak {p}^{\lambda _1} \oplus \cdots \oplus \mathfrak {o}/\mathfrak {p}^{\lambda _n}$
. Since
![]() $(\ )^{\vee }$
commutes with finite direct sums, we may further assume that
$(\ )^{\vee }$
commutes with finite direct sums, we may further assume that
![]() $M = \mathfrak {o}/\mathfrak {p}^{\lambda }$
. Then we have
$M = \mathfrak {o}/\mathfrak {p}^{\lambda }$
. Then we have
![]() $M^{\vee } \cong \mathfrak {p}^{-\lambda }/\mathfrak {o}$
. Hence by choosing a uniformiser
$M^{\vee } \cong \mathfrak {p}^{-\lambda }/\mathfrak {o}$
. Hence by choosing a uniformiser
![]() $\varpi \in \mathfrak {p}$
, we obtain a desired isomorphism
$\varpi \in \mathfrak {p}$
, we obtain a desired isomorphism
![]() $M \cong M^{\vee }$
.
$M \cong M^{\vee }$
.
Lemma 4.3. Let
![]() $M, M'$
be
$M, M'$
be
![]() $\mathfrak {o}$
-modules of finite length.
$\mathfrak {o}$
-modules of finite length.
-
(1) If there exists an injective homomorphism
 $M' \hookrightarrow M$
, then we have
$M' \hookrightarrow M$
, then we have
 $[M'] \leq [M]$
.
$[M'] \leq [M]$
. -
(2) If there exists a surjective homomorphism
 $M \twoheadrightarrow M'$
, then we have
$M \twoheadrightarrow M'$
, then we have
 $[M'] \leq [M]$
.
$[M'] \leq [M]$
.
Proof. Since an injective homomorphism
![]() $M' \hookrightarrow M$
induces a surjective homomorphism
$M' \hookrightarrow M$
induces a surjective homomorphism
![]() $M^{\vee } \twoheadrightarrow {M'}^{\vee }$
, claim (1) follows from claim (2) and Lemma 4.2. Let us prove claim (2) below.
$M^{\vee } \twoheadrightarrow {M'}^{\vee }$
, claim (1) follows from claim (2) and Lemma 4.2. Let us prove claim (2) below.
Let
![]() $M, M'$
be
$M, M'$
be
![]() $\mathfrak {o}$
-modules of finite length, and suppose that there exists a surjective homomorphism
$\mathfrak {o}$
-modules of finite length, and suppose that there exists a surjective homomorphism
![]() $M \twoheadrightarrow M'$
. Let us take an integer
$M \twoheadrightarrow M'$
. Let us take an integer
![]() $n \geq 1$
such that both
$n \geq 1$
such that both
![]() $[M]$
and
$[M]$
and
![]() $[M']$
belong to
$[M']$
belong to
![]() $|\mathcal {C}^n|$
. We prove the claim by induction on n. If
$|\mathcal {C}^n|$
. We prove the claim by induction on n. If
![]() $n=1$
, then the claim is clear. We assume
$n=1$
, then the claim is clear. We assume
![]() $n>1$
. Let us write
$n>1$
. Let us write
![]() $\mathrm {seq}_n([M])=(\lambda _1,\ldots ,\lambda _n)$
and
$\mathrm {seq}_n([M])=(\lambda _1,\ldots ,\lambda _n)$
and
![]() $\mathrm {seq}_n([M'])=(\lambda ^{\prime }_1,\ldots ,\lambda ^{\prime }_n)$
.
$\mathrm {seq}_n([M'])=(\lambda ^{\prime }_1,\ldots ,\lambda ^{\prime }_n)$
.
First, suppose that
![]() $\lambda _1> \lambda ^{\prime }_1$
. Then we have
$\lambda _1> \lambda ^{\prime }_1$
. Then we have
![]() $[M'] < [M]$
as claimed. Next, suppose that
$[M'] < [M]$
as claimed. Next, suppose that
![]() $\lambda _1 = \lambda ^{\prime }_1$
. Then both
$\lambda _1 = \lambda ^{\prime }_1$
. Then both
![]() $M/\mathfrak {p}^{\lambda _1} M$
and
$M/\mathfrak {p}^{\lambda _1} M$
and
![]() $M'/\mathfrak {p}^{\lambda _1} M'$
are isomorphic to
$M'/\mathfrak {p}^{\lambda _1} M'$
are isomorphic to
![]() $(\mathfrak {o}/\mathfrak {p}^{\lambda _1})^{\oplus n}$
, and we have
$(\mathfrak {o}/\mathfrak {p}^{\lambda _1})^{\oplus n}$
, and we have
![]() $[M] = [\mathfrak {p}^{\lambda _1} M] \vee [(\mathfrak {o}/\mathfrak {p}^{\lambda _1})^{\oplus n}]$
and
$[M] = [\mathfrak {p}^{\lambda _1} M] \vee [(\mathfrak {o}/\mathfrak {p}^{\lambda _1})^{\oplus n}]$
and
![]() $[M'] = [\mathfrak {p}^{\lambda _1} M'] \vee [(\mathfrak {o}/\mathfrak {p}^{\lambda _1})^{\oplus n}]$
. Note that the surjective homomorphism
$[M'] = [\mathfrak {p}^{\lambda _1} M'] \vee [(\mathfrak {o}/\mathfrak {p}^{\lambda _1})^{\oplus n}]$
. Note that the surjective homomorphism
![]() $M \twoheadrightarrow M'$
induces a surjective homomorphism
$M \twoheadrightarrow M'$
induces a surjective homomorphism
![]() $\mathfrak {p}^{\lambda _1} M \twoheadrightarrow \mathfrak {p}^{\lambda _1} M'$
. Hence by Lemma 4.1, we are reduced to proving claim (2) for
$\mathfrak {p}^{\lambda _1} M \twoheadrightarrow \mathfrak {p}^{\lambda _1} M'$
. Hence by Lemma 4.1, we are reduced to proving claim (2) for
![]() $\mathfrak {p}^{\lambda _1} M$
and
$\mathfrak {p}^{\lambda _1} M$
and
![]() $\mathfrak {p}^{\lambda _1} M'$
. Since both
$\mathfrak {p}^{\lambda _1} M'$
. Since both
![]() $[\mathfrak {p}^{\lambda _1} M]$
and
$[\mathfrak {p}^{\lambda _1} M]$
and
![]() $[\mathfrak {p}^{\lambda _1} M']$
belong to
$[\mathfrak {p}^{\lambda _1} M']$
belong to
![]() $|\mathcal {C}^{n-1}|$
, the inductive hypothesis proves the claim in the case where
$|\mathcal {C}^{n-1}|$
, the inductive hypothesis proves the claim in the case where
![]() $\lambda _1 = \lambda ^{\prime }_1$
.
$\lambda _1 = \lambda ^{\prime }_1$
.
Finally, suppose that
![]() $\lambda _1 < \lambda ^{\prime }_1$
. Again in this case, the surjective homomorphism
$\lambda _1 < \lambda ^{\prime }_1$
. Again in this case, the surjective homomorphism
![]() $M \twoheadrightarrow M'$
induces a surjective homomorphism
$M \twoheadrightarrow M'$
induces a surjective homomorphism
![]() $\mathfrak {p}^{\lambda _1} M \twoheadrightarrow \mathfrak {p}^{\lambda _1} M'$
. Note that
$\mathfrak {p}^{\lambda _1} M \twoheadrightarrow \mathfrak {p}^{\lambda _1} M'$
. Note that
![]() $\mathfrak {p}^{\lambda _1} M$
is generated by fewer than n elements, whereas the minimum number of generators of
$\mathfrak {p}^{\lambda _1} M$
is generated by fewer than n elements, whereas the minimum number of generators of
![]() $\mathfrak {p}^{\lambda _1} M'$
is equal to n. This leads to a contradiction.
$\mathfrak {p}^{\lambda _1} M'$
is equal to n. This leads to a contradiction.
Proposition 4.4 (Convexity)
Let
be a short exact sequence of
![]() $\mathfrak {o}$
-modules of finite length. Then we have the inequality
$\mathfrak {o}$
-modules of finite length. Then we have the inequality
Proof. Let n,
![]() $n'$
and
$n'$
and
![]() $n"$
denote the minimal numbers of generators of the
$n"$
denote the minimal numbers of generators of the
![]() $\mathfrak {o}$
-modules M,
$\mathfrak {o}$
-modules M,
![]() $M'$
and
$M'$
and
![]() $M"$
, respectively. We prove the claim by induction on
$M"$
, respectively. We prove the claim by induction on
![]() $n'+n"$
.
$n'+n"$
.
If
![]() $n'+n"=0$
, then we have
$n'+n"=0$
, then we have
![]() $M'=M"=0$
, and the claim is clear. Since
$M'=M"=0$
, and the claim is clear. Since
![]() $M \to M"$
and
$M \to M"$
and
![]() $M^{\vee } \to M^{\prime \vee }$
are surjective, we have
$M^{\vee } \to M^{\prime \vee }$
are surjective, we have
![]() $n \geq n"$
and
$n \geq n"$
and
![]() $n \geq n'$
. If
$n \geq n'$
. If
![]() $n> \max \{n',n"\}$
, then the claim is obvious. Hence we may assume that
$n> \max \{n',n"\}$
, then the claim is obvious. Hence we may assume that
![]() $n=\max \{n',n"\}$
. By considering the short exact sequence
$n=\max \{n',n"\}$
. By considering the short exact sequence
instead of equation (4.1), if necessary, we may further assume that
![]() $n=n"$
. Let us write
$n=n"$
. Let us write
![]() $\mathrm {seq}_n(M")=(\lambda ^{\prime \prime }_1,\ldots ,\lambda ^{\prime \prime }_n)$
and
$\mathrm {seq}_n(M")=(\lambda ^{\prime \prime }_1,\ldots ,\lambda ^{\prime \prime }_n)$
and
![]() $I = \mathfrak {p}^{\lambda ^{\prime \prime }_1}$
. Then both
$I = \mathfrak {p}^{\lambda ^{\prime \prime }_1}$
. Then both
![]() $M/I M$
and
$M/I M$
and
![]() $M"/I M"$
are isomorphic to
$M"/I M"$
are isomorphic to
![]() $(\mathfrak {o}/I)^{\oplus n}$
, and we have
$(\mathfrak {o}/I)^{\oplus n}$
, and we have
![]() $[M]=[I M] \vee [(\mathfrak {o}/I)^{\oplus n}]$
and
$[M]=[I M] \vee [(\mathfrak {o}/I)^{\oplus n}]$
and
![]() $[M"]=[I M"] \vee [(\mathfrak {o}/I)^{\oplus n}]$
. Moreover, equation (4.1) induces a short exact sequence
$[M"]=[I M"] \vee [(\mathfrak {o}/I)^{\oplus n}]$
. Moreover, equation (4.1) induces a short exact sequence
Since
![]() $\mathrm {seq}_n(IM")=(0,\lambda ^{\prime \prime }_2-\lambda ^{\prime \prime }_1,\ldots ,\lambda ^{\prime \prime }_n-\lambda ^{\prime \prime }_1)$
, the minimal number of generators of
$\mathrm {seq}_n(IM")=(0,\lambda ^{\prime \prime }_2-\lambda ^{\prime \prime }_1,\ldots ,\lambda ^{\prime \prime }_n-\lambda ^{\prime \prime }_1)$
, the minimal number of generators of
![]() $IM"$
is strictly smaller than
$IM"$
is strictly smaller than
![]() $n"$
. Hence, by induction, we have
$n"$
. Hence, by induction, we have
![]() $[IM] \geq [M'] \vee [IM"]$
. By adding
$[IM] \geq [M'] \vee [IM"]$
. By adding
![]() $[(\mathfrak {o}/I)^{\oplus n}]$
to both sides and using Lemma 4.1, we obtain the desired inequality.
$[(\mathfrak {o}/I)^{\oplus n}]$
to both sides and using Lemma 4.1, we obtain the desired inequality.
Lemma 4.5. Let M be an
![]() $\mathfrak {o}$
-module of finite length. Then for any nonzero ideal
$\mathfrak {o}$
-module of finite length. Then for any nonzero ideal
![]() $I \subset \mathfrak {o}$
, we have
$I \subset \mathfrak {o}$
, we have
![]() $[M] = [IM] \vee [M/IM]$
.
$[M] = [IM] \vee [M/IM]$
.
Proof. Let us write
![]() $I = \mathfrak {p}^{\lambda }$
. Let us choose a positive integer n such that
$I = \mathfrak {p}^{\lambda }$
. Let us choose a positive integer n such that
![]() $[M] \in |\mathcal {C}^n|$
. Let us write
$[M] \in |\mathcal {C}^n|$
. Let us write
![]() $\mathrm {seq}_n([M]) = (\lambda _1,\ldots ,\lambda _n)$
. For
$\mathrm {seq}_n([M]) = (\lambda _1,\ldots ,\lambda _n)$
. For
![]() $i=1,\ldots ,n$
, set
$i=1,\ldots ,n$
, set
![]() $\lambda ^{\prime \prime }_i = \min \{\lambda ,\lambda _i\}$
. Then
$\lambda ^{\prime \prime }_i = \min \{\lambda ,\lambda _i\}$
. Then
![]() $M/IM$
is isomorphic to
$M/IM$
is isomorphic to
![]() $\bigoplus _{i=1}^n\mathfrak {o}/\mathfrak {p}^{\lambda ^{\prime \prime }_i}$
and
$\bigoplus _{i=1}^n\mathfrak {o}/\mathfrak {p}^{\lambda ^{\prime \prime }_i}$
and
![]() $IM$
is isomorphic to
$IM$
is isomorphic to
![]() $\bigoplus _{i=1}^n \mathfrak {p}^{\lambda ^{\prime \prime }_i}/\mathfrak {p}^{\lambda _i}$
. Thus, we have
$\bigoplus _{i=1}^n \mathfrak {p}^{\lambda ^{\prime \prime }_i}/\mathfrak {p}^{\lambda _i}$
. Thus, we have
![]() $[M]=[IM]\vee [M/IM]$
, as desired.
$[M]=[IM]\vee [M/IM]$
, as desired.
Proposition 4.6 (Uniqueness)
Suppose that
![]() $[M], [M'], [M"] \in |\mathcal {C}|$
satisfy
$[M], [M'], [M"] \in |\mathcal {C}|$
satisfy
![]() $[M] = [M'] \vee [M"]$
. Then there exists a unique
$[M] = [M'] \vee [M"]$
. Then there exists a unique
![]() $\mathfrak {o}$
-submodule
$\mathfrak {o}$
-submodule
![]() $N \subset M$
satisfying
$N \subset M$
satisfying
![]() $[N] = [M']$
and
$[N] = [M']$
and
![]() $[M/N] = [M"]$
. Moreover, for any
$[M/N] = [M"]$
. Moreover, for any
![]() $\mathfrak {o}$
-submodule
$\mathfrak {o}$
-submodule
![]() $N' \subset M$
other than N, we have either
$N' \subset M$
other than N, we have either
![]() $[N'] < [M']$
or
$[N'] < [M']$
or
![]() $[M/N'] < [M"]$
.
$[M/N'] < [M"]$
.
Proof. First, we prove the existence and uniqueness of N. Let n,
![]() $n'$
and
$n'$
and
![]() $n"$
denote the minimal numbers of generators of the
$n"$
denote the minimal numbers of generators of the
![]() $\mathfrak {o}$
-modules M,
$\mathfrak {o}$
-modules M,
![]() $M'$
and
$M'$
and
![]() $M"$
, respectively. We prove the claim by induction on
$M"$
, respectively. We prove the claim by induction on
![]() $n'+n"$
.
$n'+n"$
.
If
![]() $n'+n"=0$
, then we have
$n'+n"=0$
, then we have
![]() $M=M'=M"=0$
, and the claim is obvious. The relation
$M=M'=M"=0$
, and the claim is obvious. The relation
![]() $[M]=[M']\vee [M"]$
implies that
$[M]=[M']\vee [M"]$
implies that
![]() $n=\max \{n',n"\}$
. By considering
$n=\max \{n',n"\}$
. By considering
![]() $M^{\vee }$
instead of M if necessary, we may assume that
$M^{\vee }$
instead of M if necessary, we may assume that
![]() $n=n"$
. Let us write
$n=n"$
. Let us write
![]() $\mathrm {seq}_n(M")=(\lambda ^{\prime \prime }_1,\ldots ,\lambda ^{\prime \prime }_n)$
and
$\mathrm {seq}_n(M")=(\lambda ^{\prime \prime }_1,\ldots ,\lambda ^{\prime \prime }_n)$
and
![]() $I = \mathfrak {p}^{\lambda ^{\prime \prime }_1}$
. Then for any
$I = \mathfrak {p}^{\lambda ^{\prime \prime }_1}$
. Then for any
![]() $\mathfrak {o}$
-submodule
$\mathfrak {o}$
-submodule
![]() $N \subset M$
satisfying
$N \subset M$
satisfying
![]() $[M/N]=[M"]$
, we have
$[M/N]=[M"]$
, we have
![]() $N \subset IM$
. Since
$N \subset IM$
. Since
![]() $\mathrm {seq}_n(IM")=(0,\lambda ^{\prime \prime }_2-\lambda ^{\prime \prime }_1,\ldots ,\lambda ^{\prime \prime }_n-\lambda ^{\prime \prime }_1)$
, the minimal number of generators of
$\mathrm {seq}_n(IM")=(0,\lambda ^{\prime \prime }_2-\lambda ^{\prime \prime }_1,\ldots ,\lambda ^{\prime \prime }_n-\lambda ^{\prime \prime }_1)$
, the minimal number of generators of
![]() $IM"$
is strictly smaller than
$IM"$
is strictly smaller than
![]() $n"$
. Hence, by induction, there exists a unique
$n"$
. Hence, by induction, there exists a unique
![]() $\mathfrak {o}$
-submodule
$\mathfrak {o}$
-submodule
![]() $N \subset IM$
satisfying
$N \subset IM$
satisfying
![]() $[N] = [M']$
and
$[N] = [M']$
and
![]() $[IM/N]=[IM"]$
. Since N is contained in
$[IM/N]=[IM"]$
. Since N is contained in
![]() $IM$
, the
$IM$
, the
![]() $\mathfrak {o}$
-module
$\mathfrak {o}$
-module
![]() $I(M/N)$
is isomorphic to
$I(M/N)$
is isomorphic to
![]() $IM/N$
, and hence
$IM/N$
, and hence
![]() $(M/N)/I(M/N)$
is isomorphic to
$(M/N)/I(M/N)$
is isomorphic to
![]() $M/IM$
. It follows from Lemma 4.5 that we have
$M/IM$
. It follows from Lemma 4.5 that we have
![]() $[M/N] = [IM/N] \vee [M/IM] = [M"]$
. Hence the claim follows.
$[M/N] = [IM/N] \vee [M/IM] = [M"]$
. Hence the claim follows.
Finally, let us prove the last assertion of the proposition. Let
![]() $N' \subset M$
be an
$N' \subset M$
be an
![]() $\mathfrak {o}$
-submodule other than N. Suppose that
$\mathfrak {o}$
-submodule other than N. Suppose that
![]() $[N'] \geq [M']$
and
$[N'] \geq [M']$
and
![]() $[M/N'] \geq [M"]$
. Since
$[M/N'] \geq [M"]$
. Since
![]() $N' \neq N$
, we have either
$N' \neq N$
, we have either
![]() $[N']>[M']$
or
$[N']>[M']$
or
![]() $[M/N']> [M"]$
. Hence it follows from Lemma 4.1 and Proposition 4.4 that
$[M/N']> [M"]$
. Hence it follows from Lemma 4.1 and Proposition 4.4 that
which is a contradiction. Hence we have either
![]() $[N'] < [M']$
or
$[N'] < [M']$
or
![]() $[M/N'] < [M"]$
. This completes the proof.
$[M/N'] < [M"]$
. This completes the proof.
Corollary 4.7. Suppose that
![]() $[M], [M_1], \ldots , [M_r] \in |\mathcal {C}|$
satisfy
$[M], [M_1], \ldots , [M_r] \in |\mathcal {C}|$
satisfy
![]() $[M] = [M_1] \vee \cdots \vee [M_r]$
. Then there exists a unique increasing filtration
$[M] = [M_1] \vee \cdots \vee [M_r]$
. Then there exists a unique increasing filtration
of M by
![]() $\mathfrak {o}$
-submodules satisfying
$\mathfrak {o}$
-submodules satisfying
![]() $[M_i]=[\mathrm {Gr}_i^{\mathrm {F}^0} M]$
for
$[M_i]=[\mathrm {Gr}_i^{\mathrm {F}^0} M]$
for
![]() $i=1,\ldots ,r$
, where
$i=1,\ldots ,r$
, where
![]() $\mathrm {Gr}_i^{\mathrm {F}^0} M = \mathrm {F}^0_i M / \mathrm {F}^0_{i-1} M$
. Moreover, for any filtration
$\mathrm {Gr}_i^{\mathrm {F}^0} M = \mathrm {F}^0_i M / \mathrm {F}^0_{i-1} M$
. Moreover, for any filtration
of M by
![]() $\mathfrak {o}$
-submodules other than
$\mathfrak {o}$
-submodules other than
![]() $\mathrm {F}^0_{\bullet } M$
, we have
$\mathrm {F}^0_{\bullet } M$
, we have
![]() $[\mathrm {Gr}_i^{\mathrm {F}} M] < [M_i]$
for some
$[\mathrm {Gr}_i^{\mathrm {F}} M] < [M_i]$
for some
![]() $i \in \{1,\ldots ,r\}$
.
$i \in \{1,\ldots ,r\}$
.
Proof. We prove the existence and uniqueness of
![]() $\mathrm {F}^0_{\bullet }M$
by induction on r. If
$\mathrm {F}^0_{\bullet }M$
by induction on r. If
![]() $r = 1$
, it is obvious. If
$r = 1$
, it is obvious. If
![]() $r> 1$
, set
$r> 1$
, set
![]() $[M'] = [M_1]$
and
$[M'] = [M_1]$
and
![]() $[M"] = [M_2] \vee \dots \vee [M_{r}]$
. By Proposition 4.6, there exists a unique
$[M"] = [M_2] \vee \dots \vee [M_{r}]$
. By Proposition 4.6, there exists a unique
![]() $\mathfrak {o}$
-submodule N of M such that
$\mathfrak {o}$
-submodule N of M such that
![]() $[N] = [M_1]$
and
$[N] = [M_1]$
and
![]() $[M/N] = [M_2] \vee \dots \vee [M_{r}]$
. By the inductive hypothesis, we have a unique filtration
$[M/N] = [M_2] \vee \dots \vee [M_{r}]$
. By the inductive hypothesis, we have a unique filtration
![]() $\mathrm {F}^0_{\bullet }(M/N)$
satisfying the conditions with respect to
$\mathrm {F}^0_{\bullet }(M/N)$
satisfying the conditions with respect to
![]() $[M/N] = [M_2] \vee \dots \vee [M_{r}]$
. By setting
$[M/N] = [M_2] \vee \dots \vee [M_{r}]$
. By setting
![]() $\mathrm {F}^0_{i+1}M$
to be the inverse image of
$\mathrm {F}^0_{i+1}M$
to be the inverse image of
![]() $\mathrm {F}^0_i(M/N)$
for
$\mathrm {F}^0_i(M/N)$
for
![]() $1 \leq i \leq r-1$
, and
$1 \leq i \leq r-1$
, and
![]() $\mathrm {F}^0_{1}M = N$
, we obtain
$\mathrm {F}^0_{1}M = N$
, we obtain
![]() $\mathrm {F}^0_{\bullet }M$
.
$\mathrm {F}^0_{\bullet }M$
.
The last assertion follows from the same argument as in the proof of Proposition 4.6.
4.2 Generators of
 $\mathfrak {o}$
-modules
$\mathfrak {o}$
-modules
Lemma 4.8. Let
![]() $f \colon M \twoheadrightarrow N$
be a surjective homomorphism of
$f \colon M \twoheadrightarrow N$
be a surjective homomorphism of
![]() $\mathfrak {o}$
-modules, and
$\mathfrak {o}$
-modules, and
![]() $M' \subset M$
an
$M' \subset M$
an
![]() $\mathfrak {o}$
-submodule. Let
$\mathfrak {o}$
-submodule. Let
![]() $x \in N$
and
$x \in N$
and
![]() $y \in M/M'$
be elements whose images in
$y \in M/M'$
be elements whose images in
![]() $N/f(M')$
coincide. Then there exists a lift
$N/f(M')$
coincide. Then there exists a lift
![]() $\widetilde {y} \in M$
of y satisfying
$\widetilde {y} \in M$
of y satisfying
![]() $f(\widetilde {y})=x$
.
$f(\widetilde {y})=x$
.
Proof. Let us take an arbitrary lift
![]() $\widetilde {y}' \in M$
of y and set
$\widetilde {y}' \in M$
of y and set
![]() $x'=f(\widetilde {y}')$
. Since the images of x and
$x'=f(\widetilde {y}')$
. Since the images of x and
![]() $x'$
coincide in
$x'$
coincide in
![]() $N/f(M')$
, there exists
$N/f(M')$
, there exists
![]() $z \in M'$
satisfying
$z \in M'$
satisfying
![]() $x-x' = f(z)$
. Then the element
$x-x' = f(z)$
. Then the element
![]() $\widetilde {y} = \widetilde {y'} + z \in M$
has the desired property.
$\widetilde {y} = \widetilde {y'} + z \in M$
has the desired property.
Lemma 4.9. Let N be an
![]() $\mathfrak {o}$
-module of finite length. Let L and
$\mathfrak {o}$
-module of finite length. Let L and
![]() $L'$
be finitely generated free
$L'$
be finitely generated free
![]() $\mathfrak {o}$
-modules of the same rank, and let
$\mathfrak {o}$
-modules of the same rank, and let
![]() $f \colon L \twoheadrightarrow N$
and
$f \colon L \twoheadrightarrow N$
and
![]() $f' \colon L'\twoheadrightarrow N$
be surjective homomorphisms of
$f' \colon L'\twoheadrightarrow N$
be surjective homomorphisms of
![]() $\mathfrak {o}$
-modules. Then there exists an isomorphism
$\mathfrak {o}$
-modules. Then there exists an isomorphism
![]() $\alpha \colon L \xrightarrow {\cong } L'$
of
$\alpha \colon L \xrightarrow {\cong } L'$
of
![]() $\mathfrak {o}$
-modules satisfying
$\mathfrak {o}$
-modules satisfying
![]() $f = f' \circ \alpha $
.
$f = f' \circ \alpha $
.
Proof. Since N is of finite length over a noetherian local ring
![]() $\mathfrak {o}$
, one can take a projective cover
$\mathfrak {o}$
, one can take a projective cover
![]() $\beta \colon P \to N$
of N (see [Reference Anderson and Fuller1, 17.16 Examples (3)]). Then there exist homomorphisms
$\beta \colon P \to N$
of N (see [Reference Anderson and Fuller1, 17.16 Examples (3)]). Then there exist homomorphisms
![]() $\gamma \colon L \to P$
and
$\gamma \colon L \to P$
and
![]() $\gamma ' \colon L' \to P$
satisfying
$\gamma ' \colon L' \to P$
satisfying
![]() $f = \beta \circ \gamma $
and
$f = \beta \circ \gamma $
and
![]() $f' = \beta \circ \gamma '$
. Since projective covers are essential surjections, the homomorphisms
$f' = \beta \circ \gamma '$
. Since projective covers are essential surjections, the homomorphisms
![]() $\gamma $
and
$\gamma $
and
![]() $\gamma '$
are surjective. Hence by the projectivity of P, one can choose a right inverse s and
$\gamma '$
are surjective. Hence by the projectivity of P, one can choose a right inverse s and
![]() $s'$
of
$s'$
of
![]() $\gamma $
and
$\gamma $
and
![]() $\gamma '$
, respectively. Since
$\gamma '$
, respectively. Since
![]() $\mathrm {Ker}\, \gamma $
and
$\mathrm {Ker}\, \gamma $
and
![]() $\mathrm {Ker}\, \gamma '$
are free
$\mathrm {Ker}\, \gamma '$
are free
![]() $\mathfrak {o}$
-modules of the same rank, there exists an isomorphism
$\mathfrak {o}$
-modules of the same rank, there exists an isomorphism
![]() $\alpha ' \colon \mathrm {Ker}\, \gamma \xrightarrow {\cong } \mathrm {Ker}\, \gamma '$
of
$\alpha ' \colon \mathrm {Ker}\, \gamma \xrightarrow {\cong } \mathrm {Ker}\, \gamma '$
of
![]() $\mathfrak {o}$
-modules. By taking the direct sum of
$\mathfrak {o}$
-modules. By taking the direct sum of
![]() $\alpha '$
and the isomorphism
$\alpha '$
and the isomorphism
![]() $s(P) \xrightarrow {\cong } s'(P)$
given by
$s(P) \xrightarrow {\cong } s'(P)$
given by
![]() $s' \circ \gamma $
, we obtain a desired isomorphism
$s' \circ \gamma $
, we obtain a desired isomorphism
![]() $\alpha \colon L \to L'$
.
$\alpha \colon L \to L'$
.
Corollary 4.10. Let N be an
![]() $\mathfrak {o}$
-module of finite length generated by n elements
$\mathfrak {o}$
-module of finite length generated by n elements
![]() $x_1,\ldots ,x_n$
. Then for any free
$x_1,\ldots ,x_n$
. Then for any free
![]() $\mathfrak {o}$
-module L of rank n and for any surjective homomorphism
$\mathfrak {o}$
-module L of rank n and for any surjective homomorphism
![]() $f \colon L \to N$
, there exists an
$f \colon L \to N$
, there exists an
![]() $\mathfrak {o}$
-basis
$\mathfrak {o}$
-basis
![]() $y_1,\ldots ,y_n$
of L satisfying
$y_1,\ldots ,y_n$
of L satisfying
![]() $f(y_i)=x_i$
for
$f(y_i)=x_i$
for
![]() $i=1,\ldots ,n$
.
$i=1,\ldots ,n$
.
Proof. Let
![]() $L' = \mathfrak {o}^{\oplus n}$
, and let
$L' = \mathfrak {o}^{\oplus n}$
, and let
![]() $f' \colon L' \twoheadrightarrow N$
denote the surjection that sends the standard basis of
$f' \colon L' \twoheadrightarrow N$
denote the surjection that sends the standard basis of
![]() $L'$
to the elements
$L'$
to the elements
![]() $x_1,\ldots ,x_n$
. By applying Lemma 4.9, we obtain an isomorphism
$x_1,\ldots ,x_n$
. By applying Lemma 4.9, we obtain an isomorphism
![]() $\alpha \colon L \xrightarrow {\cong } L'$
satisfying
$\alpha \colon L \xrightarrow {\cong } L'$
satisfying
![]() $f=f'\circ \alpha $
. Then the image under
$f=f'\circ \alpha $
. Then the image under
![]() $\alpha ^{-1}$
of the standard basis of
$\alpha ^{-1}$
of the standard basis of
![]() $L'$
gives a desired basis of L.
$L'$
gives a desired basis of L.
From now until the end of this section, we fix an integer
![]() $n \geq 1$
and a partition
$n \geq 1$
and a partition
of n. For
![]() $i=1,\ldots , r$
, we set
$i=1,\ldots , r$
, we set
We use the following terminology.
Definition 4.11. Let M be an
![]() $\mathfrak {o}$
-module generated by at most n elements.
$\mathfrak {o}$
-module generated by at most n elements.
-
(1) We say that an increasing filtration
 $\mathrm {F}_{\bullet } M$
of M by
$\mathrm {F}_{\bullet } M$
of M by
 $\mathfrak {o}$
-submodules is
$\mathfrak {o}$
-submodules is
 $\mathbf {n}$
-admissible if the following conditions are satisfied:
$\mathbf {n}$
-admissible if the following conditions are satisfied:-
•
 $\mathrm {F}_0 M = 0$
and
$\mathrm {F}_0 M = 0$
and
 $\mathrm {F}_{r} M = M$
.
$\mathrm {F}_{r} M = M$
. -
• For
 $i=1,\ldots ,r$
, the graded quotient
$i=1,\ldots ,r$
, the graded quotient
 $\mathrm {Gr}^{\mathrm {F}}_i M = \mathrm {F}_i M/\mathrm {F}_{i-1} M$
is generated by at most
$\mathrm {Gr}^{\mathrm {F}}_i M = \mathrm {F}_i M/\mathrm {F}_{i-1} M$
is generated by at most
 $n_i$
elements.
$n_i$
elements.
-
-
(2) Let
 $\mathrm {F}_{\bullet } M$
be an
$\mathrm {F}_{\bullet } M$
be an
 $\mathbf {n}$
-admissible filtration of M. We say that a sequence
$\mathbf {n}$
-admissible filtration of M. We say that a sequence
 $y_1,\ldots ,y_n$
of elements of M is compatible with
$y_1,\ldots ,y_n$
of elements of M is compatible with
 $\mathrm {F}_{\bullet } M$
if, for
$\mathrm {F}_{\bullet } M$
if, for
 $i=1,\ldots ,r$
, the
$i=1,\ldots ,r$
, the
 $b_i$
elements
$b_i$
elements
 $y_1, \ldots , y_{b_i}$
generate the
$y_1, \ldots , y_{b_i}$
generate the
 $\mathfrak {o}$
-module
$\mathfrak {o}$
-module
 $\mathrm {F}_i M$
.
$\mathrm {F}_i M$
.
Lemma 4.12. Let M be an
![]() $\mathfrak {o}$
-module of finite length. Let L be a free
$\mathfrak {o}$
-module of finite length. Let L be a free
![]() $\mathfrak {o}$
-module of rank n, and let
$\mathfrak {o}$
-module of rank n, and let
![]() $f \colon L \twoheadrightarrow M$
be a surjective homomorphism of
$f \colon L \twoheadrightarrow M$
be a surjective homomorphism of
![]() $\mathfrak {o}$
-modules. Suppose that an
$\mathfrak {o}$
-modules. Suppose that an
![]() $\mathbf {n}$
-admissible filtration
$\mathbf {n}$
-admissible filtration
![]() $\mathrm {F}_{\bullet } L$
of L is given. Let
$\mathrm {F}_{\bullet } L$
of L is given. Let
![]() $\mathrm {F}_{\bullet } M$
denote the filtration on M induced from
$\mathrm {F}_{\bullet } M$
denote the filtration on M induced from
![]() $\mathrm {F}_{\bullet } L$
via f: that is,
$\mathrm {F}_{\bullet } L$
via f: that is,
![]() $\mathrm {F}_i M = f(\mathrm {F}_i L)$
. For
$\mathrm {F}_i M = f(\mathrm {F}_i L)$
. For
![]() $i=1,\ldots ,r$
, let
$i=1,\ldots ,r$
, let
![]() $f_i \colon \mathrm {Gr}^{\mathrm {F}}_i L \twoheadrightarrow \mathrm {Gr}^{\mathrm {F}}_i M$
denote the surjective homomorphism induced by f. Then we have the following.
$f_i \colon \mathrm {Gr}^{\mathrm {F}}_i L \twoheadrightarrow \mathrm {Gr}^{\mathrm {F}}_i M$
denote the surjective homomorphism induced by f. Then we have the following.
-
(1)
 $\mathrm {F}_{\bullet } M$
is an
$\mathrm {F}_{\bullet } M$
is an
 $\mathbf {n}$
-admissible filtration of M.
$\mathbf {n}$
-admissible filtration of M. -
(2) Let
 $x_1,\ldots ,x_n$
be a sequence of elements of M compatible with
$x_1,\ldots ,x_n$
be a sequence of elements of M compatible with
 $\mathrm {F}_{\bullet } M$
. Then there exists a sequence
$\mathrm {F}_{\bullet } M$
. Then there exists a sequence
 $y_1,\ldots ,y_n$
of elements of L compatible with
$y_1,\ldots ,y_n$
of elements of L compatible with
 $\mathrm {F}_{\bullet } L$
such that
$\mathrm {F}_{\bullet } L$
such that
 $x_j=f(y_j)$
for
$x_j=f(y_j)$
for
 $j=1,\ldots ,n$
.
$j=1,\ldots ,n$
. -
(3) Let
 $x_1,\ldots ,x_n$
be a sequence of elements of M compatible with
$x_1,\ldots ,x_n$
be a sequence of elements of M compatible with
 $\mathrm {F}_{\bullet } M$
. Suppose that, for
$\mathrm {F}_{\bullet } M$
. Suppose that, for
 $i=1,\ldots ,r$
, an
$i=1,\ldots ,r$
, an
 $\mathfrak {o}$
-basis
$\mathfrak {o}$
-basis
 $z_{a_i}, \ldots , z_{b_i}$
of
$z_{a_i}, \ldots , z_{b_i}$
of
 $\mathrm {Gr}^{\mathrm {F}}_i L$
is given in such a way that for
$\mathrm {Gr}^{\mathrm {F}}_i L$
is given in such a way that for
 $j=a_i,\ldots ,b_i$
, the image
$j=a_i,\ldots ,b_i$
, the image
 $f_i(z_j)$
is equal to the class of
$f_i(z_j)$
is equal to the class of
 $x_j$
in
$x_j$
in
 $\mathrm {Gr}^{\mathrm {F}}_i M$
. Then there exists a sequence
$\mathrm {Gr}^{\mathrm {F}}_i M$
. Then there exists a sequence
 $y_1,\ldots ,y_n$
of elements of L compatible with
$y_1,\ldots ,y_n$
of elements of L compatible with
 $\mathrm {F}_{\bullet } L$
such that
$\mathrm {F}_{\bullet } L$
such that
 $x_j=f(y_j)$
for
$x_j=f(y_j)$
for
 $j=1,\ldots ,n$
and such that the class of
$j=1,\ldots ,n$
and such that the class of
 $y_j$
in
$y_j$
in
 $\mathrm {Gr}^{\mathrm {F}}_i L$
is equal to
$\mathrm {Gr}^{\mathrm {F}}_i L$
is equal to
 $z_j$
for
$z_j$
for
 $j=a_i,\ldots ,b_i$
.
$j=a_i,\ldots ,b_i$
.
Proof. Assertion (1) is clear. We can deduce assertion (2) from assertion (3), since in the situation of (2), one can find, by using Corollary 4.10, an
![]() $\mathfrak {o}$
-basis
$\mathfrak {o}$
-basis
![]() $z_{a_i}, \ldots , z_{b_i}$
of
$z_{a_i}, \ldots , z_{b_i}$
of
![]() $\mathrm {Gr}^{\mathrm {F}}_i L$
as in the statement of the assertion of (3) for
$\mathrm {Gr}^{\mathrm {F}}_i L$
as in the statement of the assertion of (3) for
![]() $i=1,\ldots ,r$
. (Here, we note that
$i=1,\ldots ,r$
. (Here, we note that
![]() $\mathrm {F}_i L$
is a free
$\mathrm {F}_i L$
is a free
![]() $\mathfrak {o}$
-module of rank
$\mathfrak {o}$
-module of rank
![]() $n_1+\dots +n_i$
.)
$n_1+\dots +n_i$
.)
We prove assertion (3). Using Lemma 4.8, one can choose an element
![]() $y_j \in \mathrm {F}_i L$
for
$y_j \in \mathrm {F}_i L$
for
![]() $j=a_i,\ldots ,b_i$
in such a way that
$j=a_i,\ldots ,b_i$
in such a way that
![]() $f(y_j)=x_j$
and the image of
$f(y_j)=x_j$
and the image of
![]() $y_j$
in
$y_j$
in
![]() $\mathrm {Gr}^{\mathrm {F}}_i L$
is equal to
$\mathrm {Gr}^{\mathrm {F}}_i L$
is equal to
![]() $z_j$
. Then the sequence
$z_j$
. Then the sequence
![]() $y_1,\ldots ,y_n$
of elements of L has the desired property.
$y_1,\ldots ,y_n$
of elements of L has the desired property.
The following is well-known.
Lemma 4.13. Let M be an
![]() $\mathfrak {o}$
-module of finite length and
$\mathfrak {o}$
-module of finite length and
![]() $m_1, \dots , m_r$
be nonnegative integers. Then the number of filtrations
$m_1, \dots , m_r$
be nonnegative integers. Then the number of filtrations
![]() $0 = \mathrm {F}_0M \subset \dots \subset \mathrm {F}_rM = M$
with
$0 = \mathrm {F}_0M \subset \dots \subset \mathrm {F}_rM = M$
with
![]() $\mathrm {Gr}_i^{\mathrm {F}} M$
generated by exactly
$\mathrm {Gr}_i^{\mathrm {F}} M$
generated by exactly
![]() $m_i$
elements for any
$m_i$
elements for any
![]() $1 \leq i \leq r$
is invariant under the permutations of
$1 \leq i \leq r$
is invariant under the permutations of
![]() $m_1, \dots , m_r$
.
$m_1, \dots , m_r$
.
Outline of proof.
First, reduce to the case where the permutation is an adjacent transposition. Then reduce to the case where
![]() $r = 2$
. Finally, use the duality (Lemma 4.2) to treat this case.
$r = 2$
. Finally, use the duality (Lemma 4.2) to treat this case.
5 The Mackey decomposition
In this section, we give the Mackey decomposition (Proposition 5.2) of the invariants by compact open subgroups of the form
![]() $\mathbb {K}_{n,\lambda }$
. As an application, we give a reduction step in the proof of our main results.
$\mathbb {K}_{n,\lambda }$
. As an application, we give a reduction step in the proof of our main results.
5.1 Invariant subspaces of parabolically induced representations
Fix an integer
![]() $n \geq 1$
. Let us consider the F-vector space
$n \geq 1$
. Let us consider the F-vector space
![]() $F^n$
. We regard an element of
$F^n$
. We regard an element of
![]() $F^n$
as a column vector. The group
$F^n$
as a column vector. The group
![]() $G_n = \mathrm {GL}_n(F)$
acts on
$G_n = \mathrm {GL}_n(F)$
acts on
![]() $F^n$
from the left by the multiplication. Let
$F^n$
from the left by the multiplication. Let
![]() $L_1,L_2 \subset F^n$
be
$L_1,L_2 \subset F^n$
be
![]() $\mathfrak {o}$
-lattices with
$\mathfrak {o}$
-lattices with
![]() $L_1 \supset L_2$
. We denote by
$L_1 \supset L_2$
. We denote by
![]() $\mathbb {K}_{L_1,L_2}$
the set of elements
$\mathbb {K}_{L_1,L_2}$
the set of elements
![]() $g \in G_n$
satisfying the following conditions:
$g \in G_n$
satisfying the following conditions:
-
• We have
 $g L_1 = L_1$
and
$g L_1 = L_1$
and
 $g L_2 = L_2$
.
$g L_2 = L_2$
. -
• The endomorphism of the
 $\mathfrak {o}$
-module
$\mathfrak {o}$
-module
 $L_1/L_2$
induced by the multiplication by g is the identity map.
$L_1/L_2$
induced by the multiplication by g is the identity map.
Then
![]() $\mathbb {K}_{L_1,L_2}$
is a compact open subgroup of
$\mathbb {K}_{L_1,L_2}$
is a compact open subgroup of
![]() $G_n$
.
$G_n$
.
Lemma 5.1. The
![]() $G_n$
-conjugacy class of
$G_n$
-conjugacy class of
![]() $\mathbb {K}_{L_1,L_2}$
depends only on n and an isomorphism class
$\mathbb {K}_{L_1,L_2}$
depends only on n and an isomorphism class
![]() $[L_1/L_2]$
of the
$[L_1/L_2]$
of the
![]() $\mathfrak {o}$
-module
$\mathfrak {o}$
-module
![]() $L_1/L_2$
.
$L_1/L_2$
.
Proof. Let
![]() $L_1, L_2, L^{\prime }_1, L^{\prime }_2$
be
$L_1, L_2, L^{\prime }_1, L^{\prime }_2$
be
![]() $\mathfrak {o}$
-lattices of
$\mathfrak {o}$
-lattices of
![]() $F^n$
such that
$F^n$
such that
![]() $L_1 \supset L_2$
,
$L_1 \supset L_2$
,
![]() $L^{\prime }_1 \supset L^{\prime }_2$
and
$L^{\prime }_1 \supset L^{\prime }_2$
and
![]() $L_1/L_2$
is isomorphic to
$L_1/L_2$
is isomorphic to
![]() $L^{\prime }_1/L^{\prime }_2$
as
$L^{\prime }_1/L^{\prime }_2$
as
![]() $\mathfrak {o}$
-modules. Let us choose an isomorphism
$\mathfrak {o}$
-modules. Let us choose an isomorphism
![]() $L_1/L_2 \cong L^{\prime }_1/L^{\prime }_2$
, and let f (respectively,
$L_1/L_2 \cong L^{\prime }_1/L^{\prime }_2$
, and let f (respectively,
![]() $f'$
) denote the composite
$f'$
) denote the composite
![]() $L_1 \twoheadrightarrow L_1/L_2 \xrightarrow {\cong } L^{\prime }_1/L^{\prime }_2$
(respectively, the quotient map
$L_1 \twoheadrightarrow L_1/L_2 \xrightarrow {\cong } L^{\prime }_1/L^{\prime }_2$
(respectively, the quotient map
![]() $L^{\prime }_1 \to L^{\prime }_1/L^{\prime }_2$
). Then it follows from Lemma 4.9 that there exists an isomorphism
$L^{\prime }_1 \to L^{\prime }_1/L^{\prime }_2$
). Then it follows from Lemma 4.9 that there exists an isomorphism
![]() $\alpha \colon L_1 \xrightarrow {\cong } L^{\prime }_1$
satisfying
$\alpha \colon L_1 \xrightarrow {\cong } L^{\prime }_1$
satisfying
![]() $f=f'\circ \alpha $
. By extending
$f=f'\circ \alpha $
. By extending
![]() $\alpha $
to an automorphism
$\alpha $
to an automorphism
![]() $F^n \xrightarrow {\cong } F^n$
by F-linearity, we obtain an element
$F^n \xrightarrow {\cong } F^n$
by F-linearity, we obtain an element
![]() $g \in G_n$
such that
$g \in G_n$
such that
![]() $\alpha (x) = gx$
. It is then straightforward to check that
$\alpha (x) = gx$
. It is then straightforward to check that
![]() $\mathbb {K}_{L^{\prime }_1,L^{\prime }_2} = g \mathbb {K}_{L_1,L_2} g^{-1}$
. This completes the proof.
$\mathbb {K}_{L^{\prime }_1,L^{\prime }_2} = g \mathbb {K}_{L_1,L_2} g^{-1}$
. This completes the proof.
By abuse of notation, we denote the group
![]() $\mathbb {K}_{L_1,L_2}$
by
$\mathbb {K}_{L_1,L_2}$
by
![]() $\mathbb {K}_{n,[L_1/L_2]}$
. We note that, for
$\mathbb {K}_{n,[L_1/L_2]}$
. We note that, for
![]() $[M]$
in
$[M]$
in
![]() $|\mathcal {C}^n|$
, the group
$|\mathcal {C}^n|$
, the group
![]() $\mathbb {K}_{n,[M]}$
is well-defined only up to
$\mathbb {K}_{n,[M]}$
is well-defined only up to
![]() $G_n$
-conjugation. If
$G_n$
-conjugation. If
![]() $\lambda = \mathrm {seq}_n([M])$
, the
$\lambda = \mathrm {seq}_n([M])$
, the
![]() $G_n$
-conjugacy class of
$G_n$
-conjugacy class of
![]() $\mathbb {K}_{n,[M]}$
is equal to the class of
$\mathbb {K}_{n,[M]}$
is equal to the class of
![]() $\mathbb {K}_{n,\lambda }$
. Indeed, if we set
$\mathbb {K}_{n,\lambda }$
. Indeed, if we set
![]() $L_1 = \mathfrak {o}^n$
and
$L_1 = \mathfrak {o}^n$
and
![]() $L_1 = \oplus _{i=1}^n\mathfrak {p}^{\lambda _i}$
with
$L_1 = \oplus _{i=1}^n\mathfrak {p}^{\lambda _i}$
with
![]() $\lambda = (\lambda _1, \dots , \lambda _n)$
, then we see that
$\lambda = (\lambda _1, \dots , \lambda _n)$
, then we see that
![]() $\mathbb {K}_{L_1,L_2} = \mathbb {K}_{n,\lambda }$
.
$\mathbb {K}_{L_1,L_2} = \mathbb {K}_{n,\lambda }$
.
Fix a partition
![]() $\mathbf {n} = (n_1,\ldots ,n_r)$
of n with integers
$\mathbf {n} = (n_1,\ldots ,n_r)$
of n with integers
![]() $n_1, \dots , n_r \geq 1$
. Let
$n_1, \dots , n_r \geq 1$
. Let
![]() $\pi _1,\ldots ,\pi _r$
be representations of
$\pi _1,\ldots ,\pi _r$
be representations of
![]() $G_{n_1}, \ldots , G_{n_r}$
of finite length, respectively. Consider the representation
$G_{n_1}, \ldots , G_{n_r}$
of finite length, respectively. Consider the representation
![]() $\pi _1 \times \cdots \times \pi _r$
of
$\pi _1 \times \cdots \times \pi _r$
of
![]() $G_n$
, which is parabolically induced from the representation
$G_n$
, which is parabolically induced from the representation
![]() $\pi _1 \boxtimes \cdots \boxtimes \pi _r$
of the standard Levi subgroup
$\pi _1 \boxtimes \cdots \boxtimes \pi _r$
of the standard Levi subgroup
![]() $G_{n_1} \times \cdots \times G_{n_r}$
of
$G_{n_1} \times \cdots \times G_{n_r}$
of
![]() $G_n$
. Then for any
$G_n$
. Then for any
![]() $[M] \in |\mathcal {C}^n|$
, the Mackey decomposition gives the following description of the
$[M] \in |\mathcal {C}^n|$
, the Mackey decomposition gives the following description of the
![]() $\mathbb {K}_{n,[M]}$
-invariant part of
$\mathbb {K}_{n,[M]}$
-invariant part of
![]() $\pi _1 \times \cdots \times \pi _r$
.
$\pi _1 \times \cdots \times \pi _r$
.
Proposition 5.2 (The Mackey decomposition)
There exists an isomorphism
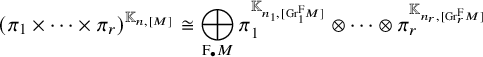 $$\begin{align*}(\pi_1 \times \cdots \times \pi_r)^{\mathbb{K}_{n,[M]}} \cong \bigoplus_{\mathrm{F}_{\bullet} M} \pi_1^{\mathbb{K}_{n_1,[\mathrm{Gr}_1^{\mathrm{F}} M]}} \otimes \cdots \otimes \pi_r^{\mathbb{K}_{n_r,[\mathrm{Gr}_r^{\mathrm{F}} M]}} \end{align*}$$
$$\begin{align*}(\pi_1 \times \cdots \times \pi_r)^{\mathbb{K}_{n,[M]}} \cong \bigoplus_{\mathrm{F}_{\bullet} M} \pi_1^{\mathbb{K}_{n_1,[\mathrm{Gr}_1^{\mathrm{F}} M]}} \otimes \cdots \otimes \pi_r^{\mathbb{K}_{n_r,[\mathrm{Gr}_r^{\mathrm{F}} M]}} \end{align*}$$
of complex vector spaces. Here
![]() $\mathrm {F}_{\bullet } M$
in the direct sum above runs over the set of
$\mathrm {F}_{\bullet } M$
in the direct sum above runs over the set of
![]() $\mathbf {n}$
-admissible filtrations of M: that is, the increasing filtrations
$\mathbf {n}$
-admissible filtrations of M: that is, the increasing filtrations
on M by
![]() $\mathfrak {o}$
-submodules such that for
$\mathfrak {o}$
-submodules such that for
![]() $i=1,\ldots ,r$
, the
$i=1,\ldots ,r$
, the
![]() $\mathfrak {o}$
-module
$\mathfrak {o}$
-module
![]() $\mathrm {Gr}_i^{\mathrm {F}} M = \mathrm {F}_{i}M/\mathrm {F}_{i-1} M$
is generated by at most
$\mathrm {Gr}_i^{\mathrm {F}} M = \mathrm {F}_{i}M/\mathrm {F}_{i-1} M$
is generated by at most
![]() $n_i$
elements.
$n_i$
elements.
Proof. Let
![]() $P_{\mathbf {n}} \subset G_n$
denote the standard parabolic subgroup corresponding to the partition
$P_{\mathbf {n}} \subset G_n$
denote the standard parabolic subgroup corresponding to the partition
![]() $\mathbf {n}=(n_1,\ldots ,n_r)$
. Consider the quotient homomorphism
$\mathbf {n}=(n_1,\ldots ,n_r)$
. Consider the quotient homomorphism
![]() $q \colon P_{\mathbf {n}} \to G_{n_1} \times \cdots \times G_{n_r}$
. Let us choose a complete set
$q \colon P_{\mathbf {n}} \to G_{n_1} \times \cdots \times G_{n_r}$
. Let us choose a complete set
![]() $S \subset G_n$
of representatives of the double coset
$S \subset G_n$
of representatives of the double coset
![]() $P_{\mathbf {n}} \backslash G_n /\mathbb {K}_{n,[M]}$
.
$P_{\mathbf {n}} \backslash G_n /\mathbb {K}_{n,[M]}$
.
Then the Mackey decomposition yields an isomorphism
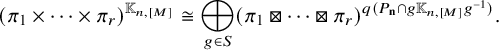 $$ \begin{align} (\pi_1 \times \cdots \times \pi_r)^{\mathbb{K}_{n,[M]}} \cong \bigoplus_{g \in S} (\pi_1 \boxtimes \cdots \boxtimes \pi_r)^{q(P_{\mathbf{n}} \cap g \mathbb{K}_{n,[M]} g^{-1})}. \end{align} $$
$$ \begin{align} (\pi_1 \times \cdots \times \pi_r)^{\mathbb{K}_{n,[M]}} \cong \bigoplus_{g \in S} (\pi_1 \boxtimes \cdots \boxtimes \pi_r)^{q(P_{\mathbf{n}} \cap g \mathbb{K}_{n,[M]} g^{-1})}. \end{align} $$
Let
![]() $\mathcal {F}_M$
denote the set of
$\mathcal {F}_M$
denote the set of
![]() $\mathbf {n}$
-admissible filtrations on M. In view of equation (5.1), it suffices to construct a bijection
$\mathbf {n}$
-admissible filtrations on M. In view of equation (5.1), it suffices to construct a bijection
![]() $\alpha \colon P_{\mathbf {n}} \backslash G_n /\mathbb {K}_{n,[M]} \xrightarrow {\cong } \mathcal {F}_M$
satisfying the following property: If
$\alpha \colon P_{\mathbf {n}} \backslash G_n /\mathbb {K}_{n,[M]} \xrightarrow {\cong } \mathcal {F}_M$
satisfying the following property: If
![]() $P_{\mathbf {n}} g \mathbb {K}_{n,[M]}$
corresponds to the filtration
$P_{\mathbf {n}} g \mathbb {K}_{n,[M]}$
corresponds to the filtration
![]() $\mathrm {F}_{\bullet } M$
via
$\mathrm {F}_{\bullet } M$
via
![]() $\alpha $
, then the subgroup
$\alpha $
, then the subgroup
![]() $q(P_{\mathbf {n}} \cap g \mathbb {K}_{n,[M]} g^{-1})$
of
$q(P_{\mathbf {n}} \cap g \mathbb {K}_{n,[M]} g^{-1})$
of
![]() $G_{n_1} \times \cdots \times G_{n_r}$
is a conjugate of the subgroup
$G_{n_1} \times \cdots \times G_{n_r}$
is a conjugate of the subgroup
![]() $\mathbb {K}_{n_1,[\mathrm {Gr}_1^{\mathrm {F}} M]} \times \cdots \times \mathbb {K}_{n_r,[\mathrm {Gr}_r^{\mathrm {F}} M]}$
.
$\mathbb {K}_{n_1,[\mathrm {Gr}_1^{\mathrm {F}} M]} \times \cdots \times \mathbb {K}_{n_r,[\mathrm {Gr}_r^{\mathrm {F}} M]}$
.
Lemma 5.3. By choosing a pair
![]() $(L_1,L_2)$
of
$(L_1,L_2)$
of
![]() $\mathfrak {o}$
-lattices with
$\mathfrak {o}$
-lattices with
![]() $L_1 \supset L_2$
and an isomorphism
$L_1 \supset L_2$
and an isomorphism
![]() $\gamma \colon L_1/L_2 \cong M$
of
$\gamma \colon L_1/L_2 \cong M$
of
![]() $\mathfrak {o}$
-modules, we identify
$\mathfrak {o}$
-modules, we identify
![]() $\mathbb {K}_{n,[M]}$
with
$\mathbb {K}_{n,[M]}$
with
![]() $\mathbb {K}_{L_1,L_2}$
. We denote the composite
$\mathbb {K}_{L_1,L_2}$
. We denote the composite
![]() $L_1 \twoheadrightarrow L_1/L_2 \xrightarrow {\gamma } M$
by
$L_1 \twoheadrightarrow L_1/L_2 \xrightarrow {\gamma } M$
by
![]() $f_1$
.
$f_1$
.
-
(1) Let
 $\mathcal {L}_{M}(F^n)$
be the set of pairs
$\mathcal {L}_{M}(F^n)$
be the set of pairs
 $(L,f)$
of an
$(L,f)$
of an
 $\mathfrak {o}$
-lattice
$\mathfrak {o}$
-lattice
 $L \subset F^n$
and a surjective homomorphism
$L \subset F^n$
and a surjective homomorphism
 $f \colon L \twoheadrightarrow M$
of
$f \colon L \twoheadrightarrow M$
of
 $\mathfrak {o}$
-modules. Then there is a (canonical) bijection
$\mathfrak {o}$
-modules. Then there is a (canonical) bijection
 $G_n/\mathbb {K}_{n,[M]} \rightarrow \mathcal {L}_{M}(F^n)$
given by
$G_n/\mathbb {K}_{n,[M]} \rightarrow \mathcal {L}_{M}(F^n)$
given by
 $g\mathbb {K}_{L_1,L_2} \mapsto (gL_1, y \mapsto f_1(g^{-1}y))$
.
$g\mathbb {K}_{L_1,L_2} \mapsto (gL_1, y \mapsto f_1(g^{-1}y))$
. -
(2) There is a bijection from
 $G_n / P_{\mathbf {n}}$
to the set of
$G_n / P_{\mathbf {n}}$
to the set of
 $\mathbf {n}$
-admissible filtrations on
$\mathbf {n}$
-admissible filtrations on
 $L_1$
given by
$L_1$
given by
 , where
, where
 $\{e_1, \dots , e_n\}$
is the standard basis of
$\{e_1, \dots , e_n\}$
is the standard basis of
 $F^n$
.
$F^n$
. -
(3) Let
 $\mathcal {L}_{M}'(F^n)$
be the set of triples
$\mathcal {L}_{M}'(F^n)$
be the set of triples
 $(L,\mathrm {F}_{\bullet } L,f)$
of an
$(L,\mathrm {F}_{\bullet } L,f)$
of an
 $\mathfrak {o}$
-lattice
$\mathfrak {o}$
-lattice
 $L \subset F^n$
, an
$L \subset F^n$
, an
 $\mathbf {n}$
-admissible filtration
$\mathbf {n}$
-admissible filtration
 $\mathrm {F}_{\bullet } L$
on L and a surjective homomorphism
$\mathrm {F}_{\bullet } L$
on L and a surjective homomorphism
 $f \colon L \twoheadrightarrow M$
of
$f \colon L \twoheadrightarrow M$
of
 $\mathfrak {o}$
-modules. We let the group
$\mathfrak {o}$
-modules. We let the group
 $G_n$
act on
$G_n$
act on
 $\mathcal {L}_M'(F^n)$
by
$\mathcal {L}_M'(F^n)$
by
 $g.(L,\mathrm {F}_{\bullet } L,f) = (gL, g \mathrm {F}_{\bullet } L, y\mapsto f(g^{-1}y))$
. Then there is a (canonical) bijection
$g.(L,\mathrm {F}_{\bullet } L,f) = (gL, g \mathrm {F}_{\bullet } L, y\mapsto f(g^{-1}y))$
. Then there is a (canonical) bijection
 $P_{\mathbf {n}} \backslash G_n /\mathbb {K}_{n,[M]} \rightarrow G_n \backslash \mathcal {L}_{M}'(F^n)$
given by sending
$P_{\mathbf {n}} \backslash G_n /\mathbb {K}_{n,[M]} \rightarrow G_n \backslash \mathcal {L}_{M}'(F^n)$
given by sending
 $P_{\mathbf {n}} g \mathbb {K}_{L_1,L_2}$
to the
$P_{\mathbf {n}} g \mathbb {K}_{L_1,L_2}$
to the
 $G_n$
-orbit of
$G_n$
-orbit of
 $(gL_1, \mathrm {F}_{\bullet } gL_1, y \mapsto f_1(g^{-1}y))$
, where
$(gL_1, \mathrm {F}_{\bullet } gL_1, y \mapsto f_1(g^{-1}y))$
, where
 .
.
Proof. We show (1). We let the group
![]() $G_n$
act from the left on the set
$G_n$
act from the left on the set
![]() $\mathcal {L}_{M}(F^n)$
by the rule
$\mathcal {L}_{M}(F^n)$
by the rule
![]() $g.(L,f) = (gL,y \mapsto f(g^{-1}y))$
. One can prove that the action of
$g.(L,f) = (gL,y \mapsto f(g^{-1}y))$
. One can prove that the action of
![]() $G_n$
on
$G_n$
on
![]() $\mathcal {L}_{M}(F^n)$
is transitive in the following way. Let
$\mathcal {L}_{M}(F^n)$
is transitive in the following way. Let
![]() $(L,f)$
and
$(L,f)$
and
![]() $(L',f')$
be two elements of
$(L',f')$
be two elements of
![]() $\mathcal {L}_{M}(F^n)$
. Then by Lemma 4.9, there exists an isomorphism
$\mathcal {L}_{M}(F^n)$
. Then by Lemma 4.9, there exists an isomorphism
![]() $\beta \colon L \xrightarrow {\cong } L'$
satisfying
$\beta \colon L \xrightarrow {\cong } L'$
satisfying
![]() $f = f' \circ \beta $
. By extending
$f = f' \circ \beta $
. By extending
![]() $\beta $
to an automorphism of
$\beta $
to an automorphism of
![]() $F^n$
by F-linearity, we obtain an element
$F^n$
by F-linearity, we obtain an element
![]() $g \in G_n$
such that
$g \in G_n$
such that
![]() $\beta (x) = gx$
. Then we have
$\beta (x) = gx$
. Then we have
![]() $(L',f') = g.(L,f)$
. Hence the map
$(L',f') = g.(L,f)$
. Hence the map
![]() $g \mapsto g.(L_1,f_1)$
gives a surjective map
$g \mapsto g.(L_1,f_1)$
gives a surjective map
![]() $G_n \rightarrow \mathcal {L}_{M}(F^n)$
. Since the stabiliser of
$G_n \rightarrow \mathcal {L}_{M}(F^n)$
. Since the stabiliser of
![]() $(L_1,f_1)$
with respect to the action of
$(L_1,f_1)$
with respect to the action of
![]() $G_n$
is equal to
$G_n$
is equal to
![]() $\mathbb {K}_{L_1,L_2}$
, it gives the desired bijection.
$\mathbb {K}_{L_1,L_2}$
, it gives the desired bijection.
It is straightforward to check that this bijection does not depend on the choice of the triple
![]() $(L_1, L_2, \gamma )$
in the following sense. Let
$(L_1, L_2, \gamma )$
in the following sense. Let
![]() $(L^{\prime }_1, L^{\prime }_2, \gamma ')$
be another choice. It follows from the proof of Lemma 5.1 that there exists
$(L^{\prime }_1, L^{\prime }_2, \gamma ')$
be another choice. It follows from the proof of Lemma 5.1 that there exists
![]() $g \in G_n$
satisfying
$g \in G_n$
satisfying
![]() $g L_1 = L^{\prime }_1$
,
$g L_1 = L^{\prime }_1$
,
![]() $g L_2 = L^{\prime }_2$
and
$g L_2 = L^{\prime }_2$
and
![]() $\gamma (y \ \ \mod {L_2}) =\gamma '(gy\ \ \mod {L^{\prime }_2})$
for all
$\gamma (y \ \ \mod {L_2}) =\gamma '(gy\ \ \mod {L^{\prime }_2})$
for all
![]() $y \in L_1$
. Then for any such
$y \in L_1$
. Then for any such
![]() $g \in G_n$
, we have
$g \in G_n$
, we have
![]() $\mathbb {K}_{L^{\prime }_1,L^{\prime }_2} = g \mathbb {K}_{L_1,L_2} g^{-1}$
, and the diagram
$\mathbb {K}_{L^{\prime }_1,L^{\prime }_2} = g \mathbb {K}_{L_1,L_2} g^{-1}$
, and the diagram
is commutative. Here the left vertical map sends
![]() $h \mathbb {K}_{L_1,L_2}$
to
$h \mathbb {K}_{L_1,L_2}$
to
![]() $h g^{-1} \mathbb {K}_{L^{\prime }_1,L^{\prime }_2}$
. Hence we obtain (1).
$h g^{-1} \mathbb {K}_{L^{\prime }_1,L^{\prime }_2}$
. Hence we obtain (1).
Note that
![]() $G_n / P_{\mathbf {n}}$
is naturally identified with the set of partial flags
$G_n / P_{\mathbf {n}}$
is naturally identified with the set of partial flags
![]() $0 = V_0 \subset \dots \subset V_r = F^n$
with
$0 = V_0 \subset \dots \subset V_r = F^n$
with
![]() $\dim (V_i/V_{i-1}) = n_i$
for
$\dim (V_i/V_{i-1}) = n_i$
for
![]() $i = 1,\dots ,r$
. Note that
$i = 1,\dots ,r$
. Note that
![]() $(L_1 \cap V') \otimes _{\mathfrak {o}} F = V'$
for any subspace
$(L_1 \cap V') \otimes _{\mathfrak {o}} F = V'$
for any subspace
![]() $V'$
of
$V'$
of
![]() $F^n$
. On the other hand, if
$F^n$
. On the other hand, if
![]() $\mathrm {F}_{\bullet } L_1$
is an
$\mathrm {F}_{\bullet } L_1$
is an
![]() $\mathbf {n}$
-admissible filtration of
$\mathbf {n}$
-admissible filtration of
![]() $L_1$
, since
$L_1$
, since
![]() $L_1$
is a free
$L_1$
is a free
![]() $\mathfrak {o}$
-module of rank
$\mathfrak {o}$
-module of rank
![]() $n=n_1 + \cdots + n_r$
, each subquotient
$n=n_1 + \cdots + n_r$
, each subquotient
![]() $\mathrm {Gr}_i^{\mathrm {F}} L_1$
is a free
$\mathrm {Gr}_i^{\mathrm {F}} L_1$
is a free
![]() $\mathfrak {o}$
-module of rank
$\mathfrak {o}$
-module of rank
![]() $n_i$
for any i. Hence we have
$n_i$
for any i. Hence we have
![]() $L_1 \cap (\mathrm {F}_i L_1 \otimes _{\mathfrak {o}} F) = \mathrm {F}_i L_1$
for any i. Therefore we have (2).
$L_1 \cap (\mathrm {F}_i L_1 \otimes _{\mathfrak {o}} F) = \mathrm {F}_i L_1$
for any i. Therefore we have (2).
Since the double cosets in
![]() $P_{\mathbf {n}} \backslash G_n /\mathbb {K}_{n,[M]}$
are in one-to-one correspondence with the
$P_{\mathbf {n}} \backslash G_n /\mathbb {K}_{n,[M]}$
are in one-to-one correspondence with the
![]() $G_n$
-orbits in
$G_n$
-orbits in
![]() $(G_n/P_{\mathbf {n}}) \times (G_n/\mathbb {K}_{n,[M]})$
with respect to the diagonal left
$(G_n/P_{\mathbf {n}}) \times (G_n/\mathbb {K}_{n,[M]})$
with respect to the diagonal left
![]() $G_n$
-action, assertion (3) follows from (1) and (2).
$G_n$
-action, assertion (3) follows from (1) and (2).
We continue the proof of Proposition 5.2. We identify
![]() $P_{\mathbf {n}} \backslash G_n /\mathbb {K}_{n,[M]}$
with
$P_{\mathbf {n}} \backslash G_n /\mathbb {K}_{n,[M]}$
with
![]() $G_n \backslash \mathcal {L}_{M}'(F^n)$
by Lemma 5.3. By sending the triple
$G_n \backslash \mathcal {L}_{M}'(F^n)$
by Lemma 5.3. By sending the triple
![]() $(L,\mathrm {F}_{\bullet } L,f) \in \mathcal {L}^{\prime }_M(F^n)$
to the filtration on M induced from
$(L,\mathrm {F}_{\bullet } L,f) \in \mathcal {L}^{\prime }_M(F^n)$
to the filtration on M induced from
![]() $\mathrm {F}_{\bullet } L$
via f, we obtain a map
$\mathrm {F}_{\bullet } L$
via f, we obtain a map
![]() $\alpha \colon P_{\mathbf {n}} \backslash G_n /\mathbb {K}_{n,[M]} \to \mathcal {F}_M$
. Let
$\alpha \colon P_{\mathbf {n}} \backslash G_n /\mathbb {K}_{n,[M]} \to \mathcal {F}_M$
. Let
![]() $\mathrm {F}^{\mathrm {st}}_{\bullet } \mathfrak {o}^n$
be the standard
$\mathrm {F}^{\mathrm {st}}_{\bullet } \mathfrak {o}^n$
be the standard
![]() $\mathbf {n}$
-admissible filtration on
$\mathbf {n}$
-admissible filtration on
![]() $\mathfrak {o}^n$
: that is, the unique
$\mathfrak {o}^n$
: that is, the unique
![]() $\mathbf {n}$
-admissible filtration on
$\mathbf {n}$
-admissible filtration on
![]() $\mathfrak {o}^n$
such that the standard basis of
$\mathfrak {o}^n$
such that the standard basis of
![]() $\mathfrak {o}^n$
is a sequence compatible with
$\mathfrak {o}^n$
is a sequence compatible with
![]() $\mathrm {F}^{\mathrm {st}}_{\bullet } \mathfrak {o}^n$
. Let us fix a surjective homomorphism
$\mathrm {F}^{\mathrm {st}}_{\bullet } \mathfrak {o}^n$
. Let us fix a surjective homomorphism
![]() $f \colon \mathfrak {o}^n \to M$
, and let L denote its kernel. Then we can regard
$f \colon \mathfrak {o}^n \to M$
, and let L denote its kernel. Then we can regard
![]() $\mathbb {K}_{n,[M]}$
as
$\mathbb {K}_{n,[M]}$
as
![]() $\mathbb {K}_{\mathfrak {o}^n,L}$
. In this case, one can describe the map
$\mathbb {K}_{\mathfrak {o}^n,L}$
. In this case, one can describe the map
![]() $\alpha $
as follows. Let
$\alpha $
as follows. Let
![]() $s \in P_{\mathbf {n}} \backslash G_n /\mathbb {K}_{\mathfrak {o}^n,L}$
. Then by the Iwasawa decomposition, we have
$s \in P_{\mathbf {n}} \backslash G_n /\mathbb {K}_{\mathfrak {o}^n,L}$
. Then by the Iwasawa decomposition, we have
![]() $s = P_{\mathbf {n}} k \mathbb {K}_{\mathfrak {o}^n,L}$
for some
$s = P_{\mathbf {n}} k \mathbb {K}_{\mathfrak {o}^n,L}$
for some
![]() $k \in \mathrm {GL}_n(\mathfrak {o})$
. Then
$k \in \mathrm {GL}_n(\mathfrak {o})$
. Then
![]() $\alpha (s)$
is the filtration
$\alpha (s)$
is the filtration
on M. We note that
![]() $k^{-1} \mathrm {F}^{\mathrm {st}}_{i} \mathfrak {o}^n$
is the
$k^{-1} \mathrm {F}^{\mathrm {st}}_{i} \mathfrak {o}^n$
is the
![]() $\mathfrak {o}$
-submodule of
$\mathfrak {o}$
-submodule of
![]() $\mathfrak {o}^n$
generated by the first
$\mathfrak {o}^n$
generated by the first
![]() $b_i$
columns of
$b_i$
columns of
![]() $k^{-1}$
.
$k^{-1}$
.
Now let us choose a filtration
![]() $\mathrm {F}_{\bullet } M$
on M in
$\mathrm {F}_{\bullet } M$
on M in
![]() $\mathcal {F}_M$
. Let us fix a sequence
$\mathcal {F}_M$
. Let us fix a sequence
![]() $x_1,\ldots ,x_n \in M$
compatible with
$x_1,\ldots ,x_n \in M$
compatible with
![]() $\mathrm {F}_{\bullet } M$
. By considering the homomorphism
$\mathrm {F}_{\bullet } M$
. By considering the homomorphism
![]() $\mathfrak {o}^n \to M$
that sends the standard basis to the sequence
$\mathfrak {o}^n \to M$
that sends the standard basis to the sequence
![]() $x_1,\ldots ,x_n$
, one can check that the map
$x_1,\ldots ,x_n$
, one can check that the map
![]() $\alpha $
is surjective. Suppose that two triples
$\alpha $
is surjective. Suppose that two triples
![]() $(L,\mathrm {F}_{\bullet } L,f)$
and
$(L,\mathrm {F}_{\bullet } L,f)$
and
![]() $(L',\mathrm {F}^{\prime }_{\bullet } L',f')$
are sent to
$(L',\mathrm {F}^{\prime }_{\bullet } L',f')$
are sent to
![]() $\mathrm {F}_{\bullet } M$
via
$\mathrm {F}_{\bullet } M$
via
![]() $\alpha $
. Let us choose a basis
$\alpha $
. Let us choose a basis
![]() $y_1,\ldots ,y_n$
of L and a basis
$y_1,\ldots ,y_n$
of L and a basis
![]() $y^{\prime }_1,\ldots ,y^{\prime }_n$
of
$y^{\prime }_1,\ldots ,y^{\prime }_n$
of
![]() $L'$
as in assertion (2) of Lemma 4.12. By considering the change-of-basis matrix, we can see that the two triples are in the same
$L'$
as in assertion (2) of Lemma 4.12. By considering the change-of-basis matrix, we can see that the two triples are in the same
![]() $G_n$
-orbit. This proves that the map
$G_n$
-orbit. This proves that the map
![]() $\alpha $
is injective. In conclusion,
$\alpha $
is injective. In conclusion,
![]() $\alpha \colon P_{\mathbf {n}} \backslash G_n /\mathbb {K}_{n,[M]} \to \mathcal {F}_M$
is bijective.
$\alpha \colon P_{\mathbf {n}} \backslash G_n /\mathbb {K}_{n,[M]} \to \mathcal {F}_M$
is bijective.
Again, we realise
![]() $\mathbb {K}_{n,[M]}$
as
$\mathbb {K}_{n,[M]}$
as
![]() $\mathbb {K}_{\mathfrak {o}^n, L}$
for a lattice
$\mathbb {K}_{\mathfrak {o}^n, L}$
for a lattice
![]() $L \subset \mathfrak {o}^n$
with a surjection
$L \subset \mathfrak {o}^n$
with a surjection
![]() $f \colon \mathfrak {o}^n \twoheadrightarrow M$
such that
$f \colon \mathfrak {o}^n \twoheadrightarrow M$
such that
![]() $\mathrm {Ker}\, f = L$
. Then by the Iwasawa decomposition, any
$\mathrm {Ker}\, f = L$
. Then by the Iwasawa decomposition, any
![]() $s \in P_{\mathbf {n}} \backslash G_n /\mathbb {K}_{\mathfrak {o}^n,L}$
is of the form
$s \in P_{\mathbf {n}} \backslash G_n /\mathbb {K}_{\mathfrak {o}^n,L}$
is of the form
![]() $s = P_{\mathbf {n}} k_s \mathbb {K}_{\mathfrak {o}^n,L}$
for some
$s = P_{\mathbf {n}} k_s \mathbb {K}_{\mathfrak {o}^n,L}$
for some
![]() $k_s \in \mathrm {GL}_n(\mathfrak {o})$
. In this case, the corresponding triple is the
$k_s \in \mathrm {GL}_n(\mathfrak {o})$
. In this case, the corresponding triple is the
![]() $G_n$
-orbit of
$G_n$
-orbit of
![]() $(\mathfrak {o}^n,\mathrm {F}^{\mathrm {st}}_{\bullet } \mathfrak {o}^n, f_s)$
, where
$(\mathfrak {o}^n,\mathrm {F}^{\mathrm {st}}_{\bullet } \mathfrak {o}^n, f_s)$
, where
![]() $f_s(y) = f(k_s^{-1}y)$
. In particular,
$f_s(y) = f(k_s^{-1}y)$
. In particular,
![]() $\mathrm {Ker}\, f_s = k_sL$
. Then
$\mathrm {Ker}\, f_s = k_sL$
. Then
where
![]() $m(p) \colon \mathfrak {o}^n \to \mathfrak {o}^n$
denotes the homomorphism given by the multiplication by p from the left. Recall that
$m(p) \colon \mathfrak {o}^n \to \mathfrak {o}^n$
denotes the homomorphism given by the multiplication by p from the left. Recall that
![]() $\{e_1, \dots , e_n\}$
is the standard basis of
$\{e_1, \dots , e_n\}$
is the standard basis of
![]() $F^n$
. For
$F^n$
. For
![]() $1 \leq i \leq r$
, we set
$1 \leq i \leq r$
, we set
![]() $L_i$
to be the image of
$L_i$
to be the image of
![]() $k_s L \cap (\mathfrak {o} e_1 + \dots + \mathfrak {o} e_{b_i})$
under the canonical projection
$k_s L \cap (\mathfrak {o} e_1 + \dots + \mathfrak {o} e_{b_i})$
under the canonical projection
Then
![]() $\mathfrak {o}^{n_i} \supset L_i$
are lattices in
$\mathfrak {o}^{n_i} \supset L_i$
are lattices in
![]() $F^{n_i} = Fe_{a_i} + \dots + Fe_{b_i}$
such that
$F^{n_i} = Fe_{a_i} + \dots + Fe_{b_i}$
such that
![]() $\mathfrak {o}^{n_i}/L_i \cong \mathrm {Gr}^{\mathrm {F}}_iM$
, where
$\mathfrak {o}^{n_i}/L_i \cong \mathrm {Gr}^{\mathrm {F}}_iM$
, where
![]() $\mathrm {F}_{\bullet } M$
is the filtration corresponding to the
$\mathrm {F}_{\bullet } M$
is the filtration corresponding to the
![]() $G_n$
-orbit of
$G_n$
-orbit of
![]() $(\mathfrak {o}^n,\mathrm {F}^{\mathrm {st}}_{\bullet } \mathfrak {o}^n, f_s)$
. Moreover, we have
$(\mathfrak {o}^n,\mathrm {F}^{\mathrm {st}}_{\bullet } \mathfrak {o}^n, f_s)$
. Moreover, we have
We show that this inclusion is indeed an equality. Let
![]() $(k_1, \dots , k_r) \in \mathbb {K}_{\mathfrak {o}^{n_1},L_1} \times \dots \times \mathbb {K}_{\mathfrak {o}^{n_r},L_r}$
be given. Set
$(k_1, \dots , k_r) \in \mathbb {K}_{\mathfrak {o}^{n_1},L_1} \times \dots \times \mathbb {K}_{\mathfrak {o}^{n_r},L_r}$
be given. Set
![]() $x_j = f_s(e_j) \in M$
for
$x_j = f_s(e_j) \in M$
for
![]() $1 \leq j \leq n$
, and set
$1 \leq j \leq n$
, and set
![]() $z_j = k_ie_j \in \mathfrak {o}^{n_i} = \mathrm {Gr}_i^{F^{\mathrm {st}}}\mathfrak {o}^n$
for
$z_j = k_ie_j \in \mathfrak {o}^{n_i} = \mathrm {Gr}_i^{F^{\mathrm {st}}}\mathfrak {o}^n$
for
![]() $a_i \leq j \leq b_i$
. Since
$a_i \leq j \leq b_i$
. Since
![]() $k_i$
fixes
$k_i$
fixes
![]() $\mathfrak {o}^{n_i} \ni x \mapsto f_s(x) \bmod \mathrm {F}_{i-1}M \in \mathrm {Gr}^{\mathrm {F}}_iM \cong \mathfrak {o}^{n_i}/L_i$
, we see that the image of
$\mathfrak {o}^{n_i} \ni x \mapsto f_s(x) \bmod \mathrm {F}_{i-1}M \in \mathrm {Gr}^{\mathrm {F}}_iM \cong \mathfrak {o}^{n_i}/L_i$
, we see that the image of
![]() $f_s(z_j)$
in
$f_s(z_j)$
in
![]() $\mathrm {Gr}^{\mathrm {F}}_iM$
is the same as the one of
$\mathrm {Gr}^{\mathrm {F}}_iM$
is the same as the one of
![]() $x_j$
. By assertion (3) of Lemma 4.12, one can take a sequence
$x_j$
. By assertion (3) of Lemma 4.12, one can take a sequence
![]() $e_1', \dots , e_n' \in \mathfrak {o}^n$
which is compatible with
$e_1', \dots , e_n' \in \mathfrak {o}^n$
which is compatible with
![]() $\mathrm {F}_{\bullet }^{\mathrm {st}} \mathfrak {o}^n$
such that
$\mathrm {F}_{\bullet }^{\mathrm {st}} \mathfrak {o}^n$
such that
![]() $x_j = f_s(e^{\prime }_j)$
and the class of
$x_j = f_s(e^{\prime }_j)$
and the class of
![]() $e^{\prime }_j$
in
$e^{\prime }_j$
in
![]() $\mathrm {Gr}_i^{\mathrm {F}^{\mathrm {st}}}\mathfrak {o}^n = \mathfrak {o}^{n_i}$
is equal to
$\mathrm {Gr}_i^{\mathrm {F}^{\mathrm {st}}}\mathfrak {o}^n = \mathfrak {o}^{n_i}$
is equal to
![]() $z_j$
. Define
$z_j$
. Define
![]() $k \in G_n$
so that
$k \in G_n$
so that
![]() $e^{\prime }_j = ke_j$
for
$e^{\prime }_j = ke_j$
for
![]() $1 \leq j \leq n$
. Since
$1 \leq j \leq n$
. Since
![]() $F e^{\prime }_1+\dots +Fe^{\prime }_{n_i} = F e_1+\dots +Fe_{n_i}$
for
$F e^{\prime }_1+\dots +Fe^{\prime }_{n_i} = F e_1+\dots +Fe_{n_i}$
for
![]() $1 \leq i \leq r$
, we have
$1 \leq i \leq r$
, we have
![]() $k \in P_{\mathbf {n}}$
. Moreover, since k preserves
$k \in P_{\mathbf {n}}$
. Moreover, since k preserves
![]() $\mathfrak {o}^n$
and
$\mathfrak {o}^n$
and
![]() $f_s(kx) = f_s(x)$
, it also preserves
$f_s(kx) = f_s(x)$
, it also preserves
![]() $k_sL = \mathrm {Ker}\, f_s$
. Hence
$k_sL = \mathrm {Ker}\, f_s$
. Hence
![]() $k \in \mathbb {K}_{\mathfrak {o}^n, k_sL} = k_s \mathbb {K}_{\mathfrak {o}^n,L} k_s^{-1}$
. Since
$k \in \mathbb {K}_{\mathfrak {o}^n, k_sL} = k_s \mathbb {K}_{\mathfrak {o}^n,L} k_s^{-1}$
. Since
![]() $q(k) = (k_1, \dots , k_r)$
, we conclude that
$q(k) = (k_1, \dots , k_r)$
, we conclude that
![]() $q(P_{\mathbf {n}} \cap k_s \mathbb {K}_{\mathfrak {o}^n,L} k_s^{-1}) = \mathbb {K}_{\mathfrak {o}^{n_1},L_1} \times \dots \times \mathbb {K}_{\mathfrak {o}^{n_r},L_r}$
. Namely,
$q(P_{\mathbf {n}} \cap k_s \mathbb {K}_{\mathfrak {o}^n,L} k_s^{-1}) = \mathbb {K}_{\mathfrak {o}^{n_1},L_1} \times \dots \times \mathbb {K}_{\mathfrak {o}^{n_r},L_r}$
. Namely,
![]() $q(P_{\mathbf {n}} \cap g \mathbb {K}_{n,[M]} g^{-1})$
is a
$q(P_{\mathbf {n}} \cap g \mathbb {K}_{n,[M]} g^{-1})$
is a
![]() $G_{n_1} \times \cdots \times G_{n_r}$
-conjugate of
$G_{n_1} \times \cdots \times G_{n_r}$
-conjugate of
![]() $\mathbb {K}_{n_1,[\mathrm {Gr}^{\mathrm {F}}_1 M]} \times \cdots \times \mathbb {K}_{n_r,[\mathrm {Gr}^{\mathrm {F}}_r M]}$
. This completes the proof of Proposition 5.2.
$\mathbb {K}_{n_1,[\mathrm {Gr}^{\mathrm {F}}_1 M]} \times \cdots \times \mathbb {K}_{n_r,[\mathrm {Gr}^{\mathrm {F}}_r M]}$
. This completes the proof of Proposition 5.2.
Remark 5.4. One can interpret the statement and the proof of Proposition 5.2 in terms of the topos theory. For more precise statements, see the previous paper of the second and third authors [Reference Kondo and Yasuda18].
5.2 Proof of the main theorems: a reduction step
Let
![]() $\pi $
be an irreducible representation of
$\pi $
be an irreducible representation of
![]() $G_n$
. Then we can write
$G_n$
. Then we can write
![]() $\pi = \pi ' \times \pi _1 \times \dots \times \pi _r$
as an irreducible parabolic induction such that
$\pi = \pi ' \times \pi _1 \times \dots \times \pi _r$
as an irreducible parabolic induction such that
-
•
 $\pi '$
is an irreducible representation such that
$\pi '$
is an irreducible representation such that
 $L(s,\pi ') = 1$
;
$L(s,\pi ') = 1$
; -
•
 $\pi _i = Z(\mathfrak {m}_i)$
with
$\pi _i = Z(\mathfrak {m}_i)$
with
 $\mathfrak {m}_i$
of type
$\mathfrak {m}_i$
of type
 $\chi _i$
for some unramified character
$\chi _i$
for some unramified character
 $\chi _i$
of
$\chi _i$
of
 $F^{\times }$
;
$F^{\times }$
; -
• if
 $i \not = j$
, then
$i \not = j$
, then
 $\chi _i\chi _j^{-1}$
is not of the form
$\chi _i\chi _j^{-1}$
is not of the form
 $|\cdot |^a$
for any
$|\cdot |^a$
for any
 $a \in \mathbb {Z}$
.
$a \in \mathbb {Z}$
.
If we knew Theorem 2.1 (respectively, Theorem 2.2) for
![]() $\pi '$
and
$\pi '$
and
![]() $\pi _i$
for
$\pi _i$
for
![]() $1 \leq i \leq r$
, by Proposition 5.2 and Corollary 4.7, we would obtain the same theorem for
$1 \leq i \leq r$
, by Proposition 5.2 and Corollary 4.7, we would obtain the same theorem for
![]() $\pi $
. In other words, Theorems 2.1 and 2.2 are reduced to the following two cases:
$\pi $
. In other words, Theorems 2.1 and 2.2 are reduced to the following two cases:
-
• The case where
 $\pi = Z(\mathfrak {m})$
with
$\pi = Z(\mathfrak {m})$
with
 $\mathfrak {m}$
of type
$\mathfrak {m}$
of type
 $\chi $
for some unramified character
$\chi $
for some unramified character
 $\chi $
of
$\chi $
of
 $F^{\times }$
;
$F^{\times }$
; -
• The case where
 $L(s,\pi ) = 1$
.
$L(s,\pi ) = 1$
.
We will deal with the first case in Section 6, and the second case will be treated in Sections 7 and 9.
6 Proof of the main theorems: the unipotent case
In this section, we prove Theorems 2.1 and 2.2 for
![]() $\pi = Z(\mathfrak {m})$
with
$\pi = Z(\mathfrak {m})$
with
![]() $\mathfrak {m}$
of type
$\mathfrak {m}$
of type
![]() $\chi $
for some unramified character
$\chi $
for some unramified character
![]() $\chi $
of
$\chi $
of
![]() $F^{\times }$
.
$F^{\times }$
.
6.1 Proof of Theorem 2.1 for ladder representations of type
 $\chi $
$\chi $
In this section, we prove Theorem 2.1 in the case where
![]() $\pi = Z([x_1,y_1]_{\chi }, \dots , [x_t,y_t]_{\chi }) \in \mathrm {Irr}(G_n)$
is of type
$\pi = Z([x_1,y_1]_{\chi }, \dots , [x_t,y_t]_{\chi }) \in \mathrm {Irr}(G_n)$
is of type
![]() $\chi $
with an unramified character
$\chi $
with an unramified character
![]() $\chi $
of
$\chi $
of
![]() $F^{\times }$
such that
$F^{\times }$
such that
![]() $\pi $
is a ladder representation: that is,
$\pi $
is a ladder representation: that is,
![]() $x_1> \dots > x_t$
and
$x_1> \dots > x_t$
and
![]() $y_1> \dots > y_t$
. Recall from Example 2.5 (2) that
$y_1> \dots > y_t$
. Recall from Example 2.5 (2) that
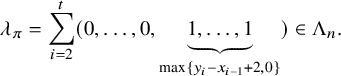 $$\begin{align*}\lambda_{\pi} = \sum_{i=2}^t(0,\dots,0, \underbrace{1,\dots,1}_{\max\{y_i-x_{i-1}+2,0\}}) \in \Lambda_n. \end{align*}$$
$$\begin{align*}\lambda_{\pi} = \sum_{i=2}^t(0,\dots,0, \underbrace{1,\dots,1}_{\max\{y_i-x_{i-1}+2,0\}}) \in \Lambda_n. \end{align*}$$
For
![]() $[M] \in |\mathcal {C}^n|$
, and for a partition
$[M] \in |\mathcal {C}^n|$
, and for a partition
![]() $\mathbf {n} = (n_1, \dots , n_{t})$
of n with
$\mathbf {n} = (n_1, \dots , n_{t})$
of n with
![]() $n_i \in \mathbb {Z}$
, we set
$n_i \in \mathbb {Z}$
, we set
![]() $\mathcal {N}_{\mathbf {n}}(M)$
to be the number of
$\mathcal {N}_{\mathbf {n}}(M)$
to be the number of
![]() $\mathbf {n}$
-admissible filtrations of M. Here, when
$\mathbf {n}$
-admissible filtrations of M. Here, when
![]() $n_i < 0$
for some i, we understand that
$n_i < 0$
for some i, we understand that
![]() $\mathcal {N}_{\mathbf {n}}(M) = 0$
.
$\mathcal {N}_{\mathbf {n}}(M) = 0$
.
Proposition 6.1. We have
where
![]() $\mathbf {n}_w = (y_1-x_{w(1)}+1,\dots , y_t-x_{w(t)}+1)$
.
$\mathbf {n}_w = (y_1-x_{w(1)}+1,\dots , y_t-x_{w(t)}+1)$
.
Proof. By the determinantal formula [Reference Lapid and Mínguez21], in the Grothendieck group of the category of representations of
![]() $G_n$
of finite length, we have
$G_n$
of finite length, we have
Here, when
![]() $x = y+1$
(respectively,
$x = y+1$
(respectively,
![]() $x> y+1$
), we formally set
$x> y+1$
), we formally set
![]() $Z([x,y]_{\chi }) = \mathbf {1}_{G_0}$
(respectively,
$Z([x,y]_{\chi }) = \mathbf {1}_{G_0}$
(respectively,
![]() $Z([x,y]_{\chi }) = 0$
). Note that in [Reference Lapid and Mínguez21], the determinantal formula was formulated using the Langlands classification, but by taking the Zelevinsky dual, it translates to the statement above.
$Z([x,y]_{\chi }) = 0$
). Note that in [Reference Lapid and Mínguez21], the determinantal formula was formulated using the Langlands classification, but by taking the Zelevinsky dual, it translates to the statement above.
Recall that for a compact open subgroup
![]() $\mathbb {K}$
of
$\mathbb {K}$
of
![]() $G_n$
, the functor
$G_n$
, the functor
![]() $\pi \mapsto \pi ^{\mathbb {K}}$
is exact. Hence, by Proposition 5.2, we have
$\pi \mapsto \pi ^{\mathbb {K}}$
is exact. Hence, by Proposition 5.2, we have
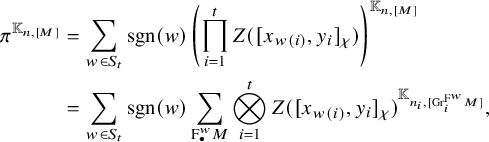 $$ \begin{align*} \pi^{\mathbb{K}_{n,[M]}} &= \sum_{w \in S_t} \mathrm{sgn}(w) \left(\prod_{i=1}^t Z([x_{w(i)}, y_i]_{\chi})\right)^{\mathbb{K}_{n,[M]}} \\ &= \sum_{w \in S_t} \mathrm{sgn}(w) \sum_{\mathrm{F}_{\bullet}^w M} \bigotimes_{i=1}^t Z([x_{w(i)}, y_i]_{\chi})^{\mathbb{K}_{n_i, [\mathrm{Gr}^{\mathrm{F}^w}_i M]}}, \end{align*} $$
$$ \begin{align*} \pi^{\mathbb{K}_{n,[M]}} &= \sum_{w \in S_t} \mathrm{sgn}(w) \left(\prod_{i=1}^t Z([x_{w(i)}, y_i]_{\chi})\right)^{\mathbb{K}_{n,[M]}} \\ &= \sum_{w \in S_t} \mathrm{sgn}(w) \sum_{\mathrm{F}_{\bullet}^w M} \bigotimes_{i=1}^t Z([x_{w(i)}, y_i]_{\chi})^{\mathbb{K}_{n_i, [\mathrm{Gr}^{\mathrm{F}^w}_i M]}}, \end{align*} $$
where
![]() $\mathrm {F}_{\bullet }^w M$
runs over the set of
$\mathrm {F}_{\bullet }^w M$
runs over the set of
![]() $\mathbf {n}_w$
-admissible filtrations with
$\mathbf {n}_w$
-admissible filtrations with
![]() $\mathbf {n}_w = (y_1-x_{w(1)}+1,\dots , y_t-x_{w(t)}+1)$
. Here, if
$\mathbf {n}_w = (y_1-x_{w(1)}+1,\dots , y_t-x_{w(t)}+1)$
. Here, if
![]() $y_i-x_{w(i)}+1 < 0$
for some i, we understand that there is no
$y_i-x_{w(i)}+1 < 0$
for some i, we understand that there is no
![]() $\mathbf {n}_w$
-admissible filtration. Since
$\mathbf {n}_w$
-admissible filtration. Since
![]() $Z([x_{w(i)},y_i]_{\chi })$
is a character which is trivial on
$Z([x_{w(i)},y_i]_{\chi })$
is a character which is trivial on
![]() $\mathrm {GL}_{y_i-x_{w(i)}+1}(\mathfrak {o})$
, the dimension of
$\mathrm {GL}_{y_i-x_{w(i)}+1}(\mathfrak {o})$
, the dimension of
![]() $Z([x_{w(i)},y_i]_{\chi })^{\mathbb {K}_{n_i, [\mathrm {Gr}^{\mathrm {F}^w}_i M]}}$
is always one if
$Z([x_{w(i)},y_i]_{\chi })^{\mathbb {K}_{n_i, [\mathrm {Gr}^{\mathrm {F}^w}_i M]}}$
is always one if
![]() $y_i-x_{w(i)}+1 \geq 0$
. Hence we obtain the assertion.
$y_i-x_{w(i)}+1 \geq 0$
. Hence we obtain the assertion.
Set
![]() $b = \max _{2 \leq i \leq t}\max \{y_i-x_{i-1}+2,0\}$
. If
$b = \max _{2 \leq i \leq t}\max \{y_i-x_{i-1}+2,0\}$
. If
![]() $b = 0$
, then
$b = 0$
, then
![]() $\pi $
is unramified so that Theorem 2.1 is trivial for
$\pi $
is unramified so that Theorem 2.1 is trivial for
![]() $\pi $
. Hence we may assume that
$\pi $
. Hence we may assume that
![]() $b> 0$
. Let
$b> 0$
. Let
![]() $[M_{\pi }] \in |\mathcal {C}^n|$
be such that
$[M_{\pi }] \in |\mathcal {C}^n|$
be such that
![]() $\mathrm {seq}_n([M_{\pi }]) = \lambda _{\pi }$
. Then
$\mathrm {seq}_n([M_{\pi }]) = \lambda _{\pi }$
. Then
![]() $M_{\pi } \cong \oplus _{i=1}^b \mathfrak {o}/\mathfrak {p}^{a_i}$
for some
$M_{\pi } \cong \oplus _{i=1}^b \mathfrak {o}/\mathfrak {p}^{a_i}$
for some
![]() $a_i \geq 1$
.
$a_i \geq 1$
.
Lemma 6.2. If
![]() $[M] \leq [M_{\pi }]$
, for any filtration
$[M] \leq [M_{\pi }]$
, for any filtration
![]() $\mathrm {F}_{\bullet } M$
, the
$\mathrm {F}_{\bullet } M$
, the
![]() $\mathfrak {o}$
-module
$\mathfrak {o}$
-module
![]() $[\mathrm {Gr}_i^{\mathrm {F}} M]$
can be generated by at most b elements.
$[\mathrm {Gr}_i^{\mathrm {F}} M]$
can be generated by at most b elements.
Proof. This follows from Lemma 4.3.
Now we calculate the alternating sum on the right-hand side of Proposition 6.1. We will see that there are many nontrivial cancellations. See Section 6.2 below for an explicit example of this calculation.
Choose
![]() $2 \leq a \leq t$
such that
$2 \leq a \leq t$
such that
![]() $y_a-x_{a-1}+2 = b$
. The following lemma is a key in computing the alternating sum in the right-hand side of Proposition 6.1.
$y_a-x_{a-1}+2 = b$
. The following lemma is a key in computing the alternating sum in the right-hand side of Proposition 6.1.
Lemma 6.3. Suppose that
![]() $[M] \leq [M_{\pi }]$
.
$[M] \leq [M_{\pi }]$
.
-
(1) Let
 $X_1$
be the subset of
$X_1$
be the subset of
 $S_t$
consisting of w such that
$S_t$
consisting of w such that
 $w(k) \geq a-1$
for any
$w(k) \geq a-1$
for any
 $k \geq a$
. For
$k \geq a$
. For
 $w \in S_t \setminus X_1$
, take
$w \in S_t \setminus X_1$
, take
 $1 \leq i,j \leq a-1$
such that
$1 \leq i,j \leq a-1$
such that
 $w(i)$
achieves the largest value and
$w(i)$
achieves the largest value and
 $w(j)$
achieves the second-largest value among
$w(j)$
achieves the second-largest value among
 $\{w(1), \dots , w(a-1)\}$
, and set
$\{w(1), \dots , w(a-1)\}$
, and set
 $w' = w(i,j)$
. Then
$w' = w(i,j)$
. Then
 $w(i), w(j) \geq a-1$
, and the map
$w(i), w(j) \geq a-1$
, and the map
 $w \mapsto w'$
is an involution on
$w \mapsto w'$
is an involution on
 $S_t \setminus X_1$
. Moreover,
$S_t \setminus X_1$
. Moreover,
 $\mathcal {N}_{\mathbf {n}_w}(M) = \mathcal {N}_{\mathbf {n}_{w'}}(M)$
. In particular,
$\mathcal {N}_{\mathbf {n}_w}(M) = \mathcal {N}_{\mathbf {n}_{w'}}(M)$
. In particular,  $$\begin{align*}\sum_{w \in S_t \setminus X_1}\mathrm{sgn}(w) \mathcal{N}_{\mathbf{n}_w}(M) = 0. \end{align*}$$
$$\begin{align*}\sum_{w \in S_t \setminus X_1}\mathrm{sgn}(w) \mathcal{N}_{\mathbf{n}_w}(M) = 0. \end{align*}$$
-
(2) Let
 $X_2$
be the subset of
$X_2$
be the subset of
 $X_1$
consisting of w such that
$X_1$
consisting of w such that
 $w(k) \geq a$
for any
$w(k) \geq a$
for any
 $k> a$
. For
$k> a$
. For
 $w \in X_1 \setminus X_2$
, take a unique
$w \in X_1 \setminus X_2$
, take a unique
 $1 \leq i \leq a-1$
such that
$1 \leq i \leq a-1$
such that
 $w(i) \geq a$
, and set
$w(i) \geq a$
, and set
 $w' = w(i,a)$
. Then the map
$w' = w(i,a)$
. Then the map
 $w \mapsto w'$
is an involution on
$w \mapsto w'$
is an involution on
 $X_1 \setminus X_2$
. Moreover,
$X_1 \setminus X_2$
. Moreover,
 $\mathcal {N}_{\mathbf {n}_w}(M) = \mathcal {N}_{\mathbf {n}_{w'}}(M)$
. In particular,
$\mathcal {N}_{\mathbf {n}_w}(M) = \mathcal {N}_{\mathbf {n}_{w'}}(M)$
. In particular,  $$\begin{align*}\sum_{w \in X_1 \setminus X_2}\mathrm{sgn}(w) \mathcal{N}_{\mathbf{n}_w}(M) = 0. \end{align*}$$
$$\begin{align*}\sum_{w \in X_1 \setminus X_2}\mathrm{sgn}(w) \mathcal{N}_{\mathbf{n}_w}(M) = 0. \end{align*}$$
-
(3) Let
 $S_{(a-1,t-a+1)}$
be the subgroup of
$S_{(a-1,t-a+1)}$
be the subgroup of
 $S_t$
consisting of w such that
$S_t$
consisting of w such that
 $w(k) \geq a$
for any
$w(k) \geq a$
for any
 $k \geq a$
, and set
$k \geq a$
, and set
 $X_3 = \{(a-1,w(a))w \;|\; w \in S_{(a-1,t-a+1)}\}$
. Then
$X_3 = \{(a-1,w(a))w \;|\; w \in S_{(a-1,t-a+1)}\}$
. Then  $$\begin{align*}X_2 = S_{(a-1,t-a+1)} \sqcup X_3. \end{align*}$$
$$\begin{align*}X_2 = S_{(a-1,t-a+1)} \sqcup X_3. \end{align*}$$
-
(4) Let
 $X_4$
be the subset of
$X_4$
be the subset of
 $S_t$
consisting of w such that
$S_t$
consisting of w such that
 $w(a) = a-1$
and
$w(a) = a-1$
and
 $w(k) < a-1$
for some
$w(k) < a-1$
for some
 $k> a$
. Then
$k> a$
. Then
 $X_4 \subset S_t \setminus X_1$
, and the involution in (1) preserves
$X_4 \subset S_t \setminus X_1$
, and the involution in (1) preserves
 $X_4$
. Moreover, the disjoint union
$X_4$
. Moreover, the disjoint union
 $X_3 \sqcup X_4$
is equal to the subset of
$X_3 \sqcup X_4$
is equal to the subset of
 $S_t$
consisting of w such that
$S_t$
consisting of w such that
 $w(a) = a-1$
.
$w(a) = a-1$
. -
(5) For
 $w \in X_4$
, take
$w \in X_4$
, take
 $1 \le i \leq a-1$
such that
$1 \le i \leq a-1$
such that
 $w(i)$
achieves the largest value among
$w(i)$
achieves the largest value among
 $\{w(1), \dots , w(a-1)\}$
, in particular
$\{w(1), \dots , w(a-1)\}$
, in particular
 $w(i) \geq a$
. Set
$w(i) \geq a$
. Set
 $\widetilde {w} = w(a,i)$
and
$\widetilde {w} = w(a,i)$
and
 $X_5 = \{\widetilde {w} \;|\; w \in X_4\}$
. Then
$X_5 = \{\widetilde {w} \;|\; w \in X_4\}$
. Then
 $X_5 \subset S_t \setminus X_1$
, and the involution in (1) preserves
$X_5 \subset S_t \setminus X_1$
, and the involution in (1) preserves
 $X_5$
.
$X_5$
.
Proof. We prove (1). Let
![]() $w \in S_t \setminus X_1$
and
$w \in S_t \setminus X_1$
and
![]() $1 \leq i,j \leq a-1$
be as in the statement. Note that i and j depend on w, but the map
$1 \leq i,j \leq a-1$
be as in the statement. Note that i and j depend on w, but the map
![]() $w \mapsto w'$
gives a well-defined involution on
$w \mapsto w'$
gives a well-defined involution on
![]() $S_t \setminus X_1$
. Since there exists
$S_t \setminus X_1$
. Since there exists
![]() $k \geq a$
such that
$k \geq a$
such that
![]() $w(k) < a-1$
, we notice that
$w(k) < a-1$
, we notice that
![]() $w(i),w(j) \geq a-1$
. Hence
$w(i),w(j) \geq a-1$
. Hence
By Lemma 6.2, we see that
![]() $\mathcal {N}_{\mathbf {n}_{w}}(M) = \mathcal {N}_{\mathbf {n}_{w'}}(M)$
. Since
$\mathcal {N}_{\mathbf {n}_{w}}(M) = \mathcal {N}_{\mathbf {n}_{w'}}(M)$
. Since
![]() $\mathrm {sgn}(w') = -\mathrm {sgn}(w)$
, the last part follows. Hence we obtain (1).
$\mathrm {sgn}(w') = -\mathrm {sgn}(w)$
, the last part follows. Hence we obtain (1).
We prove (2). When
![]() $w \in X_1 \setminus X_2$
, there exists
$w \in X_1 \setminus X_2$
, there exists
![]() $k> a$
such that
$k> a$
such that
![]() $w(k) = a-1$
. In particular,
$w(k) = a-1$
. In particular,
![]() $w(a) \geq a$
. Hence the map
$w(a) \geq a$
. Hence the map
![]() $w \mapsto w'$
gives a well-defined involution on
$w \mapsto w'$
gives a well-defined involution on
![]() $X_1 \setminus X_2$
. By the same argument as in (1), we obtain (2).
$X_1 \setminus X_2$
. By the same argument as in (1), we obtain (2).
Assertions (3) are (4) are obvious from the definitions.
We prove (5). Let
![]() $w \in X_4$
. Then
$w \in X_4$
. Then
![]() $\widetilde {w}(k) = w(k) < a-1$
for some
$\widetilde {w}(k) = w(k) < a-1$
for some
![]() $k> a$
so that
$k> a$
so that
![]() $\widetilde {w} \not \in X_1$
. Take
$\widetilde {w} \not \in X_1$
. Take
![]() $1 \leq i \leq a-1$
as in the statement so that
$1 \leq i \leq a-1$
as in the statement so that
![]() $\widetilde {w} = w(a,i)$
. Note that
$\widetilde {w} = w(a,i)$
. Note that
![]() $\widetilde {w}(a) = w(i) \geq a$
. Let
$\widetilde {w}(a) = w(i) \geq a$
. Let
![]() $1 \leq j_1,j_2 \leq a-1$
be such that
$1 \leq j_1,j_2 \leq a-1$
be such that
![]() $\widetilde {w}(j_1)$
(respectively,
$\widetilde {w}(j_1)$
(respectively,
![]() $\widetilde {w}(j_2)$
) achieves the largest (respectively, the second-largest) value among
$\widetilde {w}(j_2)$
) achieves the largest (respectively, the second-largest) value among
![]() $\{\widetilde {w}(1), \dots , \widetilde {w}(a-1)\}$
. Note that
$\{\widetilde {w}(1), \dots , \widetilde {w}(a-1)\}$
. Note that
![]() $a \leq \widetilde {w}(j_1) < w(i)$
and
$a \leq \widetilde {w}(j_1) < w(i)$
and
![]() $\widetilde {w}(j_2) \geq a-1$
. If
$\widetilde {w}(j_2) \geq a-1$
. If
![]() $\widetilde {w}(j_2) \geq a$
, then
$\widetilde {w}(j_2) \geq a$
, then
![]() $j_1,j_2,i,a$
are all distinct from each other. In this case,
$j_1,j_2,i,a$
are all distinct from each other. In this case,
Hence we have
![]() $(\widetilde {w})' \in X_5$
. If
$(\widetilde {w})' \in X_5$
. If
![]() $\widetilde {w}(j_2) = a-1$
, then
$\widetilde {w}(j_2) = a-1$
, then
![]() $j_2 = i$
. In this case,
$j_2 = i$
. In this case,
Hence we again have
![]() $(\widetilde {w})' \in X_5$
.
$(\widetilde {w})' \in X_5$
.
Now we prove Theorem 2.1 for a ladder representation
![]() $\pi = Z([x_1,y_1]_{\chi }, \dots , [x_t,y_t]_{\chi })$
of type
$\pi = Z([x_1,y_1]_{\chi }, \dots , [x_t,y_t]_{\chi })$
of type
![]() $\chi $
with unramified character
$\chi $
with unramified character
![]() $\chi $
.
$\chi $
.
Proof of Theorem 2.1 for ladder representations of type
 $\chi $
$\chi $
When
![]() $b = 0$
, since
$b = 0$
, since
![]() $\pi $
is unramified, the assertion is trivial. From now on, we assume that
$\pi $
is unramified, the assertion is trivial. From now on, we assume that
![]() $b>0$
. In particular, one has
$b>0$
. In particular, one has
![]() $t \geq 2$
.
$t \geq 2$
.
Set
This is a ladder representation of some
![]() $G_{n'}$
. We claim that
$G_{n'}$
. We claim that
where
![]() $M'$
runs over the set of
$M'$
runs over the set of
![]() $\mathfrak {o}$
-submodules of M generated by exactly b elements.
$\mathfrak {o}$
-submodules of M generated by exactly b elements.
Suppose for a moment that this claim is true. Note that
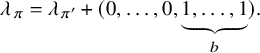 $$\begin{align*}\lambda_{\pi} = \lambda_{\pi'} + (0,\dots,0, \underbrace{1,\dots,1}_{b}). \end{align*}$$
$$\begin{align*}\lambda_{\pi} = \lambda_{\pi'} + (0,\dots,0, \underbrace{1,\dots,1}_{b}). \end{align*}$$
By induction on t, we may assume that we have
![]() $\dim (\pi ^{\prime \mathbb {K}_{n',[M/M']}}) = 0$
if
$\dim (\pi ^{\prime \mathbb {K}_{n',[M/M']}}) = 0$
if
![]() $[M/M'] < [M_{\pi '}]$
. In particular,
$[M/M'] < [M_{\pi '}]$
. In particular,
![]() $\dim (\pi ^{\mathbb {K}_{n,[M]}}) = 0$
if
$\dim (\pi ^{\mathbb {K}_{n,[M]}}) = 0$
if
![]() $[M] < [M_{\pi }]$
. Moreover, when
$[M] < [M_{\pi }]$
. Moreover, when
![]() $[M] = [M_{\pi }]$
, by Corollary 4.7, there exists a unique
$[M] = [M_{\pi }]$
, by Corollary 4.7, there exists a unique
![]() $\mathfrak {o}$
-submodule
$\mathfrak {o}$
-submodule
![]() $M'$
of M generated by exactly b elements such that
$M'$
of M generated by exactly b elements such that
![]() $[M/M'] = [M_{\pi '}]$
. Hence we have
$[M/M'] = [M_{\pi '}]$
. Hence we have
Therefore, the claim implies that
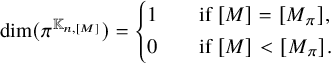 $$\begin{align*}\dim(\pi^{\mathbb{K}_{n,[M]}}) = \left\{ \begin{aligned} &1 &\quad&\text{if } [M] = [M_{\pi}], \\ &0 &\quad&\text{if } [M] < [M_{\pi}]. \end{aligned} \right. \end{align*}$$
$$\begin{align*}\dim(\pi^{\mathbb{K}_{n,[M]}}) = \left\{ \begin{aligned} &1 &\quad&\text{if } [M] = [M_{\pi}], \\ &0 &\quad&\text{if } [M] < [M_{\pi}]. \end{aligned} \right. \end{align*}$$
For the rest of the proof, we show the claim.
Let
![]() $X_1, X_2, X_3, X_4, X_5 \subset S_t$
be as in Lemma 6.3. We denote the inverse map of
$X_1, X_2, X_3, X_4, X_5 \subset S_t$
be as in Lemma 6.3. We denote the inverse map of
![]() $S_{(a-1,t-a+1)} \ni w \mapsto (a-1,w(a))w \in X_3$
by
$S_{(a-1,t-a+1)} \ni w \mapsto (a-1,w(a))w \in X_3$
by
![]() $X_3 \ni w \mapsto \widetilde {w} \in S_{(a-1,t-a+1)}$
. Then by Lemma 6.3 (1)–(3), we have
$X_3 \ni w \mapsto \widetilde {w} \in S_{(a-1,t-a+1)}$
. Then by Lemma 6.3 (1)–(3), we have
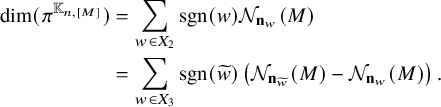 $$ \begin{align*} \dim(\pi^{\mathbb{K}_{n,[M]}}) &= \sum_{w \in X_2}\mathrm{sgn}(w) \mathcal{N}_{\mathbf{n}_w}(M) \\&= \sum_{w \in X_3}\mathrm{sgn}(\widetilde{w}) \left(\mathcal{N}_{\mathbf{n}_{\widetilde{w}}}(M) - \mathcal{N}_{\mathbf{n}_{w}}(M)\right). \end{align*} $$
$$ \begin{align*} \dim(\pi^{\mathbb{K}_{n,[M]}}) &= \sum_{w \in X_2}\mathrm{sgn}(w) \mathcal{N}_{\mathbf{n}_w}(M) \\&= \sum_{w \in X_3}\mathrm{sgn}(\widetilde{w}) \left(\mathcal{N}_{\mathbf{n}_{\widetilde{w}}}(M) - \mathcal{N}_{\mathbf{n}_{w}}(M)\right). \end{align*} $$
For
![]() $w \in X_3$
, there exists
$w \in X_3$
, there exists
![]() $1 \leq i_0 \leq a-1$
uniquely such that
$1 \leq i_0 \leq a-1$
uniquely such that
![]() $w(i_0) = \widetilde {w}(a) \geq a$
. Since
$w(i_0) = \widetilde {w}(a) \geq a$
. Since
![]() $w(a) = \widetilde {w}(i_0) = a-1$
, we have
$w(a) = \widetilde {w}(i_0) = a-1$
, we have
-
•
 $\min \{y_{i_0}-x_{w(i_0)}+1, y_{i_0}-x_{\widetilde {w}(i_0)}+1\} \geq y_a-x_{a-1}+2 = b$
;
$\min \{y_{i_0}-x_{w(i_0)}+1, y_{i_0}-x_{\widetilde {w}(i_0)}+1\} \geq y_a-x_{a-1}+2 = b$
; -
•
 $y_a-x_{\widetilde {w}(a)}+1 \geq b$
, whereas
$y_a-x_{\widetilde {w}(a)}+1 \geq b$
, whereas
 $y_a-x_{w(a)}+1 = b-1$
.
$y_a-x_{w(a)}+1 = b-1$
.
By Lemma 6.2,
![]() $\mathcal {N}_{\mathbf {n}_{\widetilde {w}}}(M)-\mathcal {N}_{\mathbf {n}_{w}}(M)$
is equal to the number of filtrations
$\mathcal {N}_{\mathbf {n}_{\widetilde {w}}}(M)-\mathcal {N}_{\mathbf {n}_{w}}(M)$
is equal to the number of filtrations
of M by
![]() $\mathfrak {o}$
-submodules such that
$\mathfrak {o}$
-submodules such that
-
•
 $\mathrm {Gr}_i^{\mathrm {F}} M$
is generated by at most
$\mathrm {Gr}_i^{\mathrm {F}} M$
is generated by at most
 $y_i-x_{w(i)}+1$
elements for
$y_i-x_{w(i)}+1$
elements for
 $i \not = a$
;
$i \not = a$
; -
•
 $\mathrm {Gr}_a^{\mathrm {F}} M$
is generated by exactly b elements.
$\mathrm {Gr}_a^{\mathrm {F}} M$
is generated by exactly b elements.
By Lemma 4.13, this number is equal to the number of pairs
![]() $(M', \mathrm {F}^{\prime }_{\bullet } (M/M'))$
, where
$(M', \mathrm {F}^{\prime }_{\bullet } (M/M'))$
, where
![]() $M' \subset M$
is an
$M' \subset M$
is an
![]() $\mathfrak {o}$
-submodule generated by exactly b elements and
$\mathfrak {o}$
-submodule generated by exactly b elements and
![]() $\mathrm {F}^{\prime }_{\bullet } (M/M')$
is a filtration
$\mathrm {F}^{\prime }_{\bullet } (M/M')$
is a filtration
of
![]() $M/M'$
by
$M/M'$
by
![]() $\mathfrak {o}$
-submodules such that
$\mathfrak {o}$
-submodules such that
![]() $\mathrm {Gr}_i^{\mathrm {F}'} (M/M')$
is generated by at most
$\mathrm {Gr}_i^{\mathrm {F}'} (M/M')$
is generated by at most
![]() $y_i-x_{w(i)}+1$
elements for
$y_i-x_{w(i)}+1$
elements for
![]() $i \not = a$
. Here, we set
$i \not = a$
. Here, we set
![]() $\mathrm {Gr}_i^{\mathrm {F}'} (M/M') = \mathrm {F}^{\prime }_i(M/M')/\mathrm {F}^{\prime }_{i-1}(M/M')$
unless
$\mathrm {Gr}_i^{\mathrm {F}'} (M/M') = \mathrm {F}^{\prime }_i(M/M')/\mathrm {F}^{\prime }_{i-1}(M/M')$
unless
![]() $i = a,a+1$
, and
$i = a,a+1$
, and
![]() $\mathrm {Gr}_{a+1}^{\mathrm {F}'} (M/M') = \mathrm {F}^{\prime }_{a+1}(M/M')/\mathrm {F}^{\prime }_{a-1}(M/M')$
. Therefore,
$\mathrm {Gr}_{a+1}^{\mathrm {F}'} (M/M') = \mathrm {F}^{\prime }_{a+1}(M/M')/\mathrm {F}^{\prime }_{a-1}(M/M')$
. Therefore,
where
![]() $M'$
runs over the set of
$M'$
runs over the set of
![]() $\mathfrak {o}$
-submodules of M generated by exactly b elements, and we set
$\mathfrak {o}$
-submodules of M generated by exactly b elements, and we set
![]() $\mathbf {n}^{\prime }_{w} = (n_{w,1},\dots ,n_{w,a-1},n_{w,a+1},\dots ,n_{w,t})$
with
$\mathbf {n}^{\prime }_{w} = (n_{w,1},\dots ,n_{w,a-1},n_{w,a+1},\dots ,n_{w,t})$
with
![]() $n_{w,i} = y_i-x_{w(i)}+1$
for
$n_{w,i} = y_i-x_{w(i)}+1$
for
![]() $i \not = a$
.
$i \not = a$
.
Note that
![]() $X_4 \cap X_5 = \emptyset $
. By the same argument as above, we have
$X_4 \cap X_5 = \emptyset $
. By the same argument as above, we have
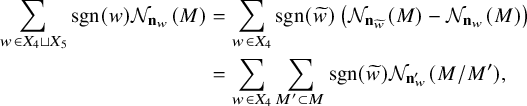 $$ \begin{align*} \sum_{w \in X_4 \sqcup X_5}\mathrm{sgn}(w) \mathcal{N}_{\mathbf{n}_w}(M) &= \sum_{w \in X_4} \mathrm{sgn}(\widetilde{w}) \left(\mathcal{N}_{\mathbf{n}_{\widetilde{w}}}(M) - \mathcal{N}_{\mathbf{n}_w}(M)\right) \\&= \sum_{w \in X_4} \sum_{M' \subset M} \mathrm{sgn}(\widetilde{w}) \mathcal{N}_{\mathbf{n}^{\prime}_{w}}(M/M'), \end{align*} $$
$$ \begin{align*} \sum_{w \in X_4 \sqcup X_5}\mathrm{sgn}(w) \mathcal{N}_{\mathbf{n}_w}(M) &= \sum_{w \in X_4} \mathrm{sgn}(\widetilde{w}) \left(\mathcal{N}_{\mathbf{n}_{\widetilde{w}}}(M) - \mathcal{N}_{\mathbf{n}_w}(M)\right) \\&= \sum_{w \in X_4} \sum_{M' \subset M} \mathrm{sgn}(\widetilde{w}) \mathcal{N}_{\mathbf{n}^{\prime}_{w}}(M/M'), \end{align*} $$
where
![]() $M'$
runs over the set of
$M'$
runs over the set of
![]() $\mathfrak {o}$
-submodules of M generated by exactly b elements, and
$\mathfrak {o}$
-submodules of M generated by exactly b elements, and
![]() $\mathbf {n}^{\prime }_{w}$
is as above. However, by Lemma 6.3 (1), (4), (5), we see that the left-hand side is zero. Therefore,
$\mathbf {n}^{\prime }_{w}$
is as above. However, by Lemma 6.3 (1), (4), (5), we see that the left-hand side is zero. Therefore,
Next, we consider the alternating sum
Here, we regard
![]() $S_{t-1}$
as the set of bijective maps
$S_{t-1}$
as the set of bijective maps
by identifying
![]() $a-1$
and a. For
$a-1$
and a. For
![]() $w \in X_3 \sqcup X_4$
, define
$w \in X_3 \sqcup X_4$
, define
![]() $w'$
to be the restriction of w to
$w'$
to be the restriction of w to
![]() $\{1,\dots ,a-1,a+1,\dots ,t\}$
. Then we have a bijective map
$\{1,\dots ,a-1,a+1,\dots ,t\}$
. Then we have a bijective map
![]() $X_3 \sqcup X_4 \rightarrow S_{t-1}$
since
$X_3 \sqcup X_4 \rightarrow S_{t-1}$
since
![]() $X_3 \sqcup X_4$
is the subset of
$X_3 \sqcup X_4$
is the subset of
![]() $S_t$
consisting of w such that
$S_t$
consisting of w such that
![]() $w(a) = a-1$
. Note that for
$w(a) = a-1$
. Note that for
![]() $w \in X_3 \sqcup X_4$
, the sign
$w \in X_3 \sqcup X_4$
, the sign
![]() $\mathrm {sgn}(w')$
of
$\mathrm {sgn}(w')$
of
![]() $w'$
as an element of
$w'$
as an element of
![]() $S_{t-1}$
is equal to
$S_{t-1}$
is equal to
![]() $\mathrm {sgn}(\widetilde {w})$
.
$\mathrm {sgn}(\widetilde {w})$
.
Therefore,
 $$ \begin{align*} \dim(\pi^{\mathbb{K}_{n,[M]}}) &= \sum_{M' \subset M} \sum_{w \in X_3 \sqcup X_4} \mathrm{sgn}(\widetilde{w}) \mathcal{N}_{\mathbf{n}^{\prime}_{w}}(M/M') \\&= \sum_{M' \subset M} \sum_{w' \in S_{t-1}} \mathrm{sgn}(w') \mathcal{N}_{\mathbf{n}^{\prime}_{w'}}(M/M') \\&= \sum_{M' \subset M} \dim(\pi^{\prime \mathbb{K}_{n',[M/M']}}). \end{align*} $$
$$ \begin{align*} \dim(\pi^{\mathbb{K}_{n,[M]}}) &= \sum_{M' \subset M} \sum_{w \in X_3 \sqcup X_4} \mathrm{sgn}(\widetilde{w}) \mathcal{N}_{\mathbf{n}^{\prime}_{w}}(M/M') \\&= \sum_{M' \subset M} \sum_{w' \in S_{t-1}} \mathrm{sgn}(w') \mathcal{N}_{\mathbf{n}^{\prime}_{w'}}(M/M') \\&= \sum_{M' \subset M} \dim(\pi^{\prime \mathbb{K}_{n',[M/M']}}). \end{align*} $$
Hence we obtain the claim. This completes the proof of Theorem 2.1 for ladder representations of type
![]() $\chi $
.
$\chi $
.
6.2 Example of calculation of the alternating sum
To understand the proof of Theorem 2.1 for ladder representations of type
![]() $\chi $
, the following explicit example may be helpful.
$\chi $
, the following explicit example may be helpful.
Example 6.4. For simplicity, we drop
![]() $\chi $
from the notation. Let us consider a ladder representation
$\chi $
from the notation. Let us consider a ladder representation
Then
![]() $\lambda _{\pi } = (0,\dots ,0,1,3,3,3) \in \Lambda _{15}$
so that
$\lambda _{\pi } = (0,\dots ,0,1,3,3,3) \in \Lambda _{15}$
so that
![]() $M_{\pi } = \mathfrak {o}/\mathfrak {p} \oplus (\mathfrak {o}/\mathfrak {p}^3)^{\oplus 3}$
. By the determinantal formula, we have
$M_{\pi } = \mathfrak {o}/\mathfrak {p} \oplus (\mathfrak {o}/\mathfrak {p}^3)^{\oplus 3}$
. By the determinantal formula, we have
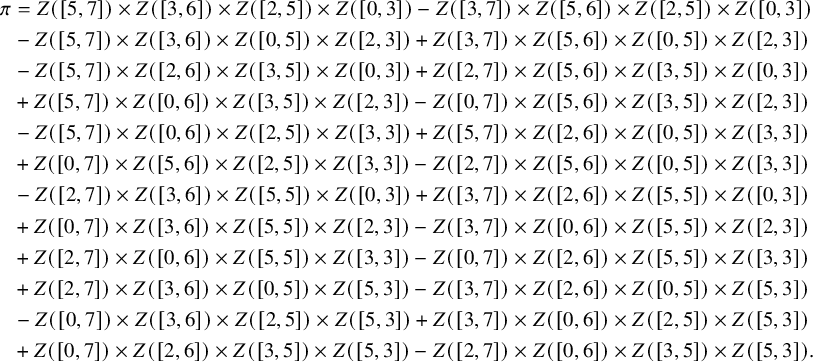 $$ \begin{align*} \pi &= Z([5,7]) \times Z([3,6]) \times Z([2,5]) \times Z([0,3]) -Z([3,7]) \times Z([5,6]) \times Z([2,5]) \times Z([0,3]) \\& -Z([5,7]) \times Z([3,6]) \times Z([0,5]) \times Z([2,3]) +Z([3,7]) \times Z([5,6]) \times Z([0,5]) \times Z([2,3]) \\& -Z([5,7]) \times Z([2,6]) \times Z([3,5]) \times Z([0,3]) +Z([2,7]) \times Z([5,6]) \times Z([3,5]) \times Z([0,3]) \\& +Z([5,7]) \times Z([0,6]) \times Z([3,5]) \times Z([2,3]) -Z([0,7]) \times Z([5,6]) \times Z([3,5]) \times Z([2,3]) \\& -Z([5,7]) \times Z([0,6]) \times Z([2,5]) \times Z([3,3]) +Z([5,7]) \times Z([2,6]) \times Z([0,5]) \times Z([3,3]) \\& +Z([0,7]) \times Z([5,6]) \times Z([2,5]) \times Z([3,3]) -Z([2,7]) \times Z([5,6]) \times Z([0,5]) \times Z([3,3]) \\& -Z([2,7]) \times Z([3,6]) \times Z([5,5]) \times Z([0,3]) +Z([3,7]) \times Z([2,6]) \times Z([5,5]) \times Z([0,3]) \\& +Z([0,7]) \times Z([3,6]) \times Z([5,5]) \times Z([2,3]) -Z([3,7]) \times Z([0,6]) \times Z([5,5]) \times Z([2,3]) \\& +Z([2,7]) \times Z([0,6]) \times Z([5,5]) \times Z([3,3]) -Z([0,7]) \times Z([2,6]) \times Z([5,5]) \times Z([3,3]) \\& +Z([2,7]) \times Z([3,6]) \times Z([0,5]) \times Z([5,3]) -Z([3,7]) \times Z([2,6]) \times Z([0,5]) \times Z([5,3]) \\& -Z([0,7]) \times Z([3,6]) \times Z([2,5]) \times Z([5,3]) +Z([3,7]) \times Z([0,6]) \times Z([2,5]) \times Z([5,3]) \\& +Z([0,7]) \times Z([2,6]) \times Z([3,5]) \times Z([5,3]) -Z([2,7]) \times Z([0,6]) \times Z([3,5]) \times Z([5,3]). \end{align*} $$
$$ \begin{align*} \pi &= Z([5,7]) \times Z([3,6]) \times Z([2,5]) \times Z([0,3]) -Z([3,7]) \times Z([5,6]) \times Z([2,5]) \times Z([0,3]) \\& -Z([5,7]) \times Z([3,6]) \times Z([0,5]) \times Z([2,3]) +Z([3,7]) \times Z([5,6]) \times Z([0,5]) \times Z([2,3]) \\& -Z([5,7]) \times Z([2,6]) \times Z([3,5]) \times Z([0,3]) +Z([2,7]) \times Z([5,6]) \times Z([3,5]) \times Z([0,3]) \\& +Z([5,7]) \times Z([0,6]) \times Z([3,5]) \times Z([2,3]) -Z([0,7]) \times Z([5,6]) \times Z([3,5]) \times Z([2,3]) \\& -Z([5,7]) \times Z([0,6]) \times Z([2,5]) \times Z([3,3]) +Z([5,7]) \times Z([2,6]) \times Z([0,5]) \times Z([3,3]) \\& +Z([0,7]) \times Z([5,6]) \times Z([2,5]) \times Z([3,3]) -Z([2,7]) \times Z([5,6]) \times Z([0,5]) \times Z([3,3]) \\& -Z([2,7]) \times Z([3,6]) \times Z([5,5]) \times Z([0,3]) +Z([3,7]) \times Z([2,6]) \times Z([5,5]) \times Z([0,3]) \\& +Z([0,7]) \times Z([3,6]) \times Z([5,5]) \times Z([2,3]) -Z([3,7]) \times Z([0,6]) \times Z([5,5]) \times Z([2,3]) \\& +Z([2,7]) \times Z([0,6]) \times Z([5,5]) \times Z([3,3]) -Z([0,7]) \times Z([2,6]) \times Z([5,5]) \times Z([3,3]) \\& +Z([2,7]) \times Z([3,6]) \times Z([0,5]) \times Z([5,3]) -Z([3,7]) \times Z([2,6]) \times Z([0,5]) \times Z([5,3]) \\& -Z([0,7]) \times Z([3,6]) \times Z([2,5]) \times Z([5,3]) +Z([3,7]) \times Z([0,6]) \times Z([2,5]) \times Z([5,3]) \\& +Z([0,7]) \times Z([2,6]) \times Z([3,5]) \times Z([5,3]) -Z([2,7]) \times Z([0,6]) \times Z([3,5]) \times Z([5,3]). \end{align*} $$
By Proposition 5.2, we have
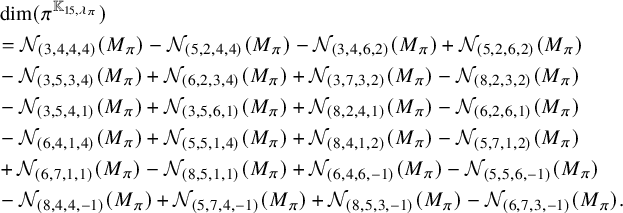 $$ \begin{align*} &\dim(\pi^{\mathbb{K}_{15,\lambda_{\pi}}}) \\&= \mathcal{N}_{(3,4,4,4)}(M_{\pi})-\mathcal{N}_{(5,2,4,4)}(M_{\pi}) -\mathcal{N}_{(3,4,6,2)}(M_{\pi})+\mathcal{N}_{(5,2,6,2)}(M_{\pi}) \\& -\mathcal{N}_{(3,5,3,4)}(M_{\pi})+\mathcal{N}_{(6,2,3,4)}(M_{\pi}) +\mathcal{N}_{(3,7,3,2)}(M_{\pi})-\mathcal{N}_{(8,2,3,2)}(M_{\pi}) \\& -\mathcal{N}_{(3,5,4,1)}(M_{\pi})+\mathcal{N}_{(3,5,6,1)}(M_{\pi}) +\mathcal{N}_{(8,2,4,1)}(M_{\pi})-\mathcal{N}_{(6,2,6,1)}(M_{\pi}) \\& -\mathcal{N}_{(6,4,1,4)}(M_{\pi})+\mathcal{N}_{(5,5,1,4)}(M_{\pi}) +\mathcal{N}_{(8,4,1,2)}(M_{\pi})-\mathcal{N}_{(5,7,1,2)}(M_{\pi}) \\& +\mathcal{N}_{(6,7,1,1)}(M_{\pi})-\mathcal{N}_{(8,5,1,1)}(M_{\pi}) +\mathcal{N}_{(6,4,6,-1)}(M_{\pi})-\mathcal{N}_{(5,5,6,-1)}(M_{\pi}) \\& -\mathcal{N}_{(8,4,4,-1)}(M_{\pi})+\mathcal{N}_{(5,7,4,-1)}(M_{\pi}) +\mathcal{N}_{(8,5,3,-1)}(M_{\pi})-\mathcal{N}_{(6,7,3,-1)}(M_{\pi}). \end{align*} $$
$$ \begin{align*} &\dim(\pi^{\mathbb{K}_{15,\lambda_{\pi}}}) \\&= \mathcal{N}_{(3,4,4,4)}(M_{\pi})-\mathcal{N}_{(5,2,4,4)}(M_{\pi}) -\mathcal{N}_{(3,4,6,2)}(M_{\pi})+\mathcal{N}_{(5,2,6,2)}(M_{\pi}) \\& -\mathcal{N}_{(3,5,3,4)}(M_{\pi})+\mathcal{N}_{(6,2,3,4)}(M_{\pi}) +\mathcal{N}_{(3,7,3,2)}(M_{\pi})-\mathcal{N}_{(8,2,3,2)}(M_{\pi}) \\& -\mathcal{N}_{(3,5,4,1)}(M_{\pi})+\mathcal{N}_{(3,5,6,1)}(M_{\pi}) +\mathcal{N}_{(8,2,4,1)}(M_{\pi})-\mathcal{N}_{(6,2,6,1)}(M_{\pi}) \\& -\mathcal{N}_{(6,4,1,4)}(M_{\pi})+\mathcal{N}_{(5,5,1,4)}(M_{\pi}) +\mathcal{N}_{(8,4,1,2)}(M_{\pi})-\mathcal{N}_{(5,7,1,2)}(M_{\pi}) \\& +\mathcal{N}_{(6,7,1,1)}(M_{\pi})-\mathcal{N}_{(8,5,1,1)}(M_{\pi}) +\mathcal{N}_{(6,4,6,-1)}(M_{\pi})-\mathcal{N}_{(5,5,6,-1)}(M_{\pi}) \\& -\mathcal{N}_{(8,4,4,-1)}(M_{\pi})+\mathcal{N}_{(5,7,4,-1)}(M_{\pi}) +\mathcal{N}_{(8,5,3,-1)}(M_{\pi})-\mathcal{N}_{(6,7,3,-1)}(M_{\pi}). \end{align*} $$
By Lemma 6.2, we have
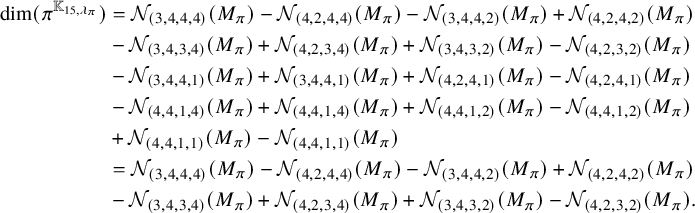 $$ \begin{align*} \dim(\pi^{\mathbb{K}_{15,\lambda_{\pi}}}) &= \mathcal{N}_{(3,4,4,4)}(M_{\pi})-\mathcal{N}_{(4,2,4,4)}(M_{\pi}) -\mathcal{N}_{(3,4,4,2)}(M_{\pi})+\mathcal{N}_{(4,2,4,2)}(M_{\pi}) \\& -\mathcal{N}_{(3,4,3,4)}(M_{\pi})+\mathcal{N}_{(4,2,3,4)}(M_{\pi}) +\mathcal{N}_{(3,4,3,2)}(M_{\pi})-\mathcal{N}_{(4,2,3,2)}(M_{\pi}) \\& -\mathcal{N}_{(3,4,4,1)}(M_{\pi})+\mathcal{N}_{(3,4,4,1)}(M_{\pi}) +\mathcal{N}_{(4,2,4,1)}(M_{\pi})-\mathcal{N}_{(4,2,4,1)}(M_{\pi}) \\& -\mathcal{N}_{(4,4,1,4)}(M_{\pi})+\mathcal{N}_{(4,4,1,4)}(M_{\pi}) +\mathcal{N}_{(4,4,1,2)}(M_{\pi})-\mathcal{N}_{(4,4,1,2)}(M_{\pi}) \\& +\mathcal{N}_{(4,4,1,1)}(M_{\pi})-\mathcal{N}_{(4,4,1,1)}(M_{\pi}) \\&= \mathcal{N}_{(3,4,4,4)}(M_{\pi})-\mathcal{N}_{(4,2,4,4)}(M_{\pi}) -\mathcal{N}_{(3,4,4,2)}(M_{\pi})+\mathcal{N}_{(4,2,4,2)}(M_{\pi}) \\& -\mathcal{N}_{(3,4,3,4)}(M_{\pi})+\mathcal{N}_{(4,2,3,4)}(M_{\pi}) +\mathcal{N}_{(3,4,3,2)}(M_{\pi})-\mathcal{N}_{(4,2,3,2)}(M_{\pi}). \end{align*} $$
$$ \begin{align*} \dim(\pi^{\mathbb{K}_{15,\lambda_{\pi}}}) &= \mathcal{N}_{(3,4,4,4)}(M_{\pi})-\mathcal{N}_{(4,2,4,4)}(M_{\pi}) -\mathcal{N}_{(3,4,4,2)}(M_{\pi})+\mathcal{N}_{(4,2,4,2)}(M_{\pi}) \\& -\mathcal{N}_{(3,4,3,4)}(M_{\pi})+\mathcal{N}_{(4,2,3,4)}(M_{\pi}) +\mathcal{N}_{(3,4,3,2)}(M_{\pi})-\mathcal{N}_{(4,2,3,2)}(M_{\pi}) \\& -\mathcal{N}_{(3,4,4,1)}(M_{\pi})+\mathcal{N}_{(3,4,4,1)}(M_{\pi}) +\mathcal{N}_{(4,2,4,1)}(M_{\pi})-\mathcal{N}_{(4,2,4,1)}(M_{\pi}) \\& -\mathcal{N}_{(4,4,1,4)}(M_{\pi})+\mathcal{N}_{(4,4,1,4)}(M_{\pi}) +\mathcal{N}_{(4,4,1,2)}(M_{\pi})-\mathcal{N}_{(4,4,1,2)}(M_{\pi}) \\& +\mathcal{N}_{(4,4,1,1)}(M_{\pi})-\mathcal{N}_{(4,4,1,1)}(M_{\pi}) \\&= \mathcal{N}_{(3,4,4,4)}(M_{\pi})-\mathcal{N}_{(4,2,4,4)}(M_{\pi}) -\mathcal{N}_{(3,4,4,2)}(M_{\pi})+\mathcal{N}_{(4,2,4,2)}(M_{\pi}) \\& -\mathcal{N}_{(3,4,3,4)}(M_{\pi})+\mathcal{N}_{(4,2,3,4)}(M_{\pi}) +\mathcal{N}_{(3,4,3,2)}(M_{\pi})-\mathcal{N}_{(4,2,3,2)}(M_{\pi}). \end{align*} $$
Note that if a filtration
![]() $\mathrm {F}_{\bullet } M_{\pi }$
satisfies that
$\mathrm {F}_{\bullet } M_{\pi }$
satisfies that
![]() $\mathrm {Gr}_3^{\mathrm {F}} M_{\pi }$
is generated by exactly
$\mathrm {Gr}_3^{\mathrm {F}} M_{\pi }$
is generated by exactly
![]() $4$
elements, then
$4$
elements, then
![]() $\mathrm {Gr}_i^{\mathrm {F}} M_{\pi }$
for
$\mathrm {Gr}_i^{\mathrm {F}} M_{\pi }$
for
![]() $i = 1,2,4$
can be generated by at most
$i = 1,2,4$
can be generated by at most
![]() $3$
elements by Lemmas 4.13, 4.3 and 6.2. Hence
$3$
elements by Lemmas 4.13, 4.3 and 6.2. Hence
 $$ \begin{align*} \mathcal{N}_{(3,4,4,4)}(M_{\pi})-\mathcal{N}_{(3,4,3,4)}(M_{\pi}) &= \mathcal{N}_{(3,3,4,3)}(M_{\pi})-\mathcal{N}_{(3,3,3,3)}(M_{\pi}), \\ \mathcal{N}_{(4,2,4,4)}(M_{\pi})-\mathcal{N}_{(4,2,3,4)}(M_{\pi}) &= \mathcal{N}_{(3,2,4,3)}(M_{\pi})-\mathcal{N}_{(3,2,3,3)}(M_{\pi}), \\ \mathcal{N}_{(3,4,4,2)}(M_{\pi})-\mathcal{N}_{(3,4,3,2)}(M_{\pi}) &= \mathcal{N}_{(3,3,4,2)}(M_{\pi})-\mathcal{N}_{(3,3,3,2)}(M_{\pi}), \\ \mathcal{N}_{(4,2,4,2)}(M_{\pi})-\mathcal{N}_{(4,2,3,2)}(M_{\pi}) &= \mathcal{N}_{(3,2,4,2)}(M_{\pi})-\mathcal{N}_{(3,2,3,2)}(M_{\pi}). \end{align*} $$
$$ \begin{align*} \mathcal{N}_{(3,4,4,4)}(M_{\pi})-\mathcal{N}_{(3,4,3,4)}(M_{\pi}) &= \mathcal{N}_{(3,3,4,3)}(M_{\pi})-\mathcal{N}_{(3,3,3,3)}(M_{\pi}), \\ \mathcal{N}_{(4,2,4,4)}(M_{\pi})-\mathcal{N}_{(4,2,3,4)}(M_{\pi}) &= \mathcal{N}_{(3,2,4,3)}(M_{\pi})-\mathcal{N}_{(3,2,3,3)}(M_{\pi}), \\ \mathcal{N}_{(3,4,4,2)}(M_{\pi})-\mathcal{N}_{(3,4,3,2)}(M_{\pi}) &= \mathcal{N}_{(3,3,4,2)}(M_{\pi})-\mathcal{N}_{(3,3,3,2)}(M_{\pi}), \\ \mathcal{N}_{(4,2,4,2)}(M_{\pi})-\mathcal{N}_{(4,2,3,2)}(M_{\pi}) &= \mathcal{N}_{(3,2,4,2)}(M_{\pi})-\mathcal{N}_{(3,2,3,2)}(M_{\pi}). \end{align*} $$
Therefore,
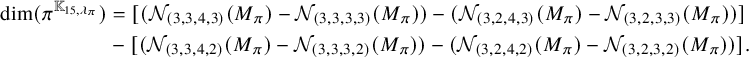 $$ \begin{align*} \dim(\pi^{\mathbb{K}_{15,\lambda_{\pi}}}) &= [(\mathcal{N}_{(3,3,4,3)}(M_{\pi})-\mathcal{N}_{(3,3,3,3)}(M_{\pi})) -(\mathcal{N}_{(3,2,4,3)}(M_{\pi})-\mathcal{N}_{(3,2,3,3)}(M_{\pi}))] \\&-[ (\mathcal{N}_{(3,3,4,2)}(M_{\pi})-\mathcal{N}_{(3,3,3,2)}(M_{\pi})) -(\mathcal{N}_{(3,2,4,2)}(M_{\pi})-\mathcal{N}_{(3,2,3,2)}(M_{\pi})) ]. \end{align*} $$
$$ \begin{align*} \dim(\pi^{\mathbb{K}_{15,\lambda_{\pi}}}) &= [(\mathcal{N}_{(3,3,4,3)}(M_{\pi})-\mathcal{N}_{(3,3,3,3)}(M_{\pi})) -(\mathcal{N}_{(3,2,4,3)}(M_{\pi})-\mathcal{N}_{(3,2,3,3)}(M_{\pi}))] \\&-[ (\mathcal{N}_{(3,3,4,2)}(M_{\pi})-\mathcal{N}_{(3,3,3,2)}(M_{\pi})) -(\mathcal{N}_{(3,2,4,2)}(M_{\pi})-\mathcal{N}_{(3,2,3,2)}(M_{\pi})) ]. \end{align*} $$
The right-hand side is equal to the number of filtrations
such that
-
•
 $\mathrm {Gr}^{\mathrm {F}}_2 M_{\pi }$
is generated by exactly
$\mathrm {Gr}^{\mathrm {F}}_2 M_{\pi }$
is generated by exactly
 $3$
elements;
$3$
elements; -
•
 $\mathrm {Gr}^{\mathrm {F}}_3 M_{\pi }$
is generated by exactly
$\mathrm {Gr}^{\mathrm {F}}_3 M_{\pi }$
is generated by exactly
 $4$
elements;
$4$
elements; -
•
 $\mathrm {Gr}^{\mathrm {F}}_4 M_{\pi }$
is generated by exactly
$\mathrm {Gr}^{\mathrm {F}}_4 M_{\pi }$
is generated by exactly
 $3$
elements.
$3$
elements.
Since
![]() $M_{\pi } = \mathfrak {o}/\mathfrak {p} \oplus (\mathfrak {o}/\mathfrak {p}^3)^{\oplus 3}$
, such a filtration exists uniquely and is given by
$M_{\pi } = \mathfrak {o}/\mathfrak {p} \oplus (\mathfrak {o}/\mathfrak {p}^3)^{\oplus 3}$
, such a filtration exists uniquely and is given by
Therefore, we conclude that
![]() $\dim (\pi ^{\mathbb {K}_{15,\lambda _{\pi }}}) = 1$
, as desired.
$\dim (\pi ^{\mathbb {K}_{15,\lambda _{\pi }}}) = 1$
, as desired.
6.3 Proof of Theorem 2.1 for general
 $Z(\mathfrak {m})$
of type
$Z(\mathfrak {m})$
of type
 $\chi $
$\chi $
Now we consider
![]() $\pi = Z(\mathfrak {m})$
with
$\pi = Z(\mathfrak {m})$
with
![]() $\mathfrak {m}$
of type
$\mathfrak {m}$
of type
![]() $\chi $
for some unramified character
$\chi $
for some unramified character
![]() $\chi $
of
$\chi $
of
![]() $F^{\times }$
.
$F^{\times }$
.
Lemma 6.5. Let
![]() $\mathfrak {m}_1$
and
$\mathfrak {m}_1$
and
![]() $\mathfrak {m}_2$
be multisegments. Then
$\mathfrak {m}_2$
be multisegments. Then
![]() $Z(\mathfrak {m}_1 + \mathfrak {m}_2)$
appears as a subquotient of
$Z(\mathfrak {m}_1 + \mathfrak {m}_2)$
appears as a subquotient of
![]() $Z(\mathfrak {m}_1) \times Z(\mathfrak {m}_2)$
with multiplicity one.
$Z(\mathfrak {m}_1) \times Z(\mathfrak {m}_2)$
with multiplicity one.
Proof. See [Reference Tadić38, Proposition 2.3] (or [Reference Lapid and Mínguez22, Proposition 3.5 (5)]).
Recall that when
![]() $\mathfrak {m} = \Delta _1+\dots +\Delta _r$
, we set
$\mathfrak {m} = \Delta _1+\dots +\Delta _r$
, we set
![]() $\mathrm {Card}(\mathfrak {m}) = r$
.
$\mathrm {Card}(\mathfrak {m}) = r$
.
Lemma 6.6. Let
![]() $\mathfrak {m}$
,
$\mathfrak {m}$
,
![]() $\mathfrak {m}_1$
and
$\mathfrak {m}_1$
and
![]() $\mathfrak {m}_2$
be multisegments. Suppose that
$\mathfrak {m}_2$
be multisegments. Suppose that
![]() $Z(\mathfrak {m})$
appears as a subquotient of
$Z(\mathfrak {m})$
appears as a subquotient of
![]() $Z(\mathfrak {m}_1) \times Z(\mathfrak {m}_2)$
. Then
$Z(\mathfrak {m}_1) \times Z(\mathfrak {m}_2)$
. Then
![]() $Z(\mathfrak {m}^{-})$
appears as a subquotient of
$Z(\mathfrak {m}^{-})$
appears as a subquotient of
![]() $Z(\mathfrak {m}_1^{-}) \times Z(\mathfrak {m}_2^{-})$
if and only if
$Z(\mathfrak {m}_1^{-}) \times Z(\mathfrak {m}_2^{-})$
if and only if
![]() $\mathrm {Card}(\mathfrak {m}) = \mathrm {Card}(\mathfrak {m}_1) + \mathrm {Card}(\mathfrak {m}_2)$
.
$\mathrm {Card}(\mathfrak {m}) = \mathrm {Card}(\mathfrak {m}_1) + \mathrm {Card}(\mathfrak {m}_2)$
.
Proof. Suppose that
![]() $Z(\mathfrak {m}^{-})$
appears as a subquotient of
$Z(\mathfrak {m}^{-})$
appears as a subquotient of
![]() $Z(\mathfrak {m}_1^{-}) \times Z(\mathfrak {m}_2^{-})$
. By considering cuspidal supports, we have
$Z(\mathfrak {m}_1^{-}) \times Z(\mathfrak {m}_2^{-})$
. By considering cuspidal supports, we have
![]() $l(\mathfrak {m}^{-}) = l(\mathfrak {m}_1^{-}) + l(\mathfrak {m}_2^{-})$
. For a similar reason, we have
$l(\mathfrak {m}^{-}) = l(\mathfrak {m}_1^{-}) + l(\mathfrak {m}_2^{-})$
. For a similar reason, we have
![]() $l(\mathfrak {m}) = l(\mathfrak {m}_1) + l(\mathfrak {m}_2)$
. Since
$l(\mathfrak {m}) = l(\mathfrak {m}_1) + l(\mathfrak {m}_2)$
. Since
![]() $l(\mathfrak {m}) = l(\mathfrak {m}^{-}) + \mathrm {Card}(\mathfrak {m})$
, we have the desired equality
$l(\mathfrak {m}) = l(\mathfrak {m}^{-}) + \mathrm {Card}(\mathfrak {m})$
, we have the desired equality
![]() $\mathrm {Card}(\mathfrak {m}) = \mathrm {Card}(\mathfrak {m}_1) + \mathrm {Card}(\mathfrak {m}_2)$
.
$\mathrm {Card}(\mathfrak {m}) = \mathrm {Card}(\mathfrak {m}_1) + \mathrm {Card}(\mathfrak {m}_2)$
.
Conversely, suppose that the equality
![]() $\mathrm {Card}(\mathfrak {m}) = \mathrm {Card}(\mathfrak {m}_1) + \mathrm {Card}(\mathfrak {m}_2)$
holds. We set
$\mathrm {Card}(\mathfrak {m}) = \mathrm {Card}(\mathfrak {m}_1) + \mathrm {Card}(\mathfrak {m}_2)$
holds. We set
![]() $c=\mathrm {Card}(\mathfrak {m})$
. Then the cth derivatives of
$c=\mathrm {Card}(\mathfrak {m})$
. Then the cth derivatives of
![]() $Z(\mathfrak {m})$
and
$Z(\mathfrak {m})$
and
![]() $Z(\mathfrak {m}_1) \times Z(\mathfrak {m}_2)$
are equal to
$Z(\mathfrak {m}_1) \times Z(\mathfrak {m}_2)$
are equal to
![]() $Z(\mathfrak {m}^{-})$
and
$Z(\mathfrak {m}^{-})$
and
![]() $Z(\mathfrak {m}_1^{-}) \times Z(\mathfrak {m}_2^{-})$
, respectively. Since the cth derivative is an exact functor (compare to [Reference Bernstein and Zelevinsky4, 3.2, 3.5]), the assertion follows.
$Z(\mathfrak {m}_1^{-}) \times Z(\mathfrak {m}_2^{-})$
, respectively. Since the cth derivative is an exact functor (compare to [Reference Bernstein and Zelevinsky4, 3.2, 3.5]), the assertion follows.
Proof of Theorem 2.1 for
 $\pi = Z(\mathfrak {m})$
of type
$\pi = Z(\mathfrak {m})$
of type
 $\chi $
$\chi $
Let
![]() $\pi = Z(\mathfrak {m})$
be an irreducible representation of
$\pi = Z(\mathfrak {m})$
be an irreducible representation of
![]() $G_n$
, where
$G_n$
, where
![]() $\mathfrak {m} = \Delta _1+\dots +\Delta _r$
is a multisegment of type
$\mathfrak {m} = \Delta _1+\dots +\Delta _r$
is a multisegment of type
![]() $\chi $
for some unramified character
$\chi $
for some unramified character
![]() $\chi $
of
$\chi $
of
![]() $F^{\times }$
. Let
$F^{\times }$
. Let
![]() $t_{\mathfrak {m}}$
be the number of pairs of linked segments in
$t_{\mathfrak {m}}$
be the number of pairs of linked segments in
![]() $\{\Delta _1, \dots , \Delta _r\}$
. Note that
$\{\Delta _1, \dots , \Delta _r\}$
. Note that
![]() $t_{\mathfrak {m}} \leq \binom {l(\mathfrak {m})}{2}$
since
$t_{\mathfrak {m}} \leq \binom {l(\mathfrak {m})}{2}$
since
![]() $r \leq l(\mathfrak {m})$
.
$r \leq l(\mathfrak {m})$
.
We prove the claim by induction on the element
![]() $(l(\mathfrak {m}),t_{\mathfrak {m}})$
in the set
$(l(\mathfrak {m}),t_{\mathfrak {m}})$
in the set
![]() $S = \{(l,t) \in \mathbb {Z}_{\ge 0}^2 \;|\; t \leq \binom {l}{2}\}$
. Here we endow this set with the following total order. We have
$S = \{(l,t) \in \mathbb {Z}_{\ge 0}^2 \;|\; t \leq \binom {l}{2}\}$
. Here we endow this set with the following total order. We have
![]() $(l,t) \le (l',t')$
if and only if we have either
$(l,t) \le (l',t')$
if and only if we have either
![]() $l<l'$
, or
$l<l'$
, or
![]() $l=l'$
and
$l=l'$
and
![]() $t \leq t'$
. Note that for a fixed element
$t \leq t'$
. Note that for a fixed element
![]() $(l,t) \in S$
, there are only finitely many elements in S that are less than
$(l,t) \in S$
, there are only finitely many elements in S that are less than
![]() $(l,t)$
.
$(l,t)$
.
Recall that we have a decomposition
![]() $\mathfrak {m} = \mathfrak {m}_{\mathrm {max}} + \mathfrak {m}^{\mathrm {max}}$
as in Section 2.3. We note that
$\mathfrak {m} = \mathfrak {m}_{\mathrm {max}} + \mathfrak {m}^{\mathrm {max}}$
as in Section 2.3. We note that
![]() $Z(\mathfrak {m}_{\mathrm {max}})$
is a ladder representation. In particular, if
$Z(\mathfrak {m}_{\mathrm {max}})$
is a ladder representation. In particular, if
![]() $\mathfrak {m} = \mathfrak {m}_{\mathrm {max}}$
, then we have the claim for
$\mathfrak {m} = \mathfrak {m}_{\mathrm {max}}$
, then we have the claim for
![]() $\mathfrak {m}$
(Section 6.1).
$\mathfrak {m}$
(Section 6.1).
From now on, we assume that
![]() $\mathfrak {m}_{\mathrm {max}} \neq \mathfrak {m}$
. Set
$\mathfrak {m}_{\mathrm {max}} \neq \mathfrak {m}$
. Set
Since
![]() $l(\mathfrak {m}^{\mathrm {max}}) < l(\mathfrak {m})$
, it follows from Proposition 5.2, Corollary 2.8 and the inductive hypothesis that
$l(\mathfrak {m}^{\mathrm {max}}) < l(\mathfrak {m})$
, it follows from Proposition 5.2, Corollary 2.8 and the inductive hypothesis that
 $$\begin{align*}\dim(\Pi^{\mathbb{K}_{n,\lambda}}) = \left\{ \begin{aligned} &1 &\quad&\text{if } \lambda = \lambda_{\mathfrak{m}}, \\ &0 &\quad&\text{if } \lambda < \lambda_{\mathfrak{m}}. \end{aligned} \right. \end{align*}$$
$$\begin{align*}\dim(\Pi^{\mathbb{K}_{n,\lambda}}) = \left\{ \begin{aligned} &1 &\quad&\text{if } \lambda = \lambda_{\mathfrak{m}}, \\ &0 &\quad&\text{if } \lambda < \lambda_{\mathfrak{m}}. \end{aligned} \right. \end{align*}$$
It follows from Lemma 6.5 that
![]() $Z(\mathfrak {m})$
appears as a subquotient of
$Z(\mathfrak {m})$
appears as a subquotient of
![]() $\Pi $
. This implies that the
$\Pi $
. This implies that the
![]() $\mathbb {K}_{n,\lambda }$
-invariant part of
$\mathbb {K}_{n,\lambda }$
-invariant part of
![]() $Z(\mathfrak {m})$
is equal to zero if
$Z(\mathfrak {m})$
is equal to zero if
![]() $\lambda < \lambda _{\mathfrak {m}}$
. Hence it remains to show that the
$\lambda < \lambda _{\mathfrak {m}}$
. Hence it remains to show that the
![]() $\mathbb {K}_{n,\lambda _{\mathfrak {m}}}$
-invariant part of
$\mathbb {K}_{n,\lambda _{\mathfrak {m}}}$
-invariant part of
![]() $Z(\mathfrak {m})$
is one-dimensional. To do this, we may assume that
$Z(\mathfrak {m})$
is one-dimensional. To do this, we may assume that
![]() $\Pi $
is reducible, which implies that
$\Pi $
is reducible, which implies that
![]() $t_{\mathfrak {m}}> 0$
.
$t_{\mathfrak {m}}> 0$
.
For an irreducible representation
![]() $\pi $
of
$\pi $
of
![]() $G_n$
and a representation
$G_n$
and a representation
![]() $\sigma $
of
$\sigma $
of
![]() $G_n$
of finite length, we write
$G_n$
of finite length, we write
![]() $\pi \dashv \sigma $
if
$\pi \dashv \sigma $
if
![]() $\pi $
appears as a subquotient of
$\pi $
appears as a subquotient of
![]() $\sigma $
. Let
$\sigma $
. Let
![]() $\mathfrak {m}' \neq \mathfrak {m}$
be a multisegment, and suppose that
$\mathfrak {m}' \neq \mathfrak {m}$
be a multisegment, and suppose that
![]() $Z(\mathfrak {m}') \dashv \Pi $
. It follows from [Reference Zelevinsky42, 7.1 Theorem] that
$Z(\mathfrak {m}') \dashv \Pi $
. It follows from [Reference Zelevinsky42, 7.1 Theorem] that
![]() $\mathfrak {m}'$
is obtained by successively applying elementary operations to
$\mathfrak {m}'$
is obtained by successively applying elementary operations to
![]() $\mathfrak {m}$
. In particular, we have
$\mathfrak {m}$
. In particular, we have
![]() $l(\mathfrak {m}') = l(\mathfrak {m})$
and
$l(\mathfrak {m}') = l(\mathfrak {m})$
and
![]() $t_{\mathfrak {m}'} < t_{\mathfrak {m}}$
. Hence, by the inductive hypothesis, we have
$t_{\mathfrak {m}'} < t_{\mathfrak {m}}$
. Hence, by the inductive hypothesis, we have
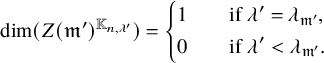 $$\begin{align*}\dim(Z(\mathfrak{m}')^{\mathbb{K}_{n,\lambda'}}) = \left\{ \begin{aligned} &1 &\quad&\text{if } \lambda' = \lambda_{\mathfrak{m}'}, \\ &0 &\quad&\text{if } \lambda' < \lambda_{\mathfrak{m}'}. \end{aligned} \right. \end{align*}$$
$$\begin{align*}\dim(Z(\mathfrak{m}')^{\mathbb{K}_{n,\lambda'}}) = \left\{ \begin{aligned} &1 &\quad&\text{if } \lambda' = \lambda_{\mathfrak{m}'}, \\ &0 &\quad&\text{if } \lambda' < \lambda_{\mathfrak{m}'}. \end{aligned} \right. \end{align*}$$
Note that this implies
![]() $\lambda _{\mathfrak {m}'} \ge \lambda _{\mathfrak {m}}$
. In fact, if
$\lambda _{\mathfrak {m}'} \ge \lambda _{\mathfrak {m}}$
. In fact, if
![]() $\lambda _{\mathfrak {m}'} < \lambda _{\mathfrak {m}}$
, then the
$\lambda _{\mathfrak {m}'} < \lambda _{\mathfrak {m}}$
, then the
![]() $\mathbb {K}_{n,\lambda _{\mathfrak {m}'}}$
-invariant part of
$\mathbb {K}_{n,\lambda _{\mathfrak {m}'}}$
-invariant part of
![]() $\Pi $
would be nonzero, which is a contradiction.
$\Pi $
would be nonzero, which is a contradiction.
Now we claim that
![]() $\lambda _{\mathfrak {m}'}> \lambda _{\mathfrak {m}}$
. For a proof by contradiction, suppose that
$\lambda _{\mathfrak {m}'}> \lambda _{\mathfrak {m}}$
. For a proof by contradiction, suppose that
![]() $\lambda _{\mathfrak {m}'} =\lambda _{\mathfrak {m}}$
. Since
$\lambda _{\mathfrak {m}'} =\lambda _{\mathfrak {m}}$
. Since
![]() $l(\mathfrak {m}^{\mathrm {ram}}) = |\lambda _{\mathfrak {m}}|$
and
$l(\mathfrak {m}^{\mathrm {ram}}) = |\lambda _{\mathfrak {m}}|$
and
![]() $l(\mathfrak {m}^{\prime \mathrm {ram}}) = |\lambda _{\mathfrak {m}'}|$
, by Proposition 2.7, we have
$l(\mathfrak {m}^{\prime \mathrm {ram}}) = |\lambda _{\mathfrak {m}'}|$
, by Proposition 2.7, we have
In particular, we have
By our assumption, we have
![]() $Z(\mathfrak {m}), Z(\mathfrak {m}') \dashv Z(\mathfrak {m}_{\mathrm {max}}) \times Z(\mathfrak {m}^{\mathrm {max}})$
. Proposition 2.7 together with Lemma 6.5 implies that
$Z(\mathfrak {m}), Z(\mathfrak {m}') \dashv Z(\mathfrak {m}_{\mathrm {max}}) \times Z(\mathfrak {m}^{\mathrm {max}})$
. Proposition 2.7 together with Lemma 6.5 implies that
![]() $Z(\mathfrak {m}^{\mathrm {ram}}) \dashv Z((\mathfrak {m}_{\mathrm {max}})^{\mathrm {ram}}) \times Z((\mathfrak {m}^{\mathrm {max}})^{\mathrm {ram}})$
. By taking the Zelevinsky duals, we have
$Z(\mathfrak {m}^{\mathrm {ram}}) \dashv Z((\mathfrak {m}_{\mathrm {max}})^{\mathrm {ram}}) \times Z((\mathfrak {m}^{\mathrm {max}})^{\mathrm {ram}})$
. By taking the Zelevinsky duals, we have
![]() $Z(\mathfrak {m}^{\sharp }), Z(\mathfrak {m}^{\prime \sharp }) \dashv Z((\mathfrak {m}_{\mathrm {max}})^{\sharp }) \times Z((\mathfrak {m}^{\mathrm {max}})^{\sharp })$
, and
$Z(\mathfrak {m}^{\sharp }), Z(\mathfrak {m}^{\prime \sharp }) \dashv Z((\mathfrak {m}_{\mathrm {max}})^{\sharp }) \times Z((\mathfrak {m}^{\mathrm {max}})^{\sharp })$
, and
![]() $Z((\mathfrak {m}^{\sharp })^{-}) \dashv Z(((\mathfrak {m}_{\mathrm {max}})^{\sharp })^{-}) \times Z(((\mathfrak {m}^{\mathrm {max}})^{\sharp })^{-})$
. Hence it follows from Lemma 6.6 that
$Z((\mathfrak {m}^{\sharp })^{-}) \dashv Z(((\mathfrak {m}_{\mathrm {max}})^{\sharp })^{-}) \times Z(((\mathfrak {m}^{\mathrm {max}})^{\sharp })^{-})$
. Hence it follows from Lemma 6.6 that
Since we have seen that
![]() $\mathrm {Card}(\mathfrak {m}^{\prime \sharp }) = \mathrm {Card}(\mathfrak {m}^{\sharp })$
, it again follows from Lemma 6.6 that
$\mathrm {Card}(\mathfrak {m}^{\prime \sharp }) = \mathrm {Card}(\mathfrak {m}^{\sharp })$
, it again follows from Lemma 6.6 that
![]() $Z((\mathfrak {m}^{\prime \sharp })^{-}) \dashv Z(((\mathfrak {m}_{\mathrm {max}})^{\sharp })^{-}) \times Z(((\mathfrak {m}^{\mathrm {max}})^{\sharp })^{-})$
. Again by taking the Zelevinsky duals, we see that
$Z((\mathfrak {m}^{\prime \sharp })^{-}) \dashv Z(((\mathfrak {m}_{\mathrm {max}})^{\sharp })^{-}) \times Z(((\mathfrak {m}^{\mathrm {max}})^{\sharp })^{-})$
. Again by taking the Zelevinsky duals, we see that
This implies that
![]() $\mathfrak {m}^{\prime \mathrm {ram}}$
is obtained from
$\mathfrak {m}^{\prime \mathrm {ram}}$
is obtained from
![]() $\mathfrak {m}^{\mathrm {ram}} = (\mathfrak {m}_{\mathrm {max}})^{\mathrm {ram}} + (\mathfrak {m}^{\mathrm {max}})^{\mathrm {ram}}$
by a successive chain of elementary operations.
$\mathfrak {m}^{\mathrm {ram}} = (\mathfrak {m}_{\mathrm {max}})^{\mathrm {ram}} + (\mathfrak {m}^{\mathrm {max}})^{\mathrm {ram}}$
by a successive chain of elementary operations.
Since we have assumed that
![]() $\lambda _{\mathfrak {m}'} = \lambda _{\mathfrak {m}}$
, it follows that
$\lambda _{\mathfrak {m}'} = \lambda _{\mathfrak {m}}$
, it follows that
![]() $\mathfrak {m}^{\prime \mathrm {ram}} = \mathfrak {m}^{\mathrm {ram}}$
and hence
$\mathfrak {m}^{\prime \mathrm {ram}} = \mathfrak {m}^{\mathrm {ram}}$
and hence
![]() $(\mathfrak {m}^{\prime \sharp })^{-} = (\mathfrak {m}^{\sharp })^{-}$
. Observe that for any integer
$(\mathfrak {m}^{\prime \sharp })^{-} = (\mathfrak {m}^{\sharp })^{-}$
. Observe that for any integer
![]() $a\in \mathbb {Z}$
, the number of segments in
$a\in \mathbb {Z}$
, the number of segments in
![]() $\mathfrak {m}'$
that contain
$\mathfrak {m}'$
that contain
![]() $\chi |\cdot |^a$
is equal to the number of segments in
$\chi |\cdot |^a$
is equal to the number of segments in
![]() $\mathfrak {m}$
that contain
$\mathfrak {m}$
that contain
![]() $\chi |\cdot |^a$
. Hence the equality
$\chi |\cdot |^a$
. Hence the equality
![]() $(\mathfrak {m}^{\prime \sharp })^{-} = (\mathfrak {m}^{\sharp })^{-}$
implies the equality
$(\mathfrak {m}^{\prime \sharp })^{-} = (\mathfrak {m}^{\sharp })^{-}$
implies the equality
![]() $\mathfrak {m}^{\prime \sharp } = \mathfrak {m}^{\sharp }$
. By taking the Zelevinsky duals, we obtain the equality
$\mathfrak {m}^{\prime \sharp } = \mathfrak {m}^{\sharp }$
. By taking the Zelevinsky duals, we obtain the equality
![]() $\mathfrak {m}' =\mathfrak {m}$
, which is a contradiction. This completes the proof of the inequality
$\mathfrak {m}' =\mathfrak {m}$
, which is a contradiction. This completes the proof of the inequality
![]() $\lambda _{\mathfrak {m}'}> \lambda _{\mathfrak {m}}$
.
$\lambda _{\mathfrak {m}'}> \lambda _{\mathfrak {m}}$
.
Since
![]() $\mathfrak {m}' \neq \mathfrak {m}$
is an arbitrary multisegment satisfying
$\mathfrak {m}' \neq \mathfrak {m}$
is an arbitrary multisegment satisfying
![]() $\mathfrak {m}' \dashv \Pi $
, we see that the equation
$\mathfrak {m}' \dashv \Pi $
, we see that the equation
![]() $\dim (\Pi ^{\mathbb {K}_{n,\lambda _{\mathfrak {m}}}}) = 1$
implies
$\dim (\Pi ^{\mathbb {K}_{n,\lambda _{\mathfrak {m}}}}) = 1$
implies
![]() $\dim (Z(\mathfrak {m})^{\mathbb {K}_{n,\lambda _{\mathfrak {m}}}}) = 1$
. This completes the proof.
$\dim (Z(\mathfrak {m})^{\mathbb {K}_{n,\lambda _{\mathfrak {m}}}}) = 1$
. This completes the proof.
6.4 Proof of Theorem 2.2 for
 $Z(\mathfrak {m})$
of type
$Z(\mathfrak {m})$
of type
 $\chi $
$\chi $
In this section, we give a proof of Theorem 2.2 for
![]() $\pi = Z(\mathfrak {m})$
with
$\pi = Z(\mathfrak {m})$
with
![]() $\mathfrak {m}$
of type
$\mathfrak {m}$
of type
![]() $\chi $
, where
$\chi $
, where
![]() $\chi $
is an unramified character of
$\chi $
is an unramified character of
![]() $F^{\times }$
.
$F^{\times }$
.
We consider the polynomial ring
![]() $R = \mathbb {Z}[x_1,x_2,\ldots ]$
in countably many variables
$R = \mathbb {Z}[x_1,x_2,\ldots ]$
in countably many variables
![]() $\{x_i\}_{i \geq 1}$
. For an
$\{x_i\}_{i \geq 1}$
. For an
![]() $\mathfrak {o}$
-module M of finite length, we define a homomorphism
$\mathfrak {o}$
-module M of finite length, we define a homomorphism
![]() $\xi _M \colon R \to \mathbb {Z}$
of
$\xi _M \colon R \to \mathbb {Z}$
of
![]() $\mathbb {Z}$
-modules as follows. We set
$\mathbb {Z}$
-modules as follows. We set
![]() $\xi _M(1)=1$
if
$\xi _M(1)=1$
if
![]() $M=0$
and
$M=0$
and
![]() $\xi _M(1)=0$
otherwise. For a monomial
$\xi _M(1)=0$
otherwise. For a monomial
![]() $x_{m_1} \cdots x_{m_s}$
in R, we define its image by
$x_{m_1} \cdots x_{m_s}$
in R, we define its image by
![]() $\xi _M$
to be the number of increasing filtrations
$\xi _M$
to be the number of increasing filtrations
on M by
![]() $\mathfrak {o}$
-submodules such that for
$\mathfrak {o}$
-submodules such that for
![]() $i=1,\ldots ,s$
, the ith graded piece
$i=1,\ldots ,s$
, the ith graded piece
![]() $\mathrm {Gr}^{\mathrm {F}}_i M$
is generated exactly by
$\mathrm {Gr}^{\mathrm {F}}_i M$
is generated exactly by
![]() $m_i$
elements. By Lemma 4.13, the homomorphism
$m_i$
elements. By Lemma 4.13, the homomorphism
![]() $\xi _M$
is well-defined.
$\xi _M$
is well-defined.
For an integer
![]() $m \geq 0$
, we set
$m \geq 0$
, we set
Lemma 6.7. Let M be an
![]() $\mathfrak {o}$
-module of finite length. Then the integer
$\mathfrak {o}$
-module of finite length. Then the integer
![]() $\xi _M(y_{m_1} \cdots y_{m_s})$
is equal to the number
$\xi _M(y_{m_1} \cdots y_{m_s})$
is equal to the number
![]() $\mathcal {N}_{(m_1,\ldots ,m_s)}(M)$
of
$\mathcal {N}_{(m_1,\ldots ,m_s)}(M)$
of
![]() $(m_1,\ldots ,m_s)$
-admissible filtrations on M.
$(m_1,\ldots ,m_s)$
-admissible filtrations on M.
Proof. This is immediate from the definition of the homomorphism
![]() $\xi _M$
and the definition of
$\xi _M$
and the definition of
![]() $(m_1,\ldots ,m_s)$
-admissible filtrations.
$(m_1,\ldots ,m_s)$
-admissible filtrations.
By setting
![]() $\deg x_m = m$
for
$\deg x_m = m$
for
![]() $m \geq 1$
, we regard R as a graded ring. For any integer
$m \geq 1$
, we regard R as a graded ring. For any integer
![]() $m \ge 0$
, let
$m \ge 0$
, let
![]() $R_m$
denote the degree-m-part of R, and set
$R_m$
denote the degree-m-part of R, and set
Then
![]() $I_m$
is an ideal of R, and we have
$I_m$
is an ideal of R, and we have
![]() $I_{m} \cdot I_{m'} \subset I_{m+m'}$
.
$I_{m} \cdot I_{m'} \subset I_{m+m'}$
.
Lemma 6.8. Let
![]() $m \ge 0$
be an integer, and let M be an
$m \ge 0$
be an integer, and let M be an
![]() $\mathfrak {o}$
-module of length less than m. Then we have
$\mathfrak {o}$
-module of length less than m. Then we have
![]() $\xi _M(I_m)=0$
.
$\xi _M(I_m)=0$
.
Proof. Let
![]() $f=x_{m_1} \cdots x_{m_s}$
be an arbitrary monomial that belongs to
$f=x_{m_1} \cdots x_{m_s}$
be an arbitrary monomial that belongs to
![]() $I_m$
. It suffices to show
$I_m$
. It suffices to show
![]() $\xi _M(f)=0$
. By definition of
$\xi _M(f)=0$
. By definition of
![]() $I_m$
, we have
$I_m$
, we have
![]() $m_1+ \cdots + m_s \ge m$
. Suppose that there exists an increasing filtration
$m_1+ \cdots + m_s \ge m$
. Suppose that there exists an increasing filtration
on M by
![]() $\mathfrak {o}$
-submodules such that for
$\mathfrak {o}$
-submodules such that for
![]() $i=1,\ldots ,s$
, the ith graded piece
$i=1,\ldots ,s$
, the ith graded piece
![]() $\mathrm {Gr}^{\mathrm {F}}_i M$
is generated exactly by
$\mathrm {Gr}^{\mathrm {F}}_i M$
is generated exactly by
![]() $m_i$
elements. Then since
$m_i$
elements. Then since
![]() $\mathrm {Gr}^{\mathrm {F}}_i M$
is of length at least
$\mathrm {Gr}^{\mathrm {F}}_i M$
is of length at least
![]() $m_i$
, the length of M is at least
$m_i$
, the length of M is at least
![]() $m_1 + \cdots + m_s \ge m$
, which is a contradiction. Hence by the definition of
$m_1 + \cdots + m_s \ge m$
, which is a contradiction. Hence by the definition of
![]() $\xi _M$
, we have
$\xi _M$
, we have
![]() $\xi _M(f)=0$
as desired.
$\xi _M(f)=0$
as desired.
Now we prove Theorem 2.2 for
![]() $\pi = Z(\mathfrak {m})$
with
$\pi = Z(\mathfrak {m})$
with
![]() $\mathfrak {m}$
of type
$\mathfrak {m}$
of type
![]() $\chi $
.
$\chi $
.
Proof of Theorem 2.2 for
 $\pi = Z(\mathfrak {m})$
of type
$\pi = Z(\mathfrak {m})$
of type
 $\chi $
$\chi $
Let us write
For
![]() $i=1,\ldots ,s$
, we set
$i=1,\ldots ,s$
, we set
![]() $\pi _i = Z(\Delta _i^{\sharp })$
. Let n and
$\pi _i = Z(\Delta _i^{\sharp })$
. Let n and
![]() $n_i$
be such that
$n_i$
be such that
![]() $\pi \in \mathrm {Irr}(G_n)$
and
$\pi \in \mathrm {Irr}(G_n)$
and
![]() $\pi _i \in \mathrm {Irr}(G_{n_i})$
. Then
$\pi _i \in \mathrm {Irr}(G_{n_i})$
. Then
![]() $\pi $
appears as a subquotient of
$\pi $
appears as a subquotient of
![]() $\pi _1 \times \cdots \times \pi _s$
, and we have
$\pi _1 \times \cdots \times \pi _s$
, and we have
![]() $|\lambda _{\pi }| = |\lambda _{\pi _1}| + \cdots + |\lambda _{\pi _s}|$
. Let
$|\lambda _{\pi }| = |\lambda _{\pi _1}| + \cdots + |\lambda _{\pi _s}|$
. Let
![]() $\lambda = (\lambda _1,\ldots ,\lambda _n) \in \Lambda _n$
be such that
$\lambda = (\lambda _1,\ldots ,\lambda _n) \in \Lambda _n$
be such that
![]() $|\lambda | < |\lambda _{\pi }|$
. Then
$|\lambda | < |\lambda _{\pi }|$
. Then
![]() $\pi ^{\mathbb {K}_{n,\lambda }}$
is a subquotient of
$\pi ^{\mathbb {K}_{n,\lambda }}$
is a subquotient of
![]() $(\pi _1 \times \cdots \times \pi _{s})^{\mathbb {K}_{n,\lambda }}$
. Let
$(\pi _1 \times \cdots \times \pi _{s})^{\mathbb {K}_{n,\lambda }}$
. Let
![]() $M = \mathfrak {o}/\mathfrak {p}^{\lambda _1} \oplus \cdots \oplus \mathfrak {o}/\mathfrak {p}^{\lambda _n}$
. By Proposition 5.2, we have
$M = \mathfrak {o}/\mathfrak {p}^{\lambda _1} \oplus \cdots \oplus \mathfrak {o}/\mathfrak {p}^{\lambda _n}$
. By Proposition 5.2, we have
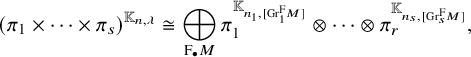 $$\begin{align*}(\pi_1 \times \cdots \times \pi_{s})^{\mathbb{K}_{n,\lambda}} \cong \bigoplus_{\mathrm{F}_{\bullet} M} \pi_1^{\mathbb{K}_{n_1,[\mathrm{Gr}^{\mathrm{F}}_1 M]}} \otimes \cdots \otimes \pi_r^{\mathbb{K}_{n_{s},[\mathrm{Gr}^{\mathrm{F}}_{s} M]}}, \end{align*}$$
$$\begin{align*}(\pi_1 \times \cdots \times \pi_{s})^{\mathbb{K}_{n,\lambda}} \cong \bigoplus_{\mathrm{F}_{\bullet} M} \pi_1^{\mathbb{K}_{n_1,[\mathrm{Gr}^{\mathrm{F}}_1 M]}} \otimes \cdots \otimes \pi_r^{\mathbb{K}_{n_{s},[\mathrm{Gr}^{\mathrm{F}}_{s} M]}}, \end{align*}$$
where
![]() $\mathrm {F}_{\bullet } M$
runs over the set of increasing filtrations
$\mathrm {F}_{\bullet } M$
runs over the set of increasing filtrations
on M by
![]() $\mathfrak {o}$
-submodules such that for
$\mathfrak {o}$
-submodules such that for
![]() $i=1,\ldots ,s,$
the
$i=1,\ldots ,s,$
the
![]() $\mathfrak {o}$
-module
$\mathfrak {o}$
-module
![]() $\mathrm {Gr}^{\mathrm {F}}_i M = \mathrm {F}_i M/\mathrm {F}_{i-1} M$
is generated by at most
$\mathrm {Gr}^{\mathrm {F}}_i M = \mathrm {F}_i M/\mathrm {F}_{i-1} M$
is generated by at most
![]() $n_i$
elements. Fix such a filtration
$n_i$
elements. Fix such a filtration
![]() $\mathrm {F}_{\bullet } M$
. Since
$\mathrm {F}_{\bullet } M$
. Since
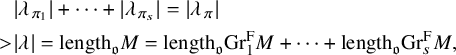 $$ \begin{align*} & |\lambda_{\pi_1}|+ \cdots + |\lambda_{\pi_{s}}| = |\lambda_{\pi}| \\> & |\lambda| = \mathrm{length}_{\mathfrak{o}} M = \mathrm{length}_{\mathfrak{o}} \mathrm{Gr}^{\mathrm{F}}_1 M + \cdots + \mathrm{length}_{\mathfrak{o}} \mathrm{Gr}^{\mathrm{F}}_{s} M, \end{align*} $$
$$ \begin{align*} & |\lambda_{\pi_1}|+ \cdots + |\lambda_{\pi_{s}}| = |\lambda_{\pi}| \\> & |\lambda| = \mathrm{length}_{\mathfrak{o}} M = \mathrm{length}_{\mathfrak{o}} \mathrm{Gr}^{\mathrm{F}}_1 M + \cdots + \mathrm{length}_{\mathfrak{o}} \mathrm{Gr}^{\mathrm{F}}_{s} M, \end{align*} $$
we have
![]() $|\lambda _{\pi _i}|> \mathrm {length}_{\mathfrak {o}} \mathrm {Gr}^{\mathrm {F}}_i M$
for some i. If we knew the claim for
$|\lambda _{\pi _i}|> \mathrm {length}_{\mathfrak {o}} \mathrm {Gr}^{\mathrm {F}}_i M$
for some i. If we knew the claim for
![]() $\pi _i$
for any
$\pi _i$
for any
![]() $i = 1,\dots , s$
, then we would have
$i = 1,\dots , s$
, then we would have
![]() $(\pi _1 \times \cdots \times \pi _{s})^{\mathbb {K}_{n,\lambda }} = 0$
, which implies that
$(\pi _1 \times \cdots \times \pi _{s})^{\mathbb {K}_{n,\lambda }} = 0$
, which implies that
![]() $\pi ^{\mathbb {K}_{n, \lambda }} = 0$
. Hence we reduce the claim to the case where
$\pi ^{\mathbb {K}_{n, \lambda }} = 0$
. Hence we reduce the claim to the case where
![]() $s=1$
.
$s=1$
.
From now on, we assume that
![]() $s=1$
. Let us write
$s=1$
. Let us write
![]() $\Delta _1 = [1,n]_{\chi }$
for some unramified character
$\Delta _1 = [1,n]_{\chi }$
for some unramified character
![]() $\chi $
. Then
$\chi $
. Then
![]() $\pi = Z([1,1]_{\chi } + \cdots + [n,n]_{\chi })$
is an unramified twist of the Steinberg representation. By Tadić’s determinantal formula [Reference Tadić39], we have
$\pi = Z([1,1]_{\chi } + \cdots + [n,n]_{\chi })$
is an unramified twist of the Steinberg representation. By Tadić’s determinantal formula [Reference Tadić39], we have
 $$\begin{align*}\pi = \sum_{r=1}^n (-1)^{n-r} \sum_{0=n_0 < n_1 < \cdots < n_r =n} Z([n_0+1,n_1]_{\chi}) \times \cdots \times Z([n_{r-1}+1,n_r]_{\chi}) \end{align*}$$
$$\begin{align*}\pi = \sum_{r=1}^n (-1)^{n-r} \sum_{0=n_0 < n_1 < \cdots < n_r =n} Z([n_0+1,n_1]_{\chi}) \times \cdots \times Z([n_{r-1}+1,n_r]_{\chi}) \end{align*}$$
in the Grothendieck group of the category of representations of
![]() $G_n$
of finite length. Then it follows from Proposition 5.2 that for any
$G_n$
of finite length. Then it follows from Proposition 5.2 that for any
![]() $\mathfrak {o}$
-module M of finite length, the dimension of the
$\mathfrak {o}$
-module M of finite length, the dimension of the
![]() $\mathbb {K}_{n,[M]}$
-invariant part
$\mathbb {K}_{n,[M]}$
-invariant part
![]() $\pi ^{\mathbb {K}_{n,[M]}}$
is equal to the number
$\pi ^{\mathbb {K}_{n,[M]}}$
is equal to the number
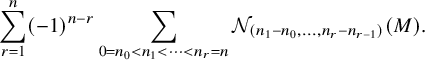 $$\begin{align*}\sum_{r=1}^n (-1)^{n-r} \sum_{0=n_0 < n_1 < \cdots < n_r =n} \mathcal{N}_{(n_1-n_0,\ldots,n_r-n_{r-1})}(M). \end{align*}$$
$$\begin{align*}\sum_{r=1}^n (-1)^{n-r} \sum_{0=n_0 < n_1 < \cdots < n_r =n} \mathcal{N}_{(n_1-n_0,\ldots,n_r-n_{r-1})}(M). \end{align*}$$
We set
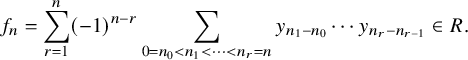 $$ \begin{align} f_n = \sum_{r=1}^n (-1)^{n-r} \sum_{0=n_0 < n_1 < \cdots < n_r =n} y_{n_1-n_0} \cdots y_{n_r-n_{r-1}} \in R. \end{align} $$
$$ \begin{align} f_n = \sum_{r=1}^n (-1)^{n-r} \sum_{0=n_0 < n_1 < \cdots < n_r =n} y_{n_1-n_0} \cdots y_{n_r-n_{r-1}} \in R. \end{align} $$
Then it follows from Lemma 6.7 that for any
![]() $\mathfrak {o}$
-module M of finite length, the dimension of
$\mathfrak {o}$
-module M of finite length, the dimension of
![]() $\pi ^{\mathbb {K}_{n,[M]}}$
is equal to
$\pi ^{\mathbb {K}_{n,[M]}}$
is equal to
![]() $\xi _M(f_n)$
. Therefore, it suffices to prove that
$\xi _M(f_n)$
. Therefore, it suffices to prove that
![]() $\xi _M(f_n) = 0$
for any
$\xi _M(f_n) = 0$
for any
![]() $\mathfrak {o}$
-module M of length at most
$\mathfrak {o}$
-module M of length at most
![]() $n-2$
. By Lemma 6.8, it suffices to show that
$n-2$
. By Lemma 6.8, it suffices to show that
![]() $f_n$
belongs to the ideal
$f_n$
belongs to the ideal
![]() $I_{n-1}$
.
$I_{n-1}$
.
Let us consider the ring
![]() $R[[t]]$
of formal power series in the variable t. We set
$R[[t]]$
of formal power series in the variable t. We set
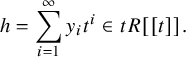 $$\begin{align*}h = \sum_{i=1}^{\infty} y_i t^i \in t R[[t]]. \end{align*}$$
$$\begin{align*}h = \sum_{i=1}^{\infty} y_i t^i \in t R[[t]]. \end{align*}$$
Then
![]() $f_n$
is equal to the coefficient of
$f_n$
is equal to the coefficient of
![]() $t^n$
in
$t^n$
in
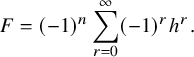 $$\begin{align*}F = (-1)^n\sum_{r=0}^{\infty} (-1)^r h^r. \end{align*}$$
$$\begin{align*}F = (-1)^n\sum_{r=0}^{\infty} (-1)^r h^r. \end{align*}$$
Since
we have
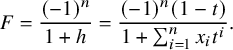 $$\begin{align*}F = \frac{(-1)^n}{1+h} = \frac{(-1)^n(1-t)}{1 + \sum_{i=1}^n x_i t^i}. \end{align*}$$
$$\begin{align*}F = \frac{(-1)^n}{1+h} = \frac{(-1)^n(1-t)}{1 + \sum_{i=1}^n x_i t^i}. \end{align*}$$
Since the coefficients of
![]() $t^i$
in
$t^i$
in
![]() $(1 + \sum _{i=1}^n x_i t^i)^{-1}$
belongs to
$(1 + \sum _{i=1}^n x_i t^i)^{-1}$
belongs to
![]() $R_i$
for any
$R_i$
for any
![]() $i \ge 0$
, the claim follows.
$i \ge 0$
, the claim follows.
7 Proof of the main theorems: the case where
 $L(s,\pi )=1$
$L(s,\pi )=1$
In this section, we prove Theorem 2.2 for
![]() $\pi \in \mathrm {Irr}(G_n)$
with
$\pi \in \mathrm {Irr}(G_n)$
with
![]() $L(s,\pi ) = 1$
, and we reduce Theorem 2.1 to the case of Speh representations.
$L(s,\pi ) = 1$
, and we reduce Theorem 2.1 to the case of Speh representations.
7.1 Proof of Theorem 2.2 when
 $L(s,\pi ) =1$
$L(s,\pi ) =1$
First, we reduce Theorem 2.2 for
![]() $\pi $
to the case where
$\pi $
to the case where
![]() $\pi $
is cuspidal. Let
$\pi $
is cuspidal. Let
![]() $(\pi ,V)$
be an irreducible representation of
$(\pi ,V)$
be an irreducible representation of
![]() $G_n$
such that
$G_n$
such that
![]() $L(s,\pi )=1$
. Note that there exists a partition
$L(s,\pi )=1$
. Note that there exists a partition
![]() $n=n_1 + \cdots + n_r$
of n and cuspidal representations
$n=n_1 + \cdots + n_r$
of n and cuspidal representations
![]() $\pi _1, \ldots , \pi _r$
of
$\pi _1, \ldots , \pi _r$
of
![]() $G_{n_1}, \ldots , G_{n_r}$
, respectively, such that the following conditions are satisfied:
$G_{n_1}, \ldots , G_{n_r}$
, respectively, such that the following conditions are satisfied:
-
• For
 $i=1,\ldots ,r$
, we have
$i=1,\ldots ,r$
, we have
 $L(s,\pi _i)=1$
;
$L(s,\pi _i)=1$
; -
•
 $\pi $
appears as a subquotient of the parabolic induction
$\pi $
appears as a subquotient of the parabolic induction
 $\pi _1 \times \cdots \times \pi _r$
;
$\pi _1 \times \cdots \times \pi _r$
; -
• We have
 $|\lambda _{\pi }| = |\lambda _{\pi _1}| + \cdots + |\lambda _{\pi _r}|$
.
$|\lambda _{\pi }| = |\lambda _{\pi _1}| + \cdots + |\lambda _{\pi _r}|$
.
Then by the same argument as in the proof of Theorem 2.2 for
![]() $\pi = Z(\mathfrak {m})$
of type
$\pi = Z(\mathfrak {m})$
of type
![]() $\chi $
in Section 6.4, we can reduce the claim for
$\chi $
in Section 6.4, we can reduce the claim for
![]() $\pi $
to the ones for
$\pi $
to the ones for
![]() $\pi _i$
for
$\pi _i$
for
![]() $i=1,\dots ,r$
: that is, the case where
$i=1,\dots ,r$
: that is, the case where
![]() $\pi $
is cuspidal.
$\pi $
is cuspidal.
To prove the claim for cuspidal
![]() $\pi $
, we consider certain Hecke operators. Let
$\pi $
, we consider certain Hecke operators. Let
![]() $X_{\lambda } \subset M_n(\mathfrak {o})$
denote the subset of matrices
$X_{\lambda } \subset M_n(\mathfrak {o})$
denote the subset of matrices
![]() $A = (a_{i,j}) \in M_n(\mathfrak {o})$
such that
$A = (a_{i,j}) \in M_n(\mathfrak {o})$
such that
![]() $a_{i,j} \equiv \delta _{i,j} \bmod \mathfrak {p}^{\lambda _i}$
for
$a_{i,j} \equiv \delta _{i,j} \bmod \mathfrak {p}^{\lambda _i}$
for
![]() $1 \leq i,j \leq n$
. Then
$1 \leq i,j \leq n$
. Then
-
•
 $X_{\lambda }$
contains
$X_{\lambda }$
contains
 $\mathbb {K}_{n,\lambda }$
;
$\mathbb {K}_{n,\lambda }$
; -
•
 $X_{\lambda }$
is closed under the multiplication of matrices; and
$X_{\lambda }$
is closed under the multiplication of matrices; and -
•
 $X_{\lambda }$
is bi-invariant under the action of
$X_{\lambda }$
is bi-invariant under the action of
 $\mathbb {K}_{n,\lambda }$
.
$\mathbb {K}_{n,\lambda }$
.
We let
![]() $\mathcal {H}_{\lambda }$
denote the complex vector space of
$\mathcal {H}_{\lambda }$
denote the complex vector space of
![]() $\mathbb {C}$
-valued compactly supported bi-
$\mathbb {C}$
-valued compactly supported bi-
![]() $\mathbb {K}_{n,\lambda }$
-invariant functions on
$\mathbb {K}_{n,\lambda }$
-invariant functions on
![]() $G_n$
whose supports are contained in
$G_n$
whose supports are contained in
![]() $X_{\lambda }$
. Then
$X_{\lambda }$
. Then
![]() $\mathcal {H}_{\lambda }$
has a structure of
$\mathcal {H}_{\lambda }$
has a structure of
![]() $\mathbb {C}$
-algebra whose multiplication law is given by the convolution with respect to the Haar measure on
$\mathbb {C}$
-algebra whose multiplication law is given by the convolution with respect to the Haar measure on
![]() $G_n$
satisfying
$G_n$
satisfying
![]() $\mathrm {vol}(\mathbb {K}_{n,\lambda }) = 1$
. The unit element
$\mathrm {vol}(\mathbb {K}_{n,\lambda }) = 1$
. The unit element
![]() $1$
of
$1$
of
![]() $\mathcal {H}_{\lambda }$
is equal to the characteristic function of
$\mathcal {H}_{\lambda }$
is equal to the characteristic function of
![]() $\mathbb {K}_{n,\lambda }$
. Let
$\mathbb {K}_{n,\lambda }$
. Let
![]() $\mathfrak {a}_{\lambda } \subset \mathcal {H}_{\lambda }$
be the subspace of functions whose supports are contained in the complement
$\mathfrak {a}_{\lambda } \subset \mathcal {H}_{\lambda }$
be the subspace of functions whose supports are contained in the complement
![]() $X_{\lambda } \setminus \mathbb {K}_{n,\lambda }$
of
$X_{\lambda } \setminus \mathbb {K}_{n,\lambda }$
of
![]() $\mathbb {K}_{n,\lambda }$
in
$\mathbb {K}_{n,\lambda }$
in
![]() $X_{\lambda }$
. Then we have
$X_{\lambda }$
. Then we have
![]() $\mathcal {H}_{\lambda } = \mathbb {C} \cdot 1 \oplus \mathfrak {a}_{\lambda }$
, and
$\mathcal {H}_{\lambda } = \mathbb {C} \cdot 1 \oplus \mathfrak {a}_{\lambda }$
, and
![]() $\mathfrak {a}_{\lambda }$
is a two-sided ideal of
$\mathfrak {a}_{\lambda }$
is a two-sided ideal of
![]() $\mathcal {H}_{\lambda }$
.
$\mathcal {H}_{\lambda }$
.
Let
![]() $(\pi ,V)$
be an irreducible representation of
$(\pi ,V)$
be an irreducible representation of
![]() $G_n$
. The action of
$G_n$
. The action of
![]() $G_n$
on V induces an action of
$G_n$
on V induces an action of
![]() $\mathcal {H}_{\lambda }$
on
$\mathcal {H}_{\lambda }$
on
![]() $V^{\mathbb {K}_{n,\lambda }}$
. We let
$V^{\mathbb {K}_{n,\lambda }}$
. We let
denote the induced homomorphism of
![]() $\mathbb {C}$
-algebras. We set
$\mathbb {C}$
-algebras. We set
![]() $\mathcal {H}_{\lambda ,V} = \theta _V(\mathcal {H}_{\lambda })$
and
$\mathcal {H}_{\lambda ,V} = \theta _V(\mathcal {H}_{\lambda })$
and
![]() $\mathfrak {a}_{\lambda ,V} = \theta _V(\mathfrak {a}_{\lambda })$
. Then
$\mathfrak {a}_{\lambda ,V} = \theta _V(\mathfrak {a}_{\lambda })$
. Then
![]() $\mathcal {H}_{\lambda ,V}$
is a finite-dimensional
$\mathcal {H}_{\lambda ,V}$
is a finite-dimensional
![]() $\mathbb {C}$
-algebra, and
$\mathbb {C}$
-algebra, and
![]() $\mathfrak {a}_{\lambda ,V}$
is a two-sided ideal of
$\mathfrak {a}_{\lambda ,V}$
is a two-sided ideal of
![]() $\mathcal {H}_{\lambda ,V}$
.
$\mathcal {H}_{\lambda ,V}$
.
Lemma 7.1. Suppose that
![]() $\pi $
is cuspidal. Then any element
$\pi $
is cuspidal. Then any element
![]() $T \in \mathfrak {a}_{\lambda ,V}$
is nilpotent.
$T \in \mathfrak {a}_{\lambda ,V}$
is nilpotent.
Proof. Since
![]() $V^{\mathbb {K}_{n,\lambda }}$
is finite-dimensional, it suffices to show that for any
$V^{\mathbb {K}_{n,\lambda }}$
is finite-dimensional, it suffices to show that for any
![]() $v \in V^{\mathbb {K}_{n,\lambda }}$
and for any linear form
$v \in V^{\mathbb {K}_{n,\lambda }}$
and for any linear form
![]() $\widetilde {v} \colon V^{\mathbb {K}_{n,\lambda }} \to \mathbb {C}$
, we have
$\widetilde {v} \colon V^{\mathbb {K}_{n,\lambda }} \to \mathbb {C}$
, we have
![]() $\widetilde {v}(T^m v) = 0$
for any sufficiently large integer m.
$\widetilde {v}(T^m v) = 0$
for any sufficiently large integer m.
Let us choose
![]() $\widetilde {T} \in \mathfrak {a}_{\lambda }$
satisfying
$\widetilde {T} \in \mathfrak {a}_{\lambda }$
satisfying
![]() $\theta _V(\widetilde {T}) =T$
. For an integer
$\theta _V(\widetilde {T}) =T$
. For an integer
![]() $m \ge 0$
, we let
$m \ge 0$
, we let
![]() $X_{\lambda }^{\ge m}$
denote the subset of matrices
$X_{\lambda }^{\ge m}$
denote the subset of matrices
![]() $A \in X_{\lambda }$
satisfying
$A \in X_{\lambda }$
satisfying
![]() $\det A \in \mathfrak {p}^m$
. We note that
$\det A \in \mathfrak {p}^m$
. We note that
![]() $X_{\lambda }^{\ge 1}$
is equal to
$X_{\lambda }^{\ge 1}$
is equal to
![]() $X_{\lambda } \setminus \mathbb {K}_{n,\lambda }$
. Since the product of any m matrices in
$X_{\lambda } \setminus \mathbb {K}_{n,\lambda }$
. Since the product of any m matrices in
![]() $X_{\lambda }^{\ge 1}$
belongs to
$X_{\lambda }^{\ge 1}$
belongs to
![]() $X_{\lambda }^{\ge m}$
, it follows that the mth power
$X_{\lambda }^{\ge m}$
, it follows that the mth power
![]() $\widetilde {T}^m$
of
$\widetilde {T}^m$
of
![]() $\widetilde {T}$
is, as a function on
$\widetilde {T}$
is, as a function on
![]() $G_n$
, supported on
$G_n$
, supported on
![]() $X_{\lambda }^{\ge m} \cap G_n$
.
$X_{\lambda }^{\ge m} \cap G_n$
.
Let
![]() $(\widetilde {\pi }, \widetilde {V})$
denote the contragredient representation of
$(\widetilde {\pi }, \widetilde {V})$
denote the contragredient representation of
![]() $(\pi ,V)$
. We regard
$(\pi ,V)$
. We regard
![]() $\widetilde {v}$
as a vector in the
$\widetilde {v}$
as a vector in the
![]() $\mathbb {K}_{n,\lambda }$
-invariant part
$\mathbb {K}_{n,\lambda }$
-invariant part
![]() $(\widetilde {V})^{\mathbb {K}_{n,\lambda }}$
of
$(\widetilde {V})^{\mathbb {K}_{n,\lambda }}$
of
![]() $\widetilde {V}$
. Since
$\widetilde {V}$
. Since
![]() $\pi $
is cuspidal, the matrix coefficient
$\pi $
is cuspidal, the matrix coefficient
of
![]() $\pi $
is compactly supported modulo the centre
$\pi $
is compactly supported modulo the centre
![]() $Z_n$
of
$Z_n$
of
![]() $G_n$
. Observe that the intersection
$G_n$
. Observe that the intersection
![]() $G_n \cap \left ( \bigcap _{m \ge 1} Z_n X_{\lambda }^{\ge m}\right )$
is empty. This implies that any subset K of
$G_n \cap \left ( \bigcap _{m \ge 1} Z_n X_{\lambda }^{\ge m}\right )$
is empty. This implies that any subset K of
![]() $G_n$
that is compact modulo
$G_n$
that is compact modulo
![]() $Z_n$
does not intersect
$Z_n$
does not intersect
![]() $X_{\lambda }^{\ge m}$
for any sufficiently large m. Thus, the function
$X_{\lambda }^{\ge m}$
for any sufficiently large m. Thus, the function
![]() $f(g)$
is identically zero on
$f(g)$
is identically zero on
![]() $X_{\lambda }^{\ge m}$
for any sufficiently large m, which implies that
$X_{\lambda }^{\ge m}$
for any sufficiently large m, which implies that
![]() $\widetilde {v}(T^m v) = 0$
as desired.
$\widetilde {v}(T^m v) = 0$
as desired.
Proof for Theorem 2.2 when
 $L(s,\pi ) = 1$
$L(s,\pi ) = 1$
As we have remarked above, we may and will assume that
![]() $(\pi ,V)$
is cuspidal.
$(\pi ,V)$
is cuspidal.
Let us assume that
![]() $V^{\mathbb {K}_{n,\lambda }} \neq 0$
. Since
$V^{\mathbb {K}_{n,\lambda }} \neq 0$
. Since
![]() $V^{\mathbb {K}_{n,\lambda }}$
is finite-dimensional, one can take a minimal nonzero left
$V^{\mathbb {K}_{n,\lambda }}$
is finite-dimensional, one can take a minimal nonzero left
![]() $\mathcal {H}_{\lambda ,V}$
-submodule W of
$\mathcal {H}_{\lambda ,V}$
-submodule W of
![]() $V^{\mathbb {K}_{n,\lambda }}$
. Lemma 7.1 implies that
$V^{\mathbb {K}_{n,\lambda }}$
. Lemma 7.1 implies that
![]() $\mathfrak {a}_{\lambda ,V}$
is contained in the Jacobson radical of
$\mathfrak {a}_{\lambda ,V}$
is contained in the Jacobson radical of
![]() $\mathcal {H}_{\lambda ,V}$
. Hence any element of
$\mathcal {H}_{\lambda ,V}$
. Hence any element of
![]() $\mathfrak {a}_{\lambda ,V}$
acts as zero on W.
$\mathfrak {a}_{\lambda ,V}$
acts as zero on W.
Let us choose nonzero vectors
![]() $w \in W$
and
$w \in W$
and
![]() $\widetilde {w} \in (\widetilde {V})^{\mathbb {K}_{n,\lambda }}$
such that
$\widetilde {w} \in (\widetilde {V})^{\mathbb {K}_{n,\lambda }}$
such that
![]() $\langle w,\widetilde {w} \rangle \neq 0$
. Let
$\langle w,\widetilde {w} \rangle \neq 0$
. Let
![]() $f(g)$
denote the matrix coefficient of
$f(g)$
denote the matrix coefficient of
![]() $\pi $
defined as
$\pi $
defined as
Let
![]() $\Phi $
denote the characteristic function of
$\Phi $
denote the characteristic function of
![]() $X_{\lambda }$
. Let us consider the zeta integral
$X_{\lambda }$
. Let us consider the zeta integral
of [Reference Godement and Jacquet8]. By definition, we have
where
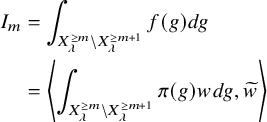 $$ \begin{align*} I_m & = \int_{X_{\lambda}^{\ge m} \setminus X_{\lambda}^{\ge m+1}} f(g) dg \\ & = \left\langle \int_{X_{\lambda}^{\ge m} \setminus X_{\lambda}^{\ge m+1}} \pi(g) w dg, \widetilde{w}\right\rangle \end{align*} $$
$$ \begin{align*} I_m & = \int_{X_{\lambda}^{\ge m} \setminus X_{\lambda}^{\ge m+1}} f(g) dg \\ & = \left\langle \int_{X_{\lambda}^{\ge m} \setminus X_{\lambda}^{\ge m+1}} \pi(g) w dg, \widetilde{w}\right\rangle \end{align*} $$
as a formal power series in
![]() $q^{-s}$
. Since
$q^{-s}$
. Since
![]() $\mathfrak {a}_{\lambda }$
annihilates w, it follows that
$\mathfrak {a}_{\lambda }$
annihilates w, it follows that
![]() $I_m =0$
for
$I_m =0$
for
![]() $m \ge 1$
. Hence
$m \ge 1$
. Hence
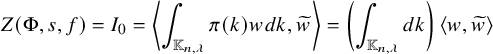 $$\begin{align*}Z(\Phi,s,f) = I_0 = \left\langle \int_{\mathbb{K}_{n,\lambda}} \pi(k) w dk, \widetilde{w}\right\rangle = \left(\int_{\mathbb{K}_{n,\lambda}} dk \right) \langle w,\widetilde{w} \rangle \end{align*}$$
$$\begin{align*}Z(\Phi,s,f) = I_0 = \left\langle \int_{\mathbb{K}_{n,\lambda}} \pi(k) w dk, \widetilde{w}\right\rangle = \left(\int_{\mathbb{K}_{n,\lambda}} dk \right) \langle w,\widetilde{w} \rangle \end{align*}$$
is a nonzero constant.
Let us consider the Fourier transform
of
![]() $\Phi $
with respect to
$\Phi $
with respect to
![]() $\psi $
, where
$\psi $
, where
![]() $dy$
is the Haar measure on
$dy$
is the Haar measure on
![]() $M_n(F)$
that is self-dual with respect to
$M_n(F)$
that is self-dual with respect to
![]() $\psi $
. Then
$\psi $
. Then
![]() $\widehat {\Phi }$
is supported on the subset
$\widehat {\Phi }$
is supported on the subset
![]() $Y_{\lambda } \subset M_n(F)$
of matrices
$Y_{\lambda } \subset M_n(F)$
of matrices
![]() $B = (b_{i,j}) \in M_n(F)$
such that
$B = (b_{i,j}) \in M_n(F)$
such that
![]() $b_{i,j} \in \mathfrak {p}^{-\lambda _j}$
for
$b_{i,j} \in \mathfrak {p}^{-\lambda _j}$
for
![]() $1 \leq i,j \leq n$
. We set
$1 \leq i,j \leq n$
. We set
![]() $\check {f} (g) = f(g^{-1})$
. Note that
$\check {f} (g) = f(g^{-1})$
. Note that
![]() $\check {f}$
is a matrix coefficient of
$\check {f}$
is a matrix coefficient of
![]() $(\widetilde {\pi },\widetilde {V})$
. Since
$(\widetilde {\pi },\widetilde {V})$
. Since
![]() $\det B \in \mathfrak {p}^{-|\lambda |}$
for any
$\det B \in \mathfrak {p}^{-|\lambda |}$
for any
![]() $B \in Y_{\lambda }$
, it follows that the zeta integral
$B \in Y_{\lambda }$
, it follows that the zeta integral
![]() $Z(\widehat {\Phi },s,\check {f})$
, as a formal power series in
$Z(\widehat {\Phi },s,\check {f})$
, as a formal power series in
![]() $q^{-s}$
, belongs to
$q^{-s}$
, belongs to
![]() $q^{|\lambda | s} \mathbb {C}[[q^{-s}]]$
.
$q^{|\lambda | s} \mathbb {C}[[q^{-s}]]$
.
By our assumption, we have
![]() $L(s,\pi ) = L(s,\widetilde {\pi }) =1$
. Hence it follows from the local functional equation that we have
$L(s,\pi ) = L(s,\widetilde {\pi }) =1$
. Hence it follows from the local functional equation that we have
 $$ \begin{align} Z\left(\widehat{\Phi},1-s+\frac{n-1}{2},\check{f}\right) = \varepsilon(s,\pi,\psi) Z\left(\Phi,s+\frac{n-1}{2},f\right), \end{align} $$
$$ \begin{align} Z\left(\widehat{\Phi},1-s+\frac{n-1}{2},\check{f}\right) = \varepsilon(s,\pi,\psi) Z\left(\Phi,s+\frac{n-1}{2},f\right), \end{align} $$
where
![]() $\varepsilon (s,\pi ,\psi )$
denotes the
$\varepsilon (s,\pi ,\psi )$
denotes the
![]() $\varepsilon $
-factor of
$\varepsilon $
-factor of
![]() $\pi $
. It is known that
$\pi $
. It is known that
![]() $\varepsilon (s,\pi ,\psi ) = cq^{-|\lambda _{\pi }| s}$
for some nonzero constant c. Since the left-hand side is in
$\varepsilon (s,\pi ,\psi ) = cq^{-|\lambda _{\pi }| s}$
for some nonzero constant c. Since the left-hand side is in
![]() $q^{-|\lambda | s} \mathbb {C}[[q^{s}]]$
, we see that
$q^{-|\lambda | s} \mathbb {C}[[q^{s}]]$
, we see that
![]() $|\lambda | \geq |\lambda _{\pi }|$
. This proves Theorem 2.2 for
$|\lambda | \geq |\lambda _{\pi }|$
. This proves Theorem 2.2 for
![]() $\pi $
.
$\pi $
.
As explained in Section 5.2, Proposition 5.2 and results in Section 6.4 and this subsection complete Theorem 2.2 in all cases.
7.2 Proof of Theorem 2.1: reduction to Speh representations
In this subsection, we prove Lemma 7.2. By this lemma, Theorem 2.1 for
![]() $\pi $
with
$\pi $
with
![]() $L(s,\pi ) = 1$
is reduced to the case where
$L(s,\pi ) = 1$
is reduced to the case where
![]() $\pi = Z(\Delta )$
.
$\pi = Z(\Delta )$
.
Lemma 7.2. Let
![]() $\pi = Z(\mathfrak {m}) \in \mathrm {Irr}(G_n)$
be such that
$\pi = Z(\mathfrak {m}) \in \mathrm {Irr}(G_n)$
be such that
![]() $L(s,\pi ) = 1$
. Write
$L(s,\pi ) = 1$
. Write
![]() $\mathfrak {m} = \Delta _1 + \dots + \Delta _r$
. Assume that
$\mathfrak {m} = \Delta _1 + \dots + \Delta _r$
. Assume that
 $$\begin{align*}\dim (Z(\Delta_i)^{\mathbb{K}_{n_i, \lambda_i}}) = \left\{ \begin{aligned} &1 &\quad&\text{if } \lambda_i = \lambda_{\Delta_i}, \\ &0 &\quad&\text{if } \lambda_i < \lambda_{\Delta_i} \end{aligned} \right. \end{align*}$$
$$\begin{align*}\dim (Z(\Delta_i)^{\mathbb{K}_{n_i, \lambda_i}}) = \left\{ \begin{aligned} &1 &\quad&\text{if } \lambda_i = \lambda_{\Delta_i}, \\ &0 &\quad&\text{if } \lambda_i < \lambda_{\Delta_i} \end{aligned} \right. \end{align*}$$
for
![]() $1 \leq i \leq r$
, where
$1 \leq i \leq r$
, where
![]() $n_i$
is such that
$n_i$
is such that
![]() $Z(\Delta _i) \in \mathrm {Irr}(G_{n_i})$
. Then we have
$Z(\Delta _i) \in \mathrm {Irr}(G_{n_i})$
. Then we have
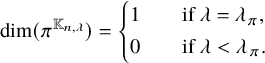 $$\begin{align*}\dim (\pi^{\mathbb{K}_{n, \lambda}}) = \left\{ \begin{aligned} &1 &\quad&\text{if } \lambda = \lambda_{\pi}, \\ &0 &\quad&\text{if } \lambda < \lambda_{\pi}. \end{aligned} \right. \end{align*}$$
$$\begin{align*}\dim (\pi^{\mathbb{K}_{n, \lambda}}) = \left\{ \begin{aligned} &1 &\quad&\text{if } \lambda = \lambda_{\pi}, \\ &0 &\quad&\text{if } \lambda < \lambda_{\pi}. \end{aligned} \right. \end{align*}$$
Proof. Set
![]() $\Pi = Z(\Delta _1) \times \dots \times Z(\Delta _r)$
. First, we claim that
$\Pi = Z(\Delta _1) \times \dots \times Z(\Delta _r)$
. First, we claim that
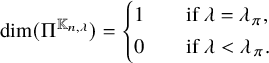 $$\begin{align*}\dim (\Pi^{\mathbb{K}_{n, \lambda}}) = \left\{ \begin{aligned} &1 &\quad&\text{if } \lambda = \lambda_{\pi}, \\ &0 &\quad&\text{if } \lambda < \lambda_{\pi}. \end{aligned} \right. \end{align*}$$
$$\begin{align*}\dim (\Pi^{\mathbb{K}_{n, \lambda}}) = \left\{ \begin{aligned} &1 &\quad&\text{if } \lambda = \lambda_{\pi}, \\ &0 &\quad&\text{if } \lambda < \lambda_{\pi}. \end{aligned} \right. \end{align*}$$
Write
![]() $\lambda _{\pi } = (\lambda _1, \dots , \lambda _n)$
, and consider
$\lambda _{\pi } = (\lambda _1, \dots , \lambda _n)$
, and consider
![]() $M = \oplus _{i=1}^n \mathfrak {o}/\mathfrak {p}^{\lambda _i}$
. Then
$M = \oplus _{i=1}^n \mathfrak {o}/\mathfrak {p}^{\lambda _i}$
. Then
![]() $\mathbb {K}_{n,\lambda _{\pi }}$
is conjugate to
$\mathbb {K}_{n,\lambda _{\pi }}$
is conjugate to
![]() $\mathbb {K}_{n,[M]}$
. By Proposition 5.2, we have
$\mathbb {K}_{n,[M]}$
. By Proposition 5.2, we have
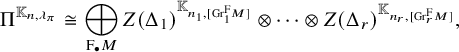 $$\begin{align*}\Pi^{\mathbb{K}_{n,\lambda_{\pi}}} \cong \bigoplus_{\mathrm{F}_{\bullet} M} Z(\Delta_1)^{\mathbb{K}_{n_1, [\mathrm{Gr}^{\mathrm{F}}_1 M]}} \otimes \dots \otimes Z(\Delta_r)^{\mathbb{K}_{n_r, [\mathrm{Gr}^{\mathrm{F}}_r M]}}, \end{align*}$$
$$\begin{align*}\Pi^{\mathbb{K}_{n,\lambda_{\pi}}} \cong \bigoplus_{\mathrm{F}_{\bullet} M} Z(\Delta_1)^{\mathbb{K}_{n_1, [\mathrm{Gr}^{\mathrm{F}}_1 M]}} \otimes \dots \otimes Z(\Delta_r)^{\mathbb{K}_{n_r, [\mathrm{Gr}^{\mathrm{F}}_r M]}}, \end{align*}$$
where
![]() $\mathrm {F}_{\bullet } M$
runs over the set of
$\mathrm {F}_{\bullet } M$
runs over the set of
![]() $\mathbf {n}$
-admissible filtrations with
$\mathbf {n}$
-admissible filtrations with
![]() $\mathbf {n} = (n_1,\dots ,n_r)$
. Since
$\mathbf {n} = (n_1,\dots ,n_r)$
. Since
![]() $\lambda _{\pi } = \lambda _{\Delta _1} + \dots + \lambda _{\Delta _r}$
, by Corollary 4.7, there exists a unique
$\lambda _{\pi } = \lambda _{\Delta _1} + \dots + \lambda _{\Delta _r}$
, by Corollary 4.7, there exists a unique
![]() $\mathbf {n}$
-admissible filtration
$\mathbf {n}$
-admissible filtration
![]() $\mathrm {F}^0_{\bullet } M$
such that
$\mathrm {F}^0_{\bullet } M$
such that
![]() $\mathrm {seq}_n([\mathrm {Gr}^{\mathrm {F}^0}_i M]) = \lambda _{\Delta _i}$
for
$\mathrm {seq}_n([\mathrm {Gr}^{\mathrm {F}^0}_i M]) = \lambda _{\Delta _i}$
for
![]() $1 \leq i \leq r$
. Moreover, for any other filtration
$1 \leq i \leq r$
. Moreover, for any other filtration
![]() $\mathrm {F}_{\bullet } M$
, it holds that
$\mathrm {F}_{\bullet } M$
, it holds that
![]() $\mathrm {seq}_n([\mathrm {Gr}^{\mathrm {F}}_i M]) < \lambda _{\Delta _i}$
for some
$\mathrm {seq}_n([\mathrm {Gr}^{\mathrm {F}}_i M]) < \lambda _{\Delta _i}$
for some
![]() $1 \leq i \leq r$
. Hence by our assumption, we have
$1 \leq i \leq r$
. Hence by our assumption, we have
![]() $Z(\Delta _1)^{\mathbb {K}_{n_1, [\mathrm {Gr}^{\mathrm {F}}_1 M]}} \otimes \dots \otimes Z(\Delta _r)^{\mathbb {K}_{n_r, [\mathrm {Gr}^{\mathrm {F}}_r M]}} = 0$
, and
$Z(\Delta _1)^{\mathbb {K}_{n_1, [\mathrm {Gr}^{\mathrm {F}}_1 M]}} \otimes \dots \otimes Z(\Delta _r)^{\mathbb {K}_{n_r, [\mathrm {Gr}^{\mathrm {F}}_r M]}} = 0$
, and
Conversely, suppose that
![]() $[M] \in |\mathcal {C}^n|$
satisfies
$[M] \in |\mathcal {C}^n|$
satisfies
![]() $\Pi ^{\mathbb {K}_{n,[M]}} \not = 0$
. Then by Propositions 5.2, 4.4 and our assumption, we have
$\Pi ^{\mathbb {K}_{n,[M]}} \not = 0$
. Then by Propositions 5.2, 4.4 and our assumption, we have
In other words, if
![]() $\lambda < \lambda _{\pi }$
, then
$\lambda < \lambda _{\pi }$
, then
![]() $\Pi ^{\mathbb {K}_{n,\lambda }} = 0$
. Hence we obtain the claim.
$\Pi ^{\mathbb {K}_{n,\lambda }} = 0$
. Hence we obtain the claim.
In particular, since
![]() $\pi $
is a subquotient of
$\pi $
is a subquotient of
![]() $\Pi $
, we have
$\Pi $
, we have
![]() $\pi ^{\mathbb {K}_{n,\lambda }} = 0$
for
$\pi ^{\mathbb {K}_{n,\lambda }} = 0$
for
![]() $\lambda < \lambda _{\pi }$
.
$\lambda < \lambda _{\pi }$
.
We show
![]() $\dim (\pi ^{\mathbb {K}_{n,\lambda }}) = 1$
by induction on the number
$\dim (\pi ^{\mathbb {K}_{n,\lambda }}) = 1$
by induction on the number
![]() $t_{\pi }$
of pairs of linked segments in
$t_{\pi }$
of pairs of linked segments in
![]() $\{\Delta _1, \dots , \Delta _r\}$
. If
$\{\Delta _1, \dots , \Delta _r\}$
. If
![]() $t_{\pi } = 0$
, then by [Reference Zelevinsky42, 4.2 Theorem],
$t_{\pi } = 0$
, then by [Reference Zelevinsky42, 4.2 Theorem],
![]() $\Pi $
is irreducible so that
$\Pi $
is irreducible so that
![]() $\pi = \Pi $
. In this case, the assertion is obtained above.
$\pi = \Pi $
. In this case, the assertion is obtained above.
Now assume that
![]() $t_{\pi }> 0$
. By [Reference Zelevinsky42, 7.1 Theorem], if
$t_{\pi }> 0$
. By [Reference Zelevinsky42, 7.1 Theorem], if
![]() $\pi ' = Z(\mathfrak {m}') \in \mathrm {Irr}(G_n)$
is an irreducible constituent of
$\pi ' = Z(\mathfrak {m}') \in \mathrm {Irr}(G_n)$
is an irreducible constituent of
![]() $\Pi $
, then the multisegment
$\Pi $
, then the multisegment
![]() $\mathfrak {m}'$
is obtained from
$\mathfrak {m}'$
is obtained from
![]() $\mathfrak {m}$
by a chain of elementary operations. In particular, if
$\mathfrak {m}$
by a chain of elementary operations. In particular, if
![]() $\pi ' \not \cong \pi $
, we have
$\pi ' \not \cong \pi $
, we have
![]() $t_{\pi '} < t_{\pi }$
. Moreover, since
$t_{\pi '} < t_{\pi }$
. Moreover, since
![]() $L(s,\pi ) = 1$
, we see that
$L(s,\pi ) = 1$
, we see that
![]() $\lambda _{\pi '}> \lambda _{\pi }$
. By the inductive hypothesis, we have
$\lambda _{\pi '}> \lambda _{\pi }$
. By the inductive hypothesis, we have
![]() $\pi ^{\prime \mathbb {K}_{n,\lambda _{\pi }}} = 0$
. Therefore, we have
$\pi ^{\prime \mathbb {K}_{n,\lambda _{\pi }}} = 0$
. Therefore, we have
![]() $\Pi ^{\mathbb {K}_{n,\lambda _{\pi }}} = \pi ^{\mathbb {K}_{n,\lambda _{\pi }}}$
since
$\Pi ^{\mathbb {K}_{n,\lambda _{\pi }}} = \pi ^{\mathbb {K}_{n,\lambda _{\pi }}}$
since
![]() $\pi $
appears in the irreducible constituents of
$\pi $
appears in the irreducible constituents of
![]() $\Pi $
with multiplicity one. It follows from the above claim that
$\Pi $
with multiplicity one. It follows from the above claim that
![]() $\pi ^{\mathbb {K}_{n,\lambda _{\pi }}}$
is one-dimensional. This completes the proof.
$\pi ^{\mathbb {K}_{n,\lambda _{\pi }}}$
is one-dimensional. This completes the proof.
Note that Theorem 2.1 for
![]() $\pi $
is equivalent to the one for its unramified twist
$\pi $
is equivalent to the one for its unramified twist
![]() $\pi |\cdot |^c$
. Therefore, we may assume that
$\pi |\cdot |^c$
. Therefore, we may assume that
![]() $\pi $
has a unitary central character. In Section 9 below, we will prove Theorem 2.1 for
$\pi $
has a unitary central character. In Section 9 below, we will prove Theorem 2.1 for
![]() $\pi = Z(\Delta )$
with a unitary central character such that
$\pi = Z(\Delta )$
with a unitary central character such that
![]() $L(s,\pi ) = 1$
. The proof of this case is rather similar to the generic case in [Reference Jacquet, Piatetski-Shapiro and Shalika14]. To carry out the proof, we will establish the theory of Rankin–Selberg integrals for
$L(s,\pi ) = 1$
. The proof of this case is rather similar to the generic case in [Reference Jacquet, Piatetski-Shapiro and Shalika14]. To carry out the proof, we will establish the theory of Rankin–Selberg integrals for
![]() $Z(\Delta )$
in Section 8.
$Z(\Delta )$
in Section 8.
Remark 7.3. We note that Lemma 7.2 does not work for
![]() $\pi $
with
$\pi $
with
![]() $L(s,\pi ) \not = 1$
since the equality
$L(s,\pi ) \not = 1$
since the equality
![]() $\lambda _{\pi } = \lambda _{\Delta _1} + \dots + \lambda _{\Delta _r}$
does not hold in general. It is one of the two reasons we should treat the case where
$\lambda _{\pi } = \lambda _{\Delta _1} + \dots + \lambda _{\Delta _r}$
does not hold in general. It is one of the two reasons we should treat the case where
![]() $L(s,\pi ) = 1$
and the other case separately. The other reason will be explained in Remark 8.8 below.
$L(s,\pi ) = 1$
and the other case separately. The other reason will be explained in Remark 8.8 below.
8 Rankin–Selberg integrals for Speh representations
In [Reference Jacquet, Piatetski-Shapiro and Shalika14], Jacquet–Piatetskii-Shapiro–Shalika proved Theorem 2.1 for
![]() $\pi $
generic. The ingredients they used are the Rankin–Selberg integrals [Reference Jacquet, Piatetski-Shapiro and Shalika15], which express the L-factors of the products of two generic representations of
$\pi $
generic. The ingredients they used are the Rankin–Selberg integrals [Reference Jacquet, Piatetski-Shapiro and Shalika15], which express the L-factors of the products of two generic representations of
![]() $G_n$
and
$G_n$
and
![]() $G_{n-1}$
. (They also have expressions for products of representations of groups of other ranks, but the one used for the study of local newforms is the one mentioned above.)
$G_{n-1}$
. (They also have expressions for products of representations of groups of other ranks, but the one used for the study of local newforms is the one mentioned above.)
In [Reference Lapid and Mao20], Lapid and Mao introduced the Rankin–Selberg integrals for the products of Speh representations in the equal rank case. To prove Theorem 2.1 for Speh representations in the next section, we introduce the Rankin–Selberg integrals for the product of Speh representations in the case
![]() $G_{nm} \times G_{(n-1)m}$
.
$G_{nm} \times G_{(n-1)m}$
.
8.1 Subgroups of
 $\mathrm {GL}_{nm}$
(F)
$\mathrm {GL}_{nm}$
(F)
Fix positive integers m and n. In this subsection, we fix notations for some subgroups of
![]() $\mathrm {GL}_{nm}(F)$
.
$\mathrm {GL}_{nm}(F)$
.
Set
![]() $G = G_{nm} = \mathrm {GL}_{nm}(F)$
and
$G = G_{nm} = \mathrm {GL}_{nm}(F)$
and
![]() $K = \mathrm {GL}_{nm}(\mathfrak {o})$
. Let
$K = \mathrm {GL}_{nm}(\mathfrak {o})$
. Let
![]() $B = TN$
be the Borel subgroup of G consisting of upper triangular matrices, where T is the diagonal torus.
$B = TN$
be the Borel subgroup of G consisting of upper triangular matrices, where T is the diagonal torus.
We write an element of G as
![]() $g = (g_{i,j})_{1 \leq i,j \leq m}$
with
$g = (g_{i,j})_{1 \leq i,j \leq m}$
with
![]() $g_{i,j} \in M_n(F)$
. Define
$g_{i,j} \in M_n(F)$
. Define
-
• L to be the subgroup of G consisting of block diagonal matrices: that is,
 $g = (g_{i,j})_{1 \leq i,j \leq m} \in G$
with
$g = (g_{i,j})_{1 \leq i,j \leq m} \in G$
with
 $g_{i,j} = 0$
for
$g_{i,j} = 0$
for
 $i \not = j$
;
$i \not = j$
; -
• U to be the subgroup of G consisting of block upper unipotent matrices: that is,
 $g = (g_{i,j})_{1 \leq i,j \leq m} \in G$
with
$g = (g_{i,j})_{1 \leq i,j \leq m} \in G$
with
 $g_{i,i} = \mathbf {1}_n$
for
$g_{i,i} = \mathbf {1}_n$
for
 $1 \leq i \leq m$
and
$1 \leq i \leq m$
and
 $g_{i,j} = 0$
for
$g_{i,j} = 0$
for
 $i> j$
;
$i> j$
; -
• S to be the subgroup of G consisting of
 $g = (g_{i,j})_{1 \leq i,j \leq m} \in G$
such that each
$g = (g_{i,j})_{1 \leq i,j \leq m} \in G$
such that each
 $g_{i,j}$
is a diagonal matrix;
$g_{i,j}$
is a diagonal matrix; -
• V to be the subgroup of G consisting of
 $g = (g_{i,j})_{1 \leq i,j \leq m} \in G$
such that each
$g = (g_{i,j})_{1 \leq i,j \leq m} \in G$
such that each
 $g_{i,j} - \delta _{i,j}\mathbf {1}_n$
is a strictly upper triangular matrix;
$g_{i,j} - \delta _{i,j}\mathbf {1}_n$
is a strictly upper triangular matrix; -
• D to be the subgroup of G consisting of
 $g = (g_{i,j})_{1 \leq i,j \leq m} \in G$
such that each
$g = (g_{i,j})_{1 \leq i,j \leq m} \in G$
such that each
 $g_{i,j}$
is of the form for some
$g_{i,j}$
is of the form for some $$\begin{align*}g_{i,j} = \begin{pmatrix} g^{\prime}_{i,j} & u_{i,j} \\ 0 & \delta_{i,j} \end{pmatrix} \end{align*}$$
$$\begin{align*}g_{i,j} = \begin{pmatrix} g^{\prime}_{i,j} & u_{i,j} \\ 0 & \delta_{i,j} \end{pmatrix} \end{align*}$$
 $g^{\prime }_{i,j} \in M_{n-1}(F)$
and
$g^{\prime }_{i,j} \in M_{n-1}(F)$
and
 $u_{i,j} \in F^{n-1}$
.
$u_{i,j} \in F^{n-1}$
.
Then
![]() $P = LU$
is the standard parabolic subgroup with
$P = LU$
is the standard parabolic subgroup with
![]() $L \cong G_n \times \dots \times G_n$
(m-times) as its Levi subgroup, and
$L \cong G_n \times \dots \times G_n$
(m-times) as its Levi subgroup, and
![]() $Q = SV$
is a nonstandard parabolic subgroup with
$Q = SV$
is a nonstandard parabolic subgroup with
![]() $S \cong G_m \times \dots \times G_m$
(n-times) as its Levi subgroup.
$S \cong G_m \times \dots \times G_m$
(n-times) as its Levi subgroup.
We set
![]() $G' = G_{(n-1)m}$
. We denote analogous subgroups by taking
$G' = G_{(n-1)m}$
. We denote analogous subgroups by taking
![]() $'$
, for example,
$'$
, for example,
![]() $K' = \mathrm {GL}_{(n-1)m}(\mathfrak {o})$
,
$K' = \mathrm {GL}_{(n-1)m}(\mathfrak {o})$
,
![]() $P' = L'U'$
,
$P' = L'U'$
,
![]() $Q' = S'V'$
and so on. Define an embedding
$Q' = S'V'$
and so on. Define an embedding
![]() $\iota \colon G' \hookrightarrow G$
by
$\iota \colon G' \hookrightarrow G$
by
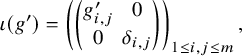 $$\begin{align*}\iota(g') = \left( \begin{pmatrix} g^{\prime}_{i,j} & 0 \\ 0 & \delta_{i,j} \end{pmatrix} \right)_{1 \leq i,j \leq m}, \end{align*}$$
$$\begin{align*}\iota(g') = \left( \begin{pmatrix} g^{\prime}_{i,j} & 0 \\ 0 & \delta_{i,j} \end{pmatrix} \right)_{1 \leq i,j \leq m}, \end{align*}$$
where we write
![]() $g' = (g^{\prime }_{i,j})_{1 \leq i,j \leq m}$
with
$g' = (g^{\prime }_{i,j})_{1 \leq i,j \leq m}$
with
![]() $g^{\prime }_{i,j} \in M_{n-1}(F)$
. Sometimes we identify
$g^{\prime }_{i,j} \in M_{n-1}(F)$
. Sometimes we identify
![]() $G'$
with the image of
$G'$
with the image of
![]() $\iota $
. Note that
$\iota $
. Note that
![]() $G'$
is contained in D.
$G'$
is contained in D.
For example, when
![]() $n = 3$
and
$n = 3$
and
![]() $m = 2$
, the subgroups above are as follows:
$m = 2$
, the subgroups above are as follows:
 $$ \begin{align*} L = \left( \begin{array}{ccc|ccc} *&*&*&&& \\ *&*&*&&& \\ *&*&*&&& \\ \hline &&&*&*&* \\ &&&*&*&* \\ &&&*&*&* \end{array} \right), &\quad U = \left( \begin{array}{ccc|ccc} 1&&&*&*&* \\ &1&&*&*&* \\ &&1&*&*&* \\ \hline &&&1&& \\ &&&&1& \\ &&&&&1 \end{array} \right), \\ S = \left( \begin{array}{ccc|ccc} *&&&*&& \\ &*&&&*& \\ &&*&&&* \\ \hline *&&&*&& \\ &*&&&*& \\ &&*&&&* \end{array} \right), &\quad V = \left( \begin{array}{ccc|ccc} 1&*&*&&*&* \\ &1&*&&&* \\ &&1&&& \\ \hline &*&*&1&*&* \\ &&*&&1&* \\ &&&&&1 \end{array} \right), \\ D = \left( \begin{array}{ccc|ccc} *&*&*&*&*&* \\ *&*&*&*&*&* \\ &&1&&& \\ \hline *&*&*&*&*&* \\ *&*&*&*&*&* \\ &&&&&1 \end{array} \right), &\quad G' = \left( \begin{array}{ccc|ccc} *&*&&*&*& \\ *&*&&*&*& \\ &&1&&& \\ \hline *&*&&*&*& \\ *&*&&*&*& \\ &&&&&1 \end{array} \right). \end{align*} $$
$$ \begin{align*} L = \left( \begin{array}{ccc|ccc} *&*&*&&& \\ *&*&*&&& \\ *&*&*&&& \\ \hline &&&*&*&* \\ &&&*&*&* \\ &&&*&*&* \end{array} \right), &\quad U = \left( \begin{array}{ccc|ccc} 1&&&*&*&* \\ &1&&*&*&* \\ &&1&*&*&* \\ \hline &&&1&& \\ &&&&1& \\ &&&&&1 \end{array} \right), \\ S = \left( \begin{array}{ccc|ccc} *&&&*&& \\ &*&&&*& \\ &&*&&&* \\ \hline *&&&*&& \\ &*&&&*& \\ &&*&&&* \end{array} \right), &\quad V = \left( \begin{array}{ccc|ccc} 1&*&*&&*&* \\ &1&*&&&* \\ &&1&&& \\ \hline &*&*&1&*&* \\ &&*&&1&* \\ &&&&&1 \end{array} \right), \\ D = \left( \begin{array}{ccc|ccc} *&*&*&*&*&* \\ *&*&*&*&*&* \\ &&1&&& \\ \hline *&*&*&*&*&* \\ *&*&*&*&*&* \\ &&&&&1 \end{array} \right), &\quad G' = \left( \begin{array}{ccc|ccc} *&*&&*&*& \\ *&*&&*&*& \\ &&1&&& \\ \hline *&*&&*&*& \\ *&*&&*&*& \\ &&&&&1 \end{array} \right). \end{align*} $$
It is easy to see the following:
Lemma 8.1.
-
(1)
 $D = VG'$
and
$D = VG'$
and
 $G' \cap V = V'$
so that
$G' \cap V = V'$
so that
 $V \backslash D \cong V' \backslash G'$
.
$V \backslash D \cong V' \backslash G'$
. -
(2)
 $N \cap D = (N \cap V) N'$
and
$N \cap D = (N \cap V) N'$
and
 $(N \cap V) \cap N' = N' \cap V'$
so that
$(N \cap V) \cap N' = N' \cap V'$
so that
 $(N \cap V) \backslash (N \cap D) \cong (N' \cap V') \backslash N'$
.
$(N \cap V) \backslash (N \cap D) \cong (N' \cap V') \backslash N'$
.
Proof. Omitted.
8.2 Two models of Speh representations
We introduce the Zelevinsky model and the Shalika model of a Speh representation. For the detail of these models and the relation between them, see [Reference Lapid and Mao20, Section 3].
We define a function
![]() $\Psi $
of
$\Psi $
of
![]() $G = G_{nm}$
by
$G = G_{nm}$
by
 $$\begin{align*}\Psi(g) = \psi \left( \sum_{\substack{1 \leq i < nm \\ n \nmid i}}g_{i,i+1} \right). \end{align*}$$
$$\begin{align*}\Psi(g) = \psi \left( \sum_{\substack{1 \leq i < nm \\ n \nmid i}}g_{i,i+1} \right). \end{align*}$$
We denote the restriction of
![]() $\Psi $
to N (respectively, V) by the same symbol
$\Psi $
to N (respectively, V) by the same symbol
![]() $\Psi $
, which is a character of N (respectively, V).
$\Psi $
, which is a character of N (respectively, V).
Let
![]() $\pi $
be an irreducible tempered representation of
$\pi $
be an irreducible tempered representation of
![]() $G_n$
. Then the parabolically induced representation
$G_n$
. Then the parabolically induced representation
of G has a unique irreducible subrepresentation
![]() $\mathrm {Sp}(\pi , m)$
. We call
$\mathrm {Sp}(\pi , m)$
. We call
![]() $\mathrm {Sp}(\pi , m)$
a Speh representation. Note that if
$\mathrm {Sp}(\pi , m)$
a Speh representation. Note that if
![]() $\pi = \rho $
is cuspidal, then
$\pi = \rho $
is cuspidal, then
![]() $\mathrm {Sp}(\rho ,m) = Z([-\frac {m-1}{2},\frac {m-1}{2}]_{\rho })$
.
$\mathrm {Sp}(\rho ,m) = Z([-\frac {m-1}{2},\frac {m-1}{2}]_{\rho })$
.
From now on, we set
![]() $\sigma = \mathrm {Sp}(\pi , m)$
for some irreducible tempered representation
$\sigma = \mathrm {Sp}(\pi , m)$
for some irreducible tempered representation
![]() $\pi $
of
$\pi $
of
![]() $G_n$
. By [Reference Zelevinsky42, 8.3], we know that
$G_n$
. By [Reference Zelevinsky42, 8.3], we know that
is one-dimensional. Following [Reference Lapid and Mao20, Section 3.1], we write
![]() $\mathcal {W}^{\psi }_{\mathrm {Ze}}(\sigma )$
for the image of a nonzero element and call it the Zelevinsky model of
$\mathcal {W}^{\psi }_{\mathrm {Ze}}(\sigma )$
for the image of a nonzero element and call it the Zelevinsky model of
![]() $\sigma $
.
$\sigma $
.
In the case
![]() $m=1$
, the Zelevinsky model
$m=1$
, the Zelevinsky model
![]() $\mathcal {W}^{\psi }(\pi ) = \mathcal {W}^{\psi }_{\mathrm {Ze}}(\pi )$
is what is known as the Whittaker model of
$\mathcal {W}^{\psi }(\pi ) = \mathcal {W}^{\psi }_{\mathrm {Ze}}(\pi )$
is what is known as the Whittaker model of
![]() $\pi $
. Note that the character
$\pi $
. Note that the character
![]() $\Psi $
is a generic character of N in this case, and the one-dimensionality above implies that every tempered representation
$\Psi $
is a generic character of N in this case, and the one-dimensionality above implies that every tempered representation
![]() $\pi $
of
$\pi $
of
![]() $G_n$
is generic.
$G_n$
is generic.
As explained in [Reference Lapid and Mao20, Section 3.1], for any
![]() $W \in \mathcal {W}^{\psi }_{\mathrm {Ze}}(\sigma )$
, we have
$W \in \mathcal {W}^{\psi }_{\mathrm {Ze}}(\sigma )$
, we have
By [Reference Mœglin and Waldspurger32], we know that
is also one-dimensional. Following [Reference Lapid and Mao20, Section 3.1], we write
![]() $\mathcal {W}^{\psi }_{\mathrm {Sh}}(\sigma )$
for the image of a nonzero element and call it the Shalika model of
$\mathcal {W}^{\psi }_{\mathrm {Sh}}(\sigma )$
for the image of a nonzero element and call it the Shalika model of
![]() $\sigma $
. As explained in [Reference Lapid and Mao20, Section 3.1], the usage of this terminology may not be a common one.
$\sigma $
. As explained in [Reference Lapid and Mao20, Section 3.1], the usage of this terminology may not be a common one.
We recall a theorem of Lapid and Mao.
Theorem 8.2 [Reference Lapid and Mao20, Theorem 4.3]
For
![]() $W_1, W_2 \in \mathcal {W}^{\psi }_{\mathrm {Sh}}(\sigma )$
, the integral
$W_1, W_2 \in \mathcal {W}^{\psi }_{\mathrm {Sh}}(\sigma )$
, the integral
converges for
![]() $\mathrm {Re}(s)> -1$
and admits meromorphic continuation to the complex plane. Moreover,
$\mathrm {Re}(s)> -1$
and admits meromorphic continuation to the complex plane. Moreover,
![]() $(W_1,W_2) \mapsto \mathcal {B}(W_1,W_2,0)$
is a G-invariant inner product on
$(W_1,W_2) \mapsto \mathcal {B}(W_1,W_2,0)$
is a G-invariant inner product on
![]() $\mathcal {W}^{\psi }_{\mathrm {Sh}}(\sigma )$
.
$\mathcal {W}^{\psi }_{\mathrm {Sh}}(\sigma )$
.
Proof. See [Reference Lapid and Mao20, Theorem 4.3]. See also [Reference Lapid and Mao20, Propositions 4.1, 6.2].
Note that
![]() $\mathcal {W}^{\psi }_{\mathrm {Ze}}(\sigma )$
and
$\mathcal {W}^{\psi }_{\mathrm {Ze}}(\sigma )$
and
![]() $\mathcal {W}^{\psi }_{\mathrm {Sh}}(\sigma )$
are isomorphic to each other since both are isomorphic to
$\mathcal {W}^{\psi }_{\mathrm {Sh}}(\sigma )$
are isomorphic to each other since both are isomorphic to
![]() $\sigma $
. We can give isomorphisms explicitly as follows.
$\sigma $
. We can give isomorphisms explicitly as follows.
Proposition 8.3 [Reference Lapid and Mao20, Lemmas 3.8, 3.11]
Let
![]() $W_{\mathrm {Ze}} \in \mathcal {W}^{\psi }_{\mathrm {Ze}}(\sigma )$
and
$W_{\mathrm {Ze}} \in \mathcal {W}^{\psi }_{\mathrm {Ze}}(\sigma )$
and
![]() $W_{\mathrm {Sh}} \in \mathcal {W}^{\psi }_{\mathrm {Sh}}(\sigma )$
. Then
$W_{\mathrm {Sh}} \in \mathcal {W}^{\psi }_{\mathrm {Sh}}(\sigma )$
. Then
![]() $W_{\mathrm {Ze}}$
(respectively,
$W_{\mathrm {Ze}}$
(respectively,
![]() $W_{\mathrm {Sh}}$
) is compactly supported on
$W_{\mathrm {Sh}}$
) is compactly supported on
![]() $(V \cap N) \backslash V$
(respectively,
$(V \cap N) \backslash V$
(respectively,
![]() $(N \cap V) \backslash (N \cap D)$
). Moreover, an isomorphism
$(N \cap V) \backslash (N \cap D)$
). Moreover, an isomorphism
![]() $\mathcal {T} = \mathcal {T}^{\psi } \colon \mathcal {W}^{\psi }_{\mathrm {Ze}}(\sigma ) \xrightarrow {\sim } \mathcal {W}^{\psi }_{\mathrm {Sh}}(\sigma )$
is given by the integral
$\mathcal {T} = \mathcal {T}^{\psi } \colon \mathcal {W}^{\psi }_{\mathrm {Ze}}(\sigma ) \xrightarrow {\sim } \mathcal {W}^{\psi }_{\mathrm {Sh}}(\sigma )$
is given by the integral
The inverse of
![]() $\mathcal {T}$
is given by the integral
$\mathcal {T}$
is given by the integral
Proof. See [Reference Lapid and Mao20, Lemmas 3.8, 3.11].
8.3 Rankin–Selberg integrals in the Zelevinsky models
For irreducible tempered representations
![]() $\pi $
and
$\pi $
and
![]() $\pi '$
of
$\pi '$
of
![]() $G_n$
and
$G_n$
and
![]() $G_{n-1}$
, respectively, we have Speh representations
$G_{n-1}$
, respectively, we have Speh representations
![]() $\sigma = \mathrm {Sp}(\pi ,m) \in \mathrm {Irr}(G)$
and
$\sigma = \mathrm {Sp}(\pi ,m) \in \mathrm {Irr}(G)$
and
![]() $\sigma ' = \mathrm {Sp}(\pi ',m) \in \mathrm {Irr}(G')$
. For
$\sigma ' = \mathrm {Sp}(\pi ',m) \in \mathrm {Irr}(G')$
. For
![]() $W \in W^{\psi }_{\mathrm {Ze}}(\sigma )$
,
$W \in W^{\psi }_{\mathrm {Ze}}(\sigma )$
,
![]() $W' \in W^{\psi ^{-1}}_{\mathrm {Ze}}(\sigma ')$
and
$W' \in W^{\psi ^{-1}}_{\mathrm {Ze}}(\sigma ')$
and
![]() $s \in \mathbb {C}$
, consider the integral
$s \in \mathbb {C}$
, consider the integral
We call this the Rankin–Selberg integral in the Zelevinsky models.
Lemma 8.4. Formally,
![]() $I_m(s,W,W')$
is equal to
$I_m(s,W,W')$
is equal to
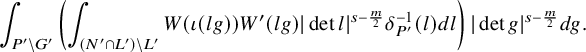 $$\begin{align*}\int_{P' \backslash G'} \left( \int_{(N' \cap L') \backslash L'}W(\iota(lg)) W'(lg) |\det l|^{s-\frac{m}{2}} \delta_{P'}^{-1}(l)dl \right) |\det g|^{s-\frac{m}{2}} dg. \end{align*}$$
$$\begin{align*}\int_{P' \backslash G'} \left( \int_{(N' \cap L') \backslash L'}W(\iota(lg)) W'(lg) |\det l|^{s-\frac{m}{2}} \delta_{P'}^{-1}(l)dl \right) |\det g|^{s-\frac{m}{2}} dg. \end{align*}$$
Proof. This follows from a well-known integral formula.
When
![]() $m = 1$
, several properties of
$m = 1$
, several properties of
![]() $I_1(s,W,W')$
were obtained in [Reference Jacquet, Piatetski-Shapiro and Shalika15]. The following is a generalisation of [Reference Jacquet, Piatetski-Shapiro and Shalika15, (2.7) Theorem], whose proof is analogous to that of [Reference Lapid and Mao20, Theorem 5.1].
$I_1(s,W,W')$
were obtained in [Reference Jacquet, Piatetski-Shapiro and Shalika15]. The following is a generalisation of [Reference Jacquet, Piatetski-Shapiro and Shalika15, (2.7) Theorem], whose proof is analogous to that of [Reference Lapid and Mao20, Theorem 5.1].
Theorem 8.5. Let
![]() $\pi $
and
$\pi $
and
![]() $\pi '$
be irreducible tempered representations of
$\pi '$
be irreducible tempered representations of
![]() $G_n$
and
$G_n$
and
![]() $G_{n-1}$
, respectively. We denote the central character of
$G_{n-1}$
, respectively. We denote the central character of
![]() $\pi '$
by
$\pi '$
by
![]() $\omega _{\pi '}$
.
$\omega _{\pi '}$
.
-
(1) The integral
 $I_m(s,W,W')$
is absolutely convergent for
$I_m(s,W,W')$
is absolutely convergent for
 $\mathrm {Re}(s) \gg 0$
.
$\mathrm {Re}(s) \gg 0$
. -
(2) The function
is in $$\begin{align*}\left(\prod_{i=1}^m L(s-m+i, \pi \times \pi')\right)^{-1} I_m(s,W,W') \end{align*}$$
$$\begin{align*}\left(\prod_{i=1}^m L(s-m+i, \pi \times \pi')\right)^{-1} I_m(s,W,W') \end{align*}$$
 $\mathbb {C}[q^{-s}, q^{s}]$
. In particular, it is entire.
$\mathbb {C}[q^{-s}, q^{s}]$
. In particular, it is entire.
-
(3) The functional equation
holds, where $$\begin{align*}I_m(m-s,\widetilde{W},\widetilde{W}') = \omega_{\pi'}(-1)^{(n-1)m} \left( \prod_{i=1}^m \gamma(s-m+i, \pi \times \pi', \psi) \right) I_m(s,W,W') \end{align*}$$
$$\begin{align*}I_m(m-s,\widetilde{W},\widetilde{W}') = \omega_{\pi'}(-1)^{(n-1)m} \left( \prod_{i=1}^m \gamma(s-m+i, \pi \times \pi', \psi) \right) I_m(s,W,W') \end{align*}$$
 $\widetilde {W}(g) = W(w_{nm} {}^tg^{-1} w^{\prime }_n)$
and
$\widetilde {W}(g) = W(w_{nm} {}^tg^{-1} w^{\prime }_n)$
and
 $\widetilde {W}'(g') = W'(w_{(n-1)m} {}^tg^{\prime -1} w^{\prime }_{n-1})$
with
$\widetilde {W}'(g') = W'(w_{(n-1)m} {}^tg^{\prime -1} w^{\prime }_{n-1})$
with  $$\begin{align*}w_{nm} = \begin{pmatrix} &&1 \\ &\unicode{x22F0}& \\ 1&& \end{pmatrix}, \quad w^{\prime}_n = \begin{pmatrix} &&\mathbf{1}_{n} \\ &\unicode{x22F0}& \\ \mathbf{1}_{n} && \end{pmatrix} \in G. \end{align*}$$
$$\begin{align*}w_{nm} = \begin{pmatrix} &&1 \\ &\unicode{x22F0}& \\ 1&& \end{pmatrix}, \quad w^{\prime}_n = \begin{pmatrix} &&\mathbf{1}_{n} \\ &\unicode{x22F0}& \\ \mathbf{1}_{n} && \end{pmatrix} \in G. \end{align*}$$
Here
 $\gamma (s, \pi \times \pi ', \psi )$
is the gamma factor defined by
$\gamma (s, \pi \times \pi ', \psi )$
is the gamma factor defined by  $$\begin{align*}\gamma(s, \pi \times \pi', \psi) = \varepsilon(s, \pi \times \pi', \psi)\frac{L(1-s,\widetilde{\pi} \times \widetilde{\pi}')}{L(s,\pi \times \pi')}. \end{align*}$$
$$\begin{align*}\gamma(s, \pi \times \pi', \psi) = \varepsilon(s, \pi \times \pi', \psi)\frac{L(1-s,\widetilde{\pi} \times \widetilde{\pi}')}{L(s,\pi \times \pi')}. \end{align*}$$
Proof. When
![]() $m=1$
, the assertions are [Reference Jacquet, Piatetski-Shapiro and Shalika15, (2.7) Theorem].
$m=1$
, the assertions are [Reference Jacquet, Piatetski-Shapiro and Shalika15, (2.7) Theorem].
Note that
![]() $\delta _{P'}(l) = \prod _{i=1}^{m}|\det l_i|^{(m+1-2i)(n-1)}$
for
$\delta _{P'}(l) = \prod _{i=1}^{m}|\det l_i|^{(m+1-2i)(n-1)}$
for
![]() $l = \mathrm {diag}(l_1, \dots , l_m) \in L'$
. Moreover,
$l = \mathrm {diag}(l_1, \dots , l_m) \in L'$
. Moreover,
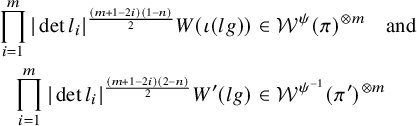 $$ \begin{align*} \prod_{i=1}^m|\det l_i|^{\frac{(m+1-2i)(1-n)}{2}}W(\iota(lg)) &\in \mathcal{W}^{\psi}(\pi)^{\otimes m} \quad\text{and}\\ \prod_{i=1}^m|\det l_i|^{\frac{(m+1-2i)(2-n)}{2}}W'(lg) &\in \mathcal{W}^{\psi^{-1}}(\pi')^{\otimes m} \end{align*} $$
$$ \begin{align*} \prod_{i=1}^m|\det l_i|^{\frac{(m+1-2i)(1-n)}{2}}W(\iota(lg)) &\in \mathcal{W}^{\psi}(\pi)^{\otimes m} \quad\text{and}\\ \prod_{i=1}^m|\det l_i|^{\frac{(m+1-2i)(2-n)}{2}}W'(lg) &\in \mathcal{W}^{\psi^{-1}}(\pi')^{\otimes m} \end{align*} $$
for fixed
![]() $g \in G'$
. It follows that the inner integral of Lemma 8.4 is of the form
$g \in G'$
. It follows that the inner integral of Lemma 8.4 is of the form
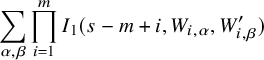 $$\begin{align*}\sum_{\alpha,\beta} \prod_{i=1}^m I_1(s-m+i, W_{i,\alpha}, W^{\prime}_{i,\beta}) \end{align*}$$
$$\begin{align*}\sum_{\alpha,\beta} \prod_{i=1}^m I_1(s-m+i, W_{i,\alpha}, W^{\prime}_{i,\beta}) \end{align*}$$
for some
![]() $W_{i,\alpha } \in \mathcal {W}^{\psi }(\pi )$
and
$W_{i,\alpha } \in \mathcal {W}^{\psi }(\pi )$
and
![]() $W^{\prime }_{i,\beta } \in \mathcal {W}^{\psi ^{-1}}(\pi ')$
(depending on g). Hence we obtain assertions (1) and (2).
$W^{\prime }_{i,\beta } \in \mathcal {W}^{\psi ^{-1}}(\pi ')$
(depending on g). Hence we obtain assertions (1) and (2).
We prove assertion (3). For
![]() $g \in G'$
and
$g \in G'$
and
![]() $l = \mathrm {diag}(l_1, \dots , l_m) \in L'$
with
$l = \mathrm {diag}(l_1, \dots , l_m) \in L'$
with
![]() $l_i \in \mathrm {GL}_{n-1}(F)$
, we note that
$l_i \in \mathrm {GL}_{n-1}(F)$
, we note that
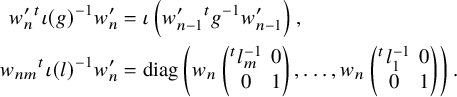 $$ \begin{align*} w^{\prime}_n{}^t\iota(g)^{-1}w^{\prime}_n &= \iota \left(w^{\prime}_{n-1}{}^tg^{-1}w^{\prime}_{n-1}\right), \\ w_{nm}{}^t\iota(l)^{-1} w^{\prime}_n &= \mathrm{diag}\left( w_n \begin{pmatrix} {}^tl_m^{-1} & 0 \\ 0 & 1 \end{pmatrix}, \dots, w_n \begin{pmatrix} {}^tl_1^{-1} & 0 \\ 0 & 1 \end{pmatrix} \right). \end{align*} $$
$$ \begin{align*} w^{\prime}_n{}^t\iota(g)^{-1}w^{\prime}_n &= \iota \left(w^{\prime}_{n-1}{}^tg^{-1}w^{\prime}_{n-1}\right), \\ w_{nm}{}^t\iota(l)^{-1} w^{\prime}_n &= \mathrm{diag}\left( w_n \begin{pmatrix} {}^tl_m^{-1} & 0 \\ 0 & 1 \end{pmatrix}, \dots, w_n \begin{pmatrix} {}^tl_1^{-1} & 0 \\ 0 & 1 \end{pmatrix} \right). \end{align*} $$
Hence we have
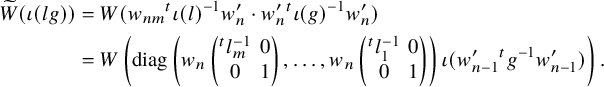 $$ \begin{align*} \widetilde{W}(\iota(lg)) &= W(w_{nm}{}^t\iota(l)^{-1} w^{\prime}_n \cdot w^{\prime}_n {}^t\iota(g)^{-1}w^{\prime}_n) \\&= W\left( \mathrm{diag}\left( w_n \begin{pmatrix} {}^tl_m^{-1} & 0 \\ 0 & 1 \end{pmatrix}, \dots, w_n \begin{pmatrix} {}^tl_1^{-1} & 0 \\ 0 & 1 \end{pmatrix} \right) \iota(w^{\prime}_{n-1}{}^tg^{-1}w^{\prime}_{n-1}) \right). \end{align*} $$
$$ \begin{align*} \widetilde{W}(\iota(lg)) &= W(w_{nm}{}^t\iota(l)^{-1} w^{\prime}_n \cdot w^{\prime}_n {}^t\iota(g)^{-1}w^{\prime}_n) \\&= W\left( \mathrm{diag}\left( w_n \begin{pmatrix} {}^tl_m^{-1} & 0 \\ 0 & 1 \end{pmatrix}, \dots, w_n \begin{pmatrix} {}^tl_1^{-1} & 0 \\ 0 & 1 \end{pmatrix} \right) \iota(w^{\prime}_{n-1}{}^tg^{-1}w^{\prime}_{n-1}) \right). \end{align*} $$
Similarly, we have
 $$ \begin{align*} \widetilde{W}'(lg) &= W'(w_{(n-1)m}{}^tl^{-1}w^{\prime}_{n-1} \cdot w^{\prime}_{n-1}{}^tg^{-1} w^{\prime}_{n-1}) \\&= W'(\mathrm{diag}(w_{n-1}{}^tl_m^{-1}, \dots, w_{n-1}{}^tl_1^{-1}) \cdot w^{\prime}_{n-1}{}^tg^{-1} w^{\prime}_{n-1}). \end{align*} $$
$$ \begin{align*} \widetilde{W}'(lg) &= W'(w_{(n-1)m}{}^tl^{-1}w^{\prime}_{n-1} \cdot w^{\prime}_{n-1}{}^tg^{-1} w^{\prime}_{n-1}) \\&= W'(\mathrm{diag}(w_{n-1}{}^tl_m^{-1}, \dots, w_{n-1}{}^tl_1^{-1}) \cdot w^{\prime}_{n-1}{}^tg^{-1} w^{\prime}_{n-1}). \end{align*} $$
Moreover, the map
![]() is a homeomorphism on
is a homeomorphism on
![]() $P' \backslash G'$
such that
$P' \backslash G'$
such that
![]() $d\theta (g) = dg$
and
$d\theta (g) = dg$
and
![]() $|\det \theta (g)| = |\det g|^{-1}$
. Hence
$|\det \theta (g)| = |\det g|^{-1}$
. Hence
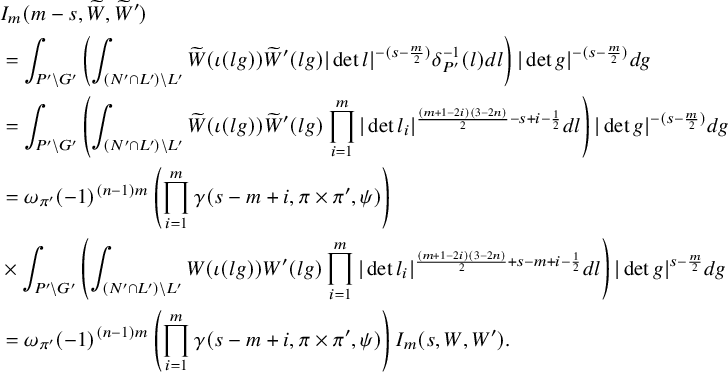 $$ \begin{align*} &I_{m}(m-s, \widetilde{W}, \widetilde{W}') \\&= \int_{P' \backslash G'} \left( \int_{(N' \cap L') \backslash L'}\widetilde{W}(\iota(lg)) \widetilde{W}'(lg) |\det l|^{-(s-\frac{m}{2})} \delta_{P'}^{-1}(l)dl \right) |\det g|^{-(s-\frac{m}{2})} dg \\&= \int_{P' \backslash G'} \left( \int_{(N' \cap L') \backslash L'}\widetilde{W}(\iota(lg)) \widetilde{W}'(lg) \prod_{i=1}^{m}|\det l_i|^{\frac{(m+1-2i)(3-2n)}{2}-s+i-\frac{1}{2}} dl \right) |\det g|^{-(s-\frac{m}{2})} dg \\&= \omega_{\pi'}(-1)^{(n-1)m} \left( \prod_{i=1}^m \gamma(s-m+i, \pi \times \pi', \psi) \right) \\&\times \int_{P' \backslash G'} \left( \int_{(N' \cap L') \backslash L'}W(\iota(lg)) W'(lg) \prod_{i=1}^{m}|\det l_i|^{\frac{(m+1-2i)(3-2n)}{2}+s-m+i-\frac{1}{2}} dl \right) |\det g|^{s-\frac{m}{2}} dg \\&= \omega_{\pi'}(-1)^{(n-1)m} \left( \prod_{i=1}^m \gamma(s-m+i, \pi \times \pi', \psi) \right) I_m(s,W,W'). \end{align*} $$
$$ \begin{align*} &I_{m}(m-s, \widetilde{W}, \widetilde{W}') \\&= \int_{P' \backslash G'} \left( \int_{(N' \cap L') \backslash L'}\widetilde{W}(\iota(lg)) \widetilde{W}'(lg) |\det l|^{-(s-\frac{m}{2})} \delta_{P'}^{-1}(l)dl \right) |\det g|^{-(s-\frac{m}{2})} dg \\&= \int_{P' \backslash G'} \left( \int_{(N' \cap L') \backslash L'}\widetilde{W}(\iota(lg)) \widetilde{W}'(lg) \prod_{i=1}^{m}|\det l_i|^{\frac{(m+1-2i)(3-2n)}{2}-s+i-\frac{1}{2}} dl \right) |\det g|^{-(s-\frac{m}{2})} dg \\&= \omega_{\pi'}(-1)^{(n-1)m} \left( \prod_{i=1}^m \gamma(s-m+i, \pi \times \pi', \psi) \right) \\&\times \int_{P' \backslash G'} \left( \int_{(N' \cap L') \backslash L'}W(\iota(lg)) W'(lg) \prod_{i=1}^{m}|\det l_i|^{\frac{(m+1-2i)(3-2n)}{2}+s-m+i-\frac{1}{2}} dl \right) |\det g|^{s-\frac{m}{2}} dg \\&= \omega_{\pi'}(-1)^{(n-1)m} \left( \prod_{i=1}^m \gamma(s-m+i, \pi \times \pi', \psi) \right) I_m(s,W,W'). \end{align*} $$
Here, in the third equation, we made the change of variables
![]() $l_i \mapsto l_{m+1-i}$
and
$l_i \mapsto l_{m+1-i}$
and
![]() $g \mapsto \theta (g)$
. This completes the proof.
$g \mapsto \theta (g)$
. This completes the proof.
Lemma 8.6. For any
![]() $W' \in W^{\psi ^{-1}}_{\mathrm {Ze}}(\sigma ')$
with
$W' \in W^{\psi ^{-1}}_{\mathrm {Ze}}(\sigma ')$
with
![]() $W'(\mathbf {1}_{(n-1)m}) \not = 0$
, there exists
$W'(\mathbf {1}_{(n-1)m}) \not = 0$
, there exists
![]() $W \in W^{\psi }_{\mathrm {Ze}}(\sigma )$
such that
$W \in W^{\psi }_{\mathrm {Ze}}(\sigma )$
such that
![]() $I_m(s,W,W') = 1$
for all
$I_m(s,W,W') = 1$
for all
![]() $s \in \mathbb {C}$
.
$s \in \mathbb {C}$
.
Proof. By [Reference Lapid and Mao20, Corollary 3.15], the space
![]() $\{W|_D \;|\; W \in W^{\psi }_{\mathrm {Ze}}(\sigma )\}$
contains the compact induction
$\{W|_D \;|\; W \in W^{\psi }_{\mathrm {Ze}}(\sigma )\}$
contains the compact induction
![]() $\mathrm {ind}_{N \cap D}^{D}(\Psi )$
. Hence the assertion follows by taking
$\mathrm {ind}_{N \cap D}^{D}(\Psi )$
. Hence the assertion follows by taking
![]() $W \in W^{\psi }_{\mathrm {Ze}}(\sigma )$
such that
$W \in W^{\psi }_{\mathrm {Ze}}(\sigma )$
such that
![]() $W|_D$
is supported on
$W|_D$
is supported on
![]() $(N \cap D)\Omega $
for a small neighbourhood
$(N \cap D)\Omega $
for a small neighbourhood
![]() $\Omega $
of
$\Omega $
of
![]() $\mathbf {1}_{nm} \in D$
.
$\mathbf {1}_{nm} \in D$
.
Proposition 8.7. The
![]() $\mathbb {C}$
-span of the integrals
$\mathbb {C}$
-span of the integrals
![]() $I_m(s,W,W')$
for
$I_m(s,W,W')$
for
![]() $W \in W^{\psi }(\sigma )$
and
$W \in W^{\psi }(\sigma )$
and
![]() $W' \in W^{\psi ^{-1}}(\sigma ')$
is a fractional ideal of
$W' \in W^{\psi ^{-1}}(\sigma ')$
is a fractional ideal of
![]() $\mathbb {C}[q^{-s},q^{s}]$
, which is generated by
$\mathbb {C}[q^{-s},q^{s}]$
, which is generated by
![]() $P_m(q^{-s})^{-1}$
for some
$P_m(q^{-s})^{-1}$
for some
![]() $P_m(X) \in \mathbb {C}[X]$
with
$P_m(X) \in \mathbb {C}[X]$
with
![]() $P_m(0) = 1$
. Moreover,
$P_m(0) = 1$
. Moreover,
![]() $P_1(q^{-s}) = L(s, \pi \times \pi ')^{-1}$
and
$P_1(q^{-s}) = L(s, \pi \times \pi ')^{-1}$
and
![]() $P_m(X)$
divides
$P_m(X)$
divides
![]() $\prod _{i=1}^mP_1(q^{m-i}X)$
.
$\prod _{i=1}^mP_1(q^{m-i}X)$
.
Proof. Note that
for
![]() $h \in G'$
, where
$h \in G'$
, where
![]() $(\iota (h)W)(g) = W(g\iota (h))$
and
$(\iota (h)W)(g) = W(g\iota (h))$
and
![]() $(hW')(g') = W'(g'h)$
. Hence the
$(hW')(g') = W'(g'h)$
. Hence the
![]() $\mathbb {C}$
-span of the integrals
$\mathbb {C}$
-span of the integrals
![]() $I_m(s,W,W')$
is a fractional ideal of
$I_m(s,W,W')$
is a fractional ideal of
![]() $\mathbb {C}[q^{-s},q^{s}]$
. The other assertions follow from Lemma 8.6 and Theorem 8.5 (2).
$\mathbb {C}[q^{-s},q^{s}]$
. The other assertions follow from Lemma 8.6 and Theorem 8.5 (2).
Remark 8.8. One might expect that
![]() $P_m(X) = \prod _{i=1}^mP_1(q^{m-i}X)$
, but we do not know if this holds in general. This is a reason we cannot prove Theorem 9.1 below for
$P_m(X) = \prod _{i=1}^mP_1(q^{m-i}X)$
, but we do not know if this holds in general. This is a reason we cannot prove Theorem 9.1 below for
![]() $\sigma = \mathrm {Sp}(\pi ,m)$
when
$\sigma = \mathrm {Sp}(\pi ,m)$
when
![]() $L(s,\pi ) \not = 1$
by a method similar to that in [Reference Jacquet, Piatetski-Shapiro and Shalika14]. However, as an application of Theorem 2.1, we will prove the equation
$L(s,\pi ) \not = 1$
by a method similar to that in [Reference Jacquet, Piatetski-Shapiro and Shalika14]. However, as an application of Theorem 2.1, we will prove the equation
![]() $P_m(X) = \prod _{i=1}^mP_1(q^{m-i}X)$
when
$P_m(X) = \prod _{i=1}^mP_1(q^{m-i}X)$
when
![]() $\pi '$
is unramified (see Theorem 9.1 below).
$\pi '$
is unramified (see Theorem 9.1 below).
8.4 Rankin–Selberg integrals in the Shalika models
Now we translate the results for the Zelevinsky models obtained in the previous subsection to those for the Shalika models.
Recall that
![]() $\sigma = \mathrm {Sp}(\pi ,m) \in \mathrm {Irr}(G)$
and
$\sigma = \mathrm {Sp}(\pi ,m) \in \mathrm {Irr}(G)$
and
![]() $\sigma ' = \mathrm {Sp}(\pi ',m) \in \mathrm {Irr}(G')$
. For
$\sigma ' = \mathrm {Sp}(\pi ',m) \in \mathrm {Irr}(G')$
. For
![]() $W_{\mathrm {Sh}} \in W^{\psi }_{\mathrm {Sh}}(\sigma )$
,
$W_{\mathrm {Sh}} \in W^{\psi }_{\mathrm {Sh}}(\sigma )$
,
![]() $W^{\prime }_{\mathrm {Sh}} \in W^{\psi ^{-1}}_{\mathrm {Sh}}(\sigma ')$
and
$W^{\prime }_{\mathrm {Sh}} \in W^{\psi ^{-1}}_{\mathrm {Sh}}(\sigma ')$
and
![]() $s \in \mathbb {C}$
, consider the integral
$s \in \mathbb {C}$
, consider the integral
We call this the Rankin–Selberg integral in the Shalika models.
Proposition 8.9. If
![]() $W_{\mathrm {Sh}} = \mathcal {T}^{\psi }W_{\mathrm {Ze}}$
and
$W_{\mathrm {Sh}} = \mathcal {T}^{\psi }W_{\mathrm {Ze}}$
and
![]() $W^{\prime }_{\mathrm {Sh}} = \mathcal {T}^{\psi ^{-1}}W^{\prime }_{\mathrm {Ze}}$
, we have
$W^{\prime }_{\mathrm {Sh}} = \mathcal {T}^{\psi ^{-1}}W^{\prime }_{\mathrm {Ze}}$
, we have
Proof. By Lemma 8.1 and Proposition 8.3, we have
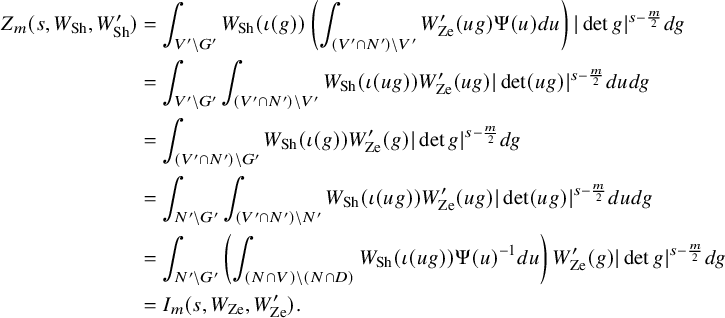 $$ \begin{align*} Z_m(s,W_{\mathrm{Sh}},W^{\prime}_{\mathrm{Sh}}) &= \int_{V' \backslash G'} W_{\mathrm{Sh}}(\iota(g)) \left( \int_{(V' \cap N') \backslash V'} W^{\prime}_{\mathrm{Ze}}(ug) \Psi(u)du \right) |\det g|^{s-\frac{m}{2}} dg \\&= \int_{V' \backslash G'} \int_{(V' \cap N') \backslash V'} W_{\mathrm{Sh}}(\iota(ug)) W^{\prime}_{\mathrm{Ze}}(ug) |\det (ug)|^{s-\frac{m}{2}} dudg \\&= \int_{(V' \cap N') \backslash G'} W_{\mathrm{Sh}}(\iota(g)) W^{\prime}_{\mathrm{Ze}}(g) |\det g|^{s-\frac{m}{2}} dg \\&= \int_{N' \backslash G'}\int_{(V' \cap N') \backslash N'} W_{\mathrm{Sh}}(\iota(ug)) W^{\prime}_{\mathrm{Ze}}(ug) |\det (ug)|^{s-\frac{m}{2}} dudg \\&= \int_{N' \backslash G'} \left(\int_{(N \cap V) \backslash (N \cap D)} W_{\mathrm{Sh}}(\iota(ug)) \Psi(u)^{-1} du \right) W^{\prime}_{\mathrm{Ze}}(g) |\det g|^{s-\frac{m}{2}} dg \\&= I_m(s,W_{\mathrm{Ze}},W^{\prime}_{\mathrm{Ze}}). \end{align*} $$
$$ \begin{align*} Z_m(s,W_{\mathrm{Sh}},W^{\prime}_{\mathrm{Sh}}) &= \int_{V' \backslash G'} W_{\mathrm{Sh}}(\iota(g)) \left( \int_{(V' \cap N') \backslash V'} W^{\prime}_{\mathrm{Ze}}(ug) \Psi(u)du \right) |\det g|^{s-\frac{m}{2}} dg \\&= \int_{V' \backslash G'} \int_{(V' \cap N') \backslash V'} W_{\mathrm{Sh}}(\iota(ug)) W^{\prime}_{\mathrm{Ze}}(ug) |\det (ug)|^{s-\frac{m}{2}} dudg \\&= \int_{(V' \cap N') \backslash G'} W_{\mathrm{Sh}}(\iota(g)) W^{\prime}_{\mathrm{Ze}}(g) |\det g|^{s-\frac{m}{2}} dg \\&= \int_{N' \backslash G'}\int_{(V' \cap N') \backslash N'} W_{\mathrm{Sh}}(\iota(ug)) W^{\prime}_{\mathrm{Ze}}(ug) |\det (ug)|^{s-\frac{m}{2}} dudg \\&= \int_{N' \backslash G'} \left(\int_{(N \cap V) \backslash (N \cap D)} W_{\mathrm{Sh}}(\iota(ug)) \Psi(u)^{-1} du \right) W^{\prime}_{\mathrm{Ze}}(g) |\det g|^{s-\frac{m}{2}} dg \\&= I_m(s,W_{\mathrm{Ze}},W^{\prime}_{\mathrm{Ze}}). \end{align*} $$
This proves the proposition.
Therefore, assertions similar to those in Theorem 8.5, Lemma 8.6 and Proposition 8.7 hold for
![]() $Z_m(s,W_{\mathrm {Sh}}, W^{\prime }_{\mathrm {Sh}})$
. Here, we note the following. If
$Z_m(s,W_{\mathrm {Sh}}, W^{\prime }_{\mathrm {Sh}})$
. Here, we note the following. If
![]() $W_{\mathrm {Ze}} \in \mathcal {W}^{\psi }_{\mathrm {Ze}}(\sigma )$
, we define
$W_{\mathrm {Ze}} \in \mathcal {W}^{\psi }_{\mathrm {Ze}}(\sigma )$
, we define
![]() $\widetilde {W}_{\mathrm {Ze}} \in \mathcal {W}^{\psi ^{-1}}_{\mathrm {Ze}}(\widetilde {\sigma })$
, where
$\widetilde {W}_{\mathrm {Ze}} \in \mathcal {W}^{\psi ^{-1}}_{\mathrm {Ze}}(\widetilde {\sigma })$
, where
![]() $\widetilde {\sigma }$
is the contragredient representation of
$\widetilde {\sigma }$
is the contragredient representation of
![]() $\sigma $
, by
$\sigma $
, by
![]() $\widetilde {W}_{\mathrm {Ze}}(g) = W_{\mathrm {Ze}}(w_{nm}{}^tg^{-1}w^{\prime }_{n})$
. One can easily check that
$\widetilde {W}_{\mathrm {Ze}}(g) = W_{\mathrm {Ze}}(w_{nm}{}^tg^{-1}w^{\prime }_{n})$
. One can easily check that
Hence we define
![]() $\widetilde {W}_{\mathrm {Sh}} \in \mathcal {W}^{\psi ^{-1}}_{\mathrm {Sh}}(\widetilde {\sigma })$
for
$\widetilde {W}_{\mathrm {Sh}} \in \mathcal {W}^{\psi ^{-1}}_{\mathrm {Sh}}(\widetilde {\sigma })$
for
![]() $W_{\mathrm {Sh}} \in \mathcal {W}^{\psi }_{\mathrm {Sh}}(\sigma )$
by
$W_{\mathrm {Sh}} \in \mathcal {W}^{\psi }_{\mathrm {Sh}}(\sigma )$
by
![]() $\widetilde {W}_{\mathrm {Sh}}(g) = W_{\mathrm {Sh}}(w_{nm}{}^tg^{-1}w^{\prime }_{n})$
.
$\widetilde {W}_{\mathrm {Sh}}(g) = W_{\mathrm {Sh}}(w_{nm}{}^tg^{-1}w^{\prime }_{n})$
.
8.5 The case where
 $\pi '$
is unramified
$\pi '$
is unramified
In the following section, we need sharper results when
![]() $\pi '$
is unramified.
$\pi '$
is unramified.
Let
![]() $\pi '$
be an irreducible unramified representation of
$\pi '$
be an irreducible unramified representation of
![]() $G_{n-1}$
with Satake parameter
$G_{n-1}$
with Satake parameter
![]() $(x_1, \dots , x_{n-1}) \in (\mathbb {C}^{\times })^{n-1}/S_{n-1}$
. Hence
$(x_1, \dots , x_{n-1}) \in (\mathbb {C}^{\times })^{n-1}/S_{n-1}$
. Hence
![]() $\pi '$
is the unique irreducible unramified constituent of
$\pi '$
is the unique irreducible unramified constituent of
where
![]() $s_j$
is a complex number such that
$s_j$
is a complex number such that
![]() $q^{-s_j} = x_j$
. Since the principal series
$q^{-s_j} = x_j$
. Since the principal series
![]() $I(s_1, \dots , s_{n-1})$
is generic and unramified, there exists a unique Whittaker function
$I(s_1, \dots , s_{n-1})$
is generic and unramified, there exists a unique Whittaker function
![]() $W^0(x_1, \dots , x_{n-1}) \in \mathcal {W}^{\psi ^{-1}}(I(s_1, \dots , s_{n-1}))$
such that
$W^0(x_1, \dots , x_{n-1}) \in \mathcal {W}^{\psi ^{-1}}(I(s_1, \dots , s_{n-1}))$
such that
![]() $W^0(k_1; x_1, \dots , x_{n-1}) = 1$
for any
$W^0(k_1; x_1, \dots , x_{n-1}) = 1$
for any
![]() $k_1 \in \mathrm {GL}_{n-1}(\mathfrak {o})$
. When
$k_1 \in \mathrm {GL}_{n-1}(\mathfrak {o})$
. When
![]() $\pi '$
is tempered, that is,
$\pi '$
is tempered, that is,
![]() $|x_j| = 1$
for any
$|x_j| = 1$
for any
![]() $1 \leq j \leq n-1$
, the function
$1 \leq j \leq n-1$
, the function
![]() $W^0(x_1, \dots , x_{n-1}) \text{ belongs to } \mathcal {W}^{\psi ^{-1}}(\pi ')$
. Note that
$W^0(x_1, \dots , x_{n-1}) \text{ belongs to } \mathcal {W}^{\psi ^{-1}}(\pi ')$
. Note that
![]() $W^0(x_1, \dots , x_{n-1})$
is a Hecke eigenfunction whose Hecke eigenvalues are uniquely determined by
$W^0(x_1, \dots , x_{n-1})$
is a Hecke eigenfunction whose Hecke eigenvalues are uniquely determined by
![]() $(x_1, \dots , x_{n-1}) \in (\mathbb {C}^{\times })^{n-1}/S_{n-1}$
.
$(x_1, \dots , x_{n-1}) \in (\mathbb {C}^{\times })^{n-1}/S_{n-1}$
.
Recall that
![]() $G' = G_{(n-1)m}$
,
$G' = G_{(n-1)m}$
,
![]() $K' = G_{(n-1)m}(\mathfrak {o})$
and that
$K' = G_{(n-1)m}(\mathfrak {o})$
and that
![]() $P' = L'U'$
is the standard parabolic subgroup of
$P' = L'U'$
is the standard parabolic subgroup of
![]() $G'$
with
$G'$
with
![]() $L' \cong G_{n-1} \times \dots \times G_{n-1}$
(m-times). Let
$L' \cong G_{n-1} \times \dots \times G_{n-1}$
(m-times). Let
![]() $\underline {x} = (x_{i,j}) \in M_{m,n-1}(\mathbb {C})$
with
$\underline {x} = (x_{i,j}) \in M_{m,n-1}(\mathbb {C})$
with
![]() $x_{i,j} \in \mathbb {C}^{\times }$
. We can define a function
$x_{i,j} \in \mathbb {C}^{\times }$
. We can define a function
by
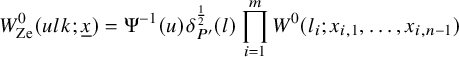 $$\begin{align*}W^0_{\mathrm{Ze}}(ulk; \underline{x}) = \Psi^{-1}(u) \delta_{P'}^{\frac{1}{2}}(l) \prod_{i=1}^m W^0(l_i; x_{i,1}, \dots, x_{i,n-1}) \end{align*}$$
$$\begin{align*}W^0_{\mathrm{Ze}}(ulk; \underline{x}) = \Psi^{-1}(u) \delta_{P'}^{\frac{1}{2}}(l) \prod_{i=1}^m W^0(l_i; x_{i,1}, \dots, x_{i,n-1}) \end{align*}$$
for
![]() $u \in U'$
,
$u \in U'$
,
![]() $l = \mathrm {diag}(l_1, \dots , l_m) \in L'$
and
$l = \mathrm {diag}(l_1, \dots , l_m) \in L'$
and
![]() $k \in K'$
. (Here, we note that
$k \in K'$
. (Here, we note that
![]() $\Psi (u) = 1$
for
$\Psi (u) = 1$
for
![]() $u \in U'$
.) As in [Reference Lapid and Mao20, Lemma 3.8],
$u \in U'$
.) As in [Reference Lapid and Mao20, Lemma 3.8],
![]() $W^0_{\mathrm {Ze}}(\underline {x})$
is compactly supported on
$W^0_{\mathrm {Ze}}(\underline {x})$
is compactly supported on
![]() $(V' \cap N') \backslash V'$
. We set
$(V' \cap N') \backslash V'$
. We set
If
![]() $\underline {x} = {}^t(q^{-\frac {m-1}{2}}x_{j}, q^{-\frac {m-3}{2}}x_{j}, \dots , q^{\frac {m-1}{2}}x_{j})_{1 \leq j \leq n-1}$
with
$\underline {x} = {}^t(q^{-\frac {m-1}{2}}x_{j}, q^{-\frac {m-3}{2}}x_{j}, \dots , q^{\frac {m-1}{2}}x_{j})_{1 \leq j \leq n-1}$
with
![]() $|x_j| = 1$
for any
$|x_j| = 1$
for any
![]() $1 \leq j \leq n-1$
, then
$1 \leq j \leq n-1$
, then
![]() $W^0_{\mathrm {Ze}}(\underline {x}) \in \mathcal {W}^{\psi ^{-1}}_{\mathrm {Ze}}(\mathrm {Sp}(\pi ',m))$
, where
$W^0_{\mathrm {Ze}}(\underline {x}) \in \mathcal {W}^{\psi ^{-1}}_{\mathrm {Ze}}(\mathrm {Sp}(\pi ',m))$
, where
![]() $\pi '$
is the irreducible unramified representation of
$\pi '$
is the irreducible unramified representation of
![]() $G_{n-1}$
with Satake parameter
$G_{n-1}$
with Satake parameter
![]() $(x_1, \dots , x_{n-1})$
. In general,
$(x_1, \dots , x_{n-1})$
. In general,
![]() $W^0_{\mathrm {Ze}}(g; \underline {x}) = l(g \cdot f^0)$
for some
$W^0_{\mathrm {Ze}}(g; \underline {x}) = l(g \cdot f^0)$
for some
![]() $l \in \mathrm {Hom}_{N'}(I(s_1, \dots , s_{(n-1)m}), \Psi )$
, where
$l \in \mathrm {Hom}_{N'}(I(s_1, \dots , s_{(n-1)m}), \Psi )$
, where
![]() $s_1, \dots , s_{(n-1)m}$
are complex numbers such that
$s_1, \dots , s_{(n-1)m}$
are complex numbers such that
as multisets, and
![]() $f^0 \in I(s_1, \dots , s_{(n-1)m})^{K'}$
. Note that
$f^0 \in I(s_1, \dots , s_{(n-1)m})^{K'}$
. Note that
![]() $W^0_{\mathrm {Ze}}(\underline {x})$
is a Hecke eigenfunction whose Hecke eigenvalues are uniquely determined by
$W^0_{\mathrm {Ze}}(\underline {x})$
is a Hecke eigenfunction whose Hecke eigenvalues are uniquely determined by
![]() $(s_1, \dots , s_{(n-1)m}) \in \mathbb {C}^{(n-1)m}/S_{(n-1)m}$
.
$(s_1, \dots , s_{(n-1)m}) \in \mathbb {C}^{(n-1)m}/S_{(n-1)m}$
.
Lemma 8.10. The Hecke eigenspace in
![]() $\mathrm {Ind}_{N'}^{G'}(\Psi )^{K'}$
with Hecke eigenvalues determined by
$\mathrm {Ind}_{N'}^{G'}(\Psi )^{K'}$
with Hecke eigenvalues determined by
![]() $(s_1, \dots , s_{(n-1)m})$
is spanned by
$(s_1, \dots , s_{(n-1)m})$
is spanned by
![]() $W^0_{\mathrm {Ze}}(\underline {x})$
for
$W^0_{\mathrm {Ze}}(\underline {x})$
for
![]() $\underline {x} = (x_{i,j}) \in M_{m,n-1}(\mathbb {C})$
such that
$\underline {x} = (x_{i,j}) \in M_{m,n-1}(\mathbb {C})$
such that
![]() $\{q^{-s_1}, \dots , q^{-s_{(n-1)m}}\} = \{x_{i,j} \;|\; 1 \leq i \leq m, \; 1 \leq j \leq n-1\}$
as multisets.
$\{q^{-s_1}, \dots , q^{-s_{(n-1)m}}\} = \{x_{i,j} \;|\; 1 \leq i \leq m, \; 1 \leq j \leq n-1\}$
as multisets.
Proof. Since
![]() $\Psi $
is trivial on
$\Psi $
is trivial on
![]() $U' \subset N'$
, we have a canonical isomorphism
$U' \subset N'$
, we have a canonical isomorphism
where
![]() $\mathrm {Jac}_{P'}$
is the unnormalised Jacquet functor along
$\mathrm {Jac}_{P'}$
is the unnormalised Jacquet functor along
![]() $P' = L'U'$
. Note that
$P' = L'U'$
. Note that
![]() $\Psi |_{N' \cap L'}$
is a generic character. Moreover, by the Geometric Lemma of Bernstein–Zelevinsky [Reference Bernstein and Zelevinsky4, 2.12], the semisimplification of
$\Psi |_{N' \cap L'}$
is a generic character. Moreover, by the Geometric Lemma of Bernstein–Zelevinsky [Reference Bernstein and Zelevinsky4, 2.12], the semisimplification of
![]() $\mathrm {Jac}_{P'}(I(s_1, \dots , s_{(n-1)m}))$
is equal to
$\mathrm {Jac}_{P'}(I(s_1, \dots , s_{(n-1)m}))$
is equal to
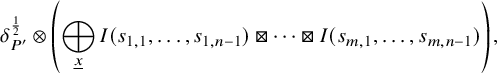 $$\begin{align*}\delta_{P'}^{\frac{1}{2}} \otimes \left( \bigoplus_{\underline{x}} I(s_{1,1}, \dots, s_{1,n-1}) \boxtimes \dots \boxtimes I(s_{m,1}, \dots, s_{m,n-1}) \right), \end{align*}$$
$$\begin{align*}\delta_{P'}^{\frac{1}{2}} \otimes \left( \bigoplus_{\underline{x}} I(s_{1,1}, \dots, s_{1,n-1}) \boxtimes \dots \boxtimes I(s_{m,1}, \dots, s_{m,n-1}) \right), \end{align*}$$
where
![]() $\underline {x} = (x_{i,j})$
runs over
$\underline {x} = (x_{i,j})$
runs over
![]() $M_{m,n-1}(\mathbb {C})/(S_{n-1})^m$
such that
$M_{m,n-1}(\mathbb {C})/(S_{n-1})^m$
such that
![]() $\{q^{-s_1}, \dots , q^{-s_{(n-1)m}}\} = \{x_{i,j} \;|\; 1 \leq i \leq m, \; 1 \leq j \leq n-1\}$
, and
$\{q^{-s_1}, \dots , q^{-s_{(n-1)m}}\} = \{x_{i,j} \;|\; 1 \leq i \leq m, \; 1 \leq j \leq n-1\}$
, and
![]() $s_{i,j}$
is a complex number such that
$s_{i,j}$
is a complex number such that
![]() $q^{-s_{i,j}} = x_{i,j}$
. Hence
$q^{-s_{i,j}} = x_{i,j}$
. Hence
![]() $\dim \mathrm {Hom}_{N'}(I(s_1, \dots , s_{(n-1)m}), \Psi )$
is less than or equal to the number of choices of such
$\dim \mathrm {Hom}_{N'}(I(s_1, \dots , s_{(n-1)m}), \Psi )$
is less than or equal to the number of choices of such
![]() $\underline {x}$
. This proves the claim.
$\underline {x}$
. This proves the claim.
Let
![]() $\pi $
be an irreducible tempered representation of
$\pi $
be an irreducible tempered representation of
![]() $G_n$
, and set
$G_n$
, and set
![]() $\sigma = \mathrm {Sp}(\pi ,m)$
. For
$\sigma = \mathrm {Sp}(\pi ,m)$
. For
![]() $W_{\mathrm {Ze}} \in \mathcal {W}^{\psi }_{\mathrm {Ze}}(\sigma )$
and
$W_{\mathrm {Ze}} \in \mathcal {W}^{\psi }_{\mathrm {Ze}}(\sigma )$
and
![]() $W_{\mathrm {Sh}} \in \mathcal {W}^{\psi }_{\mathrm {Sh}}(\sigma )$
, one can consider the integrals
$W_{\mathrm {Sh}} \in \mathcal {W}^{\psi }_{\mathrm {Sh}}(\sigma )$
, one can consider the integrals
![]() $I_m(s,W_{\mathrm {Ze}},W^0_{\mathrm {Ze}}(\underline {x}))$
and
$I_m(s,W_{\mathrm {Ze}},W^0_{\mathrm {Ze}}(\underline {x}))$
and
![]() $Z_m(s,W_{\mathrm {Sh}},W^0_{\mathrm {Sh}}(\underline {x}))$
defined by the same integrals in the previous two subsections. By the same arguments as in these subsections, we can prove the following theorem. We omit the proof of it.
$Z_m(s,W_{\mathrm {Sh}},W^0_{\mathrm {Sh}}(\underline {x}))$
defined by the same integrals in the previous two subsections. By the same arguments as in these subsections, we can prove the following theorem. We omit the proof of it.
Theorem 8.11. The integrals
![]() $I_m(s,W_{\mathrm {Ze}},W^0_{\mathrm {Ze}}(\underline {x}))$
and
$I_m(s,W_{\mathrm {Ze}},W^0_{\mathrm {Ze}}(\underline {x}))$
and
![]() $Z_m(s,W_{\mathrm {Sh}},W^0_{\mathrm {Sh}}(\underline {x}))$
have the following properties:
$Z_m(s,W_{\mathrm {Sh}},W^0_{\mathrm {Sh}}(\underline {x}))$
have the following properties:
-
(1) The integral
 $I_m(s,W_{\mathrm {Ze}},W^0_{\mathrm {Ze}}(\underline {x}))$
is absolutely convergent for
$I_m(s,W_{\mathrm {Ze}},W^0_{\mathrm {Ze}}(\underline {x}))$
is absolutely convergent for
 $\mathrm {Re}(s) \gg 0$
.
$\mathrm {Re}(s) \gg 0$
. -
(2) The function
is in $$\begin{align*}\left(\prod_{i=1}^m\prod_{j = 1}^{n-1} L\left(s+s_{i,j}-\frac{m-1}{2}, \pi \right)\right)^{-1} I_m(s,W_{\mathrm{Ze}},W^0_{\mathrm{Ze}}(\underline{x})) \end{align*}$$
$$\begin{align*}\left(\prod_{i=1}^m\prod_{j = 1}^{n-1} L\left(s+s_{i,j}-\frac{m-1}{2}, \pi \right)\right)^{-1} I_m(s,W_{\mathrm{Ze}},W^0_{\mathrm{Ze}}(\underline{x})) \end{align*}$$
 $\mathbb {C}[q^{-s}, q^{s}]$
, where
$\mathbb {C}[q^{-s}, q^{s}]$
, where
 $s_{i,j}$
is a complex number such that
$s_{i,j}$
is a complex number such that
 $q^{-s_{i,j}} = x_{i,j}$
. In particular, it is entire.
$q^{-s_{i,j}} = x_{i,j}$
. In particular, it is entire.
-
(3) The functional equation
holds, where $$ \begin{align*} &I_m(m-s,\widetilde{W}_{\mathrm{Ze}},W^0_{\mathrm{Ze}}(\underline{x}^{-1})) \\&= \left( \prod_{i=1}^m\prod_{j=1}^{n-1} \gamma\left( s+s_{i,j}-\frac{m-1}{2}, \pi, \psi \right) \right) I_m(s,W_{\mathrm{Ze}},W^0_{\mathrm{Ze}}(\underline{x})) \end{align*} $$
$$ \begin{align*} &I_m(m-s,\widetilde{W}_{\mathrm{Ze}},W^0_{\mathrm{Ze}}(\underline{x}^{-1})) \\&= \left( \prod_{i=1}^m\prod_{j=1}^{n-1} \gamma\left( s+s_{i,j}-\frac{m-1}{2}, \pi, \psi \right) \right) I_m(s,W_{\mathrm{Ze}},W^0_{\mathrm{Ze}}(\underline{x})) \end{align*} $$
 $\widetilde {W}_{\mathrm {Ze}}(g) = W_{\mathrm {Ze}}(w_{nm} {}^tg^{-1} w^{\prime }_n)$
and
$\widetilde {W}_{\mathrm {Ze}}(g) = W_{\mathrm {Ze}}(w_{nm} {}^tg^{-1} w^{\prime }_n)$
and
 $\underline {x}^{-1} = (x_{i,j}^{-1})$
.
$\underline {x}^{-1} = (x_{i,j}^{-1})$
.
-
(4) If
 $W_{\mathrm {Sh}} = \mathcal {T}^{\psi }W_{\mathrm {Ze}}$
, then
$W_{\mathrm {Sh}} = \mathcal {T}^{\psi }W_{\mathrm {Ze}}$
, then  $$\begin{align*}I_m(s,W_{\mathrm{Ze}},W^0_{\mathrm{Ze}}(\underline{x})) = Z_m(s,W_{\mathrm{Sh}},W^0_{\mathrm{Sh}}(\underline{x})). \end{align*}$$
$$\begin{align*}I_m(s,W_{\mathrm{Ze}},W^0_{\mathrm{Ze}}(\underline{x})) = Z_m(s,W_{\mathrm{Sh}},W^0_{\mathrm{Sh}}(\underline{x})). \end{align*}$$
Proof. Omitted.
9 Essential vectors for Speh representations
We continue to use the notations in the previous section. Recall that
![]() $\psi $
is unramified: that is,
$\psi $
is unramified: that is,
![]() $\psi $
is trivial on
$\psi $
is trivial on
![]() $\mathfrak {o}$
but nontrivial on
$\mathfrak {o}$
but nontrivial on
![]() $\mathfrak {p}^{-1}$
. Let
$\mathfrak {p}^{-1}$
. Let
![]() $\pi $
be an irreducible tempered representation of
$\pi $
be an irreducible tempered representation of
![]() $G_n$
, and set
$G_n$
, and set
![]() $\sigma = \mathrm {Sp}(\pi ,m)$
. In this section, we define a notion of essential vectors and prove Theorem 2.1 for Speh representations.
$\sigma = \mathrm {Sp}(\pi ,m)$
. In this section, we define a notion of essential vectors and prove Theorem 2.1 for Speh representations.
9.1 Essential vectors
The following theorem is a generalisation of [Reference Jacquet, Piatetski-Shapiro and Shalika14, (4.1) Théorème].
Theorem 9.1. Let the notation be as above. There exists a unique function
![]() $W^{\mathrm {ess}}_{\mathrm {Sh}} \in \mathcal {W}^{\psi }_{\mathrm {Sh}}(\sigma )$
such that
$W^{\mathrm {ess}}_{\mathrm {Sh}} \in \mathcal {W}^{\psi }_{\mathrm {Sh}}(\sigma )$
such that
-
(1)
 $W^{\mathrm {ess}}_{\mathrm {Sh}}(g \cdot \iota (k)) = W^{\mathrm {ess}}_{\mathrm {Sh}}(g)$
for any
$W^{\mathrm {ess}}_{\mathrm {Sh}}(g \cdot \iota (k)) = W^{\mathrm {ess}}_{\mathrm {Sh}}(g)$
for any
 $g \in G$
and
$g \in G$
and
 $k \in K'$
;
$k \in K'$
; -
(2) for all
 $s \in \mathbb {C}$
and
$s \in \mathbb {C}$
and
 $\underline {x} = (x_{i,j}) \in M_{m,n-1}(\mathbb {C})$
with
$\underline {x} = (x_{i,j}) \in M_{m,n-1}(\mathbb {C})$
with
 $x_{i,j} \in \mathbb {C}^{\times }$
, where
$x_{i,j} \in \mathbb {C}^{\times }$
, where $$\begin{align*}Z_m(s,W^{\mathrm{ess}}_{\mathrm{Sh}}, W^0_{\mathrm{Sh}}(\underline{x})) = \prod_{i=1}^m\prod_{j = 1}^{n-1} L\left( s+s_{i,j}-\frac{m-1}{2}, \pi \right), \end{align*}$$
$$\begin{align*}Z_m(s,W^{\mathrm{ess}}_{\mathrm{Sh}}, W^0_{\mathrm{Sh}}(\underline{x})) = \prod_{i=1}^m\prod_{j = 1}^{n-1} L\left( s+s_{i,j}-\frac{m-1}{2}, \pi \right), \end{align*}$$
 $s_{i,j}$
is a complex number such that
$s_{i,j}$
is a complex number such that
 $q^{-s_{i,j}} = x_{i,j}$
.
$q^{-s_{i,j}} = x_{i,j}$
.
Definition 9.2. We call the unique function
![]() $W^{\mathrm {ess}}_{\mathrm {Sh}}$
the essential vector of
$W^{\mathrm {ess}}_{\mathrm {Sh}}$
the essential vector of
![]() $\mathcal {W}^{\psi }_{\mathrm {Sh}}(\sigma )$
.
$\mathcal {W}^{\psi }_{\mathrm {Sh}}(\sigma )$
.
First we consider existence. Here, we show it only when
![]() $L(s,\pi ) = 1$
. The general case will be proven in Section 9.3 below.
$L(s,\pi ) = 1$
. The general case will be proven in Section 9.3 below.
Proof of the existence statement in Theorem 9.1 when
 $L(s,\pi )=1$
$L(s,\pi )=1$
Note that
![]() $Q' = S'V'$
is conjugate to a standard parabolic subgroup of
$Q' = S'V'$
is conjugate to a standard parabolic subgroup of
![]() $G'$
by an element of
$G'$
by an element of
![]() $K'$
. Hence we have the Iwasawa decomposition
$K'$
. Hence we have the Iwasawa decomposition
![]() $G' = Q'K'$
. Define a smooth function
$G' = Q'K'$
. Define a smooth function
![]() $\varphi $
of
$\varphi $
of
![]() $D = V \iota (G')$
by
$D = V \iota (G')$
by
![]() $\mathrm {Supp}(\varphi ) = V \iota (K')$
and
$\mathrm {Supp}(\varphi ) = V \iota (K')$
and
![]() $\varphi (u \cdot \iota (k)) = \Psi (u)$
for
$\varphi (u \cdot \iota (k)) = \Psi (u)$
for
![]() $u \in V$
and
$u \in V$
and
![]() $k \in K'$
. Then
$k \in K'$
. Then
![]() $\varphi \in \mathrm {ind}_{V}^{D}(\Psi )$
and
$\varphi \in \mathrm {ind}_{V}^{D}(\Psi )$
and
for all
![]() $s \in \mathbb {C}$
and
$s \in \mathbb {C}$
and
![]() $\underline {x} = (x_{i,j}) \in M_{m,n-1}(\mathbb {C})$
with
$\underline {x} = (x_{i,j}) \in M_{m,n-1}(\mathbb {C})$
with
![]() $x_{i,j} \in \mathbb {C}^{\times }$
. By [Reference Lapid and Mao20, Corollary 3.15], one can take
$x_{i,j} \in \mathbb {C}^{\times }$
. By [Reference Lapid and Mao20, Corollary 3.15], one can take
![]() $W_{\mathrm {Sh}} \in \mathcal {W}^{\psi }_{\mathrm {Sh}}(\sigma )$
such that
$W_{\mathrm {Sh}} \in \mathcal {W}^{\psi }_{\mathrm {Sh}}(\sigma )$
such that
![]() $W_{\mathrm {Sh}}|_D = \varphi $
. Then
$W_{\mathrm {Sh}}|_D = \varphi $
. Then
![]() $Z_m(s,W_{\mathrm {Sh}},W^0_{\mathrm {Sh}}(\underline {x})) = 1$
holds for all
$Z_m(s,W_{\mathrm {Sh}},W^0_{\mathrm {Sh}}(\underline {x})) = 1$
holds for all
![]() $s \in \mathbb {C}$
and
$s \in \mathbb {C}$
and
![]() $\underline {x} = (x_{i,j}) \in M_{m,n-1}(\mathbb {C})$
with
$\underline {x} = (x_{i,j}) \in M_{m,n-1}(\mathbb {C})$
with
![]() $x_{i,j} \in \mathbb {C}^{\times }$
. By replacing
$x_{i,j} \in \mathbb {C}^{\times }$
. By replacing
![]() $W_{\mathrm {Sh}}$
with
$W_{\mathrm {Sh}}$
with
we may assume that
![]() $W_{\mathrm {Sh}}$
is right
$W_{\mathrm {Sh}}$
is right
![]() $\iota (K')$
-invariant. Then
$\iota (K')$
-invariant. Then
![]() $W_{\mathrm {Sh}}$
satisfies the conditions in Theorem 9.1. This completes the proof of the existence statement in Theorem 9.1 when
$W_{\mathrm {Sh}}$
satisfies the conditions in Theorem 9.1. This completes the proof of the existence statement in Theorem 9.1 when
![]() $L(s,\pi ) = 1$
.
$L(s,\pi ) = 1$
.
We now prove the uniqueness statement (in general).
Proof of the uniqueness statement in Theorem 9.1
Let
![]() $L^2(V' \backslash G'; \Psi )$
denote the space of functions
$L^2(V' \backslash G'; \Psi )$
denote the space of functions
![]() $\varphi $
on
$\varphi $
on
![]() $G'$
such that
$G'$
such that
![]() $\varphi (vg) = \Psi (v)\varphi (g)$
for
$\varphi (vg) = \Psi (v)\varphi (g)$
for
![]() $v \in V'$
and
$v \in V'$
and
![]() $g \in G'$
, and
$g \in G'$
, and
![]() $\varphi $
is square-integrable on
$\varphi $
is square-integrable on
![]() $V' \backslash G'$
. Define
$V' \backslash G'$
. Define
![]() $\Pi $
to be the closure of the subspace of
$\Pi $
to be the closure of the subspace of
![]() $L^2(V' \backslash G'; \Psi )$
consisting of smooth functions
$L^2(V' \backslash G'; \Psi )$
consisting of smooth functions
![]() $\varphi _{\mathrm {Sh}}$
of
$\varphi _{\mathrm {Sh}}$
of
![]() $G'$
such that
$G'$
such that
for some smooth function
![]() $\varphi _{\mathrm {Ze}}$
that satisfies
$\varphi _{\mathrm {Ze}}$
that satisfies
![]() $\varphi _{\mathrm {Ze}}(ug) = \Psi (u)\varphi _{\mathrm {Ze}}(g)$
for
$\varphi _{\mathrm {Ze}}(ug) = \Psi (u)\varphi _{\mathrm {Ze}}(g)$
for
![]() $u \in N'$
and
$u \in N'$
and
![]() $g \in G'$
.
$g \in G'$
.
Lemma 9.3. Let
![]() $\varphi $
be a smooth function on
$\varphi $
be a smooth function on
![]() $G'$
such that
$G'$
such that
-
(1)
 $\varphi \in \Pi $
;
$\varphi \in \Pi $
; -
(2)
 $\varphi (gk) = \varphi (g)$
for
$\varphi (gk) = \varphi (g)$
for
 $g \in G'$
and
$g \in G'$
and
 $k \in K'$
;
$k \in K'$
; -
(3) for any
 $\underline {x} = (x_{i,j}) \in M_{m,n-1}(\mathbb {C})$
with
$\underline {x} = (x_{i,j}) \in M_{m,n-1}(\mathbb {C})$
with
 $x_{i,j} \in \mathbb {C}^{\times }$
,
$x_{i,j} \in \mathbb {C}^{\times }$
,  $$\begin{align*}\int_{V' \backslash G'}\varphi(g) W^0_{\mathrm{Sh}}(g; \underline{x})dg = 0. \end{align*}$$
$$\begin{align*}\int_{V' \backslash G'}\varphi(g) W^0_{\mathrm{Sh}}(g; \underline{x})dg = 0. \end{align*}$$
Then
![]() $\varphi = 0$
.
$\varphi = 0$
.
Proof. This is an analogue of [Reference Jacquet, Piatetski-Shapiro and Shalika14, (3.5) Lemme]. Consider the direct integral expression of the unitary representation
![]() $\Pi $
of
$\Pi $
of
![]() $G'$
:
$G'$
:
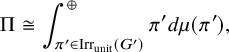 $$\begin{align*}\Pi \cong \int^{\oplus}_{\pi' \in \mathrm{Irr}_{\mathrm{unit}}(G')} \pi' d\mu(\pi'), \end{align*}$$
$$\begin{align*}\Pi \cong \int^{\oplus}_{\pi' \in \mathrm{Irr}_{\mathrm{unit}}(G')} \pi' d\mu(\pi'), \end{align*}$$
where
![]() $\mathrm {Irr}_{\mathrm {unit}}(G')$
is the set of equivalence classes of irreducible unitary representations of
$\mathrm {Irr}_{\mathrm {unit}}(G')$
is the set of equivalence classes of irreducible unitary representations of
![]() $G'$
and
$G'$
and
![]() $\mu $
is a certain Borel measure on it. For almost all
$\mu $
is a certain Borel measure on it. For almost all
![]() $\pi '$
, there exists a
$\pi '$
, there exists a
![]() $G'$
-equivariant intertwining operator
$G'$
-equivariant intertwining operator
![]() $A_{\pi '} \colon \Pi \rightarrow \pi '$
such that
$A_{\pi '} \colon \Pi \rightarrow \pi '$
such that
for
![]() $\varphi _1, \varphi _2 \in \Pi \subset L^2(V' \backslash G'; \Psi )$
, where
$\varphi _1, \varphi _2 \in \Pi \subset L^2(V' \backslash G'; \Psi )$
, where
![]() $(\cdot ,\cdot )_{\pi '}$
is a
$(\cdot ,\cdot )_{\pi '}$
is a
![]() $G'$
-invariant inner product on
$G'$
-invariant inner product on
![]() $\pi '$
.
$\pi '$
.
Now we assume that
![]() $\varphi \not = 0$
. Then there exists
$\varphi \not = 0$
. Then there exists
![]() $\pi ' \in \mathrm {Irr}(G')$
such that
$\pi ' \in \mathrm {Irr}(G')$
such that
![]() $A_{\pi '}\varphi \not = 0$
. Since
$A_{\pi '}\varphi \not = 0$
. Since
![]() $\varphi $
is right
$\varphi $
is right
![]() $K'$
-invariant,
$K'$
-invariant,
![]() $A_{\pi '}\varphi $
belongs to the subspace of
$A_{\pi '}\varphi $
belongs to the subspace of
![]() $\pi '$
consisting of
$\pi '$
consisting of
![]() $K'$
-fixed vectors. Then using Lemma 8.10, we see that
$K'$
-fixed vectors. Then using Lemma 8.10, we see that
![]() $(A_{\pi '} \varphi , A_{\pi '} \varphi )_{\pi '}$
is a linear combination of integrals of the form
$(A_{\pi '} \varphi , A_{\pi '} \varphi )_{\pi '}$
is a linear combination of integrals of the form
for some
![]() $\underline {x} = (x_{i,j}) \in M_{m,n-1}(\mathbb {C})$
with
$\underline {x} = (x_{i,j}) \in M_{m,n-1}(\mathbb {C})$
with
![]() $x_{i,j} \in \mathbb {C}^{\times }$
. This contradicts Condition (3).
$x_{i,j} \in \mathbb {C}^{\times }$
. This contradicts Condition (3).
We continue the proof of the uniqueness statement in Theorem 9.1. Now suppose that two functions
![]() $W_1, W_2 \in \mathcal {W}^{\psi }_{\mathrm {Sh}}(\sigma )$
satisfy the conditions of Theorem 9.1. Set
$W_1, W_2 \in \mathcal {W}^{\psi }_{\mathrm {Sh}}(\sigma )$
satisfy the conditions of Theorem 9.1. Set
![]() $W = W_1-W_2$
, which is square-integrable on
$W = W_1-W_2$
, which is square-integrable on
![]() $V' \backslash G'$
by Theorem 8.2. Note that
$V' \backslash G'$
by Theorem 8.2. Note that
![]() $W = \mathcal {T}^{\psi } W_{\mathrm {Ze}}$
for some
$W = \mathcal {T}^{\psi } W_{\mathrm {Ze}}$
for some
![]() $W_{\mathrm {Ze}} \in \mathcal {W}^{\psi }_{\mathrm {Ze}}(\sigma )$
. We define
$W_{\mathrm {Ze}} \in \mathcal {W}^{\psi }_{\mathrm {Ze}}(\sigma )$
. We define
![]() $V"$
to be the subgroup of V consisting of
$V"$
to be the subgroup of V consisting of
![]() $v = (v_{i,j})$
with
$v = (v_{i,j})$
with
![]() $v_{i,j} \in M_n(F)$
such that
$v_{i,j} \in M_n(F)$
such that
![]() $v_{i,j}$
is of the form
$v_{i,j}$
is of the form
 $$\begin{align*}v_{i,j} = \begin{pmatrix} \delta_{i,j}\mathbf{1}_{n-1} & u_{i,j} \\ 0 & \delta_{i,j} \end{pmatrix} \end{align*}$$
$$\begin{align*}v_{i,j} = \begin{pmatrix} \delta_{i,j}\mathbf{1}_{n-1} & u_{i,j} \\ 0 & \delta_{i,j} \end{pmatrix} \end{align*}$$
for
![]() $u_{i,j} \in F^{n-1}$
. Then
$u_{i,j} \in F^{n-1}$
. Then
![]() $V'$
normalises
$V'$
normalises
![]() $V"$
and
$V"$
and
![]() $V = V' V"$
. Hence
$V = V' V"$
. Hence
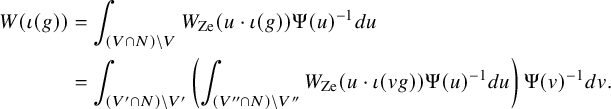 $$ \begin{align*} W(\iota(g)) &= \int_{(V \cap N) \backslash V} W_{\mathrm{Ze}}(u \cdot \iota(g)) \Psi(u)^{-1}du \\ &= \int_{(V' \cap N) \backslash V'} \left( \int_{(V" \cap N) \backslash V"} W_{\mathrm{Ze}}(u \cdot \iota(vg)) \Psi(u)^{-1} du \right) \Psi(v)^{-1} dv. \end{align*} $$
$$ \begin{align*} W(\iota(g)) &= \int_{(V \cap N) \backslash V} W_{\mathrm{Ze}}(u \cdot \iota(g)) \Psi(u)^{-1}du \\ &= \int_{(V' \cap N) \backslash V'} \left( \int_{(V" \cap N) \backslash V"} W_{\mathrm{Ze}}(u \cdot \iota(vg)) \Psi(u)^{-1} du \right) \Psi(v)^{-1} dv. \end{align*} $$
Since
![]() $\iota (G')$
normalises
$\iota (G')$
normalises
![]() $V"$
, and since the action of
$V"$
, and since the action of
![]() $\iota (N')$
on
$\iota (N')$
on
![]() $V"$
does not change the invariant measure on
$V"$
does not change the invariant measure on
![]() $(V" \cap N) \backslash V"$
, if we set
$(V" \cap N) \backslash V"$
, if we set
for
![]() $g' \in G'$
, then
$g' \in G'$
, then
![]() $\varphi _{\mathrm {Ze}}(u'g') = \Psi (u')\varphi _{\mathrm {Ze}}(g')$
for
$\varphi _{\mathrm {Ze}}(u'g') = \Psi (u')\varphi _{\mathrm {Ze}}(g')$
for
![]() $u' \in N'$
and
$u' \in N'$
and
![]() $g' \in G'$
. Therefore, we have
$g' \in G'$
. Therefore, we have
![]() $W \circ \iota \in \Pi $
. Hence we can apply Lemma 9.3 to
$W \circ \iota \in \Pi $
. Hence we can apply Lemma 9.3 to
![]() $W \circ \iota $
, and we obtain that
$W \circ \iota $
, and we obtain that
![]() $W \circ \iota = 0$
. Since
$W \circ \iota = 0$
. Since
![]() $D = V'\iota (G')$
, it follows that
$D = V'\iota (G')$
, it follows that
![]() $W|_D = 0$
. By Theorem 8.2, we conclude that
$W|_D = 0$
. By Theorem 8.2, we conclude that
![]() $W = 0$
, as desired. This completes the proof of the uniqueness statement in Theorem 9.1.
$W = 0$
, as desired. This completes the proof of the uniqueness statement in Theorem 9.1.
Corollary 9.4. Let
![]() $W \in \mathcal {W}^{\psi }_{\mathrm {Ze}}(\sigma )$
. If W is right
$W \in \mathcal {W}^{\psi }_{\mathrm {Ze}}(\sigma )$
. If W is right
![]() $\iota (K')$
-invariant, and if
$\iota (K')$
-invariant, and if
![]() $W|_L = 0$
, then
$W|_L = 0$
, then
![]() $W = 0$
.
$W = 0$
.
Proof. By the assumptions, one has
![]() $I_m(s, W, W^0_{\mathrm {Ze}}(\underline {x})) = 0$
for all
$I_m(s, W, W^0_{\mathrm {Ze}}(\underline {x})) = 0$
for all
![]() $s \in \mathbb {C}$
and
$s \in \mathbb {C}$
and
![]() $\underline {x} = (x_{i,j}) \in M_{m,n-1}(\mathbb {C})$
with
$\underline {x} = (x_{i,j}) \in M_{m,n-1}(\mathbb {C})$
with
![]() $x_{i,j} \in \mathbb {C}^{\times }$
. By the same argument as in the proof of the uniqueness statement in Theorem 9.1, we have
$x_{i,j} \in \mathbb {C}^{\times }$
. By the same argument as in the proof of the uniqueness statement in Theorem 9.1, we have
![]() $\mathcal {T}^{\psi } W = 0$
, and hence
$\mathcal {T}^{\psi } W = 0$
, and hence
![]() $W = 0$
.
$W = 0$
.
As an application, we have a part of Theorem 2.1 for Speh representations. Recall from Example 2.5 (4) that
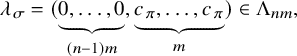 $$\begin{align*}\lambda_{\sigma} = (\underbrace{0,\dots,0}_{(n-1)m}, \underbrace{c_{\pi}, \dots, c_{\pi}}_m) \in \Lambda_{nm}, \end{align*}$$
$$\begin{align*}\lambda_{\sigma} = (\underbrace{0,\dots,0}_{(n-1)m}, \underbrace{c_{\pi}, \dots, c_{\pi}}_m) \in \Lambda_{nm}, \end{align*}$$
where
![]() $c_{\pi }$
is the conductor of
$c_{\pi }$
is the conductor of
![]() $\pi $
.
$\pi $
.
Proposition 9.5. Let
![]() $\lambda \in \Lambda _{nm}$
. If
$\lambda \in \Lambda _{nm}$
. If
![]() $\lambda < \lambda _{\sigma }$
, then
$\lambda < \lambda _{\sigma }$
, then
![]() $\sigma ^{\mathbb {K}_{nm,\lambda }} = 0$
.
$\sigma ^{\mathbb {K}_{nm,\lambda }} = 0$
.
Proof. If
![]() $\lambda < \lambda _{\sigma }$
, then the first
$\lambda < \lambda _{\sigma }$
, then the first
![]() $(n-1)m$
components of
$(n-1)m$
components of
![]() $\lambda $
are
$\lambda $
are
![]() $0$
. Hence there exists a compact subgroup
$0$
. Hence there exists a compact subgroup
![]() $K_{\lambda }$
of G conjugate to
$K_{\lambda }$
of G conjugate to
![]() $\mathbb {K}_{nm,\lambda }$
such that
$\mathbb {K}_{nm,\lambda }$
such that
-
•
 $K_{\lambda } \supset \iota (K')$
;
$K_{\lambda } \supset \iota (K')$
; -
•
 $K_{\lambda } \cap L \supset \mathbb {K}_{n,\lambda _1} \times \dots \times \mathbb {K}_{n,\lambda _m}$
with
$K_{\lambda } \cap L \supset \mathbb {K}_{n,\lambda _1} \times \dots \times \mathbb {K}_{n,\lambda _m}$
with
 $\lambda _i \in \Lambda _n$
of the form
$\lambda _i \in \Lambda _n$
of the form
 $\lambda _i = (0,\dots ,0,a_i)$
such that
$\lambda _i = (0,\dots ,0,a_i)$
such that
 $0 \leq a_i < c_{\pi }$
for some
$0 \leq a_i < c_{\pi }$
for some
 $1 \leq i \leq m$
.
$1 \leq i \leq m$
.
Let
![]() $W \in \mathcal {W}^{\psi }_{\mathrm {Ze}}(\sigma )^{K_{\lambda }}$
. Since
$W \in \mathcal {W}^{\psi }_{\mathrm {Ze}}(\sigma )^{K_{\lambda }}$
. Since
![]() $\pi ^{\mathbb {K}_{n,\lambda _i}} = 0$
by [Reference Jacquet, Piatetski-Shapiro and Shalika14, (5.1) Théorème], we see that
$\pi ^{\mathbb {K}_{n,\lambda _i}} = 0$
by [Reference Jacquet, Piatetski-Shapiro and Shalika14, (5.1) Théorème], we see that
![]() $W|_L = 0$
. It follows from Corollary 9.4 that
$W|_L = 0$
. It follows from Corollary 9.4 that
![]() $W = 0$
. Hence
$W = 0$
. Hence
![]() $\sigma ^{\mathbb {K}_{nm,\lambda }} \cong \sigma ^{K_{\lambda }} = 0$
.
$\sigma ^{\mathbb {K}_{nm,\lambda }} \cong \sigma ^{K_{\lambda }} = 0$
.
9.2 Properties of essential vectors
Recall that
![]() $G = \mathrm {GL}_{nm}(F)$
and
$G = \mathrm {GL}_{nm}(F)$
and
![]() $K= \mathrm {GL}_{nm}(\mathfrak {o})$
. For a positive integer a, define
$K= \mathrm {GL}_{nm}(\mathfrak {o})$
. For a positive integer a, define
![]() $K(a) \subset K$
to be the subgroup consisting of
$K(a) \subset K$
to be the subgroup consisting of
![]() $k = (k_{i,j})_{1 \leq i,j \leq m} \in K$
with
$k = (k_{i,j})_{1 \leq i,j \leq m} \in K$
with
![]() $k_{i,j} \in M_{n}(\mathfrak {o})$
such that the last row of
$k_{i,j} \in M_{n}(\mathfrak {o})$
such that the last row of
![]() $k_{i,j}$
is congruent to
$k_{i,j}$
is congruent to
![]() $(0,\dots ,0,\delta _{i,j}) \bmod \mathfrak {p}^a$
for
$(0,\dots ,0,\delta _{i,j}) \bmod \mathfrak {p}^a$
for
![]() $1 \leq i,j \leq m$
. Put another way, if we denote by
$1 \leq i,j \leq m$
. Put another way, if we denote by
![]() $D(\mathfrak {o}/\mathfrak {p}^a)$
the image of
$D(\mathfrak {o}/\mathfrak {p}^a)$
the image of
![]() $D \cap K$
under
$D \cap K$
under
![]() $K \rightarrow \mathrm {GL}_{nm}(\mathfrak {o}/\mathfrak {p}^a)$
, then
$K \rightarrow \mathrm {GL}_{nm}(\mathfrak {o}/\mathfrak {p}^a)$
, then
![]() $K(a)$
is the inverse image of
$K(a)$
is the inverse image of
![]() $D(\mathfrak {o}/\mathfrak {p}^a)$
. Note that
$D(\mathfrak {o}/\mathfrak {p}^a)$
. Note that
![]() $K(a)$
is conjugate to
$K(a)$
is conjugate to
![]() $\mathbb {K}_{nm,\lambda }$
with
$\mathbb {K}_{nm,\lambda }$
with
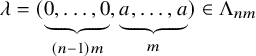 $$\begin{align*}\lambda = (\underbrace{0,\dots,0}_{(n-1)m},\underbrace{a,\dots,a}_m) \in \Lambda_{nm} \end{align*}$$
$$\begin{align*}\lambda = (\underbrace{0,\dots,0}_{(n-1)m},\underbrace{a,\dots,a}_m) \in \Lambda_{nm} \end{align*}$$
by an element of K.
Let
![]() $\pi $
be an irreducible tempered representation of
$\pi $
be an irreducible tempered representation of
![]() $G_n$
, and set
$G_n$
, and set
![]() $\sigma = \mathrm {Sp}(\pi ,m)$
. We prove the following proposition in this subsection. It together with Proposition 9.5 contains Theorem 2.1 for
$\sigma = \mathrm {Sp}(\pi ,m)$
. We prove the following proposition in this subsection. It together with Proposition 9.5 contains Theorem 2.1 for
![]() $\sigma $
when
$\sigma $
when
![]() $L(s,\sigma ) = 1$
.
$L(s,\sigma ) = 1$
.
Proposition 9.6. Suppose that
![]() $L(s, \pi ) = 1$
. Then
$L(s, \pi ) = 1$
. Then
![]() $\mathcal {W}^{\psi }_{\mathrm {Sh}}(\sigma )^{K(c_{\pi })}$
is the one-dimensional vector space spanned by the essential vector
$\mathcal {W}^{\psi }_{\mathrm {Sh}}(\sigma )^{K(c_{\pi })}$
is the one-dimensional vector space spanned by the essential vector
![]() $W^{\mathrm {ess}}_{\mathrm {Sh}}$
.
$W^{\mathrm {ess}}_{\mathrm {Sh}}$
.
The proof of Proposition 9.6 is analogous to that of [Reference Jacquet, Piatetski-Shapiro and Shalika14, (5.1) Théorème]. Suppose that
![]() $L(s, \pi ) = 1$
.
$L(s, \pi ) = 1$
.
For
![]() $d \in \mathbb {Z}$
and
$d \in \mathbb {Z}$
and
![]() $W_{\mathrm {Sh}} \in \mathcal {W}^{\psi }_{\mathrm {Sh}}(\sigma )$
, we consider
$W_{\mathrm {Sh}} \in \mathcal {W}^{\psi }_{\mathrm {Sh}}(\sigma )$
, we consider
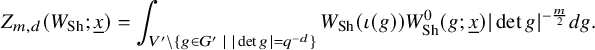 $$\begin{align*}Z_{m,d}(W_{\mathrm{Sh}}; \underline{x}) = \int_{V' \backslash \{g \in G' \;|\; |\det g| = q^{-d}\}} W_{\mathrm{Sh}}(\iota(g)) W_{\mathrm{Sh}}^0(g; \underline{x})|\det g|^{-\frac{m}{2}} dg. \end{align*}$$
$$\begin{align*}Z_{m,d}(W_{\mathrm{Sh}}; \underline{x}) = \int_{V' \backslash \{g \in G' \;|\; |\det g| = q^{-d}\}} W_{\mathrm{Sh}}(\iota(g)) W_{\mathrm{Sh}}^0(g; \underline{x})|\det g|^{-\frac{m}{2}} dg. \end{align*}$$
Note that
where
![]() $x\underline {x} = (xx_{i,j})$
if
$x\underline {x} = (xx_{i,j})$
if
![]() $\underline {x} = (x_{i,j})$
.
$\underline {x} = (x_{i,j})$
.
Lemma 9.7. There is an integer
![]() $d(W_{\mathrm {Sh}})$
such that
$d(W_{\mathrm {Sh}})$
such that
![]() $Z_{m,d}(W_{\mathrm {Sh}}; \underline {x}) = 0$
for any
$Z_{m,d}(W_{\mathrm {Sh}}; \underline {x}) = 0$
for any
![]() $d < d(W_{\mathrm {Sh}})$
and
$d < d(W_{\mathrm {Sh}})$
and
![]() $\underline {x} = (x_{i,j}) \in M_{m,n-1}(\mathbb {C})$
with
$\underline {x} = (x_{i,j}) \in M_{m,n-1}(\mathbb {C})$
with
![]() $x_{i,j} \in \mathbb {C}^{\times }$
.
$x_{i,j} \in \mathbb {C}^{\times }$
.
Proof. By (the proof of) Proposition 8.9, it is enough to show an analogous assertion for
![]() $I_m(s,W_{\mathrm {Ze}}, W^0_{\mathrm {Ze}}(\underline {x}))$
with
$I_m(s,W_{\mathrm {Ze}}, W^0_{\mathrm {Ze}}(\underline {x}))$
with
![]() $W_{\mathrm {Ze}} \in \mathcal {W}^{\psi }_{\mathrm {Ze}}(\sigma )$
. Let
$W_{\mathrm {Ze}} \in \mathcal {W}^{\psi }_{\mathrm {Ze}}(\sigma )$
. Let
![]() $g \in G'$
with
$g \in G'$
with
![]() $|\det g| = q^{-d}$
such that
$|\det g| = q^{-d}$
such that
![]() $W_{\mathrm {Ze}}(\iota (g)) W^0_{\mathrm {Ze}}(g; \underline {x}) \not = 0$
. We take
$W_{\mathrm {Ze}}(\iota (g)) W^0_{\mathrm {Ze}}(g; \underline {x}) \not = 0$
. We take
![]() $k' \in K'$
,
$k' \in K'$
,
![]() $u' \in N'$
and
$u' \in N'$
and
![]() $a_1, \dots , a_{(n-1)m} \in \mathbb {Z}$
such that
$a_1, \dots , a_{(n-1)m} \in \mathbb {Z}$
such that
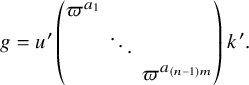 $$\begin{align*}g = u' \begin{pmatrix} \varpi^{a_1} && \\ & \ddots & \\ && \varpi^{a_{(n-1)m}} \end{pmatrix} k'. \end{align*}$$
$$\begin{align*}g = u' \begin{pmatrix} \varpi^{a_1} && \\ & \ddots & \\ && \varpi^{a_{(n-1)m}} \end{pmatrix} k'. \end{align*}$$
Since
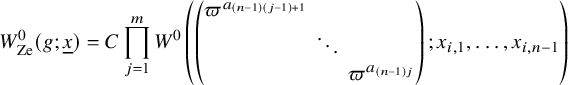 $$\begin{align*}W^0_{\mathrm{Ze}}(g; \underline{x}) = C \prod_{j=1}^mW^0\left( \begin{pmatrix} \varpi^{a_{(n-1)(j-1)+1}} && \\ & \ddots & \\ && \varpi^{a_{(n-1)j}} \end{pmatrix}; x_{i,1}, \dots, x_{i,n-1}\right) \end{align*}$$
$$\begin{align*}W^0_{\mathrm{Ze}}(g; \underline{x}) = C \prod_{j=1}^mW^0\left( \begin{pmatrix} \varpi^{a_{(n-1)(j-1)+1}} && \\ & \ddots & \\ && \varpi^{a_{(n-1)j}} \end{pmatrix}; x_{i,1}, \dots, x_{i,n-1}\right) \end{align*}$$
for some
![]() $C \not = 0$
(depending on
$C \not = 0$
(depending on
![]() $a_1, \dots , a_{(n-1)m}$
), we must have
$a_1, \dots , a_{(n-1)m}$
), we must have
![]() $a_{(n-1)(j-1)+1} \geq \dots \geq a_{(n-1)j}$
for any
$a_{(n-1)(j-1)+1} \geq \dots \geq a_{(n-1)j}$
for any
![]() $1 \leq j \leq m$
. In particular,
$1 \leq j \leq m$
. In particular,
![]() $d = \sum _{i=1}^{(n-1)m}a_i \geq \sum _{j=1}^{m}(n-1)a_{(n-1)j}$
.
$d = \sum _{i=1}^{(n-1)m}a_i \geq \sum _{j=1}^{m}(n-1)a_{(n-1)j}$
.
For
![]() $l \geq 0$
, let
$l \geq 0$
, let
![]() $V"(\mathfrak {p}^l)$
be the subgroup of K consisting of
$V"(\mathfrak {p}^l)$
be the subgroup of K consisting of
![]() $(k_{i,j})_{1 \leq i,j \leq m}$
with
$(k_{i,j})_{1 \leq i,j \leq m}$
with
![]() $k_{i,j} \in M_n(\mathfrak {o})$
such that
$k_{i,j} \in M_n(\mathfrak {o})$
such that
![]() $k_{i,j}$
is of the form
$k_{i,j}$
is of the form
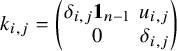 $$\begin{align*}k_{i,j} = \begin{pmatrix} \delta_{i,j}\mathbf{1}_{n-1} & u_{i,j} \\ 0 & \delta_{i,j} \end{pmatrix} \end{align*}$$
$$\begin{align*}k_{i,j} = \begin{pmatrix} \delta_{i,j}\mathbf{1}_{n-1} & u_{i,j} \\ 0 & \delta_{i,j} \end{pmatrix} \end{align*}$$
for
![]() $u_{i,j} \in (\mathfrak {p}^l)^{n-1}$
. Since
$u_{i,j} \in (\mathfrak {p}^l)^{n-1}$
. Since
![]() $W_{\mathrm {Ze}}$
is smooth, one can take sufficiently large l such that
$W_{\mathrm {Ze}}$
is smooth, one can take sufficiently large l such that
![]() $W_{\mathrm {Ze}}$
is right
$W_{\mathrm {Ze}}$
is right
![]() $V"(\mathfrak {p}^l)$
-invariant. Note that
$V"(\mathfrak {p}^l)$
-invariant. Note that
![]() $\iota (K')$
acts on
$\iota (K')$
acts on
![]() $V"(\mathfrak {p}^l)$
. In particular, for any
$V"(\mathfrak {p}^l)$
. In particular, for any
![]() $z_1, \dots , z_m \in \mathfrak {p}^l$
, we can take
$z_1, \dots , z_m \in \mathfrak {p}^l$
, we can take
![]() $u \in V"(\mathfrak {p}^l)$
such that
$u \in V"(\mathfrak {p}^l)$
such that
![]() $(\iota (k') \cdot u \cdot \iota (k')^{-1})_{nj-1,nj} = z_j$
for
$(\iota (k') \cdot u \cdot \iota (k')^{-1})_{nj-1,nj} = z_j$
for
![]() $1 \leq j \leq m$
. Then we have
$1 \leq j \leq m$
. Then we have
 $$ \begin{align*} W_{\mathrm{Ze}}(\iota(g)) &= W_{\mathrm{Ze}}\left(\iota(u') \iota\begin{pmatrix} \varpi^{a_1} && \\ & \ddots & \\ && \varpi^{a_{n-1}} \end{pmatrix} \iota(k')u\right) \\&= \left(\prod_{j=1}^m\psi(\varpi^{a_{(n-1)j}}z_j)\right) W_{\mathrm{Ze}}(\iota(g)). \end{align*} $$
$$ \begin{align*} W_{\mathrm{Ze}}(\iota(g)) &= W_{\mathrm{Ze}}\left(\iota(u') \iota\begin{pmatrix} \varpi^{a_1} && \\ & \ddots & \\ && \varpi^{a_{n-1}} \end{pmatrix} \iota(k')u\right) \\&= \left(\prod_{j=1}^m\psi(\varpi^{a_{(n-1)j}}z_j)\right) W_{\mathrm{Ze}}(\iota(g)). \end{align*} $$
Since
![]() $z_1, \dots , z_m \in \mathfrak {p}^l$
are arbitrary, if
$z_1, \dots , z_m \in \mathfrak {p}^l$
are arbitrary, if
![]() $W_{\mathrm {Ze}}(\iota (g)) \not = 0$
, then we must have
$W_{\mathrm {Ze}}(\iota (g)) \not = 0$
, then we must have
![]() $a_{(n-1)j} \geq -l$
for
$a_{(n-1)j} \geq -l$
for
![]() $1 \leq j \leq m$
. In conclusion, we have
$1 \leq j \leq m$
. In conclusion, we have
![]() $d \geq \sum _{j=1}^{m}(n-1)a_{(n-1)j} \geq -(n-1)ml$
. This completes the proof of the lemma.
$d \geq \sum _{j=1}^{m}(n-1)a_{(n-1)j} \geq -(n-1)ml$
. This completes the proof of the lemma.
By the proof of this lemma, one can take
![]() $d(W_{\mathrm {Sh}}) = -(n-1)m l$
if
$d(W_{\mathrm {Sh}}) = -(n-1)m l$
if
![]() $W_{\mathrm {Sh}}$
is right
$W_{\mathrm {Sh}}$
is right
![]() $V"(\mathfrak {p}^l)$
-invariant. In particular, if
$V"(\mathfrak {p}^l)$
-invariant. In particular, if
![]() $W_{\mathrm {Sh}} \in \mathcal {W}^{\psi }_{\mathrm {Sh}}(\sigma )^{K(a)}$
, then we can take
$W_{\mathrm {Sh}} \in \mathcal {W}^{\psi }_{\mathrm {Sh}}(\sigma )^{K(a)}$
, then we can take
![]() $d(W_{\mathrm {Sh}}) = 0$
and
$d(W_{\mathrm {Sh}}) = 0$
and
![]() $d(\widetilde {W}_{\mathrm {Sh}}) = -(n-1)ma$
.
$d(\widetilde {W}_{\mathrm {Sh}}) = -(n-1)ma$
.
Now, if we set
![]() $x = q^{-s}$
, we have
$x = q^{-s}$
, we have
 $$\begin{align*}Z_m(s,W_{\mathrm{Sh}},W^0_{\mathrm{Sh}}(\underline{x})) = \sum_{d \in \mathbb{Z}}x^d Z_{m,d}(W_{\mathrm{Sh}}; \underline{x}) = \sum_{d \geq d(W_{\mathrm{Sh}})}x^d Z_{m,d}(W_{\mathrm{Sh}}; \underline{x}). \end{align*}$$
$$\begin{align*}Z_m(s,W_{\mathrm{Sh}},W^0_{\mathrm{Sh}}(\underline{x})) = \sum_{d \in \mathbb{Z}}x^d Z_{m,d}(W_{\mathrm{Sh}}; \underline{x}) = \sum_{d \geq d(W_{\mathrm{Sh}})}x^d Z_{m,d}(W_{\mathrm{Sh}}; \underline{x}). \end{align*}$$
If we replace
![]() $\pi $
,
$\pi $
,
![]() $W_{\mathrm {Sh}}$
and
$W_{\mathrm {Sh}}$
and
![]() $\psi $
with
$\psi $
with
![]() $\widetilde {\pi }$
,
$\widetilde {\pi }$
,
![]() $\widetilde {W}_{\mathrm {Sh}}$
and
$\widetilde {W}_{\mathrm {Sh}}$
and
![]() $\psi ^{-1}$
, respectively, since
$\psi ^{-1}$
, respectively, since
![]() $\widetilde {W}^0_{\mathrm {Sh}}(\underline {x}) = W^0_{\mathrm {Sh}}(\underline {x}^{-1})$
(with respect to
$\widetilde {W}^0_{\mathrm {Sh}}(\underline {x}) = W^0_{\mathrm {Sh}}(\underline {x}^{-1})$
(with respect to
![]() $\psi $
), we have
$\psi $
), we have
 $$\begin{align*}Z_m(s,\widetilde{W}_{\mathrm{Sh}},\widetilde{W}^0_{\mathrm{Sh}}(\underline{x})) = \sum_{d \geq d(\widetilde{W}_{\mathrm{Sh}})}x^d Z_{m,d}(\widetilde{W}_{\mathrm{Sh}}; \underline{x}^{-1}), \end{align*}$$
$$\begin{align*}Z_m(s,\widetilde{W}_{\mathrm{Sh}},\widetilde{W}^0_{\mathrm{Sh}}(\underline{x})) = \sum_{d \geq d(\widetilde{W}_{\mathrm{Sh}})}x^d Z_{m,d}(\widetilde{W}_{\mathrm{Sh}}; \underline{x}^{-1}), \end{align*}$$
and hence
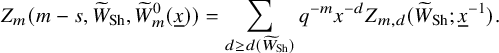 $$\begin{align*}Z_m(m-s,\widetilde{W}_{\mathrm{Sh}},\widetilde{W}^0_m(\underline{x})) = \sum_{d \geq d(\widetilde{W}_{\mathrm{Sh}})}q^{-m}x^{-d} Z_{m,d}(\widetilde{W}_{\mathrm{Sh}}; \underline{x}^{-1}). \end{align*}$$
$$\begin{align*}Z_m(m-s,\widetilde{W}_{\mathrm{Sh}},\widetilde{W}^0_m(\underline{x})) = \sum_{d \geq d(\widetilde{W}_{\mathrm{Sh}})}q^{-m}x^{-d} Z_{m,d}(\widetilde{W}_{\mathrm{Sh}}; \underline{x}^{-1}). \end{align*}$$
By the functional equation (Theorem 8.11 (3)), using the assumption that
![]() $L(s,\pi ) = 1$
, we have
$L(s,\pi ) = 1$
, we have
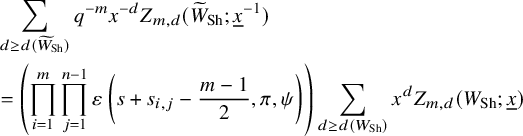 $$ \begin{align*} &\sum_{d \geq d(\widetilde{W}_{\mathrm{Sh}})}q^{-m}x^{-d} Z_{m,d}(\widetilde{W}_{\mathrm{Sh}}; \underline{x}^{-1}) \\&= \left(\prod_{i=1}^m\prod_{j=1}^{n-1} \varepsilon\left( s+s_{i,j}-\frac{m-1}{2}, \pi, \psi \right) \right) \sum_{d \geq d(W_{\mathrm{Sh}})}x^d Z_{m,d}(W_{\mathrm{Sh}}; \underline{x}) \end{align*} $$
$$ \begin{align*} &\sum_{d \geq d(\widetilde{W}_{\mathrm{Sh}})}q^{-m}x^{-d} Z_{m,d}(\widetilde{W}_{\mathrm{Sh}}; \underline{x}^{-1}) \\&= \left(\prod_{i=1}^m\prod_{j=1}^{n-1} \varepsilon\left( s+s_{i,j}-\frac{m-1}{2}, \pi, \psi \right) \right) \sum_{d \geq d(W_{\mathrm{Sh}})}x^d Z_{m,d}(W_{\mathrm{Sh}}; \underline{x}) \end{align*} $$
as a formal power series of x, where
![]() $s_{i,j}$
is a complex number such that
$s_{i,j}$
is a complex number such that
![]() $x_{i,j} = q^{-s_{i,j}}$
. If we write
$x_{i,j} = q^{-s_{i,j}}$
. If we write
![]() $\varepsilon (s,\pi , \psi ) = \varepsilon _0 q^{-c_{\pi } s} = \varepsilon _0 x^{c_{\pi }}$
, we have
$\varepsilon (s,\pi , \psi ) = \varepsilon _0 q^{-c_{\pi } s} = \varepsilon _0 x^{c_{\pi }}$
, we have
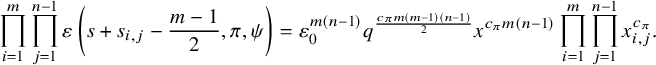 $$\begin{align*}\prod_{i=1}^m\prod_{j=1}^{n-1} \varepsilon \left(s+s_{i,j}-\frac{m-1}{2}, \pi, \psi \right) = \varepsilon_0^{m(n-1)} q^{\frac{c_{\pi} m(m-1)(n-1)}{2}} x^{c_{\pi} m(n-1)} \prod_{i=1}^m \prod_{j=1}^{n-1}x_{i,j}^{c_{\pi}}. \end{align*}$$
$$\begin{align*}\prod_{i=1}^m\prod_{j=1}^{n-1} \varepsilon \left(s+s_{i,j}-\frac{m-1}{2}, \pi, \psi \right) = \varepsilon_0^{m(n-1)} q^{\frac{c_{\pi} m(m-1)(n-1)}{2}} x^{c_{\pi} m(n-1)} \prod_{i=1}^m \prod_{j=1}^{n-1}x_{i,j}^{c_{\pi}}. \end{align*}$$
In particular, if
![]() , we must have
, we must have
![]() $Z_{m,d}(W_{\mathrm {Sh}}; \underline {x}) = 0$
. Hence we obtain the following.
$Z_{m,d}(W_{\mathrm {Sh}}; \underline {x}) = 0$
. Hence we obtain the following.
Proposition 9.8. Assume that
![]() $L(s,\pi ) = 1$
. Write
$L(s,\pi ) = 1$
. Write
![]() $\varepsilon (s,\pi , \psi ) = \varepsilon _0 q^{-c_{\pi } s}$
. For
$\varepsilon (s,\pi , \psi ) = \varepsilon _0 q^{-c_{\pi } s}$
. For
![]() $W_{\mathrm {Sh}} \in \mathcal {W}^{\psi }_{\mathrm {Sh}}(\sigma )$
, let
$W_{\mathrm {Sh}} \in \mathcal {W}^{\psi }_{\mathrm {Sh}}(\sigma )$
, let
![]() $d(W_{\mathrm {Sh}})$
and
$d(W_{\mathrm {Sh}})$
and
![]() $d(\widetilde {W}_{\mathrm {Sh}})$
be the constants in Lemma 9.7, and set
$d(\widetilde {W}_{\mathrm {Sh}})$
be the constants in Lemma 9.7, and set
![]() $d'(W_{\mathrm {Sh}}) = -c_{\pi } m(n-1)-d(\widetilde {W}_{\mathrm {Sh}})$
. Then
$d'(W_{\mathrm {Sh}}) = -c_{\pi } m(n-1)-d(\widetilde {W}_{\mathrm {Sh}})$
. Then
 $$\begin{align*}Z_m(s,W_{\mathrm{Sh}},W^0_{\mathrm{Sh}}(\underline{x})) = \sum_{d(W_{\mathrm{Sh}}) \leq d \leq d'(W_{\mathrm{Sh}})} x^d Z_{m,d}(W_{\mathrm{Sh}}; \underline{x}) \end{align*}$$
$$\begin{align*}Z_m(s,W_{\mathrm{Sh}},W^0_{\mathrm{Sh}}(\underline{x})) = \sum_{d(W_{\mathrm{Sh}}) \leq d \leq d'(W_{\mathrm{Sh}})} x^d Z_{m,d}(W_{\mathrm{Sh}}; \underline{x}) \end{align*}$$
is a finite sum. Moreover, we have a functional equation
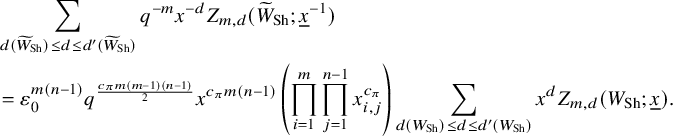 $$ \begin{align*} &\sum_{d(\widetilde{W}_{\mathrm{Sh}}) \leq d \leq d'(\widetilde{W}_{\mathrm{Sh}})}q^{-m}x^{-d} Z_{m,d}(\widetilde{W}_{\mathrm{Sh}}; \underline{x}^{-1}) \\&= \varepsilon_0^{m(n-1)} q^{\frac{c_{\pi} m(m-1)(n-1)}{2}} x^{c_{\pi} m(n-1)} \left(\prod_{i=1}^m \prod_{j=1}^{n-1}x_{i,j}^{c_{\pi}}\right) \sum_{d(W_{\mathrm{Sh}}) \leq d \leq d'(W_{\mathrm{Sh}})}x^d Z_{m,d}(W_{\mathrm{Sh}}; \underline{x}). \end{align*} $$
$$ \begin{align*} &\sum_{d(\widetilde{W}_{\mathrm{Sh}}) \leq d \leq d'(\widetilde{W}_{\mathrm{Sh}})}q^{-m}x^{-d} Z_{m,d}(\widetilde{W}_{\mathrm{Sh}}; \underline{x}^{-1}) \\&= \varepsilon_0^{m(n-1)} q^{\frac{c_{\pi} m(m-1)(n-1)}{2}} x^{c_{\pi} m(n-1)} \left(\prod_{i=1}^m \prod_{j=1}^{n-1}x_{i,j}^{c_{\pi}}\right) \sum_{d(W_{\mathrm{Sh}}) \leq d \leq d'(W_{\mathrm{Sh}})}x^d Z_{m,d}(W_{\mathrm{Sh}}; \underline{x}). \end{align*} $$
Now we prove Proposition 9.6.
Proof of Proposition 9.6
First, we show that the essential vector
![]() $W^{\mathrm {ess}}_{\mathrm {Sh}}$
is
$W^{\mathrm {ess}}_{\mathrm {Sh}}$
is
![]() $K(c_{\pi })$
-invariant. By Proposition 9.8, we have
$K(c_{\pi })$
-invariant. By Proposition 9.8, we have
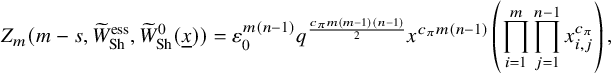 $$\begin{align*}Z_m(m-s, \widetilde{W}^{\mathrm{ess}}_{\mathrm{Sh}}, \widetilde{W}^0_{\mathrm{Sh}}(\underline{x})) = \varepsilon_0^{m(n-1)} q^{\frac{c_{\pi} m(m-1)(n-1)}{2}} x^{c_{\pi} m(n-1)} \left(\prod_{i=1}^m \prod_{j=1}^{n-1}x_{i,j}^{c_{\pi}}\right), \end{align*}$$
$$\begin{align*}Z_m(m-s, \widetilde{W}^{\mathrm{ess}}_{\mathrm{Sh}}, \widetilde{W}^0_{\mathrm{Sh}}(\underline{x})) = \varepsilon_0^{m(n-1)} q^{\frac{c_{\pi} m(m-1)(n-1)}{2}} x^{c_{\pi} m(n-1)} \left(\prod_{i=1}^m \prod_{j=1}^{n-1}x_{i,j}^{c_{\pi}}\right), \end{align*}$$
where
![]() $x = q^{-s}$
. Set
$x = q^{-s}$
. Set
![]() $a = \varpi ^{c_{\pi }}\mathbf {1}_{(n-1)m}$
, which is in the centre of
$a = \varpi ^{c_{\pi }}\mathbf {1}_{(n-1)m}$
, which is in the centre of
![]() $G'$
. We notice that
$G'$
. We notice that
![]() $|\det a^{-1}|^{\frac {m}{2}-s} = q^{\frac {c_{\pi } m^2(n-1)}{2}}x^{c_{\pi } m(n-1)}$
and
$|\det a^{-1}|^{\frac {m}{2}-s} = q^{\frac {c_{\pi } m^2(n-1)}{2}}x^{c_{\pi } m(n-1)}$
and
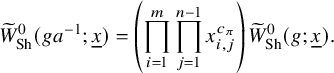 $$\begin{align*}\widetilde{W}^0_{\mathrm{Sh}}(ga^{-1}; \underline{x}) = \left(\prod_{i=1}^m\prod_{j=1}^{n-1}x_{i,j}^{c_{\pi}}\right) \widetilde{W}^0_{\mathrm{Sh}}(g; \underline{x}). \end{align*}$$
$$\begin{align*}\widetilde{W}^0_{\mathrm{Sh}}(ga^{-1}; \underline{x}) = \left(\prod_{i=1}^m\prod_{j=1}^{n-1}x_{i,j}^{c_{\pi}}\right) \widetilde{W}^0_{\mathrm{Sh}}(g; \underline{x}). \end{align*}$$
If we define
![]() $W^{\prime }_{\mathrm {Sh}} \in \mathcal {W}^{\psi ^{-1}}_{\mathrm {Sh}}(\widetilde {\sigma })$
by
$W^{\prime }_{\mathrm {Sh}} \in \mathcal {W}^{\psi ^{-1}}_{\mathrm {Sh}}(\widetilde {\sigma })$
by
then it is right
![]() $\iota (K')$
-invariant and
$\iota (K')$
-invariant and
 $$\begin{align*}Z_m(m-s, W^{\prime}_{\mathrm{Sh}}, \widetilde{W}^0_{\mathrm{Sh}}(\underline{x})) = q^{\frac{c_{\pi} m^2(n-1)}{2}}x^{c_{\pi} m(n-1)} \left(\prod_{i=1}^m\prod_{j=1}^{n-1}x_{i,j}^{c_{\pi}}\right). \end{align*}$$
$$\begin{align*}Z_m(m-s, W^{\prime}_{\mathrm{Sh}}, \widetilde{W}^0_{\mathrm{Sh}}(\underline{x})) = q^{\frac{c_{\pi} m^2(n-1)}{2}}x^{c_{\pi} m(n-1)} \left(\prod_{i=1}^m\prod_{j=1}^{n-1}x_{i,j}^{c_{\pi}}\right). \end{align*}$$
By Lemma 9.3 and Theorem 8.2, we see that
![]() $\widetilde {W}^{\mathrm {ess}}_{\mathrm {Sh}} = C W^{\prime }_{\mathrm {Sh}}$
for some constant C. Hence
$\widetilde {W}^{\mathrm {ess}}_{\mathrm {Sh}} = C W^{\prime }_{\mathrm {Sh}}$
for some constant C. Hence
Since
![]() $W^{\mathrm {ess}}_{\mathrm {Sh}}$
is right
$W^{\mathrm {ess}}_{\mathrm {Sh}}$
is right
![]() $V"(\mathfrak {o})$
-invariant, it follows that
$V"(\mathfrak {o})$
-invariant, it follows that
![]() $W^{\mathrm {ess}}_{\mathrm {Sh}}$
is right
$W^{\mathrm {ess}}_{\mathrm {Sh}}$
is right
![]() ${}^tV"(\mathfrak {p}^{c_{\pi }})$
-invariant. Therefore, we conclude that
${}^tV"(\mathfrak {p}^{c_{\pi }})$
-invariant. Therefore, we conclude that
![]() $W^{\mathrm {ess}}_{\mathrm {Sh}}$
is right
$W^{\mathrm {ess}}_{\mathrm {Sh}}$
is right
![]() $K(c_{\pi })$
-invariant.
$K(c_{\pi })$
-invariant.
Next, we show that
![]() $\dim (\sigma ^{K(c_{\pi })}) = 1$
. If
$\dim (\sigma ^{K(c_{\pi })}) = 1$
. If
![]() $\mathcal {W}_{\mathrm {Ze}} \in \mathcal {W}^{\psi }_{\mathrm {Ze}}(\sigma )^{K(c_{\pi })}$
, we have
$\mathcal {W}_{\mathrm {Ze}} \in \mathcal {W}^{\psi }_{\mathrm {Ze}}(\sigma )^{K(c_{\pi })}$
, we have
 $$\begin{align*}W_{\mathrm{Ze}}|_L \in \left(\bigotimes_{i=1}^m\mathcal{W}^{\psi}(\pi|\cdot|^{\frac{(m+1-2i)(n-1)}{2}}) \right)^{K(c_{\pi}) \cap L}, \end{align*}$$
$$\begin{align*}W_{\mathrm{Ze}}|_L \in \left(\bigotimes_{i=1}^m\mathcal{W}^{\psi}(\pi|\cdot|^{\frac{(m+1-2i)(n-1)}{2}}) \right)^{K(c_{\pi}) \cap L}, \end{align*}$$
where the right-hand side is one-dimensional and is spanned by the tensor product of essential vectors. Hence
![]() $Z_m(s,\mathcal {T}^{\psi } W_{\mathrm {Ze}},W^0_{\mathrm {Sh}}(\underline {x})) = I_m(s,W_{\mathrm {Ze}},W^0_{\mathrm {Ze}}(\underline {x}))$
does not depend on
$Z_m(s,\mathcal {T}^{\psi } W_{\mathrm {Ze}},W^0_{\mathrm {Sh}}(\underline {x})) = I_m(s,W_{\mathrm {Ze}},W^0_{\mathrm {Ze}}(\underline {x}))$
does not depend on
![]() $s \in \mathbb {C}$
and
$s \in \mathbb {C}$
and
![]() $\underline {x} = (x_{i,j}) \in M_{m,n-1}(\mathbb {C})$
with
$\underline {x} = (x_{i,j}) \in M_{m,n-1}(\mathbb {C})$
with
![]() $x_{i,j} \in \mathbb {C}^{\times }$
. Using the uniqueness statement in Theorem 9.1, we conclude that
$x_{i,j} \in \mathbb {C}^{\times }$
. Using the uniqueness statement in Theorem 9.1, we conclude that
![]() $\mathcal {T}^{\psi } W_{\mathrm {Ze}}$
is a constant multiple of
$\mathcal {T}^{\psi } W_{\mathrm {Ze}}$
is a constant multiple of
![]() $W^{\mathrm {ess}}_{\mathrm {Sh}}$
.
$W^{\mathrm {ess}}_{\mathrm {Sh}}$
.
Since
![]() $\mathbb {K}_{nm,\lambda _{\sigma }}$
is conjugate to
$\mathbb {K}_{nm,\lambda _{\sigma }}$
is conjugate to
![]() $K(c_{\pi })$
, by Propositions 9.5 and 9.6, we complete the proof of Theorem 2.1 for
$K(c_{\pi })$
, by Propositions 9.5 and 9.6, we complete the proof of Theorem 2.1 for
![]() $\sigma = \mathrm {Sp}(\pi ,m)$
such that
$\sigma = \mathrm {Sp}(\pi ,m)$
such that
![]() $L(s,\pi ) = 1$
. As explained in Section 5.2, this together with results in Sections 6.1, 6.4 and Lemma 7.2 completes Theorem 2.1 in all cases.
$L(s,\pi ) = 1$
. As explained in Section 5.2, this together with results in Sections 6.1, 6.4 and Lemma 7.2 completes Theorem 2.1 in all cases.
To prove Theorem 9.1 in Section 9.3, we use the following special case of Theorem 2.1.
Corollary 9.9. Let
![]() $\pi $
be an irreducible tempered representation of
$\pi $
be an irreducible tempered representation of
![]() $G_n$
, and set
$G_n$
, and set
![]() $\sigma = \mathrm {Sp}(\pi ,m)$
. Then we have
$\sigma = \mathrm {Sp}(\pi ,m)$
. Then we have
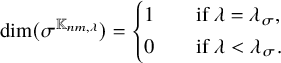 $$\begin{align*}\dim(\sigma^{\mathbb{K}_{nm,\lambda}}) = \left\{ \begin{aligned} &1 &\quad&\text{if } \lambda = \lambda_{\sigma},\\ &0 &\quad&\text{if } \lambda < \lambda_{\sigma}. \end{aligned} \right. \end{align*}$$
$$\begin{align*}\dim(\sigma^{\mathbb{K}_{nm,\lambda}}) = \left\{ \begin{aligned} &1 &\quad&\text{if } \lambda = \lambda_{\sigma},\\ &0 &\quad&\text{if } \lambda < \lambda_{\sigma}. \end{aligned} \right. \end{align*}$$
9.3 Proof of Theorem 9.1: the case where
 $L(s,\pi ) \neq 1$
$L(s,\pi ) \neq 1$
Finally, we prove the existence statement in Theorem 9.1 in general. Before doing it, we state the following consequence of Corollary 9.9.
Corollary 9.10. Let
![]() $\pi $
be an irreducible tempered representation of
$\pi $
be an irreducible tempered representation of
![]() $G_n$
, and set
$G_n$
, and set
![]() $\sigma = \mathrm {Sp}(\pi ,m)$
. Then the restriction map
$\sigma = \mathrm {Sp}(\pi ,m)$
. Then the restriction map
![]() $W_{\mathrm {Ze}} \mapsto W_{\mathrm {Ze}}|_L$
gives an isomorphism of one-dimensional vector spaces
$W_{\mathrm {Ze}} \mapsto W_{\mathrm {Ze}}|_L$
gives an isomorphism of one-dimensional vector spaces
Proof. Since the compact open subgroup
![]() $K(c_{\pi })$
is conjugate to
$K(c_{\pi })$
is conjugate to
![]() $\mathbb {K}_{nm,\lambda _{\sigma }}$
, we conclude that
$\mathbb {K}_{nm,\lambda _{\sigma }}$
, we conclude that
![]() $\sigma ^{K(c_{\pi })}$
is one-dimensional. By Lemma 9.4, the restriction map
$\sigma ^{K(c_{\pi })}$
is one-dimensional. By Lemma 9.4, the restriction map
![]() $W_{\mathrm {Ze}} \mapsto W_{\mathrm {Ze}}|_L$
is injective on
$W_{\mathrm {Ze}} \mapsto W_{\mathrm {Ze}}|_L$
is injective on
![]() $\mathcal {W}_{\mathrm {Ze}}^{\psi }(\sigma )^{K(c_{\pi })}$
. Since the image is in
$\mathcal {W}_{\mathrm {Ze}}^{\psi }(\sigma )^{K(c_{\pi })}$
. Since the image is in
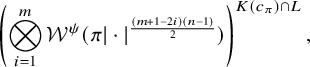 $$\begin{align*}\left(\bigotimes_{i=1}^m \mathcal{W}^{\psi}(\pi|\cdot|^{\frac{(m+1-2i)(n-1)}{2}})\right)^{K(c_{\pi}) \cap L}, \end{align*}$$
$$\begin{align*}\left(\bigotimes_{i=1}^m \mathcal{W}^{\psi}(\pi|\cdot|^{\frac{(m+1-2i)(n-1)}{2}})\right)^{K(c_{\pi}) \cap L}, \end{align*}$$
which is one-dimensional, we obtain the desired isomorphism.
Proof of the existence statement in Theorem 9.1
By Lemma 8.4 and Corollary 9.10 together with [Reference Jacquet, Piatetski-Shapiro and Shalika14, (4.1) Théorème], we can find
![]() $W_{\mathrm {Ze}}^{\mathrm {ess}} \in \mathcal {W}_{\mathrm {Ze}}^{\psi }(\sigma )^{K(c_{\pi })}$
such that
$W_{\mathrm {Ze}}^{\mathrm {ess}} \in \mathcal {W}_{\mathrm {Ze}}^{\psi }(\sigma )^{K(c_{\pi })}$
such that
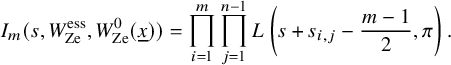 $$\begin{align*}I_m(s,W_{\mathrm{Ze}}^{\mathrm{ess}},W^0_{\mathrm{Ze}}(\underline{x})) = \prod_{i=1}^m\prod_{j = 1}^{n-1} L\left( s+s_{i,j}-\frac{m-1}{2}, \pi \right). \end{align*}$$
$$\begin{align*}I_m(s,W_{\mathrm{Ze}}^{\mathrm{ess}},W^0_{\mathrm{Ze}}(\underline{x})) = \prod_{i=1}^m\prod_{j = 1}^{n-1} L\left( s+s_{i,j}-\frac{m-1}{2}, \pi \right). \end{align*}$$
Then
![]() $W_{\mathrm {Sh}}^{\mathrm {ess}} = \mathcal {T}^{\psi } \mathcal {W}_{\mathrm {Ze}}^{\mathrm {ess}}$
satisfies the conditions in Theorem 9.1.
$W_{\mathrm {Sh}}^{\mathrm {ess}} = \mathcal {T}^{\psi } \mathcal {W}_{\mathrm {Ze}}^{\mathrm {ess}}$
satisfies the conditions in Theorem 9.1.
Acknowledgement
The authors thank the referee for careful reading of the long manuscript and for giving valuable comments.
Conflict of Interest
The authors have no conflict of interest to declare.
Financial support
The first author was supported by JSPS KAKENHI Grant Number 19K14494. The second author was supported by WPI Initiative, MEXT, Japan. The third author was supported by JSPS KAKENHI Grant Number 21H00969.





















