Article contents
The fields of values of characters of degree not divisible by p
Published online by Cambridge University Press: 15 February 2021
Abstract
We study the fields of values of the irreducible characters of a finite group of degree not divisible by a prime p. In the case where 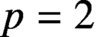 $p=2$, we fully characterise these fields. In order to accomplish this, we generalise the main result of [ILNT] to higher irrationalities. We do the same for odd primes, except that in this case the analogous results hold modulo a simple-to-state conjecture on the character values of quasi-simple groups.
$p=2$, we fully characterise these fields. In order to accomplish this, we generalise the main result of [ILNT] to higher irrationalities. We do the same for odd primes, except that in this case the analogous results hold modulo a simple-to-state conjecture on the character values of quasi-simple groups.
MSC classification
- Type
- Algebra
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
Footnotes
Dedicated to Gunter Malle on the occasion of his 60th birthday
References
 ${p}^a{q}^b$ theorem’, Invent. Math. 213 (2018), 589–695.CrossRefGoogle Scholar
${p}^a{q}^b$ theorem’, Invent. Math. 213 (2018), 589–695.CrossRefGoogle Scholar- 10
- Cited by



