Hostname: page-component-8448b6f56d-cfpbc Total loading time: 0 Render date: 2024-04-24T20:52:33.047Z Has data issue: false hasContentIssue false
  • English
  • Français

On continuous branches of very singular similarity solutions of the stable thin film equation. II – Free-boundary problems

Published online by Cambridge University Press:  21 February 2011

J. D. EVANS  and
V. A. GALAKTIONOV
J. D. EVANS
Affiliation:
Department of Mathematical Sciences, University of Bath, Bath, BA2 7AY, UK email: masjde@maths.bath.ac.uk, vag@maths.bath.ac.uk
V. A. GALAKTIONOV
Affiliation:
Department of Mathematical Sciences, University of Bath, Bath, BA2 7AY, UK email: masjde@maths.bath.ac.uk, vag@maths.bath.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

We discuss the fourth-order thin film equation 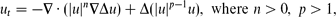with a stable second-order diffusion term, in the context of a standard free-boundary problem with zero height, zero contact angle and zero-flux conditions imposed at an interface. For the first critical exponent 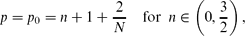where N ≥ 1 is the space dimension, there are continuous sets (branches) of source-type very singular self-similar solutions of the form 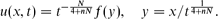For p ≠ p0, the set of very singular self-similar solutions is shown to be finite and consists of a countable family of branches (in the parameter p) of similarity profiles that originate at a sequence of critical exponents {pl, l ≥ 0}. At p = pl, these branches appear via a non-linear bifurcation mechanism from a countable set of second kind similarity solutions of the pure thin film equation 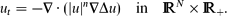Such solutions are detected by a combination of linear and non-linear ‘Hermitian spectral theory’, which allows the application of an analytical n-branching approach. In order to connect with the Cauchy problem in Part I, we identify the cauchy problem solutions as suitable ‘limits’ of the free-boundary problem solutions.

Keywords

Stable thin film equationGlobal similarity solutionsAsymptotic behaviourBranchingBifurcationsHermitian spectral theory
Type
Papers
Information
European Journal of Applied Mathematics , Volume 22 , Issue 3 , June 2011 , pp. 245 - 265
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Bernis, F. (1988) Source-type solutions of fourth order degenerate parabolic equations. In: Ni, W.-M., Peletier, L. A. & Serrin, J. (editors), Proc. Microprogram Nonlinear Diffusion Eqs Equilibrium States, Vol. 1, MSRI Publications, Berkeley, CA, USA, pp. 123–146.Google Scholar
[2]Bernis, F. & Friedman, A. (1990) Higher order nonlinear degenerate parabolic equations. J. Differ. Equ. 83, 179–206.CrossRefGoogle Scholar
[3]Bernis, F. & McLeod, J. B. (1991) Similarity solutions of a higher order nonlinear diffusion equation. Nonlinear Anal. 17, 1039–1068.Google Scholar
[4]Bernis, F., Peletier, L. A. & Williams, S. M. (1992) Source-type solutions of a fourth order nonlinear degenerate parabolic equation. Nonlinear Anal. Theory Methods Appl. 18, 217–234.CrossRefGoogle Scholar
[5]Evans, J. D., Galaktionov, V. A. & King, J. R. (2007a) Blow-up similarity solutions of the fourth-order unstable thin film equation. Eur. J. Appl. Math. 18, 195–231.CrossRefGoogle Scholar
[6]Evans, J. D., Galaktionov, V. A. & King, J. R. (2007b) Source-type solutions for the fourth-order unstable thin film equation. Eur. J. Appl. Math. 18, 273–321.CrossRefGoogle Scholar
[7]Evans, J. D., Galaktionov, V. A. & King, J. R. (2007c) Unstable sixth-order thin film equation. I. Blow-up similarity solutions; II. Global similarity patterns. Nonlinearity 20, 1799–1841, 1843–1881.CrossRefGoogle Scholar
[8]Evans, J. D., Galaktionov, V. A. & Williams, J. F. (2006) Blow-up and global asymptotics of the limit unstable Cahn–Hilliard equation. SIAM J. Math. Anal. 38, 64–102.CrossRefGoogle Scholar
[9]Ferreira, R. & Bernis, F. (1997) Source-type solutions to thin-film equations in higher dimensions. Eur. J. Appl. Math. 8, 507–534.CrossRefGoogle Scholar
[10]Galaktionov, V. A. (2010) Very singular solutions for thin film equations with absorption. Studies Appl. Math. 124, 39–63 (arXiv:0109.3982).CrossRefGoogle Scholar
[11]Galaktinov, V. A. & Harwin, P. J. (2005) Non-uniqueness and global similarity solutions for a higher-order semilinear parabolic equation. Nonlinearity 18, 717–746.CrossRefGoogle Scholar
[12]Galaktionov, V. A. & Williams, J. F. (2004) On very singular similarity solutions of a higher-order semilinear parabolic equation. Nonlinearity 17, 1075–1099.CrossRefGoogle Scholar
[13]Wu, Z., Zhao, J., Yin, J. & Li, H. (2001) Nonlinear Diffusion Equations, World Scientific Publishing Company, River Edge, NJ, USA.CrossRefGoogle Scholar