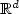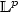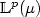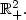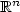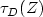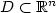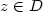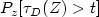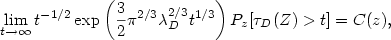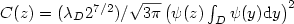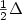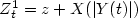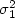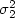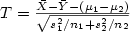Introduction
Preface
-
- Published online by Cambridge University Press:
- 01 March 2007, pp. 1-2
-
- Article
- Export citation
Research Article
Reflected backward stochastic differential equations with two RCLL barriers
-
- Published online by Cambridge University Press:
- 01 March 2007, pp. 3-22
-
- Article
- Export citation
Some short elements on hedging credit derivatives
-
- Published online by Cambridge University Press:
- 01 March 2007, pp. 23-34
-
- Article
- Export citation
Consistent price systems for subfiltrations
-
- Published online by Cambridge University Press:
- 01 March 2007, pp. 35-39
-
- Article
- Export citation
A martingale control variate method for option pricing with stochastic volatility
-
- Published online by Cambridge University Press:
- 01 March 2007, pp. 40-54
-
- Article
- Export citation
Infinite system of Brownian balls with interaction: the non-reversible case
-
- Published online by Cambridge University Press:
- 01 March 2007, pp. 55-79
-
- Article
- Export citation
Pricing rules under asymmetric information
-
- Published online by Cambridge University Press:
- 01 March 2007, pp. 80-88
-
- Article
- Export citation
Potentials of a Markov process are expected suprema
-
- Published online by Cambridge University Press:
- 01 March 2007, pp. 89-101
-
- Article
- Export citation
The empirical distribution function for dependent variables:asymptotic and nonasymptotic results in ${\mathbb L}^p$
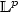
-
- Published online by Cambridge University Press:
- 31 March 2007, pp. 102-114
-
- Article
- Export citation
Approximation of the fractional Brownian sheet VIA Ornstein-Uhlenbeck sheet
-
- Published online by Cambridge University Press:
- 31 March 2007, pp. 115-146
-
- Article
- Export citation
Lifetime asymptotics of iterated Brownian motion in $\mathbb{R}^{n}$
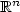
-
- Published online by Cambridge University Press:
- 31 March 2007, pp. 147-160
-
- Article
- Export citation
Convex rearrangements of Lévy processes
-
- Published online by Cambridge University Press:
- 31 March 2007, pp. 161-172
-
- Article
- Export citation
Asymptotic properties of power variations of Lévy processes
-
- Published online by Cambridge University Press:
- 19 June 2007, pp. 173-196
-
- Article
- Export citation
Entropic Conditions and Hedging
-
- Published online by Cambridge University Press:
- 19 June 2007, pp. 197-216
-
- Article
- Export citation
Discrete Lundberg-type bounds with actuarial applications
-
- Published online by Cambridge University Press:
- 19 June 2007, pp. 217-235
-
- Article
- Export citation
Behavior of the Euler scheme with decreasing stepin a degenerate situation
-
- Published online by Cambridge University Press:
- 19 June 2007, pp. 236-247
-
- Article
- Export citation
Polynomial expansions of density of power mixtures
-
- Published online by Cambridge University Press:
- 19 June 2007, pp. 248-263
-
- Article
- Export citation
Moderate deviationsfor two sample t-statistics
-
- Published online by Cambridge University Press:
- 19 June 2007, pp. 264-271
-
- Article
- Export citation
A graph-based estimator of the number of clusters
-
- Published online by Cambridge University Press:
- 19 June 2007, pp. 272-280
-
- Article
- Export citation
Macroscopic non-uniqueness and transversal fluctuation in optimal random sequence alignment
-
- Published online by Cambridge University Press:
- 19 June 2007, pp. 281-300
-
- Article
- Export citation